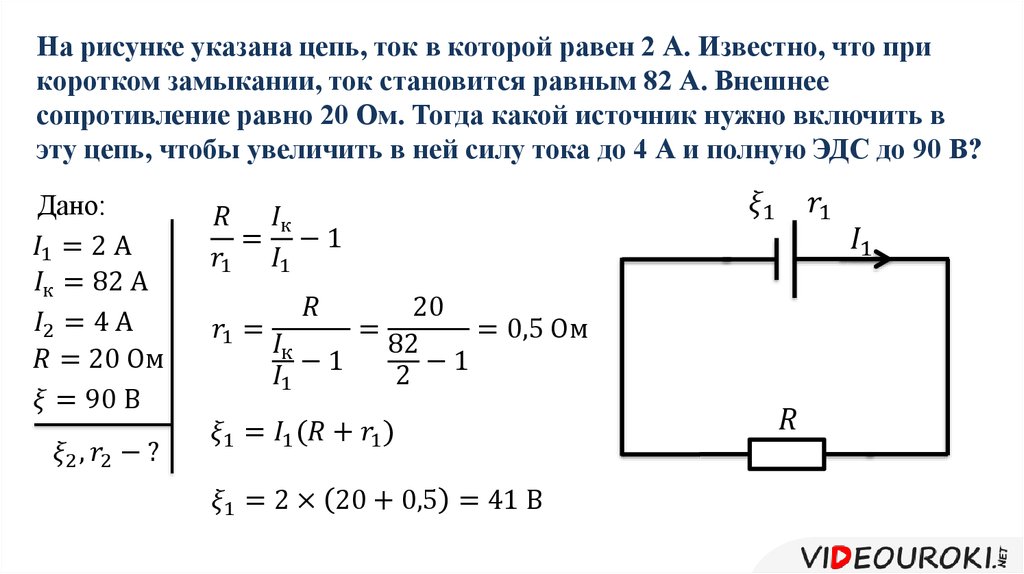
Физический смысл полного закона Ома для замкнутой цепи

Источник ЭДС

Рисунок 1 — Обозначение на схемах источника ЭДС (слева) и реального источника напряжения (справа)

ИсточникЭДС

(
идеальный источник напряжения
) — двухполюсник, напряжение на зажимах которого постоянно (не зависит от тока в цепи). Напряжение может быть задано как константа, как функция времени, либо как внешнее управляющее воздействие.

В простейшем случае напряжение определено как константа, то есть напряжение источника ЭДС постоянно.

Реальные источники напряжения

Рисунок 2

Рисунок 3 — Нагрузочная характеристика

Идеальный источник напряжения (источник ЭДС) является физической абстракцией, то есть подобное устройство не может существовать. Если допустить существование такого устройства, то электрический ток I

, протекающий через него, стремился бы к бесконечности при подключении нагрузки,сопротивление
RH
которой стремится к нулю. Но при этом получается, что мощность источника ЭДС также стремится к бесконечности, так как . Но это невозможно, по той причине, что мощность любого источника энергии конечна.

В реальности, любой источник напряжения обладает внутренним сопротивлением r

, которое имеет обратную зависимость от мощности источника. То есть, чем больше мощность, тем меньше сопротивление (при заданном неизменном напряжении источника) и наоборот. Наличие внутреннего сопротивления отличает реальный источник напряжения от идеального. Следует отметить, что внутреннее сопротивление — это исключительно конструктивное свойство источника энергии. Эквивалентная схема реального источника напряжения представляет собой последовательное включение источника ЭДС —
Е
(идеального источника напряжения) и внутреннего сопротивления —
r
.

На рисунке 3 приведены нагрузочные характеристики идеального источника напряжения (источника ЭДС) (синяя линия) и реального источника напряжения (красная линия).

где

— падение напряжения на внутреннем сопротивлении;

— падение напряжения на нагрузке.

При коротком замыкании () , то есть вся мощность источника энергии рассеивается на его внутреннем сопротивлении. В этом случае ток будет максимальным для данного источника ЭДС. Зная напряжение холостого хода и ток короткого замыкания, можно вычислить внутреннее сопротивление источника напряжения:

Рисунок 1 — схема с условным обозначением источника тока[1]

Рисунок 2.1 — Обозначение на схемах источника тока

Рисунок 3 — Генератор тока типа токовое зеркало, собранный на биполярных транзисторах

Исто́чник то́ка

(также
генератор тока
) — двухполюсник, который создаёт ток , не зависящий от сопротивления нагрузки, к которой он присоединён. В быту «источником тока» часто неточно называют любой источник электрического напряжения (батарею, генератор, розетку), но в строго физическом смысле это не так, более того, обычно используемые в быту источники напряжения по своим характеристикам гораздо ближе кисточнику ЭДС, чем к источнику тока.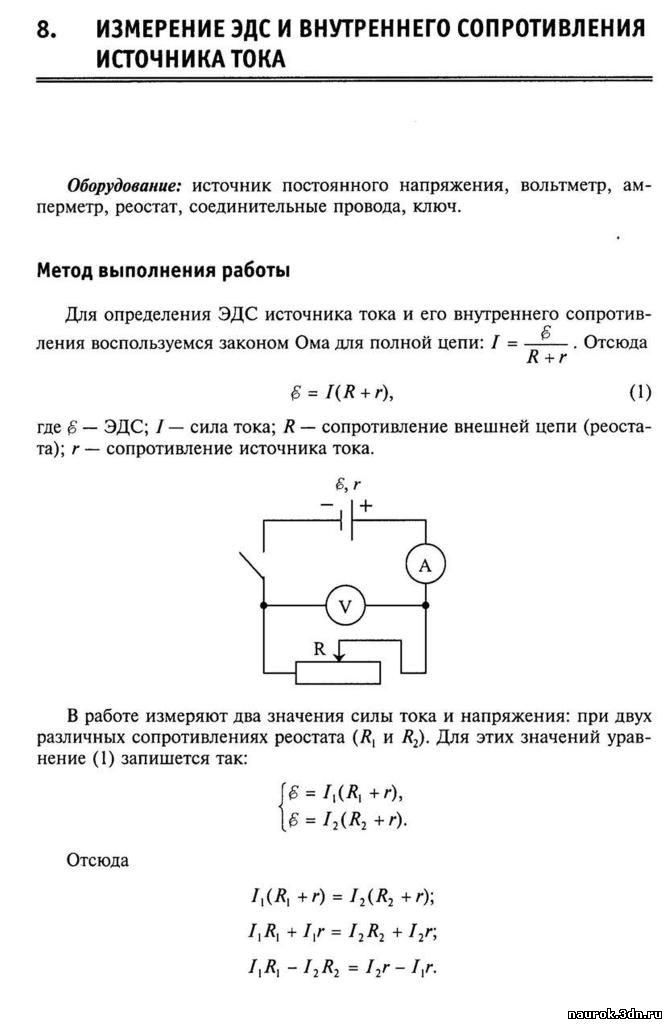

На рисунке 1 представлена схема замещения биполярного транзистора, содержащая источник тока (с указанием S·Uбэ; стрелка в кружке указывает положительное направление тока источника тока), генерирующий ток S·Uбэ, т. е. ток, зависящий от напряжения на другом участке схемы.

Идеальный источник тока

Напряжение на клеммах идеального источника тока зависит только от сопротивления внешней цепи:

Мощность, отдаваемая источником тока в сеть, равна:

Так как для источника тока , напряжение и мощность, выделяемая им, неограниченно растут при росте сопротивления..

Реальный источник тока

Реальный источник тока, так же как и источник ЭДС, в линейном приближении может быть описан таким параметром, как внутреннее сопротивление . Отличие состоит в том, что чем больше внутреннее сопротивление, тем ближе источник тока к идеальному (источник ЭДС, наоборот, чем ближе к идеальному, тем меньше его внутреннее сопротивление). Реальный источник тока с внутренним сопротивлением эквивалентен реальному источнику ЭДС, имеющему внутреннее сопротивление и ЭДС .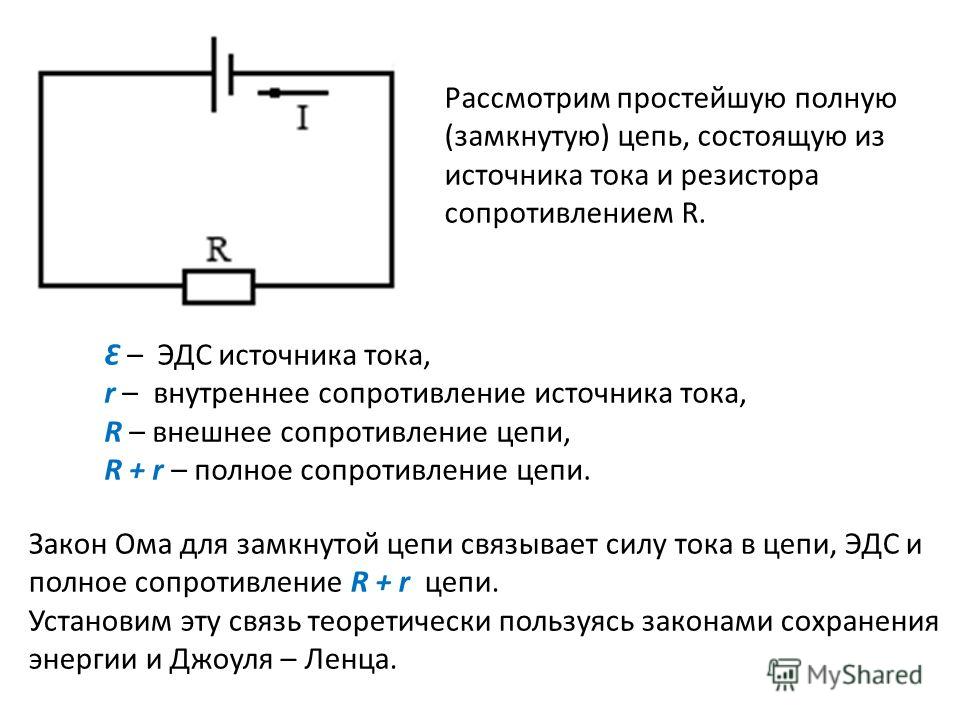

Напряжение на клеммах реального источника тока равно:

Сила тока в цепи равна:

Мощность, отдаваемая реальным источником тока в сеть, равна:

Измерение сопротивления петли фаза-нуль

Петля «фаза – нуль» – это электрическая цепь переменного тока, которая может возникнуть в результате короткого замыкания между проводами: «фаза» и «ноль» или «фаза» и «фаза». Разрушение изоляции, механические повреждения или случайное соединение оголённых участков кабеля между собой могут стать этому причиной. В установках с глухо заземлённой нейтралью нулевой проводник физически связан с нейтралью трансформатора, она подключена к контуру заземления. При замыкании на корпус или соединении фаз между собой образуется цепь (петля).

Главная задача проводимых измерений – узнавать, каким будет величина тока через петлю при КЗ. Это обязательно для расчёта и подбора защитного оборудования. Хорошим результатом будет маленькое сопротивление петли, тогда ток Iк.з. будет наибольшим. От его величины зависит, как быстро сработает защитный автоматический выключатель.

Чем меньше времени будет затрачено на отключение повреждённой или закороченной цепи, тем больше шансов предотвратить пожар от возгорания кабельной сети. При попадании человека под удар электрического тока в результате прикосновения или короткого замыкания автоматическое снятие напряжения спасёт ему жизнь.

На предприятиях ежегодно проводится комплекс измерений защитного заземления и сопротивления петли фаза – ноль. При неудовлетворительных результатах проводится ряд мероприятий:

• заменяются участки провода, не отвечающие требованиям по диаметру сечения;
• перекручиваются болтовые соединения с обязательной установкой врезных шайб;
• вскрываются контуры защитных заземлений и осматриваются на предмет целостности сварных соединений и состояния элементов заземления;
• при необходимости в контур защитного заземления добавляются дополнительные элементы;
• исключается последовательное подключение корпусов устройств к общей шине заземления.

После выполнения комплекса мероприятий измерения проводятся повторно.

Проверка сопротивления петли «фаза – ноль»

Составные части электрических цепей

Как известно, для того, чтобы электрический ток в проводниках существовал длительное время необходимо, во-первых, существование разности потенциалов или напряжения, а во-вторых, восполнение необходимого количества разноимённых зарядов для возникновения этой разности потенциалов. Данным условиям соответствует некоторая совокупность элементов называемая электрической цепью.

Таким образом, электрической цепью называется совокупность устройств и объектов, которые образуют путь для электрического тока и электромагнитные процессы, в которых могут быть описаны с помощью понятий ЭДС, напряжения и электрического тока. Кроме того, для протекания электрического тока необходима замкнутая электрическая цепь. В общем случае электрическая цепь состоит из источника электрической энергии, приемника электрической энергии, соединительных проводов, а также вспомогательных элементов, выполняющих разнообразные функции.

Источником электрической энергии является устройство, которое выполняет преобразование неэлектрической энергии в электрическую. Например, аккумуляторы осуществляют преобразование энергии химических реакций в электрическую энергию, а генераторы – преобразование механической энергии. Таким образом, как известно из предыдущей статьи источники энергии называют также источниками ЭДС.

Приёмником электрической энергии, также называемые нагрузками является устройство, в котором выполняется действие противоположное источнику энергии, то есть электрическая энергия преобразуется в неэлектрическую. Например, в лампочке электрическая энергия преобразуется в световую и тепловую энергию, а в электродвигателе – в механическую энергию.

К вспомогательным устройствам относятся различные коммутирующие, распределительные и измерительные приборы и объекты.

Электрические цепи изображают на чертежах в виде принципиальных электрических схем, где каждому элементу электрической цепи соответствует свой графический элемент. Принципиальные схемы показывают назначение каждого элемента цепи, а также его взаимодействие с остальными элементами, однако при расчётах они не очень удобны. Поэтому при расчётах пользуются так называемыми схемами замещения, которые также как и принципиальные схемы изображаются с помощью графических элементов, однако элементы схем замещения выбираются так, чтобы с необходимым приближением описать работу электрической цепи. Пример изображения принципиальных электрических схем и схем замещения показано ниже

Принципиальная схема (слева) и схема её замещения (справа).

Схемы замещения состоят из следующих элементов: контур, ветвь и узел. Ветвь – это один элемент либо последовательное соединение нескольких элементов. Узел – место соединения трёх и более ветвей. Контур – замкнутый путь, проходящий по ветвям так, чтобы ни один узел и ни одна ветвь не встречались больше одного раза.

Таким образом, зная параметры всех элементов схемы замещения, возможно при помощи законов электротехники определить электрическое состояние всей электрической цепи, то есть рассчитать режим её работы.

Идеальный источник ЭДС

Имеем источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС – это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

Или проще:

Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.

Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?

Разрядная емкость источника

Величина, зависящая от силы тока разряда, называется разрядной ёмкостью источника.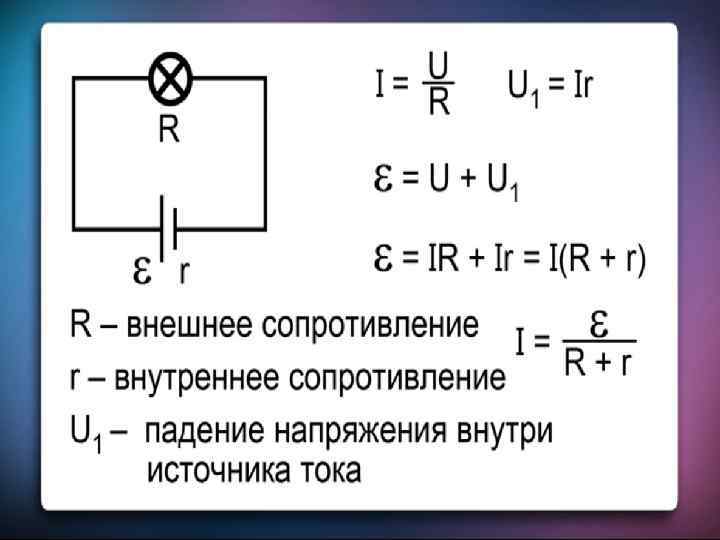 Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки. Эту величину можно считать постоянной условно. Так, стартерный аккумулятор, имеющий разрядную ёмкость С = 55 А*ч, при токе разряда 5,5 А проработает 10 часов. При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.

Для того чтобы найти остаточную разрядную ёмкость, производят циклы «заряд – разряд». Они выполняются при помощи нагрузочных сопротивлений. Разряд на нагрузочное сопротивление производят до минимально допустимых значений плотности электролита. При этом замеряется время работы под нагрузкой. Это актуально при сезонном обслуживании аккумуляторов для выявления процессов саморазряда.

Разрядная ёмкость автомобильного аккумулятора

Внутреннее сопротивление источников тока – важная величина. Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников.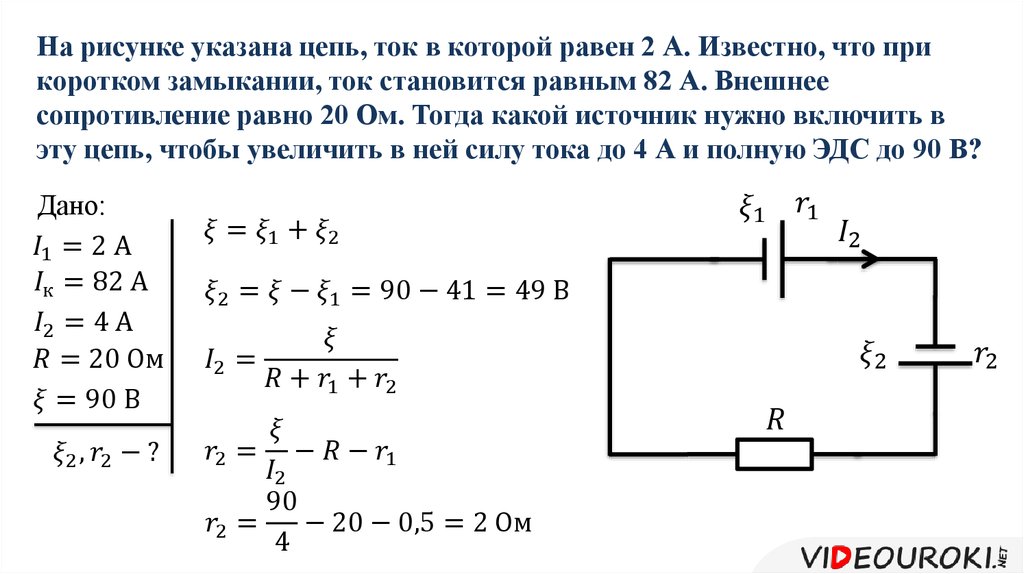 Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.

Нахождение внутреннего сопротивления

Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.

Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:

I = ε / (r + R).

Чтобы узнать силу тока, нужно напряжение ЭДС делить на сумму сопротивлений.

Выразив отсюда r, получают формулу для его вычисления:

r = (ε / I) – R,

где:

• r – внутреннее сопротивление источника;
• ε – ЭДС источника;
• I – сила тока в полной цепи;
• R – сопротивление в полной цепи.

Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.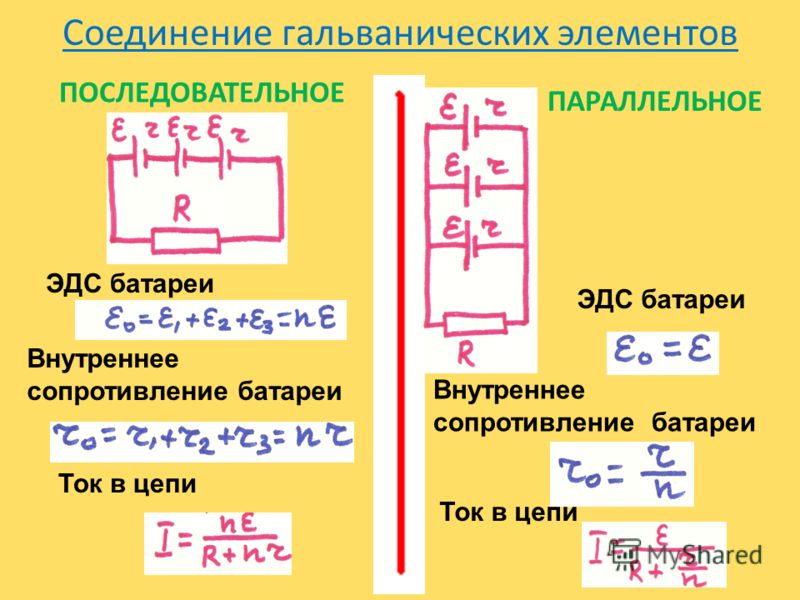

Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.

В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода. Тогда измеренное омметром Rн будет соответствовать внутреннему сопротивлению источника.

Внутреннее сопротивление источника тока

Определение и физический смысл

Приложение некоторой разности потенциалов между двумя концами проводника создаст перетекание электронов от одного конца к другому. Но этого недостаточно для поддержания потока зарядов в проводнике. Дрейф электронов приводит к уменьшению потенциала до момента его уравновешивания (прекращение тока). Таким образом, для создания постоянного тока необходимы механизмы, непрерывно возвращающие описанную систему в первоначальную конфигурацию, то есть, препятствующие агрегации зарядов в результате их движения.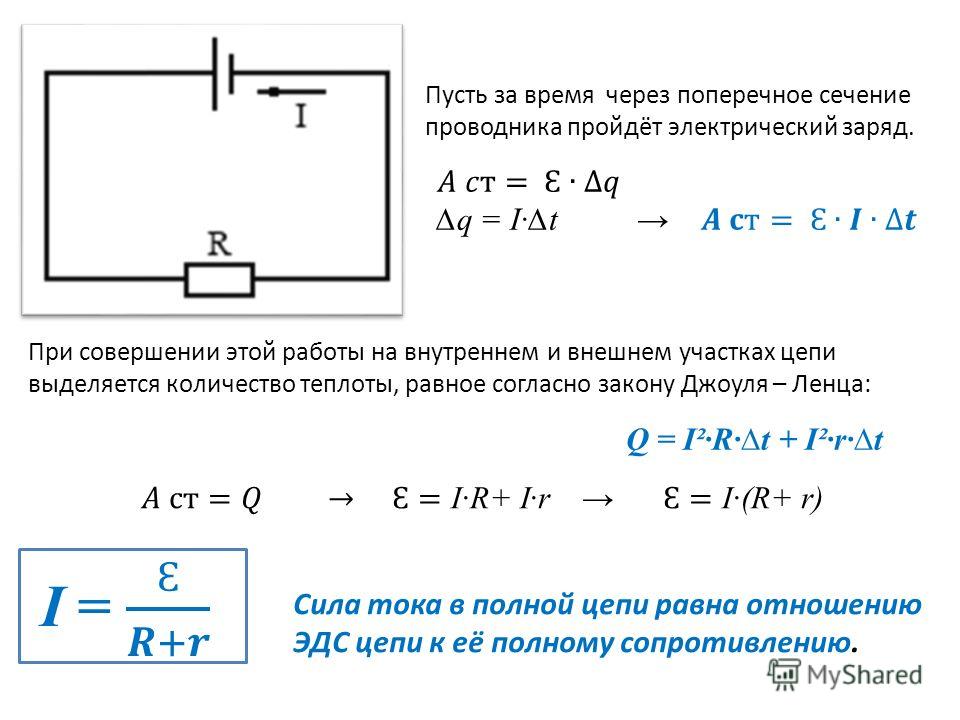 Для этой цели используются специальные устройства, называемые источники питания.

В качестве иллюстрации их работы удобно рассматривать замкнутый контур из сопротивления и гальванического источника питания (батареи). Если предположить, что внутри батареи тока нет, то описанная проблема объединения зарядов остаётся неразрешённой. Но в цепи с реальным источником питания электроны перемещаются постоянно. Это происходит благодаря тому, что поток ионов протекает и внутри батареи от отрицательного электрода к положительному. Источник энергии, перемещающий эти заряды в батарее — химические реакции. Такая энергия называется электродвижущей силой.

ЭДС является характеристикой любого источника энергии, способного управлять движением электрических зарядов в цепи. В аналогии с замкнутым гидравлическим контуром работа источника э. д. с. соответствует работе насоса для создания давления воды. Поэтому значок, обозначающий эти устройства, неотличим на гидравлических и электрических схемах.

Несмотря на название, электродвижущая сила на самом деле не является силой и измеряется в вольтах. Её численное значение равно работе по перемещению заряда по замкнутой цепи. ЭДС источника выражается формулой E=A/q, в которой:

• E — электродвижущая сила в вольтах;
• A — работа сторонних сил по перемещению заряда в джоулях;
• q — перемещённый заряд в кулонах.

Из этой формулы ЭДС следует, что электродвижущая сила не является свойством цепи или нагрузки, а есть способность генератора электроэнергии к разделению зарядов.

Двухполюсник и его эквивалентная схема

Двухполюсник представляет собой электрическую цепь, содержащую две точки присоединения к другим цепям. Бывает два вида электрических цепей:

• цепи, содержащие источник тока или напряжения;
• двухполюсники, не являющиеся источниками.

Первые характеризуются электрическими параметрами: силой тока, напряжением и импедансом. Для расчёта параметров таких двухполюсников предварительно производят замену реальных элементов цепи на идеальные элементы. Комбинация, которая получается в результате подобной замены, называется эквивалентной схемой.

Внимание! При работе со сложными электрическими схемами с учётом того, что устройство работает на одной частоте, допустимо преобразовывать последовательные и параллельные ветви до получения простой схемы, доступной для расчёта параметров.

Второй вид двухполюсников можно охарактеризовать только величиной внутреннего сопротивления.

От электростатики к электрокинетике

Между концом XVIII и началом XIX века работы таких учёных, как Кулон, Лагранж и Пуассон, заложили математические основы определения электростатических величин. Прогресс в понимании электричества на этом историческом этапе очевиден. Франклин уже ввёл понятие «количество электрической субстанции», но пока ещё и он, ни его преемники не смогли его измерить.

Следуя за экспериментами Гальвани, Вольта пытался найти подтверждения того, что «гальванические жидкости» животного были одной природы со статическим электричеством. В поисках истины он обнаружил, что когда два электрода из разных металлов контактируют через электролит, оба заряжаются и остаются заряженными несмотря на замыкание контура нагрузкой. Это явление не соответствовало существующим представлениям об электричестве потому, что электростатические заряды в подобном случае должны были рекомбинировать.

Вольта ввёл новое определение силы, действующей в направлении разделения зарядов и поддержании их в таком состоянии. Он назвал её электродвижущей. Подобное объяснение описания работы батареи не вписывалось в теоретические основы физики того времени. В Кулоновской парадигме первой трети XIX века э. д. с. Вольта определялась способностью одних тел вырабатывать электричество в других.

Важнейший вклад в объяснение работы электрических цепей внёс Ом. Результаты ряда экспериментов привели его к построению теории электропроводности. Он ввёл величину «напряжение» и определил её как разность потенциалов на контактах. Подобно Фурье, который в своей теории различал количество тепла и температуру в теплопередаче, Ом создал модель по аналогии, связывающую количество перемещаемого заряда, напряжение и электропроводность. Закон Ома не противоречил накопленным знаниям об электростатическом электричестве.

Вам это будет интересно Подключение клеммной испытательной переходной колодки (ИКК)

Затем, благодаря Максвеллу и Фарадею, пояснительные модели тока получили новую теорию поля. Это позволило разработать связанную с полем концепцию энергии как для статических потенциалов, так и для электродвижущей силы. Основные даты эволюции понятия ЭДС:

• 1800 г. — создание Вольтой гальванической батареи;
• 1826 г. — Ом формулирует свой закон для полной цепи;
• 1831 г. — обнаружение электромагнитной индукции Фарадеем.

Ссылки

• Основные определения общей электротехники
• Схема для измерения параметров аккумуляторов
• Свинцово-кислотные аккумуляторы Casil Приведены графики[8] внутреннего сопротивления.
• How does the internal battery resistance affect performance? (англ.) Как внутреннее сопротивление батареи влияет на ее эксплуатационные качества.
• Сравнение технических характеристик свинцово-кислотных аккумуляторов
• Что такое внутреннее сопротивление аккумулятора?
• Оптимальный выбор аккумулятора

Реальный генератор

Главное различие между реальным и идеальным устройством — наличие внутреннего сопротивления. Чем выше данный параметр, тем ближе элемент к улучшенному варианту. Из этого следует, что напряжение и мощность значения конечные, т. е имеют определенный рабочий диапазон. При этом система также обладает ограничением по присоединяемой нагрузке. При решении задач, реальное устройство изображают в качестве идеального, с подключенным в параллель внутренним сопротивлением.

Эксплуатация данного агрегата возможна при холостом ходе (без внешней нагрузки) вследствие того, что имеем замкнутый контур за счет внутреннего сопротивления. Ток на выходе во время такого режима снижается до нулевого значения. При подключении накоротко (режим короткого замыкания) получим максимальную величину, а выходное напряжение опустится до 0.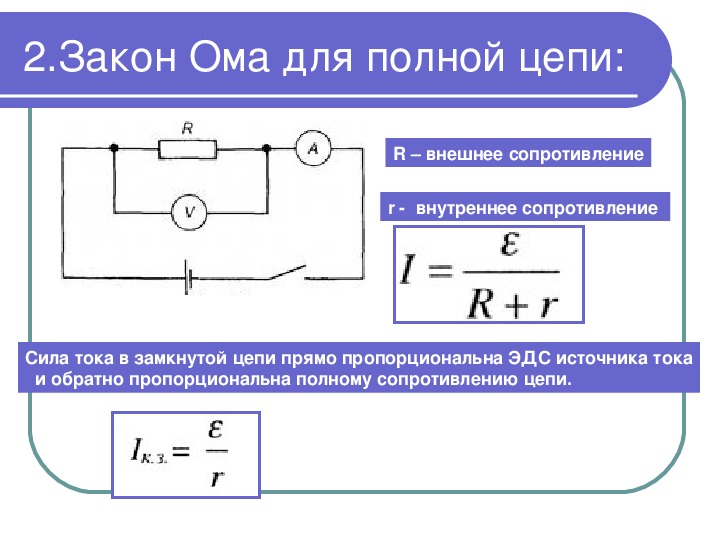

В качестве примера такого устройства, обратимся к катушке индуктивности. Это положение справедливо в момент размыкания цепи. Так разность потенциалов в таком режиме резко увеличивается по сравнению с предыдущим состоянием. Все дело в ЭДС самоиндукции возникающей в этом элементе. При увеличении напряжения катушка накапливает энергию, при снижении отдает ее в сеть.

Еще одним примером является вторичная обмотка трансформатора тока, которая в нормальных условиях работы всегда должна быть закорочена. В противном случае, если в ней произойдет разрыв, то она станет генератором. Все дело в законе сохранения энергии, так мощность на первичной и вторичной обмотке должна быть одинаковой. Параметры первичной обмотки неизменны, вследствие конструктивных особенностей трансформатора (обмотка имеет один виток). При обрыве во вторичной обмотке, упорядоченного движения заряженных частиц не будет, соответственно напряжение резко возрастет.

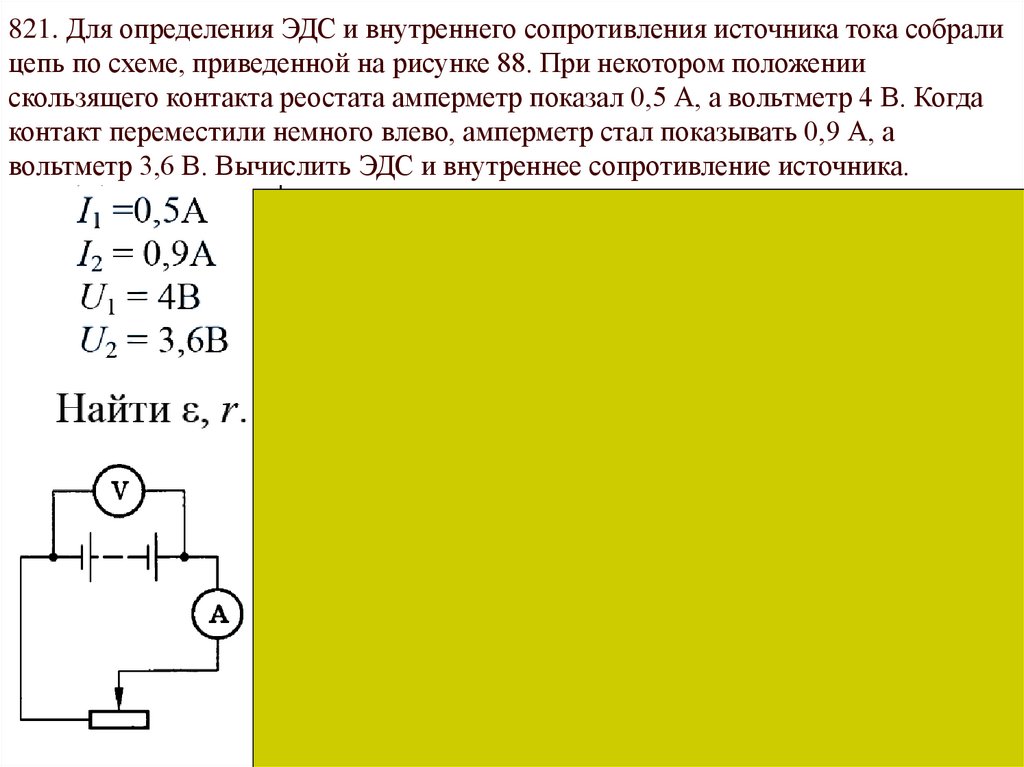
№9 ЭДС и внутреннее сопротивление

ЛАБОРАТОРНАЯ РАБОТА № 9

Тема: «Определение электродвижущей силы (ЭДС) и внутреннего сопротивления источника электрической энергии»

Цель: используя закон Ома для полной цепи, определить ЭДС и внутреннее сопротивление источника электрической энергии.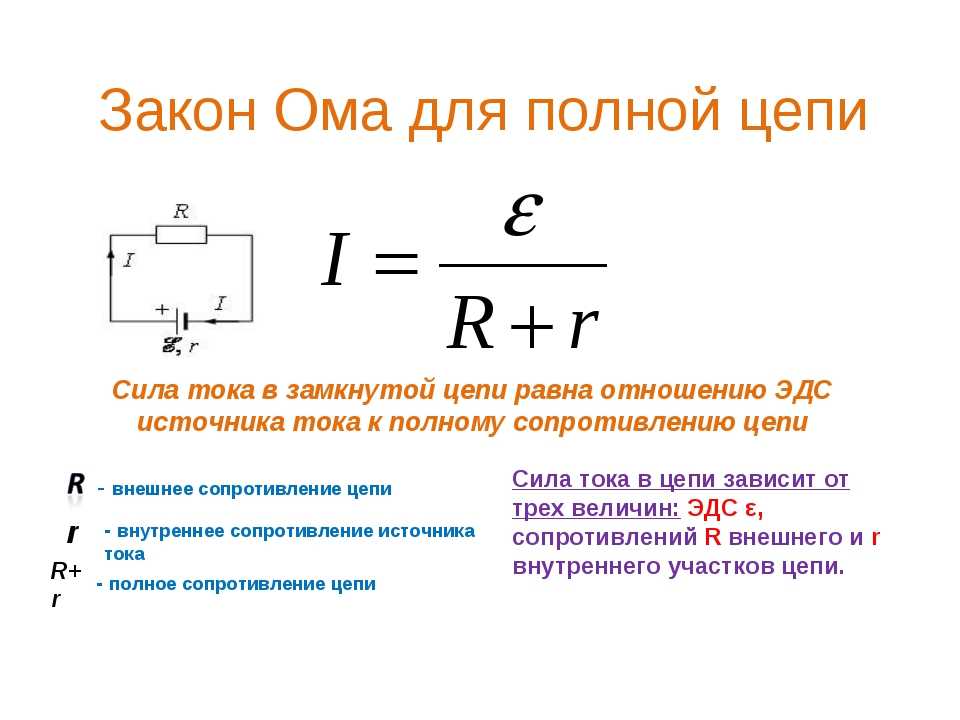

Оборудование: источник электрической энергии, реостат, амперметр, вольтметр, электрический ключ, соединительные провода.

Теоретическая часть

Для получения электрического тока в проводнике необходимо создать и поддерживать на его концах разность потенциалов (напряжение). Для этого используют источник тока. Разность потенциалов на его полюсах образуется вследствие разделения зарядов. Работу по разделению зарядов выполняют сторонние (не электрического происхождения) силы.

При разомкнутой цепи энергия, затраченная в процессе работы сторонних сил, превращается в энергию источника тока. При замыкании электрической цепи запасённая в источнике тока энергия расходуется на работу по перемещению зарядов во внешней и внутренней частях цепи с сопротивлениями соответственно

R и r.

Величина, численно равная работе, которую совершают сторонние силы при перемещении единичного заряда внутри источника, называется электродвижущей силой источника тока (ЭДС): = А/q

Согласно закону Ома сила тока в полной цепи прямо пропорциональна ЭДС и обратно пропорциональна ее полному сопротивлению: I = / (R+r)

Преобразуя закон Ома получим выражение для ЭДС: ,

где U₁ = I R – падение напряжения на внешнем участке цепи,

U₂ = I r – падение напряжения на внутреннем участке цепи.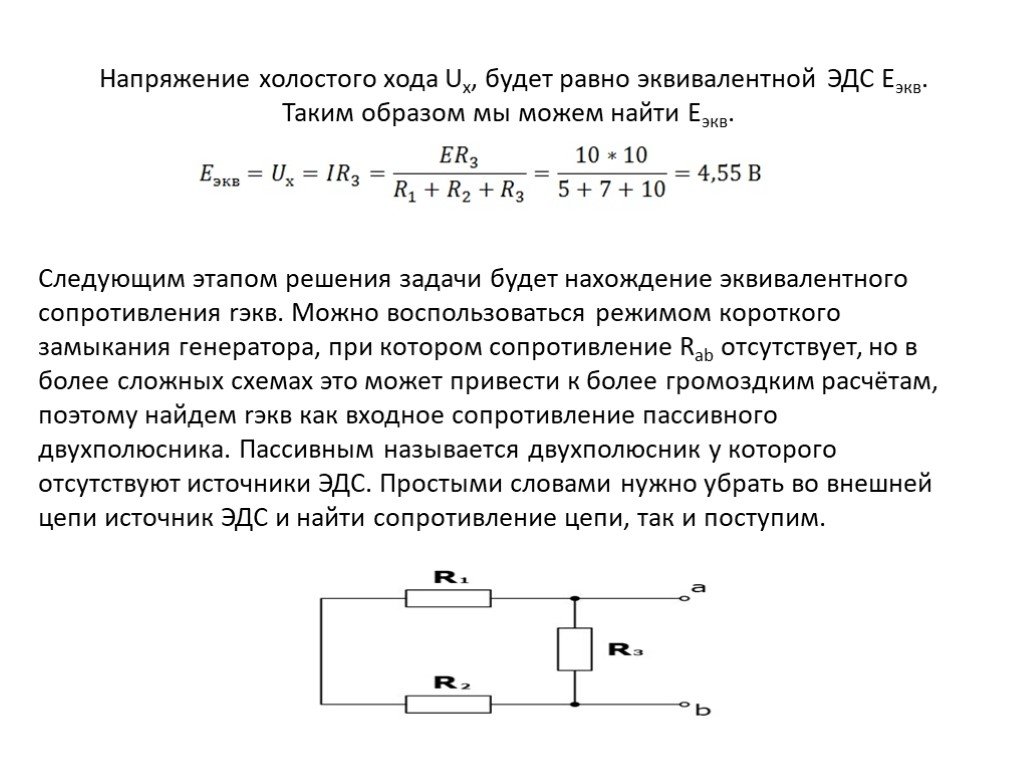

В СИ ЭДС выражается в вольтах: [] = B.

Электродвижущую силу и внутреннее сопротивление источника можно определить экспериментально.

Порядок проведения работы:

1.Определить цену деления шкалы измерительных приборов.

2. Составить электрическую цепь по схеме, изображённой на рисунке.

3. После проверки цепи преподавателем замкнуть ключ и, пользуясь реостатом, установить силу тока, соответствующую нескольким делениям шкалы амперметра. Снять показания вольтметра и амперметра.

4.Опыт повторить, изменяя сопротивление цепи при помощи реостата.

5.Результаты измерений подставить в уравнение .

Решая систему уравнений, определить r, а затем :

,

где r — внутреннее сопротивление цепи,

 — электродвижущая сила источника

№ опыта	Сила тока	Напряжение на внешнем участке	Внутреннее сопротивление цепи	ЭДС
	Цена деления амперметра:	Цена деления вольтметра:
1
2

7. После завершения работы сделать вывод.

ОТЧЕТ ПО РАБОТЕ:

Вывод:

Контрольные вопросы

1. Назвать основные характеристики внутреннего участка электрической цепи.

2. Какой источник электрической энергии использовался в ваших опытах? Укажите, какую природу имеют сторонние силы в этом источнике?

3. Укажите причины электрического сопротивления металлического проводника.

4. Какова причина электрического сопротивления внутри источника, который использовался в лабораторной работе?

ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ:

1.Назвать основные характеристики внутреннего участка электрической цепи.

2.Какой источник электрической энергии использовался в ваших опытах? Укажите, какую природу имеют сторонние силы в этом источнике?

3. Укажите причины электрического сопротивления металлического проводника.

4.Какова причина электрического сопротивления внутри источника, который использовался в лабораторной работе?

4.

7: Электродвижущая сила и внутреннее сопротивление

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

5971

• Джереми Татум
• Университет Виктории

Напоминаем читателю следующее определение из раздела 4.1:

Определение . Разность потенциалов между полюсами ячейки, когда от нее не отводится ток, называется электродвижущей силой

(ЭДС) ячейки.

Я буду использовать символ E для ЭДС.

Вопрос . К ячейке с ЭДС 2 В подключено сопротивление 4 Ом. Какой ток течет?

Непосредственный ответ: 0,5 А, но это, скорее всего, неверно. Причина в том, что у клетки есть собственное сопротивление – ее внутреннее сопротивление. Внутреннее сопротивление свинцово-кислотного элемента обычно довольно мало, но большинство сухих элементов имеют заметное внутреннее сопротивление. Если внешнее сопротивление равно \(R\), а внутреннее сопротивление равно \(r\), общее сопротивление цепи равно \(R + r\), так что протекающий ток равен E \(/( р + г)\).

Всякий раз, когда от элемента (или батареи) поступает ток, разность потенциалов между его полюсами падает до значения, меньшего, чем его ЭДС. Мы можем думать о ячейке как об ЭДС последовательно с внутренним сопротивлением:

\(\text{РИСУНОК IV.4}\)

Если мы возьмем точку A с нулевым потенциалом, мы увидим, что потенциал точки B будет равен E — \(Ir\), и это и есть разность потенциалов между полюсами ячейки, когда от нее снимается ток \(I\).

---

Эта страница под названием 4.7: Электродвижущая сила и внутреннее сопротивление распространяется под лицензией CC BY-NC 4.0 и была создана, изменена и/или курирована Джереми Татумом с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Джереми Татум

   Лицензия

   CC BY-NC

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. source@http://orca. phys.uvic.ca/~tatum/elmag.html

Mr Toogood Physics — ЭДС и внутреннее сопротивление

Внутреннее сопротивление

Элементы и батареи преобразуют химическую энергию в электрический потенциал, который затем расходуется по цепи. Однако ни одна ячейка не эффективна при таком переносе на $100\%$. Никакая передача энергии не является эффективной на $100\%$, и электрические элементы и блоки питания не являются исключением. Электрический элемент состоит из трех частей: анода, катода и электролита. Анод и катод сделаны из двух разных металлов или из одного металла и углеродной пленки, а электролит представляет собой ионную жидкость, такую ​​как гидроксид калия. Когда ячейка включается в цепь, начинают происходить химические реакции на аноде и катоде. На аноде реакция окисления удаляет электроны из металла, и они начинают поступать в цепь. Это оставляет анод заряженным положительно, что притягивает больше электронов из электролита. Анод в отрицательной клемме ячейки. Возвращающиеся электроны собираются на катоде и он восстанавливается. Катод является положительным полюсом. Через некоторое время анод потеряет почти все свои электроны, и электролит больше не сможет их поставлять, поэтому реакция замедлится, и ЭДС ячейки упадет.

Рисунок 1:  Упрощенный пример работы ячейки.

Когда происходят химические реакции, а также вырабатывается электричество, элемент выделяет небольшое количество тепла, которое излучается из системы и теряется. Поскольку энергия, теряемая ячейкой, представляет собой тепло, ее можно смоделировать так, как если бы она была резистором, генерирующим тепло, и называется внутренним сопротивлением ( r ) ячейки. Скорость потери энергии ячейкой, конечно же, измеряется в $\units{ваттах}$, и для ее описания можно использовать уравнения мощности для резистора.

Рисунок 2:  Когда ячейка генерирует ток, она также выделяет тепло.

Иногда на принципиальных схемах резистор изображается последовательно с ячейкой для представления внутреннего сопротивления; конечно, на самом деле внутри ячейки нет резистора, это просто полезный способ описания энергии, теряемой в цепи.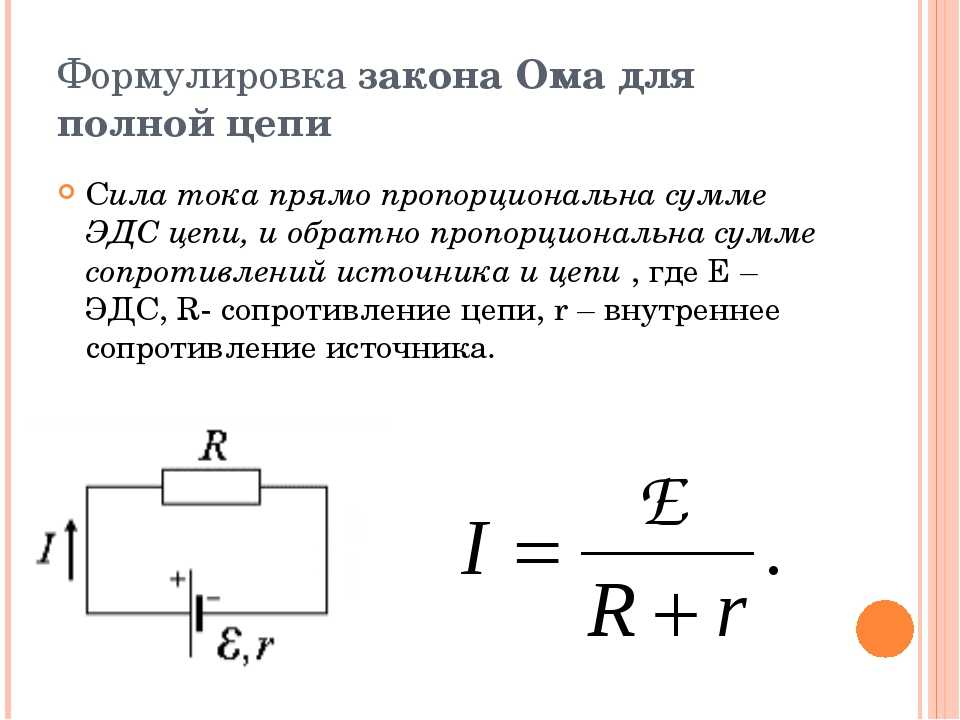 Внутреннее сопротивление является аналогом эффективности ячейки. Чем больше внутреннее сопротивление, тем больше тепла он выделяет при производстве электричества и тем менее эффективен. Внутреннее сопротивление также будет иметь разность потенциалов на нем, а это означает, что напряжение, измеренное на клеммах при протекании тока, ниже фактического истинного значения ЭДС элемента. Истинная ЭДС клетки составляет эти «потерянные вольты» плюс напряжение на клеммах .

ЭДС = клемма p.d. + потерянные вольты

Рисунок 3:  ЭДС равна клемме p.d. плюс «потерянные вольты».

Математически это можно выразить так:

$$ε=ИК+Ир$$

Где:

• ε — ЭДС в $\units{V}$
• I — ток в $\units{A}$
• R — полное сопротивление цепи в $\units{Ом}$
• r — внутреннее сопротивление ячейки в $\units{Ом}$

Термин $IR$ представляет окончание p.d. а член $Ir$ – это потерянные вольты. Приведенное выше уравнение можно упростить до:

$$\большой ε=I\влево(R+r\вправо)$$

Часто в примерах цепей внутренним сопротивлением пренебрегают и предполагают идеальную ячейку без внутреннего сопротивления. Однако на уровне A от вас ожидают выполнения расчетов в цепях со значительным внутренним сопротивлением. Типичные внутренние сопротивления для современных аккумуляторов находятся в диапазоне от $\quantity{100}{мОм}$ до $\quantity{900}{мОм}$.

Вернуться к началу

---

Рабочий пример

Батарейка соединена последовательно с резистором $\quantity{10}{Ω}$ и переключателем. Вольтметр подключен параллельно аккумулятору. Когда переключатель разомкнут (выключен), вольтметр показывает $\quantity{1.45}{V}$. Когда переключатель замкнут, показание равно $\quantity{1,26}{V}$.

Каково внутреннее сопротивление батареи?

1. $\количество{0,66}{Ом}$
2. $\количество{0,76}{Ом}$
3. $\количество{1.3}{Ω}$
4. $\количество{1,5}{Ом}$

Этот вопрос с несколькими вариантами ответов включает в себя относительно простой расчет, но важно, чтобы эти вопросы с несколькими вариантами ответов работали эффективно, чтобы вы не теряли время впустую.

Мы знаем, что ЭДС ячейки равна $\quantity{1.45}{V}$ и конечный p.d. падает до $\quantity{1,26}{V}$, когда ток протекает через резистор $\quantity{10}{Ω}$, поэтому ток через резистор можно рассчитать как:

\начать{выравнивать} I&=\frac{V}{R}\\ I & = \ гидроразрыва {\ количество {1,26} {V}} {\ количество {10} {Ω}} \\ \\ I&=\количество{0,126}{A} \end{выравнивание}

Разность потенциалов на внутреннем сопротивлении составляет $\количество{1,45}{В} — \количество{1,45}{В} = \количество{0,19}{В}$

Теперь мы можем использовать это значение тока и значение потерянных вольт, чтобы найти значение внутреннего сопротивления:

$ $ R = \ гидроразрыва {V} {I} = {\ количество {0,19}{V}}{\количество{0,126}{A}}=\количество{1,5}{Ω}$$

Вернуться к началу

---

Внутреннее сопротивление и протекание тока

Чем больше ток течет от элемента, тем выше скорость реакции в элементе и выделяется больше тепла, и, соответственно, тем выше потерянных вольт . Между током и энергией, теряемой на внутреннем сопротивлении, существует прямо пропорциональная зависимость.

Когда ток не течет, нет потерь энергии на внутреннее сопротивление и клемму p.d. будет равна ЭДС. На практике ЭДС ячейки можно определить с помощью мультиметра, который обычно имеет очень высокое сопротивление, и измерения на клемме pd, которая будет являться ЭДС, поскольку через измеритель не будет протекать ток.

Чем больше ток, протекающий через ячейку, тем больше разница между ЭДС и клеммой p.d.. Если график клеммы p.d. и ток нанесен на график, ЭДС можно найти из точки пересечения с осью y, а градиент будет представлять внутреннее сопротивление.

Рисунок 4:  График терминала p.d. против тока для ячейки. Внутреннее сопротивление можно найти по градиенту.

Вы выполните это практическое задание для своей CAP, но вам нужно будет разработать схему и предложить подходящий диапазон сопротивлений для проверки.

Вернуться к началу

---

Рабочий пример

Студент исследует, как мощность, рассеиваемая на переменном резисторе Y, изменяется при изменении сопротивления.

На приведенной ниже схеме показана схема, которую использует учащийся. Y подключен к батарее с ЭДС ε и внутренним сопротивлением r .

Рисунок 5:  Простая схема с ячейкой и переменным резистором.

На графике показаны результаты, полученные студентом при изменении сопротивления Y от $\quantity{0,5}{Ω}$ до $\quantity{6,5}{Ω}$.

Рисунок 6:  График, показывающий, как мощность, рассеиваемая переменным резистором, изменяется в зависимости от его сопротивления.

1. Опишите, как мощность, рассеиваемая в Y, изменяется при увеличении его сопротивления от $\quantity{0,5}{Ω}$ до $\quantity{6,5}{Ω}$.

Ключевое слово в этом вопросе описывает , поэтому нам просто нужно сказать, что мы видим, но чтобы получить полную оценку, мы должны использовать данные из графика. Как мы видим, мощность увеличивается до тех пор, пока сопротивление не станет равным $\quantity{3}{Ω}$ и $\quantity{3}{W}$, а затем начинает уменьшаться по мере того, как сопротивление продолжает расти.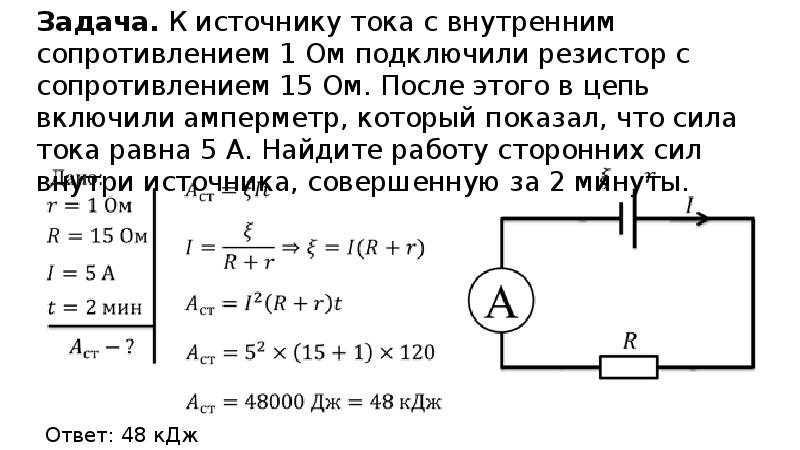 9{2}}{R}$. Когда внешнее сопротивление меньше внутреннего сопротивления, он будет иметь меньшую p.d. через него, поэтому он будет иметь меньшую мощность, чем внутреннее сопротивление. Когда внешнее сопротивление равно внутреннему сопротивлению, они оба будут иметь одинаковую разность потенциалов, и, следовательно, они будут иметь одинаковую мощность. Когда переменный резистор увеличивается настолько, что становится больше внутреннего сопротивления, мощность снова уменьшается, так как мощность обратно пропорциональна сопротивлению.

Это известно как теорема о максимальной мощности, т. е. максимальная мощность источника питания (в данном случае элемента) получается, когда нагрузка или внешнее сопротивление равны внутреннему сопротивлению источника питания.

2. ЭДС батареи равна $\quantity{6,0}{В}$, а сопротивление Y равно $\количество{0,80}{Ом}$.
1. Используйте данные из графика для расчета тока через батарею.

При чтении данных с графика рекомендуется тщательно аннотировать диаграмму с помощью карандаша и линейки, чтобы убедиться, что значения, которые вы читаете, точны. 9{2}R$, чтобы найти текущий:

\начать{выравнивать} I & = \ sqrt {\ гидроразрыва {P} {R}} \\ I & = \ sqrt {\ frac {\ количество {1,95} {Вт}} {\ количество {0,80} {Ω}}} \\ \\ I&=\количество{1.56}{A} \end{выравнивание}

В таком вопросе легко забыть найти квадратный корень из $\frac{P}{R}$, поэтому будьте особенно осторожны при использовании калькулятора.

2. Рассчитать напряжение на Y.

Теперь, когда мы знаем ток и сопротивление, мы можем использовать закон Ома, $V=IR$, чтобы найти напряжение или p.d. по Ю.

$$V=\количество{1,56}{A}\times\количество{0,80}{Ω}=\количество{1,2}{V}$$
3. Рассчитайте внутреннее сопротивление батареи.

Это можно либо рассчитать из уравнения $ε=V+Ir$, либо прочитать на графике, используя теорему о максимальной мощности, как описано выше. Мы уже вычислили значения $V$ и $I$, используя уравнение и сделав $r$ субъектом:

\начать{выравнивать} г & = \ гидроразрыва {\ влево (ε-V \ вправо)} {I} \\ r&=\frac{\left(\quantity{6. 0}{V}-\quantity{1.2}{V}\right)}{\quantity{1.56}{A}}\\ \\ r&=\количество{3.1}{Ω} \end{выравнивание}

Даже если вы не смогли вычислить прежние значения тока и разности потенциалов, вы можете прочитать значение сопротивления на пике графика, если вы указываете, что максимальная мощность будет рассеиваться, когда $Y=r $ и четко аннотировать график.

3. Учащийся повторяет эксперимент с батареей с той же ЭДС, но пренебрежимо малым внутренним сопротивлением. Сформулируйте и объясните, как теперь вы ожидаете, что мощность, рассеиваемая в Y, изменится при увеличении сопротивления Y от $\quantity{0,5}{Ω}$ до $\quantity{6,5}{Ω}$.

При незначительном внутреннем сопротивлении p.d. через Y будет равна ЭДС ячейки. Поскольку p.d. теперь постоянна, а соотношение между мощностью и сопротивлением, поскольку постоянное напряжение является обратным, мощность будет уменьшаться по мере увеличения значения Y.

Это вопрос, на который учащиеся, как правило, отвечают очень плохо, и легко предположить, что форма графика будет аналогичной, но иметь более низкое или более высокое значение пиковой мощности.