2.3. Эдс и напряжение в электрической цепи

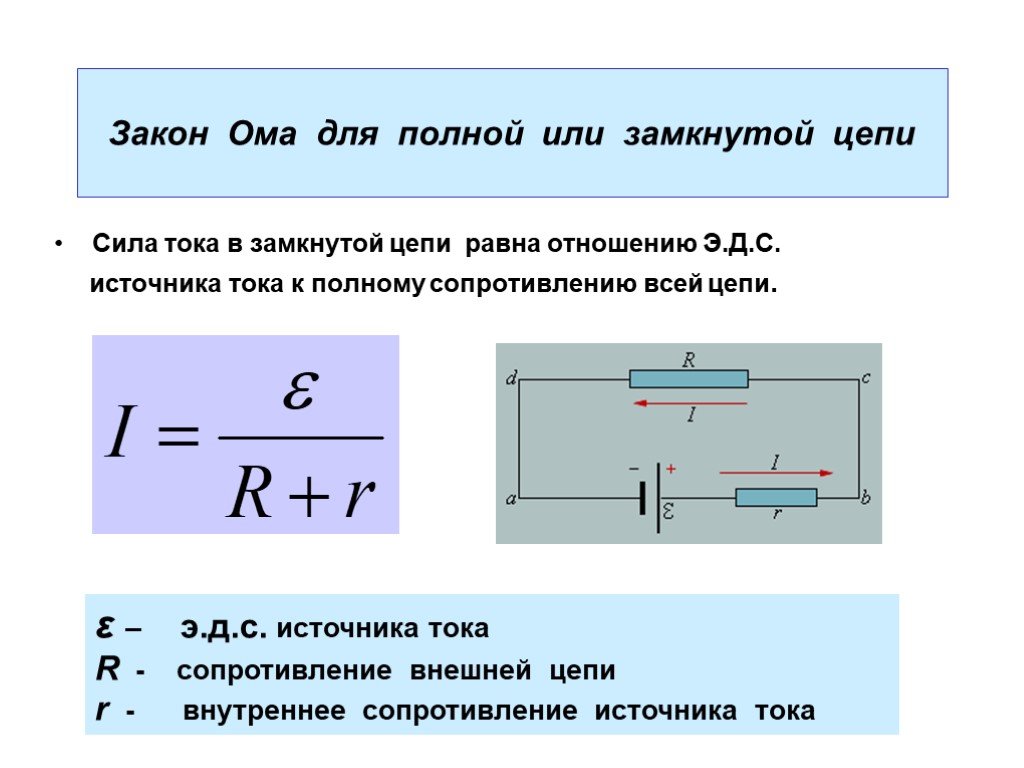
Источник электрической энергии осуществляет направленное перемещение электрических зарядов по всей замкнутой цепи (рис. 1.3.).

Энергия W, которую затрачивает или может затратить источник на перемещение единицы положительного заряда по всей замкнутой цепи, характеризует электродвижущую силу источника Е (ЭДС):

Из определения следует, что ЭДС является энергетической характеристикой источника тока, а не силовой, как можно было бы решить по названию «электродвижущая сила». Единицей измерения ЭДС является вольт:

(вольт).

Энергия, затраченная на перемещение единицы положительного заряда на каком-либо участке замкнутой цепи, характеризует напряжение или падение напряжения на этом участке (внутреннем или внешнем):

Для замкнутой электрической цепи условие равновесия напряжений

(1. 3)

Таким образом, ЭДС источника (Е) можно рассматривать как сумму падений напряжения на внутреннем (U₀) и на внешнем (U) участках замкнутой цепи (рис. 2.3).

Закон Ома для участка электрической цепи устанавливает зависимость между током, напряжением и сопротивлением на этом участке цепи.

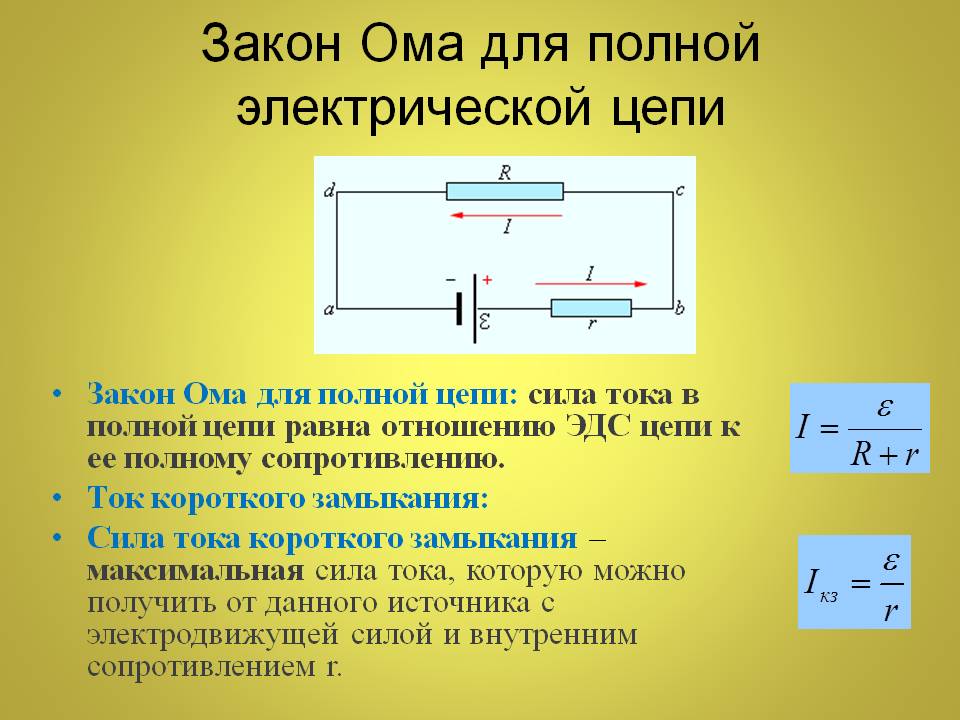
Направленное перемещение электрических зарядов в проводнике (т. е. электрический ток I) происходит под действием сил однородного электрического поля (рис. 2.4). Напряженность поля определяется из выражения

где — напряжение на участке проводника длиной l. Плотность тока в проводнике пропорциональна напряженности однородного электрического поля, силы которого направленно перемещают в нем заряды:

(1. 4)

где γ — коэффициент пропорциональности, называемый удельной проводимостью, характеризующий способность проводника проводить электрический ток.

Подставив в выражение (2.4) величину напряженности однородного электрического поля, силы которого перемещают заряды в проводнике, получим

или

где — электрическое сопротивление участка проводника (R_AB) длинной l,

Тогда (1.5)

Это и есть математическое выражение закона Ома для участка АВ электрической цепи.

Таким образом, ток на участке электрической цепи пропорционален напряжению на этом участке и обратно пропорционален сопротивлению этого участка

.

Закон Ома для участка цепи позволяет определить напряжение данном участке

(1. 6)

а также вычислить сопротивление участка электрической цепи

(1.7)

Выражения (1.6) и (1.7) являются арифметическими следствиями закона Ома, которые широко применяются для расчета электрических цепей.

Что такое электродвижущая сила (ЭДС)

Неотъемлемым элементом любой самодостаточной электрической цепи является источник (генератор) тока. Он разделяет электрические заряды, благодаря чему напряжение поддерживается в приемлемом диапазоне значений. Без этого электрический ток с точно заданными характеристиками в цепи существовать не может. Если мы поставим в цепь, например, конденсатор (пусть даже очень ёмкий), ток в ней возникнет, но через некоторое, как правило, очень непродолжительное время, он закончится. Электрическое поле переместит все имеющиеся свободные заряды, и конденсатор разрядится.

Электродвижущая сила

Определение

Электродвижущей силой источника тока называют силы не электростатического происхождения, действующие внутри указанных устройств и перемещающие электрические заряды против электростатического поля, которое создаёт необходимую разность потенциалов.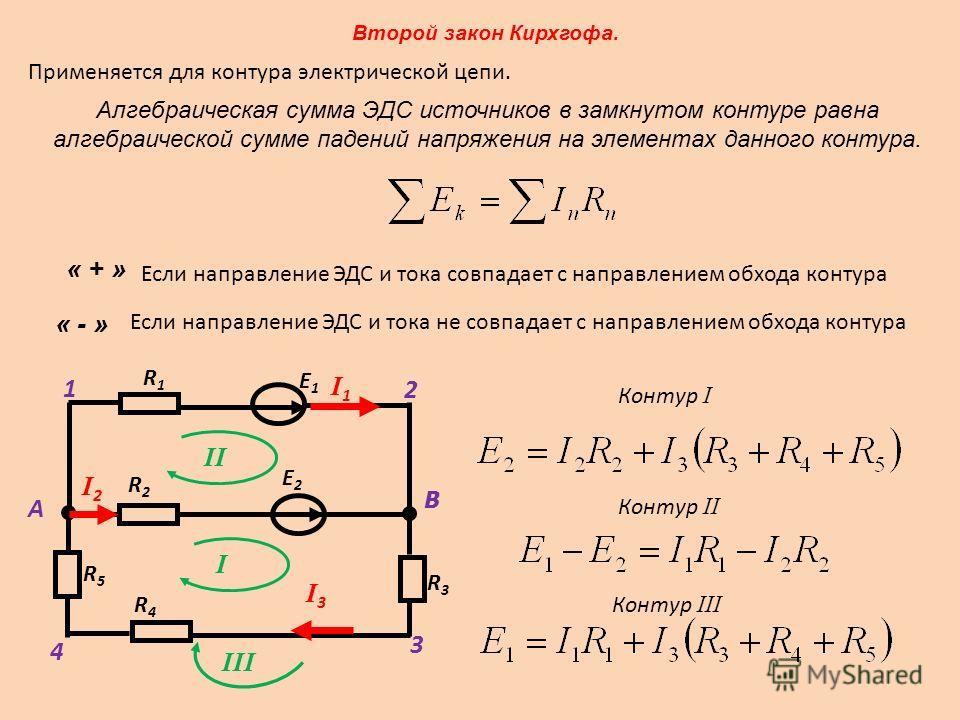

Природа у электродвижущих сил может быть самой разной. В гальванических источниках электрического тока они возникают благодаря энергии, высвобождающейся в химических реакциях между веществом электродов и электролитов. В генераторах постоянного тока они создаются энергией магнитного поля и механической энергией вращения якоря.

Формула расчета ЭДС в электрических цепях, состоящих из замкнутых контуров

Работа электростатических сил равна нулю, ведь заряды (электроны) приходят практически в то же место откуда вышли. Не равна нулю только результирующая работа электродвижущих сил цепи. 

Её величина определяется формулой электродвижущей силы:

Формула

Формула ЭДС:

\[\varepsilon=\frac{A}{q}\].

Именно этому равна электродвижущая сила. A – работа сторонних сил, т. е. ЭДС.

Обратите внимание, направлением ЭДС считается направление, в котором внутри источника перемещаются именно положительные заряды. Часто оно противоположно направлению перемещения реальных носителей заряда, в качестве которых в подавляющем большинстве случаев выполняют электроны.

Если источник тока только один, то направление ЭДС в цепи такое же, как у него.

Размерность электродвижущей силы не равна размерности силы или работы. В системе СИ величина ЭДС измеряется в вольтах. Это мера разности потенциалов, которая создаётся на зажимах при разомкнутом генераторе.

Электродвижущая сила цепи и напряжение

Представим электрическое поле. Рассмотрим в нём произвольную кривую, соединяющую между собой точки A и B. Для дальнейшего объяснения на выбранной линии следует указать положительное направление.

Напряжение на этой кривой будет равняться:

\[U=\int_{l} E d l\]

Под напряжённостью поля, как известно, понимают силу, действующую на помещённый в него единичный положительный заряд. Интеграл в данном случае – работа по перемещению заряда по кривой.

Значение напряжения станет равно разности потенциалов на концах нашей линии: U = φ1 – φ2.

Какую форму имеет кривая, совершенно безразлично. Важны лишь её начальные и конечные точки. {B} E d l=\varphi 1-\varphi 2=\varphi 2-\varphi 1=0\]

Из этого легко сделать вывод, что циркуляция вектора напряжённости по контуру, если он замкнут, равняется нулю. E и dl – векторные величины.

Определение

Электродвижущей силой в теории электричества принято считать циркуляцию вектора напряжённости по произвольному замкнутому контуру.

\[\varepsilon=\oint_{L} E d l=0\]

Если поле электростатическое, то ЭДС замкнутого контура (каким бы он ни был) равна нулю.

Закон Ома для участка цепи с электродвижущей силой тока

Рассмотрим один из самых простых случаев – электрическую цепь с химическим источником ЭДС, элементом Вольта. Он состоит из двух электродов (медного и цинкового), погружённых в раствор кислоты.

Электродвижущая сила в этом случае создаётся следующим образом: цинк при растворении в кислоте теряет положительно заряженные атомы, приобретая тем самым отрицательный потенциал, а медь становится положительно заряженной. В результате возникает сторонняя ЭДС. Находится она в очень тонком слое, отделяющем электролит от цинкового и медного электродов. Когда цепь замыкают, на сопротивлениях двух частей цепи (внешней и внутренней) возникает разность потенциалов и начинает течь ток I.

Для простоты расчётов будем исходить из того, что сопротивления на всех участках цепи распределены равномерно по всему контуру L.

Из закона сохранения энергии следует, что работа, совершаемая электрическим полем при движении заряда q по внешней цепи и в электролите будет равняться

A_q = (φ1 – φ2)*q + (φ3 – φ4)*q 

Общую работу сторонних сил можно записать как

 Ɛ_q= A_st = (φ3 – φ2)*q + (φ1 – φ4)*q

Приравняв обе части двух предыдущих выражений, получим

A_q= A_st

Формула явно указывает на то, что работа сторонних сил и работа электрического поля равны между собой.

Из закона Ома следует, что

φ1 – φ2 = I*R, а φ3 – φ4 = I*r 

От сюда следующий вид закона Ома с электродвижущей силой.

Ɛ = I*(R + r)

Справедлив он только для замкнутой цепи.

О втором правиле Кирхгофа

Полученная формула говорит, что электродвижущая сила равна сложенным друг с другом произведениям силы тока на все сопротивления, составляющих замкнутую цепь.

Ɛ = I*R + I*r

Это очень важное утверждение. Часто его именуют Вторым правилом Кирхгофа. Оно относится ко всем замкнутым цепям, какими бы они ни были.

Важно

По-другому это правило можно сформулировать так – в любом электрическом замкнутом контуре алгебраическая сумма произведений сил токов на сопротивления, через которые они протекают равняется ЭДС в указанном контуре.

Сопротивления могут считаться не только положительными, но и отрицательными. Если направление тока совпадает с выбранным направлением обхода контура, то сопротивление признают положительным. Если не совпадает – отрицательным.

Электродвижущая сила тока считается положительной, в том случае, если в его источнике произошёл переход от отрицательного полюса к положительному.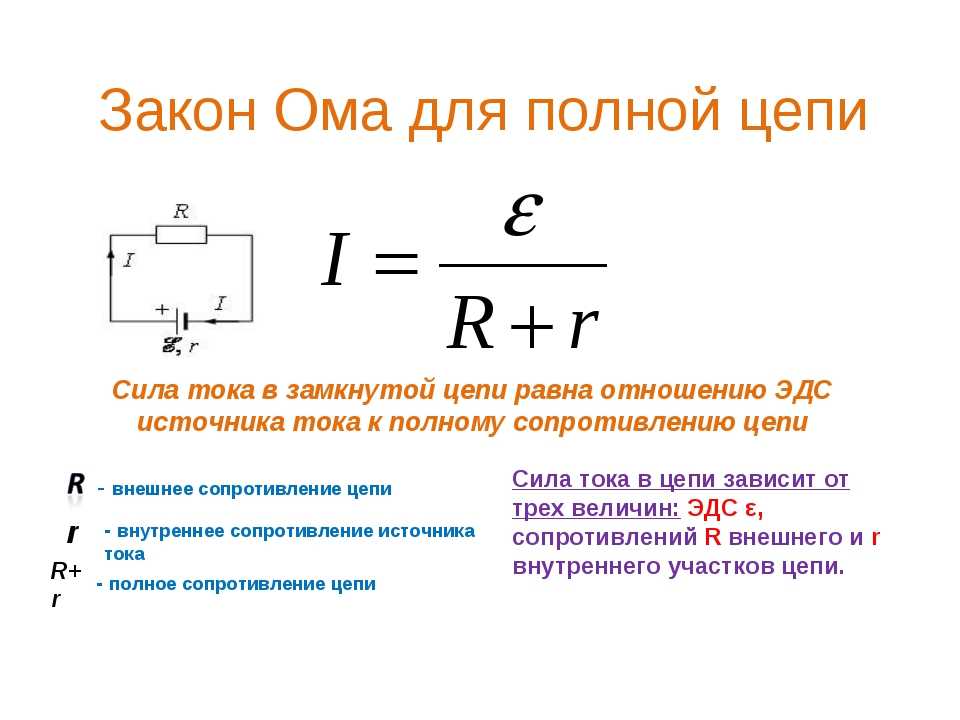 {N} I m R m\].

N – число участков, на которые мы разбили контур.

Данная формула позволяет очень легко рассчитывать достаточно сложные цепи, т. к. получаем систему независимых уравнений, легко решаемую с математической точки зрения. То что самостоятельно, на листе бумаги расчёты будут громоздкими – не проблема. Даже простейший не очень мощный компьютер с вычислениями может справиться весьма быстро.

Формула

Количество независимых контуров определяется по формуле:

\[n2 = p – m + 1\].

p – общее количество ветвей в цепи, m – общее количество узлов в цепи.

магнитных полей — Какова ЭДС в этой цепи?

Задай вопрос

спросил 1 год, 3 месяца назад

Изменено 1 год, 3 месяца назад

Просмотрено 107 раз

$\begingroup$ 92 \ гидроразрыв {дБ} {dt} \end{equation}

Это эквивалентно генератору ЭДС.

Я предполагаю, что правильная конфигурация

, где ячейка обеспечивает ЭДС $\mathcal{E}$, как указано выше. Однако в книге, которая у меня есть, соленоид считается эквивалентным следующей конфигурации:

Где каждая ячейка обеспечивает ЭДС $\mathcal{E}’=\frac{\mathcal{E}}{4}$. Эта ситуация явно отличается и дает разные результаты для токов, протекающих в петлях. На самом деле, левый контур математически ничем не отличается, а второй контур связан с генератором в общей ветви.

Какая конфигурация правильная и почему?

Я думал, что закон Фарадея должен применяться как к левой петле, так и к большой петле, включая правую и левую петлю, поэтому первая конфигурация мне подходит.

РЕДАКТИРОВАТЬ: вот рисунок в учебнике (прочитайте комментарии в принятом ответе для получения дополнительной информации). Извините за качество.

• магнитные поля
• электрические цепи
• электромагнитные индукционные

$\endgroup$

5

$\begingroup$

Вы правы. ЭДС присутствует в левом контуре и во внешнем контуре, поскольку изменяющийся поток связан с обоими этими контурами. В правой петле нет чистой ЭДС, потому что с ней не связан (изменяющийся) поток.

Таким образом, для целей теории цепей можно представить ЭДС так, как если бы она была сосредоточена в указанном вами месте (или в левой вертикальной линии схемы, или в левой части нижней линии).

[Мы можем понять, откуда взялись авторы учебников. Они видят левую петлю, окружающую соленоид, и считают, что должны быть ЭДС со всех четырех сторон квадрата, в том числе и в проводе, содержащем R2. Они забывают, что, применяя те же рассуждения к внешнему контуру, также должна быть ЭДС «вниз» в R3, как и ЭДС в других частях контура. Таким образом, ЭДС, которую они показали в проводе, содержащем R2, с этой точки зрения не является единственной ЭДС в правом контуре — и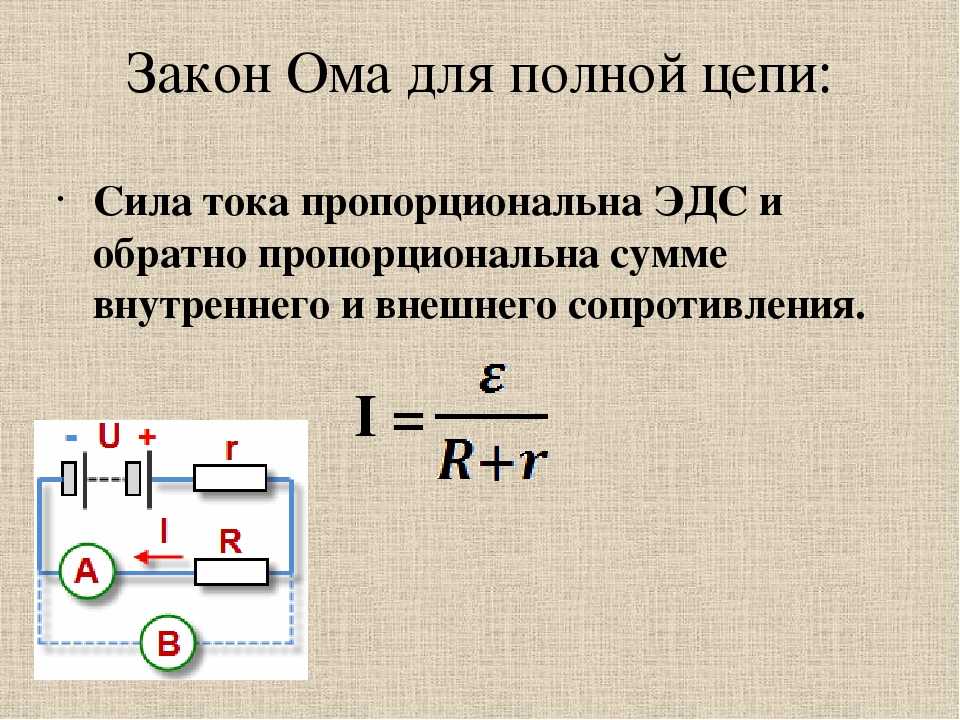

мы знаем, что результирующая ЭДС в правом контуре равна нулю. Вообще небезопасно рассуждать о других ЭДС, кроме результирующих ЭДС в петлях. ]

Какая книга дала вам другой ответ?

$\endgroup$

5

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

напряжение — ЭДС ячейки в разомкнутой цепи

Задай вопрос

спросил 6 лет, 1 месяц назад

Изменено 3 года, 3 месяца назад

Просмотрено 5к раз

$\begingroup$

Рассмотрим ячейку с напряжением на выходе $V’$ и ЭДС $V$ с внутренним сопротивлением $r$ и током $I$, протекающим по цепи, к которой подключено внешнее сопротивление $R$.

Падение потенциала на внутреннем сопротивлении = Ir

$$V= V’ + Ir = IR + Ir$$

$$V=I(R+r)$$

Теперь, если ячейка находится в разомкнутой цепи, то $I=0$ и, следовательно,
$V=0$

Но мы знаем, что ЭДС ячейки равна Окончательному напряжению ячейки в разомкнутой цепи, т.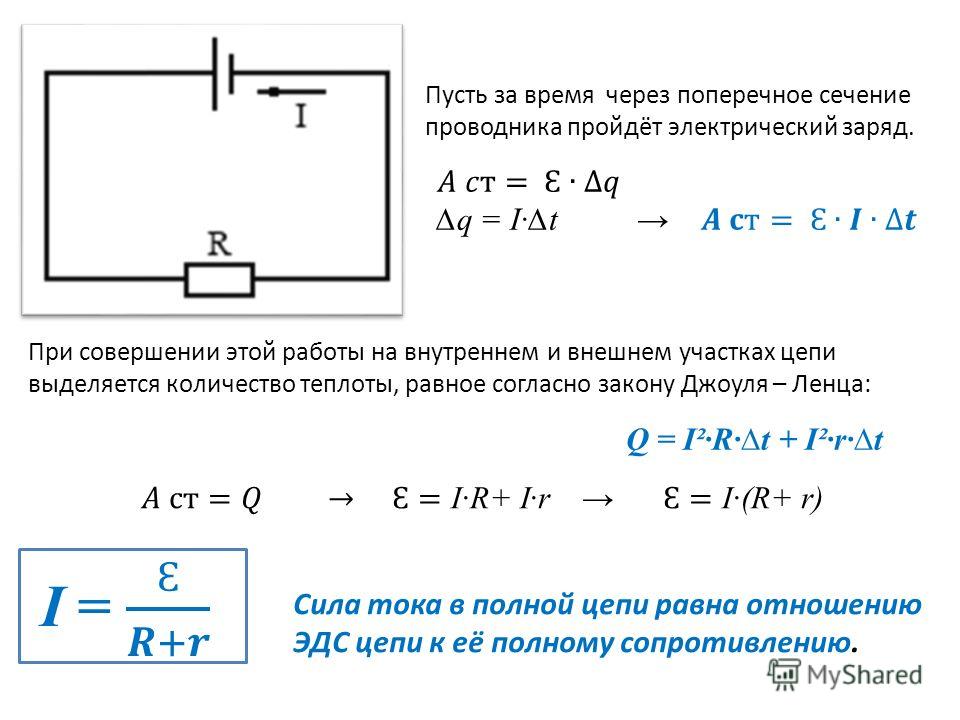 е.
V=V’

Почему такое противоречие в моей концепции?

Я знаю, как получить $V=V’$. Мне это не нужно. Я хочу знать, почему использование этой концепции делает Emf, $V= 0$, а не $V=V’$.

• напряжение
• батареи

$\endgroup$

1

$\begingroup$

Обратите внимание, что: Электродвижущая сила (ЭДС) представляет собой разность потенциалов источника при отсутствии тока. EMF не имеет ничего общего с тем, соединены ли клеммы в цепь или нет. ЭДС — это неотъемлемая характеристика клетки, обусловленная определенными химическими реакциями, необходимыми для движения электронов, чтобы вызвать ЭДС. ЭДС — это напряжение, создаваемое клеткой или магнитной силой в соответствии с законом Фарадея.

Итак, здесь

$$V=EMF$$ $$V’ = ЭДС- Ir$$

$\endgroup$

2

$\begingroup$

Вы отметили, что I равно 0 для разомкнутой цепи, но не учли сопротивление, которое действительно велико.