Расчёт эдс
Согласно [23], стр. 99 для турбогенераторов мощностью до 100 МВт рекомендуется принять .
Тогда:
.
Для системы согласно [23], стр. 99 . Тогда:
.
Расчёт сопротивлений
Сопротивления генераторов 63 МВт:
.
Сопротивления секционных реакторов:
.
Сопротивления трансформаторов ТДН-63000/110:
.
Сопротивления автотрансформаторов АТДЦТН-200000/220/110:
;
;
.
Напряжение короткого замыкания обмотки СН, имеющее отрицательное значение, в расчётах согласно [23] обычно принимают равным нулю. Тогда сопротивления обмоток автотрансформаторов:
;
;
.
Определяем сопротивления двух линий
220 кВ.
.
Сопротивление электрической системы:
.
В результате расчётов получили следующую схему замещения:
Рис. 24. Схема замещения для расчёта токов короткого замыкания
4.4. Расчёт параметров токов короткого замыкания (Iп0, Iпτ, iу, iаτ) для точки k-1
Теперь производим сворачивание схемы замещения относительно точки КЗ K-1.
Преобразование для последовательно соединённых сопротивлений (см. рис. выше):
;
;
.
Преобразуем параллельно соединенные сопротивление:
.
Затем соединим последовательно:
Преобразуем параллельно соединённые сопротивления и ЭДС эквивалентной ветви:
.
Преобразуем параллельно соединенные сопротивление:
;
;
Сопротивления иокажутся соединенными последовательно:
Преобразуем параллельно соединённые сопротивления и ЭДС эквивалентной ветви:
.
Сопротивления иокажутся соединенными последовательно:
Таким образом, получим следующие эквивалентные схемы при КЗ в точке K-1:
Рис. 25. Схемы замещения после преобразований
Приближённо считая ЭДС источников одинаковыми, находим с помощью коэффициентов токораспределения взаимные сопротивления источников относительно точки КЗ.
Зададимся коэффициентом токораспределения в ветви с сопротивлением равным единице:
.
Тогда, двигаясь от точки КЗ и осуществляя обратное преобразование схемы, находим коэффициенты токораспределения в ветвях с источниками, находящимися в различной удалённости от места КЗ:
;
.
Таким образом, коэффициенты токораспределения для всех ветвей с источниками найдены.
Взаимное сопротивление генераторов 63 МВт на ГРУ относительно точки КЗ:
.
Взаимное сопротивление генератора блока с блочным трансформатором относительно точки КЗ:
.
В результате получили трёхлучевую схему замещения:
Рис. 26. Схема замещения после преобразований
Находим значения сверхпереходных токов от каждого источника:
;
;
.
Стоит уточнить, что токи как от генераторов,
так и от системы являются величинами,
приведенными к основной ступени
напряжения (с целью упрощения символ
над токами опущен).
Теперь определим значения ударных токов для каждой ветви. Согласно [25], стр. 110 для блока генератор-трансформатор с мощностью генератора 63 МВт ударный коэффициент принимается равным 1,965, для ГРУ 1,95. Для системы по тому же источнику примем ударный коэффициент равным 1,78. Тогда ударные токи от каждого источника:
;
;
Теперь определим действующее значение периодической и мгновенное значение апериодической составляющих тока КЗ к моменту отключения. Время отключения согласно [2] определяется как:
,
.
Для генераторов периодическая составляющая тока к моменту отключения определяется по формуле:
.
Для определения по кривым из [23], стр. 113 необходимо знать электрическую удалённость точки КЗ от генератора. Удалённость определяется долей тока КЗ от генератора, отнесённой к его номинальному току, приведённому ступени напряжения, где произошло КЗ. Определим удалённость КЗ для каждого из генераторов:
;
.
Теперь по [23], стр. 113 для генераторов с тиристорной системой самовозбуждения для момента времени 0,045 с при найденной удалённости КЗ находим значения . Если, то принимается:
,.
Периодические составляющие тока КЗ от генераторов к моменту расхождения контактов:
;
.
Для системы согласно [2] обычно принимается . Поэтому.
Наконец, определяем апериодическую
составляющую тока КЗ к моменту расхождения
контактов.
По [23] постоянные времени
затухания апериодической составляющей
равны: для генератора 63 МВт – 0,39 с. Для
системы по [23], стр. 110 постоянная времени
равна 0,04 с.
;
.
Составим сводную таблицу результатов расчёта токов КЗ для точки K-1:
Таблица 10. Результаты ручного расчёта токов короткого замыкания для точки K-1
Источник | , кА | , кА | , кА | , кА |
Система | 10,96 | 27,3 | 10,96 | 4,98 |
Генераторы G1-G3 | 0. | 2,59 | 0,95 | 1,19 |
Генератор G4 | 0,5 | 1,38 | 0,435 | 0,62 |
Суммарный ток | 12,41 | 31,27 | 18,195 | 6,79 |
Расчет pH по ЭДС — Аналитическая химия — Спроси!
Спроси! | Beyond Curriculum1
катод; AgCl+e=Ag+Cl-
анод;2H+=h3
E станд.
2/1). x=0.02 M. pH=-log(0.02)=1.69, что в два раза меньше правильного ответа. Подскажите где я ошибся?
2 лайка
Alibi (Әліби)
2
Alibi:
(8.314 298)/(96500 2)
забыл знак умножения
Jeff
3
Редактировать можно
Madsoul (Madiyar Kassymaly)
9 лайков
V_V (Vadim)
6
Можно для полного понимания узнать, почему справедливо выражение [Cl-]=[H+] конкретно в нашем случае, это некое пренебрежение, связанное с чрезвычайно малым вкладом в концентрацию протонов реакции на аноде: h3 = 2H+ + 2e- ? Или это просто уравнение электронейтральности без учета автопротолиза воды из-за достаточно большой концентрации HCl?
Anton (Anton Morgunov)
7
V_V:
Или это просто уравнение электронейтральности без учета автопротолиза воды из-за достаточно большой концентрации HCl?
Угу.
И на самом деле, с сильными кислотами автопротолиз становится значительном при катастрофически маленьких концентрациях кислоты.
2 лайка
Madsoul (Madiyar Kassymaly)
8
V_V:
Можно для полного понимания узнать, почему справедливо выражение [Cl-]=[H+] конкретно в нашем случае, это некое пренебрежение, связанное с чрезвычайно малым вкладом в концентрацию протонов реакции на аноде: h3 = 2H+ + 2e- ?
Лично мне казалось, что задача требует от решателя рН раствора HCl до протекания химической реакции. В таком случае, следует рассматривать только вклад имеющихся в растворе ионов гидроксония и хлорида, которые должны иметь одинаковую концентрацию при высоких концентрациях HCl.
Тут наверное можно задать 2 вопроса :
- А вдруг там использовали солянку в чрезмерно малых количествах так, что ее диссоциация не подавляет автопротолиз воды ?
Электролит на то и есть электролит, чтобы проводить электрический ток. Поэтому, в элементах я считаю, было бы крайне неразумно использовать нереально разбавленный раствор HCl.
- А как насчет израсходования хлорид ионов на образование AgCl на электроде ?
Этот вопрос я задал себе, потому что, я предположил, что хлорсеребряный электрод готовят путем помещения серебряного электрода в соляную кислоту (как это делают с свинцовым электродом), и в следствие чего, на электроде образуется тонкий слой AgCl, а сам раствор насыщается этой солью. Так вот, в силу очень малой растворимости AgCl, можно пренебречь убытками хлорид ионов
1 лайк
Anton (Anton Morgunov)
Но вопросы плавильные задаешь
2 лайка
Madsoul (Madiyar Kassymaly)
10
Anton:
Так AgCl наоборот расходуется, а не образуется.
А лол, я почему то подумал, что сначала берут раствор солянки, помещают серебряный электрод, на котором должна образоваться тонкая пленка из хлорида серебра. Затем помещают платиновый электрод, пропускают водород при постоянном давлении, и затем измеряют ЭДС
Madsoul (Madiyar Kassymaly)
11
Хотел бы еще уточнить, в задаче спрашивают рН до протекания химической реакции, или после протекания ?
2 лайка
Anton (Anton Morgunov)
И далее, как только реакция начнет протекать, ЭДС (E) тут же начнет меняться и в равновесии придет к угадайте к чему?
значению равному нулю
Поэтому в данном случае, просят найти pH для конкретного значения ЭДС. Конкретное значение ЭДС соответствует конкретному значению концентраций.
5 лайков
gh2.xl (Мирас)
14
Я не могу понять, почему ты взял концентрацию Cl равною концентраций Н2 ?
Anton (Anton Morgunov)
15
Мирас:
почему ты взял концентрацию Cl равною концентраций Н2
вы имеете в виду \ce{[H+]=[Cl-]}?
gh2.
xl
(Мирас)
16
да именно так
Anton (Anton Morgunov)
17
таки принцип электронейтральности
1 лайк
gh2.xl (Мирас)
18
можете рассказать об этом подобное?
Anton (Anton Morgunov)
2 лайка
Alibi (Әліби)
20
Anton Morgunov:
значению равному нулю
Не могу понять, откуда это вывели
SanzharB (Sanzhar Bissenali)
21
Alibi aka Dastan:
Не могу понять, откуда это вывел
Потому что \Delta G = — nFE , а при равновесии разница в энергии Гиббса у продуктов и реагентов равна нулю.
1 лайк
Error401 (Ivan)
22
Почему в этой задачи не учитывали растворимость хлорида серебра?
1 лайк
следующая страница →
Калькулятор ЭДС самоиндукции| Icalculator ™
Меню
Population Today
- Работа калькулятора сил фрикционной силы
- Магнитное поле в центре тока калькулятора петли переноса
- Берноулли Принцип
- Калькулятор теплопередачи
- Положение и увеличение изображения в криволинейных зеркалах и калькулятор линз
- Калькулятор атомной массы
- Калькулятор электрического потока (закон Гаусса)
- Калькулятор момента равновесия с использованием моментов
- Калькулятор эффекта Доплера в звуковых волнах катушки по индуктивности и скорости изменения тока
- ЭДС самоиндукции в катушке по количеству витков и скорости изменения магнитного потока
- 16.1 — Введение в магнетизм
- 16.2 — Магнитное поле, создаваемое электрическими токами
- 16.3 — Магнитное воздействие на провод с током. Сила Ампера
- 16.4 — Магнитная сила, действующая на провод, движущийся внутри магнитного поля. Lorentz Force
- 16,5 — Магнитный дипольный момент
- 16,6 — Закон Ампер
- 16,7 — Закон Фарадея об индукции
- 16,8 — Закон Ленца
- 16,9 — Индуктивность и самоиндукция.0008
- 16.11 — Наведенные электрические поля
- 16.12 — Цепи RL
- 16.13 — Энергия, запасенная в магнитном поле. Плотность энергии магнитного поля. Взаимная индукция
- 16.14 — Переменный ток. Цепи LC
- 16.15 — Введение в цепи RLC
- 16.
16 — Цепь серии RLC - 16.17 — Питание в цепи переменного тока. Трансформаторы
- 16.18 — Уравнения Максвелла
- Eddington Luminosity Limit Calculator
- Antenna Polarization Calculator
- Conductive Heat Transfer Calculator
- Lorentz Transformation Of Coordinates Calculator
- Circuit Parallel Inductance Calculator
- Coaxial Cylinders Capacitance Calculator
- Antenna Gain Calculator
- Capacitance Calculator
- Optical Power Калькулятор
- Калькулятор гравитационной потенциальной энергии
- Larmor Radius Calculator
- Hydraulic Resistance Calculator
- Eigen Function Of Particle 3d Rectangular Box Calculator
- Parallel Plate Capacitor Calculator
- Rayleigh Jeans Relation Calculator
- Wood Density Calculator
- Vector Displacement Calculator
- Non Uniform Electric Field Calculator
- Калькулятор собственной индуктивности катушки
- Калькулятор крутильного маятника
- Рассчитать ЭДС, индуцируемую в генераторе.
- Рассчитайте пиковую ЭДС, которая может быть наведена в конкретной генераторной системе.
- Электрический генератор вращает катушку в магнитном поле, индуцируя ЭДС, определяемую как функция времени
[латекс]\text{emf}=2{B\ell v}\sin\omega t\\[/latex],
, где A – площадь витковой катушки N , вращаемой с постоянной угловой скоростью ω в однородном магнитном поле B .
- Пиковая ЭДС ЭДС 0 генератора равна
эдс 0 = NABω
- Используя RHR-1, покажите, что ЭДС на сторонах контура генератора на рисунке 4 одинаковы, и, таким образом, добавьте.
- Источником электрической энергии генератора является работа, совершаемая для вращения его катушек. Как работа, необходимая для поворота генератора, связана с законом Ленца?
- электрогенератор:
- Устройство для преобразования механической работы в электрическую энергию; он индуцирует ЭДС, вращая катушку в магнитном поле
- ЭДС, индуцированная в катушке генератора:
- эдс = NAB ω sin ωt , где A — площадь витковой катушки N , вращаемой с постоянной угловой скоростью ω в однородном магнитном поле, за период 609 610 B в однородном магнитном поле. времени т
- пик ЭДС:
- ЭДС 0 = NABω
🖹 Нормальный просмотр. Полное просмотр страницы | |
| ПРОТИВАЦИЯ Калькулятора (десятичные места) 012345101520 | |
| Количество оборотов в Solenoid Fllowing (N) | . цепь (I 0 ) A |
| Конечный ток, протекающий через цепь (I) A | |
| Время, прошедшее во время изменения (Δt) с | |
| Начальное магнитное поле, индуцированное в соленоиде (B 0 ) T | |
| Финальный магнитный поле, индуцированное в солиноидном (B) T | Финальный магнитный поле, индуцированное в солиноидном (B) T44444444444449 | . |
| Magnetic permeability of free space (vacuum) (μ 0 ) N/A 2 | (4π)× 10 power of |
| Length of inductor (solenoid) (l) m | |
| ЭДС самоиндукции в катушке с точки зрения индуктивности и скорости изменения тока составляет катушки по количеству витков и скорости изменения магнитного потока В [Вольт] | |
| ЭДС самоиндукции в катушке из-за изменения тока в цепи | |
|---|---|
| ε ‘ 1 = — μ 0 × N 2 × A / l × ∆I / ∆t ε ‘ 1 = — × 2 × / l × — / ε ‘ 1 = — × × / × / ε ‘ 1 = — / × ε ‘ 1 = — × ε ‘ 1 = | |
| Self-induced emf in the coil due to the change in magnetic flux calculation | |
| ε ‘ 2 = -N × (B — B 0 ) × A / Δt ε ‘ 2 = — × ( — ) × / ε ‘ 2 = — × × / ε ‘ 2 = — × / ε ‘ 2 = — × ε ‘ 2 = | |
| Self Induced Emf Calculator Input Values | |
| Number of количество оборотов в соленоиде (Н) | |
| Начальный ток, протекающий по цепи (I 0 ) А [А] | |
| Окончательный ток, протекающий по цепи (I) А [А] | |
| Время, прошедшее во время изменения (Δt) с [секунда] | |
| Площадь катушки соленоида (A) м 2 [квадратный метр] | 1 |
| Конечное магнитное поле, индуцируемое в соленоиде (В) Тл [Тесла] | |
| Магнитная проницаемость свободного пространства (вакуум) (мк | 1 4 Н/А 7 7 0 9090 2 [Ньютон на квадратный ампер] |
| Длина индуктора (соленоида) (л) м [метр] |
Обратите внимание, что формулы для каждого расчета вместе с подробными расчетами доступны ниже.
Когда вы вводите конкретные факторы для каждого расчета ЭДС самоиндукции, калькулятор ЭДС самоиндукции автоматически вычисляет результаты и обновляет элементы формулы физики с каждым элементом расчета ЭДС самоиндукции. Затем вы можете отправить по электронной почте или распечатать этот расчет ЭДС самоиндукции для дальнейшего использования.
Мы надеемся, что Калькулятор ЭДС самоиндукции оказался полезным для вас при изучении физики. Если это так, мы просим вас оценить этот калькулятор физики и, если у вас есть время, поделиться им в своей любимой социальной сети. Это позволяет нам распределять будущие ресурсы и сохранять эти калькуляторы по физике и учебные материалы бесплатными для всех по всему миру. Мы считаем, что у всех должен быть бесплатный доступ к учебным материалам по физике. Делясь с вами, вы помогаете нам охватить всех студентов-физиков и тех, кто интересуется физикой по всему миру.
Связанные секции физики с учебниками
Раздел 14: Электростатика
Раздел 15: Электродинамика
Раздел 16: Магнитизм
Раздел 17: Электроника
Раздел 22: космология
Тригометрия
9003.
к изменению тока в цепи Формула и расчет0128 / l × ∆I / ∆t This formula derives from
ε ‘ 1 = -L × ∆I / ∆t
где L — (собственная) индуктивность соленоида.
ЭДС самоиндукции в катушке из-за изменения магнитного потока Формула и расчет
ε ‘ 2 = -N × (B — B 0 ) × A / Δt
This formula derives from
ε ‘ 2 = -N × ∆Φ / Δt
Учебные пособия по физике магнетизма, связанные с калькулятором ЭДС самоиндукции
Следующие учебные пособия по физике представлены в разделе «Магнетизм» наших бесплатных учебных пособий по физике. Каждое руководство по магнетизму включает подробную формулу магнетизма и пример того, как рассчитать и решить конкретные вопросы и проблемы, связанные с магнетизмом.
В конце каждого учебника по магнетизму вы найдете вопросы по пересмотру магнетизма со скрытым ответом, который открывается при нажатии. Это позволяет вам узнать о магнетизме и проверить свои знания по физике, отвечая на вопросы теста по магнетизму.
16 — Цепь серии RLCКалькуляторы физики
Вам также могут пригодиться следующие калькуляторы физики.
Электрические генераторы | Физика
Цели обучения
К концу этого раздела вы сможете:
Электрические генераторы индуцируют ЭДС, вращая катушку в магнитном поле, как кратко описано в ЭДС индукции и магнитном потоке. Теперь мы рассмотрим генераторы более подробно. Рассмотрим следующий пример.
Пример 1. Расчет ЭДС, индуцированной в катушке генератора
Катушка генератора, показанная на рисунке 1, поворачивается на четверть оборота (от θ = 0° до θ = 90°) за 15,0 мс. Круглая катушка из 200 витков имеет радиус 5,00 см и находится в однородном магнитном поле 1,25 Тл. Чему равна средняя ЭДС индукции?
Рис. 1. Когда катушка этого генератора поворачивается на четверть оборота, магнитный поток Φ изменяется от своего максимума до нуля, индуцируя ЭДС.
СтратегияМы используем закон индукции Фарадея, чтобы найти среднюю ЭДС, индуцированную за время Δ t :
[латекс]\text{ЭДС}=-N\frac{\Delta\Phi}{\ Дельта т}\\[/латекс].
Мы знаем, что N = 200 и Δ t = 15,0 мс, поэтому мы должны определить изменение потока Δ Φ , чтобы найти ЭДС.
РешениеПоскольку площадь петли и напряженность магнитного поля постоянны, мы видим, что
[латекс]\Delta\Phi =\Delta\left(BA\cos\theta\right)=AB\Delta\left(\cos\theta \right)\\[/latex].
Теперь Δ (cos θ ) = −1,0, поскольку было дано, что θ изменяется от 0º до 90º . Таким образом, Δ Φ = − AB и
[латекс]\текст{ЭДС}=N\frac{AB}{\Delta t}\\[/латекс].
Площадь петли A = πr 2 = (3,14…)(0,0500м) 2 = 7,85 × 10 −3 м 2 . Ввод этого значения дает 9{-3}\text{ s}}=131\text{ V}\\[/latex].
ОбсуждениеЭто практическое среднее значение, аналогичное 120 В, используемому в домашнем хозяйстве.
ЭДС, рассчитанная в приведенном выше примере 1 , представляет собой среднее значение за одну четвертую оборота.
Чему равна ЭДС в каждый момент времени? Оно изменяется в зависимости от угла между магнитным полем и перпендикуляром к катушке. Мы можем получить выражение для ЭДС как функции времени, рассматривая ЭДС движения на вращающейся прямоугольной катушке шириной w и высотой ℓ в однородном магнитном поле, как показано на рисунке 2.
Рисунок 2. Генератор с одной прямоугольной катушкой, вращающейся с постоянной угловой скоростью в однородном магнитном поле, создает ЭДС, которая изменяется синусоидально во времени . Обратите внимание, что генератор похож на двигатель, за исключением того, что вал вращается для создания тока, а не наоборот.
Заряды в проводах петли испытывают магнитную силу, так как движутся в магнитном поле. На заряды в вертикальных проводах действуют силы, параллельные проводу, вызывающие токи. Но находящиеся в верхнем и нижнем сегментах ощущают силу, перпендикулярную проводу, которая не вызывает тока. Таким образом, мы можем найти ЭДС индукции, рассматривая только боковые провода.
ЭДС движения принимается равной ЭДС = 9.0609 Bℓv , где скорость v перпендикулярна магнитному полю B . Здесь скорость находится под углом θ с B , так что ее составляющая, перпендикулярная B , равна v sin θ (см. рис. 2). Таким образом, в этом случае ЭДС, индуцированная с каждой стороны, равна ЭДС = Bℓv sin θ , и они имеют одинаковое направление. Суммарная ЭДС вокруг петли тогда равна
[латекс]\текст{ЭДС}=2{B\ell v}\sin\theta\\[/латекс].
Это выражение верно, но оно не дает ЭДС как функцию времени. Чтобы найти зависимость ЭДС от времени, предположим, что катушка вращается с постоянной угловой скоростью ω . Угол θ связан с угловой скоростью соотношением θ = ωt , так что
[латекс]\текст{ЭДС}=2{B\ell v}\sin\omega t\\[/ латекс].
Теперь линейная скорость v связана с угловой скоростью ω соотношением v = рω .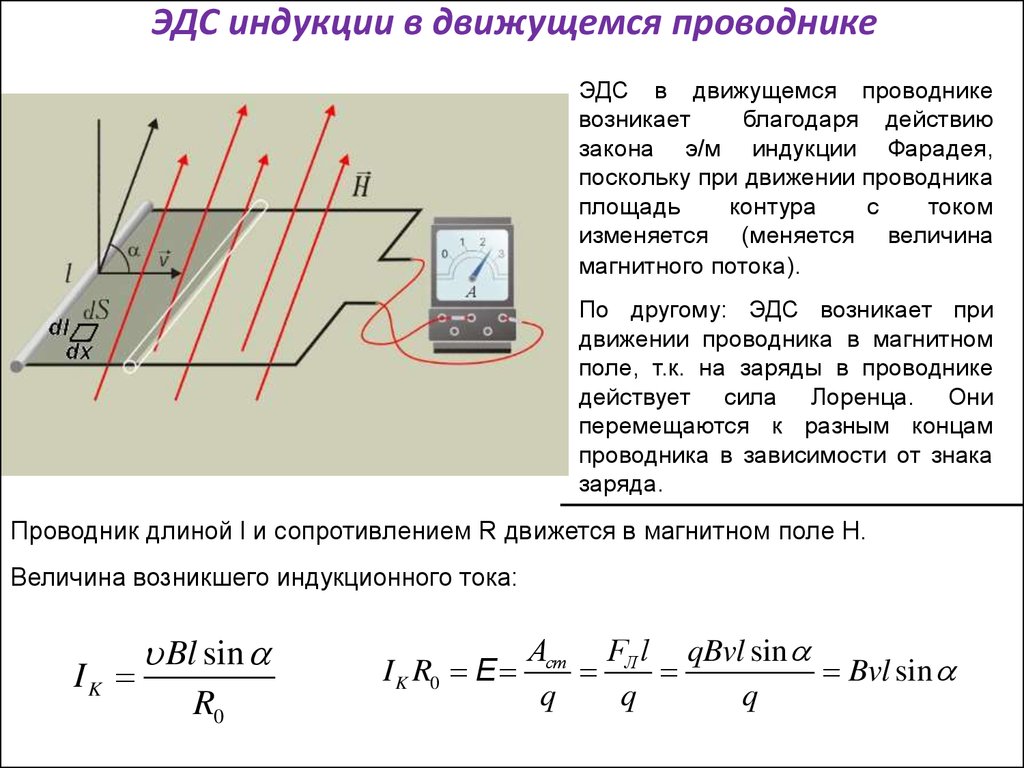
Здесь r = w /2, так что v = ( w /2) ω , и
[латекс]\text{emf}=2 B\ell \frac }{2}\omega\sin\omega t=\left(\ell w\right)B\omega\sin\omega t\\[/latex].
Заметив, что площадь петли равна A = ℓ w , и учитывая N петель, мы находим, что
[латекс]\text{emf}=NAB\omega\sin\omega t\\[/latex]
— ЭДС , индуцированная в катушке генератора N витков и площадь A вращающаяся с постоянной угловой скоростью ω в однородном магнитном поле B . Это также может быть выражено как
[латекс]\text{emf}={\text{emf}}_{0}\sin\omega t\\[/latex],
, где
[латекс]{\ text{emf}}_{0}=NAB\omega\\[/latex]
— максимальная (пиковая) emf . Обратите внимание, что частота колебаний равна f = ω /2π , а период равен Т = 1/ f = 2π/ ω .
На рис. 3 показан график зависимости ЭДС от времени, и теперь кажется разумным, что переменное напряжение является синусоидальным.
Рис. 3. ЭДС генератора подается на лампочку с показанной системой колец и щеток. На графике показана зависимость ЭДС генератора от времени. emf0 — пиковая эдс. Период T = 1/ f = 2π/ω, где f — частота. Обратите внимание, что буква E означает emf.
Тот факт, что пиковая ЭДС, ЭДС 0 = NABω , имеет смысл. Чем больше количество катушек, тем больше их площадь, и чем сильнее поле, тем больше выходное напряжение. Интересно, что чем быстрее раскручивается генератор (больше ω ), тем больше ЭДС. Это заметно на велосипедных генераторах, по крайней мере, на более дешевых. Один из авторов, будучи подростком, находил забавным ехать на велосипеде достаточно быстро, чтобы сжечь его фары, пока однажды темной ночью ему не пришлось ехать домой без света. На рисунке 4 показана схема, с помощью которой можно сделать генератор для получения импульсного постоянного тока.
Более сложное расположение нескольких катушек и разъемных колец может обеспечить более плавный постоянный ток, хотя для создания постоянного тока без пульсаций обычно используются электронные, а не механические средства.
Рис. 4. Разъемные кольца, называемые коммутаторами, в этой конфигурации создают импульсную ЭДС постоянного тока.
Пример 2. Расчет максимальной ЭДС генератора
Рассчитать максимальную ЭДС, ЭДС 0 генератора, рассмотренного в Примере 1. , определено, по ЭДС 0 = NABω можно найти ЭДС 0 . Все остальные величины известны.
РешениеУгловая скорость определяется как изменение угла в единицу времени:
[латекс]\омега =\frac{\Delta\theta}{\Delta t}\\[/latex].
Одна четвертая оборота составляет π/2 радиана, а время составляет 0,0150 с; таким образом,
[латекс]\begin{array}{lll}\omega & =& \frac{\pi /2\text{rad}}{0,0150 \text{s}}\\ & =& 104,7\text{ рад/с}\end{массив}\\[/latex].
104,7 рад/с — это ровно 1000 об/мин. Подставляем это значение на 9{2}\right)\left(1.25\text{ T}\right)\left(104.7 \text{ рад/с}\right)\\ & =& 206\text{ V}\end{массив}\\ [/латекс].
ОбсуждениеМаксимальная ЭДС больше средней ЭДС 131 В, найденной в предыдущем примере, как и должно быть.
В реальной жизни электрические генераторы выглядят совсем иначе, чем на рисунках в этом разделе, но принцип тот же. Источником механической энергии, вращающей катушку, может быть падающая вода (гидроэнергия), пар, образующийся при сжигании ископаемого топлива, или кинетическая энергия ветра. На рис. 5 показан вид в разрезе паровой турбины; пар движется по лопастям, соединенным с валом, который вращает катушку внутри генератора.
Рисунок 5. Паровая турбина/генератор. Пар, образующийся при сжигании угля, воздействует на лопатки турбины, вращая вал, соединенный с генератором. (кредит: Nabonaco, Wikimedia Commons)
Генераторы, показанные в этом разделе, очень похожи на двигатели, показанные ранее.
Это не случайно. Фактически двигатель становится генератором, когда его вал вращается. Некоторые ранние автомобили использовали свой стартер в качестве генератора. В разделе «Обратная ЭДС» мы дополнительно исследуем работу двигателя как генератора.
Резюме раздела
Концептуальные вопросы
Как работа, необходимая для поворота генератора, связана с законом Ленца?Задачи и упражнения
1. Рассчитайте пиковое напряжение генератора, который вращает свою 200-витковую катушку диаметром 0,100 м со скоростью 3600 об/мин в поле 0,800 Тл.
2. При какой угловой скорости в об/мин пиковое напряжение генератора составит 480 В, если его 500-витковая катушка диаметром 8,00 см вращается в поле 0,250 Тл?
3. Какова пиковая ЭДС, создаваемая вращением катушки с 1000 витками диаметром 20,0 см в магнитном поле Земли 5,00 × 10 −5 Тл, если плоскость катушки изначально перпендикулярна полю Земли и поворачивается параллельно полю за 10,0 мс?
4. Какова пиковая ЭДС, создаваемая катушкой радиусом 0,250 м, состоящей из 500 витков, которая поворачивается на четверть оборота за 4,17 мс, первоначально имея плоскость, перпендикулярную однородному магнитному полю. (Это 60 об/с.)
5. (a) Велосипедный генератор вращается со скоростью 1875 рад/с, производя пиковую ЭДС 18,0 В.
Он имеет прямоугольную катушку размером 1,00 на 3,00 см в поле 0,640 Тл. Сколько витков в катушке? (b) Практично ли такое количество витков провода для катушки размером 1,00 на 3,00 см?
6. Интегрированные понятия Эта задача относится к велосипедному генератору, рассмотренному в предыдущей задаче. Он приводится в движение колесом диаметром 1,60 см, которое катится по внешнему ободу велосипедной шины. а) Какова скорость велосипеда, если угловая скорость генератора равна 1875 рад/с? б) Какова максимальная ЭДС генератора, когда велосипед движется со скоростью 10,0 м/с, учитывая, что в первоначальных условиях она составляла 18,0 В? (c) Если сложный генератор может изменять свое собственное магнитное поле, какая напряженность поля ему потребуется при скорости 5,00 м/с, чтобы произвести 90,00 В максимальная ЭДС?
7. (a) Автомобильный генератор вращается со скоростью 400 об/мин, когда двигатель работает на холостом ходу. Его 300-витковая прямоугольная катушка размером 5,00 на 8,00 см вращается в регулируемом магнитном поле, так что она может создавать достаточное напряжение даже при низких оборотах. Какая напряженность поля необходима для создания пиковой ЭДС 24,0 В? (b) Обсудите, как эта требуемая напряженность поля соотносится с напряженностью поля, доступной для постоянных и электромагнитов.
8. Покажите, что если катушка вращается с угловой скоростью ω , период ее переменного тока на выходе равен 2π/ ω .
9. Катушка диаметром 10,0 см из 75 витков вращается с угловой скоростью 8,00 рад/с в поле 1,25 Тл, начиная с плоскости катушки, параллельной полю. а) Чему равна пиковая ЭДС? б) В какой момент времени достигается максимальная ЭДС? в) В какой момент ЭДС достигает своего максимального отрицательного значения? (d) Каков период выходного напряжения переменного тока?
10. а) Если ЭДС катушки, вращающейся в магнитном поле, равна нулю при t = 0 и возрастает до своего первого пика при t = 0,100 мс, какова угловая скорость катушки? б) В какое время произойдет ее следующий максимум? в) Каков период выпуска продукции? (d) Когда объем выпуска составляет первую четверть своего максимума? (e) Когда она составляет следующую четверть своего максимума?
11. Необоснованные результаты 500-витковая катушка площадью 0,250 м 2 вращается в поле Земли 5,00 × 10 −5 Тл, производя максимальную ЭДС 12,0 кВ. а) С какой угловой скоростью должна вращаться катушка? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?
Глоссарий
Избранные решения задач и упражнений
1.
