Вспомогательные приборы электрической цепи — что это, определение и ответ
Ключ – визуальное отображение разрыва цепи. При разрыве в части цепи с ключом тока быть не может.
Электродвижущая сила (ЭДС) совершает работу по перемещению зарядов в цепи, т. е. обеспечивает ток в цепи.
Электродвижущая сила равна работе, которую сторонние силы совершают по перемещению единичного положительного заряда во всей цепи:
\(\varepsilon = \frac{A_{сторонних\ сил}}{q}\), где
ε ― электродвижущая сила, [В],
Aсторонних сил ― работа сторонних сил по перемещению заряда, [Дж],
q ― величина заряда, перемещающегося в цепи, [Кл].
Сторонние силы ― это силы неэлектрического происхождения, их обеспечивают такие устройства как аккумуляторы, батареи, блоки питания.
Как видно из формулы ниже, ЭДС аналогична напряжению, но ЭДС создается неэлектрическими силами и характеризует всю цепь, а напряжение создается электрическими силами, и характеризует участок цепи.
Напряжение равно разности электрических потенциалов участков цепи, которая равна работе по перемещению единичного заряда:
\(U = \varphi_{2} — \varphi_{1} = \frac{A}{q}\), где
U ― напряжение на участке цепи, [В],
\(\varphi_{2} — \varphi_{1}\)― электрический потенциал на конечном и начальном участках цепи соответственно, [В],
A ― работа электростатического поля по перемещению заряда, [Дж],
q ― величина заряда, перемещающегося в цепи, [Кл].
Источник ЭДС обладает двумя полюсами (клеммами) ― положительным и отрицательным. На рисунке показаны примеры обозначения клемм источника ЭДС. Чаще всего положительная клемма обозначается тонкой длинной линией, а отрицательная ― короткой жирной со знаками «+» и «–» или без них.
Закон Ома для полной (замкнутой) цепи включает в себя ЭДС источника тока:
\(I = \frac{\varepsilon}{R + r}\), где
I ― сила тока [А],
ε ― ЭДС источника тока [В],
R ― сопротивление цепи [Ом],
r ― внутреннее сопротивление источника ЭДС [Ом].
Отсюда ЭДС источника тока может быть записано как:
ε = IR + Ir или ε = U + Ir, где
U ― напряжение в цепи [В].
Короткое замыкание ― это состояние, когда сопротивление нагрузки пренебрежимо мало.
Соответственно, током короткого замыкания называется сила тока, проходящего через ненагруженную сопротивлением ветвь.
Из закона Ома для полной цепи следует, что сила тока короткого замыкания равна:
\(I_{КЗ} = \frac{\varepsilon}{r}\), где
IКЗ ― сила тока короткого замыкания, [A]б
ε ― ЭДС источника тока [В],
r ― внутреннее сопротивление источника ЭДС [Ом].
Заряженные частицы, перемещаясь в электрической цепи, совершают работу. Работа силы тока равна:
A = IUt, где
A ― работа силы тока, [Дж],
I ― сила тока в цепи [А],
U ― напряжение в цепи [В],
t ― время, за которое совершается работа, [c]. {2}}{R}\)
{2}}{R}\)
Согласование цепи — настройка сопротивления цепи, обеспечивающая оптимальную передачу энергии от и источника к приемнику путем преобразования выходного сопротивления источника или входного сопротивления приемника.
То есть R = r. При абсолютном согласовании выделяемая цепью тепловая мощность максимальна.
Возможно только при использовании реостата – резистора переменного (настраиваемого) сопротивления.
Для измерения силы тока в цепи или на отдельном участке цепи используется амперметр, а для измерения напряжения ― вольтметр. При этом амперметр (А) должен подключаться к цепи последовательно (поскольку при последовательном соединении сила тока на всех участках цепи одинакова), ведь его сопротивление крайне мало, а вольтметр (V) должен подключаться параллельно (так как при этом соединении на всех участках цепи одинаково напряжение), ведь его сопротивление стремиться к бесконечности.
Пример подключения амперметра и вольтметра к электрической цепи:
Полупроводниковый диод – элемент электрической цепи, пропускающий ток только в одном направлении, то есть имеющий близкое к нулю сопротивление при протекании тока в прямом направлении, и близкое к бесконечности – при протекании тока в обратном направлении.
Контур площадью 2 м2 и сопротивлением 0,003 Ом находится в однородном поле
Условие задачи:
Контур площадью 2 м2 и сопротивлением 0,003 Ом находится в однородном поле, магнитная индукция которого возрастает на 0,5 мТл за 1 с. Определить максимальное количество теплоты, выделяющееся в контуре за 1 час.
Задача №8.4.46 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S=2\) м2, \(R=0,003\) Ом, \(\Delta B=0,5\) мТл, \(\Delta t=1\) с, \(\tau=1\) ч, \(Q-?\)
Решение задачи:
Количество теплоты \(Q\), выделяющееся в контуре за время \(\tau\) при протекании по нему электрического тока, можно определить по такой формуле:
\[Q = {I^2}R\tau \;\;\;\;(1)\]
Силу индукционного тока в контуре \(I\) будем искать, используя закон Ома:
\[I = \frac{{\rm E_i}}{R}\;\;\;\;(2)\]
Подставим выражение (2) в формулу (1), тогда:
\[Q = \frac{{{\rm E}_i^2}}{R}\tau \;\;\;\;(3)\]
Согласно закону Фарадея для электромагнитной индукции, ЭДС индукции, возникающая в контуре при изменении магнитного потока, пересекающего этот контур, равна по модулю скорости изменения магнитного потока. 2} \cdot 0,003}} = 1,2\;Дж\]
2} \cdot 0,003}} = 1,2\;Дж\]
Ответ: 1,2 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.4.45 Горизонтальные рельсы находятся на расстоянии 0,3 м друг от друга. На них лежит
8.4.47 Плоский виток провода расположен перпендикулярно однородному магнитному полю
8.4.48 Короткозамкнутая катушка, состоящая из 1000 витков проволоки, помещена в магнитное поле
Энергия
ЭнергияЭДС индукции и энергия
Проблема:
Вертикально ориентированная квадратная проволочная петля падает из области, где
магнитное поле B горизонтальное, однородное и перпендикулярное плоскости
петля, в область, где поле равно нулю. Пусть длина каждой стороны
быть s, а диаметр проволоки быть d. Удельное сопротивление провода ρ R а плотность проволоки ρ м . Если петля достигает терминала
скорости, пока его верхний сегмент еще находится в области магнитного поля, найти
выражение для конечной скорости.
Решение:
- Концепты:
ЭДС индукции ε = -∂flux/∂t, закон Ома, энергия сохранение. - Рассуждение:
Когда петля опускается, поток через петлю изменяется, и индуцируется ЭДС. в петле. Это приводит к тому, что в петле течет ток, и энергия рассеивается в виде тепла. Если петля падает с постоянной скорость, то скорость, с которой гравитационная потенциальная энергия уменьшение должно равняться скорости, с которой выделяется тепло. - Детали расчета:
|ЭДС| = |dпоток/dt| = Bsdy/dt, I = э.д.с./R. Здесь dy/dt — скорость с которой падает петля.
При достижении предельной скорости: I 2 R = ЭДС 2 /R = Fv клемма = MGV терминал .
Энергия, рассеиваемая в проводе в единицу времени, равна гравитационной потери потенциальной энергии в единицу времени.
(Bsv терминал ) 2 /R = мгв терминал , v терминал = мгР/(Вс) 2 .
R = ρ R 16s/πd 2 , m = ρ m πd 2 s, v терминал = 16g ρ m ρ R /В 2 .
Проблема:
Проводящая кольцевая петля из проволоки диаметром d, удельное сопротивление ρ и массовая плотность ρ м падает с большой высоты h в магнитном поле с компонентой B з = В 0 (1 + кз), где k — некоторая константа. Петля диаметром D всегда параллельно плоскости х-у. Сопротивлением воздуха пренебречь и найти конечная скорость контура.
Решение:
- Концепты:
ЭДС индукции ε = -∂F/∂t, Закон Ома, сохранение энергии. - Рассуждение:
Когда петля падает через неоднородное магнитное поле, поток через петля меняется, и в петле индуцируется ЭДС. Это вызывает ток течет по контуру, а энергия рассеивается в виде тепла. Если петля падает с постоянной скоростью, то скорость, с которой уменьшение потенциальной гравитационной энергии должно равняться скорости, с которой тепло сгенерировано.
- Детали расчета:
Гравитационная сила направлена в направлении -z, F g = -mg к .
Магнитный поток через контур F = BA = B
ЭДС, индуцированная в контуре, равна ε = -∂F/∂t. = -(B 0 kπD 2 /4)dz/dt.
Ток, протекающий в контуре, равен I = |ε|/R.
Скорость, с которой выделяется тепло, равна I 2 р. Курс, по которому гравитационная потенциальная энергия убывает мг dz/dt
Когда dz/dt = -v t , (v t = конечная скорость), тогда I 2 R = -mg dz/dt = mgv t .
Тогда |ε| 2 /R = мгв т , [B 0 2 k 2 π 2 D 4 /(16R)]v t
м = ρ м V = ρ м (πd 2 /4)πD. Для проволоки R = ρ длина/площадь = ρ 4Д/д 2 .
v t = 16ρ m (πd 2 /4)πDg(ρ 4D/d 2 )/(B 0 2 k 2 π 2 D 4 ) = 16ρ м гρ/(B 0 2 k 2 D 2 ).
Задача:
Тонкий диск из обычного металла с электропроводностью σ имеет радиус R и толщину d. Он фиксируется в перпендикулярное магнитное поле B(t)
(a) Найдите вектор плотности тока j (r) в точке
расстояние r от оси диска.
(b) Определить энергию/время, переданное диску
поле. Что становится с этой энергией?
(c) Предположим, что константа
a становится отрицательным, т. е. что
а —>
-α. Как ваши результаты в
части (а) и (б) меняются?
е. что
а —>
-α. Как ваши результаты в
части (а) и (б) меняются?
Решение:
- Концепты:
- Рассуждение:
Разделите диск на концентрические кольца. Магнитный поток через Кольцо меняется со временем. Это изменение потока вызывает ЭДС. Поскольку кольцо имеет конечное сопротивление, по кольцу течет ток. - Детали
расчет:
Для кольца с внутренним радиусом r и внешним радиусом r + dr имеем
ε(r) = -∂F/∂t = ЭДС индукции, ∂F/∂t = (∂B/∂t)пr 2 = αпр 2 .
E = αпr 2 /(2пr) = ар/2. Если α положителен, E указывает на направление -φ.
j = σ E , j(r) = σαr/2.
(b) Ток, текущий в кольце радиусом r, равен j(r)*d*dr. скорость, с которой энергия доставляется кольцу, равна ε(r)*j(r)*d*dr = (dпr
Скорость, с которой энергия доставляется на диск, равна
(дпσα 2 /2)∫ 0 Р р 3 др = dпσα 2 R 4 /8. Эта энергия преобразуется в тепловую энергию.
Эта энергия преобразуется в тепловую энергию.
(с) Е и j теперь укажите на направление φ. Мощность, подаваемая на диск такой же.
Задача:
Однородное магнитное поле Б = Б 0 к точки в направлении z. Частица с массой m и зарядом
q движется с кинетической энергией E
При t = 0 напряженность магнитного поля начинает изменяться
медленно, так что при t = t 1 будет B = B 1 k .
Пренебречь излучением.
(a) Чему равен радиус орбиты R 0 частицы при t < 0 в
условия B 0 и E 0 ?
(б) Предполагая, что радиус R орбиты частицы не меняется
заметно, пока частица совершает один оборот, какова кинетическая
энергия E 1 частицы в момент времени t 1 в пересчете на B 0 ,
B 1 и E 0 ?
 В
время t = 0 положение и скорость частицы равны R 0 =
(0, R 0 , 0) и v 0 = (v 0 , 0, 0).
В
время t = 0 положение и скорость частицы равны R 0 =
(0, R 0 , 0) и v 0 = (v 0 , 0, 0). (c) Напишите уравнения движения Ньютона для компонентов скорости v x , v y и v я .
(d) Постройте уравнение движения для z = v x + iv y и Найди решение.
(e) Найдите выражения для v
Решение:
- Концепты:
Закон Фарадея, ЭДС индукции, затухающие колебания - Рассуждение:
Изменяющийся магнитный поток индуцирует ЭДС, которая изменяет кинетическую энергию частица. - Детали расчета:
(а) R 0 = mv/(qB 0 ) = (2mE 0 ) ½ / (qB 0 )
б) Предположим, что радиус R орбиты частицы не меняется заметно, пока частица совершает один оборот. Тогда кинетическая энергия частицы изменится на
Тогда кинетическая энергия частицы изменится на
Время одного оборота T = 2πR/v,
поэтому dE/dt = ΔE/T = (qvR/2)(дБ/dt) = (qmv 2 R/(2mv))(дБ/dt) = (1/B)(дБ/dt)E.
(Мы использовали R = mv/(qB), qR/(mv) = 1/B, ½mv 2 = E.)
dE/E = дБ/В, ln(E 1 ) = ln(B 1 E 0 /B 0 ), Е 1 = В 1 Е 0 /В 0 .
(c) F x = mdv x /dt = qv y B 0 — mv x /τ, F y = mdv y /dt = -qv x B 0 — mv y /τ, F z = 0,
(d) dz/dt = -i(qB
= -i[(qB 0 /m)z — (i/τ)]z = gz,
где g = -i[(qB 0 /m)z — (i/τ).
z(t) = z 0 exp(gt) = z 0 exp(-t/τ) exp(-iωt), где ω = qB 0 /м.
(e) Re(z(t)) = v x (t) = v 0 exp(-t/τ) cos(ωt), Im(z(t)) = v y (t) = -v 0 exp(-t/τ) sin(ωt).
x(t) = ∫ 0 t v 0 exp(-t’/τ) cos(ωt’) dt’
= v 0 [exp(-t/τ)[- cos(ωt)/τ + ω sin(ωt)] + 1/τ]/[1/τ 2 + ω 2 ]
y(t) = -∫ 0 t v 0 exp(-t’/τ) sin(ωt’) dt’ + Р 0
= -v 0 [exp(t/τ)[ -sin(ωt)/τ — ω cos(ωt)] + ω] /[1/τ 2 + ω 2 ] + R 0
Аст —> бесконечность, x(t) —> x ∞ = (v 0 /τ)/[1/τ 2 + ω 2 ], y(t) —> г ∞ = -v 0 ω/[1/τ 2 + ω 2 ] + R 0
Частица закручивается по спирали в точку (x ∞ , y ∞ ).
Задача:
Тонкая металлическая квадратная рамка массой m, электрическая
сопротивления R, а сторона а вращается вокруг оси, перпендикулярной равномерному
магнитное поле В, как показано на рисунке. Изначально квадратная рамка
вращается с частотой ω 0 .
(a) Определите среднюю потерю энергии за цикл из-за джоулевого нагрева.
(b) Определить время, необходимое для замедления частоты вращения.
до 1/e от его первоначального значения. (Предположим, что дробное изменение кадра
частота вращения за цикл небольшая.)
Решение:
- Концепты:
ЭДС индукции e = -∂F/∂t, Закон Ома, сохранение энергии - Рассуждение:
Изменяющийся магнитный поток создает в рамке ЭДС. ЭДС вызывает протекающий ток, производящий джоулев нагрев. Кинетическая энергия преобразуется в тепловую энергию. - Детали расчета:
(а) (единицы СИ)
Магнитный поток через рамку Ва 2 cosθ. Угол меняется, dθ/dt
= ш.
Угол меняется, dθ/dt
= ш.
Индуцированная ЭДС из-за этого изменяющегося потока равна -Ba 2 sinθ ω.
Ток, протекающий в рамке, определяется как I = Ba 2 sinθ ω/R (без учета собственной индуктивности контура).
Количество кинетической энергии, преобразованной в тепловую энергию в единицу времени, равно P = B 2 a 4 sin 2 θ ω 2 /R.
Потери энергии за цикл (при условии, что ω изменяется незначительно):
∫ 0 T Pdt = ∫ 0 2π (P/ω)dθ = πω B 2 a 4 /R = ΔE.
Начальные средние потери энергии за цикл из-за джоулевого нагрева: πω 0 B 2 a 4 /R.= ΔE/T = B 2 a 4 ω 2 /(2R).
(б)
= B 2 a 4 ω 2 /2R = -dE/dt.
Е = ½Iω 2 , = ма 2 ω 2 /12, ω 2 = 12E/ma 2 , dE/dt = -E 6B 2 a 2 /(Rm).
E = E 0 exp[-6B 2 a 2 t/(Rm)], t (1/e) = Rm/(6B 2 a 2 ).
13.3 ЭДС движения — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Определять величину ЭДС индукции в проводе, движущемся с постоянной скоростью через магнитное поле. поле
- Обсудите примеры, использующие ЭДС движения, такие как рельсовая пушка и привязанный спутник
Магнитный поток зависит от трех факторов: силы магнитного поля, площади, через которую проходят силовые линии, и ориентации поля относительно площади поверхности. Если какая-либо из этих величин изменяется, происходит соответствующее изменение магнитного потока. До сих пор мы рассматривали только изменения потока из-за изменяющегося поля. Теперь мы рассмотрим другую возможность: изменение области, через которую проходят силовые линии, включая изменение ориентации области.
Два примера такого изменения потока представлены на рис. 13.11. В части (а) поток через прямоугольную петлю увеличивается по мере ее перемещения в магнитное поле, а в части (б) поток через вращающуюся катушку изменяется в зависимости от угла θθ.
Рисунок 13.11 а) изменение магнитного потока по мере того, как петля движется в магнитном поле; б) изменение магнитного потока при вращении петли в магнитном поле.
Теперь давайте посмотрим на проводящий стержень, втянутый в цепь, изменяющую магнитный поток. Площадь, ограниченная схемой «MNOP» на рисунке 13.12, равна лк и перпендикулярно магнитному полю, поэтому мы можем упростить интегрирование уравнения 13.1 в произведение магнитного поля и площади. Таким образом, магнитный поток через открытую поверхность равен
Φm=Blx.Φm=Blx.13,4
Поскольку B и l постоянны, а скорость стержня равна v=dx/dt, v=dx/dt, теперь мы можем переформулировать закон Фарадея (уравнение 13. 2) для величины ЭДС с точки зрения движущегося токопроводящего стержня как
2) для величины ЭДС с точки зрения движущегося токопроводящего стержня как
13,5
Ток, индуцированный в цепи, равен ЭДС, деленной на сопротивление, или
I=BlvR.I=BlvR.
Кроме того, направление ЭДС индукции удовлетворяет закону Ленца, в чем можно убедиться, рассмотрев рисунок.
Этот расчет ЭДС, вызванной движением, не ограничивается стержнем, движущимся по токопроводящим рельсам. Используя F→=qv→×B→F→=qv→×B→ в качестве отправной точки, можно показать, что ε=−dΦm/dtε=−dΦm/dt выполняется для любого изменения потока, вызванного движением проводник. Мы видели в законе Фарадея, что ЭДС, индуцированная изменяющимся во времени магнитным полем, подчиняется тому же соотношению, которое является законом Фарадея. Таким образом, закон Фарадея справедливо для всех изменений потока , независимо от того, вызваны ли они изменяющимся магнитным полем, движением или их комбинацией.
Рисунок
13. 12
Проводящий стержень толкают вправо с постоянной скоростью. Результирующее изменение магнитного потока индуцирует ток в цепи.
12
Проводящий стержень толкают вправо с постоянной скоростью. Результирующее изменение магнитного потока индуцирует ток в цепи.
С точки зрения энергии, F→aF→a производит мощность Fav,Fav, а резистор рассеивает мощность I2RI2R. Поскольку стержень движется с постоянной скоростью, приложенная сила FaFa должна уравновешивать магнитную силу Fm=IlBFm=IlB, действующую на стержень, когда по нему протекает индуцированный ток я . Таким образом, произведенная мощность равна
Fav=IlBv=BlvR·lBv=l2B2v2R.Fav=IlBv=BlvR·lBv=l2B2v2R.13,6
Рассеиваемая мощность равна
P=I2R=(BlvR)2R=l2B2v2RP.P=I2R=(BlvR)2R=l2B2v2R.13,7
При соблюдении принципа сохранения энергии производимая и рассеиваемая мощности равны.
Этот принцип можно увидеть в работе рельсовой пушки. Рельсовая пушка представляет собой электромагнитную метательную пусковую установку, в которой используется устройство, подобное показанному на рис. 13. 12, схематично показанное на рис. 13.13. Проводящий стержень заменяется снарядом или оружием для стрельбы. До сих пор мы слышали только о том, как движение вызывает ЭДС. В рельсовой пушке оптимальное отключение/уменьшение магнитного поля уменьшает поток между рельсами, вызывая протекание тока в стержне (якоре), который удерживает снаряд. Этот ток через якорь испытывает магнитную силу и движется вперед. Рельсовые пушки, однако, не используются широко в вооруженных силах из-за высокой стоимости производства и больших токов: требуется почти один миллион ампер для производства энергии, достаточной для того, чтобы рельсовая пушка была эффективным оружием.
12, схематично показанное на рис. 13.13. Проводящий стержень заменяется снарядом или оружием для стрельбы. До сих пор мы слышали только о том, как движение вызывает ЭДС. В рельсовой пушке оптимальное отключение/уменьшение магнитного поля уменьшает поток между рельсами, вызывая протекание тока в стержне (якоре), который удерживает снаряд. Этот ток через якорь испытывает магнитную силу и движется вперед. Рельсовые пушки, однако, не используются широко в вооруженных силах из-за высокой стоимости производства и больших токов: требуется почти один миллион ампер для производства энергии, достаточной для того, чтобы рельсовая пушка была эффективным оружием.
Рисунок 13.13 Ток через два рельса толкает токопроводящий снаряд вперед за счет создаваемой магнитной силы.
Мы можем рассчитать индуцированную движением ЭДС с помощью закона Фарадея даже при отсутствии фактической замкнутой цепи . Мы просто представляем замкнутую область, граница которой включает в себя движущийся проводник, вычисляем ΦmΦm, а затем находим ЭДС по закону Фарадея. Например, мы можем позволить движущемуся стержню на рис. 13.14 быть одной стороной воображаемой прямоугольной области, представленной пунктирными линиями. Площадь прямоугольника лк , поэтому магнитный поток через него равен Φm=Blx.Φm=Blx. Дифференцируя это уравнение, получаем
Например, мы можем позволить движущемуся стержню на рис. 13.14 быть одной стороной воображаемой прямоугольной области, представленной пунктирными линиями. Площадь прямоугольника лк , поэтому магнитный поток через него равен Φm=Blx.Φm=Blx. Дифференцируя это уравнение, получаем
13,8
, что совпадает с определенной нами ранее разностью потенциалов между концами стержня.
Рисунок 13.14 С показанным воображаемым прямоугольником мы можем использовать закон Фарадея для расчета ЭДС индукции в движущемся стержне.
ЭДС движения в слабом магнитном поле Земли обычно не очень велики, иначе мы заметили бы напряжение вдоль металлических стержней, таких как отвертка, во время обычных движений. Например, простой расчет ЭДС движения стержня длиной 1,0 м, движущегося со скоростью 3,0 м/с перпендикулярно полю Земли, дает
ЭДС=Bℓv=(5,0×10-5T)(1,0м)(3,0м/с)=150мкВ.ЭДС=Bℓv=(5,0×10-5T)(1,0м)(3,0м/с)=150мкВ.
Это небольшое значение соответствует опыту. Однако есть эффектное исключение. В 1992 и 1996 годах с помощью космического корабля «Шаттл» были предприняты попытки создать большие ЭДС движения. Привязанный спутник должен был быть выпущен по проводу длиной 20 км, как показано на рис. 13.15, для создания ЭДС 5 кВ за счет движения с орбитальной скоростью через поле Земли. Эту ЭДС можно было бы использовать для преобразования части кинетической и потенциальной энергии шаттла в электрическую энергию, если бы удалось создать полную цепь. Чтобы завершить цепь, неподвижная ионосфера должна была обеспечить обратный путь, по которому мог течь ток. (Ионосфера — это разреженная и частично ионизированная атмосфера на орбитальных высотах. Она проводит ток из-за ионизации. Ионосфера выполняет ту же функцию, что и неподвижные рельсы и соединительный резистор на рис. 13.13, без которых не было бы полной цепи.) на ток в кабеле за счет магнитной силы F=IℓBsinθF=IℓBsinθ совершает работу, уменьшающую кинетическую и потенциальную энергию челнока и позволяющую преобразовать ее в электрическую энергию. Оба теста оказались неудачными. В первом кабель болтался и его можно было протянуть только на пару сотен метров; во втором трос оборвался при почти полном вытягивании. Пример 13.4 указывает на принципиальную возможность.
Оба теста оказались неудачными. В первом кабель болтался и его можно было протянуть только на пару сотен метров; во втором трос оборвался при почти полном вытягивании. Пример 13.4 указывает на принципиальную возможность.
Рисунок 13.15 ЭДС движения как преобразование электроэнергии для космического челнока послужила мотивом для эксперимента с привязанным спутником. Было предсказано, что ЭДС напряжением 5 кВ будет индуцироваться в 20-километровом тросе при движении с орбитальной скоростью в магнитном поле Земли. Цепь завершается обратным путем через стационарную ионосферу.
Пример 13,4
Расчет большой ЭДС движения объекта на орбите
Рассчитайте ЭДС движения вдоль проводника длиной 20,0 км, движущегося с орбитальной скоростью 7,80 км/с перпендикулярно магнитному полю Земли 5,00×10-5T5,00×10-5T.Стратегия
Это отличный пример использования уравнения движения ε=Bℓv.ε=Bℓv.Раствор
Ввод заданных значений в ε=Bℓvε=Bℓv дает ε=Bℓv=(5,00×10-5Т)(2,00×104м)(7,80×103м/с)=7,80×103В. /с)=7,80×103 В.
/с)=7,80×103 В.
Значение
Полученное значение превышает измеренное напряжение 5 кВ для эксперимента с челноком, поскольку фактическое орбитальное движение троса не перпендикулярно полю Земли. Значение 7,80 кВ — это максимальная ЭДС, полученная при θ=90°θ=90°, поэтому sinθ=1.sinθ=1.Пример 13,5
Металлический стержень, вращающийся в магнитном поле
В части (а) рисунка 13.16 показан металлический стержень OS , вращающийся в горизонтальной плоскости вокруг точки O . Стержень скользит по проволоке, образующей дугу окружности PST радиусом r . Система находится в постоянном магнитном поле B→B→, которое направлено за пределы страницы. а) Если стержень вращать с постоянной угловой скоростью ωω, какова сила тока I в замкнутом контуре ОПСО ? Предположим, что резистор R обеспечивает все сопротивление в замкнутом контуре. б) Вычислите работу, совершаемую вами при вращении стержня в единицу времени, и покажите, что она равна мощности, рассеиваемой на резисторе.
б) Вычислите работу, совершаемую вами при вращении стержня в единицу времени, и покажите, что она равна мощности, рассеиваемой на резисторе.Рисунок 13.16 а) Конец вращающегося металлического стержня скользит по круглой проволоке в горизонтальной плоскости. (б) Индуцированный ток в стержне. (c) Магнитная сила на бесконечно малом отрезке тока.
Стратегия
Магнитный поток представляет собой произведение магнитного поля на площадь четверти круга или A=r2θ/2.A=r2θ/2. При нахождении ЭДС по закону Фарадея все переменные постоянны во времени, кроме θθ, при этом ω=dθ/dt.ω=dθ/dt. Чтобы рассчитать работу в единицу времени, мы знаем, что это связано с произведением крутящего момента на угловую скорость. Крутящий момент рассчитывается путем знания силы, действующей на стержень, и интегрирования ее по длине стержня.Решение
- Из геометрии площадь петли OPSO : A=r2θ2.A=r2θ2.
 Следовательно, магнитный поток через петлю равен
Следовательно, магнитный поток через петлю равенΦm=BA=Br2θ2.Φm=BA=Br2θ2.
Дифференцируя по времени и используя ω=dθ/dt, ω=dθ/dt, имеемε=|dΦmdt|=Br2ω2.ε=|dΦmdt|=Br2ω2.
При делении на сопротивление R контура это дает величину индуцированного токаI=εR=Br2ω2R.I=εR=Br2ω2R.
По мере увеличения θθ увеличивается и поток через контур из-за B→.B→. Чтобы противодействовать этому увеличению, магнитное поле из-за индуцированного тока должно быть направлено на страницу в области, ограниченной петлей. Следовательно, как показано в части (b) рис. 13.16, ток циркулирует по часовой стрелке. - Вы вращаете стержень, прикладывая к нему крутящий момент. Поскольку стержень вращается с постоянной угловой скоростью, этот крутящий момент равен и противоположен крутящему моменту, действующему на ток в стержне исходным магнитным полем. Магнитная сила на бесконечно малом отрезке длиной 90 639 d x 90 640, показанном в части (c) рис. 13.16, равна dFm=IBdx, dFm=IBdx, поэтому магнитный момент на этом отрезке равен
dτm=x·dFm=IBxdx.
Тогда чистый магнитный момент на стержне равен dτm=x·dFm=IBxdx.
dτm=x·dFm=IBxdx.τm=∫0rdτm=IB∫0rxdx=12IBr2.τm=∫0rdτm=IB∫0rxdx=12IBr2.
Крутящий момент ττ, который вы прилагаете к стержню, равен и противоположен τm, τm, а работа, которую вы совершаете, когда стержень поворачивается на угол dθdθ, равна dW=τdθ.dW=τdθ. Следовательно, работа в единицу времени, которую вы совершаете над стержнем, равнаdWdt=τdθdt=12IBr2dθdt=12(Br2ω2R)Br2ω=B2r4ω24R,dWdt=τdθdt=12IBr2dθdt=12(Br2ω2R)Br2ω=B2r4ω24R,
где мы заменили на . Мощность, рассеиваемая на резисторе, равна P=I2RP=I2R, что можно записать какP=(Br2ω2R)2R=B2r4ω24RP.P=(Br2ω2R)2R=B2r4ω24R.
Поэтому мы видим, чтоP=dWdt.P=dWdt.
Следовательно, мощность, рассеиваемая на резисторе, равна работе, совершаемой в единицу времени при вращении стержня.
Значение
Альтернативный способ рассмотрения ЭДС индукции из закона Фарадея состоит в том, чтобы интегрировать ее в пространстве, а не во времени. Однако решение будет таким же. ЭДС движения
Однако решение будет таким же. ЭДС движения|ε|=∫Bvdl.|ε|=∫Bvdl.
Скорость можно записать как произведение угловой скорости на радиус, а дифференциальную длину записать как 9dA=BAcosθ.
По закону Фарадея ЭДС, индуцированная в катушке, равна
Постоянная угловая скорость равна ω=dθ/dt.ω=dθ/dt. Угол θθ представляет изменение во времени угловой скорости или ωtωt. Это изменяет функцию на временное пространство, а не на θθ. Следовательно, ЭДС индукции изменяется синусоидально со временем согласно
ε=ε0sinωt,ε=ε0sinωt,
, где ε0=NBAω.ε0=NBAω.
Значение
Если бы напряженность магнитного поля или площадь петли также менялись со временем, эти переменные нельзя было бы извлечь из производной по времени, чтобы упростить решение, как показано на рисунке. Этот пример является основой для электрического генератора, поскольку мы дадим полное обсуждение в разделе «Электрические генераторы и обратная ЭДС».Проверьте свое понимание 13,4
Ниже показан стержень длиной l , который вращается против часовой стрелки вокруг оси через O под действием крутящего момента mg→.




 Эта энергия преобразуется в тепловую энергию.
Эта энергия преобразуется в тепловую энергию.  Тогда кинетическая энергия частицы изменится на
Тогда кинетическая энергия частицы изменится на 

 Угол меняется, dθ/dt
= ш.
Угол меняется, dθ/dt
= ш. 
 Следовательно, магнитный поток через петлю равен
Следовательно, магнитный поток через петлю равен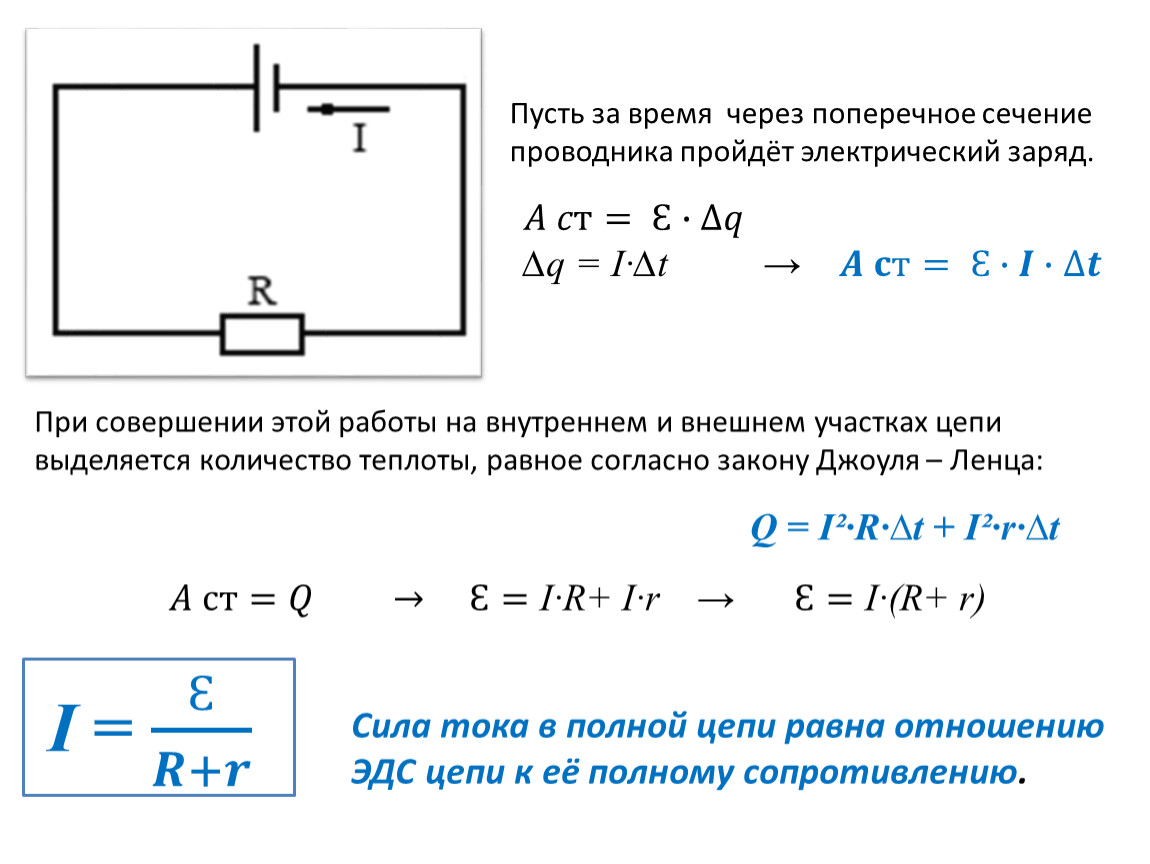 dτm=x·dFm=IBxdx.
dτm=x·dFm=IBxdx.