Единица Измерения Механического Напряжения И Давления В Системе Единиц ‘метр- Тонна- Секунда 5 Букв
Решение этого кроссворда состоит из 5 букв длиной и начинается с буквы П
Ниже вы найдете правильный ответ на Единица измерения механического напряжения и давления в системе единиц «метр- тонна- секунда 5 букв, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.
ответ на кроссворд и сканворд

ПЬЕЗА
предыдущий следующий
ты знаешь ответ ?
ответ:
связанные кроссворды
- Пьеза
- Единица давления в системе единиц мтс 5 букв
- Ед.
 давления и механическ. напряжен 5 букв
давления и механическ. напряжен 5 букв
похожие кроссворды
- Единица давления и механического напряжения
- Единица давления и механического напряжения в мтс системе единиц
- Кратная единица давления и механического напряжения в мтс системе единиц
- (единица длины) единица измерения длины 6 букв
- (единица измерения) единица кинематической вязкости 5 букв
- (единица длины) британская и американская единица измерения расстояния 4 буквы
- Действия механического манипулятора
- Часть механического прицела в виде щитка с прорезью или отверстием
- Герой никиты михалкова в фильме «неоконченная пьеса для механического пианино»
Паскаль (единица измерения) — Вики
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 сентября 2021 года; проверки требуют 6 правок.
Перейти к навигацииПерейти к поиску
У этого термина существуют и другие значения, см. Паскаль (значения).
Паска́ль (русское обозначение:
Паскаль равен давлению, вызываемому силой, равной одному ньютону, равномерно распределённой по нормальной к ней поверхности площадью один квадратный метр: 1 Па = 1 Н·м−2 (т. е. 1 Па = 1 Н/м2).
С основными единицами СИ паскаль связан следующим образом: 1 Па = 1 кг·м−1·с−2 (т. е. 1 кг/(м·с2) ).
В СИ паскаль также является единицей измерения механического напряжения, модулей упругости, модуля Юнга, объёмного модуля упругости, предела текучести, предела пропорциональности, сопротивления разрыву, сопротивления срезу, звукового давления, осмотического давления, летучести (фугитивности)
В соответствии с общими правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы паскаль пишется со строчной буквы, а её обозначение — с заглавной. Такое написание обозначения сохраняется и в обозначениях других производных единиц, образованных с использованием паскаля. Например, обозначение единицы динамической вязкости записывается как Па·с.
Единица названа в честь французского физика и математика Блеза Паскаля. Впервые наименование было введено во Франции декретом о единицах в 1961 году
Содержание
- 1 Кратные и дольные единицы
- 2 Сравнение с другими единицами измерения давления
- 3 Примечания
- 4 Ссылки
Кратные и дольные единицы
Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 Па | декапаскаль | даПа | daPa | 10−1 Па | деципаскаль | дПа | |
| 102 Па | гектопаскаль | гПа | hPa | 10−2 Па | сантипаскаль | сПа | cPa |
| 103 Па | килопаскаль | кПа | kPa | 10−3 Па | миллипаскаль | мПа | mPa |
| 106 Па | мегапаскаль | МПа | MPa | 10−6 Па | микропаскаль | мкПа | µPa |
| 109 Па | гигапаскаль | ГПа | GPa | 10−9 Па | нанопаскаль | нПа | nPa |
| 1012 Па | терапаскаль | ТПа | TPa | 10−12 Па | пикопаскаль | пПа | pPa |
| 1015 Па | петапаскаль | ППа | PPa | 10−15 Па | фемтопаскаль | фПа | fPa |
| 1018 Па | эксапаскаль | ЭПа | EPa | 10−18 Па | аттопаскаль | аПа | aPa |
| 1021 Па | зеттапаскаль | ЗПа | ZPa | 10−21 Па | зептопаскаль | зПа | zPa |
| 1024 Па | иоттапаскаль | ИПа | YPa | 10−24 Па | иоктопаскаль | иПа | yPa |
| рекомендовано к применению применять не рекомендуется | |||||||
Сравнение с другими единицами измерения давления
| Паскаль (Pa, Па) | Бар (bar, бар) | Техническая атмосфера (at, ат) | Физическая атмосфера (atm, атм) | Миллиметр ртутного столба (мм рт.  ст., mm Hg, Torr, торр) ст., mm Hg, Torr, торр) | Миллиметр водяного столба (мм вод. ст., mm H2O) | Фунт-сила на квадратный дюйм (psi) | |
|---|---|---|---|---|---|---|---|
| 1 Па | 1 | 10−5 | 1,01972⋅10−5 | 9,8692⋅10−6 | 7,5006⋅10−3 | 0,101972 | 1,4504⋅10−4 |
| 1 бар | 105 | 1 | 1,01972 | 0,98692 | 750,06 | 10197,2 | 14,504 |
| 1 ат | 98066,5 | 0,980665 | 1 | 0,96784 | 735,56 | 104 | 14,223 |
| 1 атм | 101325 | 1,01325 | 1,03323 | 1 | 760 | 10332,3 | 14,696 |
| 1 мм рт. ст. | 133,322 | 1,3332⋅10−3 | 1,3595⋅10−3 | 1,3158⋅10−3 | 1 | 13,595 | 0,019337 |
1 мм вод.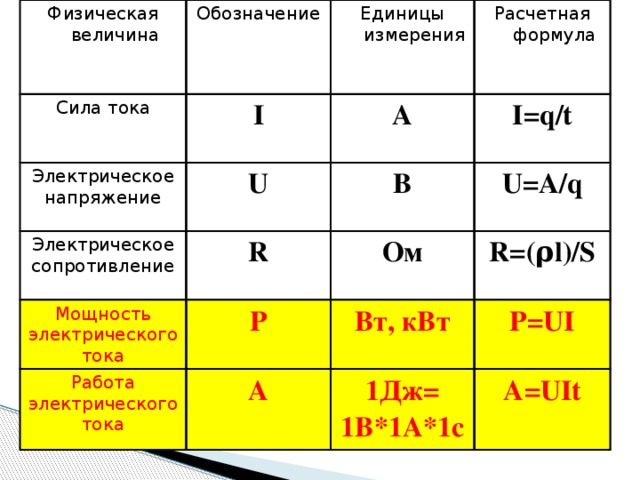 ст. ст. | 9,80665 | 9,80665⋅10−5 | 10-4 | 9,6784⋅10-5 | 0,073556 | 1 | 1,4223⋅10-3 |
| 1 psi | 6894,76 | 0,068948 | 0,070307 | 0,068046 | 51,715 | 703,07 | 1 |
На практике применяют приближённые значения: 1 атм = 0,1 МПа и 1 МПа = 10 атм. 1 мм водяного столба примерно равен 10 Па, 1 мм ртутного столба равен приблизительно 133 Па.
Значение технической атмосферы (at, ат) не равно значению физической атмосферы (atm, атм).
Нормальное атмосферное давление принято считать равным 760 мм ртутного столба, или 101 325 Па (101 кПа).
Размерность единицы давления (Н/м²) совпадает с размерностью единицы плотности энергии (Дж/м³), но с точки зрения физики эти единицы не эквивалентны, так как описывают разные физические свойства. В связи с этим некорректно использовать Паскали для измерения плотности энергии, а давление записывать как Дж/м³.
Примечания
- ↑ Паскаль // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 549—550. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ 1 2 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь справочник. — М.: Издательство стандартов, 1990. — 240 с. — ISBN 5-7050-0118-5.
- ↑ The International System of Units (SI) / Bureau International des Poids et Mesures. — Paris, 2006. — P. 156. — 180 p. — ISBN 92-822-2213-6. (англ.)
Ссылки
- Перевод единиц давления друг в друга Архивная копия от 15 марта 2016 на Wayback Machine
- Таблица перевода единиц измерения давления. Архивная копия от 11 марта 2016 на Wayback Machine
Паскаль (единица измерения)
Википедия
Август 05, 2021
Паска́ль (русское обозначение: Па, международное: Pa) — единица измерения давления (механического напряжения) в Международной системе единиц (СИ).
| Паскаль | |
|---|---|
| Па, Pa | |
| Величина | давление, механическое напряжение |
| Система | СИ |
| Тип | производная |
У этого термина существуют и другие значения, см. Паскаль (значения).
Паскаль равен давлению, вызываемому силой, равной одному ньютону, равномерно распределённой по нормальной к ней поверхности площадью один квадратный метр: 1 Па = 1 Н·м−2 (т. е. 1 Па = 1 Н/м2).
С основными единицами СИ паскаль связан следующим образом: 1 Па = 1 кг·м−1·с−2 (т. е. 1 кг/(м·с2) ).
В СИ паскаль также является единицей измерения механического напряжения, модулей упругости, модуля Юнга, объёмного модуля упругости, предела текучести, предела пропорциональности, сопротивления разрыву, сопротивления срезу, звукового давления, осмотического давления, летучести (фугитивности).
В соответствии с общими правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы паскаль пишется со строчной буквы, а её обозначение — с заглавной. Такое написание обозначения сохраняется и в обозначениях других производных единиц, образованных с использованием паскаля. Например, обозначение единицы динамической вязкости записывается как Па·с.
Единица названа в честь французского физика и математика Блеза Паскаля. Впервые наименование было введено во Франции декретом о единицах в 1961 году.
Содержание
- 1Кратные и дольные единицы
- 2Сравнение с другими единицами измерения давления
- 3Примечания
- 4Ссылки
Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 Па | декапаскаль | даПа | daPa | 10−1 Па | деципаскаль | дПа | dPa |
| 102 Па | гектопаскаль | гПа | hPa | 10−2 Па | сантипаскаль | сПа | cPa |
| 103 Па | килопаскаль | кПа | kPa | 10−3 Па | миллипаскаль | мПа | mPa |
| 106 Па | мегапаскаль | МПа | MPa | 10−6 Па | микропаскаль | мкПа | µPa |
| 109 Па | гигапаскаль | ГПа | GPa | 10−9 Па | нанопаскаль | нПа | nPa |
| 1012 Па | терапаскаль | ТПа | TPa | 10−12 Па | пикопаскаль | пПа | pPa |
| 1015 Па | петапаскаль | ППа | PPa | 10−15 Па | фемтопаскаль | фПа | fPa |
| 1018 Па | эксапаскаль | ЭПа | EPa | 10−18 Па | аттопаскаль | аПа | aPa |
| 1021 Па | зеттапаскаль | ЗПа | ZPa | 10−21 Па | зептопаскаль | зПа | zPa |
| 1024 Па | иоттапаскаль | ИПа | YPa | 10−24 Па | иоктопаскаль | иПа | yPa |
| рекомендовано к применению применять не рекомендуется | |||||||
| Паскаль (Pa, Па) | Бар (bar, бар) | Техническая атмосфера (at, ат) | Физическая атмосфера (atm, атм) | Миллиметр ртутного столба (мм рт.  ст., mm Hg, Torr, торр) ст., mm Hg, Torr, торр) | Миллиметр водяного столба (мм вод. ст., mm H2O) | Фунт-сила на квадратный дюйм (psi) | |
|---|---|---|---|---|---|---|---|
| 1 Па | 1 | 10−5 | 1,01972⋅10−5 | 9,8692⋅10−6 | 7,5006⋅10−3 | 0,101972 | 1,4504⋅10−4 |
| 1 бар | 105 | 1 | 1,01972 | 0,98692 | 750,06 | 10197,2 | 14,504 |
| 1 ат | 98066,5 | 0,980665 | 1 | 0,96784 | 735,56 | 104 | 14,223 |
| 1 атм | 101325 | 1,01325 | 1,03323 | 1 | 760 | 10332,3 | 14,696 |
| 1 мм рт. ст. | 133,322 | 1,3332⋅10−3 | 1,3595⋅10−3 | 1,3158⋅10−3 | 1 | 13,595 | 0,019337 |
1 мм вод. ст. ст. | 9,80665 | 9,80665⋅10−5 | 10-4 | 9,6784⋅10-5 | 0,073556 | 1 | 1,4223⋅10-3 |
| 1 psi | 6894,76 | 0,068948 | 0,070307 | 0,068046 | 51,715 | 703,07 | 1 |
На практике применяют приближённые значения: 1 атм = 0,1 МПа и 1 МПа = 10 атм. 1 мм водяного столба примерно равен 10 Па, 1 мм ртутного столба равен приблизительно 133 Па.
Значение технической атмосферы (at, ат) не равно значению физической атмосферы (atm, атм).
Нормальное атмосферное давление принято считать равным 760 мм ртутного столба, или 101 325 Па (101 кПа).
Размерность единицы давления (Н/м²) совпадает с размерностью единицы плотности энергии (Дж/м³), но с точки зрения физики эти единицы не эквивалентны, так как описывают разные физические свойства. В связи с этим некорректно использовать Паскали для измерения плотности энергии, а давление записывать как Дж/м³.
- // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 549—550. — 672 с. —48 000 экз. — ISBN 5-85270-019-3.
- Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь справочник. — М.: Издательство стандартов, 1990. — 240 с. — ISBN 5-7050-0118-5.
- / Bureau International des Poids et Mesures. — Paris, 2006. — P. 156. — 180 p. — ISBN 92-822-2213-6.(англ.)
Паскаль, единица, измерения, Язык, Следить, Править, Текущая, версия, страницы, пока, не, проверялась, опытными, участниками, может, значительно, отличаться, от, версии, проверенной, июня, 2020, проверки, требуют, правки, Паска, ль, русское, обозначение, Па, м. Paskal edinica izmereniya Yazyk Sledit Pravit Tekushaya versiya stranicy poka ne proveryalas opytnymi uchastnikami i mozhet znachitelno otlichatsya ot versii proverennoj 17 iyunya 2020 proverki trebuyut 2 pravki Paska l russkoe oboznachenie Pa mezhdunarodnoe Pa edinica izmereniya davleniya mehanicheskogo napryazheniya v Mezhdunarodnoj sisteme edinic SI 1 PaskalPa PaVelichina davlenie mehanicheskoe napryazhenieSistema SITip proizvodnayaU etogo termina sushestvuyut i drugie znacheniya sm Paskal znacheniya Paskal raven davleniyu vyzyvaemomu siloj ravnoj odnomu nyutonu ravnomerno raspredelyonnoj po normalnoj k nej poverhnosti ploshadyu odin kvadratnyj metr 1 Pa 1 N m 2 t e 1 Pa 1 N m2 S osnovnymi edinicami SI paskal svyazan sleduyushim obrazom 1 Pa 1 kg m 1 s 2 t e 1 kg m s2 V SI paskal takzhe yavlyaetsya edinicej izmereniya mehanicheskogo napryazheniya modulej uprugosti modulya Yunga obyomnogo modulya uprugosti predela tekuchesti predela proporcionalnosti soprotivleniya razryvu soprotivleniya srezu zvukovogo davleniya osmoticheskogo davleniya letuchesti fugitivnosti 2 V sootvetstvii s obshimi pravilami SI kasayushimisya proizvodnyh edinic nazvannyh po imeni uchyonyh naimenovanie edinicy paskal pishetsya so strochnoj bukvy a eyo oboznachenie s zaglavnoj Takoe napisanie oboznacheniya sohranyaetsya i v oboznacheniyah drugih proizvodnyh edinic obrazovannyh s ispolzovaniem paskalya Naprimer oboznachenie edinicy dinamicheskoj vyazkosti zapisyvaetsya kak Pa s Edinica nazvana v chest francuzskogo fizika i matematika Bleza Paskalya Vpervye naimenovanie bylo vvedeno vo Francii dekretom o edinicah v 1961 godu 2 3 Soderzhanie 1 Kratnye i dolnye edinicy 2 Sravnenie s drugimi edinicami izmereniya davleniya 3 Primechaniya 4 SsylkiKratnye i dolnye edinicy PravitDesyatichnye kratnye i dolnye edinicy obrazuyut s pomoshyu standartnyh pristavok SI Kratnye Dolnyevelichina nazvanie oboznachenie velichina nazvanie oboznachenie101 Pa dekapaskal daPa daPa 10 1 Pa decipaskal dPa dPa102 Pa gektopaskal gPa hPa 10 2 Pa santipaskal sPa cPa103 Pa kilopaskal kPa kPa 10 3 Pa millipaskal mPa mPa106 Pa megapaskal MPa MPa 10 6 Pa mikropaskal mkPa µPa109 Pa gigapaskal GPa GPa 10 9 Pa nanopaskal nPa nPa1012 Pa terapaskal TPa TPa 10 12 Pa pikopaskal pPa pPa1015 Pa petapaskal PPa PPa 10 15 Pa femtopaskal fPa fPa1018 Pa eksapaskal EPa EPa 10 18 Pa attopaskal aPa aPa1021 Pa zettapaskal ZPa ZPa 10 21 Pa zeptopaskal zPa zPa1024 Pa iottapaskal IPa YPa 10 24 Pa ioktopaskal iPa yPa rekomendovano k primeneniyu primenyat ne rekomenduetsyaSravnenie s drugimi edinicami izmereniya davleniya PravitEdinicy davleniya Paskal Pa Pa Bar bar bar Tehnicheskaya atmosfera at at Fizicheskaya atmosfera atm atm Millimetr rtutnogo stolba mm rt st mm Hg Torr torr Millimetr vodyanogo stolba mm vod st mm h3O Funt sila na kvadratnyj dyujm psi 1 Pa 1 10 5 1 01972 10 5 9 8692 10 6 7 5006 10 3 0 101972 1 4504 10 41 bar 105 1 1 01972 0 98692 750 06 10197 2 14 5041 at 98066 5 0 980665 1 0 96784 735 56 104 14 2231 atm 101325 1 01325 1 03323 1 760 10332 3 14 6961 mm rt st 133 322 1 3332 10 3 1 3595 10 3 1 3158 10 3 1 13 595 0 0193371 mm vod st 9 80665 9 80665 10 5 10 4 9 6784 10 5 0 073556 1 1 4223 10 31 psi 6894 76 0 068948 0 070307 0 068046 51 715 703 07 1 Na praktike primenyayut priblizhyonnye znacheniya 1 atm 0 1 MPa i 1 MPa 10 atm 1 mm vodyanogo stolba primerno raven 10 Pa 1 mm rtutnogo stolba raven priblizitelno 133 Pa Znachenie tehnicheskoj atmosfery at at ne ravno znacheniyu fizicheskoj atmosfery atm atm Normalnoe atmosfernoe davlenie prinyato schitat ravnym 760 mm rtutnogo stolba ili 101 325 Pa 101 kPa Razmernost edinicy davleniya N m sovpadaet s razmernostyu edinicy plotnosti energii Dzh m no s tochki zreniya fiziki eti edinicy ne ekvivalentny tak kak opisyvayut raznye fizicheskie svojstva V svyazi s etim nekorrektno ispolzovat Paskali dlya izmereniya plotnosti energii a davlenie zapisyvat kak Dzh m Primechaniya Pravit Paskal Fizicheskaya enciklopediya v 5 t Gl red A M Prohorov M Bolshaya rossijskaya enciklopediya 1992 T 3 Magnitoplazmennyj Pojntinga teorema S 549 550 672 s 48 000 ekz ISBN 5 85270 019 3 1 2 Dengub V M Smirnov V G Edinicy velichin Slovar spravochnik M Izdatelstvo standartov 1990 240 s ISBN 5 7050 0118 5 The International System of Units SI Bureau International des Poids et Mesures Paris 2006 P 156 180 p ISBN 92 822 2213 6 angl Ssylki PravitPerevod edinic davleniya drug v druga Tablica perevoda edinic izmereniya davleniya Istochnik https ru wikipedia org w index php title Paskal edinica izmereniya amp oldid 112264800, Википедия, чтение, книга, библиотека, поиск, нажмите,
истории
, книги, статьи, wikipedia, учить, информация, история, секс, порно, скачать, скачать, sex, seks, porn, porno, скачать, бесплатно, скачать бесплатно, mp3, видео, mp4, 3gp, jpg, jpeg, gif, png, картинка, музыка, песня, фильм, игра, игрыИзмерение механических напряжений с помощью тензометров
Перейти к основному содержаниюБыстрое и надежное измерение механических напряжений и усилий в сборках: измерения деформации и сжатия с помощью тензометров обеспечивают точные результаты сил, действующих на узлы, для структурных испытаний, измерений усталостной прочности и испытаний изделий и материалов.
Для оптимального проектирования компонентов необходимо точное знание типа, направления и величины действующих на них сил. Для их определения к образцу прикладывают тензорезисторы. CSM поддерживает все распространенные типы мостов (четвертные, половинные и полные мосты) с помощью своих измерительных модулей.
- Профили напряжений измерения
- Определите механические нагрузки
- Измерение давления с датчиками
- Измерение сил натяжения и сжатия
- Обеспечить безопасность
- Проверка симуляции
Transducers
CRANE BOOMS, RIE ROD -ROD, или автомобиль A. приложения, в которых действующие силы и механические нагрузки должны часто проверяться на протяжении всего процесса разработки продукта. Они измеряются в ходе дорожных и полевых испытаний или на испытательном стенде. Геометрия исследуемого объекта или доступное общее пространство не всегда позволяют установить дополнительные датчики для измерения силы или кручения. В таких случаях сам объект становится датчиком. Тензорезисторы крепятся непосредственно к компоненту и калибруются без приложения какой-либо нагрузки. Затем компонент повторно устанавливается в систему, где он измеряется в рабочих условиях. Это делается, например, с помощью тяги, на которой измеряются силы растяжения и сжатия.
приложения, в которых действующие силы и механические нагрузки должны часто проверяться на протяжении всего процесса разработки продукта. Они измеряются в ходе дорожных и полевых испытаний или на испытательном стенде. Геометрия исследуемого объекта или доступное общее пространство не всегда позволяют установить дополнительные датчики для измерения силы или кручения. В таких случаях сам объект становится датчиком. Тензорезисторы крепятся непосредственно к компоненту и калибруются без приложения какой-либо нагрузки. Затем компонент повторно устанавливается в систему, где он измеряется в рабочих условиях. Это делается, например, с помощью тяги, на которой измеряются силы растяжения и сжатия.
Измерительные модули CSM STGMM для измерений с помощью тензодатчиков обеспечивают высокое разрешение при возбуждении датчика 5 В и небольшой диапазон измерений. Таким образом, можно легко проводить измерения в рабочих условиях или на испытательном стенде.
При эксплуатационных испытаниях модули тензометрических измерений CSM ECAT STGMM подвергаются экстремальным условиям и точно регистрируют напряжения, возникающие на объекте испытаний. Даже сильные вибрации не снижают надежность измерительных модулей. В соответствии с методом «от дороги до стенда» измеренные значения затем можно легко перенести на стенд для испытаний на усталость. На испытательном стенде используются те же измерительные модули ECAT STGMM, что и ранее при дорожных испытаниях, что позволяет легко сравнивать измеренные данные. С помощью программного обеспечения CSMconfig настройки конфигурации из дорожных испытаний передаются в измерительные модули на испытательном стенде (или наоборот) в виде файлов .dBc или .a2l. Это значительно ускоряет тест за счет сокращения времени настройки.
Даже сильные вибрации не снижают надежность измерительных модулей. В соответствии с методом «от дороги до стенда» измеренные значения затем можно легко перенести на стенд для испытаний на усталость. На испытательном стенде используются те же измерительные модули ECAT STGMM, что и ранее при дорожных испытаниях, что позволяет легко сравнивать измеренные данные. С помощью программного обеспечения CSMconfig настройки конфигурации из дорожных испытаний передаются в измерительные модули на испытательном стенде (или наоборот) в виде файлов .dBc или .a2l. Это значительно ускоряет тест за счет сокращения времени настройки.
С помощью HV STG4 тензометрические измерения могут быть легко реализованы в средах с высоким напряжением, например, при измерении динамических сил транспортного средства, передаваемых на аккумуляторную батарею электромобиля.
Механические нагрузки воздействуют на все компоненты. Для подходящей конструкции усилия должны быть измерены во время разработки — предпочтительно в реальных условиях во время дорожных испытаний.
Экспериментальный анализ напряжения
Розетку тензодатчика можно использовать для анализа кривых напряжения для неизвестного главного направления напряжения.С помощью тензорезисторов можно быстро и надежно проверить рассчитанные механические напряжения в сборках. Для этой цели часто используются четвертьмосты (схема моста Уитстона с одним активным тензодатчиком и тремя резисторами), поскольку их можно реализовать быстро и экономично.
Если известно основное направление главного напряжения, достаточно четвертьмостика.
Если направление главного напряжения неизвестно до измерения, к образцу прикрепляют две-три четверти перемычки в виде розетки. Каждый из трех отдельных тензорезисторов розетки может быть дополнен кабелем завершения четверти моста CSM (K356) до полумоста и, таким образом, легко интегрирован в измерительный модуль STGMM. Благодаря широкому диапазону измерения STGMM можно измерять как очень малые, так и очень большие деформации.
На крупных объектах, таких как строительная техника, требуемые точки измерения часто находятся далеко друг от друга. При использовании ECAT STGMM это не проблема: точки измерения могут находиться на расстоянии до 100 метров друг от друга.
При использовании ECAT STGMM это не проблема: точки измерения могут находиться на расстоянии до 100 метров друг от друга.
Измерение механических нагрузок с помощью датчиков
Если позволяют условия, механические нагрузки можно также измерять с помощью датчиков. Большинство доступных датчиков излучают сигнал без усиления или модификации встроенной электроникой. Очень слабый сигнал, излучаемый датчиком, предъявляет особые требования к используемой технологии измерения. STGMM отвечает этим требованиям, точно обнаруживая даже небольшие напряжения сигнала и обеспечивая требуемое возбуждение датчика.
Если места достаточно, датчики также могут определять механические нагрузки. Таким образом, автомобили оптимально спроектированы для требовательных условий эксплуатации.Сопутствующие товары
Тип STG6 pro BS20 |
Варианты использования0004
Измерение напряжения в высоковольтных батареях
CSM Xplained: Измерение долговечности электромобилей
Инженеры-механики должны уметь считать! Одна из самых важных вещей, которую должен знать инженер-механик, — это базовый анализ напряжений . 4 расчета. Это руководство охватывает все основные аспекты этой области.
4 расчета. Это руководство охватывает все основные аспекты этой области.
Но сначала давайте приступим к основам. Что такое стресс? Напряжение — это величина внутренней силы, которая сохраняется и действует на молекулярном уровне между частицами материала. Напряжение является результатом приложения внешних сил к чему-либо, поэтому оно всегда присутствует во всех вещах на нашей планете, поскольку гравитация создает силу веса для всего, что имеет массу. Все виды и виды сил, приложенных к материалу, создают в нем напряжение, и это напряжение, как правило, невидимо для нашего глаза, поскольку оно происходит на молекулярном уровне. Вот почему напряжение возникает не только из-за приложения внешней нагрузки или силы, но также из-за температурных или химических изменений, которые могут увеличить молекулярную активность материала, или благодаря специальным методам производства, которые обеспечивают своего рода накопление напряжения. во что-то вроде бетона и стекла.
Единственным способом, которым мы можем заметить наличие напряжения, является наблюдение за своего рода деформацией, которая имеет место. Например, когда тяжелоатлет поднимает металлическую штангу, мы можем заметить заметный изгиб по бокам возле весовых пластин. Эта временная деформация называется «упругим напряжением» или деформацией и имеет определенный предел, до которого она остается временной. Если этот предел превышен, деформация становится постоянной, а напряжение называется вязким или пластик стресс. Проще говоря, напряжение — это внутреннее сопротивление тела его деформации, поэтому оно имеет предел, и этот предел определяется молекулярной структурой материала, из которого состоит тело.
Например, когда тяжелоатлет поднимает металлическую штангу, мы можем заметить заметный изгиб по бокам возле весовых пластин. Эта временная деформация называется «упругим напряжением» или деформацией и имеет определенный предел, до которого она остается временной. Если этот предел превышен, деформация становится постоянной, а напряжение называется вязким или пластик стресс. Проще говоря, напряжение — это внутреннее сопротивление тела его деформации, поэтому оно имеет предел, и этот предел определяется молекулярной структурой материала, из которого состоит тело.
Типы напряжений
Существует три типа основных напряжений, которые подразделяются на категории в зависимости от того, как именно они воздействуют на тело, которое их выдерживает, а именно напряжение сжатия, напряжение сдвига и напряжение растяжения.
- Напряжение растяжения — это сопротивление материала разрыву, поэтому оно возникает, когда силы противоположных направлений разрывают его на части.
 Классическим примером напряжения растяжения является игра «перетягивание каната», в которой две команды тянут веревку в стороны.
Классическим примером напряжения растяжения является игра «перетягивание каната», в которой две команды тянут веревку в стороны. - Напряжение сжатия противоположно напряжению растяжения, что означает, что силы сжимают материал. Примером этого является то, что вы сидите на своем стуле, ваш вес давит на стержень стула вниз, а сила сопротивления земли толкает его вверх. Это приводит к возникновению сжимающих напряжений в центре стержня.
- Напряжение сдвига — это сопротивление, создаваемое материалом в определенной точке поперечного сечения, а также сопротивление деформирующим противоположным силам, приложенным к самому себе или объектам/материалам, которые с ним связаны. Примером этого является разрезание листа бумаги ножницами с приложением к его сторонам противоположных сил, которые разрезают бумажный материал в точке поперечного сечения, где создается напряжение сдвига.
Основные расчеты анализа напряжения
Напряжение обозначается буквой «σ» и измеряется в Н/м 2 или Паскаль (Па), который на самом деле является единицей давления в системе СИ. Напряжение сдвига обозначено буквой «τ» для дифференциации. Как ожидается в единицах измерения, напряжение определяется путем деления силы на площадь ее возникновения, и, поскольку эта площадь («А») является либо секционной, либо осевой, основная формула напряжения « σ = F/A ».
Напряжение сдвига обозначено буквой «τ» для дифференциации. Как ожидается в единицах измерения, напряжение определяется путем деления силы на площадь ее возникновения, и, поскольку эта площадь («А») является либо секционной, либо осевой, основная формула напряжения « σ = F/A ».
Путем эксперимента или с помощью программного моделирования мы можем выяснить, когда материал растягивается или сжимается, с помощью формулы деформации, которая выглядит следующим образом: « ε = ΔL/L ». Это деление изменения длины материала на его первоначальную длину. По мере увеличения значения напряжения деформация увеличивается пропорционально до точки предела упругости, где напряжение из упругого становится вязким/пластичным.
Рассчитав напряжение и деформацию, можно рассчитать модуль упругости, который находится по формуле: « Ε = σ/ε ». Это также называется «модулем Юнга» и является мерой жесткости материала.
Другим важным элементом, который мы можем рассчитать в контексте базового анализа напряжений, является «коэффициент Пуассона» (μ) или отношение поперечной деформации к продольной деформации. Это соотношение особенно интересно для анализа конструктивных элементов, таких как балки, плиты и колонны.
Это соотношение особенно интересно для анализа конструктивных элементов, таких как балки, плиты и колонны.
Кроме того, если у нас есть элементы, которые одновременно подвергаются растяжению и сжатию, мы используем формулу напряжения изгиба, которая выглядит следующим образом: « σb = 3 FL/2wt 2 », где F — усилие, L — длина элемента конструкции, w — ширина, t — его толщина. Точно так же для расчета модуля изгиба мы используем формулу « Eb = FL 3 /4wt 3 y », где y — прогиб в точке нагрузки.
Наконец, ни одно руководство по «базовым расчетам напряжения» не будет полным без объяснения того, как рассчитать максимальное напряжение на основе выбранного коэффициента безопасности. Коэффициент запаса находится по формуле « 92 или паскалях (Па). Вместо σ используйте τ для напряжения сдвига.
A = Площадь (может быть как в разрезе, так и по оси)
ΔL = Изменение длины
L = Исходная длина
ε = Деформация
ε t = поперечная деформация
ε l = продольная или осевая деформация
L = Длина элемента конструкции
w = Ширина
t = Толщина
L = длина элемента конструкции
w = ширина
t = толщина
y = прогиб в точке приложения нагрузки
Ys = предел текучести материала
Ds = расчетное напряжение
fs = Коэффициент запаса прочности (FoS)
Механическая ячейка — PMC
- Список журналов
- Рукописи авторов HHS
- PMC2888099
Карр Биол. Авторская рукопись; доступно в PMC 2010 21 июня.
Авторская рукопись; доступно в PMC 2010 21 июня.
Опубликовано в окончательной редакции как:
Curr Biol. 2009 г., 15 сентября; 19(17): Р745–Р748.
doi: 10.1016/j.cub.2009.06.034
PMCID: PMC2888099
NIHMSID: NIHMS208256
PMID: 19906576
, 1 , 2 и 1
. механические свойства материалов и для измерения сил, приложенных к нам. Мы выбираем спелые фрукты частично, сжимая их, делаем выводы, основываясь на твердости рукопожатия человека, и часто нас привлекает или отталкивает то, мягкое или липкое что-то, что представляет большой интерес для дизайнеров продуктов и производителей косметики. Эти сенсорные способности зависят от нашей способности функционировать как реометры: мы применяем силы контролируемой величины и продолжительности и обнаруживаем результирующую деформацию или скорость потока. То есть мы одновременно осознаем напряжение (силу/площадь) и напряжение (деформацию) или скорость деформации, когда оцениваем, как ощущается объект или как сильно нас толкают или тянут. Клетки одинаково чувствительны к информации о силе, жесткости и адгезивности. Диапазон силы и жесткости, на которые реагируют разные типы клеток, а также характер их реакции при столкновении с материалами, жесткость которых отличается от жесткости ткани, в которой они обычно находятся, столь же индивидуальны, как и их ответы на химические раздражители.
Клетки одинаково чувствительны к информации о силе, жесткости и адгезивности. Диапазон силы и жесткости, на которые реагируют разные типы клеток, а также характер их реакции при столкновении с материалами, жесткость которых отличается от жесткости ткани, в которой они обычно находятся, столь же индивидуальны, как и их ответы на химические раздражители.
Способность клеток реагировать на внешние силы или обнаруживать механику их субстратов при приложении внутренних сил зависит от механических свойств самих клеток. Те же методы и приборы, которые используются для измерения механических свойств синтетических материалов — область реологии, — были применены к тканям и изолированным клеткам. В последнем случае потребовалась модификация традиционных методов и изобретение новых, чтобы справиться с небольшими размерами и хрупкостью отдельной клетки. В этом учебнике мы попытаемся обобщить некоторые из текущих открытий в области клеточной механики и то, как они, как считается, влияют на то, как клетки функционируют или неправильно функционируют 9. 0093 in vivo .
0093 in vivo .
Идея о том, что физические свойства клеток важны для их биологической функции, не нова. Многие ранние клеточные биологи подчеркивали, что определение физических характеристик клеток необходимо для понимания того, как они функционируют [1]. Клеточные функции, которые определяются механической работой, выполняемой клеткой, такой как подвижность и цитокинез, особенно мотивировали исследования механических свойств клетки и механизмов производства силы. Но помимо тех процессов, которые, подобно мышечному сокращению и передвижению клеток, явно выполняют механическую работу и требуют эластичной цитоплазмы или перехода гелеобразования-соляции для выполнения этой работы, физическое состояние клетки иногда оказывается просто побочным эффектом структуры и реакции, необходимые для более важных генетических и биохимических процессов, управляющих функционированием клетки. Однако в последнее время интерес к клеточной физике стимулировался данными широкого круга исследований о том, что внешняя сила, приложенная к клетке, и сопротивление, которое внеклеточный матрикс оказывает клеточным силам, также генерируют сигналы, столь же мощные, как и химические стимулы для управления ростом, выживанием, дифференцировкой и функцией клеток [2]. Изменения этих физических особенностей или реакции клеток на них начинают восприниматься всерьез как способствующие факторы, а не только как последствия таких патологий, как рубцевание, фиброзная болезнь и рак [3].
Изменения этих физических особенностей или реакции клеток на них начинают восприниматься всерьез как способствующие факторы, а не только как последствия таких патологий, как рубцевание, фиброзная болезнь и рак [3].
Несколькими примерами важности внешних сил являются способность стимулировать удлинение аксонов за счет приложения сил шкалы от pN до nN к кончикам конуса роста нейронов, влияние потока жидкости на морфологию и передачу сигналов эндотелиальных клеток сосудов, а также внезапная потеря костной или мышечной массы при снижении силы тяжести или физической нагрузки. Чтобы понять, как эти силы передаются по молекулярным структурам клетки и как они могут быть преобразованы в биохимические реакции, необходима детальная количественная характеристика механических свойств клеток в точках приложения этих сил. Точно так же, как трехмерная атомная структура гормонального рецептора необходима для полного понимания того, как этот химический раздражитель активирует клеточную функцию, так же необходимо определить, как деформируются клетки и макромолекулы внутри них при воздействии сил.
Клетки не только реагируют на силы, приложенные извне, но также часто сильно реагируют на пассивное сопротивление их субстратов активным силам, которые они сами генерируют. Эта область исследований, во многом стимулированная исследованием, которое показало, как по-разному фибробласты выглядели и двигались на гелях с одинаковыми химическими характеристиками, но разной жесткостью [4], выявило множество случаев, когда механические свойства окружающей среды изменяют или даже подавляют сильные химические сигналы. . Например, саркомеры не будут образовываться в культивируемых миоцитах, если только они не растут на материалах с приблизительной жесткостью мышцы, а мезенхимальные стволовые клетки не могут эффективно дифференцироваться в остеоциты, когда они растут на мягких материалах, даже при наличии химических факторов, подходящих для этот тип клеток [5].
Как клетки реагируют на силы, какие сигнальные пути используются, какие гены активируются и т. д., в настоящее время в некоторых случаях начинает выясняться, например, эндотелиальные клетки в средах с нарушенным потоком, но какие молекулы первыми реагируют на силу часто остается неизвестным. Еще меньше известно о том, как клетки исследуют свое механическое окружение, то есть как они функционируют как реометры.
Еще меньше известно о том, как клетки исследуют свое механическое окружение, то есть как они функционируют как реометры.
По сути, ячеистый датчик силы может быть пассивным компонентом, который просто реагирует на изменения сил. Возможно, самым известным примером датчика физиологической силы является волосковая клетка в ухе, которая преобразует звуковые волны в нервные импульсы, инициируемые изменениями в активности мембранных ионных каналов. Однако датчик жесткости или дуросенсор должен активно применить напряжение и измерить деформацию или наоборот и затем вычислить отношение этих двух переменных. Чтобы выполнить этот анализ напряжение-деформация, дуросенсор должен использовать молекулярные моторы, чтобы приложить силу к своей подложке, измерить результирующее движение и вычислить отношение напряжения/деформации для считывания эластичности.
Большинство, но не все испытанные до сих пор типы клеток могут реагировать на широкий, но ограниченный диапазон эластичности субстрата, и их дуросенсоры должны быть в состоянии активно контролировать этот анализ стресс-деформация, по-видимому, путем изменения исходного напряжения или деформации.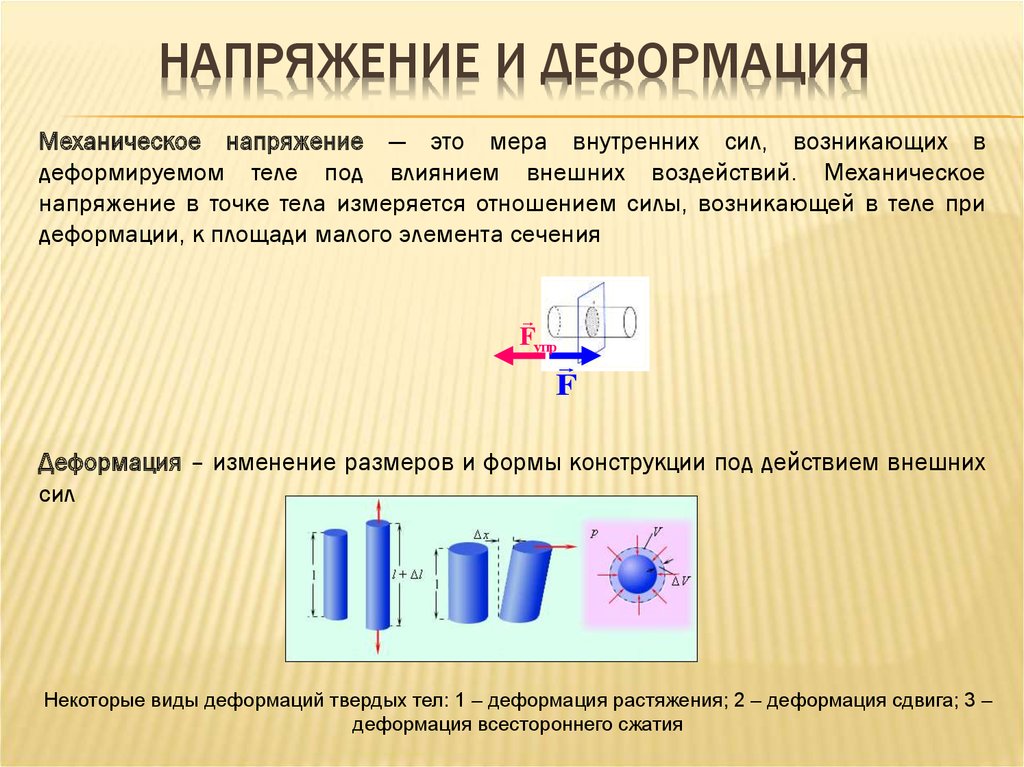 Чувство жесткости сильно различается среди разных типов клеток, и величина стресса, который они прикладывают к своему субстрату, также сильно различается. Большинство типов клеток тканей лучше распространяются на более твердом субстрате, но некоторые, такие как нейроны, гораздо лучше распространяются на мягких матрицах, которые напоминают эластичность мозга и не могут распространяться на жестких поверхностях. Количественные и качественные различия в дурозенсинге и дуротаксисе имеют много значений для заживления ран и формирования паттерна во время развития, которые только начинают изучаться.
Чувство жесткости сильно различается среди разных типов клеток, и величина стресса, который они прикладывают к своему субстрату, также сильно различается. Большинство типов клеток тканей лучше распространяются на более твердом субстрате, но некоторые, такие как нейроны, гораздо лучше распространяются на мягких матрицах, которые напоминают эластичность мозга и не могут распространяться на жестких поверхностях. Количественные и качественные различия в дурозенсинге и дуротаксисе имеют много значений для заживления ран и формирования паттерна во время развития, которые только начинают изучаться.
По аналогии с реометрами дуросенсор клетки может управляться напряжением или напряжением. Хотя механизм неизвестен, кажется правдоподобным, что после того, как молекулярные моторы генерируют напряжение на границе клетка-субстрат, результирующее напряжение приводит к структурным изменениям в белке или внутри липидного двойного слоя, и эти структурные изменения активируют некоторые сигнальные пути. Это означает, что для дуросенсора требуется активный генератор стресса или деформации, набор молекул или белков для передачи стресса или деформации от клетки через ее плазматическую мембрану на лиганд, связанный с внешним субстратом, и сенсорный блок для измерения считывания и преобразования что к биохимическому сигналу. Многие эксперименты предполагают, что миозин является активным генератором стресса [6] и что стресс передается через актиновые филаменты на гибкие белки, такие как talin или filamin, которые связываются с трансмембранными белками, такими как интегрины, а затем на внешний лиганд, как показано на рис.
Это означает, что для дуросенсора требуется активный генератор стресса или деформации, набор молекул или белков для передачи стресса или деформации от клетки через ее плазматическую мембрану на лиганд, связанный с внешним субстратом, и сенсорный блок для измерения считывания и преобразования что к биохимическому сигналу. Многие эксперименты предполагают, что миозин является активным генератором стресса [6] и что стресс передается через актиновые филаменты на гибкие белки, такие как talin или filamin, которые связываются с трансмембранными белками, такими как интегрины, а затем на внешний лиганд, как показано на рис.
Открыть в отдельном окне
Клеточные компоненты, предполагаемые для участия в определении жесткости
(A) Клетка в состоянии покоя. Молекулярные моторы, такие как немышечный миозин, двигаются по актиновым филаментам, создавая силы через белки фокальной адгезии. Белки фокальной адгезии связаны с трансмембранными белками, такими как интегрины, посредством связей скольжения или захвата. Таким образом, тяговые силы передаются на внешний субстрат посредством интегрин-лигандных взаимодействий. В принципе, любой белок в этой «силовой цепи» от молекулярного мотора к актину к белку фокальной адгезии к интегрину к лиганду к внеклеточному матриксу может быть растянут и, следовательно, активирован. Внешне лиганды, такие как фибронектин или ламинин, также могут быть активированы силой. На плазматической мембране интегрины или белки фокальной адгезии могут активироваться растяжением; сама мембрана может быть деформирована или срезана, чтобы вызвать кластеризацию или рекрутирование белков. Внутренне натяжение самой актиновой нити может влиять на сродство молекулярных моторов и, следовательно, на транспорт белков; ядро также может быть напрямую деформировано, чтобы повлиять на транскрипцию. (B) Клетка, которая применяет напряжение или деформацию, получит ответ, зависящий от жесткости субстрата. Основная идея заключается в том, что на способность клеток растягивать белки, генерировать напряжение и деформировать мембраны или ядра сильно влияет эластичность их субстрата.
Таким образом, тяговые силы передаются на внешний субстрат посредством интегрин-лигандных взаимодействий. В принципе, любой белок в этой «силовой цепи» от молекулярного мотора к актину к белку фокальной адгезии к интегрину к лиганду к внеклеточному матриксу может быть растянут и, следовательно, активирован. Внешне лиганды, такие как фибронектин или ламинин, также могут быть активированы силой. На плазматической мембране интегрины или белки фокальной адгезии могут активироваться растяжением; сама мембрана может быть деформирована или срезана, чтобы вызвать кластеризацию или рекрутирование белков. Внутренне натяжение самой актиновой нити может влиять на сродство молекулярных моторов и, следовательно, на транспорт белков; ядро также может быть напрямую деформировано, чтобы повлиять на транскрипцию. (B) Клетка, которая применяет напряжение или деформацию, получит ответ, зависящий от жесткости субстрата. Основная идея заключается в том, что на способность клеток растягивать белки, генерировать напряжение и деформировать мембраны или ядра сильно влияет эластичность их субстрата.
В последнее время особое внимание было сосредоточено на белках, которые могут действовать как сцепления, опосредующие напряжение между внутренней и внешней частью клетки, особенно в тех случаях, когда их аффинность связывания с цитоскелетом увеличивается или уменьшается принудительно. Некоторые белок-белковые контакты характеризуются как защелкивающиеся связи, которые стабилизируются за счет снижения скорости диссоциации при приложении силы, а другие представляют собой скользящие связи, которые быстрее диссоциируют при стрессе. То, как молекулярные сцепления реагируют на механическое напряжение, может определять, будут ли клетки лучше растягиваться на мягких или твердых субстратах [7]. Белки, которые связаны с интегринами, фокальными адгезиями или актином, или которые встроены поблизости в липидный бислой, являются всеми возможными дуросенсорами, особенно те, которые могут разворачиваться, обнажая скрытые сайты активации, открывая или закрывая ионные каналы, или рекрутируя/вытесняя белки в качестве результате увеличенной или уменьшенной кривизны мембраны. Др. возможность заключается в том, что натяжение, создаваемое предполагаемым белком сцепления, опосредованное либо скользящими, либо зацепляющими связями, может влиять на сродство связывания белка, например, с актиновыми филаментами и, таким образом, является показателем эластичности. Поскольку структуры, наиболее вероятно деформирующиеся, находятся в самых мягких частях внутриклеточно-внеклеточной связи, жесткость клетки по отношению к ее окружению имеет решающее значение для способности клетки воспринимать дюросенсию.
Др. возможность заключается в том, что натяжение, создаваемое предполагаемым белком сцепления, опосредованное либо скользящими, либо зацепляющими связями, может влиять на сродство связывания белка, например, с актиновыми филаментами и, таким образом, является показателем эластичности. Поскольку структуры, наиболее вероятно деформирующиеся, находятся в самых мягких частях внутриклеточно-внеклеточной связи, жесткость клетки по отношению к ее окружению имеет решающее значение для способности клетки воспринимать дюросенсию.
Было использовано множество различных методов для приложения сил к ячейкам и измерения результирующего смещения, но получить однозначное значение жесткости ячейки трудно. Жесткость клетки или ткани — это не простая скалярная величина, такая как температура или концентрация фактора роста, а скорее функция, зависящая от масштаба времени, степени деформации, направления приложенной силы и пространственного распределения деформации. Клетки и внеклеточный матрикс не являются ни простыми твердыми телами, ни жидкостями, ни однородными материалами.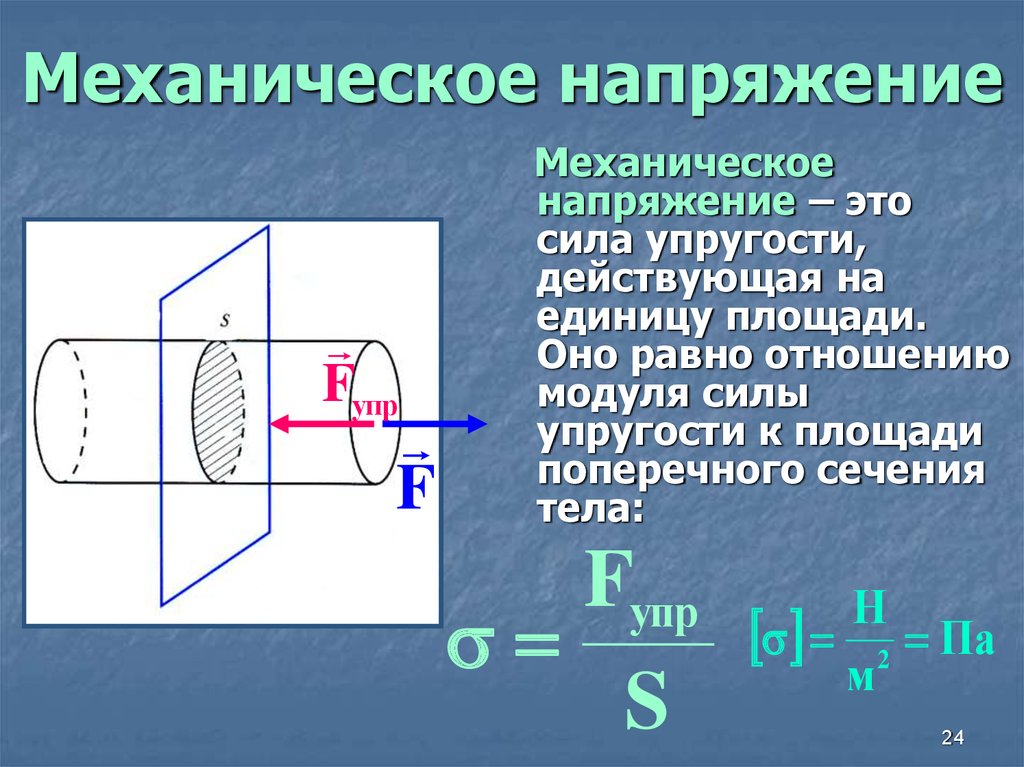 Действительно, определяющей характеристикой большинства клеточных и тканевых жесткостей является то, что они нелинейный ; их жесткость обычно увеличивается с ростом деформации [8]. Более того, наличие молекулярных двигателей и других активных процессов внутри клеток приводит к преобразованию химической энергии в механическую, что еще больше усложняет механическое поведение [9]. Эта сложность усугубляется тем фактом, что почти все исследования клеточной механики in vitro применимы к клеткам, выращенным на жестких поверхностях.
Действительно, определяющей характеристикой большинства клеточных и тканевых жесткостей является то, что они нелинейный ; их жесткость обычно увеличивается с ростом деформации [8]. Более того, наличие молекулярных двигателей и других активных процессов внутри клеток приводит к преобразованию химической энергии в механическую, что еще больше усложняет механическое поведение [9]. Эта сложность усугубляется тем фактом, что почти все исследования клеточной механики in vitro применимы к клеткам, выращенным на жестких поверхностях.
Замечательная особенность, по крайней мере, некоторых тканевых клеток заключается в том, что они настраивают свою жесткость в соответствии с жесткостью субстрата, к которому они прикрепляются, по крайней мере, в ограниченном диапазоне жесткости, как показано на рис. Механизмы, с помощью которых они изменяют жесткость, включают увеличение сборки цитоскелета, активацию сшивающих агентов и создание внутреннего напряжения, которое использует усиливающую напряжение нелинейную эластичность цитоскелета. Возможно, самое большее, что можно четко вывести из реологических исследований клеток, — это верхний предел их модуля упругости, который, вероятно, определяется максимальной концентрацией сшитых цитоскелетных сетей, которые они могут производить. Измеренная в масштабе времени примерно в одну секунду и при деформации в несколько процентов, это значение, по-видимому, составляет около 20 кПа для типичной животной клетки, но для других областей внутри клетки и в других условиях это значение может быть намного меньше.
Возможно, самое большее, что можно четко вывести из реологических исследований клеток, — это верхний предел их модуля упругости, который, вероятно, определяется максимальной концентрацией сшитых цитоскелетных сетей, которые они могут производить. Измеренная в масштабе времени примерно в одну секунду и при деформации в несколько процентов, это значение, по-видимому, составляет около 20 кПа для типичной животной клетки, но для других областей внутри клетки и в других условиях это значение может быть намного меньше.
Открыть в отдельном окне
Изменение формы клетки и модуля упругости в зависимости от жесткости субстрата
Многие типы клеток изменяют форму в зависимости от жесткости субстрата, как показано двумя клетками меланомы A7, окрашенными для F- актин после инкубации на покрытых коллагеном полиакриламидных гелях с жесткостью 500 или 15000 Па. В некоторых условиях, таких как фибробласты или клетки меланомы, прилипшие к гелю, покрытым коллагеном, апикальная жесткость клеток, измеренная с помощью атомно-силового микроскопа, приблизительно равна жесткость подложки варьируется от 1 до 10 кПа, при которой жесткость клетки достигает максимума, аналогичного жесткости клеточной культуры на стекле или пластике, как показано темно-синей кривой. ингибирование миозина, удаление сшивающих агентов актина, таких как филамин А, или деполимеризация актина, как показано голубой кривой.
ингибирование миозина, удаление сшивающих агентов актина, таких как филамин А, или деполимеризация актина, как показано голубой кривой.
Как и все сложные материалы, клетки и ткани не являются ни чистыми твердыми телами, ни чистыми жидкостями. То, кажутся ли они твердыми (обычно определяемыми их способностью восстанавливать форму) или жидкими (определяемыми их необратимым изменением формы), зависит от того, как долго и насколько они деформированы. Например, в течение нескольких секунд большинство клеток и тканей восстанавливают форму и, следовательно, являются твердыми, но при длительных нагрузках они перестраиваются как активными, так и пассивными процессами и, следовательно, кажутся жидкими. Даже на субклеточном уровне способность амебоидных клеток совершать переходы из твердого состояния в жидкое, судя по наличию или отсутствию броуновского движения в жидких или стекловидных частях цитоплазмы, столетия назад была признана существенной чертой локомоции. Точная функциональная форма масштабирования модулей упругости со временем привлекла большое внимание клеточных биологов и физиков мягкой материи.
Интересной особенностью графиков модуля упругости в зависимости от времени (или, что эквивалентно, модуля накопления сдвига в зависимости от частоты из колебательных измерений) является то, что в логарифмическом масштабе графики модуля в зависимости от времени являются линейными с очень пологими наклонами. Это так называемое степенное поведение наблюдается в масштабе от внутриклеточных частиц до целых клеток и тканей, а также сообщается в исследованиях восстановленных сетей цитоскелета. Молекулярное объяснение этого степенного закона поведения и его значение для клетки вызвало большой интерес и споры [10]. Однако биологическое значение зависящей от времени эластичности клетки представляется очевидным. Чтобы оптимизировать конструкцию шлема, чтобы защитить мозг от быстрой деформации, вызванной травмой, подходящей величиной является модуль упругости мозга в масштабе доли секунды, но при попытке понять, как нейрон или глиальная клетка исследует окружающую среду, мозг реология в гораздо более длительном временном масштабе актуальна.
Механобиология и, в частности, определение эластичности все чаще рассматриваются как важные эпигенетические факторы, которые могут влиять на поведение клеток и играть центральную роль в индукции генов, синтезе белка, росте и дифференцировке клеток. Недавние успехи в создании мягких биосовместимых материалов и приборов, способных измерять деформации и силы в масштабе клетки, дали множество примеров того, как физические факторы изменяют клеточную биологию. Молекулярные механизмы механосенсорного восприятия или, по крайней мере, некоторые белки, важные для этой функции, начинают выявляться. Многие основные характеристики жесткости и восприятия силы остаются неизвестными, например, время, которое требуется, или степень деформации, необходимая для того, чтобы клетка оценила материал как слишком мягкий, слишком твердый или в самый раз. Весьма вероятно, что в результате исследований клеточной физики будет получено много удивительных результатов, которые помогут определить, как оптимизировать биомиметические материалы и как можно контролировать клетки, когда их нормальные функции нарушаются.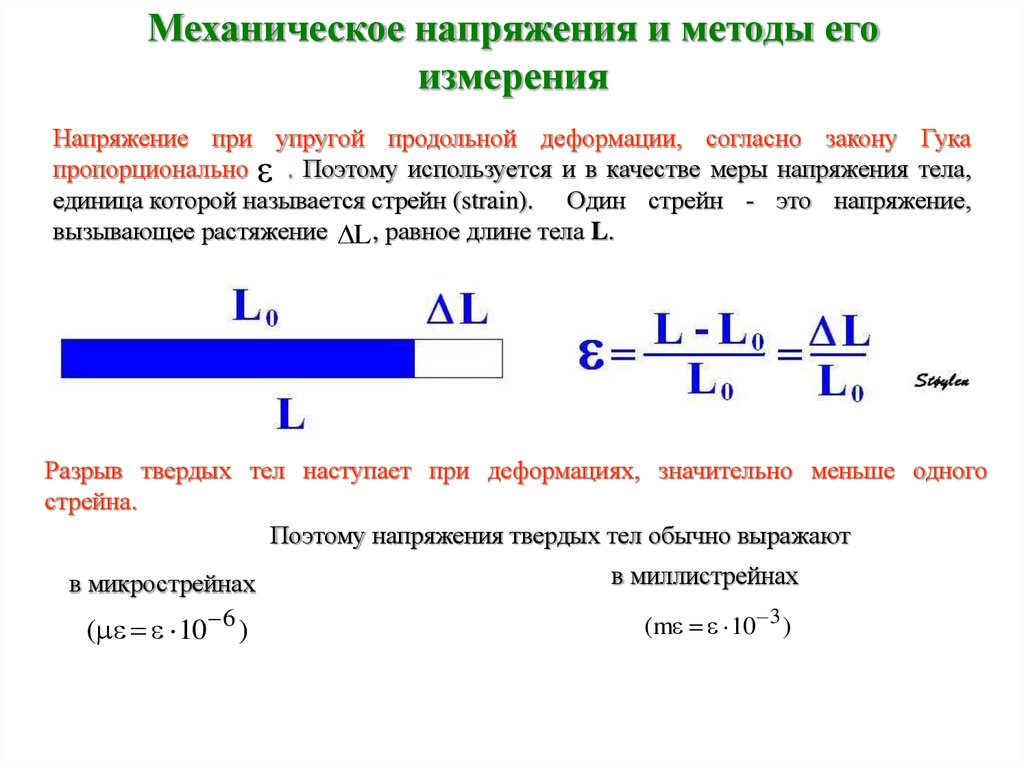
Вставка 1. Краткий глоссарий по клеточной механике
Сила
Величина, которая заставляет объект с массой изменять свою скорость. Это вектор, который имеет как величину, так и направление. Формально Ньютон определил силу как прямо пропорциональную массе и ускорению. Его единицей СИ является ньютон, Н. В одноклеточном масштабе полезной единицей является пН, а один моторный белок создает максимальную силу в несколько пН.
Напряжение
Сила, действующая на объект, нормированная по площади, на которую действует сила. Например, когда мы ударяем молотком по куску твердого дуба, мы в лучшем случае делаем неглубокую вмятину, но, максимально увеличивая нагрузку с помощью гвоздя с очень малой площадью, мы можем легко пробить дуб. Единицей напряжения в системе СИ является паскаль, Па или Н/м 9 .0127 2 . 1 Па = 1 пН/мкм 2 . Биологические нагрузки сильно различаются: от < 1 Па для напряжения сдвига из-за кровотока до > 10 6 Па на коленный хрящ каждый раз, когда средний взрослый человек встает.
Деформация
Безразмерное число, которое является формальным определением деформации; он сообщает о геометрическом изменении формы материала под нагрузкой. Очень приблизительно это расстояние, на которое материал растягивается или сжимается относительно его длины в состоянии покоя. Клетки обычно испытывают напряжение в 10–100 % при растяжении легких, сокращении мышц и т. д.
Модуль упругости
Это мера жесткости. Формально это отношение напряжения к деформации и, следовательно, также вектор, и действительно, большинство биологических материалов анизотропны и, следовательно, жестче в одном направлении, чем в другом. Важной сложностью является то, что большинство биологических материалов являются вязкоупругими, а не просто эластичными, и, следовательно, модуль упругости не является простой жесткой константой, но также зависит от количества времени и степени деформации амбра. Единицей измерения также является Па, и большинство мягких тканей имеют модули упругости от 10 до 50 000 Па, измеренные по шкале времени в одну секунду и с деформацией в один процент.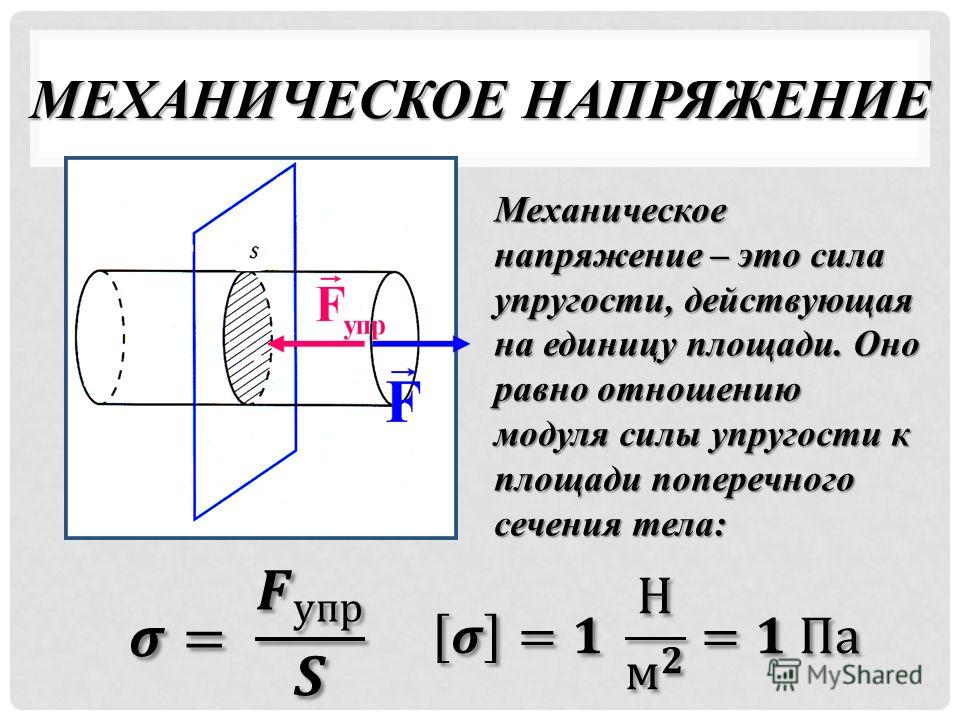 Модуль упругости часто измеряется путем приложения постоянной деформации и измерения напряжения, но также может быть измерен путем приложения контролируемого напряжения и измерения результирующей деформации.
Модуль упругости часто измеряется путем приложения постоянной деформации и измерения напряжения, но также может быть измерен путем приложения контролируемого напряжения и измерения результирующей деформации.
Вязкость
Для жидкостей это отношение напряжения к скорости деформации (или скорости потока). Единицей СИ является Па.с = 10 пуаз. Вязкость воды, например, составляет примерно 1 мПа·с.
Вязкоупругий
Сочетание вязкости и эластичности материала. Вязкоупругие материалы, подобно жидкостям, обладают существенно зависящей от времени текучестью, но также имеют некоторую способность восстанавливать свою первоначальную форму после снятия деформирующего напряжения (отличительный признак эластичности).
Соответствие
Способность изменять форму в ответ на стресс. Грубо говоря, податливость обратно пропорциональна модулю упругости, и ее единицей измерения является соответственно 1/Па. Податливость обычно измеряют путем приложения постоянного напряжения и измерения результирующей деформации, которая может медленно увеличиваться со временем по мере ползучести образца.
Нелинейная упругость
Для идеального эластичного материала напряжение пропорционально деформации, а модуль упругости представляет собой наклон линейной зависимости напряжения от деформации при любом значении напряжения или деформации. Многие сложные материалы обладают нелинейной упругостью. То есть их модуль упругости изменяется с увеличением деформации. Такие материалы могут быть либо смягчающими, либо усиливающими растяжение, как в случае перекрестно-сшитых сетей цитоскелета и внеклеточных филаментов.
1. Пеллинг А.Е., Хортон М.А. Исторический взгляд на клеточную механику. Арка Пфлюгера. 2008; 456:3–12. [PubMed] [Google Scholar]
2. Эйнсворт К. Биология клетки: расширение воображения. Природа. 2008; 456: 696–699. [PubMed] [Google Scholar]
3. Huang S, Ingber DE. Натяжение клеток, матричная механика и развитие рака. Раковая клетка. 2005; 8: 175–176. [PubMed] [Google Scholar]
4. Pelham RJ, Jr, Wang Y. Движение клеток и фокальные спайки регулируются гибкостью субстрата. проц. Натл. акад. науч. США. 1997;94:13661–13665. [Бесплатная статья PMC] [PubMed] [Google Scholar]
проц. Натл. акад. науч. США. 1997;94:13661–13665. [Бесплатная статья PMC] [PubMed] [Google Scholar]
5. Engler AJ, Sen S, Sweeney HL, Discher DE. Эластичность матрикса определяет спецификацию линии стволовых клеток. Клетка. 2006; 126: 677–689. [PubMed] [Google Scholar]
6. Cai Y, член парламента Sheetz. Распространение силы по клеткам: механическая когерентность динамических цитоскелетов. Курс. мнение Клеточная биол. 2009; 21:47–50. [Бесплатная статья PMC] [PubMed] [Google Scholar]
7. Chan CE, Odde DJ. Тракционная динамика филоподий на податливых субстратах. Наука. 2008; 322:1687–1691. [PubMed] [Google Scholar]
8. Фернандес П., Отт А. Механика одиночных ячеек: жесткость под напряжением и кинематическое упрочнение. физ. Преподобный Летт. 2008;100 238102. [PubMed] [Google Scholar]
9. Mizuno D, Tardin C, Schmidt CF, Mackintosh FC. Неравновесная механика активных цитоскелетных сетей. Наука. 2007; 315:370–373. [PubMed] [Google Scholar]
10.


 давления и механическ. напряжен 5 букв
давления и механическ. напряжен 5 букв Классическим примером напряжения растяжения является игра «перетягивание каната», в которой две команды тянут веревку в стороны.
Классическим примером напряжения растяжения является игра «перетягивание каната», в которой две команды тянут веревку в стороны.