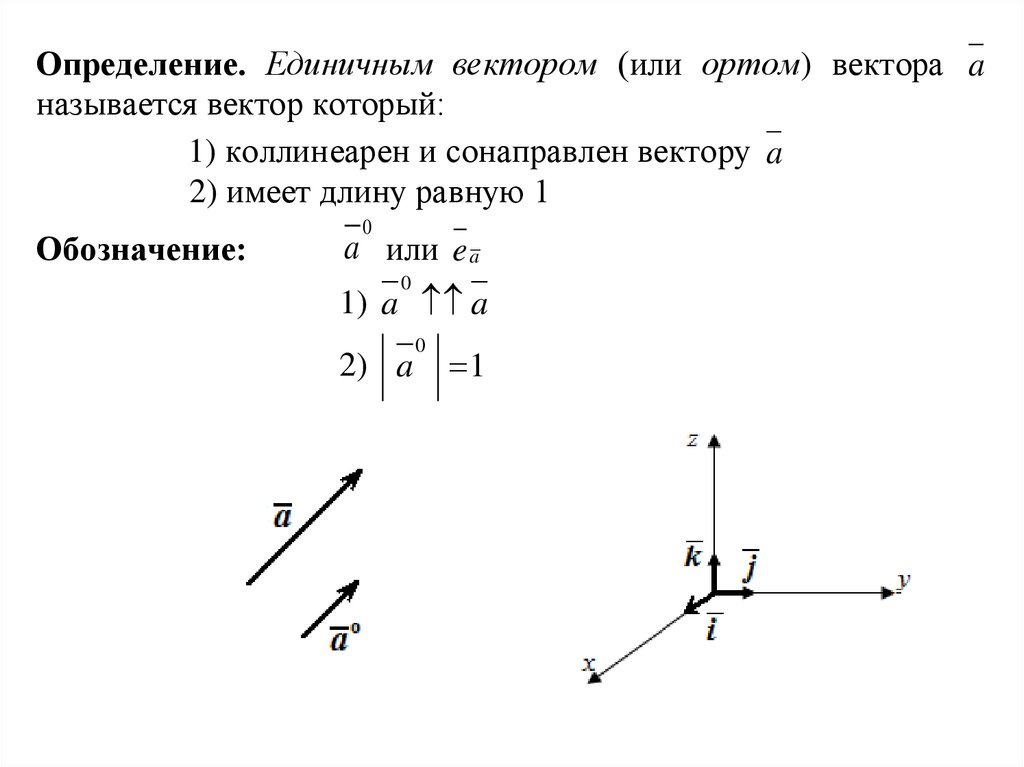
4. Единичный вектор

Определение 9. Любой вектор, длина которой равна единице, называется единичным вектором.

Пусть задан вектор . Обозначим через единичный вектор, сонаправленный с вектором . Из определения умножения вектора на число следует, что

или .

Для каждой числовой оси определен единичный вектор , с началом в точке ( – центр числовой оси) и концом в точке с координатой (рис. 12). Направление единичного вектора совпадает с положительным направлением числовой оси .

Рис. 12

5. Угол между векторами

Определение 10. Пусть векторы и имеют общее начало. Углом между векторами и называется наименьший угол , на который нужно повернуть один из этих векторов до совпадения с другим (рис. 13). Под термином совпадение понимается, что векторы и окажутся сонаправленными. Угол между векторами и обозначают .

Из определения вытекает, что угол между произвольными векторами содержится в промежутке: .

Определение 11. Пусть начало вектора находится в центре числовой оси . Углом между вектором и осью называется угол между вектором и единичным вектором оси (рис. 14).

Рис. 13 Рис. 14

6. Проекция вектора на ось

Определение 12. Проекцией точки на ось называется точка пересечения плоскости , проходящей через точку перпендикулярно оси с осью (рис. 15).

Рис. 15

Определение 13. Проекцией вектора

на ось называется число, равное разности координат проекций конца и начала (рис. 16).

Рис. 16

Проекция вектора на ось обозначается . Имеем

.

Обозначим через угол между вектором и осью .

Проекция вектора может быть: 1) положительной, если угол острый. В этом случае (рис 16), 2) отрицательной, если угол тупой. В этом случае (рис. 17), 3) нулевой, если угол или . В этом случае (рис. 18).

Рис. 17 Рис. 18

Определение 13. Составляющей вектора по оси называется произведение проекции вектора на ось на единичный вектор этой оси и обозначается .

Составляющей вектора по оси есть вектор, соединяющий проекцию начала и проекцию конца вектора:

.

Отметим некоторые свойства проекции вектора на ось.

Свойство 1. Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью :

.

Свойство 2. Проекция произведения вектора на число на ось равна произведению числа на проекцию вектора на ось :

.

Свойство 3. Проекция суммы двух векторов и на ось равна сумме проекций этих векторов на ось :

.

Свойство 4. Проекция разности двух векторов и на ось равна разности проекций этих векторов на ось :

.

7. Системы координат

7.1. Декартова система координат на плоскости

Определение 14. Прямоугольной системой координат на плоскости называется пара взаимно перпендикулярных числовых осей, имеющие общее начало . Общее начало совпадает с точкой пересечения (рис. 19).

Определение 15. Плоскость в которой, расположены оси, называется координатной плоскостью .

Осей, составляющих прямоугольную систему координат на плоскости обозначим и . Как правило, ось на чертеже располагают горизонтально, а ось – вертикально. Произвольной точке плоскости соответствуют два вещественных числа (рис. 20):

1) проекция точки на ось и обозначают ;

2) проекция точки на ось и обозначают .

Рис. 19 Рис. 20

Определение 16. Число называется абсциссой

точки , число – ординатой этой точки.

Определение 17. Ось называется осью абсцисс, ось – осью ординат.

Определение 18. Упорядоченная пара чисел называется прямоугольными (декартовыми) координатами точки координатной плоскости и обозначается .

Каждой точке координатной плоскости соответствует единственная упорядоченная пара чисел и, наоборот, каждой упорядоченной паре чисел соответствует единственная точка координатной плоскости .

Координатные оси и делят координатную плоскость на четыре четверти (на четыре квадранты). Каждая точка , не принадлежащая координатным осям, содержится в одной из четырех четвертей.

Обозначение этих четвертей и знаки координат точки:

1) первая четверть – ; ;

2) вторая четверть – ; ;

3) третья четверть – ; ;

4) четвёртая четверть – ; .

Алгебра свободных и скользящих векторов

Алгебра свободных и скользящих векторов

Меркин Д.Р. Алгебра свободных и скользящих векторов. М: изд-во «Физматгиз», 1962 — 165 с. В книге дается подробное изложение алгебры свободных и скользящих векторов. Содержание первой главы соответствует в основном программе по векторной алгебре курса высшей математики втузов. Во второй главе рассматривается теория преобразования системы скользящих векторов и приведения их к простейшему виду. Эта теория имеет важное значение в различных вопросах физики и техники; она может рассматриваться также, как вводная глава винтового исчисления. В книге большое внимание уделено примерам и разъяснению некоторых деталей и особенностей векторного исчисления, весьма важных в приложениях. Книга может служить учебным пособием для студентов и преподавателей втузов и университетов. Она рассчитана также на инженеров, желающих повысить свою теоретическую подготовку. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА 2. Определение вектора. 3. Классификация векторов. 4. Равенство векторов. 5. Перенос вектора. 6. Нуль-вектор. 7. Компланарность и коллинеарность векторов. 8. Прямопротивоположные векторы. § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ 2. Сумма векторов. 3. Свойства суммы векторов. 4. Правила параллелограмма и параллелепипеда. 5. Разность двух векторов. 6. Свойства модуля суммы векторов. § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО 2. Свойства произведения. 3. Деление вектора на число. 4. Единичные векторы. 5. Орт оси. 6. Коллинеарность двух векторов. § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ 3. Разложение вектора по трем другим векторам. 4. Разложение вектора по ортам базиса. § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ 2. Условие коллинеарности двух векторов. 3. Условие компланарности трех векторов. 4. Линейная зависимость четырех векторов. § 6. ПРОЕКЦИИ ВЕКТОРА 2. Свойства составляющих вектора. 3. Проекция вектора на ось. 4. Свойства проекций. 5. Угол между векторами. 6. Вычисление проекций вектора. 7. Теорема о проекции сумммы векторов. 8. Псевдоскаляры. § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА 2. Естественный способ задания свободного вектора. 3. Задание свободного вектора с помощью его проекций (координатный метод). 4. Связь между естественным и координатным способами задания вектора. 5. Задание несвободного вектора. 6. Задание скользящего вектора. 7. Некоторые приложения. § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ 2. Свойства скалярного произведения. 3. Выражение скалярного произведения через проекции векторов. 4. Векторные уравнения геометрических мест. 5. Уравнение плоскости. 7. Изменение проекций вектора при преобразовании координат. 8. Другое определение вектора. § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ 2. Примеры из физики. 3. Способ Н. Е. Жуковского построения векторного произведения. 4. Свойства векторного произведения. 5. Разложение вектора-произведения по координатным ортам. 6. Условие коллинеарности двух векторов. 7. Тождество Лагранжа. 8. Полярные и аксиальные векторы. § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 2. Двойное векторное произведение. 3. Разложение вектора по трем другим векторам. 4. Скалярное произведение двух векторных произведений. 5. Векторное произведение двух векторных произведений. 6. Произведение двух смешанных произведений. 7. Взаимные реперы. § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ 2. Уравнение прямой, проходящей через две заданные точки. 3. Плюкерово уравнение прямой в пространстве. 4. Прямая как пересечение двух плоскостей. § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ ГЛАВА II. АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА 2. Момент вектора относительно точки. 3. Проекции момента. 4. Момент вектора относительно оси. 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей. § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ 2. Главный вектор системы векторов. 3. Главный момент системы векторов. 4. Система двух равнопротивоположных векторов. 5. Первая теорема Вариньона. 6. Изменение главного момента с изменением полюса. 7. Инварианты системы векторов. 8. Минимальный момент и центральная ось системы. 9. Распределение главных моментов в пространстве. 10. Понятие о винте. 11. Винт системы векторов. § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ 2. Основные определения и аксиомы. § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение). § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Условия эквивалентности двух систем скользящих векторов. 3. Преобразование эквивалентных систем. § 19. ТЕОРИЯ ПАР 1. Пара векторов и ее момент. 2. Свойства пар. 3. Винт § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение). 3. Приведение системы скользящих векторов к вектору и паре. 4. Пример из кинематики. 5. Приведение системы скользящих векторов к винту. 6. Примеры. 7. Уравнения равновесия векторов. 8. Вторая теорема Вариньона. § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ 2. Плоская система скользящих векторов. 3. Система параллельных скользящих векторов. 4. Центр системы параллельных векторов.

Единица измерения вектора — объяснение, формула, пример и часто задаваемые вопросы

Единицы измерения вектора имеют как направление, так и величину. Однако иногда интересует только направление, а не величина. В таком случае векторы часто считаются единичной длиной. Эти единичные векторы обычно используются для представления направления со скалярным коэффициентом, обеспечивающим величину. Векторное разложение может быть выражено как сумма единичного вектора и скалярных коэффициентов.

Векторные единицы часто используются для представления величин в физике, таких как сила, ускорение, количество или крутящий момент. В этой статье мы обсудим, как найти единичные векторы.

Геометрические объекты, имеющие как величину, так и направление, называются векторами. Векторы начинаются с начальной точки и достигают конечной точки, которая представляет собой конечное положение.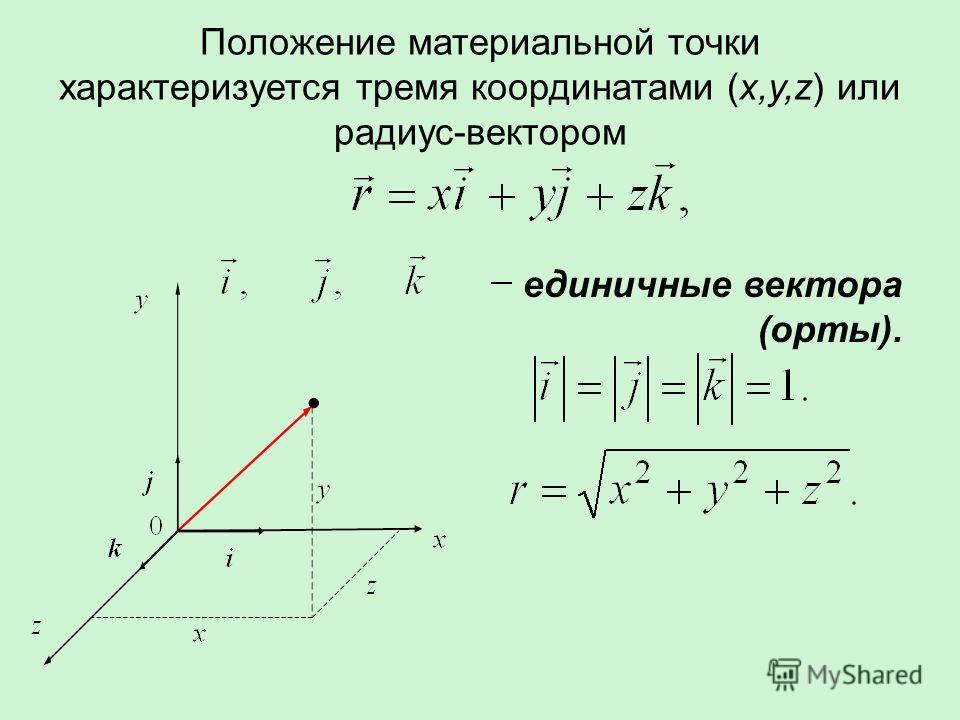 Векторы можно складывать, вычитать или умножать.

Вектор, имеющий величину 1, известен как единичный вектор. Вектор, который при делении на величину того же заданного вектора дает единичный вектор. Единичные векторы также известны как векторы направления. Единичные векторы обозначаются \[\hat{a}\], а их длины равны 1,9.{2}}\]

\[\text{Единичный вектор} = \frac{\text{Вектор}}{\text{Амплитуда вектора}}\]

Представление вектора

Существует два способа вектор может быть представлен —

1. \[\vec{a}\] = (x,y,z)

2. \[\vec{a} = \widehat{xi} + \widehat{yj} + \widehat{zk}\]

Единичный вектор нормали

Вектор, перпендикулярный поверхности в определенной точке , определяется как «нормальный» вектор. Его также можно определить как вектор нормали к поверхности, содержащей вектор. После нормализации вектора нормали полученный единичный вектор известен как единичный вектор нормали, иногда называемый единичной нормалью. 9{2}}\]

\[|\vec{a}|= \sqrt{4+9+1}\]

\[|\vec{a}|= \sqrt{14}\]

Единичный вектор в направлении \[\vec{a} = \frac{1}{Величина \vec{a}} \times \vec{a}\]

\[\hat{a} = \frac{1} {\ sqrt {14}} [\ widehat {2i} + \ widehat {3j} + \ hat {k}] \]

\[\ hat {a} = \ frac {2} {\ sqrt {14}} \hat{i} + \frac{3}{\sqrt{14}}\hat{j} + \frac{1}{\sqrt{14}}\hat{k}\]

Пример 2. Определить единичный вектор в направлении суммы векторов, \[\vec{a} = \widehat{2i} + \widehat{2j} — \widehat{5k}\] & \[\vec{b} = \widehat{2i } + \widehat{j} + \widehat{3k}\]. 9{2}}\]

\[|\vec{c}| = \sqrt{16 + 9 + 4}\]

\[|\vec{c}| = \sqrt{29}\]

Единичный вектор в направлении \[\vec{c} = \frac{1}{|\vec{c}|}\vec{c}\]

\[\hat {c} = \frac{1}{\sqrt{29}} [\widehat{4i} +\widehat{3j} — \widehat{2k}]\]   

\[\hat{c} = \frac{ 4}{\sqrt{29}}\шляпа{i} + \frac{3}{\sqrt{29}}\шляпа{j} — \frac{2}{\sqrt{29}}\шляпа{k} \]

Единичный вектор сферических координат

Единичные векторы в сферических системах координат определяются как функция положения. Единичные векторы сферических координат удобно выражать в терминах прямоугольных систем координат, которые сами по себе не являются функцией положения.

\[\шляпа{r}\] = \[\frac{\шляпа{r}}{r}\] = \[\frac{x\шляпа{x} + y\шляпа{y} + z\ hat{z}}{r}\] = \[\hat{x}\] sinθ cosØ + \[\hat{y}\]sinθ sinØ — \[\hat{z}\]cosθ

\[\ frac{\hat{z \times r}}{Sin \theta}\] = — \[\hat{x}\] sinØ + \[\hat{y}\] sinØ

\[\ hat{\theta }\] = \[\шляпа{\varnothing}\] х \[\шляпа{r}\] = \[\шляпа{х}\]cos θ cos Ø + \[\шляпа{y}\]cos θ sin Ø — \[\hat{z}\] sin θ

Единичный касательный вектор

Рассматривая гладкую вектор-функцию \[\vec{V}\](t), любой вектор, параллельный \[\vec{ V}\]'(t₀) рассматривается как касательная к графику \[\vec{V}\](t) при t = t₀. Обычно он используется для представления направления \[\vec{V}\]’(t), а не величины.

Следовательно, мы рассматриваем единичный вектор в направлении \[\vec{V}\]’(t). Это дает определение единичного касательного вектора следующим образом:

Рассмотрим \[\vec{V}\]'(t) как гладкую функцию на открытом интервале I. Тогда единичный касательный вектор \[\hat{t }\](t) в этом случае:

 \[\hat{t}\](t) = \[\vec{V}\]'(t) / |\[\vec{V}\] ‘(т)|

Единичный вектор

Единичный вектор — это вектор, величина которого равна 1 единице. Единичные векторы обычно обозначаются строчной буквой с символом циркумфлекса («шляпы») выше, например: .

Единичный вектор можно масштабировать таким образом, чтобы он образовывал вектор, величина которого является некоторым скалярным числом, кратным единичному вектору. При умножении на скаляр величина единичного вектора изменяется, но его направление сохраняется, если только скаляр не является отрицательным; если скаляр отрицательный, направление нового вектора указывает на направление, противоположное единичному вектору, как показано на рисунке ниже.

Положительный k	Отрицательный k

Величина вектора, образованного умножением единичного вектора на скаляр k, обозначается следующим образом:

Как найти единичный вектор заданного вектора

вектор, разделить на величину (или норму) вектора. Единичный вектор для , равен

,

, где величина . Процесс нахождения единичного вектора иногда называют нормализацией вектора.

Пример

Найдите единичный вектор для .

Сначала найдите величину v:

Тогда единичный вектор:

Чтобы подтвердить, что это единичный вектор, вычислите величину:

Стандартные единичные векторы орты параллельны осям системы координат. В двумерной системе координат стандартные единичные векторы могут быть записаны как . Любой вектор в двумерной координатной плоскости можно представить как линейную комбинацию i и j. Например, мы можем написать так:

В общем виде, если задано , то:

,

где v ₁ и v ₂ скаляры.

Пример

Пусть вектор v имеет хвост в точке (3, 5) и голову в точке (-2, 1). Запишите v как линейную комбинацию i и j.

Компоненты v равны

или в виде столбца

, что может быть записано как линейная комбинация i и j следующим образом:

Вектор показан на рисунке ниже:

Стоит отметить, что стандартные единичные векторы в 2D или любом другом измерении не зависят друг от друга, а это означает, что они не могут быть записаны как линейная комбинация любых других векторов в этом конкретном измерении.

В трехмерной координатной плоскости стандартные единичные векторы: и к.

Запись параллельных векторов с помощью единичных векторов

Единичные векторы можно использовать для записи параллельных векторов. Два вектора параллельны, если один из них можно представить как скалярное кратное другому. Таким образом, единичные векторы можно использовать для записи любого количества параллельных векторов.

Пример

Запишите вектор w в компонентной форме, учитывая, что он имеет величину 5 единиц и параллелен

Сначала найдите единичный вектор для v:

Поскольку имеет единичную длину и направлен в том же направлении, что и v, он параллелен v, поэтому мы можем записать w как скаляр, кратный такому, что . Таким образом:

Использование единичных векторов и углов направления для записи векторов

Если – вектор-столбец, – его единичный вектор, а θ – угол между осью x и , то компоненты лежат на единичной окружности, и мы можно использовать функции косинуса и синуса для определения таких компонентов, что

, так как .