Единица измерения ускорения, теория и онлайн калькуляторы
Для того чтобы определить в каких единицах измеряется любое ускорение ($\overline{a}$) (среднее или мгновенное, постоянное или переменное) достаточно дать определение среднего ускорения.
ОпределениеСредним ускорением ($\left\langle a\right\rangle $) в рассматриваемый промежуток времени называют физическую величину, равную отношению изменения скорости ($\Delta v$) к величине промежутка времени ($\Delta t$) за которое это изменение произошло:
\[\left\langle \overline{a}\right\rangle =\frac{\Delta \overline{v}}{\Delta t}\left(1\right).\]Ускорение — это векторная величина, его направление зависит от характера движения тела (материальной точки).
Единица измерения ускорения в Международной системе единиц
Из определения (1) следует, что ускорение имеет единицу измерения:
\[\left[a\right]=\frac{\left[v\right]}{\left[t\right]}=\frac{м/с}{с}=\frac{м}{с^2}.\]Единицы измерения ускорения являются производными единицами в Международной системе единиц. Специального наименования у единиц ускорения нет. Говорят, что метр, деленный на секунду в квадрате — единица измерения ускорения в системе СИ.
Единицы измерения ускорения, не относящиеся к системе СИ
В системе СГС (сантиметр, грамм, секунда) сантиметр, деленный на секунду в квадрате ($\frac{см}{с^2}$) — единица измерения ускорения. Единица измерения ускорения в системах СГС и СИ соотносятся как:
\[1\frac{м}{с^2}=100\frac{см}{с^2}.\]В гравиметрии (метод изучения поля силы тяжести) используют, как внесистемную единицу измерения ускорения, единицу измерения гал. Иногда говорят, что гал — единица измерения ускорения в СГС, так как:
\[1\ Гал=1\frac{см}{с^2}.\]Гал (иногда галилео) был назван в честь Г. Галилея. Чаще всего гал используют в гравиметрии при обозначении единиц ускорения свободного падения. Так, стандартная величина ускорения свободного падения составляет:
\[g=980,665\ Гал.\]В Британских системах единиц встречается единица измерения ускорения фут, деленный на секунду в квадрате:
\[\left[a\right]=\frac{фут}{с^2}.\]$\frac{фут}{с^2}$ соотносится с $\frac{м}{с^2}$ (единицей измерения ускорения в СИ), как:
\[1\frac{фут}{с^2}=0,3048\frac{м}{с^2}.\ \]Примеры задач с решением
Пример 1Задание. Каково центростремительное ускорение точек обода ($a_n$), если скорость поступательного движения обода постоянна и составляет $v=$20 $\frac{м}{с},$ при частоте вращения обода $\nu =$8 $с^{-1}$? В каких единицах будет измеряться полученное ускорение (проверьте результирующую формулу)?
Решение. Центростремительное ускорение можно найти, если использовать формулу:
\[a_n=\frac{v^2}{R}\left(1.1\right),\]В нашей задаче $R$ — радиус обода. Время, которое затрачивает обод на полный оборот равно:
\[T=\frac{2\pi R}{v}=\frac{1}{\nu }\left(1.2\right),\]где $T$ — период обращения обода, величина о
Таблица единиц измерения ускорения в СИ (по ОКЕИ ОК 015-94)
Таблица с единицами измерения ускорения приведена в ОК 015-94 (MK 002-9) ОКЕИ. Единицы измерения ускорения входят в таблицу измерения технических единиц.
ОКЕИ — это Общероссийский классификатор единиц измерения (ОКЕИ), который является документом в области национальной системы стандартизации.
ОКЕИ разработан на основе:
- Международной классификации единиц измерения ЕЭК ООН «Коды для единиц измерения, используемых в международной торговле»
- Товарной номенклатуры внешнеэкономической деятельности (ТН ВЭД) в части используемых единиц измерения и с учетом требований международных стандартов ИСО 31/0-92 «Величины и единицы измерения. Часть 0. Общие принципы» и ИСО 1000-92 «Единицы СИ и рекомендации по применению кратных единиц и некоторых других единиц».
СИ — международная система единиц физических величин, современный вариант метрической системы. (метрическая система — это общее название международной десятичной системы единиц, основанной на использовании метра и килограмма)
Выделим из таблиц с техническими единицами только таблицу с величинами измерения ускорения.
Согласно разделу 1 ОК 015-94 (MK 002-9):
Международные единицы измерения ускорения (СИ), включенные в ОКЕИ
| Код ОКЕИ | Наименование единицы измерения | Условное обозначение | Кодовое буквенное обозначение | ||
| национальное | международное | национальное | международное | ||
| 335 | Метр на секунду в квадрате | м/с2 | m/s2 | М/С2 | MSK |
Таблица единиц измерения длины СИ (по ОКЕИ ОК 015-94)
Таблица единиц измерения времени СИ (по ОКЕИ ОК 015-94)
Таблица единиц скорости в СИ (по ОКЕИ ОК 015-94)
Ускорение — это… Что такое Ускорение?
Падающий мяч при отсутствии сопротивления воздуха ускоряется, то есть движется все быстрее и быстрее.Ускоре́ние (обычно обозначается , в теоретической механике ) — производная скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости точки (тела) при её (его) движении за единицу времени (то есть ускорение учитывает не только изменение величины скорости, но и её направления).
Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².
Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (m/s2
Производная ускорения по времени, то есть величина, характеризующая скорость изменения ускорения, называется рывок:
- , где: — вектор рывка.
Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:
- .
Ускорение точки при прямолинейном движении
Если вектор не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:
- .
Из вышеприведённых двух формул можно вывести ещё одну, связывающую скалярные величины:
Здесь — начальная скорость тела, — конечная скорость тела; — ускорение тела; — пройденный телом путь.
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное, вообще говоря, не верно).
Ускорение точки при движении по окружности
Вектор ускорения
при движении точки по окружности можно разложить на два слагаемых (компоненты):
Тангенциальное ускорение — направлено по касательной к траектории (обозначается иногда и т. д., в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.
Центростремительное или Нормальное ускорение — возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда и т. д.). Является составляющей вектора ускорения a, перпендикулярной вектору мгновенной скорости. Характеризует изменение скорости по направлению. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен:
Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.
Ускорение точки при движении по кривой
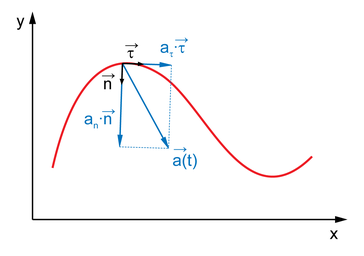
Вектор ускорения можно разложить по сопутствующему базису :
- ,
где
, называемое бинормальным ускорением, всегда равно нулю. Это можно считать прямым следствием определения векторов : можно сказать, что они выбираются именно так, чтобы первый всегда совпадал с нормальным ускорением, второй же ортогонально первому.
Векторы и называются касательным (тангенциальным) и нормальным ускорениями соответственно.
Итак, учитывая сказанное выше, вектор ускорения всегда можно записать как:
- ,
Ускорения в твёрдом теле
Связь ускорений двух точек можно получить, продифференцировав формулу Эйлера для скоростей по времени:
- ,
где — вектор угловой скорости тела, а — вектор углового ускорения тела.
Второе слагаемое называется осестремительным
Ускорение при сложном движении
Говорят, что материальная точка (тело) совершает сложное движение, если она движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. Тогда абсолютное ускорение тела равно сумме относительного, переносного и кориолисова:
- .
Первый закон Ньютона постулирует существование инерциальных систем отсчёта. В этих системах отсчёта равномерное прямолинейное движение имеет место в том случае, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом, постулируется, что причиной возникновения ненулевого ускорения
Второй закон Ньютона утверждает, что ускорение материальной точки всегда пропорционально приложенной к ней и порождающей ускорение силе, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется массой материальной точки):
Единицы измерения ускорения
- метр на секунду в квадрате (метр в секунду за секунду), м/с², производная единица системы СИ
- сантиметр на секунду в квадрате (сантиметр в секунду за секунду), см/с², производная единица системы СГС
| м/с2 | фут/с2 | g0 | см/с2 | |
|---|---|---|---|---|
| 1 м/с2 = | 1 | 3.28084 | 0.101972 | 100 |
| 1 фут/с2 = | 0.304800 | 1 | 0.0310810 | 30.4800 |
| 1 g0 = | 9.80665 | 32.1740 | 1 | 980.665 |
| 1 см/с2 = | 0.01 | 0.0328084 | 0.00101972 | 1 |
Измерение ускорения
Приборы для измерения ускорения называются акселерометрами. Они не измеряют ускорение непосредственно, а измеряют силу реакции (укр.)русск. опоры, которая возникает при ускоренном движении. Поскольку аналогичные силы сопротивления возникают также и в поле тяготения, то с помощью акселерометров можно измерять также и гравитацию.
Акселерографы — приборы, измеряющие и автоматически записывающие (в виде графиков) значения ускорения поступательного и вращательного движения.
Примеры ускорений
Значения ускорений различных движений:[1]
Примечание: g ≈ 9,81 м/с2.
См. также
Примечания
- ↑ Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике. — 10-е, испр. и доп.. — М.: Наука, 1988. — С. 61. — 256 с. — ISBN 5-02-013833-9
Ссылки
- Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 5-е, стереотипное. — М.: Физматлит, 2004. — 224 с. — («Теоретическая физика», том I). — ISBN 5-9221-0055-6
Угловое ускорение — Википедия
Угловое ускорение — псевдовекторная физическая величина, равная первой производной от псевдовектора угловой скорости по времени
ε→=dω→dt{\displaystyle {\vec {\varepsilon }}={\frac {d{\vec {\omega }}}{dt}}}
Угловое ускорение характеризует интенсивность изменения модуля и направления угловой скорости при движении твёрдого тела.
Как приходят к понятию углового ускорения: ускорение точки твердого тела при свободном движении[править | править код]
К понятию углового ускорения можно прийти, рассматривая вычисление ускорения точки твердого тела, совершающего свободное движение. Скорость точки тела B{\displaystyle B} при свободном движении, согласно формуле Эйлера, равна
v→B=v→A+ω→×AB→{\displaystyle {\vec {v}}_{B}={\vec {v}}_{A}+{\vec {\omega }}\times {\vec {AB}}}
где v→A{\displaystyle {\vec {v}}_{A}} — скорость точки тела A{\displaystyle A}, принятой в качестве полюса; ω→{\displaystyle {\vec {\omega }}} — псевдовектор угловой скорости тела; AB→{\displaystyle {\vec {AB}}} — вектор, выпущенный из полюса в точку, скорость которой вычисляется. Дифференцируя по времени данное выражение и используя формулу Ривальса[1], имеем
aB→=aA→+ε→×AB→+ω→×(ω→×AB→){\displaystyle {\vec {a_{B}}}={\vec {a_{A}}}+{\vec {\varepsilon }}\times {\vec {AB}}+{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {AB}})}
aB→=aA→+aBArot→+aBAaxis→{\displaystyle {\vec {a_{B}}}={\vec {a_{A}}}+{\vec {a_{BA}^{rot}}}+{\vec {a_{BA}^{axis}}}}
где a→A{\displaystyle {\vec {a}}_{A}} — ускорение полюса A{\displaystyle A}; ε→=dω→dt{\displaystyle {\vec {\varepsilon }}={\frac {d{\vec {\omega }}}{dt}}} — псевдовектор углового ускорения. Составляющая ускорения точки B{\displaystyle B}, вычисляемая через угловое ускорение называется вращательным ускорением точки B{\displaystyle B} вокруг полюса A{\displaystyle A}
a→BArot=ε→×AB→{\displaystyle {\vec {a}}_{BA}^{\,rot}={\vec {\varepsilon }}\times {\vec {AB}}}
Последнее слагаемое в полученной формуле, зависящее от угловой скорости, называют осестремительным ускорением ускорением точки B{\displaystyle B} вокруг полюса A{\displaystyle A}
a→BAaxis=ω→×(ω→×AB→){\displaystyle {\vec {a}}_{BA}^{\,axis}={\vec {\omega }}\times \left({\vec {\omega }}\times {\vec {AB}}\right)}
Геометрический смысл псевдовектора углового ускорения[править | править код]
Псевдовектор ε→{\displaystyle {\vec {\varepsilon }}} направлен по касательной к годографу угловой скорости. Действительно, рассмотрим два значения вектора угловой скорости, в момент времени t{\displaystyle t} и в момент времени t+Δt{\displaystyle t+\Delta t}. Оценим изменение угловой скорости за рассматриваемый промежуток времени Δt{\displaystyle \Delta t}
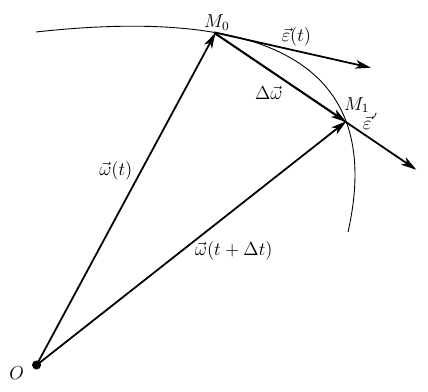
Δω→=ω→(t+Δt)−ω→(t){\displaystyle \Delta {\vec {\omega }}={\vec {\omega }}(t+\Delta t)-{\vec {\omega }}(t)}
Отнесем это изменение к тому промежутку времени, за которое оно произошло
Δω→Δt=ε→′{\displaystyle {\frac {\Delta {\vec {\omega }}}{\Delta t}}={\vec {\varepsilon }}^{\,\,’}}
Получившийся вектор называется вектором среднего углового ускорения. Он занимает положение секущей, пересекая годограф вектора угловой скорости в точках M0{\displaystyle M_{0}} и M1{\displaystyle M_{1}}. Перейдем к пределу при Δt→0{\displaystyle \Delta t\to 0}
limΔt→0Δω→Δt=dω→dt=ε→{\displaystyle \lim _{\Delta t\to 0}{\frac {\Delta {\vec {\omega }}}{\Delta t}}={\frac {d{\vec {\omega }}}{dt}}={\vec {\varepsilon }}}
Вектор среднего углового ускорения перейдет в вектор мгновенного углового ускорения и займет положение касательной в точке M0{\displaystyle M_{0}} к годографу угловой скорости.
Выражение вектора углового ускорения через параметры конечного поворота[править | править код]
При рассмотрении вращения тела через параметры конечного поворота, вектор углового ускорения можно расписать формулой
ε→=(1−cosφ)(u→×d2u→dt2)+φ˙(1+cosφ)du→dt+φ˙sinφ(u→×du→dt)+sinφd2u→dt2+φ¨u→{\displaystyle {\vec {\varepsilon }}=\left(1-\cos \varphi \right)\left({\vec {u}}\times {\frac {d^{2}{\vec {u}}}{dt^{2}}}\right)+{\dot {\varphi }}\left(1+\cos \varphi \right){\frac {d{\vec {u}}}{dt}}+{\dot {\varphi }}\sin \varphi \left({\vec {u}}\times {\frac {d{\vec {u}}}{dt}}\right)+\sin \varphi \,{\frac {d^{2}{\vec {u}}}{dt^{2}}}+{\ddot {\varphi }}\,{\vec {u}}}
где u→{\displaystyle {\vec {u}}} — орт, задающий направление оси поворота; φ{\displaystyle \varphi } — угол, на который совершается поворот вокруг оси u→{\displaystyle {\vec {u}}}.
Угловое ускорение при вращении тела вокруг неподвижной оси[править | править код]
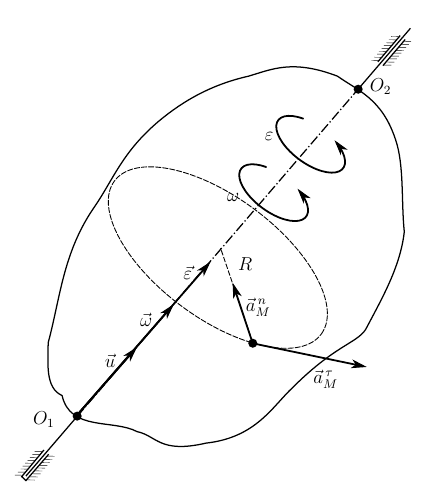
При вращении тела вокруг неподвижной оси, проходящей через неподвижные точки тела O1{\displaystyle O_{1}} и O2{\displaystyle O_{2}}, производные орта оси вращения равны нулю
du→dt=d2u→dt2=0{\displaystyle {\frac {d{\vec {u}}}{dt}}={\frac {d^{2}{\vec {u}}}{dt^{2}}}=0}
В этом случае вектор углового ускорения определяется тривиально через вторую производную угла поворота
ε→=φ¨u→{\displaystyle {\vec {\varepsilon }}={\ddot {\varphi }}\,{\vec {u}}}
или
ε→=εu→{\displaystyle {\vec {\varepsilon }}=\varepsilon \,{\vec {u}}}
где ε=φ¨{\displaystyle \varepsilon ={\ddot {\varphi }}} — алгебраическая величина углового ускорения. В этом случае псевдовектор углового ускорения, как и угловая скорость, направлен вдоль оси вращения тела. Если первая и вторая производные угла поворота имеют одинаковый знак
φ˙φ¨>0{\displaystyle {\dot {\varphi }}\,{\ddot {\varphi }}>0}
то вектор углового ускорения и вектор угловой скорости совпадают по направлению (тело вращается ускоренно). В противном случае, при φ˙φ¨<0{\displaystyle {\dot {\varphi }}\,{\ddot {\varphi }}<0}, векторы угловой скорости и углового ускорения направлены в противоположные стороны (тело вращается замедленно).
В курсе теоретической механики традиционным является подход, при котором понятие угловой скорости и углового ускорения вводится при рассмотрении вращения тела вокруг неподвижной оси. При этом в качестве закона движения рассматривается зависимость от времени угла поворота тела
φ=φ(t){\displaystyle \varphi =\varphi (t)}
В этом случае закон движения точки тела может быть выражен естественным способом, как длина дуги окружности, пройденная точкой при повороте тела от некоторого начального положения φ0=φ(t0){\displaystyle \varphi _{0}=\varphi (t_{0})}
s(t)=R(φ(t)−φ0){\displaystyle s(t)=R\,\left(\varphi (t)-\varphi _{0}\right)}
где R{\displaystyle R} — расстояние от точки до оси вращения (радиус окружности, по которой движется точка). Дифференцируя последнее соотношение по времени получаем алгебраическую скорость точки
dsdt=vτ=Rdφdt=ωR{\displaystyle {\frac {ds}{dt}}=v_{\tau }=R\,{\frac {d\varphi }{dt}}=\omega \,R}
где ω=dφdt{\displaystyle \omega ={\frac {d\varphi }{dt}}} — алгебраическая величина угловой скорости. Ускорение точки тела при вращении может быть представлено как геометрическая сумма тангенциального и нормального ускорения
a→M=a→Mτ+a→Mn{\displaystyle {\vec {a}}_{M}={\vec {a}}_{M}^{\,\tau }+{\vec {a}}_{M}^{\,n}}
причем тангенциальное ускорение получается как производная от алгебраической скорости точки
aMτ=dvτdt=ddt(ωR)=Rdωdt=εR{\displaystyle a_{M}^{\,\tau }={\frac {dv_{\tau }}{dt}}={\frac {d}{dt}}\left(\omega \,R\right)=R\,{\frac {d\omega }{dt}}=\varepsilon \,R}
где ε=dωdt=d2φdt2{\displaystyle \varepsilon ={\frac {d\omega }{dt}}={\frac {d^{2}\varphi }{dt^{2}}}} — алгебраическая величина углового ускорения. Нормальное ускорение точки тела может быть вычислено по формулам
aMn=vτ2R=ω2R{\displaystyle a_{M}^{\,n}={\frac {v_{\tau }^{2}}{R}}=\omega ^{2}\,R}
Выражение псевдовектора углового ускорения через тензор поворота тела[править | править код]
Если поворот твёрдого тела задан тензором ранга (1,1){\displaystyle \left(1,\,1\right)} (линейным оператором), выраженным, например, через параметры конечного поворота
Bmp=(1−cosφ)upum+cosφδmp+sinφgplϵlkmuk{\displaystyle B_{\,m}^{\,p}=\left(1-\cos \varphi \right)\,u^{\,p}\,u_{\,m}+\cos \varphi \,\delta _{\,m}^{\,p}+\sin \varphi \,g^{\,pl}\,\epsilon _{\,lkm}\,u^{\,k}}
где δmp{\displaystyle \delta _{\,m}^{\,p}} — символ Кронекера; ϵlkj{\displaystyle \epsilon _{\,lkj}} — тензор Леви-Чивиты, то, псевдовектор углового ускорения может быть вычислен по формуле
εi=12ϵiklglp(Bm′pB¨km+B˙m′pB˙km){\displaystyle \varepsilon ^{\,i}={\frac {1}{2}}\,\epsilon ^{ikl}\,g_{\,lp}\,\left(B_{\,m}^{‘\,p}\,{\ddot {B}}_{\,k}^{\,m}+{\dot {B}}_{\,m}^{‘\,p}\,{\dot {B}}_{\,k}^{\,m}\right)}
где Bm′p{\displaystyle B_{\,m}^{‘\,p}} — тензор обратного преобразования, равный
Bm′p=(1−cosφ)upum+cosφδmp−sinφgplϵlkmuk{\displaystyle B_{\,m}^{‘\,p}=\left(1-\cos \varphi \right)\,u^{\,p}\,u_{\,m}+\cos \varphi \,\delta _{\,m}^{\,p}-\sin \varphi \,g^{\,pl}\,\epsilon _{\,lkm}\,u^{\,k}}
- ↑ В.И. Дронг, В.В. Дубинин, М.М. Ильин и др.; под ред. К.С. Колесникова, В.В. Дубинина. Курс теоретической механики: учебник для вузов. — 2017. — С. 101, 111. — 580 с. — ISBN 978-5-7038-4568-4.
- Тарг С. М. Краткий курс теоретической механики — 10-е изд., перераб. и доп. — М.: Высш. шк., 1986 — 416 С.
- Погорелов Д. Ю. Введение в моделирование динамики систем тел: Учебное пособие. — Брянск: БГТУ, 1997. — 197 С.
Ускорение тела в физике
Важно помнить, что ускорение – величина векторная. Говорить об ускорении можно, когда скорость изменяется как по величине, так и по направлению.
Единицей измерения ускорения в системе СИ является м/с .
Примеры ускоренного движения – разгон, торможение, падение, различные маневры.
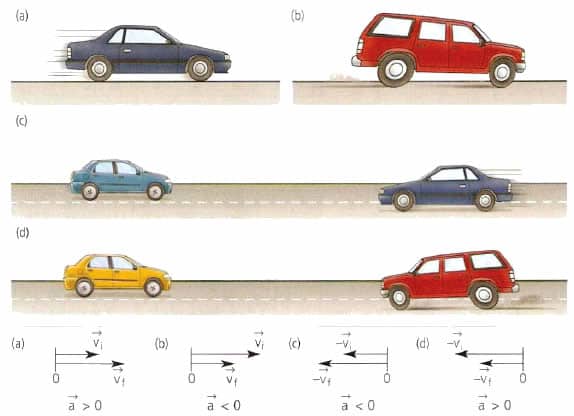
Если скорость всегда направлена по касательной к траектории движения, и направление вектора скорости совпадает с направлением движения, то вектор ускорения в общем случае может составлять любой угол с вектором скорости. Так, при разгоне по прямолинейному участку пути направления векторов скорости и ускорения совпадают (угол между векторами скорости и ускорения ) (рис.1,а). При торможении на прямолинейном участке шоссе вектора скорости и ускорения противоположно направлены (угол между векторами скорости и ускорения ) (рис.1,б).
При равномерном движении по окружности вектор ускорения перпендикулярен вектору скорости (угол между векторами скорости и ускорения ) (рис.1,в). В более общем сложном случае движения по криволинейной траектории угол между векторами скорости и ускорения зависит от кривизны траектории и интенсивности разгона/торможения, т.е. может принимать любое значение (рис.1,г).
Ускорение может быть как положительным, так и отрицательным. Если , говорят об ускоренном движении, если , движение замедленное.
Примеры решения задач по теме «Ускорение»
| Понравился сайт? Расскажи друзьям! | |||
В чем измеряется ускорение в физике? Центростремительное и угловое ускорение. Измерение ускорения свободного падения
При решении задач по физике часто приходится выводить рабочие формулы с учетом предоставленного условия. Одной из самых надежных проверок правильности полученной формулы является совпадение единиц измерения в правой и левой частях равенства. В данной статье рассмотрим вопрос, в чем измеряется ускорение.
Дадим сразу определение этой величины, а затем поясним ее особенности. Под ускорением понимают быстроту, с которой изменяется скорость в каждый момент времени при движении тела. Поскольку скорость — это величина векторная, то изменяться может ее модуль и направление. Оба типа изменения описываются понятием ускорения.
Для определения мгновенного ускорения используют следующее выражение:
a¯ = dv¯/dt.
Взяв первую производную по времени от скорости, мы получим зависимость ускорения от t.
Помимо мгновенного ускорения (значение a¯ в конкретный момент времени), на практике часто применяют среднее ускорение. Оно определяется так:
acp¯ = Δv¯/Δt.
Здесь Δv¯ — это разность скоростей в конце и в начале промежутка времени Δt. В отличие от мгновенной величины, среднее ускорение характеризует весь процесс движения, поэтому на практике оно оказывается более полезным. Очевидно, если Δt->dt, то acp¯->a¯.
В чем измеряется ускорение?
Несложно ответить на этот вопрос, если рассмотреть записанные в предыдущем пункте формулы для мгновенной и средней величины. Как известно, скорость определяется в метрах в секунду (м/с). Конечно, можно применять и другие единицы измерения для v¯, например, километры или мили в час, однако мы ведем разговор о единицах международной системы СИ. Время в СИ измеряется в секундах (c). Взяв отношение этих величин, приходим к ответу на вопрос, в чем измеряется ускорение. Его единицами являются метр в квадратную секунду или сокращенно м/с².
Что означает запись: a = 1 м/с²? Это означает, что за каждую секунду перемещения тело увеличивает свою скорость на 1 м/с.
Далее будут приведены другие возможные единицы измерения ускорения, однако м/с² является базовой, и все другие единицы сводятся к ней.
Сила и ускорение
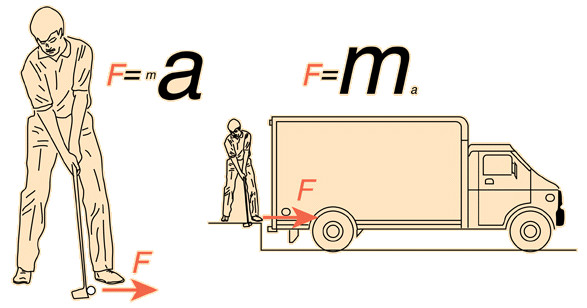
Записанное выше математическое определение ускорения не содержит никакой информации о том, откуда оно появляется, и что заставляет тела ускоряться. Ответы на эти вопросы можно понять, если вспомнить, в чем состоит второй закон Ньютона. Он гласит, что как только появляется ненулевая внешняя сила F¯, действующая на тело массой m, то она неминуемо ведет к появлению ускорения a¯. Соответствующее выражение записывается в виде:
F¯ = m*a¯.
Мы можем, используя эту формулу, определить, в чем измеряется ускорение в данном случае. Сила выражается в ньютонах, а масса в килограммах, тогда получаем:
a¯ = F¯/m [Н/кг].
Ньютон не является базовой единицей в системе СИ, поэтому Н/кг редко применяется в задачах для выражения ускорения. Тем не менее, эту единицу можно встретить в некоторых задачах по динамике движения.
Движение по окружности
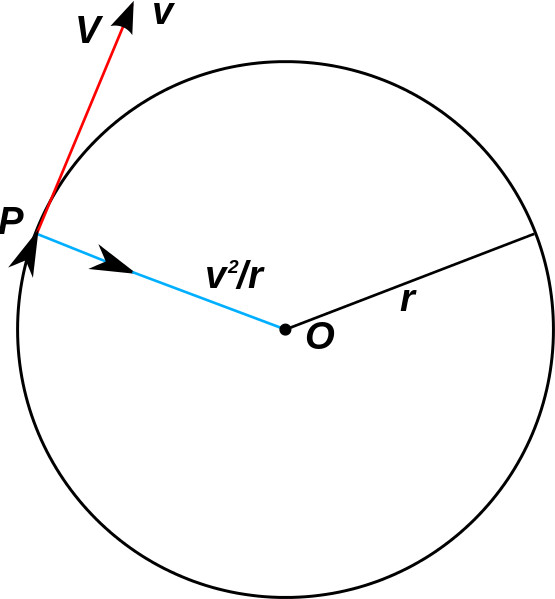
Мы специально выделили в отдельный пункт статьи вопрос перемещения тела по окружности. Дело в том, что во время вращения вокруг некоторой оси изменяться может не только абсолютное значение скорости тела, но и ее направление. Такой характер движения приводит к появлению у тела двух компонентов ускорения: нормального или центростремительного и тангенциального или касательного.
Касательная компонента описывает изменение модуля v¯, поэтому для нее используют единицу м/с². Тем не менее, вращение часто описывают в угловых величинах. Угловое же ускорение выражается в радианах в секунду в квадрате (рад/с²). Напомним, что радиан — это мера угла, который опирается на дугу длиною в один радиус окружности.
Что касается центростремительной компоненты ускорения, то для ее вычисления используют следующую формулу:
ac = v²/r.
Где r — радиус вращения. В чем измеряется центростремительное ускорение? Подставим в это выражение соответствующие единицы для v и r, получим:
ac = [м²/с²/м] = [м/с²].
Таким образом, нормальное ускорение измеряется в тех же единицах, что и полное ускорение (м/с²).
Измерение ускорения свободного падения
Это ускорение (его будем обозначать буквой g) возникает за счет действия на все тела, которые нас окружают, силы тяжести Земли. Среднее значение g на нашей планете равно 9,81 м/с², тем не менее эта величина колеблется на несколько процентов в зависимости от местности.
Наука, которая занимается измерением величины g, называется гравиметрией. Отвечая на вопрос, каким прибором измеряется ускорение, следует сказать, что это или абсолютный, или относительный гравиметр. Абсолютный гравиметр измеряет g в лоб, рассчитывая время падения тела в безвоздушном пространстве с некоторой высоты. Относительный гравиметр представляет собой пружину с грузом, удлинение которой калибруется согласно некоторому известному ускорению g в данной местности.

С помощью гравиметра ускорение свободного падения измеряется в галах. Эта единица названа в честь Галилея, который впервые в истории использовал математический маятник для вычисления ускорения g. Один гал равен сотой части м/с².
Измерение g в данной местности проводят с целью анализа состава горных пород, во время поиска полезных ископаемых или подземных вод. Применяют гравиметры также в археологии и сейсмологии.
Рывок (кинематика) — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Рывок.Рыво́к — векторная физическая величина, характеризующая темп (скорость) изменения ускорения тела. Является третьей производной по времени от радиус-вектора.
Вектор рывка ȷ→{\displaystyle {\vec {\jmath }}} в любой момент времени находится путём дифференцирования вектора ускорения частицы по времени:
- ȷ→=da→dt=d2v→dt2=d3r→dt3,{\displaystyle {\vec {\jmath }}={\frac {d{\vec {a}}}{dt}}={\frac {d^{2}{\vec {v}}}{dt^{2}}}={\frac {d^{3}{\vec {r}}}{dt^{3}}},}
где:
- a→{\displaystyle {\vec {a}}} — ускорение,
- v→{\displaystyle {\vec {v}}} — скорость,
- r→{\displaystyle {\vec {r}}} — радиус-вектор.
Соответственно формулы для движения с постоянным рывком имеют вид:
- a(t)=a0+jt,{\displaystyle a(t)=a_{0}+jt,}
- v(t)=v0+a0t+12jt2,{\displaystyle v(t)=v_{0}+a_{0}t+{\frac {1}{2}}jt^{2},}
- x(t)=x0+v0t+12a0t2+16jt3.{\displaystyle x(t)=x_{0}+v_{0}t+{\frac {1}{2}}a_{0}t^{2}+{\frac {1}{6}}jt^{3}.}
Формулы можно обобщать и далее на более высокие производные радиус-вектора, вводя в разложение координаты в степенной ряд всё новые и новые члены. По традиции или просто для удобства из-за частого использования первые 3 коэффициента в разложении имеют собственные названия: скорость, ускорение и рывок соответственно.
Сила, действующая на ускоренно движущийся заряд (радиационное трение, или реакция излучения), пропорциональна третьей производной координаты (т. e. первой производной ускорения) по времени.
- F→=q26πϵ0c3⋅d3r→dt3{\displaystyle {\vec {F}}={\frac {q^{2}}{6\pi \epsilon _{0}c^{3}}}\cdot {\frac {d^{3}{\vec {r}}}{{dt}^{3}}}}
(в системе СИ).
Транспорт[править | править код]
Понятие рывка применяется при перевозке пассажиров, а также хрупких и ценных грузов.
Пассажир приспосабливается к ускорению, напрягая мышцы и подбирая позу. При изменении ускорения поза, естественно, тоже меняется. Пассажиру нужно дать время, чтобы отреагировать и сменить её — иначе стоячий пассажир потеряет равновесие, а сидячий — ударится. Типичный пример — момент полной остановки вагона метро после процесса торможения: стоячие пассажиры, наклонившиеся вперёд в процессе торможения, не успевают приспособиться к новому ускорению, возникающему в момент остановки, и наклоняются назад.
Аналогично, груз, к которому приложено ускорение, деформируется. Частое и быстрое изменение ускорения означает частую и быструю деформацию, что может привести к разрушению хрупкого груза. Частично рывок можно уменьшить, использовав амортизирующую упаковку.
Для многих приборов и устройств в технических условиях нормируется предельное значение рывка.
Производные большего порядка в транспорте применяются редко. Известный случай, когда радиус-вектор исследовался до четвёртой производной — вывод на орбиту телескопа Хаббла[1].
В теоретической механике[править | править код]
 Рывок в четырёхзвеннике
Рывок в четырёхзвенникеПрименяется в интегрировании по Верле для быстрого численного решения дифференциальных уравнений движения материальных точек.
В статье И. И. Смульского и Я. И. Смульского «Астероид Апофис: эволюция орбиты и возможное использование» используются производные до шестого порядка и ряд Маклорена в программе расчёта[источник не указан 2573 дня].
В работе финского математика К. Зундмана, посвящённой решению «задачи трёх тел», используются высшие производные и ряды[источник не указан 2573 дня].
Понятие рывка находит применение и в задаче о вычислении угловых скоростей и угловых ускорений звеньев шарнирного четырёхзвенника — в ситуации, когда все шарниры лежат на одной прямой[2].
Металлорежущие станки[править | править код]
В металлорежущих станках с электронным управлением изменение ускорения также важно — быстрые деформации инструмента, случающиеся при высоком рывке, преждевременно выводят инструмент из строя.

