Единица измерения сила лоренца: Attention Required! | Cloudflare – Сила Лоренца — Википедия — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Сила Лоренца — Википедия

Материал из Википедии — свободной энциклопедии

Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью v{\displaystyle \mathbf {v} } заряд q {\displaystyle q\ } лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического E{\displaystyle \mathbf {E} } и магнитного B{\displaystyle \mathbf {B} } полей. В Международной системе единиц (СИ) выражается как:

F=q(E+[v×B]).{\displaystyle \mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).}

Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом^[2].

Макроскопическим проявлением силы Лоренца является сила Ампера.

Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца^[3].

Уравнение (единицы СИ)

Заряженная частица

Сила F{\displaystyle \mathbf {F} }, действующая на частицу с электрическим зарядом q{\displaystyle q}, движущуюся со скоростью v{\displaystyle \mathbf {v} }, во внешнем электрическом E{\displaystyle \mathbf {E} } и магнитном B{\displaystyle \mathbf {B} } полях, такова:

F=q(E+v×B),{\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}

где ×{\displaystyle \times } — векторное произведение. Все величины, выделенные жирным, являются векторами. Более явно:

F(r,t,q)=qE(r,t)+qr˙×B(r,t),{\displaystyle \mathbf {F} (\mathbf {r} ,t,q)=q\mathbf {E} (\mathbf {r} ,t)+q\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t),}

где r{\displaystyle \mathbf {r} } — радиус-вектор заряженной частицы, t{\displaystyle t} — время, точкой обозначена производная по времени.

Непрерывное распределение заряда

Для непрерывного распределения заряда, сила Лоренца принимает вид:

dF=dq(E+v×B),{\displaystyle d\mathbf {F} =dq\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),}

где dF{\displaystyle d\mathbf {F} } — сила, действующая на маленький элемент dq{\displaystyle dq}.

Ковариантная запись

4-сила выражается через вектор 4-скорости частицы по формуле

Fμ=qFνμuν,{\displaystyle {\mathcal {F}}^{\mu }=qF^{\nu \mu }u_{\nu },}

где Fμ{\displaystyle {\mathcal {F}}^{\mu }} — 4-сила, q{\displaystyle q} — заряд частицы, Fνμ{\displaystyle F^{\nu \mu }} — тензор электромагнитного поля, uν{\displaystyle u_{\nu }} — 4-скорость.

Частные случаи

Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)

В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r{\displaystyle r} (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:

СГС	СИ
mv2r=\|q\|cvB⇒r=cm\|q\|⋅vB{\displaystyle {mv^{2} \over r}={\|q\| \over c}vB\Rightarrow r={cm \over \|q\|}\cdot {v \over B}}	mv2r=\|q\|vB⇒r=m\|q\|⋅vB{\displaystyle {mv^{2} \over r}=\|q\|vB\Rightarrow r={m \over \|q\|}\cdot {v \over B}}

Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости v {\displaystyle v\ }, намного меньшей скорости света, круговая частота ω {\displaystyle \omega \ } не зависит от v {\displaystyle v\ }:

СГС	СИ
ω=\|q\|Bmc{\displaystyle \omega ={\|q\|B \over mc}}	ω=\|q\|Bm{\displaystyle \omega ={\|q\|B \over m}}

Если заряженная частица движется в магнитном поле так, что вектор скорости v {\displaystyle v\ } составляет с вектором магнитной индукции B{\displaystyle \mathbf {B} } угол α {\displaystyle \alpha \ }, то траекторией движения частицы является винтовая линия с радиусом r {\displaystyle r\ } и шагом винта h {\displaystyle h\ }:

СГС	СИ
r=mc\|q\|⋅vsin⁡αB{\displaystyle r={mc \over \|q\|}\cdot {v\sin \alpha \over B}}, h=2πB⋅mc\|q\|⋅vcos⁡α{\displaystyle h={2\pi \over B}\cdot {mc \over \|q\|}\cdot v\cos \alpha }	r=m\|q\|⋅vsin⁡αB{\displaystyle r={m \over \|q\|}\cdot {v\sin \alpha \over B}}, h=2πB⋅m\|q\|⋅vcos⁡α{\displaystyle h={2\pi \over B}\cdot {m \over \|q\|}\cdot v\cos \alpha }

Использование

Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне

См. также

Примечания

↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.

Формула Лоренца — Лоренца — Википедия

Фо́рмула Ло́ренца — Ло́ренца связывает показатель преломления вещества с электронной поляризуемостью частиц (атомов, ионов, молекул), из которых оно состоит. Формулу получили датский физик Людвиг В. Лоренц (дат. Ludvig Valentin Lorenz ) и голландский физик Хендрик А. Лоренц (нидерл. Hendrik Antoon Lorentz) в 1880 году независимо друг от друга^[1]^[2].

Если вещество состоит из частиц одного сорта, то формула имеет вид^[3]:

n2−1n2+2=4π3Nα,{\displaystyle {\frac {n^{2}-1}{n^{2}+2}}={\frac {4\pi }{3}}N\alpha ,}

где n{\displaystyle n} — показатель преломления, N{\displaystyle N} — количество частиц в единице объёма, а α{\displaystyle \alpha } — их поляризуемость.

Уточним, что под поляризуемостью частицы здесь понимается коэффициент α{\displaystyle \alpha }, связывающий напряжённость электрического поля E{\displaystyle {\boldsymbol {E}}}, действующего на частицу, с дипольным моментом p{\displaystyle {\boldsymbol {p}}}, образующимся у частицы под действием этого поля^[4]:

p=αE.{\displaystyle {\boldsymbol {p}}=\alpha {\boldsymbol {E}}.}

Здесь и далее жирным шрифтом выделяются векторные величины.

Формулу записывают также в виде:

n2−1n2+2⋅Mρ=4π3NAα,{\displaystyle {\frac {n^{2}-1}{n^{2}+2}}\cdot {\frac {M}{\rho }}={\frac {4\pi }{3}}N_{\mathrm {A} }\alpha ,}

где M{\displaystyle M} — молекулярная масса вещества, ρ{\displaystyle \rho } — его плотность, а NA{\displaystyle N_{\mathrm {A} }} — постоянная Авогадро. При этом величину 4π3NAα{\displaystyle {\frac {4\pi }{3}}N_{\mathrm {A} }\alpha } называют молекулярной рефракцией.

Если вещество состоит из частиц нескольких сортов с поляризуемостями αi{\displaystyle \alpha _{i}} и объёмными концентрациями Ni{\displaystyle N_{i}}, то формула принимает вид:

n2−1n2+2=4π3[N1α1+N2α2+⋯+Nnαn].{\displaystyle {\frac {n^{2}-1}{n^{2}+2}}={\frac {4\pi }{3}}\left[N_{1}\alpha _{1}+N_{2}\alpha _{2}+\cdots +N_{n}\alpha _{n}\right].}

Вывод формулы основан на рассмотрении микроскопического поля и его взаимодействия с атомами, молекулами и ионами вещества. При выводе предполагается, что среда является изотропной, а составляющие её частицы собственным дипольным моментом не обладают^[5].

Воздействие внешнего электромагнитного поля с относительно высокими частотами, соответствующими видимому и УФ-диапазону спектра, приводит к смещению только электронных оболочек относительно атомных ядер, в то время как более массивные частицы (атомы и ионы) за период колебаний поля сместиться с занимаемых ими мест не успевают. Соответственно, в поляризацию среды вносит вклад только электронная поляризация, и показатель преломления оказывается связан с электронной поляризуемостью частиц формулой Лоренца — Лоренца.

При более низких частотах колебаний поля атомы и ионы успевают смещаться под действием поля, и поэтому вносят свой вклад в общую поляризацию. В результате становится необходимым, помимо электронной поляризуемости, учитывать атомную и ионную поляризуемости. Аналогом формулы Лоренца — Лоренца для постоянных полей является формула Клаузиуса — Моссотти^[6], описывающая связь диэлектрической проницаемости вещества с поляризуемостями составляющих его частиц:

ε−1ε+2⋅Mρ=4π3NAα.{\displaystyle {\frac {\varepsilon -1}{\varepsilon +2}}\cdot {\frac {M}{\rho }}={\frac {4\pi }{3}}N_{\mathrm {A} }\alpha .}

В полярных диэлектриках частицы среды обладают собственным дипольным моментом, то есть таким, который они имеют и в отсутствие внешнего электрического поля. Непосредственное применение формулы Лоренца — Лоренца в её обычном виде в таких случаях невозможно. Дальнейшим развитием формулы Лоренца — Лоренца, пригодным в том числе и для случая полярных диэлектриков (но для относительно низких частот колебаний поля), стала формула формула Ланжевена — Дебая^[7].

Формула Лоренца — Лоренца лежит в основе структурной рефрактометрии. Она широко используется при изучении и контроле составов различных веществ, для исследования их строения и превращений, происходящих в результате протекания химических реакций^[8]^[9].

Формула Лоренца — Лоренца является одним из оснований теории дисперсии света в классическом приближении^[5]^[10]. В этой теории оптические электроны рассматриваются как дипольные осцилляторы, характеризуемые собственной частотой ω0{\displaystyle \omega _{0}}. В случае, когда затуханием колебаний электронов можно пренебречь^[11], уравнение колебаний имеет вид:

r¨+ω02r=emE(t),{\displaystyle {\ddot {\boldsymbol {r}}}+\omega _{0}^{2}{\boldsymbol {r}}={\frac {e}{m}}{\boldsymbol {E}}(t),}

где r{\displaystyle {\boldsymbol {r}}} — смещение электрона из положения равновесия, r¨{\displaystyle {\ddot {\boldsymbol {r}}}} — вторая производная r{\displaystyle {\boldsymbol {r}}} по времени (ускорение электрона), e{\displaystyle e} и m{\displaystyle m} — заряд и масса электрона соответственно, а E(t){\displaystyle {\boldsymbol {E}}(t)} — напряжённость электрического поля.

В результате решения уравнения для монохроматического поля, изменяющегося с частотой ω{\displaystyle \omega }, сначала получается зависимость r(t){\displaystyle {\boldsymbol {r}}(t)}, а затем и поляризуемость α{\displaystyle \alpha }:

α=e2m1ω02−ω2.{\displaystyle \alpha ={\frac {e^{2}}{m}}{\frac {1}{\omega _{0}^{2}-\omega ^{2}}}.}

После подстановки полученного выражения в формулу Лоренца — Лоренца возникает дисперсионная формула вида:

n2−1n2+2=4πNe23m1ω02−ω2.{\displaystyle {\frac {n^{2}-1}{n^{2}+2}}={\frac {4\pi Ne^{2}}{3m}}{\frac {1}{\omega _{0}^{2}-\omega ^{2}}}.}

Обычно свой вклад в формирование показателя преломления вносят несколько линий поглощения с частотами ω0i{\displaystyle \omega _{0i}}. В таком случае дисперсионная формула принимает вид:

n2−1n2+2=4πNe23m∑ifiω0i2−ω2,{\displaystyle {\frac {n^{2}-1}{n^{2}+2}}={\frac {4\pi Ne^{2}}{3m}}\sum _{i}{\frac {f_{i}}{\omega _{0i}^{2}-\omega ^{2}}},}

где fi{\displaystyle f_{i}} — безразмерные коэффициенты (силы осцилляторов), показывающие эффективность участия соответствующих осцилляторов в явлениях дисперсии и удовлетворяющие правилу ∑ifi=1{\displaystyle \sum _{i}f_{i}=1}.

Хендрик А. Лоренц

Людвиг В. Лоренц

Статьи Людвига В. Лоренца^[12] и Хендрика А. Лоренца^[13] с сообщениями о получении формулы были опубликованы практически одновременно в 1880 году. М. Борн и Э. Вольф такое одновременное получение результата учёными с почти одинаковыми (в оригинальном написании) фамилиями называют «удивительным совпадением»^[5].

Сам Хендрик Лоренц в своей книге писал так: «…этот результат был найден Лоренцом в Копенгагене за несколько времени до того, как я вывел его из электромагнитной теории света, что, конечно, является любопытным случаем совпадения»^[14].

Хотя Хендрик А. Лоренц не был тем, кто первым вывел формулу, и на эту роль не претендовал, в её наименовании, обычно употребляемом в англоязычной литературе, его имя стоит в начале: «Lorentz — Lorenz equation», «Lorentz — Lorenz formula» или «Lorentz — Lorenz relation».

Ранее, до того, как в русской научно-технической литературе сложилась общепринятая традиция, использовались различные варианты наименования формулы, включая такие, как формула «Лоренц — Лоренца», «Лоренц — Лорентца», «Лорентц — Лоренца» и «Лорентца — Лоренца».

В своё время значение формулы Лоренца — Лоренца не исчерпывалось только тем, что она дала возможность количественного описания формирования значения показателя преломления веществ. Как писали М. Борн и Э. Вольф, «…она служит мостом, связывающим феноменологическую теорию Максвелла с теорией атомного строения вещества»^[5].

Несмотря на солидный «возраст», формулу Лоренца — Лоренца в настоящее время не только достаточно широко применяют, но и продолжают развивать, расширяя возможности её использования^[15].

↑ Лоренца — Лоренца формула // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 611. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
↑ Лоренца — Лоренца формула / Короленко П. В. // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
↑ Здесь и далее используется система единиц измерения СГС.
↑ Гусев А. А. Поляризуемость // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 72-74. — 704 с. — 40 000 экз.
↑ ¹ ² ³ ⁴ Борн М., Вольф Э. Основы оптики. Изд. 2-е. — М.: «Наука», 1973. — 720 с. — 20 000 экз.
↑ Леванюк А. П. Клаузиуса — Мосотти формула // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. Добротность — Магнитооптика. — С. 373-374. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
↑ Ланжевена — Дебая формула. Статья в Физическом энциклопедическом словаре.
↑ Бацанов С. С. Структурная рефрактометрия. Изд. 2-е. — М.: «Высшая школа», 1976. — 304 с.
↑ Иоффе Б. В. Рефрактометрические методы химии. — Л.: «Химия», Ленинградское отделение, 1983. — 350 с.

↑ Бутиков Е. И. Оптика. — 2-е изд., перераб. и доп.. — СПб.: Невский Диалект, БХВ-Петербург, 2003. — 480 с. — 3 000 экз. — ISBN 5-94157-380-4.
↑ Затухание мало, если частота света существенно отличается от частот, на которых располагаются линии поглощения вещества.
↑ L. Lorenz. «Über die Refractionsconstante, » Ann. Phys. 1880. V. 11, 70—103.
↑ H. A. Lorentz, Über die Beziehung zwischen der Fortpflanzungsgeschwindigkeit des Lichtes und der Körperdichte. Ann. Phys. 1880. V. 9, 641—665.
↑ Лорентц Г. А. Теория электронов и её применение к явлениям света и теплового излучения. — М.: Государственное издательство технико-теоретической литературы, 1956. — С. 215. — 472 с. — (Классики естествознания). — 5 000 экз.
↑ Mário G. Silveirinha. Generalized Lorentz-Lorenz formulas for microstructured materials. Phys. Rev. B. 2007, Vol.76, Issue 24, 245117, 17 December 2007.

Сила Лоренца — Википедия. Что такое Сила Лоренца

[1], иначе говоря, со стороны электрического E{\displaystyle \mathbf {E} } и магнитного B{\displaystyle \mathbf {B} } полей. В Международной системе единиц (СИ) выражается как:

F=q(E+[v×B]).{\displaystyle \mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).}

Макроскопическим проявлением силы Лоренца является сила Ампера.

[3].

Уравнение (единицы СИ)

Заряженная частица

$\mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).$

F=q(E+v×B),{\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}

где ×{\displaystyle \times } — векторное произведение. Все величины, выделенные жирным, являются векторами. Более явно:

F(r,t,q)=qE(r,t)+qr˙×B(r,t),{\displaystyle \mathbf {F} (\mathbf {r} ,t,q)=q\mathbf {E} (\mathbf {r} ,t)+q\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t),}

Непрерывное распределение заряда

Для непрерывного распределения заряда, сила Лоренца принимает вид:

dF=dq(E+v×B),{\displaystyle d\mathbf {F} =dq\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),}

где dF{\displaystyle d\mathbf {F} } — сила, действующая на маленький элемент dq{\displaystyle dq}.

Ковариантная запись

4-сила выражается через вектор 4-скорости частицы по формуле

Fμ=qFνμuν,{\displaystyle {\mathcal {F}}^{\mu }=qF^{\nu \mu }u_{\nu },}

Частные случаи

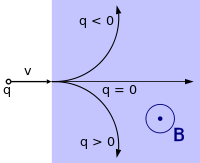$u_{\nu }$ Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)

СГС	СИ
mv2r=\|q\|cvB⇒r=cm\|q\|⋅vB{\displaystyle {mv^{2} \over r}={\|q\| \over c}vB\Rightarrow r={cm \over \|q\|}\cdot {v \over B}}	mv2r=\|q\|vB⇒r=m\|q\|⋅vB{\displaystyle {mv^{2} \over r}=\|q\|vB\Rightarrow r={m \over \|q\|}\cdot {v \over B}}

СГС	СИ
ω=\|q\|Bmc{\displaystyle \omega ={\|q\|B \over mc}}	ω=\|q\|Bm{\displaystyle \omega ={\|q\|B \over m}}

СГС	СИ
r=mc\|q\|⋅vsin⁡αB{\displaystyle r={mc \over \|q\|}\cdot {v\sin \alpha \over B}}, h=2πB⋅mc\|q\|⋅vcos⁡α{\displaystyle h={2\pi \over B}\cdot {mc \over \|q\|}\cdot v\cos \alpha }	r=m\|q\|⋅vsin⁡αB{\displaystyle r={m \over \|q\|}\cdot {v\sin \alpha \over B}}, h=2πB⋅m\|q\|⋅vcos⁡α{\displaystyle h={2\pi \over B}\cdot {m \over \|q\|}\cdot v\cos \alpha }

Использование

Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы ${\displaystyle h={2\pi \over B}\cdot {m \over$

Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне

См. также

Примечания

↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.

Сила Лоренца

msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist> msimagelist>

	Адроны
	Альфа-распад
	Альфа-частица
	Аннигиляция
	Антивещество
	Антинейтрон
	Антипротон
	Античастицы
	Атом
	Атомная единица массы
	Атомная электростанция
	Барионное число
	Барионы
	Бета-распад
	Бетатрон
	Бета-частицы
	Бозе – Эйнштейна статистика
	Бозоны
	Большой адронный коллайдер
	Большой Взрыв
	Боттом. Боттомоний
	Брейта-Вигнера формула
	Быстрота
	Векторная доминантность
	Великое объединение
	Взаимодействие частиц
	Вильсона камера
	Виртуальные частицы
	Водорода атом
	Возбуждённые состояния ядер
	Волновая функция
	Волновое уравнение
	Волны де Бройля
	Встречные пучки
	Гамильтониан
	Гамма-излучение
	Гамма-квант
	Гамма-спектрометр
	Гамма-спектроскопия
	Гаусса распределение
	Гейгера счётчик
	Гигантский дипольный резонанс
	Гиперядра
	Глюоны
	Годоскоп
	Гравитационное взаимодействие
	Дейтрон
	Деление атомных ядер
	Детекторы частиц
	Дирака уравнение
	Дифракция частиц
	Доза излучения
	Дозиметр
	Доплера эффект
	Единая теория поля
	Зарядовое сопряжение
	Зеркальные ядра
	Избыток массы (дефект массы)
	Изобары
	Изомерия ядерная
	Изоспин
	Изоспиновый мультиплет
	Изотопов разделение
	Изотопы
	Ионизирующее излучение
	Искровая камера
	Квантовая механика
	Квантовая теория поля
	Квантовые операторы
	Квантовые числа
	Квантовый переход
	Квант света
	Кварк-глюонная плазма
	Кварки
	Коллайдер
	Комбинированная инверсия
	Комптона эффект
	Комптоновская длина волны
	Конверсия внутренняя
	Константы связи
	Конфайнмент
	Корпускулярно волновой дуализм
	Космические лучи
	Критическая масса
	Лептоны
	Линейные ускорители
	Лоренца преобразования
	Лоренца сила
	Магические ядра
	Магнитный дипольный момент ядра
	Магнитный спектрометр
	Максвелла уравнения
	Масса частицы
	Масс-спектрометр
	Массовое число
	Масштабная инвариантность
	Мезоны
	Мессбауэра эффект
	Меченые атомы
	Микротрон
	Нейтрино
	Нейтрон
	Нейтронная звезда
	Нейтронная физика
	Неопределённостей соотношения
	Нормы радиационной безопасности
	Нуклеосинтез
	Нуклид
	Нуклон
	Обращение времени
	Орбитальный момент
	Осциллятор
	Отбора правила
	Пар образование
	Период полураспада
	Планка постоянная
	Планка формула
	Позитрон
	Поляризация
	Поляризация вакуума
	Потенциальная яма
	Потенциальный барьер
	Принцип Паули
	Принцип суперпозиции
	Промежуточные W-, Z-бозоны
	Пропагатор
	Пропорциональный счётчик
	Пространственная инверсия
	Пространственная четность
	Протон
	Пуассона распределение
	Пузырьковая камера
	Радиационный фон
	Радиоактивность
	Радиоактивные семейства
	Радиометрия
	Расходимости
	Резерфорда опыт
	Резонансы (резонансные частицы)
	Реликтовое микроволновое излучение
	Светимость ускорителя
	Сечение эффективное
	Сильное взаимодействие
	Синтеза реакции
	Синхротрон
	Синхрофазотрон
	Синхроциклотрон
	Система единиц измерений
	Слабое взаимодействие
	Солнечные нейтрино
	Сохранения законы
	Спаривания эффект
	Спин
	Спин-орбитальное взаимодействие
	Спиральность
	Стандартная модель
	Статистика
	Странные частицы
	Струи адронные
	Субатомные частицы
	Суперсимметрия
	Сферическая система координат
	Тёмная материя
	Термоядерные реакции
	Термоядерный реактор
	Тормозное излучение
	Трансурановые элементы
	Трек
	Туннельный эффект
	Ускорители заряженных частиц
	Фазотрон
	Фейнмана диаграммы
	Фермионы
	Формфактор
	Фотон
	Фотоэффект
	Фундаментальная длина
	Хиггса бозон
	Цвет
	Цепные ядерные реакции
	Цикл CNO
	Циклические ускорители
	Циклотрон
	Чарм. Чармоний
	Черенковский счётчик
	Черенковсое излучение
	Черные дыры
	Шредингера уравнение
	Электрический квадрупольный момент ядра
	Электромагнитное взаимодействие
	Электрон
	Электрослабое взаимодействие
	Элементарные частицы
	Ядерная физика
	Ядерная энергия
	Ядерные модели
	Ядерные реакции
	Ядерный взрыв
	Ядерный реактор
	Ядра энергия связи
	Ядро атомное
	Ядерный магнитный резонанс (ЯМР)

Сила Лоренца — это… Что такое Сила Лоренца?

Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического и магнитного полей. Выражается в СИ как:

Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено Хевисайдом^[2].

Макроскопическим проявлением силы Лоренца является сила Ампера.

Уравнение (единицы СИ)

Заряженная частица

Сила Лоренца f действующая на заряженную частицу (заряда q) при движении (с постоянной скоростью v). E поле и B поле меняются в пространстве и во времени.

Сила F действующая на частицу с электрическим зарядом q, движущуюся с постоянной скоростью v, во внешнем электрическом E и магнитном B полях, такова:

где × векторное произведение. Все величины выделенные жирным являются векторами. Более явно:

где r — радиус-вектор заряженной частицы, t — время, точкой обозначена производная по времени.

Непрерывное распределение заряда

Сила Лоренца (на единичный 3-объём) f действующая на непрерывное распределение заряда (зарядовая плотность ρ) при движении. 3-плотность потока J соответствует движению заряженного элемента dq в объеме dV .

Для непрерывного распределения заряда, сила Лоренца принимает вид:

где dF — сила, действующая на маленький элемент dq.

Ковариантная запись

4-сила выражается через вектор 4-скорости частицы по формуле

, где — 4-сила, q — заряд частицы, — тензор электромагнитного поля, — 4-скорость.

Частные случаи

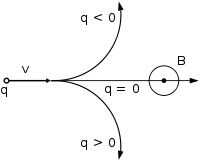$u_\nu$ Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)

В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:

Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости , намного меньшей скорости света, круговая частота не зависит от :

Если заряженная частица движется в магнитном поле так, что вектор скорости составляет с вектором магнитной индукции угол , то траекторией движения частицы является винтовая линия с радиусом и шагом винта :

Применение силы Лоренца

В электроприборах

Основным применением силы Лоренца (точнее, её частного случая — силы Ампера) являются электрические машины (электродвигатели и генераторы). Сила Лоренца широко используется в электронных приборах для воздействия на заряженные частицы (электроны и иногда ионы), например, в телевизионных электронно-лучевых трубках, а также в масс-спектрометрии и МГД генераторах.

В ускорителях заряженных частиц

Сила Лоренца также используется в ускорителях заряженных частиц, задавая орбиту, по которой движутся эти частицы.

В вооружении

См. рельсотрон, или, как его ещё называют, рэйлган («рельсовая пушка»)

Другие применения

Примечания

↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.

Сила Лоренца — Википедия

Уравнение (единицы СИ)

Заряженная частица

Непрерывное распределение заряда

Ковариантная запись

Частные случаи

Использование

См. также

Примечания

Формула Лоренца — Лоренца — Википедия

Сила Лоренца — Википедия. Что такое Сила Лоренца

Уравнение (единицы СИ)

Заряженная частица

Непрерывное распределение заряда

Ковариантная запись

Частные случаи

Использование

См. также

Примечания

Сила Лоренца

Сила Лоренца — это… Что такое Сила Лоренца?

Уравнение (единицы СИ)

Заряженная частица

Непрерывное распределение заряда

Ковариантная запись

Частные случаи

Применение силы Лоренца

В электроприборах

В ускорителях заряженных частиц

В вооружении

Другие применения

Примечания

См. также

alexxlab

Добавить комментарий Отменить ответ

Рубрики