Какая единица используется для измерения электродвижущей силы — MOREREMONTA
ЭДС. Численно электродвижущая сила измеряется работой, совершаемой источником электрической энергии при переносе единичного положительного заряда по всей замкнутой цепи. Если источник энергии, совершая работу A, обеспечивает перенос по всей замкнутой цепи заряда q, то его электродвижущая сила (Е) будет равна
За единицу измерения электродвижущей силы в системе СИ принимается вольт (в). Источник электрической энергии обладает эдс в 1 вольт, если при перемещении по всей замкнутой цепи заряда в 1 кулон совершается работа, равная 1 джоулю. Физическая природа электродвижущих сил в разных источниках весьма различна.
Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре при изменении тока, протекающего по контуру. При изменении тока I в контуре пропорционально меняется и магнитный поток Bчерез поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС
Понятие родственно понятию взаимоиндукции, являясь его частным случаем.
Мощность. Мощность – это работа производимая единицу времени.Мощность-это работа производимая в еденицу времени, т.е для переноса заряда в эл. цепи или в замкнутой затрачивается энергия, которая равна А=U*Q так как кол-во электричества равна произведению силы тока , то Q=I*t отсюда следует что A=U*I*t. P=A/t=U*Q/t=U*I=I*t*R=P=U*I(И)
1Вт=1000мВ, 1кВт=1000В, Pr=Pп+Po-формула баланса мощности. Pr-мощность генератора(ЭДС)
Pr=Е*I,Pп=I*U полезная мощность, т.е мощность которая расходуется без потерь. Po=I^2*R-теряемая мощность. Для того что бы цепь функционировала необходимо соблюдать баланс мощности в эл.цепи.
12.Закон Ома для участка цепи.
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого проводника и обратно пропорциональна его сопротивлению:
I = U / R; [A = В / Ом]
13.Закон Ома для полной цепи.
Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.

 — ЭДС источника напряжения(В),
— ЭДС источника напряжения(В),  — сила тока в цепи (А),
— сила тока в цепи (А),  — сопротивление всех внешних элементов цепи(Ом),
— сопротивление всех внешних элементов цепи(Ом),  — внутреннее сопротивление источника напряжения(Ом) .1)E=I(R+r)? 2)R+r=E/I
— внутреннее сопротивление источника напряжения(Ом) .1)E=I(R+r)? 2)R+r=E/I
14.Последовательное, параллельное соединение резисторов, эквивалентное сопротивление. Распределение токов и напряжения.
При последовательном соединении нескольких резисторов конец первого резисторасоединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I. 
Uэ=U1+U2+U3. Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Rэ=R1+R2+R3, Iэ=I1=I2=I3, Uэ=U1+U2+U3.
При последовательном соединении сопротивление цепи увеличивается.
Параллельное соединение резисторов. Параллельным соединением сопротивлений называется такое соединение, при котором к одному зажиму источника подключаются начала сопротивлений, а к другому зажиму — концы.

Общее сопротивление параллельно включенных сопротивлений определяется по формуле

Общее сопротивление параллельно включенных сопротивлений всегда меньше наименьшего сопротивления, входящего в данное соединение.
при параллельном соединении сопротивлений напряжения на них равны между собой. Uэ=U1=U2=U3 В цепи притекает ток I, а токи I1, I2, I3 утекают из нее. Так как движущиеся электрические заряды не скапливаются в точке, то очевидно, что суммарный заряд, притекающий к точке разветвления, равен суммарному заряду утекающему от нее:Iэ=I1+I2+I3 Следовательно, третье свойство параллельного соединения может сформулирована так: Величина тока в не разветвленной части цепи равна сумме токов в параллельных ветвях. Для двух парал.резисторов: 
Для поддержания электрического тока в проводнике требуется внешний источник энергии, создающий все время разность потенциалов между концами этого проводника. Такие источники энергии получили название источников электрической энергии (или источников тока).
Источники электрической энергии обладают определенной электродвижущей силой (сокращенно ЭДС), которая создает и длительное время поддерживает разность потенциалов между концами проводника. Иногда говорят, что ЭДС создает электрический ток в цепи. Нужно помнить об условности такого определения, так как выше мы уже установили, что причина возникновения и существования электрического тока — электрическое поле.
Источник электрической энергии производит определенную работу, перемещая электрические заряды по всей замкнутой цепи..
Определение: Работа, совершаемая источником электрической энергии при переносе единицы положительного заряда по всей замкнутой цепи, называется ЭДС источника
За единицу измерения электродвижущей силы принят вольт (сокращенно вольт обозначается буквой В или V — «вэ» латинское).
ЭДС источника электрической энергии равна одному вольту, если при перемещении одного кулона электричества по всей замкнутой, цепи источник электрической энергии совершает работу, равную одному джоулю:
В практике для измерения ЭДС используются как более крупные, так и более мелкие единицы, а именно:
1 киловольт (кВ, kV), равный 1000 В;
1 милливольт (мВ, mV), равный одной тысячной доле вольта (10-3 В),
1 микровольт (мкВ, μV), равный одной миллионной доле вольта (10-6 В).
Очевидно, что 1 кВ = 1000 В; 1 В = 1000 мВ = 1 000 000 мкВ; 1 мВ= 1000 мкВ.
В настоящее, время существует несколько видов источников электрической энергии. Впервые в качестве источника электрической энергии была использована гальваническая батарея, состоящая из нескольких цинковых и медных кружков, между которыми была проложена кожа, смоченная в подкисленной воде. В гальванической батарее химическая энергия превращалась в электрическую (подробнее об этом будет рассказано в главе XVI). Свое название гальваническая батарея получила по имени итальянского физиолога Луиджи Гальвани (1737—1798), одного из основателей учения об электричестве.
Многочисленные опыты по усовершенствованию и практическому использованию гальванических батарей были проведены русским ученым Василием Владимировичем Петровым. Еще в начале прошлого века он создал самую большую в мире гальваническую батарею и использовал ее для ряда блестящих опытов.
Источники электрической энергии, работающие по принципу преобразования химической энергии в электрическую, называются химическими источниками электрической энергии.
Другим основным источником электрической энергий, получившим широкое применение в электротехнике и радиотехнике, является генератор. В генераторах механическая энергия преобразуется в электрическую.
На электрических схемах источники электрической энергии и генераторы обозначаются так, как это показано на рис. 1.
Рисунок 1. Условные обозначения источников электрической энергии: а — источник ЭДС, общее обозначение, б — источник тока, общее обозначение; в — химический источник электрической энергии; г — батарея химических источников; д — источник потоянного напряжения; е — источник переменного нарияжения; ж — генератор.
У химических источников электрической энергии и у генераторов электродвижущая сила проявляется одинаково, создавая на зажимах источника разность потенциалов и поддерживая ее длительное время. Эти зажимы называются
От источников электрической энергии электрическая энергия передается по проводам к ее потребителям (электрические лампы, электродвигатели, электрические дуги, электронагревательные приборы и т. д.).
Определение : Совокупность источника электрической энергии, ее потребителя и соединительных проводов называется электрической цепью.
Простейшая электрическая цепь показана на рис. 2.
Рисунок 2. Простейшая электрическая цепь: Б — источник электрической энергии; SA — выключатель; EL — потребитель электрической энергии (лампа).
Для того чтобы по цепи проходил электрический ток, она должна быть замкнутой. По замкнутой электрической цепи непрерывно проходит ток, так как между полюсами источника электрической энергии существует некоторая разность потенциалов. Эта разность потенциалов называется
Для измерения величины ЭДС и напряжения применяется прибор, называемый вольтметром. Если вольтметр подключить непосредственно к полюсам источника электрической энергии, то при разомкнутой электрической цепи он покажет ЭДС источника электрической энергии, а при замкнутой — напряжение на его зажимах: (рис. 3).
Рисунок 3. Измерение ЭДС и напряжения источника электрической энергии: а— измерение ЭДС источника электрической энергии; б — измерение напряжения на зажимах источника электрической энергии..
Заметим, что напряжение на зажимах источника электрической энергии всегда меньше его ЭДС.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Что такое ЭДС (электродвижущая сила) в физике? Электрический ток понятен далеко не каждому. Как космическая даль, только под самым носом. Вообще, он и ученым понятен не до конца. Достаточно вспомнить Николу Тесла с его знаменитыми экспериментами, на века опередившими свое время и даже в наши дни остающимися в ореоле тайны. Сегодня мы не разгадываем больших тайн, но пытаемся разобраться в том,
Определение ЭДС в физике
ЭДС – электродвижущая сила. Обозначается буквой E или маленькой греческой буквой эпсилон.
Электродвижущая сила — скалярная физическая величина, характеризующая работу сторонних сил (сил неэлектрического происхождения), действующих в электрических цепях переменного и постоянного тока.
ЭДС, как и напряжение, измеряется в вольтах. Однако ЭДС и напряжение – явления разные.
Напряжение (между точками А и Б) – физическая величина, равная работе эффективного электрического поля, совершаемой при переносе единичного пробного заряда из одной точки в другую.
Объясняем суть ЭДС «на пальцах»
Чтобы разобраться в том, что есть что, можно привести пример-аналогию. Представим, что у нас есть водонапорная башня, полностью заполненная водой. Сравним эту башню с батарейкой.
 Схема водонапорной башни
Схема водонапорной башни
Вода оказывает максимальное давление на дно башни, когда башня заполнена полностью. Соответственно, чем меньше воды в башне, тем слабее давление и напор вытекающей из крана воды. Если открыть кран, вода будет постепенно вытекать сначала под сильным напором, а потом все медленнее, пока напор не ослабнет совсем. Здесь напряжение – это то давление, которое вода оказывает на дно. За уровень нулевого напряжения примем само дно башни.
 Водокачка
Водокачка
То же самое и с батарейкой. Сначала мы включаем наш источник тока (батарейку) в цепь, замыкая ее. Пусть это будут часы или фонарик. Пока уровень напряжения достаточный и батарейка не разрядилась, фонарик светит ярко, затем постепенно гаснет, пока не потухнет совсем.
Но как сделать так, чтобы напор не иссякал? Иными словами, как поддерживать в башне постоянный уровень воды, а на полюсах источника тока – постоянную разность потенциалов. По примеру башни ЭДС представляется как бы насосом, который обеспечивает приток в башню новой воды.
 Советская батарейка
Советская батарейка
Природа ЭДС
Причина возникновения ЭДС в разных источниках тока разная. По природе возникновения различают следующие типы:
- Химическая ЭДС. Возникает в батарейках и аккумуляторах вследствие химических реакций.
- Термо ЭДС. Возникает, когда находящиеся при разных температурах контакты разнородных проводников соединены.
- ЭДС индукции. Возникает в генераторе при помещении вращающегося проводника в магнитное поле. ЭДС будет наводиться в проводнике, когда проводник пересекает силовые линии постоянного магнитного поля или когда магнитное поле изменяется по величине.
- Фотоэлектрическая ЭДС. Возникновению этой ЭДС способствует явление внешнего или внутреннего фотоэффекта.
- Пьезоэлектрическая ЭДС. ЭДС возникает при растяжении или сдавливании веществ.
Дорогие друзья, сегодня мы рассмотрели тему «ЭДС для чайников». Как видим, ЭДС – сила неэлектрического происхождения, которая поддерживает протекание электрического тока в цепи. Если Вы хотите узнать, как решаются задачи с ЭДС, советуем обратиться к нашим авторам – скрупулезно отобранным и проверенным специалистам, которые быстро и доходчиво разъяснят ход решения любой тематической задачи. И по традиции в конце предлагаем Вам посмотреть обучающее видео. Приятного просмотра и успехов в учебе!
Электродвижущая сила — Википедия
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил, то есть любых сил неэлектрического происхождения, действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура[1][2].
По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил E→ex{\displaystyle {\vec {E}}_{ex}}, под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд к величине этого заряда. Тогда в замкнутом контуре L{\displaystyle L} ЭДС будет равна:
- E=∮LE→ex⋅dl→,{\displaystyle {\mathcal {E}}=\oint \limits _{L}{\vec {E}}_{ex}\cdot {\vec {dl}},}
где dl→{\displaystyle {\vec {dl}}} — элемент контура.
ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами источника тока вне самого́ источника равна нулю.
ЭДС и закон Ома
Электродвижущая сила источника связана с электрическим током, протекающим в цепи, соотношениями закона Ома. Закон Ома для неоднородного участка цепи имеет вид[1]:
- φ1−φ2+E=IR,{\displaystyle \varphi _{1}-\varphi _{2}+{\mathcal {E}}=IR,}
где φ1−φ2{\displaystyle \varphi _{1}-\varphi _{2}} — разность между значениями потенциала в начале и в конце участка цепи, I{\displaystyle I} — сила тока, текущего по участку, а R{\displaystyle R} — сопротивление участка.
Если точки 1 и 2 совпадают (цепь замкнута), то φ1−φ2=0{\displaystyle \varphi _{1}-\varphi _{2}=0} и предыдущая формула переходит в формулу закона Ома для замкнутой цепи[1]:
- E=IR,{\displaystyle {\mathcal {E}}=IR,}
где теперь R{\displaystyle R} — полное сопротивление всей цепи.
В общем случае полное сопротивление цепи складывается из сопротивления внешнего по отношению к источнику тока участка цепи (Re{\displaystyle R_{e}}) и внутреннего сопротивления самого́ источника тока (r{\displaystyle r}). С учётом этого следует:
- E=IRe+Ir.{\displaystyle {\mathcal {E}}=IR_{e}+Ir.}
ЭДС источника тока
Если на участке цепи не действуют сторонние силы (однородный участок цепи) и, значит, источника тока на нём нет, то, как это следует из закона Ома для неоднородного участка цепи, выполняется:
- φ1−φ2=IR.{\displaystyle \varphi _{1}-\varphi _{2}=IR.}
Значит, если в качестве точки 1 выбрать анод источника, а в качестве точки 2 — его катод, то для разности между потенциалами анода φa{\displaystyle \varphi _{a}} и катода φk{\displaystyle \varphi _{k}} можно записать:
- φa−φk=IRe,{\displaystyle \varphi _{a}-\varphi _{k}=IR_{e},}
где как и ранее Re{\displaystyle R_{e}} — сопротивление внешнего участка цепи.
Из этого соотношения и закона Ома для замкнутой цепи, записанного в виде E=IRe+Ir{\displaystyle {\mathcal {E}}=IR_{e}+Ir} нетрудно получить
- φa−φkE=ReRe+r{\displaystyle {\frac {\varphi _{a}-\varphi _{k}}{\mathcal {E}}}={\frac {R_{e}}{R_{e}+r}}} и затем φa−φk=ReRe+rE.{\displaystyle \varphi _{a}-\varphi _{k}={\frac {R_{e}}{R_{e}+r}}{\mathcal {E}}.}
Из полученного соотношения следуют два вывода:
- Во всех случаях, когда по цепи течёт ток, разность потенциалов между клеммами источника тока φa−φk{\displaystyle \varphi _{a}-\varphi _{k}} меньше, чем ЭДС источника.
- В предельном случае, когда Re{\displaystyle R_{e}} бесконечно (цепь разорвана), выполняется E=φa−φk.{\displaystyle {\mathcal {E}}=\varphi _{a}-\varphi _{k}.}
Таким образом, ЭДС источника тока равна разности потенциалов между его клеммами в состоянии, когда источник отключён от цепи[1].
ЭДС индукции
Причиной возникновения электродвижущей силы в замкнутом контуре может стать изменение потока магнитного поля, пронизывающего поверхность, ограниченную данным контуром. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением
- E=−dΦdt,{\displaystyle {\mathcal {E}}=-{\frac {d\Phi }{dt}},}
где Φ{\displaystyle \Phi } — поток магнитного поля через замкнутую поверхность, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца). В свою очередь причиной изменения магнитного потока может быть как изменение магнитного поля, так и движение контура в целом или его отдельных частей.
Неэлектрический характер ЭДС
Внутри источника ЭДС ток течёт в направлении, противоположном нормальному. Это невозможно без дополнительной силы неэлектрической природы, преодолевающей силу электрического отталкиванияКак показано на рисунке, электрический ток, нормальное направление которого — от «плюса» к «минусу», внутри источника ЭДС (например, внутри гальванического элемента) течёт в противоположном направлении. Направление от «плюса» к «минусу» совпадает с направлением электрической силы, действующей на положительные заряды. Поэтому для того, чтобы заставить ток течь в противоположном направлении, необходима дополнительная сила неэлектрической природы (центробежная сила, сила Лоренца, силы химической природы) которая бы преодолевала электрическую силу.
Сторонние силы
Сторонними силами называются силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля. Например, в гальваническом элементе или аккумуляторе сторонние силы возникают в результате электрохимических процессов, происходящих на границе соприкосновения электрода с электролитом; в электрическом генераторе постоянного тока сторонней силой является сила Лоренца[3].
См. также
Примечания
Электродвижущая сила — Википедия. Что такое Электродвижущая сила
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил, то есть любых сил неэлектрического происхождения, действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура[1][2].
По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил E→ex{\displaystyle {\vec {E}}_{ex}}, под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд к величине этого заряда. Тогда в замкнутом контуре L{\displaystyle L} ЭДС будет равна:
- E=∮LE→ex⋅dl→,{\displaystyle {\mathcal {E}}=\oint \limits _{L}{\vec {E}}_{ex}\cdot {\vec {dl}},}
где dl→{\displaystyle {\vec {dl}}} — элемент контура.
ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами источника тока вне самого́ источника равна нулю.
ЭДС и закон Ома
Электродвижущая сила источника связана с электрическим током, протекающим в цепи, соотношениями закона Ома. Закон Ома для неоднородного участка цепи имеет вид[1]:
- φ1−φ2+E=IR,{\displaystyle \varphi _{1}-\varphi _{2}+{\mathcal {E}}=IR,}
где φ1−φ2{\displaystyle \varphi _{1}-\varphi _{2}} — разность между значениями потенциала в начале и в конце участка цепи, I{\displaystyle I} — сила тока, текущего по участку, а R{\displaystyle R} — сопротивление участка.
Если точки 1 и 2 совпадают (цепь замкнута), то φ1−φ2=0{\displaystyle \varphi _{1}-\varphi _{2}=0} и предыдущая формула переходит в формулу закона Ома для замкнутой цепи[1]:
- E=IR,{\displaystyle {\mathcal {E}}=IR,}
где теперь R{\displaystyle R} — полное сопротивление всей цепи.
В общем случае полное сопротивление цепи складывается из сопротивления внешнего по отношению к источнику тока участка цепи (Re{\displaystyle R_{e}}) и внутреннего сопротивления самого́ источника тока (r{\displaystyle r}). С учётом этого следует:
- E=IRe+Ir.{\displaystyle {\mathcal {E}}=IR_{e}+Ir.}
ЭДС источника тока
Если на участке цепи не действуют сторонние силы (однородный участок цепи) и, значит, источника тока на нём нет, то, как это следует из закона Ома для неоднородного участка цепи, выполняется:
- φ1−φ2=IR.{\displaystyle \varphi _{1}-\varphi _{2}=IR.}
Значит, если в качестве точки 1 выбрать анод источника, а в качестве точки 2 — его катод, то для разности между потенциалами анода φa{\displaystyle \varphi _{a}} и катода φk{\displaystyle \varphi _{k}} можно записать:
- φa−φk=IRe,{\displaystyle \varphi _{a}-\varphi _{k}=IR_{e},}
где как и ранее Re{\displaystyle R_{e}} — сопротивление внешнего участка цепи.
Из этого соотношения и закона Ома для замкнутой цепи, записанного в виде E=IRe+Ir{\displaystyle {\mathcal {E}}=IR_{e}+Ir} нетрудно получить
- φa−φkE=ReRe+r{\displaystyle {\frac {\varphi _{a}-\varphi _{k}}{\mathcal {E}}}={\frac {R_{e}}{R_{e}+r}}} и затем φa−φk=ReRe+rE.{\displaystyle \varphi _{a}-\varphi _{k}={\frac {R_{e}}{R_{e}+r}}{\mathcal {E}}.}
Из полученного соотношения следуют два вывода:
- Во всех случаях, когда по цепи течёт ток, разность потенциалов между клеммами источника тока φa−φk{\displaystyle \varphi _{a}-\varphi _{k}} меньше, чем ЭДС источника.
- В предельном случае, когда Re{\displaystyle R_{e}} бесконечно (цепь разорвана), выполняется E=φa−φk.{\displaystyle {\mathcal {E}}=\varphi _{a}-\varphi _{k}.}
Таким образом, ЭДС источника тока равна разности потенциалов между его клеммами в состоянии, когда источник отключён от цепи[1].
ЭДС индукции
Причиной возникновения электродвижущей силы в замкнутом контуре может стать изменение потока магнитного поля, пронизывающего поверхность, ограниченную данным контуром. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением
- E=−dΦdt,{\displaystyle {\mathcal {E}}=-{\frac {d\Phi }{dt}},}
где Φ{\displaystyle \Phi } — поток магнитного поля через замкнутую поверхность, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца). В свою очередь причиной изменения магнитного потока может быть как изменение магнитного поля, так и движение контура в целом или его отдельных частей.
Неэлектрический характер ЭДС
Внутри источника ЭДС ток течёт в направлении, противоположном нормальному. Это невозможно без дополнительной силы неэлектрической природы, преодолевающей силу электрического отталкиванияКак показано на рисунке, электрический ток, нормальное направление которого — от «плюса» к «минусу», внутри источника ЭДС (например, внутри гальванического элемента) течёт в противоположном направлении. Направление от «плюса» к «минусу» совпадает с направлением электрической силы, действующей на положительные заряды. Поэтому для того, чтобы заставить ток течь в противоположном направлении, необходима дополнительная сила неэлектрической природы (центробежная сила, сила Лоренца, силы химической природы) которая бы преодолевала электрическую силу.
Сторонние силы
Сторонними силами называются силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля. Например, в гальваническом элементе или аккумуляторе сторонние силы возникают в результате электрохимических процессов, происходящих на границе соприкосновения электрода с электролитом; в электрическом генераторе постоянного тока сторонней силой является сила Лоренца[3].
См. также
Примечания
Эдс индукции
Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением
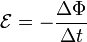
где 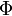 — поток
магнитного поля через
замкнутую поверхность
— поток
магнитного поля через
замкнутую поверхность 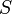 ,
ограниченную контуром. Знак «−» перед
выражением показывает, что индукционный
ток, созданный ЭДС индукции, препятствует
изменению магнитного потока в контуре
(см. правило
Ленца).
,
ограниченную контуром. Знак «−» перед
выражением показывает, что индукционный
ток, созданный ЭДС индукции, препятствует
изменению магнитного потока в контуре
(см. правило
Ленца).
41. Индуктивность, ее единица СИ. Индуктивность длинного соленоида.
Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур.[2][3][4].
В формуле

 —
магнитный
поток,
—
магнитный
поток, 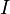 —
ток в контуре,
—
ток в контуре, 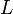 —
индуктивность.
—
индуктивность.
Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока[4]:
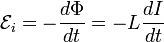 .
.
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током[4]:
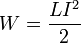 .
.
Обозначение и единицы измерения
В системе единиц СИ индуктивность измеряется в генри[7], сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 109см)[4]. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени.
Символ 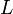 ,
используемый для обозначения индуктивности,
был взят в честь Ленца
Эмилия Христиановича (Heinrich
Friedrich Emil Lenz)[источник не указан 1017 дней].
Единица измерения индуктивности названа
в честь Джозефа
Генри (Joseph
Henry)[8].
Сам термин индуктивность был
предложен Оливером
Хевисайдом (Oliver
Heaviside) в феврале 1886
года[источник не указан 1017 дней].
,
используемый для обозначения индуктивности,
был взят в честь Ленца
Эмилия Христиановича (Heinrich
Friedrich Emil Lenz)[источник не указан 1017 дней].
Единица измерения индуктивности названа
в честь Джозефа
Генри (Joseph
Henry)[8].
Сам термин индуктивность был
предложен Оливером
Хевисайдом (Oliver
Heaviside) в феврале 1886
года[источник не указан 1017 дней].
Электрический
ток, который течет в замкнутом контуре,
создает вокруг себя магнитное поле,
индукция которого, согласно закону
Био-Савара-Лапласа, пропорциональна
току. Сцепленный с контуром магнитный
поток Ф поэтому прямо пропорционален
току I в контуре: 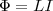 (1) где
коэффициент пропорциональности L
называетсяиндуктивностью
контура. При
изменении в контуре силы тока будет
также изменяться и сцепленный с ним
магнитный поток; значит, в контуре будет
индуцироваться э.д.с. Возникновение
э.д.с. индукции в проводящем контуре при
изменении в нем силы тока
называетсясамоиндукцией. Из
выражения (1) задается единица
индуктивности генри (Гн):
1 Гн — индуктивность контура, магнитный
поток самоиндукции которого при токе
в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В
(1) где
коэффициент пропорциональности L
называетсяиндуктивностью
контура. При
изменении в контуре силы тока будет
также изменяться и сцепленный с ним
магнитный поток; значит, в контуре будет
индуцироваться э.д.с. Возникновение
э.д.с. индукции в проводящем контуре при
изменении в нем силы тока
называетсясамоиндукцией. Из
выражения (1) задается единица
индуктивности генри (Гн):
1 Гн — индуктивность контура, магнитный
поток самоиндукции которого при токе
в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В
·c/А .
Вычислим
индуктивность бесконечно длинного
соленоида. Полный магнитный поток сквозь
соленоид (потокосцепление) равен
μ0μ(N2I/l)S
. Подставив в (1), найдем 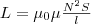 (2) т.
е. индуктивность соленоида зависит от
длиныl солениода,
числа его витков N, его , площади S и
магнитной проницаемости μ вещества, из
которого изготовлен сердечник
соленоида. Доказано, что
индуктивность контура зависит в общем
случае только от геометрической формы
контура, его размеров и магнитной
проницаемости среды, в которой он
расположен, и можно провести аналог
индуктивности контура с электрической
емкостью уединенного проводника, которая
также зависит только от формы проводника,
его размеров и диэлектрической
проницаемости среды. Найдем,
применяя к явлению самоиндукции закон
Фарадея, что э.д.с. самоиндукции
равна
(2) т.
е. индуктивность соленоида зависит от
длиныl солениода,
числа его витков N, его , площади S и
магнитной проницаемости μ вещества, из
которого изготовлен сердечник
соленоида. Доказано, что
индуктивность контура зависит в общем
случае только от геометрической формы
контура, его размеров и магнитной
проницаемости среды, в которой он
расположен, и можно провести аналог
индуктивности контура с электрической
емкостью уединенного проводника, которая
также зависит только от формы проводника,
его размеров и диэлектрической
проницаемости среды. Найдем,
применяя к явлению самоиндукции закон
Фарадея, что э.д.с. самоиндукции
равна 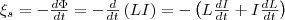 Если
контур не претерпевает деформаций и
магнитная проницаемость среды остается
неизменной (в дальнейшем будет показано,
что последнее условие выполняется не
всегда), то L = const и
Если
контур не претерпевает деформаций и
магнитная проницаемость среды остается
неизменной (в дальнейшем будет показано,
что последнее условие выполняется не
всегда), то L = const и (3) где
знак минус, определяемый правилом Ленца,
говорит о том, чтоналичие
индуктивности в контуре приводит к
замедлению изменения тока в нем. Если
ток со временем увеличивается, то
(dI/dt<0) и ξs>0
т. е. ток самоиндукции направлен навстречу
току, обусловленному внешним источником,
и замедляет его увеличение. Если ток со
временем уменьшается, то (dI/dt>0) и ξs<0
т. е. индукционный ток имеет такое же
направление, как и уменьшающийся ток в
контуре, и замедляет его уменьшение.
Значит, контур, обладая определенной
индуктивностью, имеет электрическую
инертность, заключающуюся в том, что
любое изменение тока уменьшается тем
сильнее, чем больше индуктивность
контура.
(3) где
знак минус, определяемый правилом Ленца,
говорит о том, чтоналичие
индуктивности в контуре приводит к
замедлению изменения тока в нем. Если
ток со временем увеличивается, то
(dI/dt<0) и ξs>0
т. е. ток самоиндукции направлен навстречу
току, обусловленному внешним источником,
и замедляет его увеличение. Если ток со
временем уменьшается, то (dI/dt>0) и ξs<0
т. е. индукционный ток имеет такое же
направление, как и уменьшающийся ток в
контуре, и замедляет его уменьшение.
Значит, контур, обладая определенной
индуктивностью, имеет электрическую
инертность, заключающуюся в том, что
любое изменение тока уменьшается тем
сильнее, чем больше индуктивность
контура.
42. Ток при размыкании и замыкании цепи.
При всяком изменении силы тока в проводящем контуре возникает э. д. с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.

Рассмотрим
процесс выключения тока в цепи, содержащей
источник тока с э.д.с. 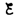 ,
резистор сопротивлением R и
катушку индуктивностью L. Под
действием внешней э. д. с. в цепи течет
постоянный ток
,
резистор сопротивлением R и
катушку индуктивностью L. Под
действием внешней э. д. с. в цепи течет
постоянный ток
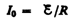
(внутренним сопротивлением источника тока пренебрегаем).
В
момент времени t=0
отключим источник тока. Ток в катушке
индуктивностью L начнет
уменьшаться, что приведет к возникновению
э.д.с. самоиндукции  препятствующей,
согласно правилу Ленца, уменьшению
тока. В каждый момент времени ток в
цепи определяется законом Ома I=
препятствующей,
согласно правилу Ленца, уменьшению
тока. В каждый момент времени ток в
цепи определяется законом Ома I=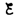 s/R, или
s/R, или
 (127.1)
(127.1)
Разделив
в выражении (127.1) переменные,
получим  Интегрируя
это уравнение по I (от I0 до I)
и t (от
0 до t),
находим ln (I /I0)
= –Rt/L, или
Интегрируя
это уравнение по I (от I0 до I)
и t (от
0 до t),
находим ln (I /I0)
= –Rt/L, или
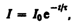 (127.2)
(127.2)
где =L/R — постоянная, называемая временем релаксации. Из (127.2) следует, что есть время, в течение которого сила тока уменьшается в е раз.
Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону (127.2) и определяется кривой 1 на рис. 183. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.
При
замыкании цепи помимо внешней э. д.
с. 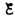 возникает
э. д. с. самоиндукции
возникает
э. д. с. самоиндукции 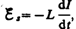 препятствующая,
согласно правилу Ленца, возрастанию
тока. По закону Ома,
препятствующая,
согласно правилу Ленца, возрастанию
тока. По закону Ома, 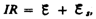 или
или
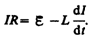
Введя
новую переменную 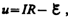 преобразуем
это уравнение к виду
преобразуем
это уравнение к виду
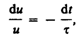
где — время релаксации.

В
момент замыкания (t=0)
сила тока I =
0 и u =
–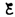 .
Следовательно, интегрируя по и (от
–
.
Следовательно, интегрируя по и (от
–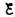 до IR–
до IR– )
и t (от
0 до t),
находим ln[(IR–
)
и t (от
0 до t),
находим ln[(IR–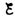 )]/–
)]/–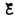 = —t/, или
= —t/, или
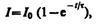 (127.3)
(127.3)
где 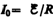 —
установившийся ток (при t).
—
установившийся ток (при t).
Таким
образом, в процессе включения источника
тока нарастание силы тока в цепи задается
функцией (127.3) и определяется кривой 2
на рис. 183. Сила тока возрастает от
начального значения I=0
и асимптотически стремится к установившемуся
значению  . Скорость
нарастания тока определяется тем же
временем релаксации =L/R, что
и убывание тока. Установление тока
происходит тем быстрее, чем меньше
индуктивность цепи и больше ее
сопротивление.
. Скорость
нарастания тока определяется тем же
временем релаксации =L/R, что
и убывание тока. Установление тока
происходит тем быстрее, чем меньше
индуктивность цепи и больше ее
сопротивление.
Оценим
значение э.д.с. самоиндукции  , возникающей
при мгновенном увеличении сопротивления
цепи постоянного тока от R0 до R.
Предположим, что мы размыкаем контур,
когда в нем течет установившийся ток
, возникающей
при мгновенном увеличении сопротивления
цепи постоянного тока от R0 до R.
Предположим, что мы размыкаем контур,
когда в нем течет установившийся ток 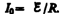 .
При размыкании цепи ток изменяется по
формуле (127.2). Подставив в нее выражение
дляI0 и ,
получим
.
При размыкании цепи ток изменяется по
формуле (127.2). Подставив в нее выражение
дляI0 и ,
получим
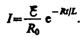
Э.д.с. самоиндукции

т. е. при значительном увеличении сопротивления цепи (R/R0>>1), обладающей большой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникновение значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.
43. Явление взаимной индукции. Трансформатор.
Рассмотрим
два неподвижных контура (1 и 2), которые
расположены достаточно близко друг от
друга (рис. 1). Если в контуре 1 протекает
ток I1,
то магнитный поток, который создавается
этим током (поле, создающее этот поток,
на рисунке изображено сплошными линиями),
прямо пропорционален I1.
Обозначим через Ф21 часть
потока,пронизывающая контур 2.
Тогда 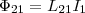 (1) где
L21 —
коэффициент пропорциональности.
(1) где
L21 —
коэффициент пропорциональности.
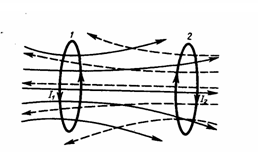
Рис.1
Если
ток I1 меняет
свое значение, то в контуре 2 индуцируется
э.д.с. ξi2 ,
которая по закону Фарадея будет равна
и противоположна по знаку скорости
изменения магнитного потока Ф21,
который создается током в первом контуре
и пронизыващет второй:  Аналогичным
образом, при протекании в контуре 2 тока
I2 магнитный
поток (его поле изображено на рис. 1
штрихами) пронизывает первый контур.
Если Ф12 —
часть этого потока, который пронизывает
контур 1, то
Аналогичным
образом, при протекании в контуре 2 тока
I2 магнитный
поток (его поле изображено на рис. 1
штрихами) пронизывает первый контур.
Если Ф12 —
часть этого потока, который пронизывает
контур 1, то 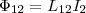 Если
ток I2 меняет
свое значение, то в контуре 1 индуцируется
э.д.с. ξi1 ,
которая равна и противоположна по знаку
скорости изменения магнитного потока
Ф12,
который создается током во втором
контуре и пронизывает первый:
Если
ток I2 меняет
свое значение, то в контуре 1 индуцируется
э.д.с. ξi1 ,
которая равна и противоположна по знаку
скорости изменения магнитного потока
Ф12,
который создается током во втором
контуре и пронизывает первый: 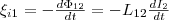 Явление
возникновения э.д.с. в одном из контуров
при изменении силы тока в другом
называется взаимной
индукцией.
Коэффициенты пропорциональности L21 и
L12 называются взаимной
индуктивностью контуров.
Расчеты, которые подтверждены опытом,
показывают, что L21 и
L12 равны
друг другу, т. е.
Явление
возникновения э.д.с. в одном из контуров
при изменении силы тока в другом
называется взаимной
индукцией.
Коэффициенты пропорциональности L21 и
L12 называются взаимной
индуктивностью контуров.
Расчеты, которые подтверждены опытом,
показывают, что L21 и
L12 равны
друг другу, т. е.  (2) Коэффициенты
пропорциональности L12 и
L21 зависят
от размеров, геометрической формы,
взаимного расположения контуров и от
магнитной проницаемости среды, окружающей
контуры. Единица взаимной индуктивности
та же, что и для индуктивности, — генри
(Гн). Найдем
взаимную индуктивность двух катушек,
которые намотаны на общий тороидальный
сердечник. Этот случай имеет большое
практическое значение (рис. 2). Магнитная
индукция поля, которое создавается
первой катушкой с числом витков N1,
током I1 и
магнитной проницаемостью μ сердечника,
B = μμ0(N1I1/l)
где l —
длина сердечника по средней линии.
Магнитный поток сквозь один виток второй
катушки Ф2 =
BS = μμ0(N1I1/l)S
(2) Коэффициенты
пропорциональности L12 и
L21 зависят
от размеров, геометрической формы,
взаимного расположения контуров и от
магнитной проницаемости среды, окружающей
контуры. Единица взаимной индуктивности
та же, что и для индуктивности, — генри
(Гн). Найдем
взаимную индуктивность двух катушек,
которые намотаны на общий тороидальный
сердечник. Этот случай имеет большое
практическое значение (рис. 2). Магнитная
индукция поля, которое создавается
первой катушкой с числом витков N1,
током I1 и
магнитной проницаемостью μ сердечника,
B = μμ0(N1I1/l)
где l —
длина сердечника по средней линии.
Магнитный поток сквозь один виток второй
катушки Ф2 =
BS = μμ0(N1I1/l)S

Значит,
полный магнитный поток (потокосцепление)
сквозь вторичную обмотку, которая
содержит N2 витков,  Поток
Ψ создается током I1,
поэтому, используя (1), найдем
Поток
Ψ создается током I1,
поэтому, используя (1), найдем 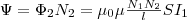 (3) Если
рассчитать магнитный поток, который
создавается катушкой 2 сквозь катушку
1, то для L12 получим
выражение в соответствии с формулой
(3). Значит, взаимная индуктивность двух
катушек, которые намотаны на общий
тороидальный сердечник,
(3) Если
рассчитать магнитный поток, который
создавается катушкой 2 сквозь катушку
1, то для L12 получим
выражение в соответствии с формулой
(3). Значит, взаимная индуктивность двух
катушек, которые намотаны на общий
тороидальный сердечник, 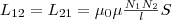
Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока
ЭДС
ЭДС расшифровывается как электродвижущая сила или физическое значение, которое характеризует работу посторонних сил в блоках неизменного либо переменного токов. При закрытом проводном контуре равняется действию работы данных сил при перемещении одиночного заряда с плюсовым значением, по всему контуру. Обозначая напряжение поля посторонних сил с помощью электродвижущей силы, получается что эдс неизвестна в закрытом контуре L равняется.
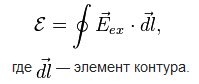
Допустимые силы электростатического поля постоянно не смогут держать одно напряжение в цепи, потому что работая по закрытому пути, данные силы равны нулю. А когда ток проходит через проводники, то данную работу сопровождает выделение энергии и нагревание проводников. Посторонние силы заставляют двигаться заряженные частицы в генераторе, гальванических элементах, аккумуляторах и всевозможных источниках. При чем возникновение посторонних сил различное. К примеру: В генераторе используются от вихревого электрического поля, которые возникают от изменения магнитного поля; У гальванических элементов и аккумуляторов используются химические силы. Эдс источника тока зависит от напряжения в местах зажимов если цепь разомкнута. По закону Ома сила тока цепи с заданным сопротивлением также находит эдс. Единица измерения Вольт.

Эдс индукции это своего рода явление которое обусловлено изменением магнитного поля в замкнутом пространстве. Находится по формуле:
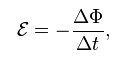
в которой: Ф — магнитное поле в закрытом пространстве S, закрытую контуром. При этом знак минус служит для неизменности магнитного поля благодаря индукции электродвижущей силы.
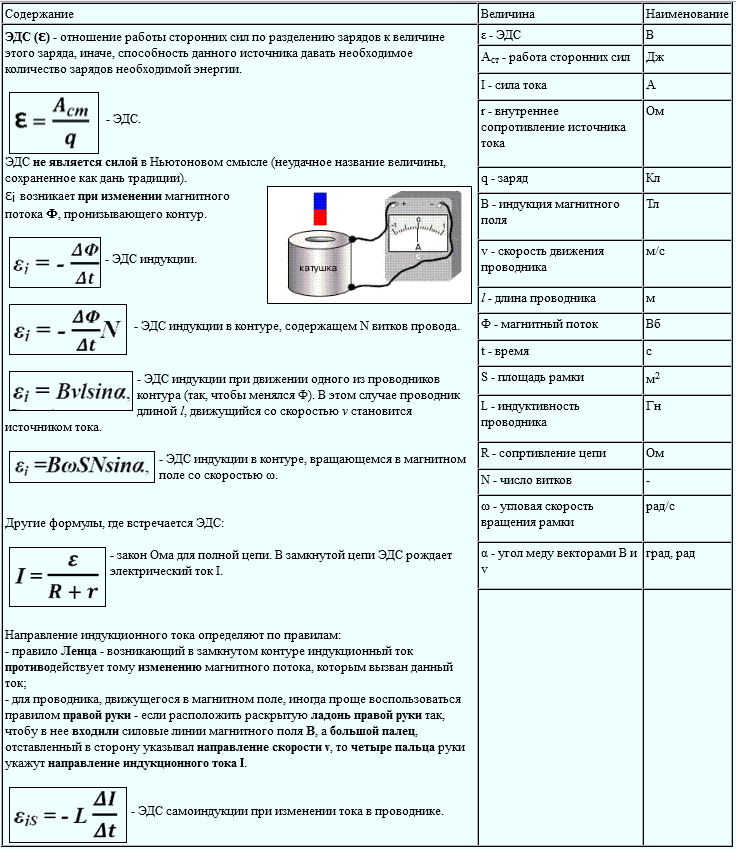
Электродвижущая сила это описание закрытого контура, невозможно точно показать её точку пребывания. Но практически всегда эдс считают приблизительно сосредоточенной в некоторых устройствах либо элементов цепи. При этом её называют описанием данного устройства, определяя как потенциальную разность в его разомкнутых полюсах.
Такие устройства разделяют на несколько видов зависящих от типа преобразования:
— Химические — это аккумуляторы, ванны, гальванические батареи;
— Электромагнитные — это электродвижущая сила электромагнитной индукции, которая бывает в трансформаторах, динамо-машинах, электромоторах, дросселях;
— Фотоэлектрические — это внешние или внутренние фотоэффекты;
— Электростатические — это возникающее напряжение в механическом трении электрофорных машин или как пример грозовые облака.
— Пьезоэлектрические — это сдавливание либо растяжение пьезэлектрических датчиков.
Так же существуют термоионные и термоэлектрические эдс.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Магнитодвижущая сила — Википедия
Материал из Википедии — свободной энциклопедии
Магнѝтодви́жущая си́ла (МДС) — физическая величина, характеризующая способность электрических токов создавать магнитные потоки. Используется при расчётах магнитных цепей; является аналогом ЭДС в электрических цепях.
Величина измеряется в амперах (СИ) или же в гилбертах (СГС), причём 1 А = 4π10{\displaystyle {\frac {4\pi }{10}}} Гб ≈ 1,257 Гб. На практике для обозначения единицы МДС часто используется термин «ампер-виток», численно равный единице в СИ.
Магнитодвижущая сила F{\displaystyle {\mathcal {F}}} в катушке или электромагните вычисляется по формуле
- F=wI,{\displaystyle {\mathcal {F}}=wI,}
где w{\displaystyle w} — количество витков в обмотке, I{\displaystyle I} — ток в проводнике.
Выражение для магнитного потока в магнитной цепи, называемое иногда законом Гопкинсона, имеет следующий вид:
- F=ΦRm{\displaystyle {\mathcal {F}}=\Phi R_{m}}
где Φ{\displaystyle \Phi } — величина магнитного потока, Rm{\displaystyle R_{m}} — магнитное сопротивление проводника. Данная запись является аналогом закона Ома в магнитных цепях.

