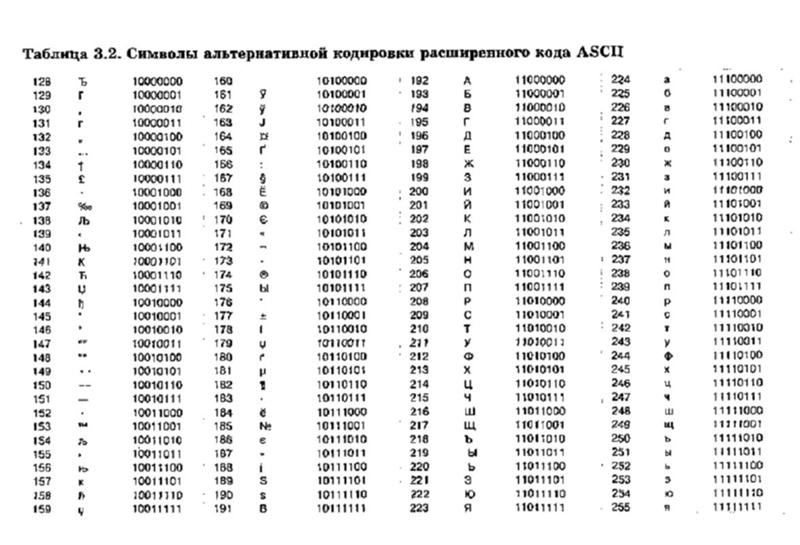
Шестнадцатеричный код

Код широко используется в вычислительной технике. Еще он называется кодом с основанием 16 (двоичный с основанием 2). В отображении шестнадцатеричного кода используются цифры от 0 до 9 и первые буквы латинского алфавита A, B, C, D, E, F. Если в двоичном коде используются степени числа 2, то в шестнадцатеричном коде — степени числа 16. Например, число 157 представляется, как

9 x 16¹ + D x 16⁰, т. е. 157₁₀ = 9D₁₆.

Для отображения чисел в разных системах используются нижние индексы, например, число₁₀ — десятичное число, число₂ — двоичное число, число₁₆ или число _H — 16-тиричное число.

Шестнадцатеричный код в основном используется для упрощения представления двоичных чисел. Например, для отображения числа 157 потребовался бы 8-ми разрядный двоичный код (а именно 1001 1101), а в 16-тиричном коде число содержит всего 2 символа (9D).

В следующем году студенты САПР, а конструктора через год, будут сворачивать 16-разрядные двоичные сигнатуры в 4-разрядные 16-ричные при диагностике цифровых устройств для удобства запоминания сигнатур (особенности человеческой памяти).

Сами цифровые устройства эти коды не воспринимают и никак на них не реагируют. В устройствах работают лишь перепады напряжения, которые мы символически и обозначаем 0 и 1, для объяснения работы устройств, их проектирования, программирования и контроля.

Перевод чисел из разных систем счисления

Перевод десятичного числа в двоичное.

Для перевода десятичного числа в двоичное нужно десятичное число делить на 2 до получения минимального остатка. При делении образуются остатки, равные 0 или 1. Первый остаток будет младшим разрядом. Последний остаток будет предпоследним перед старшим разрядом. Результат деления последнего числа является старшим разрядом и он всегда равен 1.

Например, переведем число 21 в двоичный код.

21/2=10	Остаток 1
10/2=5	Остаток 0
5/2=2	Остаток 1
2/2=1	Остаток 0

Последнее число 2/2=1. Эта единица идет в старший разряд. В следующий разряд идет остаток от этого деления (0) и т. д. до последнего разряда, т. е. считаем снизу вверх. В результате деления получили код 10101. Проверим: 1 x 16 + 0 x 8 + 1 x 4 + 0 x 2 + 1 x 1 = 21.

Переведем число 274.

274/2=137	Остаток 0
137/2=68	Остаток 1
68/2=34	Остаток 0
34/2=17	Остаток 0
17/2=8	Остаток 1
8/2=4	Остаток 0
4/2=2	Остаток 0
2/2=1	Остаток 0

Полученное число 1 0001 0010. Проверим: 256 + 16 + 2 = 274.

Это рассмотрено раньше, где проверяется результат перевода десятичного числа в двоичное. Допустим, есть число 1011 0101. Где стоит 1, имеет право стоять весовой коэффициент, где 0 — весовые коэффициенты «обнулились». Считаем: 128 + 0 + 32 + 16 + 0 + 4 + 0 + 1 = 181.

Перевод шестнадцатеричных чисел  осуществляется аналогично. Делим десятичное число на 16 до получения остатка меньшего 16. При делении десятичного числа остатки получаются в виде ряда чисел от 0 до 15. Числа от 10 до 15 заменяются буквами латинского алфавита A, B, C, D, E, F. Как и при переводе в двоичный код, последний остаток предшествует старшему разряду, результат деления последнего числа есть старший разряд. Переведем число 845 в 16-тиричный код.

845/16 = 52	Остаток 13 = D
52/16= 3	Остаток 4

Полученное число 34D. Проверим: 3 х 16² + 4 x 16¹ + D x 16⁰ = 845. D в шестнадцатеричном коде эквивалентно 13. Здесь также показан и обратный перевод. Умножаем числа 16-тиричного кода на 16 в степени и складываем.

Для перевода 16-тиричного кода в двоичный код достаточно разбить число на отдельные символы (числа) которым соответствуют четырёхразрядные двоичные эквиваленты. То есть, то же число 34D разбиваем на 3, 4 и D и записываем двоичный код каждого элемента: 3 = 0011, 4 = 0100, D = 1101. 34D = 0011 0100 1101. Вот так 10-разрядное двоичное число в 16-тиричном эквиваленте записывается всего тремя символами.

Понятно, зачем шестнадцатеричный код? Для обратного перевода двоичное число разбивается на тетрады и каждой тетраде ставится в соответствие шестнадцатеричный эквивалент. Причем разбиение ведется справа налево от младших разрядов к старшим. Если последняя, левая тетрада не получается, т.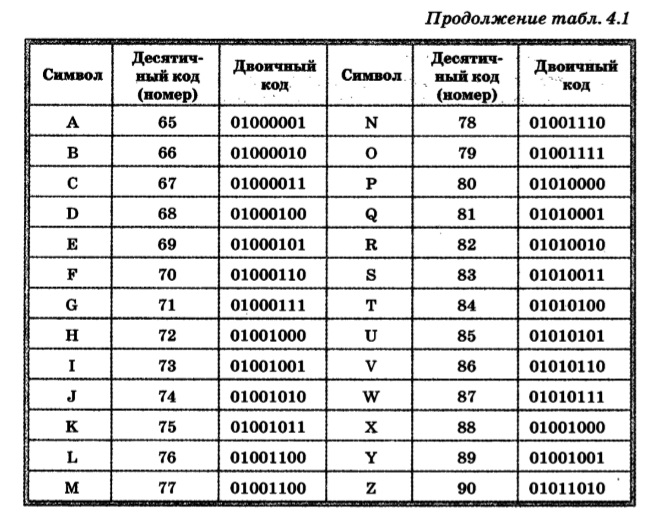

е. в старшей тетраде всего 1, 2 или 3 разряда, к ним слева дописывают нули. Получается как в последнем примере, первые два нуля образуют тетраду совместно с единицами (число 3).

Иногда, кстати, удобней переводить шестнадцатеричные числа в двоичные, а потом в десятичные и наоборот.

Существуют и другие, специальные, коды. С ними имеет смысл знакомиться при изучении использующих эти коды устройств.

Шестнадцатеричный код в текст

Как преобразовать шестнадцатеричный код в текст и наоборот — текст в шестнадцатеричный код?

Нежели следовать стандартному двоичному методу преобразования, используйте наш онлайновый Hex-конвертер для быстрого перевода кода в текст. Это просто, быстро и дает результаты, которые вы можете легко скопировать и вставить в нужный документ или на сайт. 

С помощью конвертера шестнадцатеричного кода в текст мы’облегчили вам понимание смысла кода. Это сделано за счет исключения необходимости писать общий код или использовать калькуляторы для понимания длинных числовых значений. Теперь вы можете просто свободно ввести нужный код, нажать на кнопку преобразования шестнадцатеричного кода в текстовый, и инструкции будут легко видны в следующем окне.

Почему стоит использовать наш конвертер?

Мир движется быстрыми темпами, и все так или иначе становится автоматизированным. Умение быстро преобразовывать числа и записи из одной системы в другую важно для студентов и профессионалов, работающих с компьютерами.

Наш конвертер позволяет быстро преобразовывать числа и записи из одной системы в другую.

Наш конвертер Hex в текст разработан таким образом, чтобы помочь вам получить более быстрые результаты без необходимости вручную преобразовывать код. Все, что вам нужно сделать, — это ввести числовой код, нажать кнопку преобразования, и результаты будут видны в мгновение ока. И что самое приятное — никаких ошибок или препятствий, поскольку результаты гарантированно верны.

Так что попробуйте!

С помощью нескольких простых шагов вы сможете справиться с большими заданиями за считанные секунды.

1. Введите шестнадцатеричный код в текстовое поле экрана
2. Вы можете также добавить пробелы после каждого слова в поле.
3. Выберите нужные вам параметры преобразования.
4. Нажмите на кнопку Конвертировать
5. Вы’получите результат в окне вывода справа. 
6. Вы можете скопировать результат в ваш документ/страницу CMS/файл веб-сайта.

Этот конвертер также может использоваться для преобразования текста в Hex и работает с тысячами символов одновременно.

Функции конвертации шестнадцатеричного кода в текстовый

• Быстрые и точные результаты
• Не требуется регистрация
• Надежная платформа для всех типов пользователей

Почему используется шестнадцатеричная система счисления?

Это используется в информатике, потому что это более эффективный способ представления данных, чем двоичное число

Какие примеры шестнадцатеричной системы счисления?

Примерами шестнадцатеричных чисел являются 3F, 1A и 0B. Все эти числа представляют различные буквы английского алфавита. Например, число 3F обозначает букву ‘P’. Число 1A представляет букву ‘j’, а число 0B — букву ‘L’.

Преобразование шестнадцатеричного кода

Преобразование шестнадцатеричного кода всегда преподается на курсах программирования. Это первый строительный блок для понимания базовых чисел, которые включают двоичные числа, десятичные числа, а затем шестнадцатеричное число с основанием 16.

Код шестнадцатеричного кода — это 16-значное число.

Эта 16-разрядная система счисления разработана для замены 8-разрядного двоичного числа при кодировании данных в компьютере более организованным способом. Она набирается с помощью различных типов шестнадцатеричных цифр, обычно 4-битным форматом или нибблом. Шестнадцатеричная система счисления считается более эффективной по сравнению с тремя другими типами числовых систем (десятичной и двоичной).

Как этот ресурс может помочь в преобразовании шестнадцатеричных чисел?

• Приложение экономит ваше время, быстро преобразуя код в читаемый обычный текст
• Пользователи также могут загрузить обычный файл и преобразовать его в английский язык
• Пользователи могут просматривать результаты и вставлять их в обычный текстовый файл.
• Этот конвертер можно также использовать для преобразования шестнадцатеричного кода в XML, шестнадцатеричного кода в JSON или YAML. XML, JSON и YAML — это языки разметки, аналогичные HTML. JSON является подмножеством JavaScript, а YAML — подмножеством Ruby. Файлы XML, JSON или YAML часто используются для веб-разработки или хранения и передачи данных. Эти форматы легко читаются и понимаются, что делает их хорошим выбором.

Нужно ли вам какое-либо специальное программное обеспечение для использования этого конвертера?

Нет, для использования этого ресурса вам не нужны никакие специальные приложения или программы. Конвертер работает во всех браузерах, включая Chrome, Safari, Firefox и Edge. Он также работает как на настольных компьютерах, так и на мобильных (iOS, Android и другие операционные системы телефонов)

FAQ02201 для дисковых переключателей | Промышленная автоматизация OMRON

Вопрос

Что такое двоично-шестнадцатеричный код?

Двоичный шестнадцатеричный код использует двоичный код для выражения каждой цифры шестнадцатеричного числа.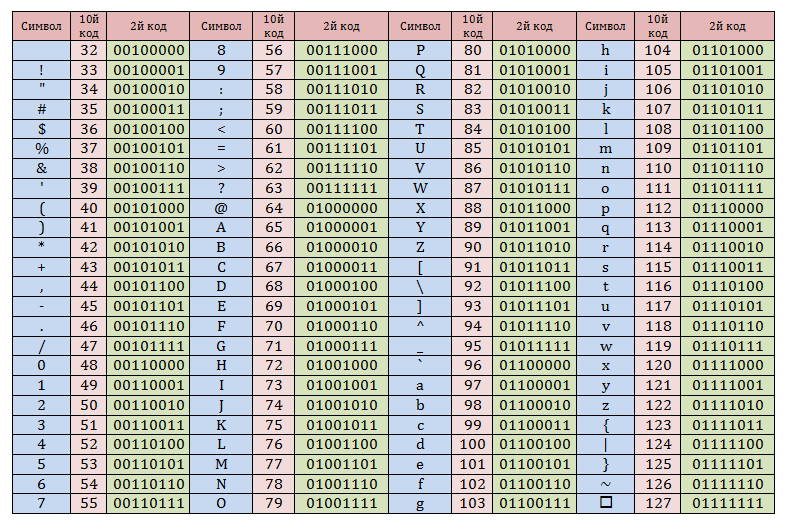 Используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Примеры:

Шестнадцатеричный	Двоичный шестнадцатеричный код
	1	2	4	8
0	0	0	0	0
1	1	0	0	0
2	0	1	0	0
3	1	1	0	0
4	0	0	1	0
5	1	0	1	0
6	0	1	1	0
7	1	1	1	0
8	0	0	0	1
9	1	0	0	1
A	0	1	0	1
B	1	1	0	1
C	0	0	1	1
D	1	0	1	1
E	0	1	1	1
F	1	1	1	1

Dial	Output
0
1	●
2		●
3	●	●
4			●
5	●		●
6		●	●
7	●	●	●
8				●
9	●			●
A		●		●
B	●	●		●
C			●	●
D	●		●	●
E		●	●	●
F	●	●	●	●

Преобразование шестнадцатеричных чисел в двоично-десятичные

Скоро Эти инструменты для работы с бинарными файлами находятся в пути

Редактор двоичных файлов

Просматривайте и редактируйте двоичные значения в своем браузере.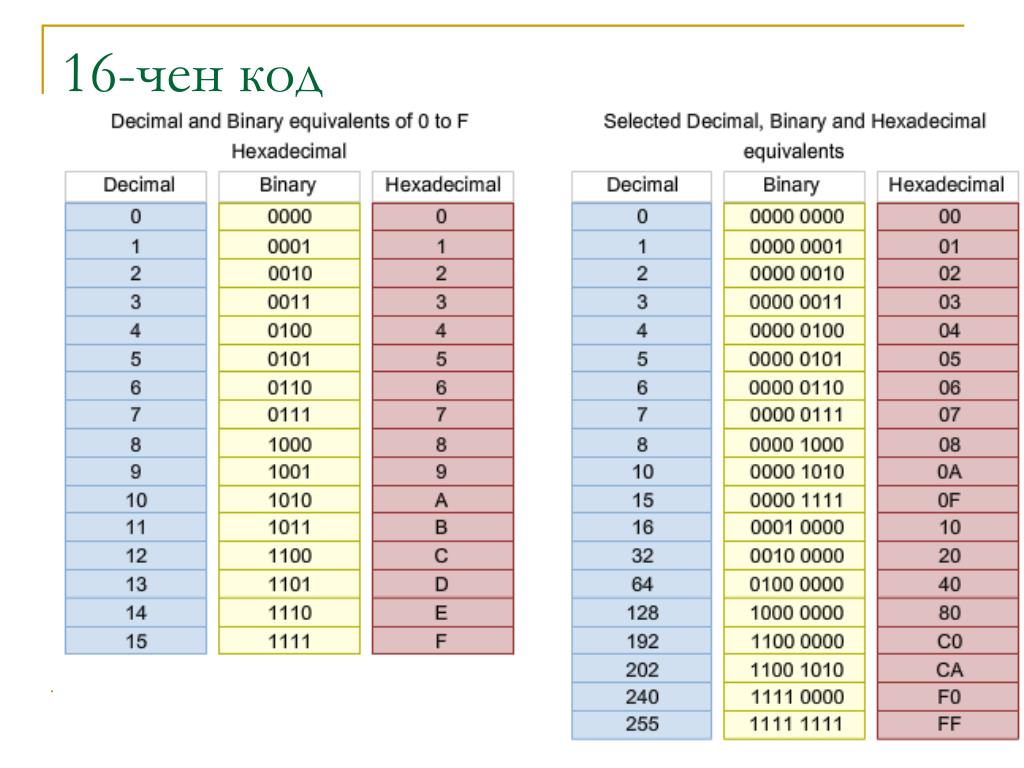

Создание файла из двоичных значений

Преобразование двоичных чисел в двоичный файл.

Двоичный дамп файла

Создайте двоичный дамп файлов в браузере.

Преобразование двоичных значений в произвольные.

Преобразование двоичных значений в любое основание (до основания 64).

Преобразование двоичных чисел в римские

Преобразование двоичных чисел в римские.

Преобразование римских чисел в двоичные

Преобразование римских цифр в двоичные значения.

Создать двоичную последовательность

Создать список возрастающих или убывающих двоичных чисел.

Двоичный штрих Шеффера

Вычислить побитовый оператор штриха Шеффера для двоичных значений.

Преобразовать двоичное число в двоично-десятичное

Кодировать каждый двоичный бит как двоично-десятичное число.

Преобразовать двоично-десятичные числа в двоичные

Декодировать двоично-десятичные числа в двоичные биты.

Разделить двоичные числа

Выполнить операцию деления нескольких двоичных чисел.

Повернуть двоичное число вправо

Повернуть биты двоичного числа вправо.

Повернуть двоичное число влево

Повернуть биты двоичного числа влево.

Извлечение битов из двоичных чисел

Извлечение n-го бита из двоичного числа.

Расчет четности

Подсчет четности двоичного числа.

Преобразование символов EBCDIC в двоичные значения

Преобразование символов EBCDIC в двоичные значения.

Преобразовать двоичные данные в символы EBCDIC

Преобразовать двоичные биты в символы EBCDIC.

Замена двоичного порядка байтов

Изменить порядок байтов двоичного числа.

Преобразование двоичного числа с прямым порядком байтов в двоичное число с прямым порядком байтов

Преобразование двоичного числа из двоичного числа с прямым порядком байтов в двоичное число с прямым порядком байтов.

Преобразовать двоичный код с прямым порядком байтов в двоичный код с прямым порядком байтов

Преобразовать двоичное число с прямого порядка байтов в прямой.

Преобразование числа с плавающей запятой в двоичное

Найдите двоичное представление числа с плавающей запятой.

Преобразование двоичных значений в растровое изображение

Преобразование двоичной строки в растровое изображение.

Преобразование растрового изображения в двоичные числа

Преобразование растрового изображения в нули и единицы.

Преобразование битов в байты

Группировка битов для создания байтов.

Преобразовать байты в биты

Разложить байты на отдельные биты.

Разделить двоичные значения

Разделить двоичное число на более мелкие двоичные числа.

Объединить двоичные значения

Объединить несколько меньших двоичных чисел в одно двоичное.

Разрезать двоичные значения

Извлечь часть двоичного числа.

Замена двоичных значений

Замена единиц и нулей любыми другими значениями.

Заполнение двоичных значений

Добавляет заполнение со знаком или без знака к двоичным числам.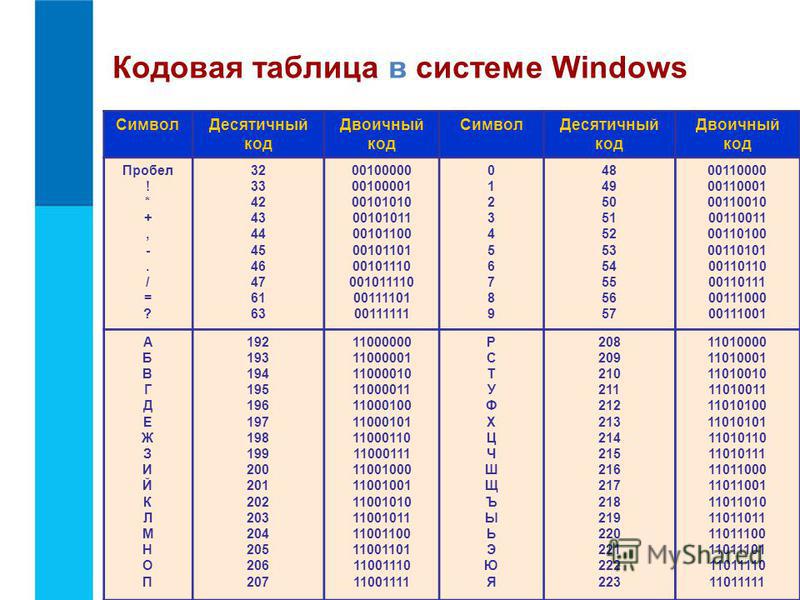

Усечение двоичных значений

Удаление начальных и конечных битов и сокращение двоичного значения.

Произвольное переключение двоичных битов

Внесение случайных ошибок в двоичные значения.

Цветные двоичные числа

Печать одинаковых двоичных чисел одинаковыми цветами.

Двоичные биты цвета

Используйте два разных цвета для двоичных нулей и единиц.

Создать двоичную спираль

Заставить двоичные биты идти по спирали.

Создать двоичный круг

Заставить двоичные биты идти по кругу.

Создать двоичный квадрат

Создать квадрат из двоичных битов.

Генерировать случайные биты

Создать последовательность случайных двоичных битов.

Генерация случайных полубайтов

Создание последовательности случайных двоичных полубайтов.

Создать случайные байты

Создать последовательность случайных двоичных октетов.

Создать случайные слова

Создать последовательность случайных двоичных слов.