Двоичный код — представление данных в виде комбинации двух знаков
Двоичный код — это представление информации в комбинации 2-х знаков 1 или 0, как говориться в программирование есть или нет, истина или лож, true или false. Обычному, человеку трудно понять, как информацию можно представить в виде нулей и единиц. Я постараюсь немного прояснить эту ситуацию.
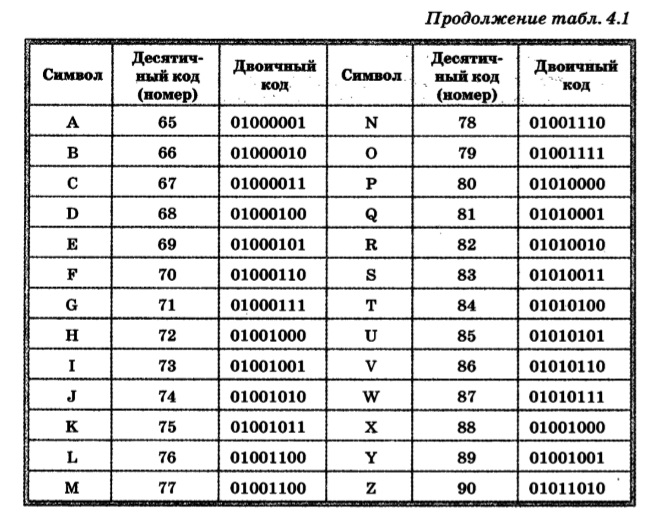
На самом деле двоичный код — это просто! Например, любую букву алфавита можно представить в виде набора нулей и единиц. Например, буква H латинского алфавита будет иметь такой вид в двоичной системе – 01001000, буква E – 01000101, бука L имеет такое двоичное представление – 01001100, P – 01010000.
Теперь не сложно догадаться, что для того чтобы написать английское слово HELP на машинном языке нужно использовать вот такой двоичный код:
01001000 01000101 01001100 01010000
Именно такой код использует для своей работы наш домашний компьютер.
Обычному человеку читать такой код очень сложно, а вот для вычислительных машин он самый понятный.
Двоичный код (машинный код) в наше время используется в программировании, ведь компьютер работает именно благодаря двоичному коду. Но не стоит думать, что процесс программирования сводится к набору единиц и нулей. Специально, чтобы упростить понимание между человеком и компьютером придумали языки программирования (си++, бейсик и т.п.). Программист пишет программу на понятом ему языке, а потом с помощью специальной программы-компилятора переводит свое творение в машинный код, который и запускает компьютер.
Переводим натуральное число десятичной системы счисления в двоичную
Берем нужное число, у меня это будет 5, делим число на 2:
5 : 2 = 2,5 есть остаток, значит, первое число двоичного кода будет 1(если нет — 0). Откидываем остаток и снова делим число на 2:
2 : 2 = 1 ответ без остатка, значит, второе число двоичного кода будет — 0.
0) = 4 + 0 + 1 = 5.
История двоичной системы счисления
Впервые двоичную систему предложил Лейбиц, он полагал, что данная система поможет в сложных математических вычислениях, да и вообще принесет пользу науке. Но по некоторым данным, до того как Лейбиц предложил двоичную систему счисления в Китае на стене появилась надпись, которую можно было расшифровать используя двоичный код. На этой надписи были нарисованы длинные и короткие палочки и если предположить, что длинная это 1, а короткая 0, вполне возможно, что в Китае идея двоичного кода ходила за много лет до его изобретения. Хотя расшифровка кода найденного на стене выявила там простое натуральное число, но все же факт остается фактом.
Виды двоичных кодов
В микропроцессорах двоичные коды используются
для представления любой обрабатываемой
информации. При этом разрядность
обрабатываемых чисел может превышать
разрядность самого процессора и используемой
в нЈм памяти. В этом случае длинное число может
занимать несколько ячеек памяти и
обрабатываться несколькими командами
процессора.
При обработке все ячейки памяти,
выделенные под многобайтное число,
рассматриваются как одно число.
Для представления числовой информации могут использоваться знаковые и беззнаковые коды. Для определЈнности примем длину слова процессора равной восьми битам.
Беззнаковые двоичные коды.
Первый вид двоичных кодов, который мы рассмотрим — это целые беззнаковые коды. В этих кодах каждый двоичный разряд представляет собой степень цифры 2:
При этом минимально возможное число, которое можно записать таким двоичным кодом, равно 0. Максимально возможное число, которое можно записать таким двоичным кодом, можно определить как:
Этими двумя числами полностью можно определить
диапазон, чисел которые можно представить таким
двоичным кодом. В случае двоичного
восьмиразрядного беззнакового целого числа
диапазон будет: диапазон чисел, которые можно
записать таким кодом: 0 .. 255. Для
шестнадцатиразрядного кода этот 0 .. 65535. В
восьмиразрядном процессоре для хранения такого
числа используется две ячейки памяти,
расположенные в соседних адресах.
Для работы с
такими числами используются специальные
команды.
Второй вид двоичных кодов, который мы рассмотрим — это прямые целые знаковые коды. В этих кодах старший разряд в слове используется для представления знака числа. В прямом знаковом коде нулем обозначается знак ‘+’, а единицей — знак ‘-‘. В результате введения знакового разряда диапазон чисел смещается в сторону отрицательных чисел:
В случае двоичного восьмиразрядного знакового целого числа диапазон чисел, которые можно записать таким кодом: -127 .. +127. Для шестнадцатиразрядного кода этот диапазон будет: -32767 .. +32767. В восьмиразрядном процессоре для хранения такого числа тоже используется две ячейки памяти, расположенные в соседних адресах.
Недостатком такого кода является то, что
знаковый разряд и цифровые разряды приходится
обрабатывать раздельно. Алгоритм программ,
работающий с такими кодами получается сложный.
Для выделения и изменения знакового разряда
приходится применять механизм маскирования
разрядов, что резко увеличивает размер программы
и уменьшает ее быстродействие.
Знаковые обратные двоичные коды.
Обратные двоичные коды отличаются от прямых только тем, что отрицательные числа в них получаются инвертированием всех разрядов числа. При этом знаковый и цифровые разряды не различаются. Алгоритм работы с такими кодами резко упрощается.
Тем не менее при работе с обратными кодами требуется специальный алгоритм распознавания знака, вычисления абсолютного значения числа, восстановления знака результата числа. Кроме того, в прямом и обратном коде числа для запоминания числа 0 используется два кода, тогда как известно, что число 0 положительное и отрицательным не может быть никогда.
Знаковые дополнительные двоичные коды.
От перечисленных недостатков свободны
дополнительные коды. Эти коды позволяют
непосредственно суммировать положительные и
отрицательные числа не анализируя знаковый
разряд и при этом получать правильный результат.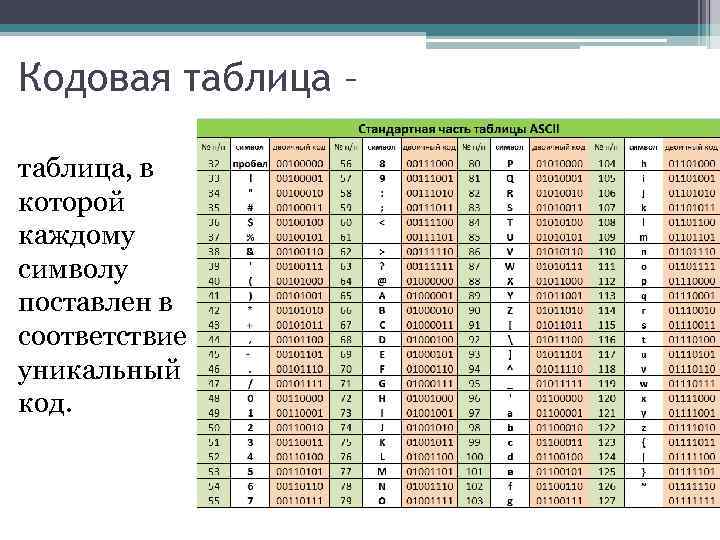
Диапазон чисел, которые можно записать таким кодом: -128 .. +127. Для шестнадцатиразрядного кода этот диапазон будет: -32768 .. +32767. В восьмиразрядном процессоре для хранения такого числа используется две ячейки памяти, расположенные в соседних адресах.
В обратных и дополнительных кодах наблюдается интересный эффект, который называется эффект распространения знака. Он заключается в том, что при преобразовании однобайтного числа в двухбайтное достаточно всем битам старшего байта присвоить значение знакового бита младшего байта. То есть для хранения знака числа можно использовать сколько угодно старших бит. При этом значение кода совершенно не изменяется.
Использование для представления знака числа
двух бит предоставляет интересную возможность
контролировать переполнения при выполнении
арифметических операций.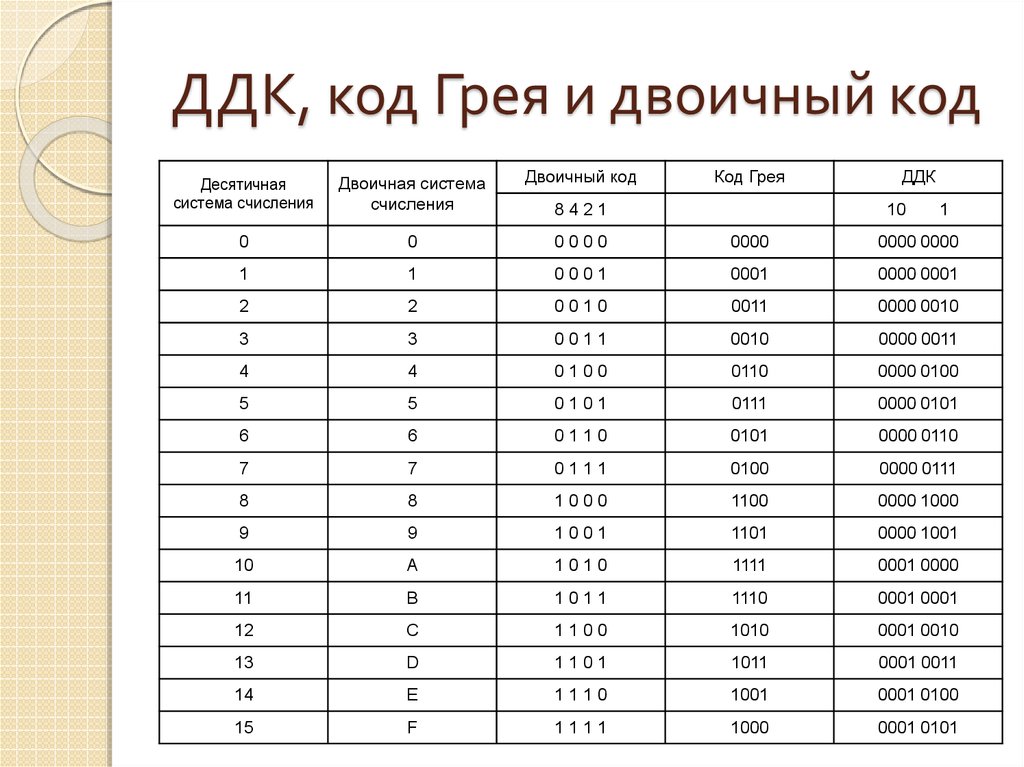
Рассмотрим несколько
примеров.
1) Просуммируем числа 12 и 5
В этом примере видно, что в результате суммирования получается правильный результат. Это можно проконтролировать по флагу переноса C, который совпадает со знаком результата (действует эффект распространения знака).
2) Просуммируем два отрицательных числа -12 и -5
В этом примере флаг переноса C тоже совпадает со знаком результата, то есть переполнения не произошло и в этом случае
3) Просуммируем положительное и отрицательное число -12 и +5
В этом примере при суммировании положительного и отрицательного числа автоматически получается правильный знак результата. В данном случае знак результата отрицательный. Флаг переноса совпадает со знаком результата, поэтому переполнения не было (мы можем убедиться в этом непосредственными вычислениями на бумаге или на калькуляторе).
4) Просуммируем положительное и отрицательное число +12 и -5
В данном примере знак результата
положительный.
Флаг переноса совпадает со знаком
результата, поэтому переполнения не было и в этом
случае.
5)Просуммируем числа 100 и 31
В этом примере видно, что в результате суммирования произошло переполнение восьмибитовой переменной, т.к. в результате операции над положительными числами получился отрицательный результат. Однако если рассмотреть флаг переноса, то он не совпадает со знаком результата. Эта ситуации является признаком переполнения результата и легко обнаруживается при помощи операции «исключающее ИЛИ» над старшим битом результата и флагом переноса C. Большинство процессоров осуществляют эту операцию аппаратно и помещают результат во флаг переполнения OV.
В этом примере результате операции над
отрицательными числами в результате
суммирования произошло переполнение
восьмибитовой переменной, т.к. получился
положительный результат. И в этом случае если
рассмотреть флаг переноса C, то он не совпадает со
знаком результата. Отличие от предыдущего случая
только в комбинации этих бит.
Представление дробных чисел в двоичном коде с фиксированной запятой.
Кроме целых чисел часто требуется работать с дробными числами. Следующий вид двоичных кодов, который мы рассмотрим — это дробные коды. Как и в случае целых чисел, дробные числа могут быть беззнаковые и знаковые. Для записи знаковых чисел могут быть использованы прямые, обратные и дополнительные коды. Принцип их построения точно такой же, как и в случае целых чисел.
Рассмотрим, как можно записать дробное число. До сих пор мы предполагали, что двоичная запятая находится правее самого младшего разряда. Но кто сказал, что она должна всегда находиться в этом месте? Мы можем договориться, что запятая находится слева от самого старшего разряда, и тогда в такой переменной можно будет записывать только дробные числа:
Или договоримся, что она находится точно посередине переменной, и тогда мы сможем записывать смешанные числа:
Остальные случаи рассматривать не будем.
Они
строятся точно так же как и для целых чисел.
Представление чисел в двоичном коде с плавающей запятой.
Часто приходится обрабатывать очень большие числа (например, расстояние между звЈздами) или наоборот очень маленькие числа (например, размеры атомов или электронов). При таких вычислениях пришлось бы использовать числа с очень большой разрядностью. В то же время нам не нужно знать расстояние между звЈздами с точностью до миллиметра. Для вычислений с такими величинами числа с фиксированной запятой неэффективны.
В десятичной арифметике для записи таких чисел используется алгебраическая форма. При этом число записывается в виде мантиссы, умноженной на 10 в степени, отображающей порядок числа, Например:
0,2*105; 0,16*10-38
Для записи двоичных чисел тоже используется
такая форма записи. Эта форма записи называется
запись числа с плавающей точкой. Напомним, что
мантисса не может быть больше единицы и после
запятой в мантиссе не может записываться ноль.
А теперь рассмотрим промышленные стандарты, используемые для представления чисел в компьютерах. Существует стандарт IEEE 754 для представления чисел с одинарной точностью (float) и с двойной точностью (double). Для записи числа в формате с плавающей запятой одинарной точности требуется тридцатидвухбитовое слово. Для записи чисел с двойной точностью требуется шестидесятичетырЈхбитовое слово. Чаще всего числа хранятся в нескольких соседних ячейках памяти процессора. Форматы числа в формате с плавающей запятой одинарной точности и числа в формате с плавающей запятой удвоенной точности приведены на рисунке
На рисунке буквой S обозначен знак числа, 0 — это
положительное число, 1 — отрицательное число. e
обозначает смещЈнный порядок числа. Смещение
требуется, чтобы не вводить в число еще один знак.
СмещЈнный порядок всегда положительное число.
Для одинарной точности для порядка выделено
восемь бит. Для смещЈнного порядка двойной
точности отводится 11 бит. Для одинарной точности
смещение принято 127, а для двойной точности — 1023.
В
десятичной мантиссе после запятой могут
присутствовать цифры 1:9, а в двоичной — только 1.
Поэтому для хранения единицы после двоичной
запятой не выделяется отдельный бит в числе с
плавающей запятой. Единица подразумевается, как
и двоичная запятая. Кроме того, в формате чисел с
плавающей запятой принято, что мантисса всегда
больше 1. То есть диапазон значений мантиссы
лежит в диапазоне от 1 до 2.
Рассмотрим несколько примеров:
1) Определить число с плавающей запятой, лежащее в четырЈх соседних байтах:
11000001 01001000 00000000 00000000
— Знаковый бит, равный 1 показывает, что число отрицательное.
— Экспонента 10000010 в десятичном виде соответствует числу 130. Вычтя число 127 из 130, получим число 3.
— Теперь запишем мантиссу: 1,100 1000 0000 0000 0000 0000
— И, наконец, определим десятичное число: 1100,1b = 12,5d
2) Определить число с плавающей запятой, лежащее в четырЈх соседних байтах:
11000011 00110100 00000000 00000000
— Знаковый бит, равный 1 показывает, что число
отрицательное.
— Экспонента 10000110 в десятичном виде соответствует числу 134. Вычтя число 127 из 134, получим число 7.
— Теперь запишем мантиссу: 1,011 0100 0000 0000 0000 0000
— И, наконец, определим десятичное число: 10110100b=180d
Для того чтобы записать ноль, достаточно записать в смещенный порядок число 00000000b. Значение мантиссы при этом не имеет значения. Число, в котором все байты равны 0, тоже попадает в этот диапазон значений.
Бесконечность соответствует смещенному порядку 11111111b и мантиссе, равной 1,0. При этом существует минус бесконечность и плюс бесконечность (переполнение и антипереполнение), которые часто отображаются на экран монитора как +INF и -INF.
Все остальные комбинации битов (в том числе и все единицы) воспринимаются как не числа и отображаются на экран: NaN.
Запись десятичных чисел.
Иногда бывает удобно хранить числа в памяти
процессора в десятичном виде (Например, для
вывода на экран дисплея). Для записи таких чисел
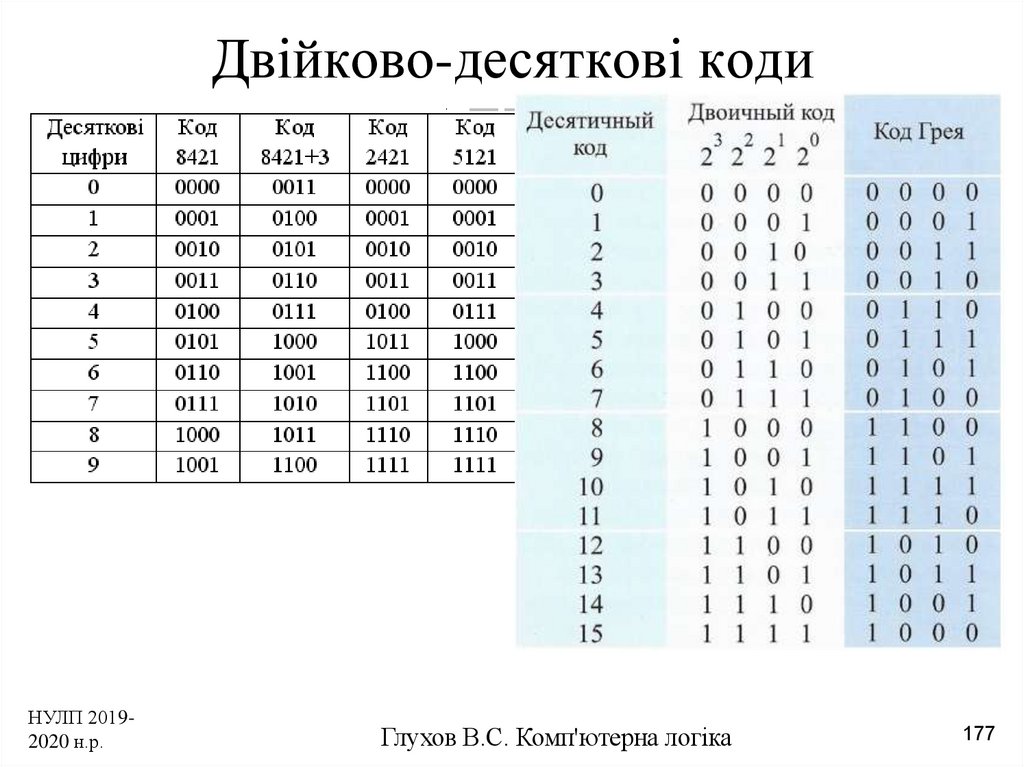
используются двоично-десятичные коды.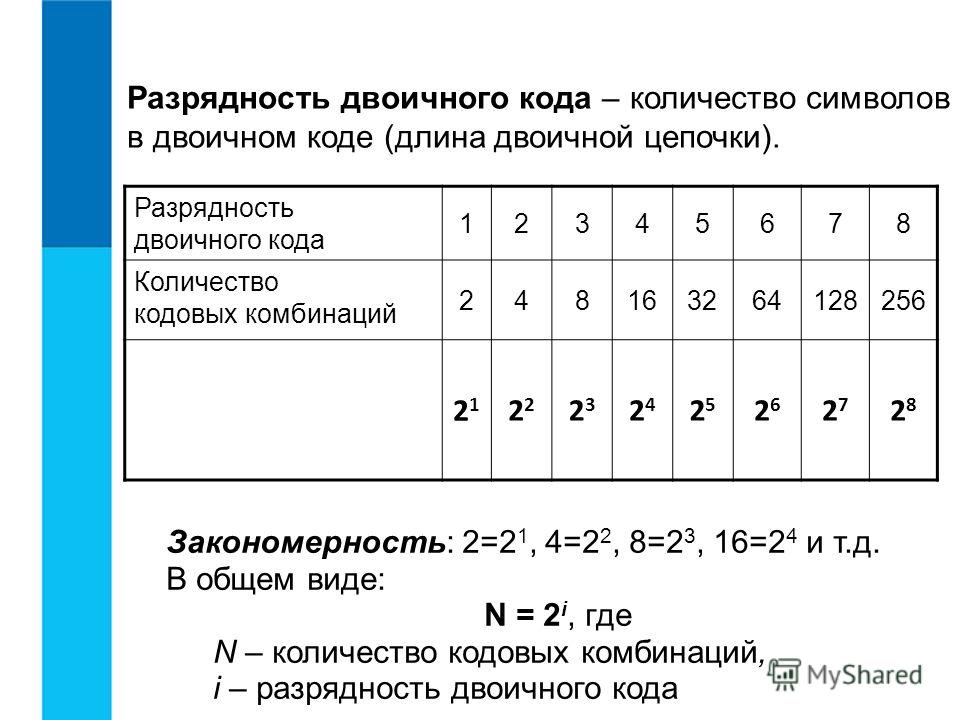
Для записи
одного десятичного разряда используется четыре
двоичных бита. Эти четыре бита называются
тетрадой. Иногда встречается название, пришедшее
из англоязычной литературы: нибл. При помощи
четырех бит можно закодировать шестнадцать цифр.
Лишние комбинации в двоично-десятичном коде
являются запрещенными. Таблица соответствия
двоично-десятичного кода и десятичных цифр
приведена ниже:
Остальные комбинации двоичного кода в тетраде являются запрещенными. Запишем пример двоично-десятичного кода:
1258 = 0001 0010 0101 1000
589 = 0000 0101 1000 1001
Достаточно часто в памяти процессора для хранения одной десятичной цифры выделяется одна ячейка памяти (восьми, шестнадцати или тридцатидвухразрядная). Это делается для повышения скорости работы программы. Для того, чтобы отличить такой способ записи двоично-десятичного числа от стандартного, способ записи десятичного числа, как это показано в примере, называется упакованной формой двоично-десятичного числа.
Суммирование двоично-десятичных чисел.
Суммирование двоично-десяичных чисел можно производить по правилам обычной двоичной арифметики, а затем производить двоично-десятичную коррекцию. Двоично-десятичная коррекция заключается в проверке каждой тетрады на допустимые коды. Если в какой либо тетраде обнаруживается запрещенная комбинация , то это говорит о переполнении. В этом случае необходимо произвести двоично-десятичную коррекцию. Двоично-десятичная коррекция заключается в дополнительном суммировании числа шесть (число запрещенных комбинаций) с тетрадой, в которой произошло переполнение или произошЈл перенос в старшую тетраду. ПриведЈм два примера:
Запись текстов в памяти процессора.
Все символы и буквы могут быть закодированы при
помощи восьми двоичных символов. Наиболее
распространенными таблицами являются таблицы
ASCII с национальными расширениями, применяющиеся
в DOS (и которые можно использовать для записи
текстов в микропроцессорах), и таблицы ANSI,
применяющиеся в WINDOWS.
В таблицах ASCII и ANSI первые 128
символов совпадают. В этой части таблицы
содержатся символы цифр, знаков препинания,
латинские буквы верхнего и нижнего регистров и
управляющие символы. Национальные расширения
символьных таблиц и символы псевдографики
содержатся в последних 128 кодах этих таблиц,
поэтому русские тексты в операционных системах
DOS и WINDOWS не совпадают.
[Назад] [Содержание] [Вперёд]
Двоичный код | Определение, цифры и факты
- Связанные темы:
- кодировка
Просмотреть весь связанный контент →
двоичный код , код, используемый в цифровых компьютерах, основанный на двоичной системе счисления, в которой есть только два возможных состояния, выключено и включено, обычно обозначаемое 0 и 1. В то время как в десятичной системе, в котором используется 10 цифр, каждая позиция цифры представляет степень числа 10 (100, 1000 и т. д.), в двоичной системе каждая позиция цифры представляет степень числа 2 (4, 8, 16 и т.
д.). Двоичный кодовый сигнал представляет собой серию электрических импульсов, которые представляют собой числа, символы и операции, которые необходимо выполнить. Устройство, называемое часами, посылает регулярные импульсы, а такие компоненты, как транзисторы, включаются (1) или выключаются (0), чтобы пропускать или блокировать импульсы. В двоичном коде каждое десятичное число (0–9) представлен набором из четырех двоичных цифр или битов. Четыре основные арифметические операции (сложение, вычитание, умножение и деление) могут быть сведены к комбинациям основных булевых алгебраических операций над двоичными числами. ( См. в таблице ниже, как десятичные числа от 0 до 10 представлены в двоичном формате.)
| десятичная дробь | бинарный | преобразование |
|---|---|---|
| 0 | 0 | 0 ( 2 0 ) |
| 1 | 1 | 1 ( 2 0 ) |
| 2 | 10 | 1 ( 2 1 ) + 0 ( 2 0 ) |
| 3 | 11 | 1 ( 2 1 ) + 1 ( 2 0 ) |
| 4 | 100 | 1 ( 2 2 ) + 0 ( 2 1 ) + 0 ( 2 0 ) |
| 5 | 101 | 1 ( 2 2 ) + 0 ( 2 1 ) + 1 ( 2 0 ) |
| 6 | 110 | 1 ( 2 2 ) + 1 ( 2 1 ) + 0 ( 2 0 ) |
| 7 | 111 | 1 ( 2 2 ) + 1 ( 2 1 ) + 1 ( 2 0 ) |
| 8 | 1000 | 1 ( 2 3 ) + 0 ( 2 2 ) + 0 ( 2 1 ) + 0 ( 2 0 ) |
| 9 | 1001 | 1 ( 2 3 ) + 0 ( 2 2 ) + 0 ( 2 1 ) + 1 ( 2 0 ) |
| 10 | 1010 | 1 ( 2 3 ) + 0 ( 2 2 ) + 1 ( 2 1 ) + 0 ( 2 0 ) |
Редакторы Британской энциклопедии Эта статья была недавно отредактирована и дополнена Адамом Августином.
Что такое двоичный код и как он используется в вычислениях?
К
- Рахул Авати
Двоичный описывает схему нумерации, в которой есть только два возможных значения для каждой цифры — 0 или 1 — и является основой для всего двоичного кода, используемого в вычислительных системах. Эти системы используют этот код для понимания операционных инструкций и пользовательского ввода, а также для представления пользователю соответствующих выходных данных.
Термин двоичный также относится к любой системе цифрового кодирования/декодирования, в которой есть ровно два возможных состояния. В памяти, хранении, обработке и передаче цифровых данных значения 0 и 1 иногда называют 9.0013 младшая и высшая соответственно. В транзисторах 1 означает поток электричества, а 0 означает отсутствие потока электричества.
Двоичная система счисления была усовершенствована в 17 веке Готфридом Лейбницем. В математике и вычислительных системах двоичная цифра или бит — это наименьшая единица данных. Каждый бит имеет единственное значение либо 1, либо 0, что означает, что он не может принимать никакое другое значение.
Компьютеры могут представлять числа с помощью двоичного кода в виде цифровых единиц и нулей внутри центрального процессора (ЦП) и ОЗУ. Эти цифровые числа являются электрическими сигналами, которые либо включены, либо выключены внутри ЦП или ОЗУ.
Двоичный и десятичный Поскольку двоичная система использует только две цифры или бита и представляет числа, используя различные комбинации единиц и нулей, она известна как система с основанием 2 .
Здесь 1 означает «включено» или «истинно», а 0 означает «выключено» или «ложно».
Напротив, десятичная система счисления представляет собой систему с основанием 10 , где каждое возможное место в числе может быть одним из 10 цифр (0-9). В многозначном числе крайняя правая цифра стоит на первом месте, цифра рядом с ней слева — на 10-м месте, цифра левее — на 100-м месте и так далее.
Пример
В четырехзначном числе 1980 вот места, занимаемые каждой цифрой.
| 1 | 9 | 8 | 0 |
1000 место | 100 место | 10 место | 1 место |
Двоичная система счисления является основой всех вычислительных систем и операций.
Он позволяет устройствам хранить, получать доступ и манипулировать всеми типами информации, направляемой в ЦП или память и из них. Это позволяет разрабатывать приложения, которые позволяют пользователям делать следующее:
- просмотр веб-сайтов;
- создавать и обновлять документы;
- играть в игры;
- просмотра потокового видео и других видов графической информации; программное обеспечение доступа
- ; и
- выполнять расчеты и анализ данных.
Двоичная схема цифровых единиц и нулей предлагает простой и элегантный способ работы компьютеров. Он также предлагает эффективный способ управления логическими схемами и определения истинного (1) и ложного (0) состояний электрического сигнала.
Как работают двоичные числа Двоичная система является основным языком вычислительных систем. Внутри этих систем двоичное число состоит из последовательности восьми битов. Эта серия известна как байт .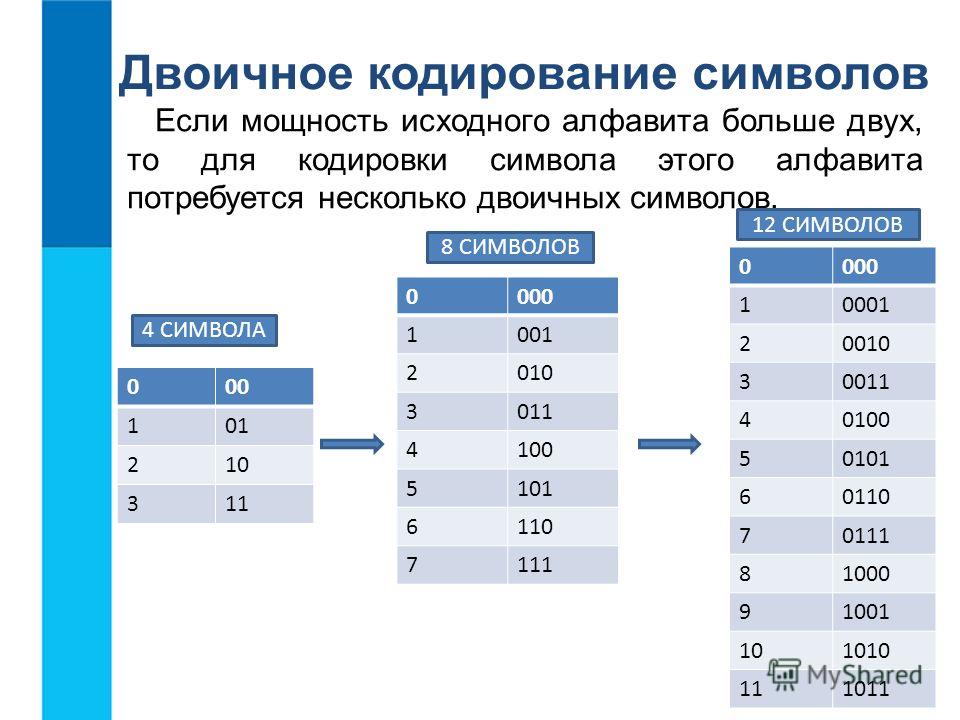
В двоичной схеме положение каждой цифры определяет ее десятичное значение. Таким образом, зная положение каждого бита, двоичное число можно преобразовать в десятичное число.
В десятичных числах каждое дополнительное место умножается на 10 при движении справа налево (первое место, 10-е место, 100-е место и т. д.). Но в двоичных числах каждое дополнительное место при движении справа налево умножается на два. Два приведенных ниже примера поясняют эту идею.
Пример 1
Вот как вычисляются десятичные значения для 8-битного (байтового) двоичного числа 01101000.
В этом номере первая цифра крайняя справа, а восьмая цифра крайняя левая. Цифры со второй (0) по седьмую (1) читаются справа налево.
Битовая позиция | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Бит | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
Двоично-десятичный расчет (экспонента) | 2 0 | 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 | 2 7 |
Десятичное значение (x2) | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
По мере увеличения позиции бита с единицы до восьми предыдущее десятичное значение умножается на два.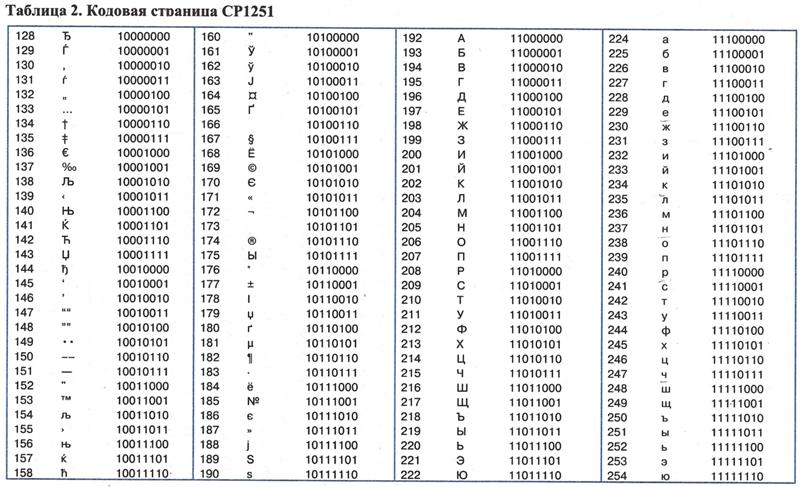
Вот почему первый бит имеет значение 1, второй бит имеет значение 2, третий бит имеет значение 4 и так далее.
Окончательное значение десятичного числа вычисляется путем сложения отдельных значений из приведенной выше таблицы. Однако следует добавлять только те значения, в которых бит равен 1. Эти значения представляют положение «включено». Нули представляют положение «выключено», поэтому они не учитываются при вычислении десятичного значения.
Итак, для двоичного числа 01101000 десятичное значение вычисляется следующим образом:
8 + 32 + 64 = 104
Пример 2
Вот как вычисляются десятичные значения для двоичного числа 11111111.
Битовая позиция | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Бит | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Двоично-десятичный расчет (экспонента) | 2 0 | 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 | 2 7 |
Десятичное значение | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
В этом двоичном числе каждый бит имеет значение 1, поэтому складываются все отдельных значений.
Итак, для этого числа , десятичное значение следующее:
1 + 2 + 4 + 8 + 16+ 32 + 64 +128 = 255
Представление десятичных чисел в двоичном форматеКак упоминалось ранее, двоичная система счисления работает только с 1 и 0. Однако положение только этих двух цифр может представлять гораздо больше чисел. Примеры в предыдущем разделе показывают, как любое десятичное число от 0 до 255 может быть представлено с помощью двоичных чисел. Числа больше 255 также можно представить, добавив больше битов к 8-битному двоичному числу.
Вот десятичные числа от нуля до 20 и их двоичные эквиваленты.
| Десятичное число | Двоичный номер | Десятичное число | Двоичный номер |
0 | 0 | 11 | 1011 |
1 | 1 | 12 | 1100 |
2 | 10 | 13 | 1101 |
3 | 11 | 14 | 1110 |
4 | 100 | 15 | 1111 |
5 | 101 | 16 | 10000 |
6 | 110 | 17 | 10001 |
7 | 111 | 18 | 10010 |
8 | 1000 | 19 | 10011 |
9 | 1001 | 20 | 10100 |
10 | 1010 | — | — |
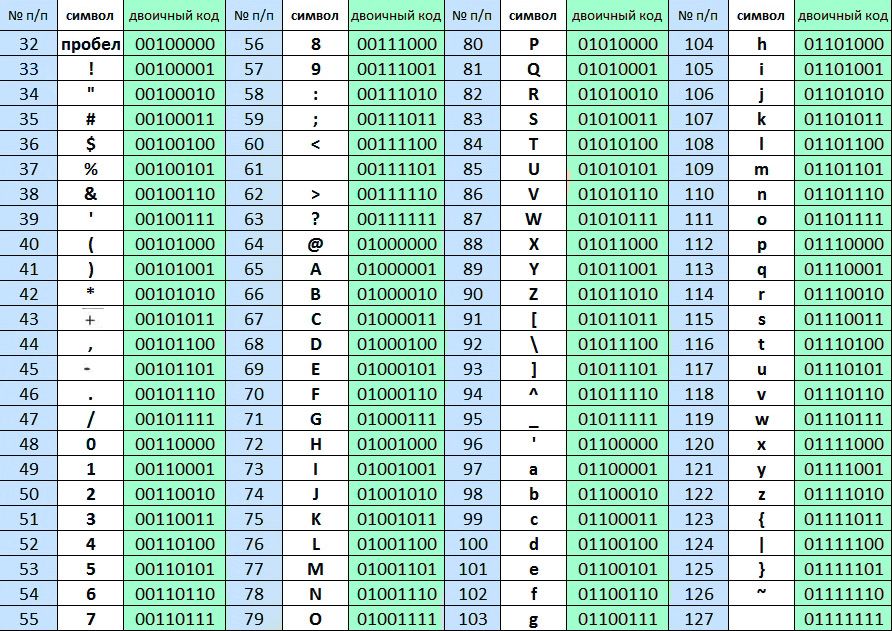
Преобразование двоичных чисел в текстовые символыДвоичные числа можно преобразовать в текстовые символы, используя коды американского стандарта для обмена информацией (ASCII) для хранения информации в ОЗУ или ЦП компьютера. Приложения с поддержкой ASCII, такие как текстовые процессоры, могут считывать текстовую информацию из ОЗУ или ЦП. Они также могут хранить текстовую информацию, которая затем может быть извлечена пользователем позднее. Коды ASCII хранятся в таблице ASCII, состоящей из 128 текстовых или специальных символов. Каждый символ имеет соответствующее десятичное значение.
символов ASCII включают символы a-z, A-Z, 0-9 и набор знаков препинания. В первом примере предыдущего раздела двоичное число равно 01101000 (десятичное число 104). В ASCII это число будет h в нижнем регистре. Чтобы образовать слова, нужно добавить больше букв к h . В двоичном выражении это означает добавление дополнительных двоичных чисел к двоичному числу для h .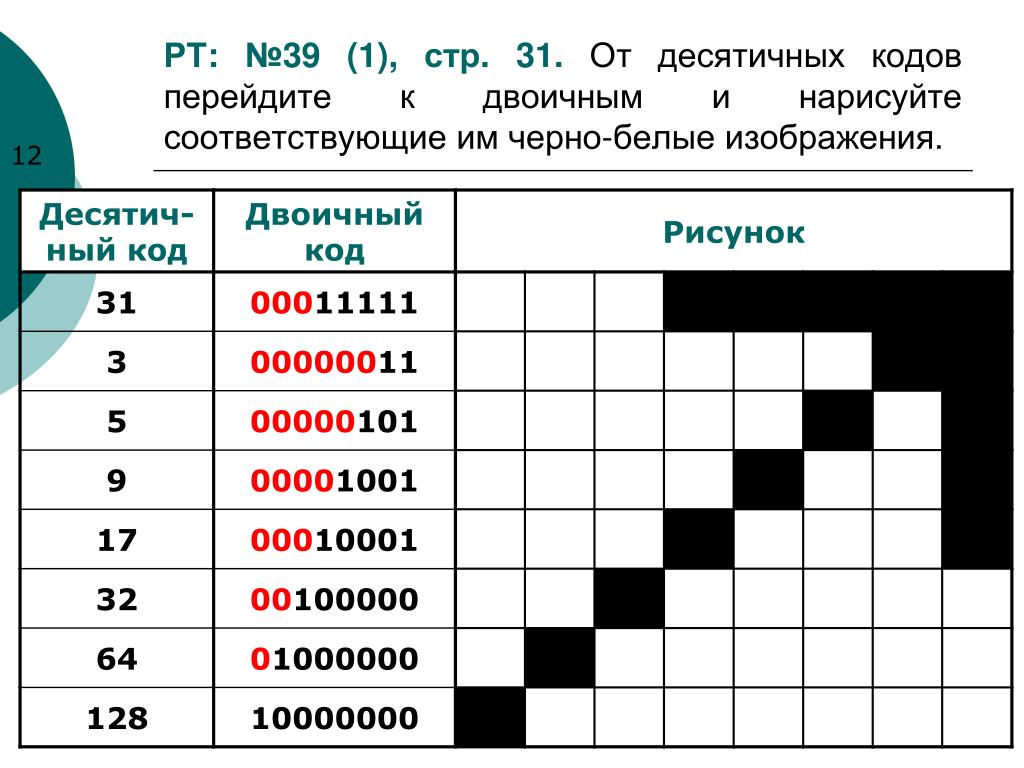
Пример
Двоичный код строчной буквы ASCII i равно 01101001. Таким образом, чтобы создать слово hi , двоичное число для i добавляется к двоичному числу для h . Это дает следующее двоичное число:
01101000 + 01101001 = 0110100001101001
В десятичном выражении десятичные числа для h и i равны 104 и 105 соответственно.
Другими распространенными примерами преобразования двоичных чисел в текстовый код ASCII являются следующие.
| Двоичный номер | Десятичное число | Код ASCII |
110000 | 48 | 0 |
1000001 | 65 | А (верхний регистр) |
1111111 | 127 | Клавиша DEL |
11011 | 27 | Клавиша ESC |
См.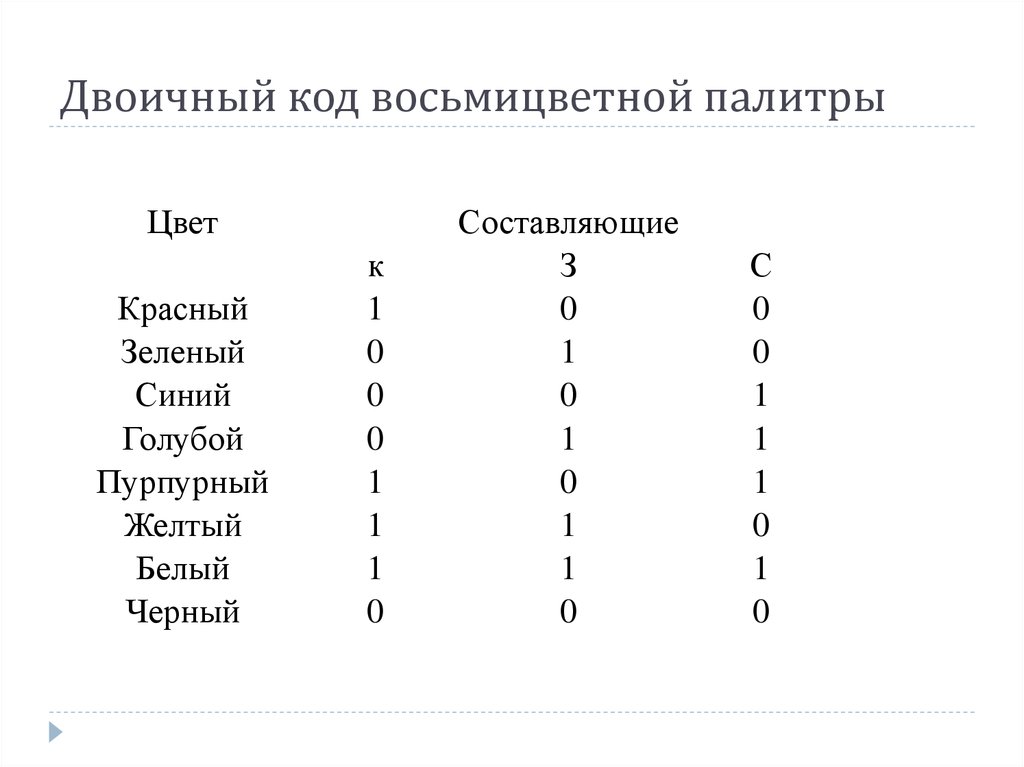
также: Символы ASCII ; киби, меби, гиби, теби, пеби и эксби ; кодирование и декодирование ; старший бит или байт ; и Расширенный двоично-десятичный код обмена .
Последнее обновление: май 2022 г.
Продолжить чтение о бинарнике- Объяснение двоичных и шестнадцатеричных чисел для разработчиков
- Новые функции Java 7: двоичная запись и литеральная инициализация переменных
- Введение в бинарное сравнение для этичных хакеров
- ТБ и ГБ: терабайт больше гигабайта?
- Преобразование двоичного кода в десятичный
управление мобильными устройствами
Программное обеспечение для управления мобильными устройствами (MDM) позволяет ИТ-администраторам контролировать, защищать и применять политики на смартфонах, планшетах и других конечных устройствах.
Сеть
- коаксиальный кабель
Коаксиальный кабель — это тип медного кабеля, специально изготовленного с металлическим экраном и другими компонентами, предназначенными для блокирования сигнала …
- мегагерц (МГц)
мегагерц (МГц) — это множитель, равный одному миллиону герц (106 Гц). Герц — стандартная единица измерения частоты в …
- Стандарты беспроводной связи IEEE 802
IEEE 802 — это набор сетевых стандартов, которые охватывают спецификации физического уровня и уровня канала передачи данных для таких технологий, как…
Безопасность
- SOAR (организация безопасности, автоматизация и реагирование)
Управление безопасностью, автоматизация и реагирование, или SOAR, представляет собой набор совместимых программ, который позволяет организации.
.. - цифровая подпись
Цифровая подпись — это математический метод, используемый для проверки подлинности и целостности сообщения, программного обеспечения или цифрового…
- судо (су ‘делать’)
Sudo — это утилита командной строки для Unix и операционных систем на базе Unix, таких как Linux и macOS.
..ИТ-директор
- хорошие навыки
Твердые навыки — это определенные способности, способности и наборы навыков, которыми человек может обладать и демонстрировать взвешенно.
- управление корпоративными проектами (EPM)
Управление корпоративными проектами (EPM) представляет собой профессиональные практики, процессы и инструменты, используемые для управления несколькими …
- Управление портфелем проектов: руководство для начинающих
Управление портфелем проектов — это формальный подход, используемый организациями для выявления, определения приоритетов, координации и мониторинга проектов .
..
..HRSoftware
- пассивный кандидат
Пассивный кандидат (пассивный кандидат на работу) — это любой сотрудник, который не занимается активным поиском работы.
- проверка сотрудников
Проверка сотрудников — это процесс проверки, проводимый работодателями для проверки биографических данных и проверки информации о новом…
- Эффект хоторна
Эффект Хоторна — это изменение поведения участников исследования в ответ на их знание о том, что они …
Отдел обслуживания клиентов
- квалифицированный маркетолог лид (MQL)
Квалифицированный маркетолог (MQL) — это посетитель веб-сайта, уровень вовлеченности которого указывает на то, что он может стать клиентом.
- автоматизация маркетинга
Автоматизация маркетинга — это тип программного обеспечения, которое позволяет компаниям эффективно ориентироваться на клиентов с помощью автоматизированного маркетинга .
