Что такое двоичный код и почему компьютеры используют его

Компьютеры не понимают слов и цифр так, как это делают люди. Современное программное обеспечение позволяет конечному пользователю игнорировать это, но на самых низких уровнях ваш компьютер оперирует двоичным электрическим сигналом, который имеет только два состояния: есть ток или нет тока. Чтобы «понять» сложные данные, ваш компьютер должен закодировать их в двоичном формате.

Двоичная система основывается на двух цифрах – 1 и 0, соответствующим состояниям включения и выключения, которые ваш компьютер может понять. Вероятно, вы знакомы с десятичной системой. Она использует десять цифр – от 0 до 9, а затем переходит к следующему порядку, чтобы сформировать двузначные числа, причем цифра из каждого следующего порядка в десять раз больше, чем предыдущая. Двоичная система аналогична, причем каждая цифра в два раза больше, чем предыдущая.

Подсчет в двоичном формате

В двоичном выражении первая цифра равноценна 1 из десятичной системы. Вторая цифра равна 2, третья – 4, четвертая – 8, и так далее – удваивается каждый раз. Добавление всех этих значений даст вам число в десятичном формате.

1111 (в двоичном формате) = 8 + 4 + 2 + 1 = 15 (в десятичной системе)

Учет 0 даёт нам 16 возможных значений для четырех двоичных битов. Переместитесь на 8 бит, и вы получите 256 возможных значений. Это занимает намного больше места для представления, поскольку четыре цифры в десятичной форме дают нам 10000 возможных значений. Конечно, бинарный код занимает больше места, но компьютеры понимают двоичные файлы намного лучше, чем десятичную систему. И для некоторых вещей, таких как логическая обработка, двоичный код лучше десятичного.

Следует сказать, что существует ещё одна базовая система, которая используется в программировании: шестнадцатеричная. Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют её для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять собой целый байт, то есть заменяют восемь цифр в двоичном формате. Шестнадцатеричная система использует цифры 0-9, а также буквы от A до F, чтобы получить дополнительные шесть цифр.

Почему компьютеры используют двоичные файлы

Короткий ответ: аппаратное обеспечение и законы физики. Каждый символ в вашем компьютере является электрическим сигналом, и в первые дни вычислений измерять электрические сигналы было намного сложнее. Было более разумно различать только «включенное» состояние, представленное отрицательным зарядом, и «выключенное» состояние, представленное положительным зарядом.

Для тех, кто не знает, почему «выключено» представлено положительным зарядом, это связано с тем, что электроны имеют отрицательный заряд, а больше электронов – больше тока с отрицательным зарядом.

Таким образом, ранние компьютеры размером с комнату использовали двоичные файлы для создания своих систем, и хотя они использовали более старое, более громоздкое оборудование, они работали на тех же фундаментальных принципах. Современные компьютеры используют, так называемый,

транзистор для выполнения расчетов с двоичным кодом.

Вот схема типичного транзистора:

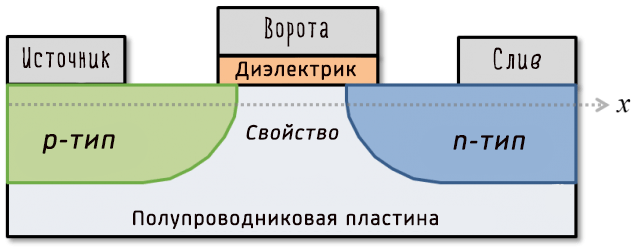
По сути, он позволяет току течь от источника к стоку, если в воротах есть ток. Это формирует двоичный ключ. Производители могут создавать эти транзисторы невероятно малыми – вплоть до 5 нанометров или размером с две нити ДНК. Это то, как работают современные процессоры, и даже они могут страдать от проблем с различением включенного и выключенного состояния (хотя это связано с их нереальным молекулярным размером, подверженным 

странностям квантовой механики).

Почему только двоичная система

Поэтому вы можете подумать: «Почему только 0 и 1? Почему бы не добавить ещё одну цифру?». Хотя отчасти это связано с традициями создания компьютеров, вместе с тем, добавление ещё одной цифры означало бы необходимость выделять ещё одно состояние тока, а не только «выключен» или «включен».

Проблема здесь в том, что если вы хотите использовать несколько уровней напряжения, вам нужен способ легко выполнять вычисления с ними, а современное аппаратное обеспечение, способное на это, не жизнеспособно как замена двоичных вычислений. Например, существует, так называемый,

тройной компьютер, разработанный в 1950-х годах, но разработка на том и прекратилась. Тернарная логика более эффективна, чем двоичная, но пока ещё нет эффективной замены бинарного транзистора или, по крайней мере, нет транзистора столь же крошечных масштабов, что и двоичные.

Причина, по которой мы не можем использовать тройную логику, сводится к тому, как транзисторы соединяются в компьютере  и как они используются для математических вычислений. Транзистор получает информацию на два входа, выполняет операцию и возвращает результат на один выход.

Таким образом, бинарная математика проще для компьютера, чем что-либо ещё. Двоичная логика легко преобразуется в двоичные системы, причем True и False соответствуют состояниям Вкл и Выкл.

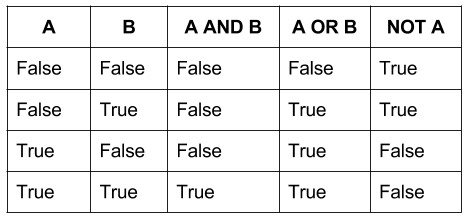
Бинарная таблица истинности, работающая на двоичной логике, будет иметь четыре возможных выхода для каждой фундаментальной операции. Но, поскольку тройные ворота используют три входа, тройная таблица истинности имела бы 9 или более. В то время как бинарная система имеет 16 возможных операторов (2^2^2), троичная система имела бы 19683 (3^3^3). Масштабирование становится проблемой, поскольку, хотя троичность более эффективна, она также экспоненциально более сложна.

Кто знает? В будущем мы вполне возможно увидим тройничные компьютеры, поскольку бинарная логика столкнулась с проблемами миниатюризации. Пока же мир будет продолжать работать в двоичном режиме.

Что такое двоичный код?

Дата

Категория: it

Всем известно, что компьютеры могут выполнять вычисления с большими группами данных на огромной скорости. Но не все знают, что эти действия зависят всего от двух условий: есть или нет ток и какое напряжение.

Каким же образом компьютер умудряется обрабатывать такую разнообразную информацию?
Секрет заключается в двоичной системе исчисления. Все данные поступают в компьютер, представленные в виде единиц и нулей, каждому из которых соответствует одно состояние электропровода: единицам — высокое напряжение, нулям — низкое или же единицам — наличие напряжения, нулям — его отсутствие. Преобразование данных в нули и единицы называется двоичной конверсией, а окончательное их обозначение — двоичным кодом.
В десятичном обозначении, основанном на десятичной системе исчисления, которая используется в повседневной жизни, числовое значение представлено десятью цифрами от 0 до 9, и каждое место в числе имеет ценность в десять раз выше, чем место справа от него. Чтобы представить число больше девяти в десятичной системе исчисления, на его место ставится ноль, а на следующее, более ценное место слева — единица. Точно так же в двоичной системе, где используются только две цифры — 0 и 1, каждое место в два раза ценнее, чем место справа от него. Таким образом, в двоичном коде только ноль и единица могут быть изображены как одноместные числа, и любое число, больше единицы, требует уже два места. После ноля и единицы следующие три двоичных числа это 10 (читается один-ноль) и 11 (читается один-один) и 100 (читается один-ноль-ноль). 100 двоичной системы эквивалентно 4 десятичной. На верхней таблице справа показаны другие двоично-десятичные эквиваленты.
Любое число может быть выражено в двоичном коде, просто оно займет больше места, чем в десятичном обозначении. В двоичной системе можно записать и алфавит, если за каждой буквой закрепить определенное двоичное число.

Две цифры на четыре места
16 комбинаций можно составить, используя темные и светлые шары, комбинируя их в наборах из четырех штук Если темные шары принять за нули, а светлые за единицы, то и 16 наборов окажутся 16-единичным двоичным кодом, числовая ценность которого составляет от нуля до пяти (см. верхнюю таблицу на стр. 27). Даже с двумя видами шаров в двоичной системе можно построить бесконечное количество комбинаций, просто увеличивая число шариков в каждой группе — или число мест в числах. 

Биты и байты

Самая маленькая единица в компьютерной обработке, бит — это единица данных, которая может обладать одним из двух возможных условий. К примеру, каждая из единиц и нулей (справа) означает 1 бит. Бит можно представить и другими способами: наличием или отсутствием электрического тока, дырочкой и ее отсутствием, направлением намагничивания вправо или влево. Восемь битов составляют байт. 256 возможных байтов могут представить 256 знаков и символов. Многие компьютеры обрабатывают байт данных одновременно.

Двоичная конверсия. Четырехцифровой двоичный код может представить десятичные числа от 0 до 15.

Кодовые таблицы

Когда двоичный код используется для обозначения букв алфавита или пунктуационных знаков, требуются кодовые таблицы, в которых указано, какой код какому символу соответствует. Составлено несколько таких кодов. Большинство ПК приспособлено под семицифровой код, называемый ASCII, или американский стандартный код для информационного обмена. На таблице справа показаны коды ASCII для английского алфавита. Другие коды предназначаются для тысяч символов и алфавитов других языков мира.

 Часть таблицы кода ASCII

Бинарный код — Binary code

Для двоичной формы компьютерного программного обеспечения, см машинного кода .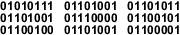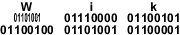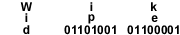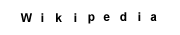 Слово представлено в «Википедии» ASCII двоичный код, состоящий из 9 байт (72 бита).

Двоичный код представляет собой текст , инструкции , процессор компьютера , или любые другие данные , используя систему из двух символов. Система два-символа , используемая часто «0» и «1» из двоичной системы счисления . Двоичный код присваивает шаблон двоичных цифр, также известные как бит , для каждого символа, инструкции и т.д. Например, двоичная строка из восьми бит может представлять любого из 256 возможных значений и может, таким образом, представляет собой широкий спектр различных Предметы.

В вычислительной технике и телекоммуникациях, двоичные коды используются для различных методов кодирования данных, таких как строки символов , в битовые строки. Эти методы могут использовать фиксированную ширину или переменную ширину строку. В фиксированной ширины двоичного кода, каждой буквы, цифры, или другой символ представлен битовой строки той же длины; что битовая строка, интерпретируется как двоичное число , обычно отображается в кодовых таблиц в восьмеричной , десятичной или шестнадцатеричной системе счисления. Есть много наборов символов и много кодировок символов для них.

Битовая строка, интерпретируется как двоичное число, может быть переведена в десятичное число . Например, нижний корпус , если представлена битовой строки (как в стандартном ASCII коде), также могут быть представлены в виде десятичного числа «97». 01100001

История двоичного кода

Современная двоичная система счисления, основа для двоичного кода, была изобретена Готфридом Лейбницем в 1689 и появляется в своей статье экспликация де l’Arithmétique Binaire . Полное название переводится на английский язык как «Объяснение двоичной арифметики», в котором используются только символы 1 и 0, с некоторыми замечаниями о его полезности, и на свете она бросает на древних китайских деятелей Фу Си .»( 1703). система Лейбница использует 0 и 1, как современную двоичную систему счисления. Лейбниц столкнулся с I Ching через французский иезуит Йоахим Буве и с восхищением заметил , как его гексаграммы соответствуют двоичным числам от 0 до 111111, и пришел к выводу , что это отображение было свидетельство крупных китайских достижений в своем роде философской математики , которыми он восхищался. Лейбниц видели гексаграммы как подтверждение универсальности своей собственной религиозной веры.

Бинарные позиции занимают центральное место в теологии Лейбница. Он считал , что двоичные числа были символом христианской идеи CREATIO экс тНИо или создания из ничего. Лейбниц пытался найти систему , которая преобразует словесные заявления Логики в чисто математический. После того, как его идеи были проигнорированы, он наткнулся на классический китайский текст под названием I Ching или «Книга перемен», в котором используется тип двоичного кода. Книга подтвердил свою теорию , что жизнь может быть упрощена или уменьшенное до ряда простых предложений. Он создал систему , состоящую из ряда нулей и единиц. В течение этого периода времени, Лейбниц еще не нашел применение для этой системы.

Бинарные системы предшествовавшие Лейбниц также существовали в древнем мире. Вышеупомянутый I Ching , что Лейбниц столкнулся с датой БЛА 9 века в Китае. Двоичная система цзин , текст для гаданий, основывается на двойственности инь и янь . Щелевые барабаны с бинарными тонами используются для кодирования сообщений по всей Африке и Азии. Индийский ученый Пингала (около 5-го 2 — го века до н.э.) разработал двоичную систему для описания просодии в его Chandashutram.

Жители острова Мангареве в Французской Полинезии использовали гибридную Binary- десятичную систему до 1450. В 11 — м веке, ученый и философ Шао Юн разработал метод для организации гексаграммы , которая соответствует, хотя и непреднамеренно, к последовательности 0 до 63 , как представлено в двоичной системе , с инь как 0, яН как 1 и наименее значимый бит на вершине. Упорядочение также лексикографическое упорядочение на sextuples элементов , выбранных из набора из двух элементов.

В 1605 году Фрэнсис Бэкон обсудили систему , в которой буквы алфавита может быть сведена к последовательности двоичных цифр, которые затем могут быть закодированы в виде едва заметных вариаций в шрифте в любом случайном тексте. Важно для общей теории двоичного кодирования, он добавил , что этот метод может быть использован с любыми объектами на всех: «если эти объекты будут способны лишь двукратная разница; также колокольчики, по Труб, фонарями и факелами, в докладе мушкетов, и любые инструменты , как природа».

Джордж Буль опубликовал статью , в 1847 году под названием «Математический анализ логики» , которая описывает алгебраическую систему логики, теперь известную как булева алгебра . Система Буля была основана на двоичной, Да нет, двухпозиционный подход , который состоял из трех самых основных операций: AND, OR, и NOT. Эта система не была введена в эксплуатацию до аспиранта из Массачусетского технологического института , Клода Шеннона , заметил , что Булева алгебра он узнал , был подобен электрической цепи. Шеннон написал свою диссертацию в 1937 году, в котором реализованы свои выводы. Тезис Шеннона стал отправной точкой для использования двоичного кода в практических приложениях , такие как компьютеры, электрические схемы, и многие другие.

Другие формы двоичного кода

Даосская Багуа

Битовая строка не является единственным типом двоичного кода. Двоичная система, в общем, любая система, которая позволяет только два варианта, такие как переключатель в электронной системе или простое истинное или ложное испытание.

шрифт Брайля

Шрифт Брайля является тип бинарного кода , который широко используется слепым читать и писать на ощупь, названный в честь его создателя, Луи Брайля. Эта система состоит из сетки из шести точек каждый, три на каждый столбец, в котором каждая точка имеет два состояния: поднятые или не подняты. Различные комбинации поднятых и уплощенных точек способны представлять все буквы, цифры и знаки препинания.

Багуа

Багуа представляют собой схемы , используемые в фэн — шуй , даосской космологии и я Ching исследований. Ба гуа состоит из 8 триграмм; bâ означает 8 и Гуа смысл прорицания фигуру. Же слово используется для 64 Gua (гексаграмм). Каждая цифра включает в себя три линии (

Yao ), которые либо сломаны ( инь ) или ненарушенной ( янь ). Отношения между триграммами представлены в двух положениях, исконных, «Ранее Heaven» или «Фусите» Багуа , и проявляющиеся, «Позже Небеса» или «King Wen» Багуа. (Смотри также, в последовательность короля Wen из 64 гексаграмм).

системы кодирования

код ASCII

Американский стандартный код для обмена информацией (ASCII), использует 7-битный двоичный код для представления текста и других символов внутри компьютеров, оборудования связи и других устройств. Каждая буква или символ присваивается число от 0 до 127. Например, в нижнем регистре «а» представлен 1100001в виде битовой строки (то есть «97» в десятичной системе ).

Двоично-кодированное десятичное число

Двоично-десятичном (BCD) представляет собой двоичное кодированное представление целочисленных значений , который использует 4-битовое откусывание для кодирования десятичных цифр. Четыре двоичный бит может кодировать до 16 различных значений; но, в двоично-кодированных чисел, только первые десять значений в каждом клев являются законными, и кодировать десятичные цифры ноль, через девять. Остальные шесть значений являются незаконными и могут привести либо исключение машины или неопределенное поведение, в зависимости от компьютерной реализации BCD арифметики.

BCD арифметика иногда предпочтительнее с плавающей точкой числовых форматов в коммерческих и финансовых приложениях, где сложное округления поведение чисел с плавающей точкой является несоответствующим.

Раннее использование двоичных кодов

В настоящее время использование двоичного файла

Большинство современных компьютеров используют двоичную кодировку для инструкций и данных. Компакт — диски , DVD — диски и Blu-Ray диски представляют звук и видео в цифровой форме в виде двоичного кода. Телефонные звонки осуществляются в цифровом виде на междугородную и сетей мобильной связи с использованием импульсно-кодовой модуляции , и голоса по IP — сетям.

Масса двоичных кодов

Вес двоичного кода, как определено в таблице кодов постоянного веса , является вес Хэмминга двоичных слов , кодирующих представленных слов или последовательностей.

Смотрите также

Рекомендации

внешняя ссылка

• Система Двухбуквенный Cypher сэра Фрэнсиса Бэкона , еще до двоичную систему счисления.
• Weisstein, Eric W. «код коррекции ошибок» . MathWorld .
• Таблица общих двоичных кодов . Обновленная версия таблиц оценок для небольших общих двоичных кодов , приведенных в MR Best; AE Брауэр; МакВильямс; AM Одлыжко; NJA Sloane (1978), «Граница для двоичных кодов длины Меньше чем 25», IEEE Trans. Inf. Теория , 24 : 81-93, CiteSeerX  10.1.1.391.9930 , DOI : 10,1109 / tit.1978.1055827,
• Таблица нелинейных двоичных кодов . Поддерживает Simon Лицын, EM Дождей и NJA Sloane. Обновлено до 1999 года.
• Glaser, Антон (1971). «Глава VII Приложения к компьютерам». История Binary и других Nondecimal нумерации . Томаш. ISBN  978-0-938228-00-4 . приводит некоторые предварительно ENIAC вехи.

Двоичное кодирование — урок. Информатика, 7 класс.

Известно множество способов записи чисел.

Мы пользуемся десятичной позиционной системой счисления. Десятичной она называется потому, что в этой системе счисления десять единиц одного разряда составляют одну единицу следующего старшего разряда.

 

Число \(10\) называется основанием десятичной системы счисления. Для записи чисел в десятичной системе счисления используются десять цифр:

\(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\) и \(9\).

Позиционной эта система счисления называется потому, что одна и та же цифра получает различные количественные значения в зависимости от места или позиции, которую она занимает в записи числа.

Пример:

В записи числа \(555\) цифра \(5\), стоящая на первом месте справа, обозначает \(5\) единиц, на втором — \(5\) десятков, на третьем — \(5\) сотен.

Рассмотрим два числовых ряда:
\(1\), \(10\), \(100\), \(1000\), \(10 000\), \(100 000\) …
\(1\), \(2\), \(4\), \(8\), \(16\), \(32\), \(64\), \(128\), \(256\), \(512\), \(1024\), \(2048\) …
Оба этих ряда начинаются с единицы.

Каждое следующее число первого ряда получается путём умножения предыдущего числа на \(10\).

Каждое следующее число второго ряда получается путем умножения предыдущего числа на \(2\).
Любое целое число можно представить в виде суммы разрядных слагаемых — единиц, десятков, сотен, тысяч и так далее, записанных в первом ряду. При этом каждый член этого ряда может либо не входить в сумму, либо входить в нее от \(1\) до \(9\) раз.

Пример:

1409=1⋅1000+4⋅100+0⋅10+9⋅1

 

Числа \(1\), \(4\), \(0\), \(9\), на которые умножаются члены первого ряда, составляют исходное число \(1409\).

Перевод целых десятичных чисел в двоичный код

Способ 1

Попробуем представить число \(1409\) в виде суммы членов второго ряда.

Воспользуемся методом разностей. Возьмём ближайший к исходному числу, но не превосходящий его член второго ряда и составим разность:

\(1409 — 1024 = 385\).

 

Возьмём ближайший к полученной разности, но не превосходящий её член второго ряда и составим разность:

\(385 — 256 = 129\).

 

Аналогично составим разность:

\(129 — 128 = 1\).

 

В итоге получим:

1409=1024+256+128+1=1⋅1024+0⋅512+1⋅256+1⋅128+ 0⋅64+0⋅32+0⋅16+0⋅8+0⋅4+0⋅2+1⋅1

 

Мы видим, что каждый член второго ряда может либо не входить в сумму, либо входить в неё только один раз.

Числа \(1\) и \(0\), на которые умножаются члены второго ряда, также составляют исходное число \(1409\), но в его другой, двоичной записи: \(10110000001\).

 

Результат записывают так:

140910=101100000012

 

Исходное число мы записали с помощью \(0\) и \(1\), другими словами, получили двоичный код этого числа или представили число в двоичной системе счисления.

 

Способ 2

Этот способ получения двоичного кода десятичного числа основан на записи остатков от деления исходного числа и получаемых частных на \(2\), продолжаемого до тех пор, пока очередное частное не окажется равным \(0\).

Пример:

В первую ячейку верхней строки записано исходное число, а в каждую следующую — результат целочисленного деления предыдущего числа на \(2\).
В ячейках нижней строки записаны остатки от деления стоящих в верхней строке чисел на \(2\).
Последняя ячейка нижней строки остается пустой. Двоичный код исходного десятичного числа получается при последовательной записи всех остатков, начиная с последнего: 140910=101100000012.

Первые \(20\) членов натурального ряда в двоичной системе счисления записываются так: \(1\), \(10\), \(11\), \(100\), \(101\), \(110\), \(111\), \(1000\), \(1001\), \(1010\), \(1011\), \(1100\), \(1101\), \(1110\), \(1111\), \(10000\), \(10001\), \(10010\), \(10011\), \(10100\).

Перевод целых чисел из двоичной системы счисления в десятичную

Способ 1

Пусть имеется число 1111012. Его можно представить так:

  

Способ 2

Возьмем то же число 1111012. Переведём единицу \(0\)-го разряда (первая слева в записи числа) в единицы \(5\)-го разряда, для чего \(1\) умножим на \(2\), так как единица \(6\)-го разряда в двоичной системе содержит \(2\) единицы \(5\)-го разряда.
К полученным \(2\) единицам \(5\)-го разряда прибавим имеющуюся единицу \(5\)-го разряда. Переведём эти \(3\) единицы \(5\)-го разряда в \(4\)-й разряд и прибавим имеющуюся единицу \(4\)-го разряда:

3⋅2+1=7

 

Переведём \(7\) единиц \(4\)-го разряда в \(3\)-й разряд и прибавим имеющуюся единицу \(3\)-го разряда:

\(7 · 2 + 1 = 15\)

Переведём \(15\) единиц \(3\)-го разряда во \(2\)-й разряд:

\(15 · 2 = 30\)

\( \) 

В исходном числе во \(2\)-м разряде единиц нет.

Переведем \(30\) единиц \(2\)-го разряда в \(1\)-й разряд и прибавим имеющуюся там единицу:

\(30 · 2 + 1 = 61\)

 

Мы получили, что исходное число содержит \(61\) единицу \(1\)-го разряда. Письменные вычисления удобно располагать так:

\(((((1 · 2 + 1) · 2 + 1) · 2 + 1) · 2 + 0) · 2 + 1 = 61\)

 

Переводить целые числа из десятичной системы счисления в двоичную систему счисления и обратно можно с помощью приложения Калькулятор.

 

 

Источники:

Босова Л.Л. Информатика и ИКТ. Учебник для 6 класса. 4 – е издание. — М.: БИНОМ. Лаборатория знаний, 2012 — 217 с.

Двоичный код что это такое

Сегодня я по-особому рад своей встрече с вами, дорогие мои читатели, ведь я чувствую себя учителем, который на самом первом уроке начинает знакомить класс с буквами и цифрами. А поскольку мы живем в мире цифровых технологий, то я расскажу вам, что такое двоичный код, являющийся их основой.

Начнем с терминологии и выясним, что означит двоичный. Для пояснения вернемся к привычному нам исчислению, которое называется «десятичным». То есть, мы используем 10 знаков-цифр, которые дают возможность удобно оперировать различными числами и вести соответствующую запись.

Следуя этой логике, двоичная система предусматривает использование только двух знаков. В нашем случае, это всего лишь «0» (ноль) и «1» единица. И здесь я хочу вас предупредить, что гипотетически на их месте могли бы быть и другие условные обозначения, но именно такие значения, обозначающие отсутствие (0, пусто) и наличие сигнала (1 или «палочка»), помогут нам в дальнейшем уяснить структуру двоичного кода.

Зачем нужен двоичный код?

До появления ЭВМ использовались различные автоматические системы, принцип работы которых основан на получении сигнала. Срабатывает датчик, цепь замыкается и включается определенное устройство. Нет тока в сигнальной цепи – нет и срабатывания. Именно электронные устройства позволили добиться прогресса в обработке информации, представленной наличием или отсутствием напряжения в цепи.

Дальнейшее их усложнение привело к появлению первых процессоров, которые так же выполняли свою работу, обрабатывая уже сигнал, состоящий из импульсов, чередующихся определенным образом. Мы сейчас не будем вникать в программные подробности, но для нас важно следующее: электронные устройства оказались способными различать заданную последовательность поступающих сигналов. Конечно, можно и так описать условную комбинацию: «есть сигнал»; «нет сигнала»; «есть сигнал»; «есть сигнал». Даже можно упростить запись: «есть»; «нет»; «есть»; «есть».

Но намного проще обозначить наличие сигнала единицей «1», а его отсутствие – нулем «0». Тогда мы вместо всего этого сможем использовать простой и лаконичный двоичный код: 1011.

Безусловно, процессорная техника шагнула далеко вперед и сейчас чипы способны воспринимать не просто последовательность сигналов, а целые программы, записанные определенными командами, состоящими из отдельных символов.

Но для их записи используется все тот же двоичный код, состоящий из нулей и единиц, соответствующий наличию или отсутствию сигнала. Есть он, или его нет – без разницы. Для чипа любой из этих вариантов – это единичная частичка информации, которая получила название «бит» (bit — официальная единица измерения).

Условно, символ можно закодировать последовательностью из нескольких знаков. Двумя сигналами (или их отсутствием) можно описать всего четыре варианта: 00; 01;10; 11. Такой способ кодирования называется двухбитным. Но он может быть и:

• Четырехбитным (как в примере на абзац выше 1011) позволяет записать 2^4 = 16 комбинаций-символов;
• Восьмибитным (например: 0101 0011; 0111 0001). Одно время он представлял наибольший интерес для программирования, поскольку охватывал 2^8 = 256 значений. Это давало возможность описать все десятичные цифры, латинский алфавит и специальные знаки;
• Шестнадцатибитным (1100 1001 0110 1010) и выше. Но записи с такой длинной – это уже для современных более сложных задач. Современные процессоры используют 32-х и 64-х битную архитектуру;

Скажу честно, единой официальной версии нет, то так сложилось, что именно комбинация из восьми знаков стала стандартной мерой хранящейся информации, именуемой «байт». Таковая могла применяться даже к одной букве, записанной 8-и битным двоичным кодом. Итак, дорогие мои друзья, запомните пожалуйста (если кто не знал):

Так принято. Хотя символ, записанный 2-х или 32-х битным значением так же номинально можно назвать байтом. Кстати, благодаря двоичному коду мы можем оценивать объемы файлов, измеряемые в байтах и скорость передачи информации и интернета (бит в секунду).

Бинарная кодировка в действии

Для стандартизации записи информации для компьютеров было разработано несколько кодировочных систем, одна из которых ASCII, базирующаяся на 8-и битной записи, получила широкое распространение. Значения в ней распределены особым образом:

• первый 31 символ – управляющие (с 00000000 по 00011111). Служат для служебных команд, вывода на принтер или экран, звуковых сигналов, форматирования текста;
• следующие с 32 по 127 (00100000 – 01111111) латинский алфавит и вспомогательные символы и знаки препинания;
• остальные, до 255-го (10000000 – 11111111) – альтернативная, часть таблицы для специальных задач и отображения национальных алфавитов;

Расшифровка значений в ней показано в таблице.

Если вы считаете, что «0» и «1» расположены в хаотичном порядке, то глубоко ошибаетесь. На примере любого числа я вам покажу закономерность и научу читать цифры, записанные двоичным кодом. Но для этого примем некоторые условности:

• Байт из 8 знаков будем читать справа налево;
• Если в обычных числах у нас используются разряды единиц, десятков, сотен, то здесь (читая в обратном порядке) для каждого бита представлены различные степени «двойки»: 256-124-64-32-16-8- 4-2-1;
• Теперь смотрим на двоичный код числа, например 00011011. Там, где в соответствующей позиции есть сигнал «1» – берем значения этого разряда и суммируем их привычным способом. Соответственно: 0+0+0+32+16+0+2+1 = 51. В правильности данного метода вы можете убедиться, взглянув на таблицу кодов.

Теперь, мои любознательные друзья, вы не только знаете что такое двоичный код, но и умеете преобразовать зашифрованную им информацию.

Язык, понятный современной технике

Конечно, алгоритм считывания двоичного кода процессорными устройствами намного сложнее. Но зато его помощью можно записать все что угодно:

• Текстовую информацию с параметрами форматирования;
• Числа и любые операции с ними;
• Графические и видео изображения;
• Звуки, в том числе и выходящие и за предел нашей слышимости;

Помимо этого, благодаря простоте «изложения» возможны различные способы записи бинарной информации:

• Дырочки на перфоленте и перфокарте, соответствующие «1», были одновременно и одним из языков программирования;

• Чередование ровной поверхности и выжженных впадин используется в CD и DVD дисках;

• Состоянием отдельных элементов группы транзисторов в USB накопителях;
• Изменением магнитного поля на HDD дисках;

Дополняет преимущества двоичного кодирования практически неограниченные возможности по передаче информации на любые расстояния. Именно такой способ связи используется с космическими кораблями и искусственными спутниками.

Так что, сегодня двоичная система счисления является языком, понятным большинству используемых нами электронных устройств. И что самое интересное, никакой другой альтернативы для него пока не предвидится.

Думаю, что изложенной мною информации для начала вам будет вполне достаточно. А дальше, если возникнет такая потребность, каждый сможет углубиться в самостоятельное изучение этой темы.

Я же буду прощаться и после небольшого перерыва подготовлю для вас новую статью моего блога, на какую-нибудь интересную тему.

Двоичный код — это подача информации путем сочетания символов 0 или 1. Порою бывает очень сложно понять принцип кодирования информации в виде этих двух чисел, однако мы постараемся все подробно разъяснить.

Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн.

Видя что-то впервые, мы зачастую задаемся логичным вопросом о том, как это работает. Любая новая информация воспринимается нами, как что-то сложное или созданное исключительно для разглядываний издали, однако для людей, желающих узнать подробнее о двоичном коде, открывается незамысловатая истина – бинарный код вовсе не сложный для понимания, как нам кажется. К примеру, английская буква T в двоичной системе приобретет такой вид – 01010100, E – 01000101 и буква X – 01011000. Исходя из этого, понимаем, что английское слово TEXT в виде двоичного кода будет выглядеть таким вот образом: 01010100 01000101 01011000 01010100. Компьютер понимает именно такое изложение символов для данного слова, ну а мы предпочитаем видеть его в изложении букв алфавита.

На сегодняшний день двоичный код активно используется в программировании, поскольку работают вычислительные машины именно благодаря ему. Но программирование не свелось до бесконечного набора нулей и единиц. Поскольку это достаточно трудоемкий процесс, были приняты меры для упрощения понимания между компьютером и человеком. Решением проблемы послужило создание языков программирования (бейсик, си++ и т.п.). В итоге программист пишет программу на языке, который он понимает, а потом программа-компилятор переводит все в машинный код, запуская работу компьютера.

Перевод натурального числа десятичной системы счисления в двоичную систему.

Чтобы перевести числа из десятичной системы счисления в двоичную пользуются «алгоритмом замещения», состоящим из такой последовательности действий:

1. Выбираем нужное число и делим его на 2. Если результат деления получился с остатком, то число двоичного кода будет 1, если остатка нет – 0.

2. Откидывая остаток, если он есть, снова делим число, полученное в результате первого деления, на 2. Устанавливаем число двоичной системы в зависимости от наличия остатка.

3. Продолжаем делить, вычисляя число двоичной системы из остатка, до тех пор, пока не дойдем до числа, которое делить нельзя – 0.

4. В этот момент считается, что двоичный код готов.

Для примера переведем в двоичную систему число 7:

1. 7 : 2 = 3.5. Поскольку остаток есть, записываем первым числом двоичного кода 1.

2. 3 : 2 = 1.5. Повторяем процедуру с выбором числа кода между 1 и 0 в зависимости от остатка.

3. 1 : 2 = 0.5. Снова выбираем 1 по тому же принципу.

4. В результате получаем, переведенный из десятичной системы счисления в двоичную, код – 111.

Таким образом можно переводить бесконечное множество чисел. Теперь попробуем сделать наоборот – перевести число из двоичной в десятичную.

Перевод числа двоичной системы в десятичную.

Для этого нам нужно пронумеровать наше двоичное число 111 с конца, начиная нулем. Для 111 это 1^2 1^1 1^0. Исходя из этого, номер для числа послужит его степенем. Далее выполняем действия по формуле: (x * 2^y) + (x * 2^y) + (x * 2^y), где x – порядковое число двоичного кода, а y – степень этого числа. Подставляем наше двоичное число под эту формулу и считаем результат. Получаем: (1 * 2^2) + (1 * 2^1) + (1 * 2^0) = 4 + 2 + 1 = 7.

Немного из истории двоичной системы счисления.

Принято считать, что впервые двоичную систему предложил Готфрид Вильгельм Лейбниц, который считал систему полезной в сложных математических вычислениях и науке. Но по неким данным, до его предложения о двоичной системе счисления, в Китае появилась настенная надпись, которая расшифровывалась при использовании двоичного кода. На надписи были изображены длинные и короткие палочки. Предполагая, что длинная это 1, а короткая палочка — 0, есть доля вероятности, что в Китае идея двоичного кода существовала многим ранее его официального открытия. Расшифровка кода определила там только простое натуральное число, однако это факт, который им и остается.

Компьютеры не понимают слов и цифр так, как это делают люди. Современное программное обеспечение позволяет конечному пользователю игнорировать это, но на самых низких уровнях ваш компьютер оперирует двоичным электрическим сигналом, который имеет только два состояния: есть ток или нет тока. Чтобы «понять» сложные данные, ваш компьютер должен закодировать их в двоичном формате.

Двоичная система основывается на двух цифрах – 1 и 0, соответствующим состояниям включения и выключения, которые ваш компьютер может понять. Вероятно, вы знакомы с десятичной системой. Она использует десять цифр – от 0 до 9, а затем переходит к следующему порядку, чтобы сформировать двузначные числа, причем цифра из каждого следующего порядка в десять раз больше, чем предыдущая. Двоичная система аналогична, причем каждая цифра в два раза больше, чем предыдущая.

Подсчет в двоичном формате

В двоичном выражении первая цифра равноценна 1 из десятичной системы. Вторая цифра равна 2, третья – 4, четвертая – 8, и так далее – удваивается каждый раз. Добавление всех этих значений даст вам число в десятичном формате.

Учет 0 даёт нам 16 возможных значений для четырех двоичных битов. Переместитесь на 8 бит, и вы получите 256 возможных значений. Это занимает намного больше места для представления, поскольку четыре цифры в десятичной форме дают нам 10000 возможных значений. Конечно, бинарный код занимает больше места, но компьютеры понимают двоичные файлы намного лучше, чем десятичную систему. И для некоторых вещей, таких как логическая обработка, двоичный код лучше десятичного.

Следует сказать, что существует ещё одна базовая система, которая используется в программировании: шестнадцатеричная. Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют её для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять собой целый байт, то есть заменяют восемь цифр в двоичном формате. Шестнадцатеричная система использует цифры 0-9, а также буквы от A до F, чтобы получить дополнительные шесть цифр.

Почему компьютеры используют двоичные файлы

Короткий ответ: аппаратное обеспечение и законы физики. Каждый символ в вашем компьютере является электрическим сигналом, и в первые дни вычислений измерять электрические сигналы было намного сложнее. Было более разумно различать только «включенное» состояние, представленное отрицательным зарядом, и «выключенное» состояние, представленное положительным зарядом.

Для тех, кто не знает, почему «выключено» представлено положительным зарядом, это связано с тем, что электроны имеют отрицательный заряд, а больше электронов – больше тока с отрицательным зарядом.

Таким образом, ранние компьютеры размером с комнату использовали двоичные файлы для создания своих систем, и хотя они использовали более старое, более громоздкое оборудование, они работали на тех же фундаментальных принципах. Современные компьютеры используют, так называемый, транзистор для выполнения расчетов с двоичным кодом.

Вот схема типичного транзистора:

По сути, он позволяет току течь от источника к стоку, если в воротах есть ток. Это формирует двоичный ключ. Производители могут создавать эти транзисторы невероятно малыми – вплоть до 5 нанометров или размером с две нити ДНК. Это то, как работают современные процессоры, и даже они могут страдать от проблем с различением включенного и выключенного состояния (хотя это связано с их нереальным молекулярным размером, подверженным странностям квантовой механики).

Почему только двоичная система

Поэтому вы можете подумать: «Почему только 0 и 1? Почему бы не добавить ещё одну цифру?». Хотя отчасти это связано с традициями создания компьютеров, вместе с тем, добавление ещё одной цифры означало бы необходимость выделять ещё одно состояние тока, а не только «выключен» или «включен».

Проблема здесь в том, что если вы хотите использовать несколько уровней напряжения, вам нужен способ легко выполнять вычисления с ними, а современное аппаратное обеспечение, способное на это, не жизнеспособно как замена двоичных вычислений. Например, существует, так называемый, тройной компьютер, разработанный в 1950-х годах, но разработка на том и прекратилась. Тернарная логика более эффективна, чем двоичная, но пока ещё нет эффективной замены бинарного транзистора или, по крайней мере, нет транзистора столь же крошечных масштабов, что и двоичные.

Причина, по которой мы не можем использовать тройную логику, сводится к тому, как транзисторы соединяются в компьютере и как они используются для математических вычислений. Транзистор получает информацию на два входа, выполняет операцию и возвращает результат на один выход.

Таким образом, бинарная математика проще для компьютера, чем что-либо ещё. Двоичная логика легко преобразуется в двоичные системы, причем True и False соответствуют состояниям Вкл и Выкл .

Бинарная таблица истинности, работающая на двоичной логике, будет иметь четыре возможных выхода для каждой фундаментальной операции. Но, поскольку тройные ворота используют три входа, тройная таблица истинности имела бы 9 или более. В то время как бинарная система имеет 16 возможных операторов (2^2^2), троичная система имела бы 19683 (3^3^3). Масштабирование становится проблемой, поскольку, хотя троичность более эффективна, она также экспоненциально более сложна.

Кто знает? В будущем мы вполне возможно увидим тройничные компьютеры, поскольку бинарная логика столкнулась с проблемами миниатюризации. Пока же мир будет продолжать работать в двоичном режиме.

Бинарный код — это… Что такое Бинарный код?

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).

Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:

• Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток — нет тока, индукция магнитного поля больше пороговой величины или нет и т. д.
• Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину индукции магнитного поля, потребуется ввести два пороговых значения, что не будет способствовать помехоустойчивости и надёжности хранения информации.
• Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.
• Возможно применение аппарата алгебры логики для выполнения побитовых операций над числами.

В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).

1 + 0 = 1
1 + 1 = 10
10 + 10 = 100

Таблица умножения двоичных чисел

0 • 0 = 0
0 • 1 = 0
1 • 0 = 0
1 • 1 = 1

Использование двоичной системы при измерении дюймами

При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7¹⁵/₁₆″, 3¹¹/₃₂″ и т. д.

Преобразование чисел

Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:

512

256

128

64

32

16

8

4

2

1

Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1 называется двоичной точкой.

Преобразование двоичных чисел в десятичные

Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:

512	256	128	64	32	16	8	4	2	1
				1	1	0	0	1	1
				32	+16			+2	+1

Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Либо .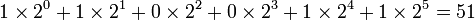

Преобразование методом Горнера

Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.

Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа

Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.

unsigned int to_deg_2(unsigned int num){
  int i;
  if ( num == 1 ) return 2;
  for( num-=1,i=1; i < sizeof(unsigned int)*8; i*=2 ) num = num|(num>>i);
  return num+1;
}

Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

19 /2 = 9  с остатком 1
9  /2 = 4  c остатком 1
4  /2 = 2  с остатком 0
2  /2 = 1  с остатком 0
1  /2 = 0  с остатком 1

Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.

Другие системы счисления

В статье «Системы счисления (продолжение)»^[1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.

См. также

Ссылки

1. ↑ http://potan.livejournal.com/91399.html Системы счисления (продолжение)

Wikimedia Foundation. 2010.

Перевод информации в двоичный код – что это такое, его виды, расшифровка

Оглавление:

1. Что такое двоичный код?
2. Разрядность двоичного кода
3. Расшифровка двоичного кода
4. Виды двоичных кодов

Всем известна такая способность компьютеров, как вычисление больших групп данных практически за считанные секунды. Однако не каждый знает, что это умение электронных машин зависит от наличия тока и напряжения.

Что такое двоичный код?

Как же компьютеру удаётся быстро обрабатывать огромные объёмы информации? Помогает ему в этом двоичная система исчисления. Данные, поступающие в это умное устройство, выглядят как единицы и нули. Каждой единице и каждому нулю соответствует определённое состояние электропровода:

• 1 — высокое напряжение.
• 0 — низкое.

Или же для единиц — наличие напряжения, а для нулей — отсутствие.

Основой двоичной системы исчисления являются двоичные коды. Что такое двоичный код?

Процесс, когда данные преобразуются в нули и единицы, называют «двоичная конверсия», а окончательное их обозначение — «двоичный код».

Разрядность двоичного кода

Все двоичные числа являются совокупностью битов, то есть, единиц и нулей, а каждый бит является одним разрядом или одной позицией в двоичном числе. Часто в задачах по информатике встречается вопрос, какое количество информации несёт тот или иной двоичный код. Следует знать, что в каждой цифре двоичного кода содержится количество информации, которое равно одному биту.

Что такое разрядность двоичного кода? Если смотреть с точки зрения арифметики, то под разрядностью понимается место, которое занимает цифра при записи чисел. Тогда под разрядностью двоичного кода подразумевается количество мест знаков (разрядов) или количество битов, которые заранее отведены для того, чтобы записать число.

Расшифровка двоичного кода

Как же расшифровать двоичный код? Десятичное обозначение основано на десятичной системе исчисления, которую обычно используют в повседневной жизни и числовые значения здесь представлены в виде десяти цифр от нуля до девяти. Каждое из мест в числах в десять раз больше по ценности, чем место, находящееся справа. Для представления числа больше 9 в десятичной системе используется ноль, который ставится справа. А единица расположена слева на следующем, более ценном месте.

Подобным образом устроена и двоичная система, в которой используют только две цифры — ноль и единицу. Места слева ценнее в два раза, чем места справа. Так, для двоичного кода характерно, что одноместными числами могут быть только 0 и 1, а для любых чисел больше единицы требуется уже 2 места.

После 0 и 1 следуют такие двоичные числа:

• 10 (то есть, 1,0).
• 11 (1,1).
• 100 (1,0,0).

В двоичной системе 100 — это эквивалент цифры 4 десятичной системы. Таким образом, любое число можно выразить в виде двоичного кода, но оно будет занимать больше места. Также, закрепив за каждой буквой алфавита определённые двоичные числа, можно осуществить перевод в двоичный код любое слово.

Видео о переводе чисел в двоичный код

К примеру, для передачи сообщения по цифровому каналу связи, его кодируют, то есть, сопоставляют каждый символ исходного сообщения с некоторым кодом (кодовым словом). Для этого используются двоичные коды — последовательность единиц и нулей.

Например, чтобы закодировать слово «мама» выбирается следующий код:

• М — 00.
• А — 1.
• Ы — 01.
• Л — 0.
• У — 10.

Пробел — 11.

Закодированные буквы соединятся в одну битовую строчку и будут переданы по сети в таком виде:

МАМА МЫЛА ЛАМУ → 0010011100010111010010

После того как эта строка будет доставлена к пункту назначения, следует решить проблему восстановления исходного сообщения. Так, получив сообщение «001001», его раскодирование можно осуществить несколькими способами. К примеру, предположив, что оно состоит только из букв Л (код 0) и А (код 1), получится:

ЛЛАЛЛАААЛЛЛАЛАААЛАЛЛАЛ

Это значит, что вышеприведённый код не декодируется однозначно. Однозначно декодируемые коды — это такие коды, в которых любые кодовые сообщения расшифровываются только одним способом.

Равномерные коды

Данная проблема решается путём правильного разбития битовой цепочки на отдельно закодированные слова. Это можно сделать, к примеру, с использованием равномерного кода, длина слов в котором всегда одинакова. К примеру, данная фраза состоит из шести символов, а это значит, что можно применить трехбитный код.

Например, если закодировать вышеприведённую фразу с помощью такого кода:

• М — 000.
• А — 001.
• Ы — 010.
• Л — 011.
• Пробел — 101, то получится следующее:

МАМА МЫЛА ЛАМУ → 000001000001101000010011001101011001000100

Это сообщение имеет длину 42 бита. Несмотря на то что оно длиннее, чем первое, состоящее всего из 22 бит, его значительно легче разобрать на отдельные слова для раскодирования:

000 001 000 001 101 000 010 011 001 101 011 001 000 100

М  А  М  А  _  М  Ы  Л  А  _  Л  А  М  У 

Хотя такой равномерный код нельзя назвать экономичным, зато его можно однозначно декодировать.

Видео о переводе букв в двоичный код

Неравномерные коды

Неравномерный двоичный код — что это такое? Его иногда применяют для сокращения длины сообщений. В неравномерном коде кодовое слово, соответствующее определённому символу в алфавите, может отличаться по длине от других слов.

Например, если использовать для кодирования «Мама мыла ламу» такой код:

• М — 01.
• А — 00.
• Ы — 1011
• Л — 100.
• У — 1010.
• Пробел — 11, то получится:

МАМА МЫЛА ЛАМУ → 0100010011011011100001110000011010

Данное сообщение состоит из 34 бит. Эту битовую цепочку можно декодировать однозначно, поскольку в первой букве — М, имеющей код 01, код является уникальным, ведь другие кодовые слова не начинаются с 01. Таким же образом можно определить вторую букву — А. Свойство, когда кодовые слова не совпадают с началом других кодовых слов, называют условием Фано, а коды, декодируемые с помощью свойства Фано, называются префиксными.

Префиксные коды отличаются важным практическим значением — с их помощью декодируются символы получаемых сообщений по мере их поступления, не ожидая, когда всё сообщение придёт к получателю.

Виды двоичных кодов

Для представления целых чисел существуют следующие виды двоичных кодов:

• Знаковые.
• Беззнаковые.

Отрицательные числа могут быть представлены только в знаковом виде. Хранение целых чисел в компьютере осуществляется в формате с фиксированной запятой.

Беззнаковые коды

В целых беззнаковых двоичных кодах все двоичные разряды представлены в степени цифры 2:

Значение минимально возможного числа равняется нулю, а максимальное определяется по формуле:

С помощью этих двух чисел определяется диапазон чисел, представленных в виде двоичного кода.

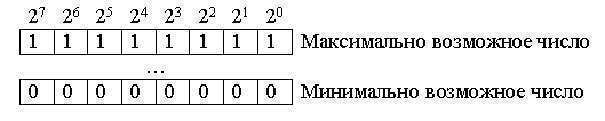
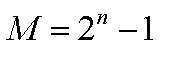
• Если представлено восьмиразрядное беззнаковое целое число, то диапазон чисел записывается с помощью кода: 0…255.
• Если представлен шестнадцатиразрядный код — 0…65535.

В восьмиразрядных процессорах такие числа хранятся в двух ячейках памяти, которые расположены в соседних адресах. Работа с подобными числами осуществляется с помощью специальных команд.

Знаковые коды

В прямых целых знаковых кодах представление знака числа осуществляется с помощью старшего разряда в слове. Для прямого знакового кода для обозначения знака «+» используется ноль, а знака «-» — единица. При введении знакового разряда произойдёт смещение диапазона чисел в сторону отрицательных значений.

• Двоичное восьмиразрядное знаковое целое число записывается с помощью такого диапазона: -127…+127.
• Шестнадцатиразрядный код будет записан в диапазоне: -32767…+32767.

В восьмиразрядных процессорах такие числа хранятся также в двух ячейках памяти, адреса которых расположены рядом.

В качестве недостатка этого кода можно назвать необходимость раздельной обработки знакового и цифрового разрядов. Программы, работающие в таких алгоритмах, являются довольно сложными. Для того чтобы выделить и изменить знаковый разряд, придётся применить метод маскирования разрядов, что приводит к увеличению размера программы и уменьшению её быстродействия. Для предотвращения возникновения различий в алгоритме обработки цифрового и знакового разрядов используются обратные двоичные коды.

Отличие знаковых обратных двоичных кодов от прямых заключается в образовании отрицательных чисел с помощью инвертирования всех разрядов чисел. Однако при этом цифровой и знаковый разряды не имеют различий. Такие коды позволяют значительно упростить алгоритм работы.

Но, несмотря на это, работа с обратными кодами требует специального алгоритма для того, чтобы распознавать знаки, вычислять абсолютные значения чисел, восстанавливать знак результата числа. Также прямой обратный код числа требует для запоминания нуля использовать два кода в то время, когда известно, что ноль является положительным числом, и отрицательным он быть не может никогда.

А Вы знаете, что такое двоичный код и как его расшифровать? Помогли ли Вам в жизни эти знания? Расскажите об этом в комментариях.