Двоичное кодирование (8 класс) Информатика и ИКТ

В общем случае, чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка. Таких языков тысячи. Каждый язык имеет свой алфавит.

Алфавит — набор отличных друг от друга символов (знаков), используемых для представления информации. Мощность алфавита — это количество входящих в него символов (знаков).

Алфавит, содержащий два символа, называется двоичным алфавитом (см. рис. ниже). Представление информации с помощью двоичного алфавита называют двоичным кодированием. Закодировав таким способом информацию, мы получим её двоичный код.

Рассмотрим в качестве символов двоичного алфавита цифры 0 и 1.

Покажем, что любой алфавит можно заменить двоичным алфавитом. Прежде всего, присвоим каждому символу рассматриваемого алфавита порядковый номер. Номер представим с помощью двоичного алфавита. Полученный двоичный код будем считать кодом исходного символа.

Если мощность исходного алфавита больше двух, то для кодирования символа этого алфавита потребуется не один, а несколько двоичных символов. Другими словами, порядковому номеру каждого символа исходного алфавита будет поставлена в соответствие цепочка (последовательность) из нескольких двоичных символов.

Правило двоичного кодирования символов алфавита мощности больше двух представим схемой на рисунке ниже.

Двоичные символы (0, 1) здесь берутся в заданном алфавитном порядке и размещаются слева направо. Двоичные коды (цепочки символов) читаются сверху вниз. Все цепочки из двух двоичных символов (кодовые комбинации) позволяют представить четыре различных символа произвольного алфавита:

Цепочки из трёх двоичных символов получаются дополнением двузначных двоичных кодов справа символом 0 или 1. В итоге трёхзначных двоичных кодовых комбинаций получается 8 – вдвое больше, чем двузначных:

Соответственно, четырёхзначный двоичный код позволяет получить 16 кодовых комбинаций, пятизначный — 32, шестизначный — 64 и т. д.

Длину двоичной цепочки — количество символов в двоичном коде – называют разрядностью двоичного кода.

Обратите внимание, что 2= 2¹, 4 = 2², 8 = 2³, 16 = 2⁴, 32 = 2⁵ и т. д.

Если количество кодовых комбинаций обозначить буквой N, а разрядность двоичного кода — буквой i, то выявленная закономерность в общем виде будет записана так: N=2ⁱ.

Задача. Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию. Какой разрядности потребуется двоичный код, если алфавит, используемый племенем Мульти, содержит 16 символов? Выпишите все кодовые комбинации.

Решение. Так как алфавит племени Мульти состоит из 16 символов, то и кодовых комбинаций им нужно 16. В этом случае длина (разрядность) двоичного кода определяется из соотношения: 16 = 2ⁱ. Отсюда i=4.

Чтобы выписать все кодовые комбинации из четырёх 0 и 1, воспользуемся схемой на рисунке выше: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.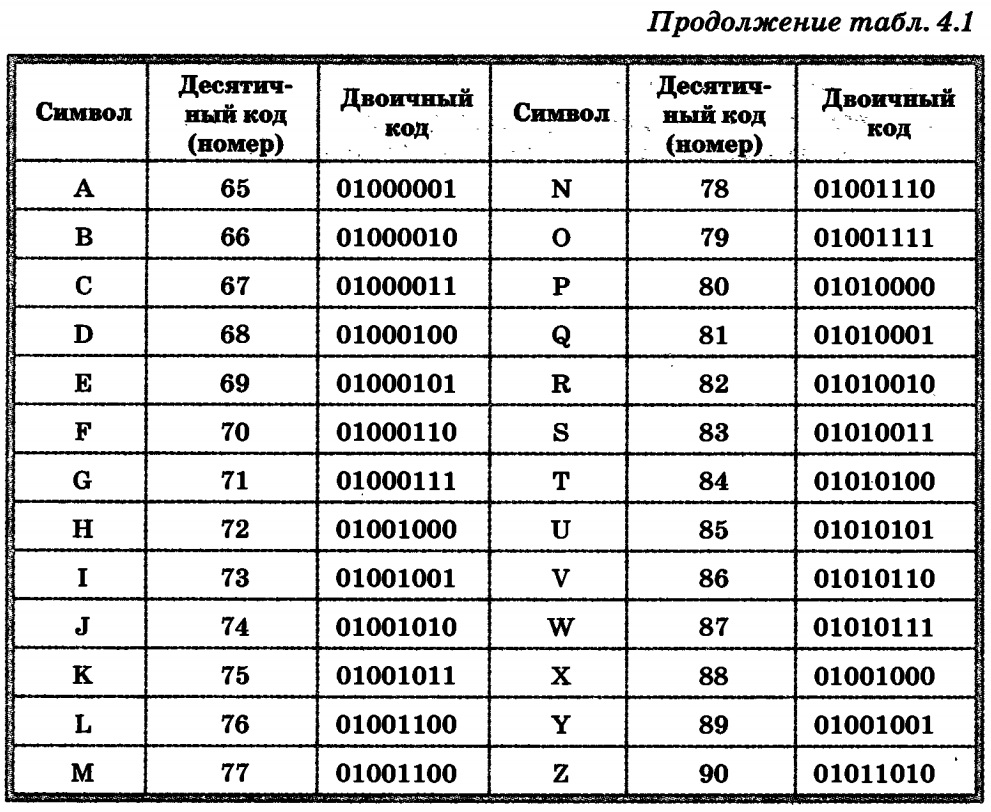

Самое главное:

• Чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка.
• Алфавит языка — набор отличных друг от друга символов, используемых для представления информации. Мощность алфавита — это количество входящих в него символов.
• Алфавит, содержащий два символа, называется двоичным алфавитом. Представление информации с помощью двоичного алфавита называют двоичным кодированием.

Вопросы и задания:

1. Что такое алфавит языка?
2. Что такое мощность алфавита? Может ли алфавит состоять из одного символа?
3. Какие символы могут входить в двоичный алфавит?
4. Сколько существует различных последовательностей из символов «плюс» и «минус» длиной ровно пять символов?
5. Как связаны мощность алфавита и разрядность двоичного кода, достаточного для кодирования всех символов этого алфавита?
6. Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию. Достаточно ли пятиразрядного двоичного кода, если алфавит, используемый племенем Мульти, содержит 26 символов?
   (Решение:
   С помощью пятиразрядного двоичного кода можно закодировать 2⁵ = 32 различных символов алфавита. Поэтому для кодирования 26 символов алфавита достаточно пятиразрядного кода.)
7. От разведчика была получена следующая шифрованная радиограмма, переданная с использованием азбуки Морзе: — • • — • • — — • • — — — — •
   При передаче радиограммы было потеряно разбиение на буквы, но известно, что в радиограмме использовались только следующие буквы:
   Определите текст радиограммы.
   
   (Решение:
   НАИГАЧ)

Содержание

Понравилось?

Нравится

Твитнуть



Page not found — Сайт skobelevserg!

• Главная
• Информатика
• Практикумы
• Подготовка к ОГЭ
• Рабочие программы
• Используемая литература
• Об авторах

Unfortunately the page you’re looking doesn’t exist (anymore) or there was an error in the link you followed or typed. This way to the home page.

• Главная
• Информатика
• • 5 класс (ФГОС)
  • • Информация вокруг нас
    • Компьютер — универсальная машина для работы с информацией
    • Ввод информации в память компьютера
    • Управление компьютером
    • Хранение информации
    • Передача информации
    • Кодирование информации
    • Текстовая информация
    • Представление информации в виде таблиц
    • Наглядные формы представления информации
    • Компьютерная графика
    • Обработка информации
  • 6 класс (ФГОС)
  • • Объекты окружающего мира
    • Компьютерные объекты
    • Отношения объектов и их множеств
    • Разновидности объектов и их классификация
    • Системы объектов
    • Персональный компьютер как система
    • Как мы познаем окружающий мир
    • Понятие как форма мышления
    • Информационное моделирование
    • Знаковые информационные модели
    • Табличные информационные объекты
    • Графики и диаграммы
    • Схемы
    • Что такое алгоритм
    • Исполнители вокруг нас
    • Формы записи алгоритмов
    • Типы алгоритмов
    • Управление исполнителем Чертежник
    • Компьютерный практикум
  • 7 класс (ФГОС)
  • • Информация и информационные процессы
    • Компьютер универсальное устройство для работы с информацией
    • Обработка графической информации
    • Обработка текстовой информации
    • Технология мультимедиа
  • 8 класс (ФГОС)
  • • Математические основы информатики
    • Основы алгоритмизации
    • Начала программирования
  • 9 класс (ФГОС)
  • • Моделирование и формализация
    • Алгоритмизация и программирование
    • Обработка числовой информации в электронных таблицах
    • Коммуникационные технологии
  • 10 класс (ФГОС)
  • • Информация и информационные процессы
    • Компьютер и его программное обеспечение
    • Представление информации в компьютере
    • Элементы теории множеств и алгебры логики
    • Современные технологии создания и обработки информационных объектов
  • 11 класс (ФГОС)
  • • Обработка информации в электронных таблицах
    • Алгоритмы и элементы программирования
    • Информационное моделирование
    • Сетевые информационные технологии
    • Основы социальной информатики
  • Безопасность в сети Интернет
• Практикумы
• • Google формы
  • Основы работы в Microsoft PowerPoint
  • Создание анимации в презентациях
  • Основы работы в Microsoft Word
  • Основы работы в Microsoft Excel
  • Создание простейшей базы данных
  • Практикум по MS Excel
• Подготовка к ОГЭ
• Рабочие программы
• Используемая литература
• Об авторах
• • Блоги
  • Сайты

блестящих проектов с двоичным кодом для детей

Коллин Розенталь Обновлено 24. 07.2022

Могут ли дети выучить двоичный код? Они точно могут! Давайте изучим и поймем основы двоичного кода. Двоичный код — это способ, с помощью которого компьютер понимает, что ему нужно делать, используя код для чтения и передачи информации. Вы можете увидеть в приветственном сообщении ниже, как буквы представлены в двоичном коде.

ДВОИЧНЫЙ БЛЕСТЯЩИЙ!

Что вы узнаете из этой статьи!

Отказ от ответственности: эта статья может содержать комиссионные или партнерские ссылки. Как партнер Amazon я зарабатываю на соответствующих покупках.
Не видите наши видео? Отключите все блокировщики рекламы, чтобы наш видеопоток был виден. Или посетите наш канал на YouTube, чтобы узнать, загружено ли туда видео. Мы потихоньку загружаем наши архивы. Спасибо!

ДОБРО ПОЖАЛОВАТЬ! 1111 01000010 01001001 01001110 01000001 01010010 01011001

Что такое двоичный код?

Ну, начнем с самого слова. Би означает два. Бинар — это нечто, состоящее из 2-х частей. В случае кода bi относится к нулям и единицам, которые являются единственными двумя числами, составляющими двоичный код. Каждая появляющаяся последовательность из восьми цифр напрямую связана с буквой в алфавите. Например, 01000001 — это двоичная заглавная буква А.

Давайте представим это как игру красный-зеленый свет. Мы знаем, что когда мы слышим «красный свет», мы останавливаемся, а когда мы слышим «зеленый свет», мы идем — компьютер понимает различные последовательности чисел и преобразует их в язык. Вы можете найти похожие коды из двух частей и в других областях! Азбуку Морзе можно использовать, посылая длинные и короткие световые или звуковые сигналы, которые можно перевести на язык. Азбука Морзе использовалась много до того, как появилась возможность озвучивать радиосигналы. Другим примером является шрифт Брайля, используемый слабовидящими. Буквы, цифры и знаки препинания представлены на странице приподнятыми и опущенными выступами.

Как работает двоичный код?

Откуда мы знаем, что обозначают нули и единицы? В таблице ниже приведен основной перевод алфавита в двоичном коде для заглавных букв, строчных букв и цифр от одного до десяти.

Мы можем использовать эту таблицу, чтобы проводить всевозможные забавные мероприятия с нашими детьми дома или с учениками в школе. Я включил пакет с некоторыми готовыми, минимальными подготовительными действиями, чтобы практиковать этот увлекательный код с детьми. Есть 5 занятий, так что вы можете легко включить их в неделю занятий по программированию! Отличная идея для летнего лагеря STEM!

ДВОИЧНЫЙ КОД ПРОЕКТ ИДЕИ ДЛЯ ДЕТЕЙ

Двоичный код для печати

Для некоторых из этих действий с двоичным кодом требуются рабочие листы для печати. Просто введите свой адрес электронной почты в форму, чтобы разблокировать печатную форму. Печатная форма идеально подходит для классной комнаты или лагеря STEM.

Напишите и раскрасьте свое имя в двоичном формате

Попросите детей выбрать 2 цвета — они могут использовать мелки, цветные карандаши или фломастеры! Раскрасьте два прямоугольника, помеченные цифрами 0 и 1, — это поможет им легко ориентироваться во время работы.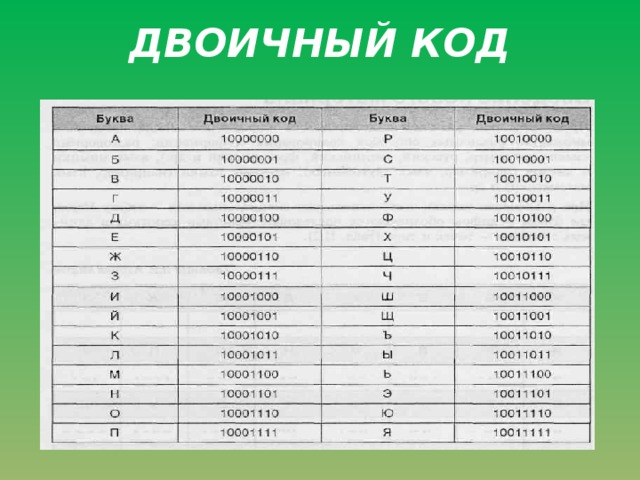 Затем попросите их написать свое имя сбоку распечатанной таблицы. Каждая буква должна соответствовать строке в таблице. Используя таблицу двоичного алфавита, заполните нули и единицы, соответствующие каждой букве вашего имени. Наконец, раскрасьте коробки.

Изготовление браслета с двоичным кодом

Для этого задания нам понадобятся бусины трех цветов и ершик для труб. Как и в первом упражнении, у нас будет код и цвет детей, но на этот раз только их инициалы. Теперь, когда они знают код своих инициалов, попросите их выбрать бусинки для обозначения нулей и единиц. Не волнуйтесь, если ваши бусины не соответствуют цветам ваших маркеров — есть круги, которые они могут раскрасить, чтобы представить бусины, или они могут просто поместить бусину в каждый круг, чтобы они знали, что есть что. Есть три круга: нули, единицы и пробелы.

Загните один конец ершика, чтобы шарики не соскальзывали во время работы. Я начал и закончил свой браслет бусинкой-пространством, чтобы показать разделение. Просто нанижите бусины в том порядке, в котором вы написали свой код инициалов. Поместите пробел между каждой буквой. Когда вы закончите, вы можете скрутить два конца вокруг друг друга, чтобы завершить браслет.

Binary Computer Jokes

Знаете, что получится, если скрестить жука и компьютер? Используйте свою таблицу, чтобы перевести двоичный код и узнать кульминацию! Есть две шутки для детей, чтобы перевести.

Секретное сообщение в двоичном коде

Объедините детей в пары и попросите их написать секретное сообщение в двоичном коде. Когда они закончат, они могут поменяться со своим партнером и посмотреть, смогут ли они перевести сообщение. Я предлагаю, чтобы дети написали свое сообщение на другом листе бумаги, чтобы у них была простая ссылка, пока они пишут свой код.

Binary Scavenger Hunt

Попросите детей перевести подсказки по поиску мусора, а затем найдите предметы дома или в классе!

Быстрая и легкая минимальная подготовительная неделя программирования! Закрепление кода в течение недели поможет детям действительно понять, как нули и единицы представляют разные буквы.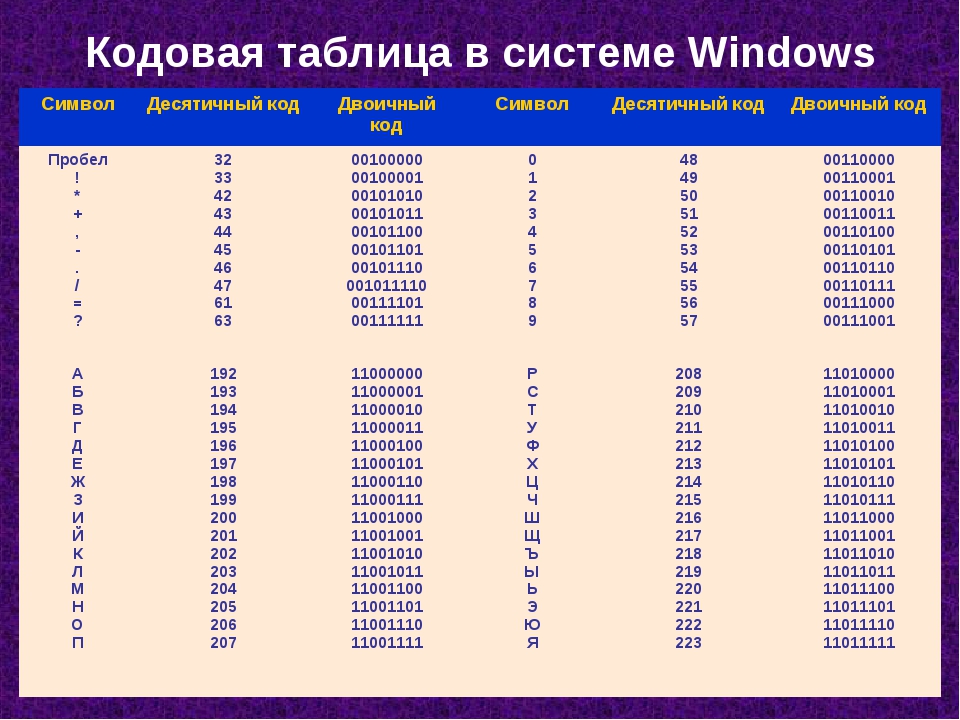 Хотите знать, как еще вы могли бы включить этот код? А как насчет списков правописания? Если вы заставите своих детей каждую неделю записывать свои орфографические слова, почему бы не перевести их в код — еще лучше, если у вас есть имена собственные, им придется помнить, что заглавные и строчные буквы представлены по-разному. Вместо браслета предложите ему застегнуть молнию для своего рюкзака или подвесное украшение в подарок! Существует множество простых способов включить двоичный алфавит и двоичный код в повседневное обучение!

БОНУС Испытание на расшифровку двоичного кода

Примите участие в нашем популярном занятии «Взломщики двоичного кода», в котором задействованы немного науки.

---

Больше программ для детей

7.3: От символов к двоичным кодам

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

9991

• Louis Scharf
• Университет штата Колорадо через OpenStax CNX
901 05

Возможно, самая фундаментальная идея теории коммуникации состоит в том, что произвольные символы могут быть представлены строками двоичных цифр. {\text {th}}\) быть двоичным представлением индекса \(i\): 9{N} \номер \]

Грубо говоря, что \(N=\log _{2} M\).

Восьмеричные коды

Когда количество символов велико и соответствующие двоичные коды содержат много битов, мы обычно группируем биты в группы по три и заменяем двоичный код соответствующим восьмеричным кодом. Например, семибитный двоичный код отображается в трехзначный восьмеричный код следующим образом:

\[\begin{gathered}
0000000 \sim 000 \\
0000001 \sim 001 \\
\vdots \\
0100110 \сим 046 \
\вточки\
101111 \сим 137\
\вточки\
1111111 \сим 177 .
\end{gathered} \nonumber \]

Восьмеричные коды ASCII для представления букв, цифр и специальных символов приведены в таблице 1.

Упражнение \(\PageIndex{1}\)

Запишите семь- битовые коды ASCII для \(A,q,7\) и {.

9

Таблица 1: Восьмеричные коды ASCII (из Дональда Кнута, The TEXbook, © 1986 Американского математического общества, Провиденс, Род-Айленд, стр. 367, опубликовано Addison-Wesley Publishing Co.)

	‘0	‘1	‘2	‘3	‘4	‘5	‘6	‘7
’00x	␀	␁	␂	␃	␄	␅	␆	␇
’01x	␈	␉	␊	␋	␌	␍	␎	␏
’02x	␐	␑	␒	␓	␔	␕	␖	␗
’03x	␘	␙	␚	␛	␜	␝	␞	␟
’04x	␠	!	»	#	$	%	и	‘
’05x	(	)	*	+	,	—	.	/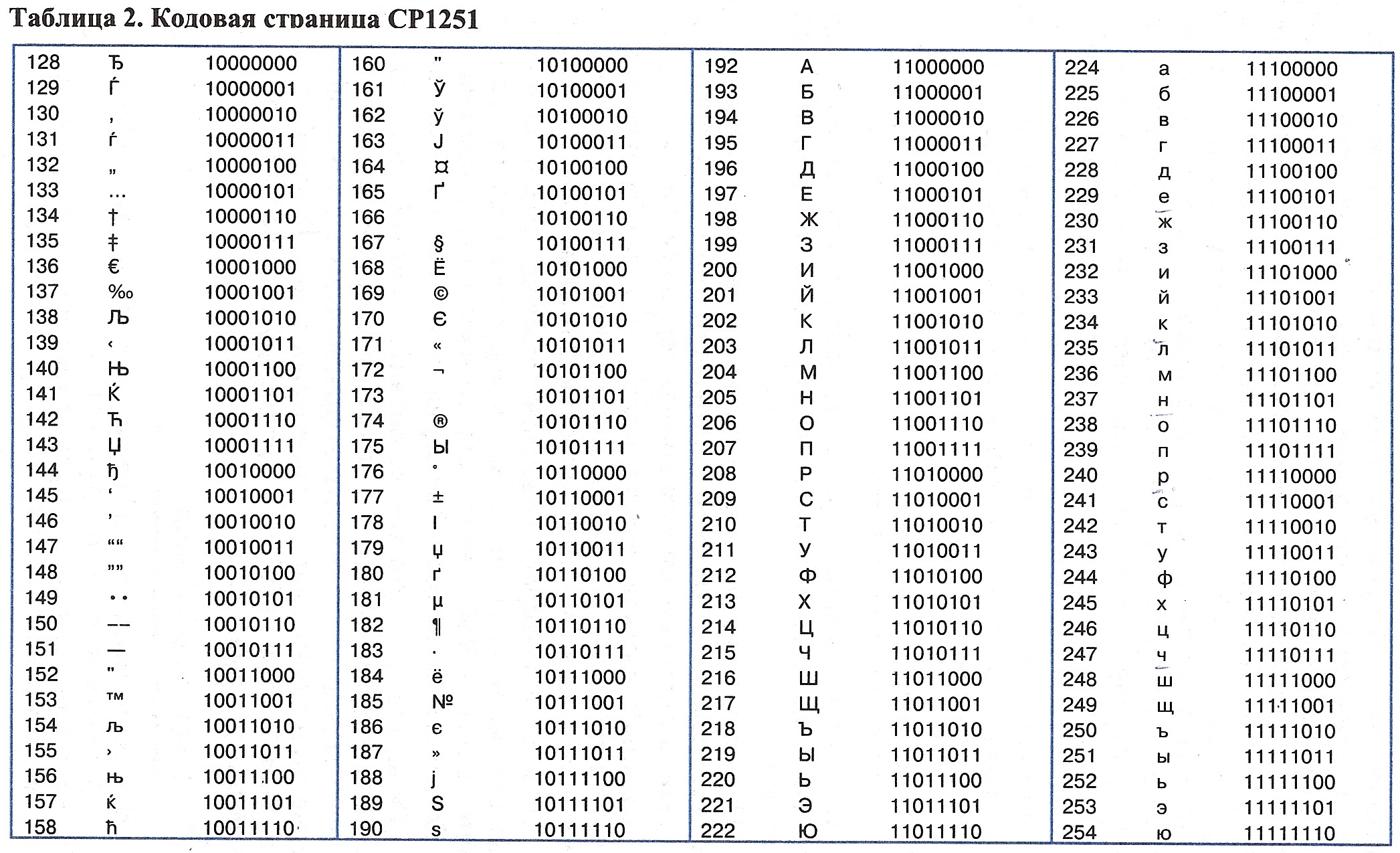
’06x	0	1	2	3	4	5	6	7
’07x	8	9	:	;	<	=	>	?
’10x	@	А	Б	С	Д	Э	Ф	Г
’11x	Х	я	Дж	К	л	М	Н	О
’12x	П	В	Р	С	Т	У	В	Вт
’13x	_
’14x	`	и	б	в	д	и	ф	г
’15x	ч	я	и	к	л	м	п	или
’16x	р	д	р	с	т	и	против	с
’17x	х	г	с	{	|	}	~	␡

Упражнение \(\PageIndex{2}\)

Добавьте 1 или 0 к самой значащей (самой левой) позиции семибитного кода ASCII, чтобы получить восьмибитный код с четной четностью. {\mathrm{A}}\): 9{\underline{2} V_{0}}\) с двоичными кодами, просто представляя нижний индекс ячейки двоичным словом. В последующем курсе по цифровой электронике и микропроцессорам вы изучите аналого-цифровые (аналогово-цифровые) преобразователи для квантования переменных.

Рисунок \(\PageIndex{1}\): Квантизатор

Пример \(\PageIndex{1}\)

Если \(M=8\), что соответствует трехбитному квантователю, мы можем связать ячейки квантователя и квантованных уровней с двоичными кодами следующим образом:

\(\begin{array}{ll}
В \in C_{-3} & \Rightarrow V_{-3}=(-3) \frac{2 V_{0}}{8} \sim 111 \\
В \in C_{-2} & \ Rightarrow V_{-2}=(-2) \frac{2 V_{0}}{8} \sim 110 \\
V \in C_{-1} & \Rightarrow V_{-1}=(-1) \frac{2 В_{0}}{8} \sim 101 \\
В \in C_{0} & \Rightarrow \quad V_{0}=0 \sim 000 \\
В \in C_{1} & \Rightarrow V_{1}=(1) \frac{2 V_{0}}{8} \sim 001 \\
V \in C_{2} & \Rightarrow V_{2}=(2) \frac{2 V_{0}}{8} \sim 010 \\
V \in C_{3} & \Rightarrow V_{3}=(3) \frac{2 V_{0}}{8} \sim 011 .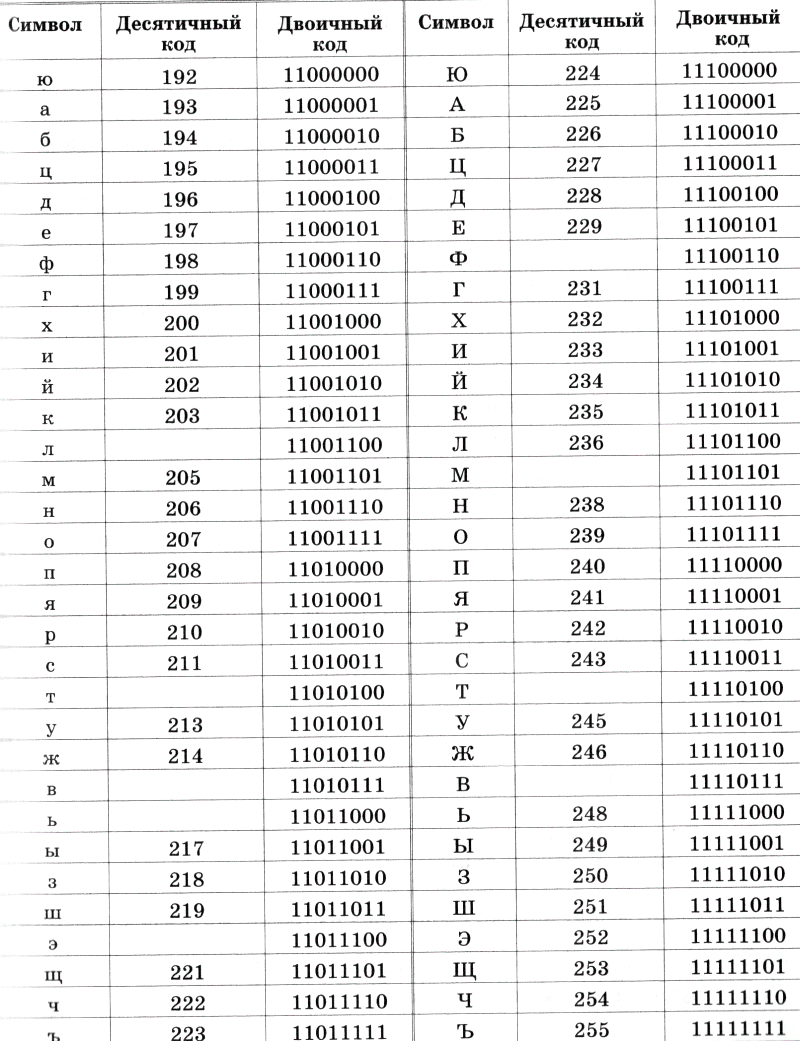
\end{array}\)

Этот конкретный код называется кодом знака-величины , в котором старший бит является знаковым битом, а остальные биты являются битами модуля (например, \(110 \sim−2\ ) и \(010 \sim 2\)). Один из недостатков кода знак-величина состоит в том, что он тратит впустую один код, используя 000 для 0 и 100 для -0. Альтернативным кодом, который имеет много других преимуществ, является код дополнения до 2 . Коды с дополнением до 2 для положительных чисел такие же, как коды со знаком, но коды для отрицательных чисел генерируются путем дополнения всех битов для соответствующего положительного числа и добавления 1:

\(\begin{align}
-4 & \sim 100 & \\
-3 &\sim 101 &(100+1) \\
-2 & \sim 110 &(101+1) \\
-1 &\sim 111 &(110+1) \\
0 & \sim 000 \\
1 & \sim 001 \\
2 & \sim 010 \\
3 & \sim 011 .
\end{выровнено }\)

Упражнение \(\PageIndex{3}\)

Сгенерировать четырехбитный двоичный код величины знака и четырехбитный дополнительный двоичный код для чисел \(-8,-7, \ldots,-1, 0,1,2, \ldots, 7\).

Упражнение \(\PageIndex{4}\)

Докажите, что в представлении с дополнением до 2 сумма двоичных кодов для \(−n\) и \(+n\) равна нулю. Например,

\[\begin{gathered}
101+011=000 \\
(-3)(3)(0) .
\end{gathered} \nonumber \]

На курсах компьютерной арифметики вы научитесь выполнять арифметические операции в различных двоично-кодированных системах. Следующая задача показывает, насколько проста арифметика в дополнении до 2.

Упражнение \(\PageIndex{5}\)

9N\) символов. В случае, когда \(M=8\) и \(N=3\), восемь возможных трехбитовых кодов могут быть представлены как листья на ветвящемся дереве, показанном на рисунке 2(a). У дерева растет левая ветвь для 0 и правая ветвь для 1, пока оно не прекратится после трех ветвлений. Трехбитные коды, которые мы до сих пор изучали, находятся на конечных листьях двоичного дерева. Но что, если наш исходный алфавит содержит всего пять символов или букв? Мы можем представить эти пять символов как трехбитные символы от 000 до 100 в двоичном дереве. Это генерирует код постоянной длины с тремя неиспользуемыми или недопустимыми символами от 101 до 111. Они отмечены знаком «\(x\)» на рисунке 2(a). Эти неиспользуемые листья и ветви, ведущие к ним, можно обрезать, чтобы получить бинарное дерево, показанное на рис. 2(b).

Если мы допустим коды переменной длины, то у нас есть несколько других вариантов использования двоичного дерева для построения двоичных кодов. Два из этих кодов и соответствующие им двоичные деревья показаны на рис. 3. Если мы избавимся от представления о том, что каждое кодовое слово должно содержать три или меньше битов, то мы можем построить двоичные деревья, подобные показанным на рис. 4, и сгенерировать соответствующие им двоичные коды. . На рис. 4(а) мы выращиваем правую ветвь после каждой левой ветви и помечаем каждый лист кодовым словом. На рис. 4(b) мы отсекаем последнюю правую ветвь и связываем кодовое слово с листом последней левой ветви.

Рисунок \(\PageIndex{2}\): Двоичные деревья и коды постоянной длины; (a) Двоичное дерево и (b) Сокращенное двоичное дерево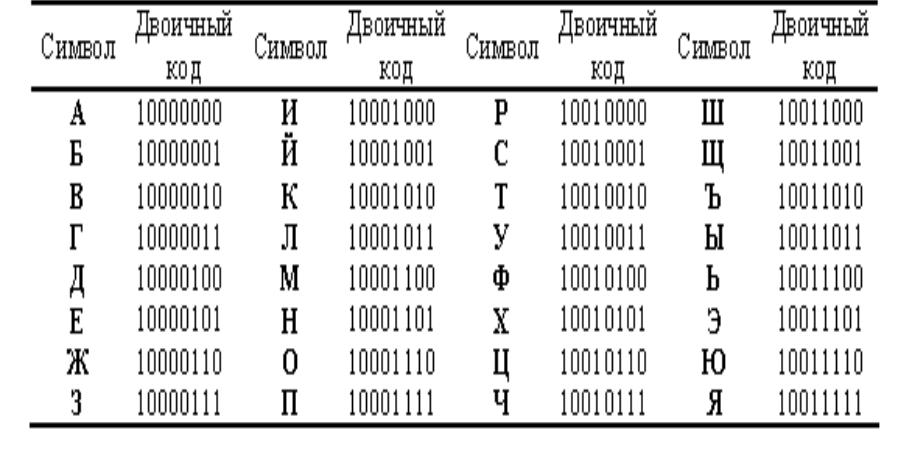

. Все коды, которые мы сгенерировали до сих пор, организованы в Таблице 2. Для каждого кода указано среднее количество бит/символ. Этот средний показатель колеблется от 2,4 до 3,0. Если вероятность появления всех символов одинакова, то лучшим кодом переменной длины будет код 2.

Рисунок \(\PageIndex{3}\): Двоичные деревья и коды переменной длины; (a) Двоичное дерево для кода переменной длины и (b) Другое двоичное дерево для кода переменной длины

Все построенные нами коды имеют общую характеристику: каждое кодовое слово является конечным листом бинарного дерева, а это означает, что ни одно кодовое слово не лежит на ветви ветвей до другого кодового слова. Мы говорим, что никакое кодовое слово не является префиксом к другому кодовому слову. Это свойство делает каждый из кодов мгновенно декодируемым , что означает, что каждый бит в строке битов может обрабатываться мгновенно (или независимо) независимо от последующих битов.

Упражнение \(\PageIndex{6}\)

Декодируйте следующую последовательность битов, используя код 2:

0111001111000000101100111.

(a)(b) Рисунок \(\PageIndex{4}\): левосторонние двоичные деревья для кодов переменной длины; (a) Левое двоичное дерево и (b) Усеченное двоичное дерево

Таблица 2: Коды переменной длины

Код №	S0S0	С1С1	С2С2	S3S3	С4С4	Среднее число бит/символ
1	000	001	010	011	100	15/5=3,015/5=3,0
2	000	001	01	10	11	12/5=2,412/5=2,4
3	000	001	010	011	1	13/5=2,613/5=2,6
4	1	01	001	0001	00001	15/5=3,015/5=3,0
5	1	01	001	0001	0000	14/5=2,8

Упражнение \(\PageIndex{7}\)

Проиллюстрируйте следующие коды на двоичном дереве. Какие из них мгновенно декодируются? Какие из них можно обрезать, оставив мгновенно декодируемыми?

\(\begin{array}{ccccc}
S_{0} & S_{1} & S_{2} & S_{3} & S_{4} \\
011 & 100 & 00 & 11 & 101 \\
011 & 100 & 00 & 0 & 01 \\
010 & 000 & 100 & 101 & 111 .
\end{array}\)

Код № 2, сгенерированный в таблице 2, кажется лучшим кодом, чем код № 5, поскольку его среднее число бит/символ (2.4) меньше. Но что, если символ \(S_0\) является очень вероятным символом, а символ \(S_4\) — очень маловероятным? Тогда вполне может оказаться, что среднее количество битов, используемых кодом №5, меньше, чем среднее количество битов, используемых кодом №2. Так какой же лучший код? Ответ зависит от относительной частоты использования каждого символа. Мы исследуем этот вопрос в следующем разделе.

---

Эта страница под названием 7.3: От символов к двоичным кодам распространяется под лицензией CC BY 3.0 и была создана, изменена и/или курирована Луи Шарфом (OpenStax CNX) посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.