[Решение] Перевод из двоичной системы в десятичную
[Решение] Перевод из двоичной системы в десятичную — онлайн калькулятор CALC.WSДвоичная система счисления — Двоичная система счисления — позиционная система счисления с основанием 2. Благодаря непосредственной реализации в цифровых электронных схемах на логических вентилях, двоичная система используется практически во всех современных компьютерах и прочих вычислительных электронных устройствах.
C помощью данного калькулятора, вы можете перевести из десятичной системы исчисления в двоичную, например из 66 получить 1000010 или наоборот.
Переводим из системы исчисления в :
В двоичной системе счисления числа записываются с помощью двух символов (0 и 1). Чтобы не путать, в какой системе счисления записано число, его снабжают указателем справа внизу. Например, число в десятичной системе 5
Например, число в десятичной системе 5
В двоичной системе счисления (как и в других системах счисления, кроме десятичной) знаки читаются по одному. Например, число 1012 произносится «один ноль один».
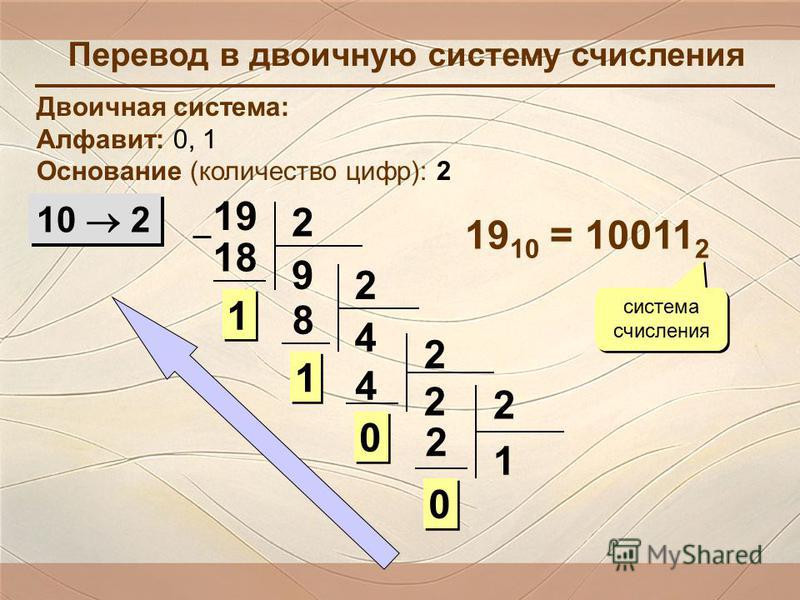
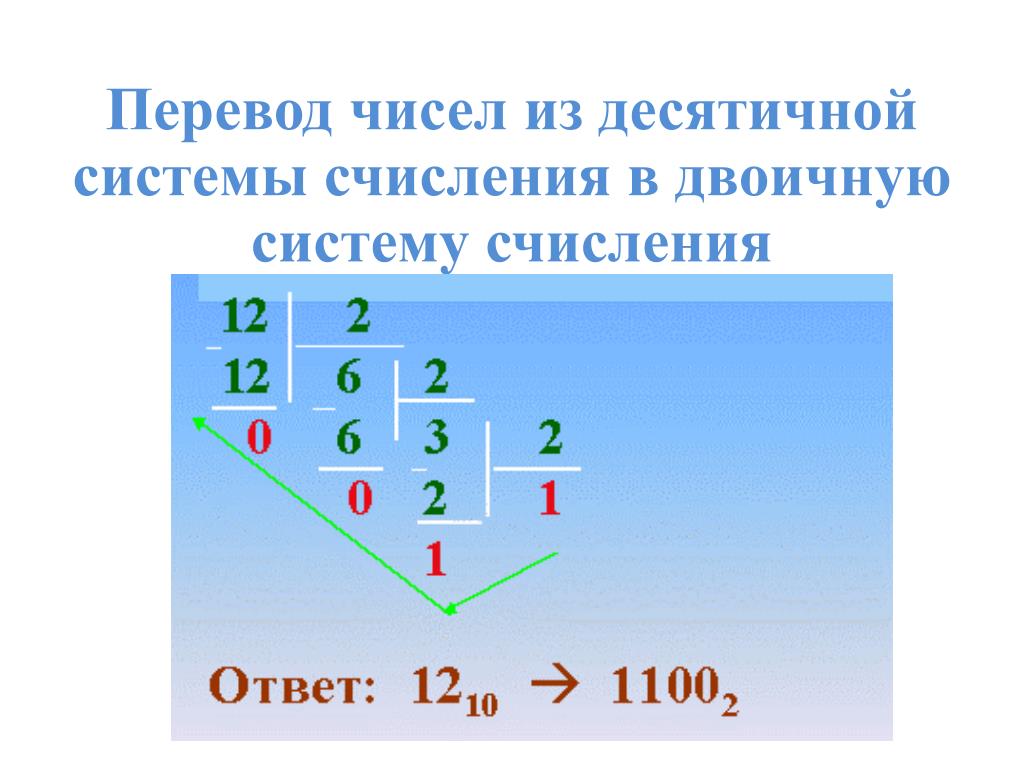
Допустим, нам нужно перевести число 19 в двоичное. Для того, чтобы перевести десятичное число в двоичное, нужно разделить каждое частное на 2 и записать отстаток в конец двоичной записи. Продолжаем деление до тех пор, пока в частном не будет 0. Результат записываем справа налево. То есть нижняя цифра (1) будет самой левой и т. д. В результате получаем число 19 в двоичной записи: 10011.
Видео
Подробно про двоичную систему счисления можно узнать из видео:
Примеры
-
Задание: переведите двоичное число 1101101 в десятичную систему
Решение: 109
11011012 = 1*26 + 1*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 32 + 0 + 8 + 4 + 0 + 1 = 109
-
Задание: двоичное число 100012 соответствует десятичному числу
Решение: 100012 = 1*24 + 0*23 + 0*22 + 0*21 + 1*20 = 16 + 0 + 0 + 0 + 1 = 17
-
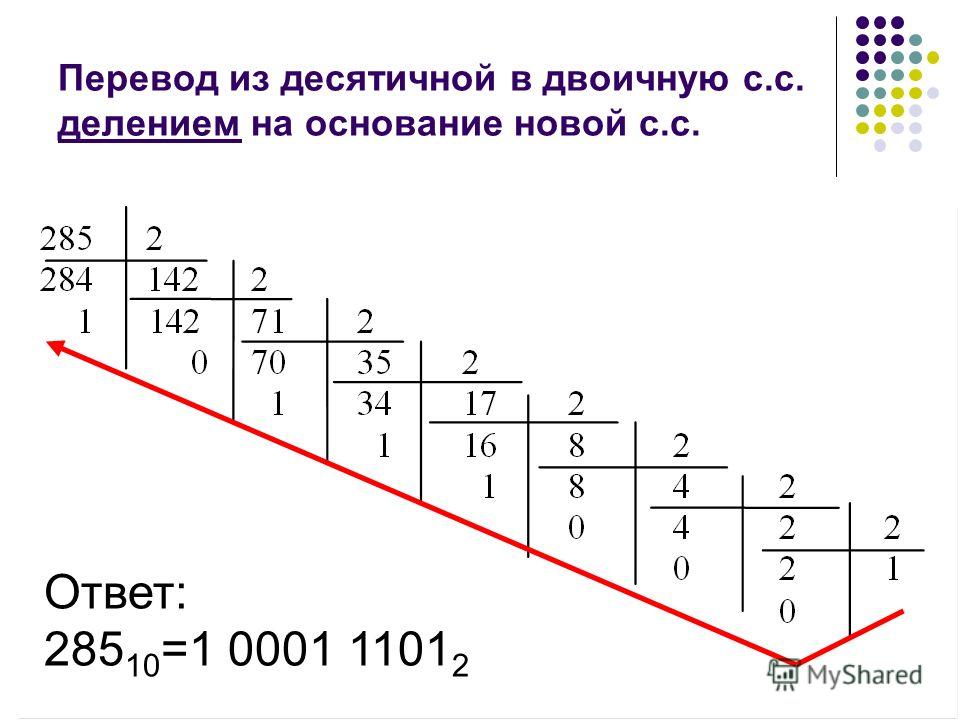
Задание: десятичное число 35 соответствует двоичному числу:
Решение: 1000112
35 2 34 17 2 1 16 8 2 1 8 4 2 0 4 2 2 0 2 1 0
Как перевести из двоичной в восьмеричную, шестнадцатеричную и четвертичную системы
Перевод чисел из двоичной системы счисления в восьмеричную, шестнадцатеричную или четвертичную и наоборот часто требуется для решения задач по теме Системы счисления. Чтобы перевести число из одной системы в другую, нужно использовать таблицу перевода чисел. А также можно воспользоваться онлайн калькулятором для перевода чисел из одной системы счисления в другую.
Чтобы перевести число из одной системы в другую, нужно использовать таблицу перевода чисел. А также можно воспользоваться онлайн калькулятором для перевода чисел из одной системы счисления в другую.
Таблица перевода чисел
| Десятичная СС | Двоичная СС | Четвертичная СС | Восьмеричная СС | Шестнадцатеричная СС |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 | 2 |
| 3 | 11 | 3 | 3 | 3 |
| 4 | 100 | 10 | 4 | 4 |
| 5 | 101 | 11 | 5 | 5 |
| 6 | 110 | 12 | 6 | 6 |
| 7 | 111 | 13 | 7 | 7 |
| 8 | 1000 | 20 | 10 | 8 |
| 9 | 1001 | 21 | 11 | 9 |
| 10 | 1010 | 22 | 12 | A |
| 11 | 1011 | 23 | 13 | B |
| 12 | 1100 | 30 | 14 | C |
| 13 | 1101 | 31 | 15 | D |
| 14 | 1110 | 32 | 16 | E |
| 15 | 1111 | 33 | 17 | F |
| 16 | 10000 | 100 | 20 | 10 |
Как перевести число из двоичной системы счисления
Чтобы перевести число из двоичной системы счисления в четвертичную, восьмеричную или шестнадцатеричную систему, нужно воспользоваться алгоритмом перевода:
- Разбить двоичное число справа налево на группы по 2 (для четвертичной СС), 3 (для восьмеричной СС) или 4 (для шестнадцатеричной СС) цифры.
 Если слева не будет хватать цифр для полной группы, нужно дописать необходимое количество незначащих нулей.
Если слева не будет хватать цифр для полной группы, нужно дописать необходимое количество незначащих нулей. - Заменить каждую группу цифр на ее аналог в соответствующей системе счисления.
Пример 1:
Перевести число 1111001102 из двоичной системы в четвертичную.
Решение:
Разбиваем число на группы по 2 цифры справа налево и заменяем каждую группу на аналог в четвертичной системе счисления из таблицы:
1111001102 = 01 11 10 01 10 = 132124
Пример 2:
Перевести число 1111001102 из двоичной системы в восьмеричную.
Решение:
Разбиваем число на группы по 3 цифры справа налево и заменяем каждую группу на аналог в восьмеричной системе счисления из таблицы:
1111001102 = 111 100 110 = 7468
Пример 3:
Перевести число 1111001102 из двоичной системы в шестнадцатеричную.
Решение:
Разбиваем число на группы по 4 цифры справа налево и заменяем каждую группу на аналог в шестнадцатеричной системе счисления из таблицы:
1111001102 = 0001 1110 0110 = 1E616
Как перевести число в двоичную систему счисления
Чтобы перевести число из четвертичной, восьмеричной или шестнадцатеричной системы счисления в двоичную, нужно воспользоваться алгоритмом перевода:
- Заменить каждую цифру на двоичный аналог, состоящий из 2 (для четвертичной), 3 (для восьмеричной) или 4 (для шестнадцатеричной) цифр.
 Если нужно, число дополняется нулями слева.
Если нужно, число дополняется нулями слева. - Вычеркнуть из числа незначащие нули.
Пример 4:
Перевести число 1203234 из четвертичной системы в двоичную.
Решение:
Выполняем замену каждой цифры на группу из 2 цифр в двоичной системе счисления:
1203234 = 01 10 00 11 10 11 = 110001110112
Пример 5:
Перевести число 264750308 из восьмеричной системы в двоичную.
Решение:
Выполняем замену каждой цифры на группу из 3 цифр в двоичной системе счисления:
264750308 = 010 110 100 111 101 000 011 000 = 101101001111010000110002
Пример 6:
Перевести число 2AC0F7416 из шестнадцатеричной системы в двоичную.
Решение:
Выполняем замену каждой цифры на группу из 4 цифр в двоичной системе счисления:
2AC0F7416 = 0010 1010 1100 0000 1111 0111 0100 = 101010110000001111011101002
Преобразователь двоичного кода в десятичный
Преобразователь двоичного кода в десятичныйГлавная›Преобразование›Преобразование чисел›Двоичный код в десятичный
От BinaryDecimalOctalHexadecimalText
Кому BinaryDecimalOctalHexadecimalText
Введите двоичное число
Десятичное число
Десятичное число из дополнения до 2 со знаком
Шестнадцатеричный номер
Десятичные шаги вычисления
Преобразователь десятичной системы в двоичную ►
Как преобразовать двоичную систему в десятичную
для двоичного номера с n цифрами:
D N-1 . .. D 3 D 2 D 1 D 0
.. D 3 D 2 D 1 D 0
(d n ) times their power of 2 (2 n ):
decimal = d 0 ×2 0 + d 1 ×2 1 + d 2 ×2 2 + …
Пример
Найдите десятичное значение 111001 2 :
| двоичное число: | 1 | 1 | 1 | 0 | 0 | 1 |
|---|---|---|---|---|---|---|
| степень двойки: | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
111001 2 = 1⋅2 5 +1⋅2 4 +1⋅2 3 +0⋅2 2 +0⋅2 1 +1⋅2 0 = 57 10
Таблица преобразования двоичного кода в десятичный
| Двоичный Число | 3 | Десятичный Числовой | Шестнадцатеричный Номер |
|---|---|---|---|
| 0 | 0 | 0 | |
| 1 | 1 | 1 | |
| 10 | 2 | 2 | |
| 11 | 3 | 3 | |
| 100 | 4 | 4 | |
| 101 | 5 | 5 | |
| 110 | 6 | 6 | |
| 111 | 7 | 7 | |
| 1000 | 8 | 8 | |
| 1001 | 9 | 9 | |
| 1010 | 10 | А | |
| 1011 | 11 | Б | |
| 1100 | 12 | С | |
| 1101 | 13 | Д | |
| 1110 | 14 | Э | |
| 1111 | 15 | Ф | |
| 10000 | 16 | 10 | |
| 10001 | 17 | 11 | |
| 10010 | 18 | 12 | |
| 10011 | 19 | 13 | |
| 10100 | 20 | 14 | |
| 10101 | 21 | 15 | |
| 10110 | 22 | 16 | |
| 10111 | 23 | 17 | |
| 11000 | 24 | 18 | |
| 11001 | 25 | 19 | |
| 11010 | 26 | 1А | |
| 11011 | 27 | 1Б | |
| 11100 | 28 | 1С | |
| 11101 | 29 | 1Д | |
| 11110 | 30 | 1Э | |
| 11111 | 31 | 1F | |
| 100000 | 32 | 20 | |
| 1000000 | 64 | 40 | |
| 10000000 | 128 | 80 | |
| 100000000 | 256 | 100 |
См.
 также
также- Преобразователь десятичной системы в двоичную
- Как преобразовать двоичный код в десятичный
- Преобразователь двоичного кода в шестнадцатеричный
- Двоичный калькулятор
- Преобразователь двоичного кода в текст ASCII
- Преобразователь шестнадцатеричного кода в десятичный
- Преобразователь восьмеричного числа в десятичное
- Шестнадцатеричный/десятичный/восьмеричный/двоичный преобразователь
- Системы счисления
- Преобразование
Напишите как улучшить эту страницу
ПРЕОБРАЗОВАНИЕ ЧИСЕЛ
- ASCII, шестнадцатеричный, двоичный, десятичный преобразователь
- ASCII в двоичный код
- ASCII в шестнадцатеричный
- Базовый преобразователь
- Двоичный преобразователь
- Двоичный код в ASCII
- Двоичное преобразование в десятичное
- Двоичный код в шестнадцатеричный
- Дата романа
- Десятичная дробь
- Десятичный до процентов
- Преобразование десятичного числа в двоичное
- Десятичный в восьмеричный
- Десятичный в шестнадцатеричный
- Градусов в минуты, секунды
- Градусов в Радиан
- Дробь до десятичной дроби
- Дробь до процента
- Шестнадцатеричный/десятичный/восьмеричный/двоичный преобразователь
- Шестнадцатеричный код в ASCII
- Шестнадцатеричный код в двоичный
- Шестнадцатеричный в десятичный
- Минуты, секунды в градусы
- Восьмеричный в десятичный
- Проценты до десятичной дроби
- Проценты в дроби
- Проценты к ppm
- ppm в процентов
- частей на миллион до частей на миллиард
- частей на миллион до частей на миллион
- частей на миллиард до частей на миллион от
- ppt до ppm Преобразователь
- частей на миллион
- радиан в градусов
- Преобразователь римских цифр
RAPID TABLES
- Рекомендовать сайт
- Отправить отзыв
- О
Преобразователь двоичного кода в десятичный
Чтобы использовать этот новый двоично-десятичный преобразователь 9инструмент 0558,
введите любое двоичное значение, например 1010, в левое поле ниже, а затем нажмите кнопку «Преобразовать».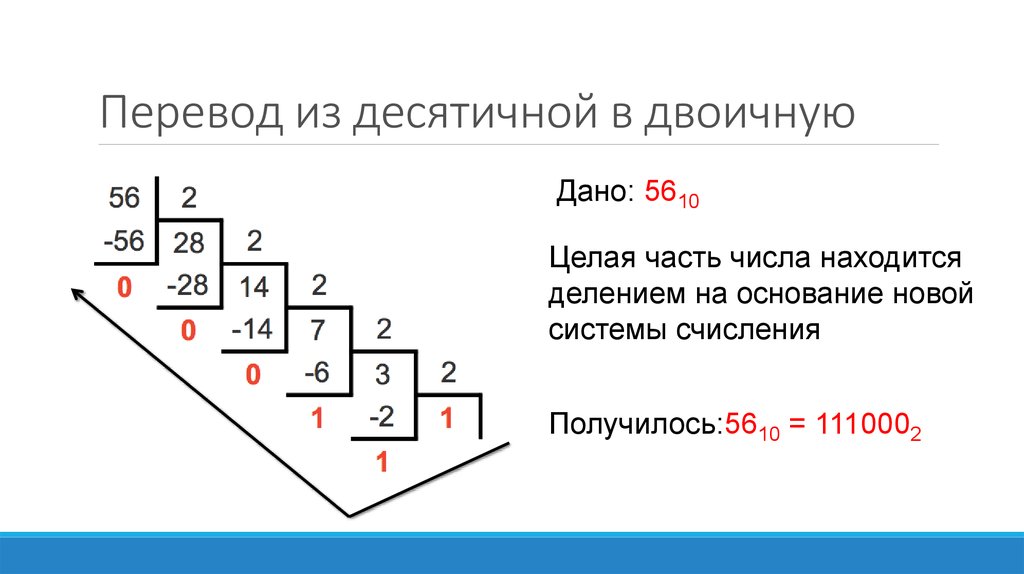 Вы можете увидеть результат в правом поле ниже.
Можно преобразовать до 63 двоичных символов в десятичные.
Вы можете увидеть результат в правом поле ниже.
Можно преобразовать до 63 двоичных символов в десятичные.
Двоичное значение
Десятичное значение Преобразование подкачки: Преобразователь десятичного числа в двоичный
Двоичное преобразование в десятичное приводит к базовым числам
Двоичная система счисления
Двоичная система счисления использует число 2 в качестве основы (основания). Как система счисления с основанием 2, она состоит только из двух чисел: 0 и 1.
Хотя она применялась в Древнем Египте, Китае и Индии для различных целей, двоичная система стала языком электроники и компьютеров в современный мир. Это наиболее эффективная система для обнаружения выключенного (0) и включенного (1) состояния электрического сигнала. Это также основа для двоичного кода, который используется для составления данных в компьютерных машинах. Даже цифровой текст, который вы сейчас читаете, состоит из двоичных чисел.
Чтение двоичного числа проще, чем кажется: это позиционная система; поэтому каждая цифра в двоичном числе возводится в степень 2, начиная с самой правой с 2 0 . В двоичной системе каждая двоичная цифра соответствует 1 биту.
Десятичная система счисления
Десятичная система счисления является наиболее часто используемой и стандартной системой в повседневной жизни. В качестве основы (основания) используется число 10. Следовательно, он имеет 10 символов: Цифры от 0 до 9; а именно 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.
Как одна из старейших известных систем счисления, десятичная система счисления использовалась многими древними цивилизациями. Трудность представления очень больших чисел в десятичной системе была преодолена индо-арабской системой счисления. Индо-арабская система счисления дает позиции цифрам в числе, и этот метод работает с использованием степени основания 10; цифры возводятся в степень n -й в соответствии с их положением.
Например, возьмем число 2345,67 в десятичной системе:
- Цифра 5 стоит на позиции единиц (10 0 , что равно 1),
- 4 стоит на позиции десятков (10 1 )
- 3 стоит на позиции сотен (10 2 )
- 2 находится в позиции тысяч (10 3 )
- При этом цифра 6 после запятой находится в десятых долях (1/10, что равно 10 -1 ), а 7 — в сотых долях (1/100, что равно 10 9 ).0041 -2 ) позиция
- Таким образом, число 2345,67 также можно представить следующим образом: (2 * 10 3 ) + (3 * 10 2 ) + (4 * 10 1 ) + (5 * 10 0 ) + (6 * 10 -1 ) + (7 * 10 -2 )
Как читать двоичные числа
Чтобы преобразовать двоичные числа в десятичные, могут помочь базовые знания о том, как читать двоичные числа. Как упоминалось выше, в позиционной двоичной системе каждый бит (двоичная цифра) является степенью числа 2.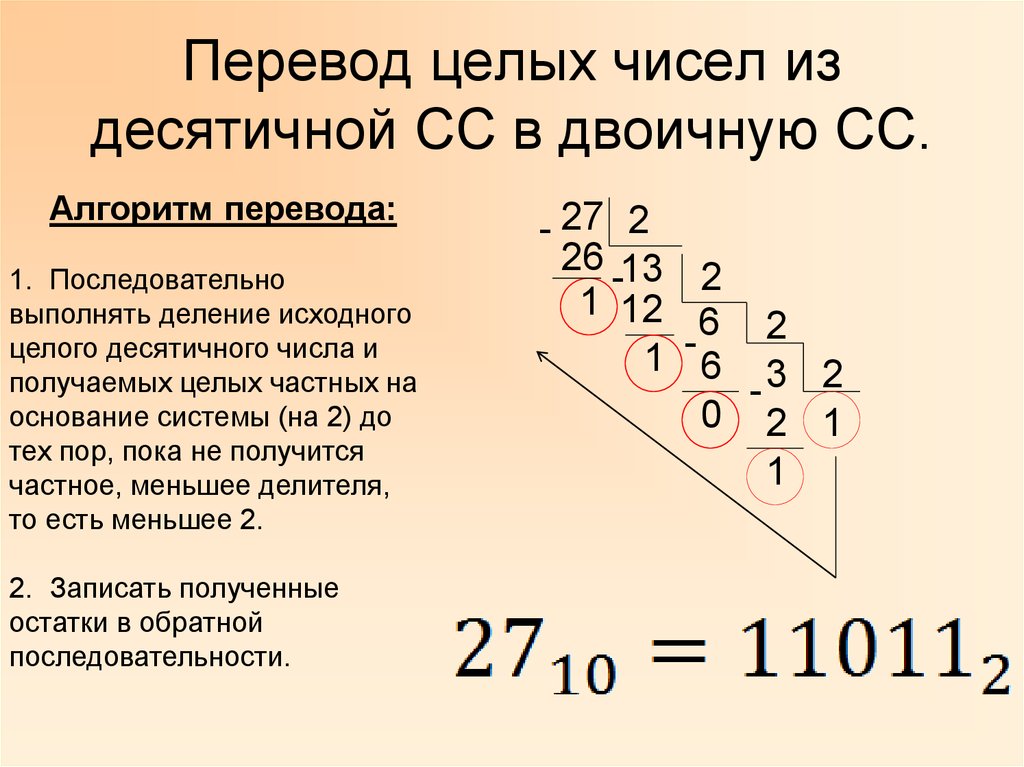 Это означает, что каждое двоичное число может быть представлено как степень числа 2, причем крайний правый из них находится в позиции 2 0 .
Это означает, что каждое двоичное число может быть представлено как степень числа 2, причем крайний правый из них находится в позиции 2 0 .
Пример : Двоичное число (1010) 2 также можно записать следующим образом: (1 * 2 3 ) + (0 * 2 2 ) + (1 * 2 1 ) + ( 0 * 2 0 )
Как преобразовать двоичное число в десятичное
Существует два метода преобразования двоичного числа в десятичное. Первый использует позиционное представление бинарника, описанное выше. Второй метод называется double dabble и используется для более быстрого преобразования более длинных двоичных строк. Он не использует позиции.
Метод 1: Использование позиций
Шаг 1 : Запишите двоичное число.
Шаг 2 : Начиная с младшей значащей цифры (LSB — самая правая), умножьте цифру на значение позиции. Продолжайте делать это, пока не дойдете до старшей значащей цифры (MSB — самая левая).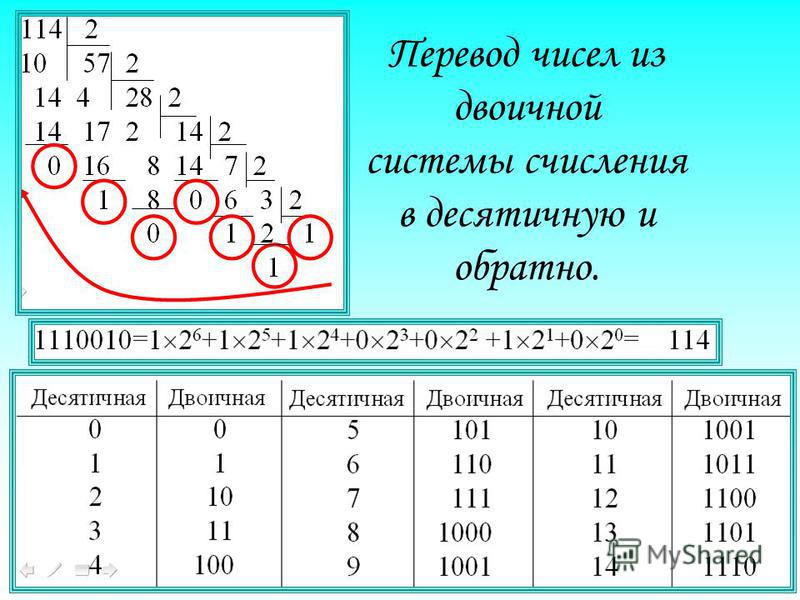
Шаг 3 : Сложите результаты, и вы получите десятичный эквивалент данного двоичного числа.
Теперь давайте применим эти шаги, например, к приведенному выше двоичному числу, которое равно (1010) 9.0026 2
- Шаг 1 : Запишите (1010) 2 и определите позиции, а именно степени числа 2, которым принадлежит цифра.
- Шаг 2 : Представьте число с точки зрения его позиций. (1 * 2 3 ) + (0 * 2 2 ) + (1 * 2 1 ) + (0 * 2 0 )
- Шаг 3 : (1 * 8) + (0 * 4) + (1 * 2) + (0 * 1) = 8 + 0 + 2 + 0 = 10
- Следовательно, (1010) 2 = (10) 10
(Обратите внимание, что цифры 0 в двоичной системе также дают нулевые значения в десятичной дроби.)
Метод 2: Double Dabble любое данное основание к десятичному. Double dabble помогает преобразовать более длинные двоичные строки в вашей голове, и единственное, что нужно помнить, это «удвоить сумму и добавить следующую цифру».

- Шаг 1: Запишите двоичное число. Начиная слева, вы будете удваивать предыдущую сумму и добавлять текущую цифру. На первом шаге предыдущая сумма всегда равна 0, потому что вы только начинаете. Поэтому удвойте сумму (0 * 2 = 0) и добавьте крайнюю левую цифру.
- Шаг 2: Удвойте сумму и добавьте следующую крайнюю левую цифру.
- Шаг 3: Удвойте сумму и добавьте следующую крайнюю левую цифру. Повторяйте это, пока не закончатся цифры.
- Шаг 4: Результат, полученный после прибавления последней цифры к предыдущему удвоенному итогу, является десятичным эквивалентом.
Теперь давайте применим метод двойного мазка к тому же двоичному числу, (1010) 2
- Ваша предыдущая сумма 0. Ваша самая левая цифра равна 1. Удвойте сумму и добавьте самую левую цифру
(0 * 2) + 1 = 1 - Шаг 2: Удвойте предыдущую сумму и добавьте следующую крайнюю левую цифру.
(1 * 2) + 0 = 2 - Шаг 3: Удвойте предыдущую сумму и добавьте следующую крайнюю левую цифру.

(2 * 2) + 1 = 5 - Шаг 4: Удвойте предыдущую сумму и добавьте следующую крайнюю левую цифру.
(5 * 2) + 0 = 10
В этом примере у вас закончились цифры. Следовательно, (1010) 2 = (10) 10
Примеры преобразования двоичного кода в десятичный
Пример 1 : (1110010) 2 = (114) 10
Метод 1:
(0 * 2 0 ) + (1 * 2 1 ) + (0 * 2 2) + (1 * 2 1 ) + (0 * 2 2) + (1 * 2 1 ) + (0 * 2 2) + (1 * 2 1 ). ) + (0 * 2 3 )
+ (1 * 2 4 ) + (1 * 2 5 ) + (1 * 2 6 )
= (0 * 1) + (1 * 2) + (0 * 4) + (0 * 8) + (1 * 16) + (1 * 32) + (1 * 64)
= 0 + 2 + 0 + 0 + 16 + 32 + 64 = 114
Метод 2:
0 (предыдущая сумма в начальной точке)
(0 + 1) * 2 = 2
2 + 1 = 3
3 * 2 = 6
6 + 1 = 7
7 * 2 = 14
14 + 0 = 14
14 * 2 = 28
28 + 0 = 28
28 * 2 = 56
56 + 1 = 57
57 * 2 = 114
Пример 2 : (11011) 2 = (27) 10
Метод 1:
(0 * 2 0 ) + (1 * 2 1 ) + ( 0 * 2 2 ) + (1 * 2 3 )
+ (1 * 2 4 )
= (1 * 1) + (1 * 2) + (0 * 4) + (1 * 8) + (1 * 16)
= 1 + 2 + 0 + 8 + 16 = 27
Способ 2:
(0 * 2) + 1 = 1
(1 * 2) + 1 = 3
(3 * 2) + 0 = 6
(6 * 2) + 1 = 13
(13 * 2) + 1 = 27
Связанные преобразователи:
Конвертер десятичных чисел в двоичные
Таблица преобразования двоично-десятичных чисел
| Двоичные числа | Десятичные числа | |
|---|---|---|
| 00000001 | 1 | |
| 00000010 | 2 | |
| 00000011 | 3 | |
| 00000100 | 4 | |
| 00000101 | 5 | |
| 00000110 | 6 | |
| 00000111 | 7 | |
| 00001000 | 8 | |
| 00001001 | 9 | |
| 00001010 | 10 | |
| 00001011 | 11 | |
| 00001100 | 12 | |
| 00001101 | 13 | |
| 00001110 | 14 | |
| 00001111 | 15 | |
| 00010000 | 16 | |
| 00010001 | 17 | |
| 00010010 | 18 | |
| 00010011 | 19 | |
| 00010100 | 20 | |
| 00010101 | 21 | |
| 00010110 | 22 | |
| 00010111 | 23 | |
| 000 | 23 | |
| 000 | 23 | |
| 000 | 23 | |
| 000 | 0075 | 24 |
| 00011001 | 25 | |
| 00011010 | 26 | |
| 00011011 | 27 | |
| 00011100 | 28 | |
| 00011101 | 29 | |
| 00011110 | 30 | |
| 00011111 | 31 | |
| 00100000 | 32 | |
| 00100001 | 33 | |
| 00100010 | 34 | |
| 00100011 | 35 | |
| 00100100 | 36 | |
| 00100101 | 37 | |
| 00100110 | 38 | |
| 00100111 | 39 | |
| 00101000 | 40 | |
| 00101001 | 41 | |
| 00101010 | 42 | |
| 00101011 | 43 | |
| 00101100 | 44 | |
| 00101101 | 45 | |
| 00101110 | 46 | |
| 00101111 | 47 | |
| 00110000 | 48 | |
| 00110001 | 49 | |
| 00110010 | 50 | |
| 00110011 | 51 | |
| 00110100 | 52 | |
| 00110101 | 53 | |
| 00110110 | 54 | |
| 00110111 | 55 | |
| 00111000 | 56 | |
| 00111001 | 57 | |
| 00111010 | 58 | |
| 00111011 | 59 | |
| 00111100 | 60 | |
| 00111101 | 61 | |
| 00111110 | 62 | |
| 00111111 | 63 | |
| 01000000 | 64 |
| Двоичный | 2 Десятичный|||||||
|---|---|---|---|---|---|---|---|
| 01000001 | 65 | ||||||
| 01000010 | 66 | ||||||
| 01000011 | 67 | ||||||
| 01000100 | 68 | ||||||
| 01000101 | 69 | ||||||
| 01000110 | 70 | ||||||
| 01000111 | 71 | ||||||
| 01001000 | 72 | ||||||
| 01001001 | 73 | ||||||
| 01001010 | 74 | ||||||
| 01001011 | 75 | ||||||
| 01001100 | 76 | ||||||
| 01001101 | 77 | ||||||
| 01001110 | 78 | ||||||
| 01001111 | 79 | ||||||
| 01010000 | 80 | ||||||
| 01010001 | 81 | ||||||
| 01010010 | 82 | ||||||
| 01010011 | 83 | ||||||
| 01010100 | 84 | ||||||
| 01010101 | 85 | ||||||
| 01010110 | 86 | ||||||
| 01010111 | 87 | ||||||
| 01011000 | 88 | ||||||
| 01011001 | |||||||
| 01011010 | 9075 | ||||||
| 9075 | |||||||
| 9075 | |||||||
| 91 | |||||||
| 01011100 | 92 | ||||||
| 01011101 | 93 | ||||||
| 01011110 | 94 | ||||||
| 01011111 | 95 | ||||||
| 01100000 | 96 | ||||||
| 01100001 | 97 | ||||||
| 01100010 | 98 | ||||||
| 01100011 | 99 | ||||||
| 01100100 | 100 | ||||||
| 01100101 | 101 | ||||||
| 01100110 | 102 | ||||||
| 01100111 | 103 | ||||||
| 01101000 | 104 | ||||||
| 01101001 | 105 | ||||||
| 01101010 | 106 | ||||||
| 01101011 | 107 | ||||||
| 01101100 | 108 | ||||||
| 01101101 | 109 | ||||||
| 01111110 | 109 | .0075110 | |||||
| 01101111 | 111 | ||||||
| 01110000 | 112 | ||||||
| 01110001 | 113 | ||||||
| 01110010 | 114 | ||||||
| 01110011 | 115 | ||||||
| 01110100 | 116 | ||||||
| 01110101 | 117 | ||||||
| 01110110 | 118 | ||||||
| 01110111 | 119 | 01110111 | 119 | 01110111 | 119 | 01110111 | |
| 01110111 | |||||||
| 01110111 | |||||||
| 01111000 | 120 | ||||||
| 01111001 | 121 | ||||||
| 01111010 | 122 | ||||||
| 01111011 | 123 | ||||||
| 01111100 | 124 | ||||||
| 01111101 | 125 | ||||||
| 01111110 | 126 | ||||||
| 01111111 | 127 | ||||||
| 10000000 | 128 |


 Если слева не будет хватать цифр для полной группы, нужно дописать необходимое количество незначащих нулей.
Если слева не будет хватать цифр для полной группы, нужно дописать необходимое количество незначащих нулей.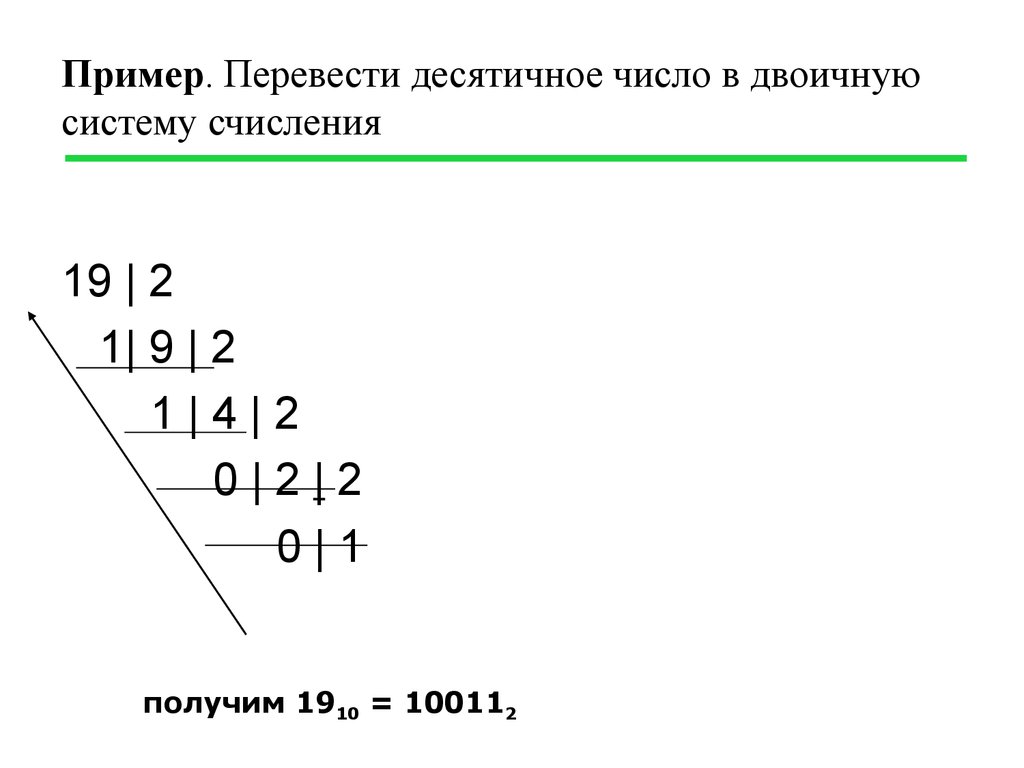 Если нужно, число дополняется нулями слева.
Если нужно, число дополняется нулями слева.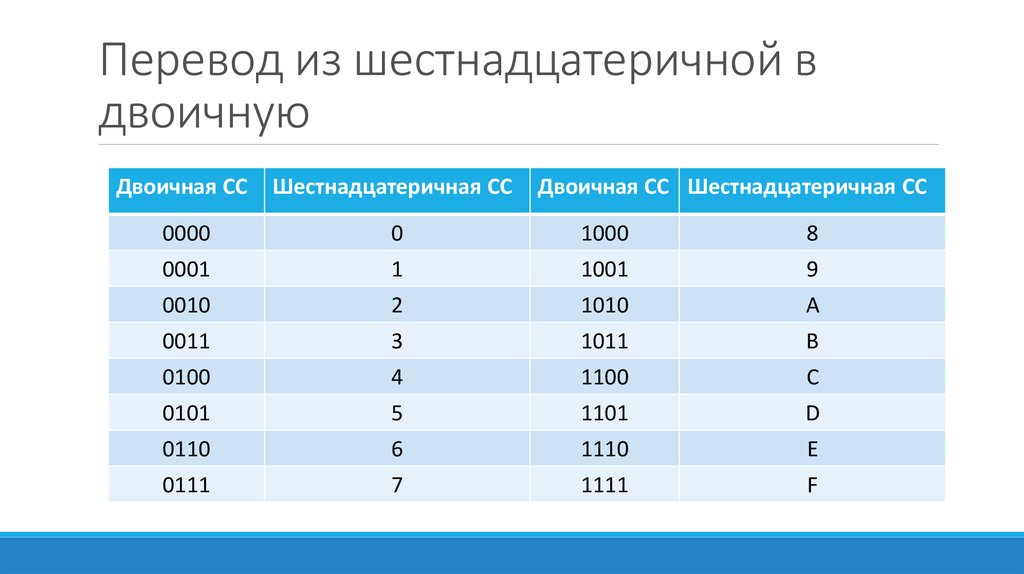
 0074 01011011
0074 01011011