Как объяснять двоичную систему счисления / Хабр

alex4 5 мая 2020 в 12:16

Время на прочтение 2 мин

Количество просмотров 16K

Блог компании Zero to Hero Учебный процесс в IT

Кто-то только входит в IT-мир, кто-то объясняет информатику своему чаду.

Довольно быстро вы обнаружите, что не так-то просто объяснить, как работает двоичный счёт.

Это вам очевидно, что после 11 идёт 100, а новичку это ещё долго может быть непонятно.

Так вот, чтобы увеличить скорость понимания, мы решили сделать дидактический материал.

Проблема

Важно отметить, что даже распиаренный курс Гарвардского университета по компьютерным наукам «CS50» не помогает.

Парень из американского университета просто заявляет, что «нуль — это нуль», «один — это один», а потом идёт 10, а потом 11. Понятно? Думаю, нет. Вот спросите кого-то, кто не программист, а каким будет следующее число — высока вероятность, что он не сможет ответить.

Слишком быстро проскочили идею о переносе разряда.

То же самое касается школьных методов перевода: во-первых, методы эти академически сухи, во-вторых, не интуитивны — например, не очевидно, почему после каскадного деления на 2 нужно ставить биты задом наперёд.

А если непонятно, то и не интересно. А если нет интереса, то и запоминается с трудом.

Мы это всё учли, и решили сделать интересное и постепенное объяснение.

Что мы предлагаем

Сначала нужно объяснить, как вообще работает обычная десятичная система счисления — и про конечный «алфавит» цифр, и про идею переноса разряда. Так развивается понимание принципа «системы счисления».

Только потом можно переходить к идее двоичной системы — и вот обучаемый уже медленно, но довольно уверенно говорит «1, 10, 11, 100».

Далее, мы решили попробовать совсем не школьный метод — объяснение двоичного счёта на пальцах: это когда загнутый палец это 0, а разогнутый это 1.

Я проверял это на подростках: показываешь им: «это 1, это 2, это 3 — теперь покажите мне 4». И весь класс сосредоточенно, медленно показывает средние пальцы. Отличницы в эсхатологическом восторге, задние парты тыкают друг другу в лицо и кричат «на тебе четвёрку!».

Провокативно? Да. Запоминается? 100%.

Теперь, когда тема стала «своей», можно переходить к теме перевода чисел из одной системы счисления в другую — начать лучше с классического школьного сухого перевода (если честно, то больше чтобы постращать).

А уже потом с помощью анимации объяснить идею перевода прямо на пальцах, и потом опять же на пальцах пересчитать число 132 в средние пальцы уже на обеих руках.

На десерт показываем, где двоичная и 16-ричная системы применяется в реальной жизни.

Двоичная система — это например QR-коды вокруг нас.

А 16-ричная система это в основном коды цветов в CSS и хеши разных стилей, от MD5 до UUID.

Итак, вот весь пакет видео-уроков (они бесплатные, в Ютубе):

• Двоичная система счисления
• Перевод из 2 в 10 систему счисления
• Перевод из 10 в 2 систему счисления
• Применение двоичной системы счисления в реальной жизни
• Шестнадцатеричная система счисления
• Применение шестнадцатеричной системы счисления в жизни
• Применение восьмиричной системы счисления — права доступа к файлу

Надеемся, этот материал будет вам полезен в нелёгком деле обучения программированию.

Теги:

• обучение
• обучение программированию
• двоичная система счисления
• двоичный код
• обучение детей программированию

Хабы:

• Блог компании Zero to Hero
• Учебный процесс в IT

Системы исчисления [АйТи бубен]

Системы исчисления: двоичная, восьмеричная, десятичная, шестнадцатеричная.

• Двоичная система счисления Материал из Википедии

• Представление числовых данных в памяти ЭВМ

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов (1 и 0). Компьютер может различить только нулевое и единичное состояние бита, и работает компьютер в системе исчисления с основанием 2 или в двоичной системе.

Бит получил свое название от английского Binary digit (двоичная цифра).

Сочетанием двоичных цифр (битов) можно представить любое значение. Значение двоичного числа определяется относительной позицией каждого бита и наличием единичных битов.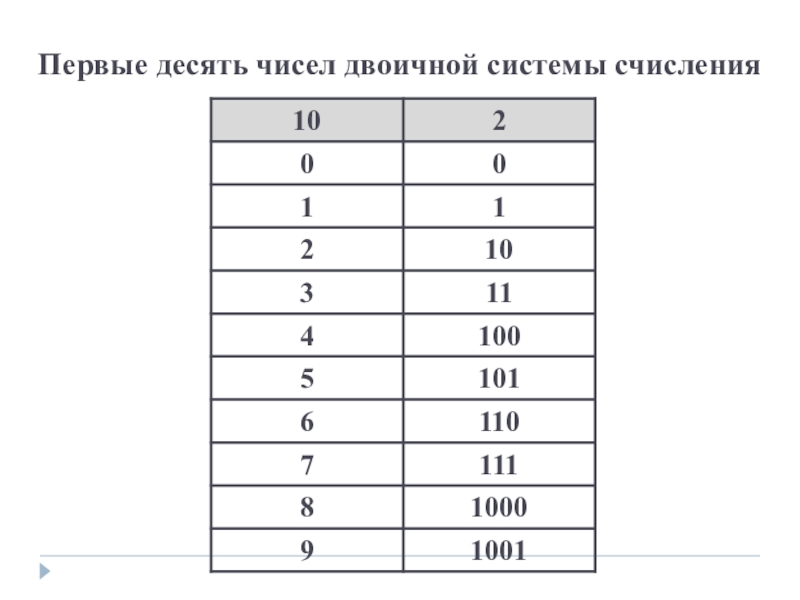 Ниже показано восьмибитовое число, содержащее все единичные биты:

значения:  128  64  32  16  8  4  2  1
биты:    1   1   1   1  1  1  1  1

Самая правая цифра имеет весовое значение 1, следующая цифра влево — 2, следующая — 4 и т.д. Общая сумма для восьми единичных битов в данном случае составит 255:

(1+2+4+8+16+32+64+128=255)

Преобразование чисел

Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:

512	256	128	64	32	16	8	4	2	1

Начиная с цифры 1 все цифры умножаются на два.

Допустим, нам нужно перевести число 17 в двоичное. Согласно таблице степеней оснований (см. выше) 17=16+1. Значит на место значимых цифр 16 и 1 ставим 1 — остальные нули. Получаем 17=10001

512	256	128	64	32	16	8	4	2	1
0       0       0       0       0       1       0       0       0       1

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

19 /2 = 9  с остатком 1
9  /2 = 4  c остатком 1
4  /2 = 2  с остатком 0
2  /2 = 1  с остатком 0
1  /2 = 0  с остатком 1

Итак, мы делим каждое частное на 2 и записываем остаток в начало двоичной записи. Продолжаем делить на 2 частные от деления до тех пор, пока частное не станет равным 0. В результате получаем число 19 в двоичной записи: 10011.

В обратную сторону нужно десятичные сложить, основываясь на таблице степеней основания 2.

Арифметические действия в двоичном формате

Компьютер выполняет арифметические действия только в двоичном формате. Поэтому, необходимо знать правила сложения в двоичной системе исчисления. Напомним их:

0 + 0 = 0
1 + 0 = 1
1 + 1 = 10

Давайте рассмотрим использование этих правил на конкретном примере.

• Пример: сложить числа 65 и 42, представленные в двоичной системе исчисления.

В десятичной системе исчисления все осуществляется достаточно просто: 65+42=107. Для сложения этих чисел в двоичной системе исчисления нужно сначала перевести их в эту систему, например, как показано на рисунке: Таким образом, получаем: 65 в 10-ой системе = 01000001 в 2-ой системе. Обратите внимание на то, что ведущий ноль в двоичном представлении числа добавлен для дополнения двоичного представления до восьми бит.

Аналогично: 42 в 10 = 00101010 в 2. Выполним сложение этих чисел:

   01000001
+
   00101010
   --------
   01101011

Можете перепроверить и убедиться, что 01101011 в 2=107 в 10:

0*27+1*26+1*25+0*24+1*23+0*22+1*21+1*20 = 64+32+8+2+1 = 107

• Вычитание

Для выполнения операции вычитания последнее заменяется сложением, а в качестве второго слагаемого берется противоположное число. Например, пусть надо выполнить вычитание: 65 — 42. Заменим его сложением: 65 + (-42).

Двоичные числа имеют положительные значения, что обозначается нулевым значением самого левого, старшего разряда. Отрицательные двоичные числа содержат единичный бит в старшем разряде.

27 /16 = 1  с остатком 11
11 /16 = 0  c остатком 1

И того получим 1B.

Остаток от деления на 16 всегда меньше 16. Это относится ко всем системам счисления.

Рассмотрим несколько простых примеров шестнадцатеричной арифметики. Следует помнить, что после шестнадцатеричного числа F следует шестнадцатеричное 10, что равно десятичному числу 16:

6+4=A 
5+8=D
F+1=10 
F+F=1E 
10+10=20 
FF+1=100

Двоичное+исчисление Финансовое определение двоичного+исчисления

Двоичное+исчисление Финансовое определение двоичного+исчисления Двоичное+исчисление Финансовое определение двоичного+исчисления

---

Слово, не найденное в Словаре и Энциклопедии.

Возможно, Вы имели в виду:

Пожалуйста, попробуйте слова по отдельности:

двоичный исчисление

Некоторые статьи, соответствующие вашему запросу:

• Двоичная комбинаторная логика
• деонтическая логика
• Chef (язык программирования)

• Функция истинности
• Оператор Лейбница
• Цифровая логика

• Комбинаторное исчисление SKI
• Ассоциативность
• Текущее исчисление

• Мереотопология
• Алгебра сообщающихся процессов
• Йота и Йота

• Булева алгебра
• Смена основания
• Список математических категорий

Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.

Полный браузер ?

• ▲
• Двоичная универсальная форма для представления метеорологических данных
• Представление универсального двоичного формата
• Бинарный университетский колледж менеджмента и предпринимательства
• Двоичный файл обновления
• двоичных значений
• двоичных значений
• двоичных значений
• двоичных значений
• двоичных значений
• Двоичная переменная
• Двоичная переменная
• Двоичная переменная
• Двоичная переменная
• Двоичная переменная
• Бинарный вектор
• Бинарный вид
• Двоичный визуальный редактор
• Бинарное голосование
• Бинарное голосование
• Бинарное вейвлет-преобразование

• Бинарное оружие
• Бинарное оружие
• Двоичный файл с последующими действиями
• двоичное слово
• Двоичный XML
• Двоичный XML
• Двоичный XML
• Двоичный XML
• Двоичный XML
• Передаточный элемент с бинарным ярмом
• двоичный код + исчисление
• Совместимость с двоичным кодом
• Двоично-десятичный
• Двоично-десятичный код
• Двоично-десятичный
• Двоично-десятичный
• Двоично-десятичный
• Двоично-десятичная запись
• Метод двоичных элементов
• Binary-Encounter-Bethe
• Аддитивный белый гауссовский шум с двоичным входом

• Двоичный ввод Двоичный вывод
• Симметричный канал без памяти с двоичным вводом
• Двоичный вход Симметричный выход
• Двоичный вход/несимметричный выход
• Двоичный ввод/симметричный вывод
• Канал с двоичной маркировкой
• Цикл отслеживания перехода двоично-квантованных данных
• Двоичный сейф
• Двоичный сейф
• Бинарно-симметричный марковский источник
• Бинарно-симметричный источник
• Преобразование двоичного кода в десятичный
• Преобразование двоичного кода в десятичный
• Бинарно-четырехфазный
• Преобразователь/преобразование двоичного кода в символ
• Преобразование двоичного кода в текст
• Оптимизированная архитектура двоичного перевода
• Двоичное дерево на двоичном дереве
• BinaryObject (метаданные)
• БИНАС
• ▼

Сайт: Следовать:

Делиться:

Открыть / Закрыть

 

Подход на основе SAT для расчета индексов на бинарных эллиптических кривых

Paper 2019/313

Подход на основе SAT для расчета индексов на бинарных эллиптических кривых

Моника Тримоска, Сорина Ионика и Жиль Декен

Abstract

Логический криптоанализ, впервые представленный Массаччи в 2000 году, является жизнеспособной альтернативой обычным методам алгебраического криптоанализа над булевыми полями. n}$ с использованием методов решения SAT. Мы экспериментировали с различными решателями SAT и решили использовать WDSat, решатель, предназначенный для этой конкретной проблемы. Мы расширяем этот решатель, добавляя новый метод нарушения симметрии и оптимизируя временную сложность шага точечной декомпозиции с коэффициентом $m!$ для многочлена суммирования $(m+1)$\textsuperscript{th} Семаева. Хотя асимптотическое решение задачи точечной декомпозиции с помощью этого метода имеет экспоненциальную наихудшую временную сложность в размерности $l$ векторного пространства, определяющего факторную базу, экспериментальное время выполнения показывает, что представленный метод решения SAT значительно быстрее, чем современные алгебраические методы, основанные на Расчет базиса Грёбнера. Для значений $l$ и $n$, рассматриваемых в экспериментах, решатель WDSat в сочетании с нашей техникой нарушения симметрии работает до 300 раз быстрее, чем реализация MAGMA F4, и этот коэффициент растет с ростом $l$ и $n$.

Метаданные

Доступный(е) формат(ы)

PDF

Категория

Криптография с открытым ключом

Информация о публикации

Опубликовано в другом месте. Прогресс в криптологии — AFRICACRYPT 2020

ДОИ

10.1007/978-3-030-51938-4_11

Ключевые слова

дискретный логарифманализ индексовэллиптические кривыеточечная декомпозициясимметрияудовлетворительностьалгоритм DPLL

Связаться с автором(ами)

моника тримоска @ u-picardie fr
sorina ionica @ u-picardie fr
gilles dequen @ u-picardie fr

История

18.12.2020: последняя из 6 ревизий

21.03.2019: получен

Посмотреть все версии

Короткий URL-адрес

https://ia.