Почему компьютеры используют двоичную систему счисления
Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.
А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
представление информации посредством только двух состояний надежно и помехоустойчиво;
возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.
Применение восьмеричной и шестнадцатеричной систем счисления
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре(шестнадцатеричная) раза меньше разрядов, чем в двоичной системе
Перевод восьмеричных и шестнадцатеричных чисел в
двоичную систему очень
прост: достаточно каждую цифру заменить
эквивалентной ей двоичной триадой (тройкой
цифр) или тетрадой (четверкой
цифр).
Например:
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную
Например,
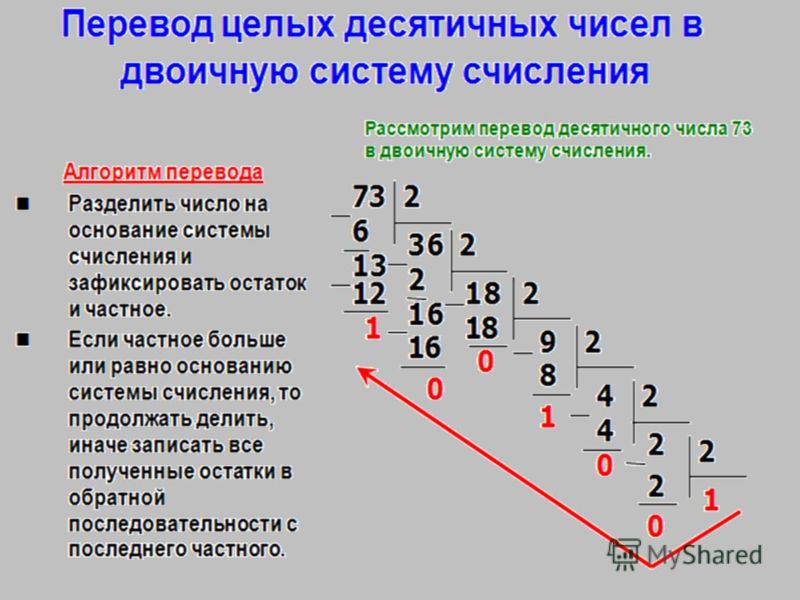
Перевод чисел из десятичной системы счисления в другие позиционные системы счисления
При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q-1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.
Пример: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Ответ: 7510 =
1 001 0112 =
1138 =
4B16.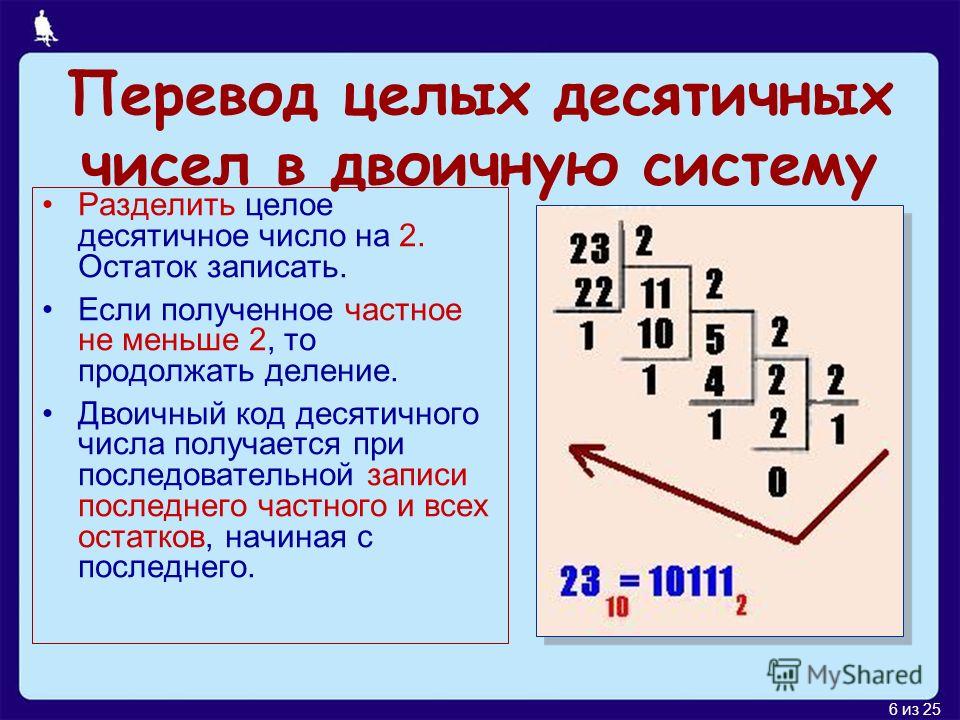
Перевод простой десятичной дроби в другие позиционные системы счисления
Пpи переводе правильной десятичной дpоби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть пpоизведения. Число в новой системе счисления записывается как последовательность полученных целых частей пpоизведения.
Умножение пpоизводится до тех поp, пока дpобная часть пpоизведения не станет pавной нулю. Это значит, что сделан точный пеpевод. В пpотивном случае пеpевод осуществляется до заданной точности. Достаточно того количества цифp в pезультате, котоpое поместится в ячейку.
Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Ответ: 0,3510 =
0,010112 =
0,2638 =
0,5916 .
Ипользование двоичной системы счисления — Секреты двоичной системы счисления
В КОМПЬЮТЕРНОЙ ТЕХНИКЕ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЯХ.
Столь привычная для нас десятичная система оказалась
неудобной для ЭВМ. Если в механических вычислительных устройствах, использующих
десятичную систему, достаточно просто применить элемент с множеством состояний
(колесо с девятью зубьями), то в электронных машинах надо было бы иметь 10
различных потенциалов в цепях. Наиболее просто реализуется элементы с двумя
состояниями — триггеры. Поэтому естественным был переход на двоичную систему,
т.е. системы по основанию 2. В этой системе всего две цифры — 0 и 1. Каждая
цифра называется двоичной (от английского binarydigit — двоичная цифра). Бит — это минимальная единица измерения информации (0 mini). За битом следует байт, состоящий из восьми бит, затем килобайт (кбайт) — 1024 байта, мегабайт (мбайт) — 1024 кбайта, гигобайт (гбайт) — 1024мбайт.
Двоичное кодирование информации в компьютере Для обмена информацией с другими людьми человек
использует естественные языки (русский, английский, китайский и т.д.), те есть
информация представляется с помощью естественных языков. В основе языка лежит
алфавит, то есть набор символов (знаков, которые человек различает по их
начертанию. Последовательности символов алфавита в соответствии с правилами
грамматики образуют основные объекты языка -слова. Правила, согласно которым
образуются предложения из слов данного языка называются синтаксисом. Необходимо
от метить, что в естественных языках грамматика и синтаксис языка формируются с
помощью большого количество правил, из которых существуют исключения, так как
такие правила складывались исторически. Наряду с естественными языками были разработаны формальные языки (системы счисления, язык алгебры, языки программирования и др.). Основное отличие формальных языков от естественных состоит в наличии жестких правил грамматики и синтаксиса. Эти языки были разработаны людьми, для упрощения каких-либо действий. Как, например, системы счисления были придуманы для упрощения подсчетов чего-либо. Создатели первых компьютеров столкнулись с проблемой
представления и обработки информации. Так как компьютер это всего лишь машина у
которой нет ни интеллекта, ни логики, и мыслить она не способна, разработчикам
пришлось найти такой способ представления информации, который был бы
максимально прост для восприятия компьютером. Столь привычная для нас
десятичная система оказалась неудобной для ЭВМ. Если в механических
вычислительных устройствах, использующих десятичную систему, достаточно просто
применить элемент с множеством состояний (колесо с девятью зубьями), то в
электронных машинах надо было бы иметь 10 различных потенциалов в цепях. Бит — это минимальная единица измерения информации (0 или1). За битом следует байт, состоящий из восьми бит, затем килобайт (кбайт) — 1024 байта, мегабайт (мбайт) — 1024 кбайта, гигобайт (гбайт) — 1024мбайт. Таким образом, в компьютере для представления информации используется двоичное кодирование, так как удалось создать надежные работающие технические устройства, которые могут со стопроцентной надежностью сохранять и распознавать не более двух различных состояний (цифр). Все виды информации в компьютере кодируются на машинном языке, в виде логических последовательностей нулей и единиц. Таким
образом, информация представляется в виде конечной последовательности 0 и 1.
Значит, мы можем записать все числа от 0 до 255 в двоичной системе счисления в 1 ячейке памяти. 2 Представление чисел в компьютере Целые числа в компьютере хранятся в ячейках памяти, в этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа. Для хранения целых неотрицательных чисел отводится одна ячейка памяти состоящая из восьми бит. Например, число 1910 будет выглядеть: 0111 Для хранения целых чисел со знаком (отрицательных) отводиться две ячейки памяти (16 битов), причем старший (левый) разряд отводиться под знак числа (если число положительное, то в знаковый разряд записывается 0, если отрицательное — 1). Например, число -9810 будет выглядеть: 1111
Представление целых чисел в компьютере в формате
«знак — величина» называется прямым кодом числа. Для представления отрицательных чисел используется дополнительный код. Дополнительный код позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Дополнительный код представляет собой дополнение модуля отрицательного числа А до О, 2n -|А|+|А| =0 поскольку в компьютерной 2n =0. Алгоритм построения такого кода довольно прост: 1. Записать модуль числа в прямом коде. 2. Получить обратный код числа (то есть заменить все нули на единицы, а все единицы на нули). 3. К полученному результату прибавить единицу. Запишем дополнительный код отрицательного числа -2002 для 16-разрядного представления: Запишем дополнительный код отрицательного числа -16320 для 16-разрядного представления: 2.3 Способы построения двоичных кодов Начиная с конца 60-х годов, компьютеры все больше
использовать для обработки текстовой информации и в настоящее время большая
часть компьютеров в мире занято именно обработкой текстовой информации. Традиционно для кодирования одного символа используется количество информации равное 1 байту, то есть 8 бит. Если рассматривать символы как возможные события, то получаем, что количество различных символов, которые можно закодировать, будет равно 256. Такое количество символов вполне достаточно для представления текстовой информации, включая прописные и строчные буквы русского и латинского алфавитов, а так же цифры, знаки препинания и математических операций, графические символы и так далее.
Одной из наиболее совершенных релейных вычислительных машин была машина РВМ-1, сконструированная и построенная под руководством советского инженера Н.И.Бессонова в середине 50-х годов. Благодаря применению каскадного принципа выполнения арифметических операций, изобретённого самим Бессоновым, машина производила до 1250 умножений в минуту. Она содержала 5500 реле. Целый ряд усовершенствований настолько улучшил её надёжность и эксплуатационные качества, что она работала до 1965 года. Компьютерный мир с каждым годом усложняется. Мощность вычислительной техники удваивается каждые полтора года. Персональные компьютеры, на которых сегодня играют школьники, мощнее суперкомпьютеров недавнего прошлого. Выпускаются всё более производительные операционные системы, появляются совершенно новые области применения компьютеров.
1. v Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями v Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать v Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.
2. В английской системе мер v При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 715/16″, 311/32″ и т. д. |
Binary — Computer Science Wiki
Из Computer Science Wiki
Перейти к навигацииПерейти к поиску
Это основное понятие в информатике
В математике и цифровой электронике двоичное число — это число, выраженное в двоичной системе счисления или система счисления с основанием 2, которая представляет числовые значения с использованием двух разных символов: обычно 0 (ноль) и 1 (единица). Система с основанием 2 представляет собой позиционную систему с основанием 2. Из-за ее простой реализации в цифровых электронных схемах с использованием логических вентилей двоичная система используется внутри почти всех современных компьютеров и компьютерных устройств. Каждая цифра называется битом. [1]
Система с основанием 2 представляет собой позиционную систему с основанием 2. Из-за ее простой реализации в цифровых электронных схемах с использованием логических вентилей двоичная система используется внутри почти всех современных компьютеров и компьютерных устройств. Каждая цифра называется битом. [1]
Содержание
- 1 Двоичный
- 2 Основные определения
- 3 Двоичная таблица перевода
- 4 Полезная шпаргалка
- 5 Как сложить два двоичных числа
- 6 Что вы должны знать
- 7 Почему это так важно?
- 8 Ресурсы
- 9 Каталожные номера
Это одно из лучших видео, которые я видел в двоичном формате. Контент с благодарностью используется с разрешения : [2]
Основные определения
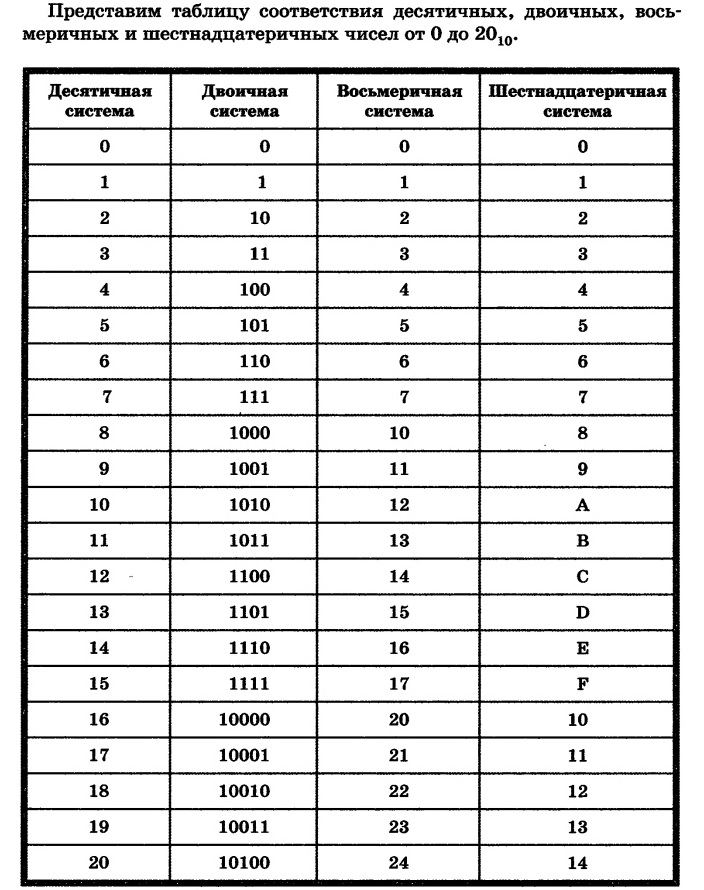
. Таблица двоичного перевода[править]
Я нахожу полезным рисовать эту таблицу, когда мне нужно преобразовать двоичную систему в 10-ю. Это также помогает при просмотре видео выше.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| |
Полезная шпаргалка[править]
Как сложить два двоичных числа[править]
Сложение двоичных чисел очень просто. Выровняйте числа, как если бы вы складывали числа с основанием 10.
Выровняйте числа, как если бы вы складывали числа с основанием 10.
Запомните это:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10, поэтому запишите 0 и перенесите 1 в следующий столбец.
Что вы должны знать[править]
Вы должны быть в состоянии правильно ответить на следующие вопросы:
- Определение термина: бит
- Определить термин: байт
- Определить термин: двоичный
- Определите термин: десятичный/десятичный (они относятся к одному и тому же)
- Дайте определение термину: шестнадцатеричное
Почему это так важно? Если мы можем представить буквы как числа (A = 65, B = 66), не можем ли мы также сказать, что A = 01000001 и B = 01000010? Мы можем следовать этой линии мышления и делать север/юг, вверх/вниз и низкий/высокий. Простые конструкции, которые мы можем использовать для представления более сложных чисел и даже букв.

Двоичное представление — суть работы компьютеров.
ресурсы
Ссылки[править]
- ↑ https://en.wikipedia.org/wiki/Binary_number
- ↑ http://cs50.tv/2015/fall/#license,psets
- ↑ https://en.wikipedia.org/wiki/Decimal
- ↑ https://en.wikipedia.org/wiki/Hexadecimal
Единица абстрактной математической системы, подчиняющаяся законам арифметики.
Дайте конкретное имя, значение или другой краткий ответ без объяснений или вычислений.
Изобразить с помощью маркированной точной диаграммы или графика с помощью карандаша. Для прямых линий следует использовать линейку (линейку). Схемы должны быть выполнены в масштабе. На графиках должны быть правильно нанесены точки (если это уместно) и соединены прямой линией или плавной кривой.
Укажите точное значение слова, фразы, понятия или физической величины.
Двоичные числа и работа компьютеров
Несмотря на то, что для изучения компьютерного программирования не обязательно обладать обширными познаниями в области математики, это, безусловно, помогает иметь базовые знания некоторых фундаментальных математических знаний, которые делают возможными вычисления.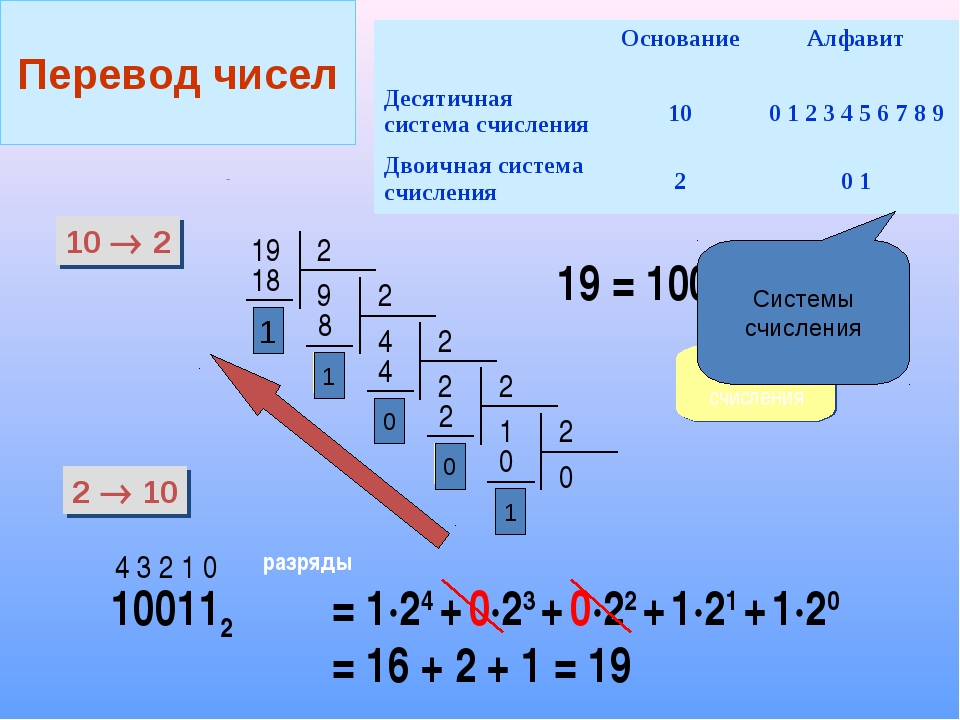 А что может быть более фундаментальным для современных вычислений, чем бинарная математика?
А что может быть более фундаментальным для современных вычислений, чем бинарная математика?
Термин «двоичный» означает нечто, имеющее только два возможных объекта или состояния. В двоичной системе счисления этими двумя объектами являются числа 0 и 1 . Эти два числа могут представлять множество вещей.
Например, в компьютерной логике 0 означает «ложь», а 1 — «истина». Или их можно использовать для представления обычных чисел в виде комбинаций единиц и нулей. Примером этого может быть представление чисел 0, 1, 2, 3 и 4 тремя двоичными цифрами как 000, 001, 010, 011 и 100 соответственно.
Но что все это означает на фундаментальном уровне вычислений? Почему двоичная система счисления используется в качестве основы для всех наших вычислений?
Возможно, было бы легче понять все это, если бы мы могли понять основы работы компьютеров на машинном уровне.
0 и 1: интерпретация работы компьютерной схемы
компьютеры работают на электрических сигналах, генерируемых этими схемами.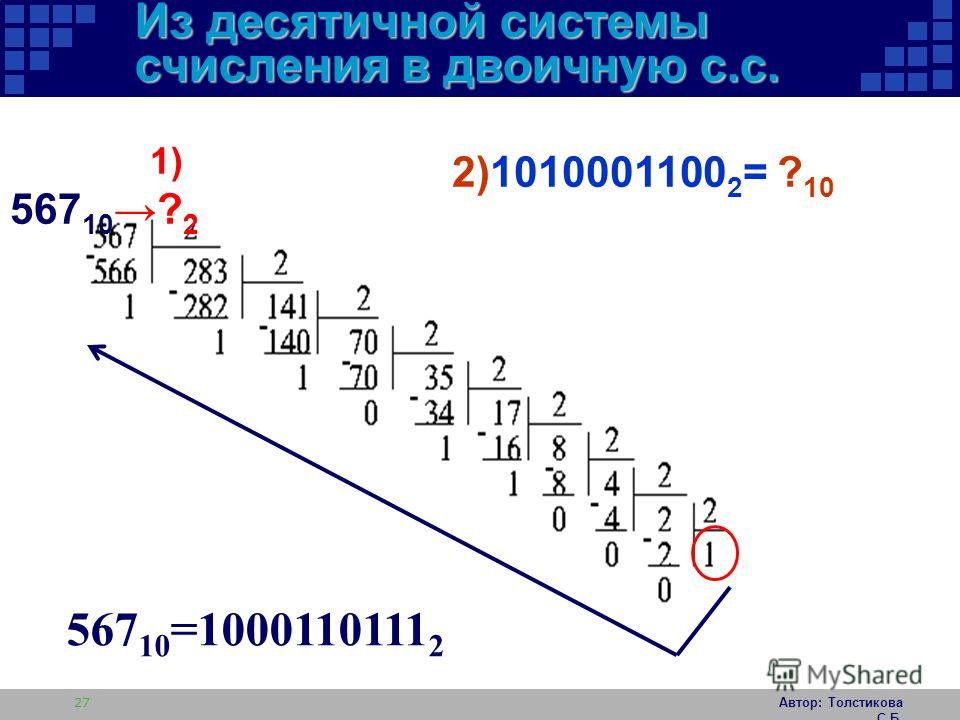 Чтобы спроектировать компьютер, который работает эффективно, нам нужна система, которая может интерпретировать электрические сигналы простым и эффективным способом.
Чтобы спроектировать компьютер, который работает эффективно, нам нужна система, которая может интерпретировать электрические сигналы простым и эффективным способом.
Хороший способ сделать это — интерпретировать электрические сигналы как двоичные значения: 0 для низкого значения напряжения и 1 для высокого напряжения. Более простой способ подумать об этом — представить себе лампочку. Если лампочка отключена от , это состояние интерпретируется как имеющее значение 0 . Если это на , оно интерпретируется как имеющее значение 1.
Интерпретация состояний лампы в двоичном форматеЭто широкое обобщение сводит диапазон интерпретации каждого электрического сигнала к двум различным значениям вместо бесконечного диапазона непрерывных значений. значения напряжения.
С помощью этого метода работы и интерпретации электронных схем мы можем приступить к разработке кодированных систем на основе двоичных битов, чтобы помочь в наших вычислительных задачах. Эти системы могут быть двоичной логикой (ограничены только истинными или ложными значениями), числовым представлением числовых значений с основанием 2 или использованием других систем, которые полагаются на серию двоичных чисел для представления текста, изображений или звуков.
Эти системы могут быть двоичной логикой (ограничены только истинными или ложными значениями), числовым представлением числовых значений с основанием 2 или использованием других систем, которые полагаются на серию двоичных чисел для представления текста, изображений или звуков.
По сути, наши компьютеры используют серию высоковольтных и низковольтных электрических сигналов (двоичных значений) для представления всего, от текстов и чисел до изображений и звуков. Существуют специальные электронные схемы, такие как триггеры и другие схемы, которые могут «хранить» или сохранять эти определенные схемы электрических сигналов для длительного использования.
Например, один триггер может иметь ряд входов, которые в настоящее время имеют выход высокого напряжения (что мы интерпретируем как 1 ). Предположим, следующие два триггера имеют низковольтные выходы 0 . Мы могли бы объединить эти три вывода, чтобы получить значение 100 , которое в двоичном виде совпадает с числом 4 .
Таким образом, понимание двоичных чисел может помочь нам понять некоторые основы компьютерных операций на достаточно абстрактной основе , даже если наш слабый человеческий интеллект никогда не позволит нам понять всю сложность компьютерных операций.
И это даже хорошо, поскольку работа с упрощенными и абстрактными представлениями о компьютерных операциях более чем достаточна для нас, студентов информатики. В следующих разделах мы кратко рассмотрим некоторые из различных способов, которыми компьютеры используют двоичные символы для выполнения некоторых из своих наиболее фундаментальных операций.
Булева логика: использование двоичных чисел для понимания компьютерной логики
Компьютерные программы используют очень специфическую логическую систему для выполнения своих инструкций. Это известно как булева логика, сформулированная английским математиком Джорджем Булем в 19 веке.
Буль разработал систему арифметических и логических операций, использующих двоичную систему чисел. Булева логика имеет дело только с двумя возможными значениями: true или false . True представлен 1 и false представлен 0 . Все логические операции приводят только к одному из этих двух двоичных значений.
Булева логика имеет дело только с двумя возможными значениями: true или false . True представлен 1 и false представлен 0 . Все логические операции приводят только к одному из этих двух двоичных значений.
Современные компьютеры постоянно используют эту форму логики для принятия решений. Эти решения приводят к тому, что наши компьютеры принимают определенный курс действий вместо другого.
Принятие решений в компьютерахЧтобы понять, насколько важна эта система для компьютеров, не нужно смотреть дальше, чем существование логических операторов в большинстве языков программирования: операторы И, ИЛИ и НЕ.
Эти операторы напрямую взяты из операций И, ИЛИ и НЕ булевой логики. И любой, кто хоть немного знаком с программированием, знает, что эти операции являются центральными в программировании.
Но на этом влияние работ Буля не заканчивается. Фактически, многие языки программирования имеют тип данных с именем boolean , который может хранить только «true» или «false», то есть 1 или 0.
Эти логические переменные и логические операторы являются фундаментальными компонентами, используемыми в реализации условных операторов и управления операторы в языках программирования. В результате их важность невозможно переоценить, так как это Программирование 101.
Существует множество других, более творческих и более сложных способов использования двоичных чисел в языках программирования. Тем не менее, этот пост в блоге служит простым обзором некоторых вещей, для которых можно использовать двоичные числа.
Таким образом, мы не будем углубляться в технические детали программирования. Возможно, я рассмотрю больше этих тем в следующих постах в блоге. А пока давайте просто рассмотрим более простую тему числовых представлений в компьютерах.
Представление числовых значений в базе 2 92 = 100)
. Чем больше цифр, тем больше последовательность степеней 10. Вот почему эта система счисления называется системой счисления с основанием 10. Система счисления с основанием 2 работает таким же образом, за исключением того, что мы умножаем каждый бит (двоичную «цифру») на последовательные степени 2. В качестве примера возьмем число с основанием 2 1011 и посмотрим какое число с основанием 10 он представляет.
В качестве примера возьмем число с основанием 2 1011 и посмотрим какое число с основанием 10 он представляет.
Как мы видим, двоичное число 1011 эквивалентно числу одиннадцать (11) по основанию 10.
Конечно, способ группировки двоичных чисел также имеет значение. Мы знаем, что 1011 представляет собой число 11 в системе счисления 10. Но что, если мы сгруппируем ту же серию битов, что и 10 11? Это два разных числа 10 и 11? Или это единый номер 1011?
Это показывает нам важность того, как мы группируем наши числа. А в компьютерах числа группируются по-разному. Например, целочисленный тип данных int в C++ хранит одно число в последовательности из 32 двоичных чисел. Итак, основание-10 число 0 представлен серией из 32 нулей, а число 1 представлено 1, перед которой стоит 31 ноль слева от него.
Текстовое и символьное представление
Мы видели, что система счисления с основанием 2 формирует основу числового представления в наших электронных устройствах. И хотя это верно для систем текстового представления, их работа совершенно иная.
И хотя это верно для систем текстового представления, их работа совершенно иная.
Наиболее распространенными системами представления символов являются ASCII (американский стандартный код для обмена информацией) и Unicode (который является расширением ASCII). Эти системы присваивают символам уникальные числовые значения и сохраняют их в двоичном формате.
Например, система ASCII изначально использовала 7 бит для представления символа. В настоящее время это было расширено до 8 бит. Например, символ A представлен числовым значением 65 в ASCII. Двоичный код для 65 равен 1000001 9.0219 . Обратите внимание, что двоичное представление состоит из 7 бит. В расширенном ASCII это будет сохранено как 01000001 , так что общее количество битов равно 8.
Аналогично, код ASCII для символа a равен 97 и представлен как 01100001 в расширенном ASCII. Есть также очень специальные символы, которые представлены 0 , 1 , 2 и так далее. И они представлены как 00000000 , 00000001 , 00000010 и так далее.
Есть также очень специальные символы, которые представлены 0 , 1 , 2 и так далее. И они представлены как 00000000 , 00000001 , 00000010 и так далее.
Эта система хорошо подходит для представления английских и некоторых европейских знаков и символов, но совершенно неадекватна для представления символов из языков со всего мира. Для размещения дополнительных символов был разработан Unicode .
Unicode изначально использовал 21 бит на символ, в отличие от 7 бит, которые изначально использовались ASCII. Это значительно расширяет диапазон значений, которые можно использовать для представления символов. Исходные коды ASCII размещаются в системе Unicode.
В настоящее время система кодирования на основе Unicode, называемая UTF-8 , является наиболее часто используемой системой кодирования в веб-приложениях. UTF-8 может использовать до 32 бит на символ, что означает, что он может представлять еще большее количество символов.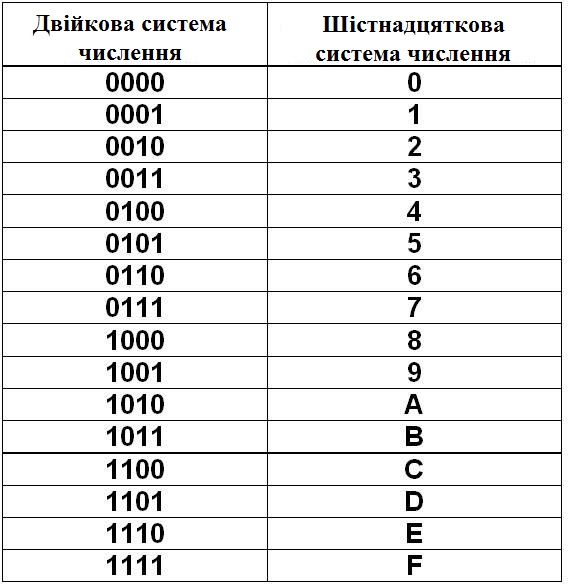
Пиксели и изображения
Неудивительно, что изображения также часто представляются числами. В компьютерах изображения чаще всего создаются с помощью крошечных цветных квадратов, называемых пикселями. Подумайте о мозаике в реальной жизни: изображение или узор создаются путем объединения множества маленьких цветных кусочков. Или головоломка, в которой мы объединяем более мелкие части, чтобы создать более крупную законченную картинку.
Пиксели работают аналогичным образом. Тысячи крошечных цветных квадратов составляют изображения, которые отображаются на наших экранах. Существует множество способов кодирования цветов в пикселях, но чаще всего используется код RGB (красный, зеленый, синий).
Коды RGB работают, комбинируя красный, зеленый и синий цвета для получения всех оттенков цветов, которые мы видим в наших современных устройствах. Каждый из трех цветовых компонентов кодируется числом, значения которого находятся в диапазоне от 0 до 255. Таким образом, существует три набора чисел, описывающих пиксель.
В качестве примера рассмотрим цвет, представленный кодом RGB (142, 150, 123). Этот цветовой код состоит из 3 компонентов: красный = 142 , зеленый = 150 и синий = 123 .
В наших компьютерах каждый из этих цветовых компонентов представлен их двоичными эквивалентами с использованием 8 бит, а затем объединен. Например, двоичный код для числа 142 (красный компонент) — 10001110, двоичный код для числа 150 — 10010110, а двоичный код для числа 123 — 1111011.
Красный = 142 = 10001110
Зеленый = 150 = 10010110
Синий = 123 = 01111011
Компьютер хранит свои коды в памяти справа от RGB.
Полный код RGB = 100011101001011001111011
Работа кода RGB Таким образом, мы видим, что даже изображения представлены в двоичном виде. На самом деле, знание двоичных кодов пикселей изображения открывает двери для небольших забавных приложений манипулирования изображениями, таких как сокрытие одного изображения внутри другого.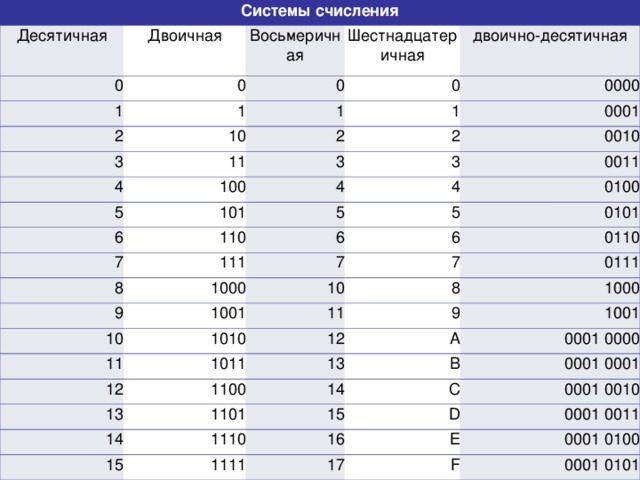 Я уже писал о простом методе сокрытия изображений в моем предыдущем блоге Steganography: Hiding Information Inside Pictures. Вы можете проверить это для фактического практического применения двоичных чисел в информатике.
Я уже писал о простом методе сокрытия изображений в моем предыдущем блоге Steganography: Hiding Information Inside Pictures. Вы можете проверить это для фактического практического применения двоичных чисел в информатике.
Заключительные мысли и выводы
Двоичные числа составляют одну из основных основ современных вычислений. И хотя мы кратко рассмотрели некоторые способы использования двоичных чисел в наших компьютерах, мы также многое упустили, поскольку исчерпывающий список приложений и объяснений выходит за рамки этого блога.
При этом мы рассмотрели довольно много интересных тем, хотя они могут быть и базовыми. Мы видели, что
- физических действий компьютерной схемы интерпретируются с использованием двоичной записи, то есть в одной цепи значения низкого напряжения интерпретируются как 0 и значения высокого напряжения интерпретируются как 1 . Компьютеры
- используют булеву логику, интерпретируя 1 как true и 0 как false при выполнении логических операций.







 Например целое неотрицательное число А2 =Т 111100002 будет храниться в ячейке
следующим образом:
Например целое неотрицательное число А2 =Т 111100002 будет храниться в ячейке
следующим образом: Например, число
200210=111110100102 будет представлено в шестнадцатиразрядном представлении
следует следующим образом: 1111111
Например, число
200210=111110100102 будет представлено в шестнадцатиразрядном представлении
следует следующим образом: 1111111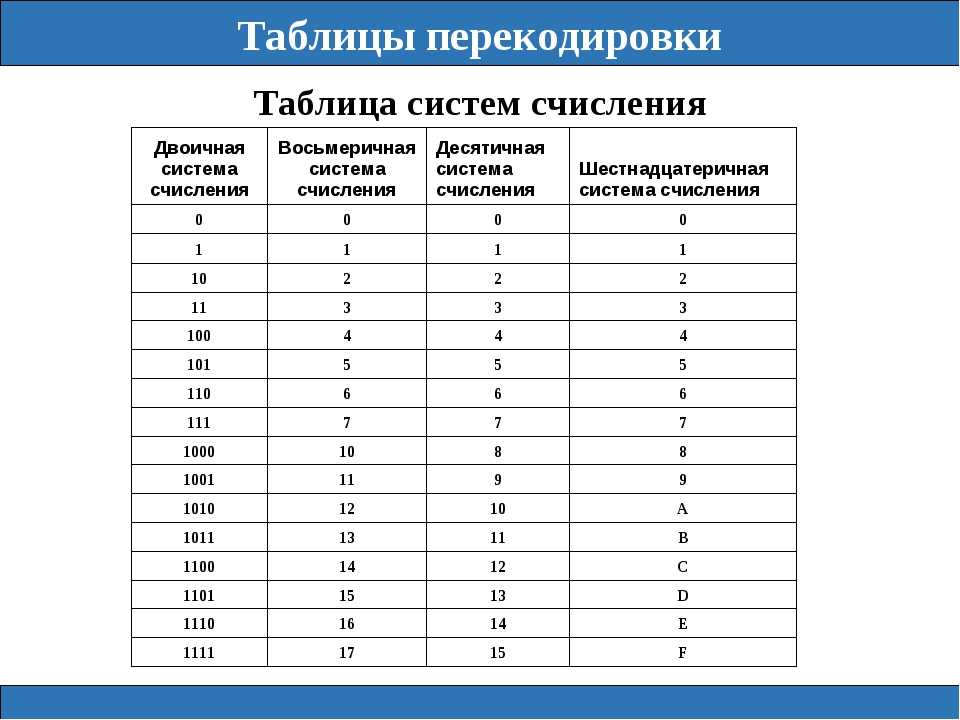
 С помощью алгебры Буля
можно просто составить схему автомата, работающего на реле.
С помощью алгебры Буля
можно просто составить схему автомата, работающего на реле. В цифровых устройствах
В цифровых устройствах