Двоичная система счисления

<<Назад  |  Содержание  |  Далее>>

 

 

Двоичная (бинарная) система счисления имеет основание 2. Ее алфавит – цифры 0 и 1. Для перевода числа из двоичной системы счисления в десятичную также справедливо правило (6). Представим в десятичном виде число 1101₍₂₎, или, что то же самое, &1101 (& — амперсант, — этим символом принято указывать то, что следующая за ним запись двоичная).

1101₍₂₎=1*2³+1*2²+0*2¹+1*2⁰=1*8+1*4+0*2+1*1=13₍₁₀₎

 

 

Рис. 14. Перевод числа из двоичной СС в десятичную.

Но двоичная система имеет некоторые приятные особенности, т.к. коэффициентами при степенях двойки в ней могут быть только либо нули (и тогда можно просто игнорировать разряд числа, имеющий значение “0”), либо единицы (умножение на “1” также можно опустить).

Т.е. достаточно просуммировать “два в соответствующей степени” только в тех позициях двоичного числа, в которых находятся единицы. Степень же, в которую нужно возводить число 2, равна номеру позиции.

Арифметические операции в любой позиционной системе счисления также имеют общую логику.

Таблица 4.

 

1		“Круглые” числа в двоичной СС
&101	= 5(10)	&1	= 20	= 1
+        1		&10	= 21	= 2
&110	= 6(10)	&100	= 22	= 4
+        1		&1000	= 23	= 8
&111	= 7(10)	&10000	= 24	= 16

 

 

Каждый разряд двоичного числа имеет информационную емкость 1 бит. На основании одного двоичного разряда можно закодировать только два десятичных числа — &0=0₍₁₀₎, &1=1₍₁₀₎, на основании двух двоичных разрядов можно закодировать уже четыре десятичных числа – &00=0₍₁₀₎, &01=1₍₁₀₎ , &10=2₍₁₀₎, &11=3₍₁₀₎ , тремя двоичными разрядами можно представить восемь десятичных чисел  и т.д. в соответствии с формулой Хартли (2).

Таблица 5.

 

	20	десятичное		22	21	20	десятичное
	1	1		1	1	1	7
	0	0		1	1	0	6
				1	0	1	5
21	20	десятичное		1	0	0	4
1	1	3		0	1	1	3
1	0	2		0	1	0	2
0	1	1		0	0	1	1
0	0	0		0	0	0	0

 

Мы видим, что добавление каждого следующего разряда вдвое увеличивает количество двоичных комбинаций. Графически это может быть представлено так:

Рис. 15. Каждый следующий разряд двоичного числа удваивает количество возможных комбинаций из нулей и единиц.

 

 

Таблицу степеней числа 2 от 2⁰ до 2¹⁰ следует знать наизусть.

Таблица 6.

N	0	1	2	3	4	5	6	7	8	9	10
2N	1	2	4	8	16	32	64	128	256	512	1024

 

Открытие двоичного способа представления чисел приписывают китайскому императору Фо Ги, жизнь которого относится к 4-му тысячелетию до новой эры. Известный немецкий математик Лейбниц (1646-1716) в 1697 г. разработал правила двоичной арифметики. Он подчеркивал, что «вычисление с помощью двоек, то есть 0 и 1, в вознаграждение его длиннот, является для науки основным и порождает новые открытия, которые оказываются полезными впоследствии, даже в практике чисел, а особенно в геометрии: причиной чего служит то обстоятельство, что при сведении чисел к простейшим началам, каковы 0 и 1, всюду выявляется чудесный порядок».

Блестящие предсказания Лейбница сбылись только через 2,5 столетия, когда именно двоичная система счисления нашла применение в качестве универсального способа кодирования информации в компьютерах.

<<Назад  |  Содержание  |  Далее>>

Общие сведения о системах счисления. Двоичная система счисления

В современной жизни человек постоянно сталкивается с числами. К примерам можно отнести номера телефонов, цены в магазинах, адреса проживания и много другое.

На протяжение долгого времени у каждого народа формировалось своё написание чисел, с помощью которых они писали и считали. Но принципы записи чисел были совершенно другими, не такими, как сейчас.

В наше время для записи числа человек использует десятичную систему счисления.

На этом уроке мы с вами узнаем, что такое система счисления, какие существуют разновидности систем счисления, а также подробно остановимся на двоичной системе счисления.

Итак, система счисления – это знаковая система, в которой приняты определённые правила записи чисел.

Цифры – это знаки, с помощью которых записываются числа.

Алфавит системы счисления – это совокупность цифр.

В любой системе счисления цифры служат для обозначения чисел, которые называются узловыми.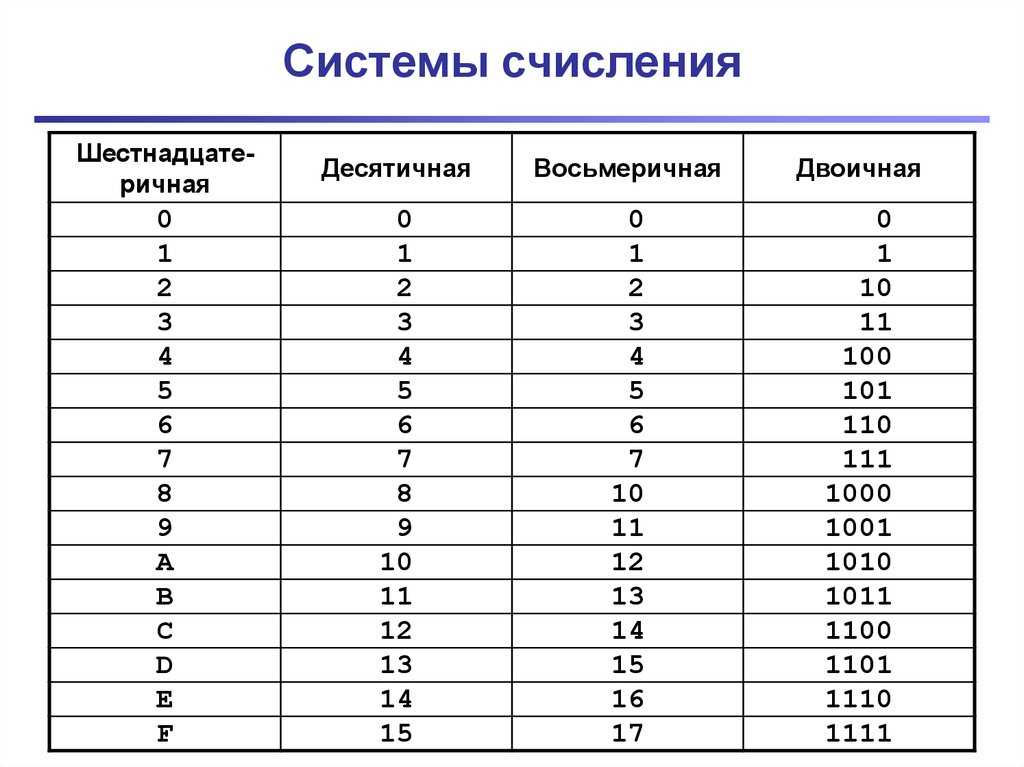

Остальные числа, которые называются алгоритмическими, получаются в результате каких-либо операций из узловых чисел.

Давайте разберёмся на примере.

Рассмотрим вавилонскую систему счисления. В ней узловыми являлись числа один, десять и шестьдесят.

Чтобы досчитать до девяти нужно было поставить девять единичек.

Например, число пятнадцать будет состоять из десяти и пяти единичек.

Число двадцать будет состоять из двух десяток и так далее.

А теперь перейдём к видам систем счисления. Системы счисления различаются выбором узловых чисел и способами образования алгоритмических чисел. Можно выделить унарную, непозиционные и позиционные системы счисления.

Унарная система счисления – это самая древняя и простейшая система счисления. В качестве единственной цифры в ней используется единица.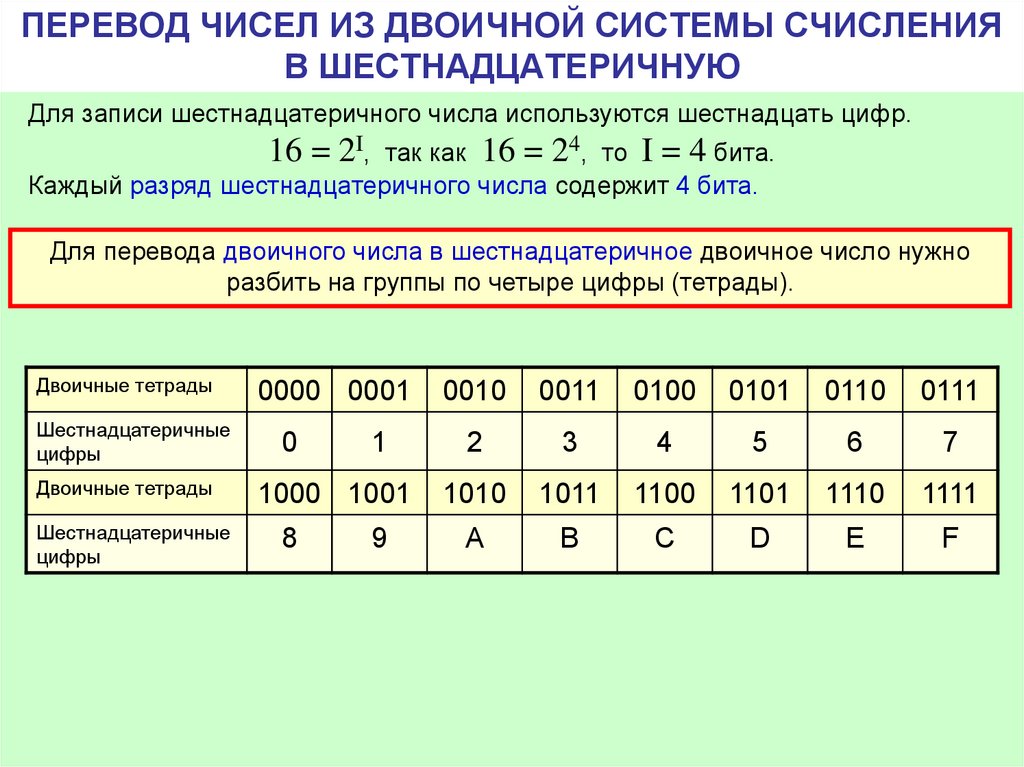 Она может быть изображена в виде чёрточки, камушка, палочки и так далее.

Длина записи числа при таком кодировании прямо связана с его величиной. Эта система счисления используется для обучения детей счёту, при подсчёте голосов на выборах в маленьких группах, в домино при подсчёте очков.

Такую систему счисления использовал Робинзон Крузо в виде зарубок на дереве для ведения календаря на необитаемом острове.

Переходим к непозиционным системам счисления.

Непозиционная система счисления – это система счисления, в которой количественный эквивалент (количество значений) цифры в числе не зависит от её положения в записи числа.

То есть можно сказать, что каждая цифра имеет своё значение, и от перестановки местами таких цифр значение числа не меняется.

В большинстве таких систем числа образуются путём сложения узловых чисел.

К примерам таких систем относится египетская система.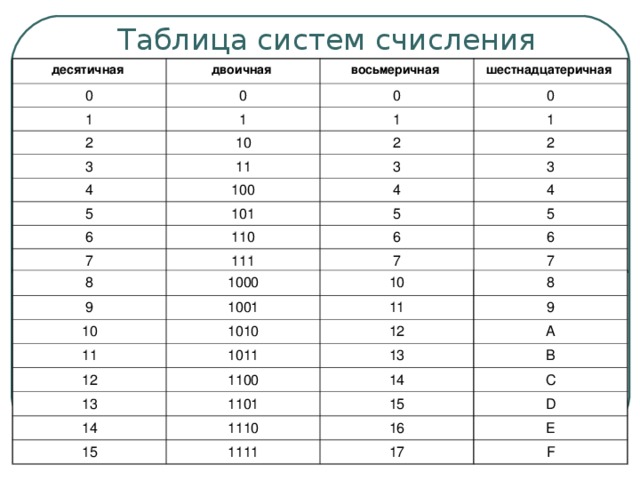 Рассмотрим её.

Вам предоставлена таблица с символами и с их значениями. В этой системе счисления числа, которые не являлись степенью десяти, записывались путём повторения этих цифр. Каждая цифра могла повторяться от одного до девяти раз. Например, число две тысячи триста пятьдесят шесть будет выглядеть следующим образом.

Определённого порядка в записи числа нет. Числа могли записываться слева направо или справа налево и даже вертикально.

Например, две следующие иероглифические записи обозначают одно и то же число – двенадцать.

Римская система счисления также относится к непозиционным. Рассмотрим таблицу с обозначениями чисел.

В этой системе числа получаются путём сложения и вычитания узловых чисел.

Для подсчёта следует придерживаться определённого правила: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитает его.

Позиционная система счисления – это система счисления, в которой количественный эквивалент цифры зависит от её положения (позиции) в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.

То есть, можно сказать, что один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места, где он расположен.

К примеру позиционной системы счисления относится десятичная, которой мы привыкли пользоваться в повседневной жизни.

Десятичная система счисления – это позиционная система по целочисленному основанию десять. Она является одной из наиболее распространённых систем. В ней используются цифры от 0 до 9. Эти цифры называются арабскими.

Есть предположение, что основание системы, число 10 связано с количеством пальцев на руках у человека.

Алгоритмические числа образуются в ней следующим образом: значения цифр умножаются на «веса» соответствующих разрядов, и все полученные значения складываются. Мы с вами знаем следующие виды разрядов: единицы, десятки, сотни и так далее. Число сто двадцать три получается следующим образом:

Основанием позиционной системы счисления может служить любое натуральное число q > 1. Алфавитом позиционной системы счисления с основанием q служат числа 0, 1 … q – 1, каждое из которых может быть записано с помощью одного уникального символа. Младшей цифрой всегда будет являться 0.

Разберёмся на примере. Нам дана знакомая всем десятичная система счисления. То есть q=10. Алфавитом этой системы будут цифры от 0 до q – 1. То есть q – 1 = 9. Получим следующие цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Если сосчитать их, то получится 10.

При кодировании информации в компьютере используется двоичная система. То есть q=2. Цифры, которые входят в эту систему будут начинаться с 0 и до q – 1.

2 – 1 = 1. Соответственно в двоичной системе счисления будет использоваться алфавит из двух цифр 0 и 1.

В позиционной системе счисления с основанием q любое число можно представить в виде:

А – это само число.

q – основание системы счисления.

a_i – цифры, принадлежащие алфавиту данной системы счисления.

n – количество целых разрядов числа.

m – количество дробных разрядов числа.

qⁱ – «вес» итого разряда.

Наша формула записана в развёрнутом виде. Свёрнутая форма записи числа – это представление числа в следующем виде:

Разберёмся на примере. Итак, перед нами представлено число 1 675,21 в свёрнутой форме.

Записано это число в десятичной системе счисления. Давайте распишем это число и посмотрим, как оно выглядит в развёрнутой форме.

Поставим знак равно. Из условия понятно, что q=10. Остаётся определиться с n. Для этого расставим над цифрами числа, которые будут обозначать степень числа q в развёрнутой записи числа.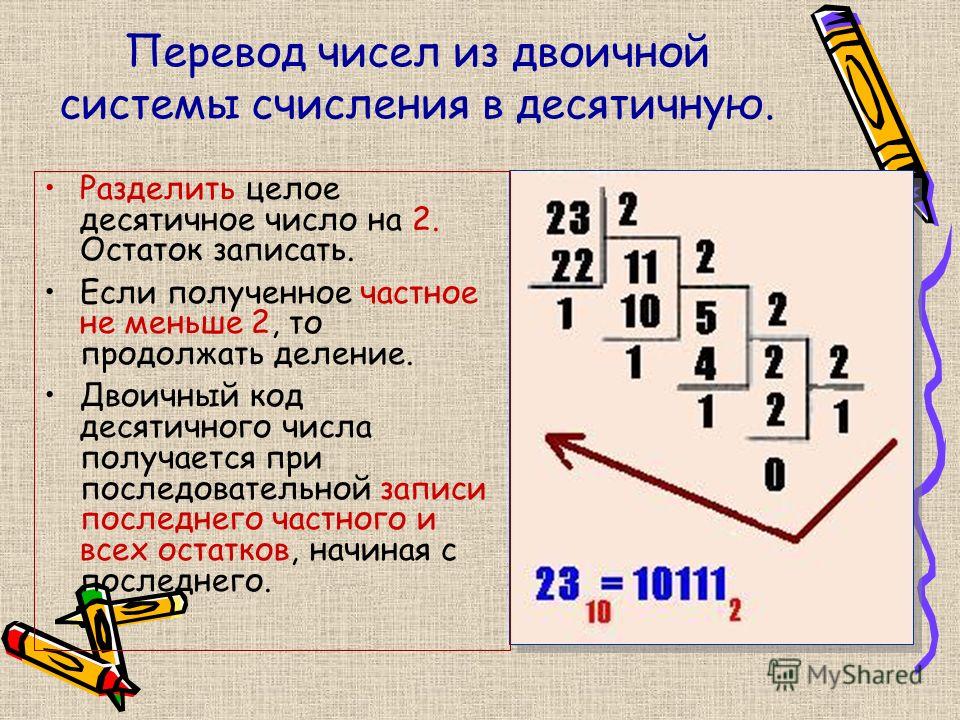 Обратимся к математике. Запишем степени числа десять.

Из этой записи видно, что разряд единиц соответствует нулевой степени числа десять, разряд десятков соответствует первой степени числа десять и так далее. Запишем эти степени над цифрами нашего числа.

Над цифрами, которые располагаются после запятой, поставим числа минус один и минус два.

Теперь мы можем записать развёрнутую форму нашего числа.

a_{n– 1} – это первая цифра нашего числа, то есть 1. Она умножается на q^{n– 1}, то есть на 10³. Ставим плюс. a_{n– 2} – это вторая цифра нашего числа, то есть 6. Умножаем её на 10². Аналогичным образом распишем всё число.

Нам не привычно видеть его таким, но это – развёрнутая форма записи числа 1 675,21.

А сейчас давайте перейдём к двоичной системе счисления. Двоичная система счисления – это позиционная система счисления с основанием два. Как мы уже знаем, для записи чисел в этой системе используются только две цифры: 0 и 1. Например, число 16 в двоичной системе счисления будет выглядеть следующим образом: .

Для обозначения системы счисления, в которой представляется число, используется нижний индекс, указывающий на основание системы.

Так мы можем сразу видеть, что число 16 записано в десятичной системе, а второе – в двоичной.

Формула развёрнутой формы записи числа для целых двоичных чисел будет выглядеть следующим образом:

Из этой формулы можно вывести правило перевода натуральных двоичных чисел в десятичную систему счисления: необходимо вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.

Давайте проверим и переведём следующее число  из двоичной системы счисления в десятичную. Для начала над всеми цифрами напишем степени для q начиная с 0 справа налево.

Ставим равно. Пишем первую 1 и умножаем её на 2³, прибавляем 0, умноженный на 2², затем прибавим 1, умноженную на 2¹ и 1, умноженную на 2⁰.

Ставим равно и посчитаем всё это.

1 · 2³ = 8.

Ставим плюс.

0 · 2² = 0.

1 · 2¹ = 2.

1 · 2⁰ = 1.

Посчитав это всё получим число одиннадцать в десятичной системе счисления.

Для закрепления давайте переведём ещё одно число 10001₂ из двоичной в десятичную систему счисления. Но перед этим запишем чему равны степени числа два.

Итак, снова проставляем степени начиная с нуля справа налево.

Ставим равно. После равно слаживаем цифры, умноженные на два в соответствующей степени.

После подсчёта получим число семнадцать.

Для перевода чисел из десятичной системы счисления в двоичную, нужно делить число на 2. Если полученное частное больше нуля, то его снова необходимо разделить на два и т. д., пока частное не станет равным 0. В результате нужно записать в одну строку, справа налево все остатки, начиная с последнего.

Давайте посмотрим на примерах, как это делается. Переведём число 25 из десятичной системы счисления в двоичную. Будем делить в столбик. Итак, делим 25 на 2. Получится 12, а в остатке 1.

Теперь число 12 делим на 2. Получается 6, а в остатке 0.

Делим число 6 на 2, получаем 3, а в остатке 0.

Далее разделим 3 на 2, получим 1 и 1 в остатке.

Делим 1 на 2, получим 0 и 1 в остатке.

Больше число не будет делиться на цело. А теперь обведём все наши остатки.

Они нам понадобятся для записи числа в двоичной системе счисления. Записывать их будем справа налево.

Первая идёт 1. Запишем её.

25₁₀ = 1

Затем идёт ещё одна 1 из остатка, также её запишем.

25₁₀ = 11

Аналогично перепишем все наши остатки в одну строку.

25₁₀ = 11001₂

Мы перевели с вами число двадцать пять из десятичной системы счисления в двоичную.

Если число большое, то будет более удобно представить его в виде таблицы.

Давайте посмотрим, как это можно сделать. Переведём число 142 в двоичную систему счисления. Наша таблица будет содержать две строки. В первой будем записывать число, которое получается при делении на 2, а во второй остаток. Итак, в первой строке первого столбца запишем число 142.

При делении этого числа на 2 получим 71 и 0 в остатке. Число 71 запишем во второй столбец первой строки, а остаток в первый столбец второй строки.

Делим 71 на 2. Получим 35 и 1 в остатке. 35 запишем в третью ячейку первой строки, а остаток 1 во вторую ячейку второй строки.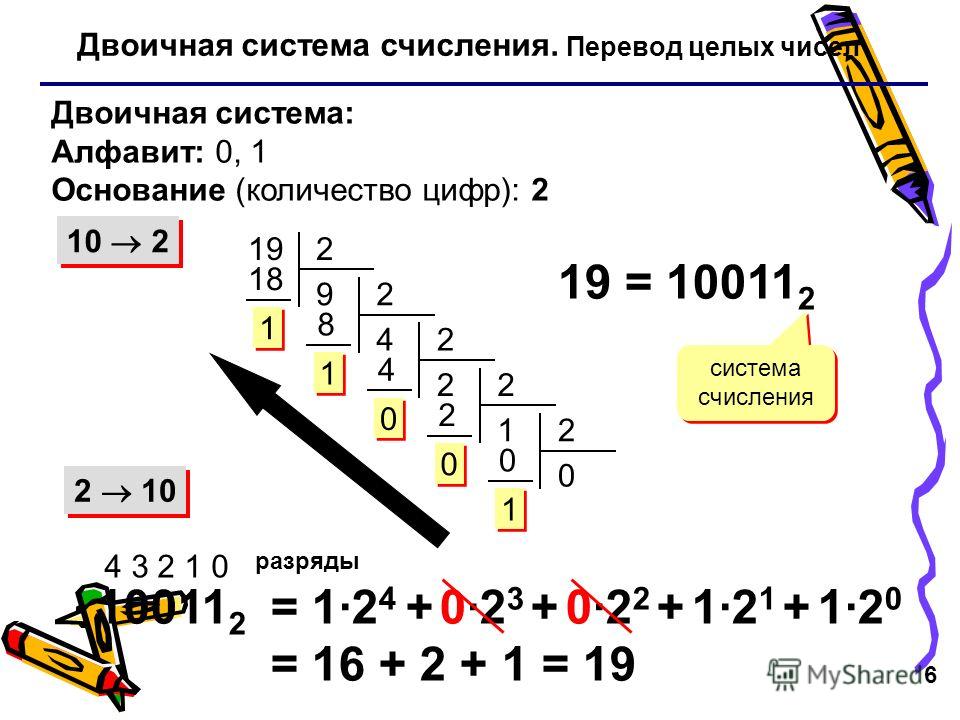

35 : 2 = 17 и 1 в остатке. 17 запишем в следующую ячейку после 35, а остаток – под число 35.

Далее 17 делим на 2 получим 8 и 1 в остатке. Запишем наши числа в соответствующие ячейки.

8 :2 = 4 и 0 остаток. Заполним таблицу.

4 :2 = 2 и 0 в остатке. Также запишем их.

2 :2 = 1 и 0 в остатке. Пишем 1 в следующую ячейку после 2, а под 2 запишем 0.

Делим 1 на 2 получим 0 и 1 в остатке. Не будем наш 0 записывать в таблицу. Внесём в неё только остаток от деления – 1 в соответствующую ячейку.

Теперь нам осталось записать наше число в строку. Для этого перепишем все числа, которые находятся во второй строке, справа налево и получим следующее:

141₁₀ = 10001110₂

Мы перевели число 142 из десятичной системы счисления в двоичную.

Пришла пора подвести итоги урока.

Сегодня мы узнали, что такое система счисления, познакомились с унарной, непозиционными и позиционными системами счисления. Также мы научились переводить из двоичной системы счисления в десятичную и наоборот.

Почему в компьютерах используются двоичные числа

Все, кто изучает компьютеры, и большинство людей, которые используют компьютеры более чем случайно известно, что современные компьютеры используют внутри себя двоичные числа. Когда мы используем слово бит, , мы используем сокращение для bi nary digi t , что-то, что может содержать ноль или единицу и ничего больше. Организуем биты в группы из восьми, называемых байтами или октетами, и мы организуем октеты в слова, часто 32 или 64 бита. Все это знают. Но почему? Почему компьютеры используют двоичные числа? Почему бы ученым и инженерам, которые проектировать современные компьютеры проектировать их для использования знакомых десятичных чисел, которые мы изучили в начальной школе? Таким образом, нам не пришлось бы изучать новую систему счисления, и мы могли бы иметь дело с величинами в знакомых нам степенях десяти вместо степеней двойки.

Оказывается, существуют веские причины, по которым компьютеры используют двоичные числа, и причины легко понять; мы можем свести причины к двум важным фактам. Чтобы понять, почему в компьютерах используются двоичные числа, нам нужно совершить небольшое путешествие по производственным процессам. и электротехника.

Производство, электроника и допуски

Нет двух абсолютно одинаковых изготовленных деталей, но небольшие различия не ухудшают полезность конечного продукта. Для механических частей мы могли бы сказать, что разница десятитысячных дюйма, плюс-минус, от номинального, или расчетного значения достаточно. В зависимости от детали, величины отклонения или допуск , может быть больше или меньше, но всегда есть понятие достаточно хорошо. Кроме то, что находится в пределах допуска, достаточно хорошо; тот, который не является дефектным.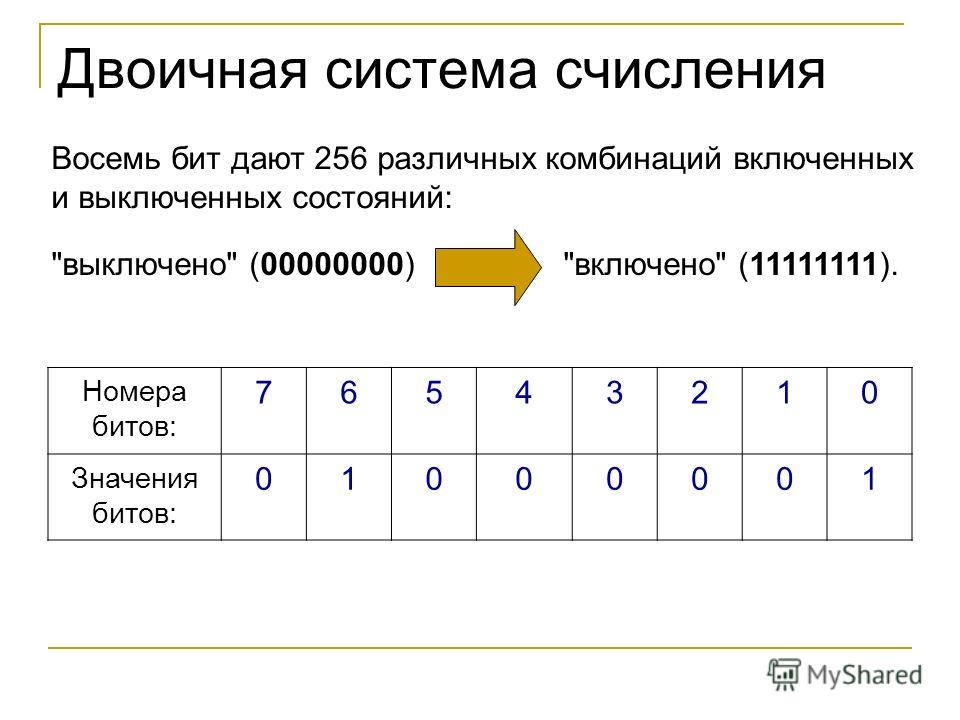

Подобно механическим деталям, электрические и электронные компоненты не всегда совершенны, когда они сделаны. Имеют производственный допуск. Часто это ±10%. Итак, 100 Ом резистор может иметь фактическое сопротивление от 90 Ом до 110 Ом и все еще быть в порядке достаточно, потому что это находится в пределах этого допуска 10%. Возможно изготовление электронных деталей с более жесткими допусками 5% или даже 1%. Более жесткие допуски делают детали более дорогими и, для многих приложений, на самом деле не нужны. Инженеры берутся за производство допуски, учитываемые при проектировании схем.

Дополнительная сложность заключается в том, что электронные компоненты меняются со временем. Компонент которое было в пределах ±10%, может стать на 15 или 20% от его номинального значения через несколько лет эксплуатации. Инженеры это тоже учитывают, поэтому электронные устройства имеют проектный срок службы.

Компьютеры с цифрами, электронными компонентами и десятичными числами

Современные компьютеры работают с дискретными значениями — цифрами — вместо использования электрических ценности как аналоги физических величин. Вот почему они называются цифровых компьютеров. Чтобы спроектировать десятичный цифровой компьютер, нам нужно десять электрических величин, чтобы представляют цифры от нуля до девяти. Гипотетически мы могли бы решить использовать сигнал ноль вольт для представления цифры ноль, один вольт для представления цифры один и и так до девяти вольт, чтобы представить цифру девять.

Звучит нормально, но производственные допуски делают это очень сложным на практике. Принимая с учетом допусков, мы бы разработали схемы так, чтобы, если цифра семь представлена на семь вольт, 6,7 вольта и 7,2 вольта также будут интерпретироваться как цифра семь.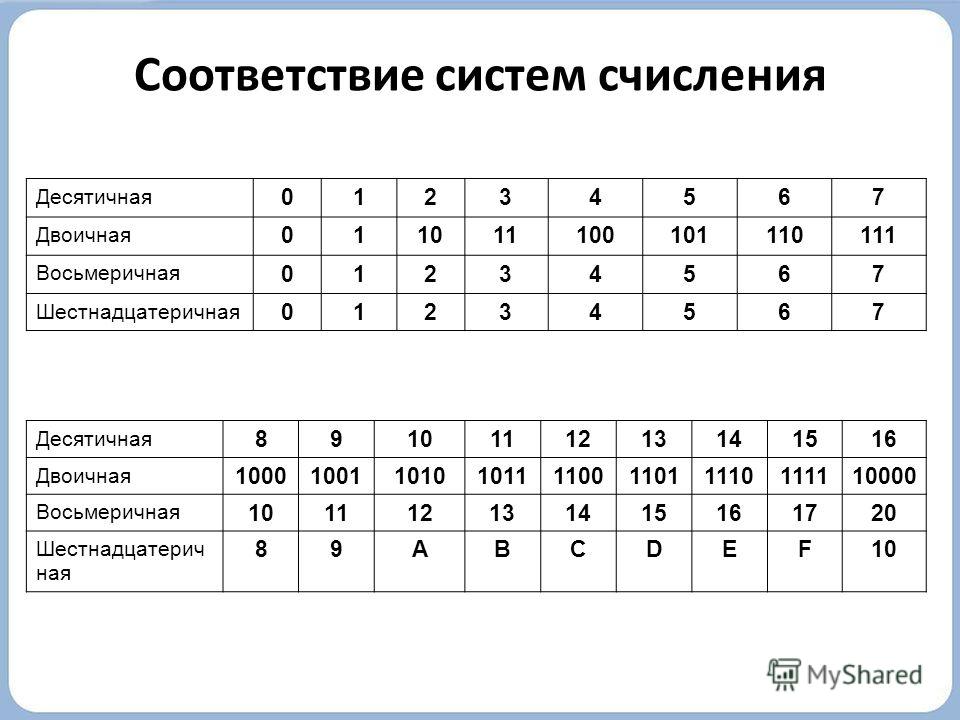 Если 6,7 вольта — это семерка, то 7,7 вольта надо интерпретировать как восемь, но это только 10% от проектной или номинальной стоимости. Отклонение в 10% приводит к необнаруживаемому ошибка! Но производственные допуски могут означать, что разница компонентов в 10% должны быть допущены конструкцией. Мы в ловушке; наш дизайн не может работать на практике при серийном производстве. Чрезвычайно сложно спроектировать и построить электронные устройства, которые надежно различают десять дискретных значений.

Бинарные электронные устройства

Хотя в электронике сложно выделить десять дискретных состояний, легко различить два. Один тип цифровой логической схемы использует напряжение нуля для представления цифры ноль и пяти вольт для представления цифры один. По сути, мы различаем между выключенным и включенным.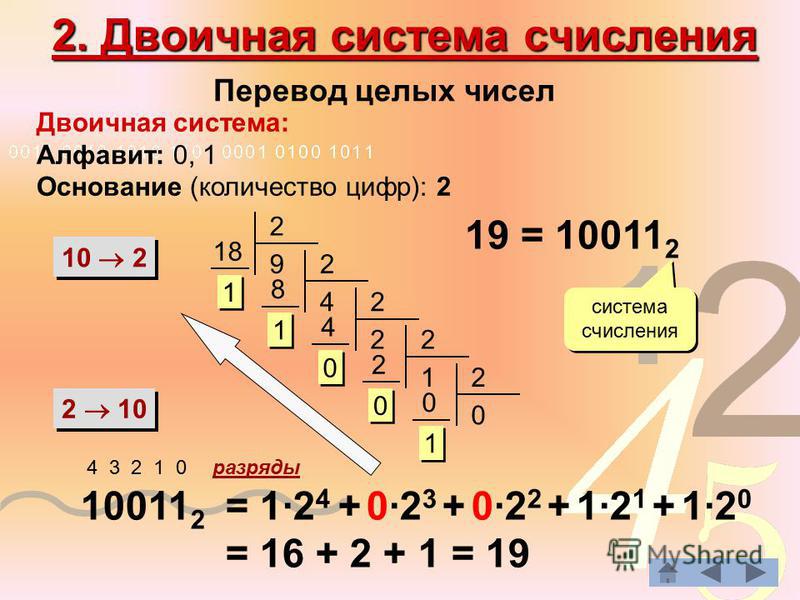 Все, что меньше 2,5 вольта, является нуль; все, что больше, является единицей. Такая схема имеет допуск около 50%. это относительно легко построить схемы, которые надежно различают два значения. первый из наших двух фактов таков: двоичные электронные схемы надежный .

Десятичные компьютеры с двоичными схемами

Если вы читали историю вычислительной техники, то знаете, что ENIAC, электронный числовой интегратор и компьютер, был первой крупной электронной вычислительной машиной, построенной во время Второй мировой войны. для расчета таблиц артиллерийского огня. Вы также можете знать, что ENIAC был десятичным компьютером; он работал с цифрами от нуля до девяти.

Инженеры 1940-е знали сложность представления десяти дискретных значений и надежность двоичных схем, поэтому они разработали ENIAC с использованием двоичных электронных схемы.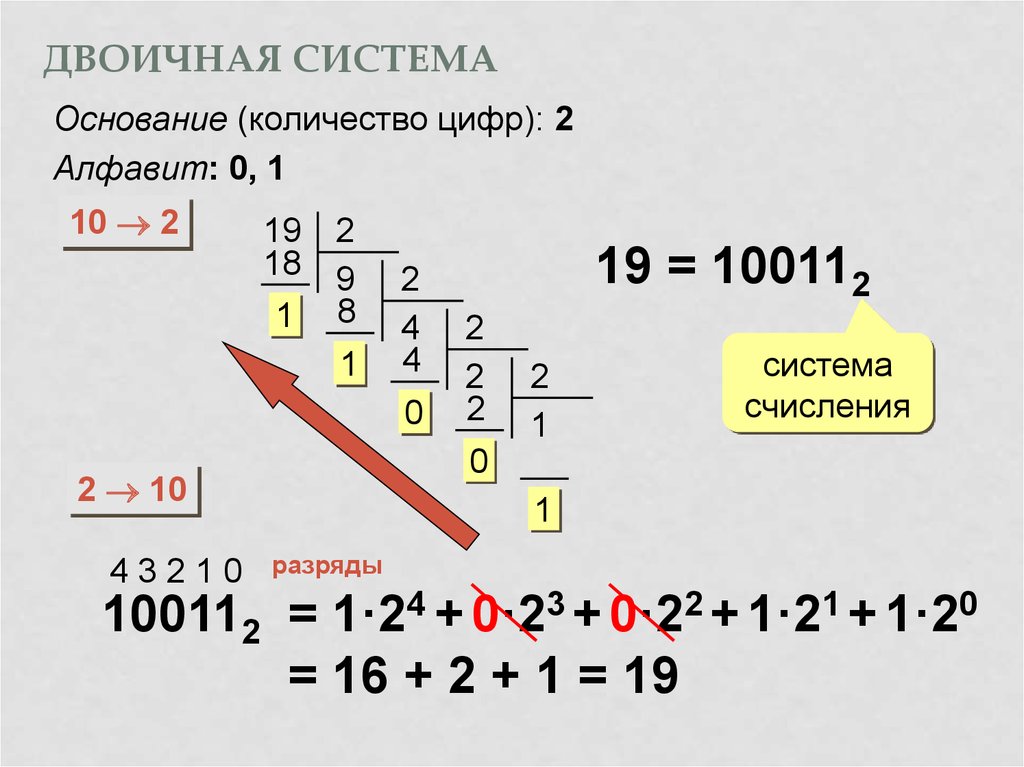 Каждая десятичная цифра требовала десяти двоичных знаков, расположенных так, чтобы один был включен, а остальные девять выключены. Схема, которая была включена, указывала на представленную цифру. Для десятизначного числа требовалось более 100 электронных ламп, сотня которых представляла собой цифры и некоторые другие для управления операциями и соединения цепей вместе.

От двоичных цепей к двоичным числам

Джон фон Нейман консультировал по созданию ENIAC и внес большой вклад в дизайн последующего компьютера, EDVAC. В ходе этого процесса фон Нейман наблюдал что десять устройств, необходимых для одной десятичной цифры, если используется как десятибитное двоичное число, может представлять значения от нуля до 1023, а не только от нуля до девяти. Использование двоичные числа увеличили выразительную силу двоичных схем.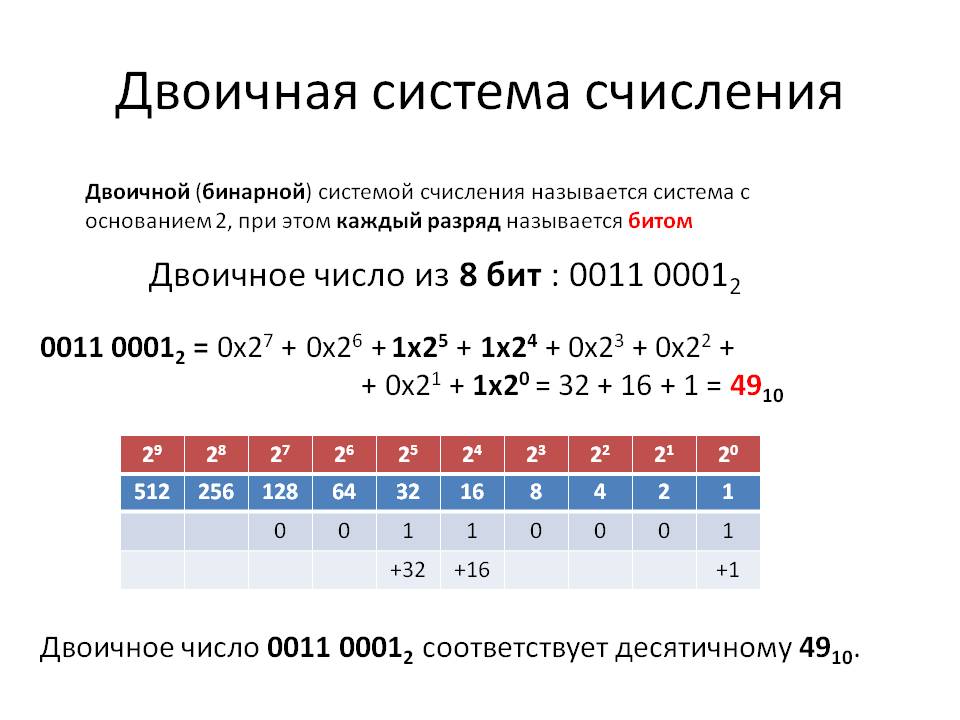 Это может быть используется для снижения стоимости компьютера или для создания более мощного компьютера в такая же стоимость. Это наш второй факт: использование двоичных чисел максимизирует выразительную силу двоичных цепей.

Важно отметить, что фон Нейман не изобретал двоичные числа. Двоичный файл Система была известна математикам сотни лет. Готфрид Лейбниц написал статью о двоичных числах в 1679 году. Джордж Буль разработал алгебру двоичных чисел в 1850-х годах, а Клод Шеннон использовал двоичные числа для вычислений с телефонным коммутационным оборудованием в 1930-х годах. Вклад фон Неймана заключался в том, что он признал, что двоичные схемы компьютеров, необходимые для надежности, лучше всего использовать для представления двоичных чисел.

Два наших важных факта

• Двоичные схемы необходимы в компьютерах из соображений надежности.
• Использование двоичных чисел в компьютерах максимально увеличивает выразительную силу двоичного числа. схемы.

---

Copyright © 2018 by Bob Brown

Последнее обновление: 2020-01-09 10:14
Первоначально опубликовано: 18.04.2018

Все, что вам нужно знать о Binary | Брэндон Скеррит | Заметки по информатике

Фото Антуана Дотри на Unsplash

Система счисления — это система чисел, используемая для представления количества объектов. В англоязычном мире мы используем систему счисления, называемую основанием 10. У нас есть 10 чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, и когда мы хотим посчитать после 9, мы добавляем 1 и 0 вместе, чтобы сделать 10, а затем мы повторяем.

Но мы можем иметь столько чисел, сколько захотим, мы можем иметь от 0 до 8 или от 0 до 1, о чем мы и поговорим.

Двоичная система счисления, в которой есть только 2 числа, 0 и 1. Мы можем посчитать любое число в двоичной системе счисления. Чтобы сделать двоичные числа более читабельными, вот краткий перевод двоичных чисел в десятичные (десятичные) числа.

0 равно 0, а 1 равно 1. Чтобы получить число 2, пишем «10», потому что физически невозможно написать что-либо > 1, приходится начинать заново в новом столбце. Очень похоже на то, как мы не можем записать 11 как одно число (если только вы не считаете в базовых системах более 10).

Двоичный код часто используется в логике, 0 представляет False или Off, а 1 представляет True или On.

Относительно легко преобразовать двоичное число в десятичное. Есть два популярных метода.

Запишите десятичное число и постоянно делите на 2, чтобы получить результат и остаток от «1» или «0», пока окончательный результат не будет равен 0.

Это мой любимый метод, но для этого вам нужно знать свои степени двойки.

Степени двойки очень важны в компьютерных науках.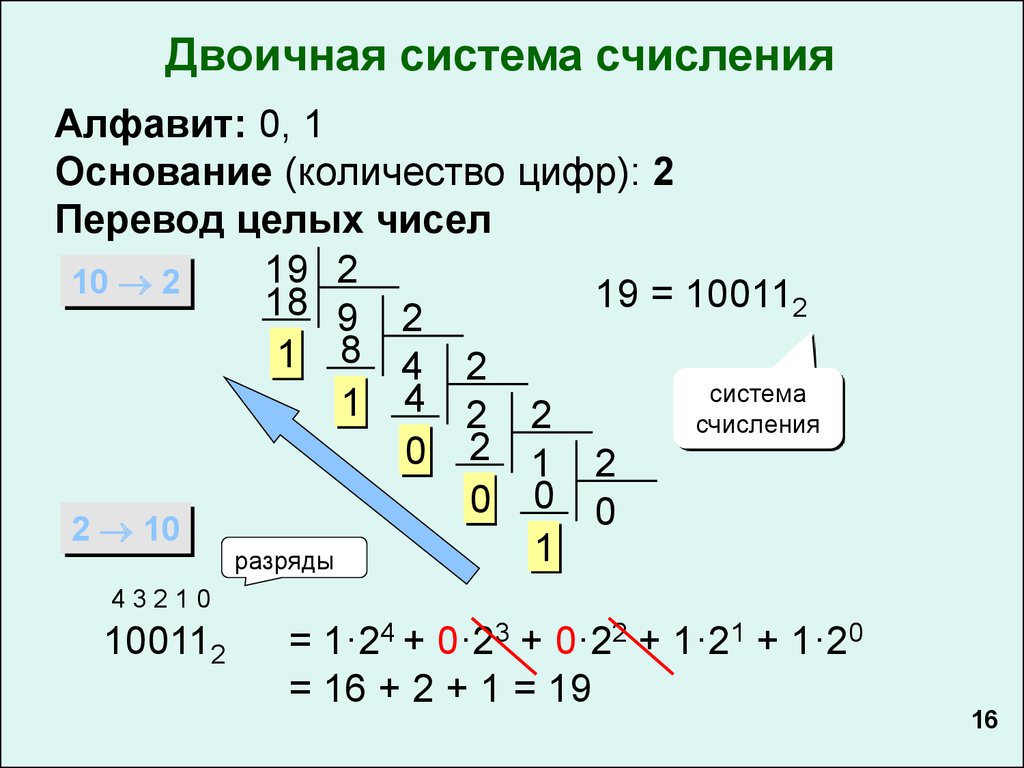 Двоичный код представлен в виде 2 чисел, поэтому, если у вас есть 3 цепи, у вас будет 2³ числа, от 0 до 7.

Степени двойки:

2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192.

И чтобы получить нечетное число, мы добавляем 1 к list, чтобы список чисел, которые нам нужно знать, стал следующим: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192.

Хорошо, скажем, мы хотим представить 15 как двоичное число. Сначала нам нужно разделить 15, чтобы его можно было составить из степеней 2 + числа 1. Ближайшая степень двойки, которая меньше 15, равна 8, поэтому мы будем использовать ее. 8 + 4 равно 12. 8 + 4 + 2 равно 14, так что мы почти у цели! Теперь мы просто добавим 1,15, представленное как степень двойки, равна 8 + 4 + 2 + 1, 9.0011

Теперь, когда мы это знаем, мы можем просто преобразовать это.

Двоичный график в степени двойки выглядит следующим образом.

Если число использует 8, поставьте 1 в двоичном поле под ним, чтобы обозначить, что оно использует 8. Хотя я предпочитаю использовать этот метод:

И тогда обычно нам нужно инвертировать двоичные числа, но в этом случае, потому что это всего лишь 1, нам не нужно реверсировать. Если мы не поменяем их местами, то получим неправильное двоичное число, поскольку двоичное число читается с наивысшим порядком слева, а не с низшим. Как и в «10», 1 на целую позицию выше, чем 0; то же самое относится и к бинарному.

Вы можете преобразовать двоичное число в десятичное обратным методом.

Давайте сначала рассмотрим сложение в десятичном виде.

 23 + 11 

Сначала мы прибавляем 3 + 1, что равно 4. Затем мы прибавляем 2 + 1, что равно 3. Таким образом, ответ равен 34. Прибавляем справа налево.

Двоичное сложение работает так же.

Мы начнем с добавления одного бита (двоичной цифры).

 0 + 0 = 1 

и

 0 + 1 = 1 

и

 1 + 1 = 10 

1 + 1 переносит нас в следующий столбец.

Попробуйте сами:

 111 + 110 = ??? 

Кроме того, практически все операторы работают так же, как и с двоичными, и с десятичными числами.

Мы можем представить двоичное число, применив к нему «знак».

В двоичном формате числа могут быть 4-битными, 8-битными, 16-битными, 32-битными и так далее. Если у нас есть 8-битное число, оно будет состоять из 8 цифр.

Итак, допустим, у нас есть число 1 в 8-битном двоичном коде, которое будет представлено как: 00000001 чтобы превратить это в отрицательное, мы добавляем 1 впереди него 10000001

Хотя это иногда вызывает проблемы. Учитывая число 0 в 8-битном двоичном формате: 00000000, мы можем сделать его отрицательным, добавив 1 перед ним. 10000000 Но -0, что это? Это ничто. Это невозможно. И вот откуда эта проблема.

Мы можем сделать двоичное число отрицательным, применив к нему дополнение до двух без необходимости подписывать его.

Дополнение до двух — очень простой алгоритм:

• инвертировать все цифры так, чтобы 0 стал 1, а 1 стал 0
• добавьте +1 к номеру

и это сделает его отрицательным!

Таким образом, учитывая число 15, которое равно 1111, в 8-битном двоичном формате оно будет: 00001111 Итак, чтобы сделать это отрицательным, мы инвертируем все цифры: 11110000, затем мы добавляем 1 к концу 11110001, и теперь это представляет -15 ! Как креативно и круто!

Допустим, у нас есть 2 числа, -3 и -5. В двоичном формате это: 11, 101, и мы хотим сложить их вместе.

Но на этот раз мы можем игнорировать любые переносы, которые идут не в конце.

Итак, мы используем наибольшую степень двойки, которая может поместить в нее и 5, и 3, то есть 8. Но на этот раз мы делаем ее отрицательной.

Теперь просто добавляем их. 1 + 1 — это 0, перенос 1, следующая строка — 1 + 1, что равно 0, поэтому перенос, следующая строка — 1 + 1, что равно 0, поэтому перенос, следующая строка — 1 + 1 + 1, что равно 1, перенос 1 , но на этот раз мы можем отбросить перенос, и у нас останется 1000 в качестве ответа.

Большое спасибо Джахану Улхаке, студенту компьютерных наук Ливерпульского университета, за то, что он показал мне этот метод.

Считать это сложением, но отрицать второй операнд. Таким образом, 4–3 — это просто 4 + (-3)

, что равно

 0100 + 1101 = 001, поскольку мы снова игнорируем перенос. 

Переполнение — это когда в двоичном значении хранится больше битов, чем оно может вместить.