Двоичная система счисления
Главная / Ассемблер / Для чайников / Системы счисления /
Чисто технически было бы очень сложно сделать компьютер, который бы «понимал» десятичные числа.
А вот сделать компьютер, который понимает двоичные числа достаточно легко. Двоичное число
оперирует только двумя цифрами – 0 и 1. Несложно сопоставить с этими цифрами два
состояния – вЫключено и включено (или нет напряжения – есть напряжение).
Процессор – это микросхема с множеством выводов. Если принять, что отсутствие напряжения
на выводе – это 0 (ноль), а наличие напряжения на выводе – это 1 (единица), то каждый вывод
может работать с одной двоичной цифрой. Сейчас мы говорим о процессоре очень упрощённо,
потому что мы изучаем не процессоры, а системы исчисления. Об устройстве процессора вы можете
почитать здесь: Структура процессора.
Конечно, это касается не только процессоров, но и других составляющих компьютера, например, шины данных или шины адреса. И когда мы говорим, например, о разрядности шины данных, мы имеем ввиду количество выводов на шине данных, по которым передаются данные, то есть о количестве двоичных цифр в числе, которое может быть передано по шине данных за один раз. Но о разрядности чуть позже.
Итак, процессор (и компьютер в целом) использует двоичную систему, которая оперирует всего двумя цифрами: 0 и 1. И поэтому основание двоичной системы равно 2. Аналогично, основание десятичной системы равно 10, так как там используются 10 цифр.
Каждая цифра в двоичном числе называется бит (или разряд).
Четыре бита – это полубайт (или тетрада), 8 бит – байт,
16 бит – слово, 32 бита – двойное слово.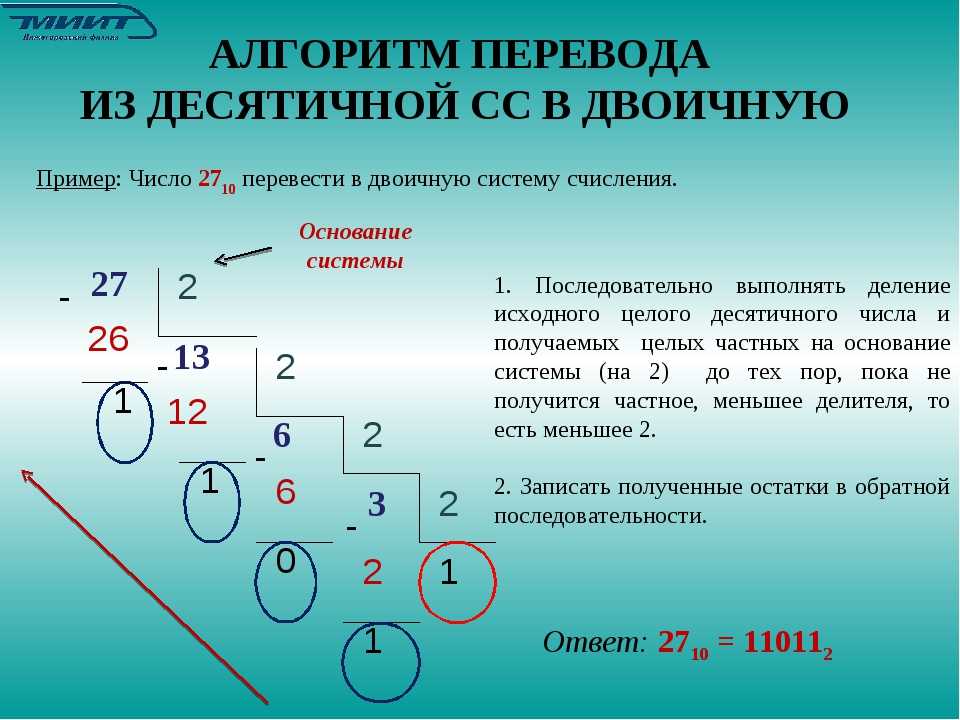
Запомните эти термины,
потому что в программировании они используются очень часто. Возможно, вам уже приходилось
слышать фразы типа слово данных или байт данных. Теперь,
я надеюсь, вы понимаете, что это такое.
Отсчёт битов в числе начинается с нуля и справа. То есть в двоичном числе самый младший бит (нулевой бит) является крайним справа. Слева находится старший бит. Например, в слове старший бит – это 15-й бит, а в байте – 7-й. В конец двоичного числа принято добавлять букву b. Таким образом вы (и ассемблер) будете знать, что это двоичное число. Например,
101 – это десятичное число 101b – это двоичное число, которое эквивалентно десятичному числу 5.
А теперь попробуем понять, как формируется двоичное число.
Ноль, он и в Африке ноль. Здесь вопросов нет.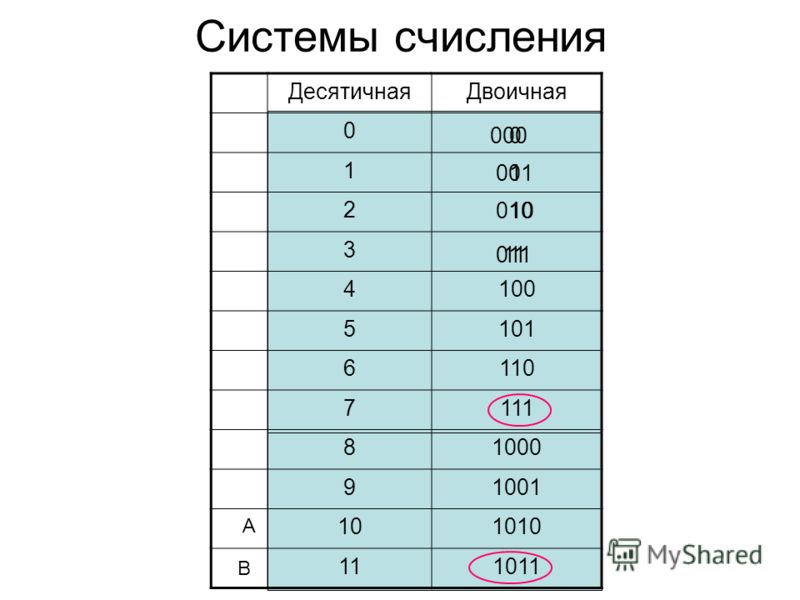
| Двоичное | Десятичное | Пояснения |
| 0000 | 0 | — |
| 0001 | 1 | В младший бит устанавливается 1. |
| 0010 | 2 | В следующий бит (бит 1) устанавливается 1, предыдущий бит (бит 0) очищается. |
| 0011 | 3 | В младший бит устанавливается 1. |
| 0100 | 4 | В следующий бит (бит 2) устанавливается 1, младшие биты (бит 0 и 1) очищаются. |
| 0101 | 5 | В младший бит устанавливается 1. |
| 0110 | 6 | Продолжаем в том же духе… |
| 0111 | 7 | … |
| 1000 | 8 | … |
| 1001 | 9 | … |
| 1010 | 10 | … |
| 1011 | 11 | … |
| 1100 | 12 | … |
| 1101 | 13 | . .. |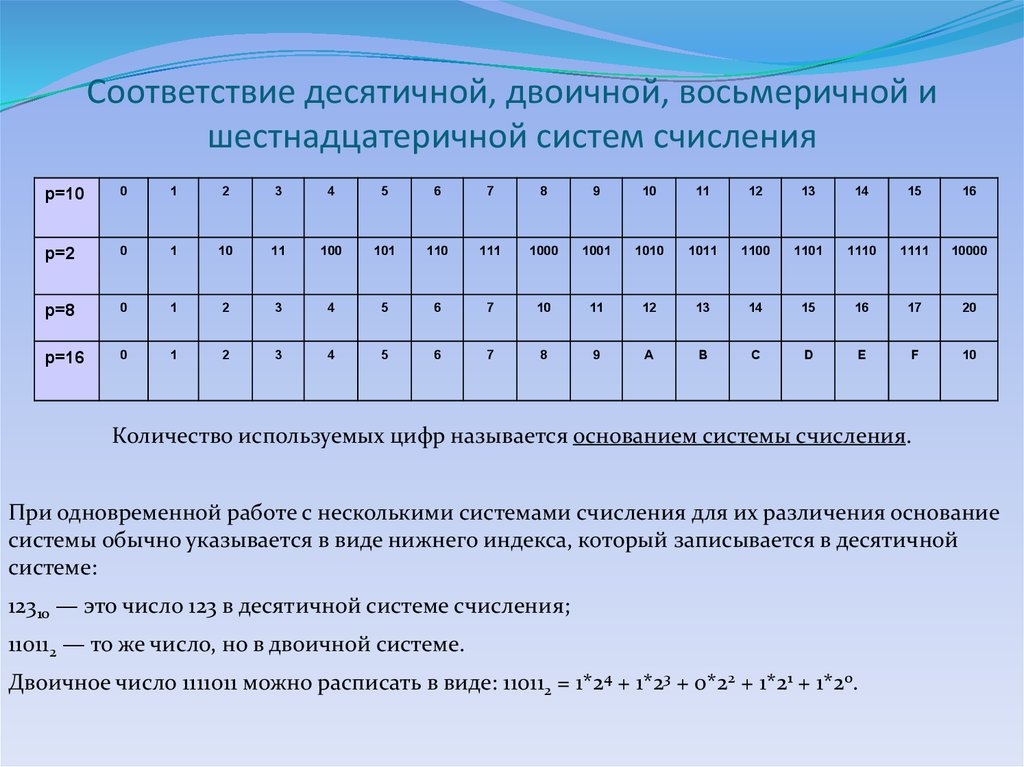
| 1110 | 14 | … |
| 1111 | 15 | … |
Итак, мы видим, что при формировании двоичных чисел разряды числа заполняются нулями и единицами в определённой последовательности:
Если младший равен нулю, то мы записываем туда единицу. Если в младшем бите единица, то мы переносим её в старший бит, а младший бит очищаем. Тот же принцип действует и в десятичной системе:
0…9 10 – очищаем младший разряд, а в старший добавляем 1
Всего для тетрады у нас получилось 16 комбинаций. То есть в тетраду можно записать 16 чисел от 0 до 15. Байт – это уже 256 комбинаций и числа от 0 до 255. Ну и так далее. На рис. 2.2 показано наглядно представление двоичного числа (двойное слово).
Рис.
Двоичная система счисления – таблица последовательности, примеры (8 класс, информатика)
4.7
Средняя оценка: 4.7
Всего получено оценок: 215.
4.7
Средняя оценка: 4.7
Всего получено оценок: 215.
Информация в компьютере обрабатывается в цифровом формате, в виде набора нулей и единиц, поэтому все числа переводятся в двоичный вид. Система счисления, в которой для обозначения чисел применяется всего два знака, называется двоичной. Метод представления чисел в двоичном формате изучается в курсе информатики 8 класса.
Двоичная система
Система счисления, которая в своем арсенале использует только две цифры, то есть имеющая основание два, называется двоичной или бинарной. В такой системе числа заменяются последовательностью нулей и единиц. Например, десятичное число 134 в двоичном формате выглядит как 10000110. Для того чтобы понять, как это работает, следует придерживаться правил перевода чисел из одной системы счисления в другую.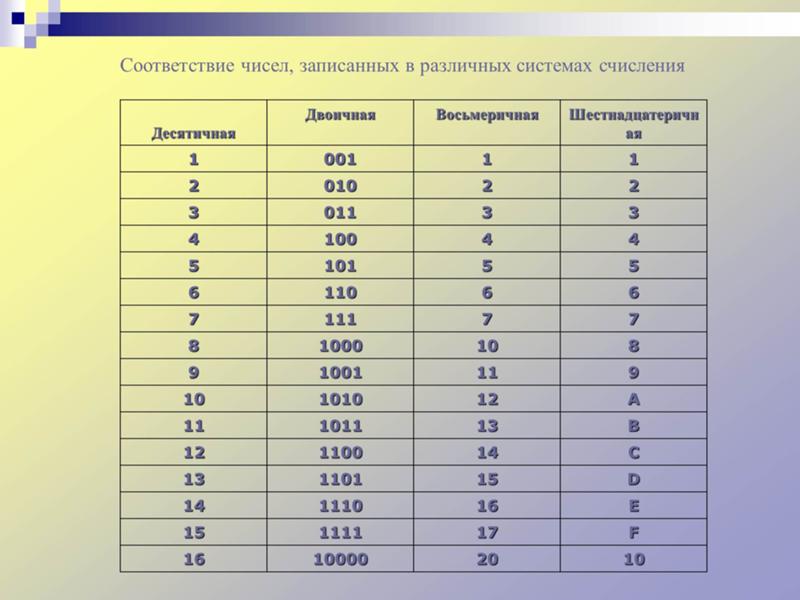
Перевод чисел из десятичной системы счисления в двоичную
Перевод целой части десятичного числа производится путем поочередного деления частного на основание двоичной системы, то есть на два. В остатке от деления останется либо ноль, либо единица. Эти остатки записываются, начиная с последнего частного в направлении слева направо. Это и будет двоичным представлением десятичного числа.
Рассмотрим примеры.
Для перевода десятичного числа 29 в двоичный формат:
Делят 29 на два, получают 14 и в остатке 1. Остаток следует запомнить.
Затем частное от деления, то есть число 14 снова делят на два, получено 7 и в остатке 0 (ноль).
Разделим 7 на два, получим частное 3 и остаток 1.
Три делят на два, получено в частном 1 и остаток 1.
Так как последнее частное 1 меньше основания системы счисления, то есть числа 2, то последовательное деление прекращают.
Затем записывают остатки, начиная с последнего частного, и получают последовательность чисел: 11101.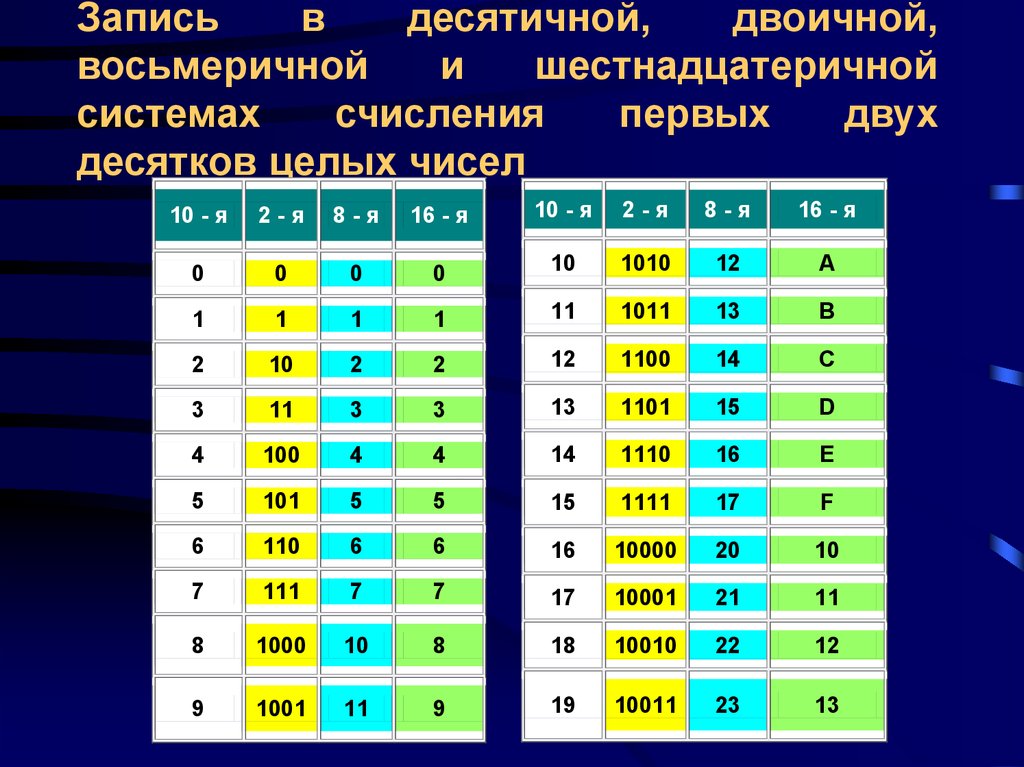
Еще один пример: перевод числа 37 в двоичный формат.
37 / 2 = 18 (1)
18 / 2 = 9 (0)
9 / 2 = 4 (1)
4 / 2 = 2 (0)
2 / 2 = 1 (0)
Получен результат: 100101.
Если десятичные числа расположить последовательно и сопоставить с их двоичными эквивалентами, то можно увидеть некоторую закономерность.
Таблица двоичной системы счисления
0 | 0 | 8 | 1000 |
1 | 01 | 9 | 1001 |
2 | 10 | 10 | 1010 |
3 | 11 | 11 | 1011 |
4 | 100 | 12 | 1100 |
5 | 101 | 13 | 1101 |
6 | 110 | 14 | 1110 |
7 | 111 | 15 | 1111 |
Как видно из таблицы, после 11 в числовом ряду двоичных чисел идет число 100.
Так как в двоичной системе счисления только два знака 0 и 1 для обозначения числа, то происходит сдвиг разрядной сетки влево. После двузначного числа 11 идет трехзначное число 100.
Таблицей двоичной системы удобно пользоваться для перевода только небольших десятичных чисел. Ее даже рекомендуется запомнить, как таблицу умножения в математике. Но ни в коем случае нельзя по таблице переводить отдельные цифры числа в десятичный формат. Это приведет к ошибке. Например, десятичное число 15 это не 1 и 101, (вместе 1101), а все-таки 1111.
Перевод двоичных чисел в десятичную систему счисления
Обратный перевод двоичного числа в десятичную систему производится также строго по правилу перевода.
Рис. 2. Портрет Г. В. Лейбница.Сначала нумеруются разряды двоичного числа справа налево, начиная с нулевого, а затем каждая цифра двоичного числа умножается на основание двоичной системы, то есть на два, возведенной в степень соответствующего разряда. Полученные произведения суммируются, и получается десятичное число.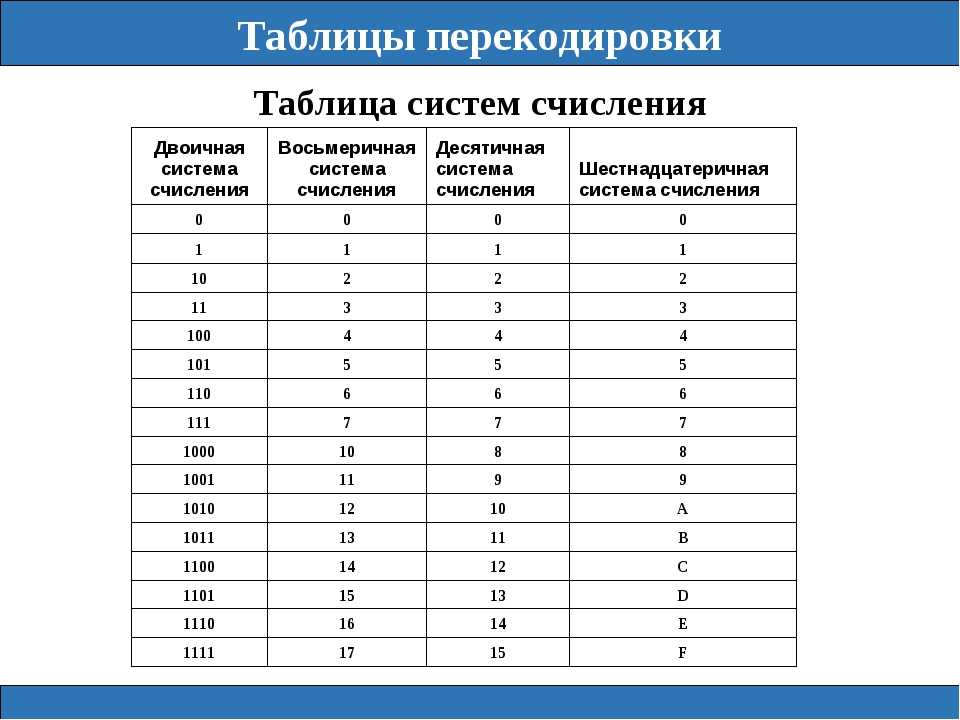
Например: двоичное число 1110001 в десятичной системе равно 113.
Нумеруем разряды числа, начиная с нуля: 1(6) 1(5) 1(4) 0(3) 0(2) 0(1) 1(0).
Каждую цифру двоичного числа умножаем на два в степени разряда и суммируем:
1*26 + 1*25 + 1*24 +0*23 + 0*22 + 0*21 + 1*20 = 64 + 32 + 16 + 0 + 0 + 0 +1 = 113
Следует помнить, что любое число в степени ноль равно единице.
Двоичная система счисления была описана Готфридом Вильгельмом Лейбницем в 18 веке. На это его вдохновили гексограммы из китайской книги Перемен, которые соответствовали двоичным числам от 0 до 111111.
Рис. 3. Гексаграммы книги перемен.Что мы узнали?
Данные в ЭВМ представляются в двоичном формате. Двоичная система счисления оперирует для записи чисел только двумя символами 0 и 1. Перевод десятичных чисел в двоичную систему и обратно производится строго по правилам.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Альбина Авезова
5/10
Оценка статьи
4.7
Средняя оценка: 4.7
Всего получено оценок: 215.
А какая ваша оценка?
Двоичный код для начинающих — Двойная спираль
Двоичный код для начинающих
Дэвид, 14 января 2014 г. , но это основа того, как почти все компьютеры выполняют арифметические действия!
Чтение двоичного числа
Каждый столбец двоичного числа в два раза больше предыдущего столбца.
Двоичное число похоже на стандартное десятичное число, но оно состоит только из цифр 1 и 0. Чтобы отличить двоичное число от стандартного, мы поместим букву «В» в конце любого двоичного числа. Некоторые люди вместо этого пишут «0b» в начале или «9».0013 2 » в конце, чтобы показать то же самое.
Стандартный номер имеет столбец единиц, столбец десятков, столбец сотен и так далее. Если бы двоичный код использовал одни и те же значения для каждого столбца, единственными числами были бы 1, 10, 11, 100 и так далее.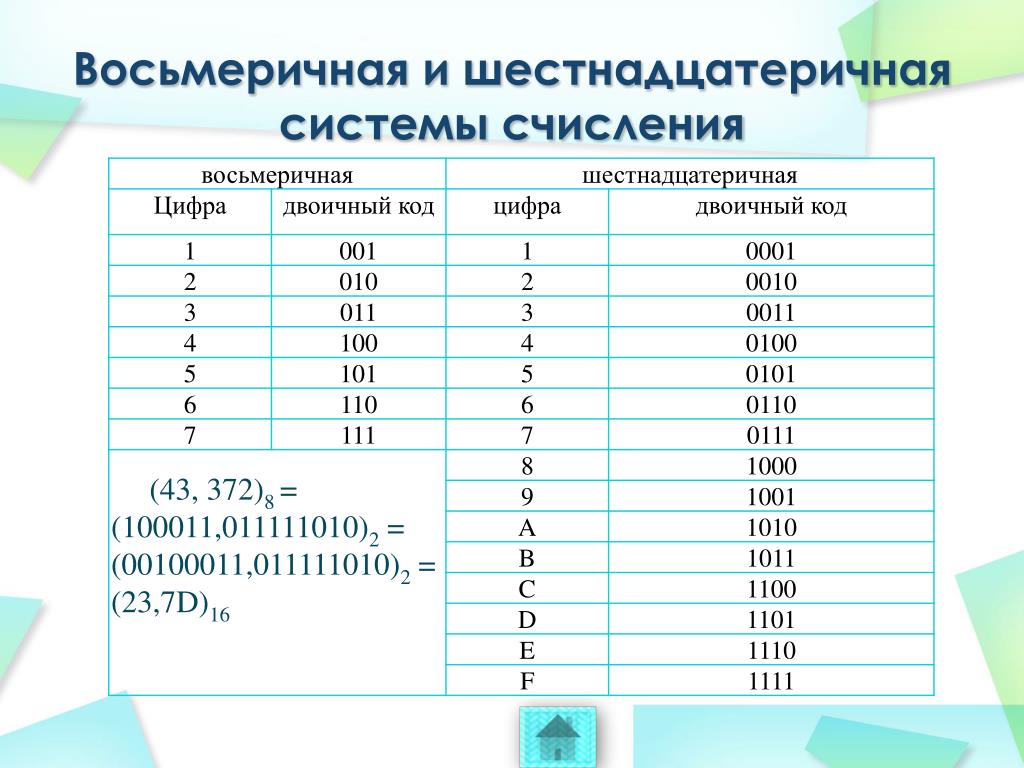
Двоичные столбцы оцениваются по-разному. Двоичное число имеет столбец единиц, столбец двоек, столбец четверок, столбец восьмерок и так далее. Каждый столбец в два раза больше предыдущего столбца. Чтобы прочитать двоичное число, сложите значения столбцов вместе. Например:
Двоичное сложение устанавливается как обычное сложение.
1011B
Имеет 1 в столбце единиц, 1 в столбце двоек, 0 в столбце четверок и 1 в столбце восьмерок, поэтому
1011B = один + два + восемь = одиннадцать
И для более крупного примера:
1000110B = два + четыре + шестьдесят четыре = семьдесят
Сложение двоичных чисел
Двоичное сложение основано на одном простом факте:
1B + 1B = 10B
Посмотрите, сможете ли вы декодировать это двоичное число!
Чтобы выполнить двоичное сложение, запишите числа, выровняв их столбцы, как если бы вы записывали обычные числа:
111B
+ 110B
Затем добавьте столбцы, начиная со столбца единиц, и продвигайтесь вверх.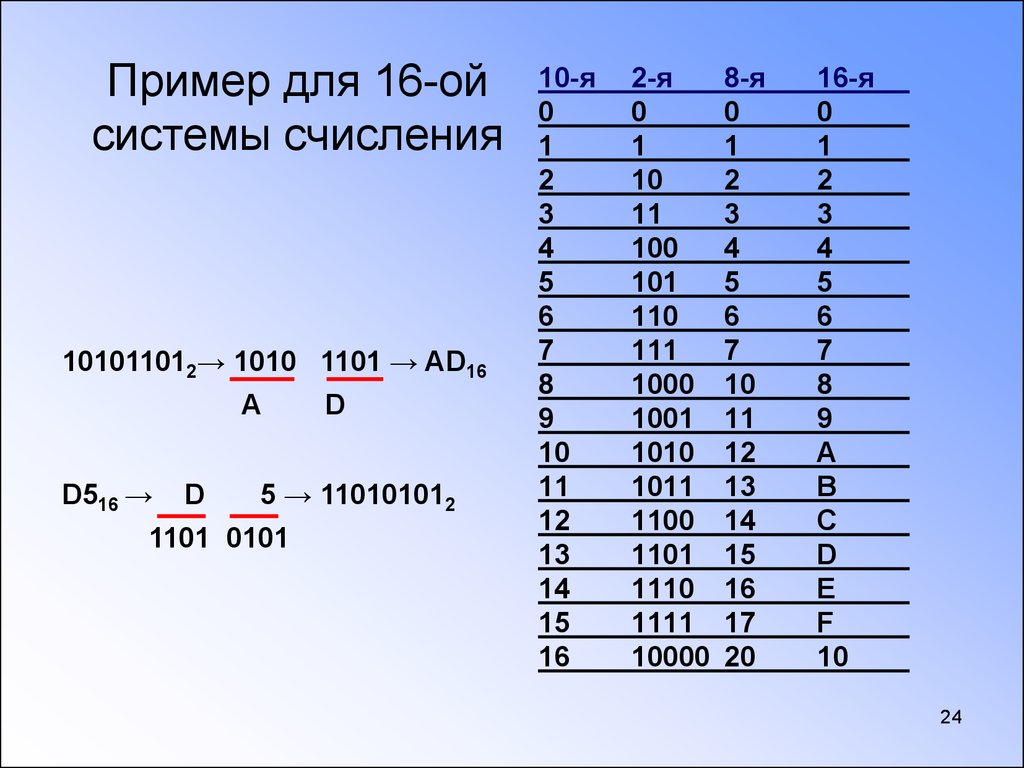
Вам должны помочь следующие три факта:
0B + 0B = 0B
1B + 0B = 1B
1B + 1B = 10B
Не забудьте взять с собой две единицы вместе!
111B
+ 110B
––––––
1101B
Чтобы проверить свой ответ, вы можете преобразовать его в стандартные десятичные числа:
111B = семь, 110B = шесть, 1101B = тринадцать, поэтому:
Семь + шесть = тринадцать
Что происходит?
Если вы выполняете это задание, вы можете подумать, что двоичный код сложный и медленный. В приведенном выше примере требуется четыре шага, чтобы сложить шесть и семь. Однако большая часть арифметики в мире выполняется в двоичном формате, потому что большая часть арифметики выполняется компьютерами.
Двоичные числа записываются только двумя цифрами: 1 и 0. Компьютер может хранить двоичные числа, используя открытые или закрытые переключатели для представления каждой цифры. Также проще проектировать микросхемы для добавления двоичных файлов.
Для работы двоичного сумматора необходимы только три факта сложения (0 + 0 = 0, 1 + 0 = 1, 1 + 1 = 10). Десятичной счетной машине потребовалось бы 55 фактов.
Двоичная система была формально описана Готфридом Лейбницем около 300 лет назад. Готфрид основал свою двоичную систему на идеях, которые он нашел в системе гадания, известной как И Цзин. Лейбниц считал, что эта бинарная система могла бы стать хорошей системой для вычислений, но до того, как были созданы первые бинарные компьютеры, прошли сотни лет.
Если вам нужно больше математических занятий для детей, подпишитесь на журнал Double Helix!
Похожие посты
Двоичный файл для чайников. «Все, что можно представить с помощью… | Уилл Бейнтон
«Все, что может быть представлено каким-либо шаблоном, может быть представлено набором битов».
-Клод Шеннон
Сам человек, возможно, наиболее известный своими Математическая теория связи, и основателем теории цифровых цепей, которая утверждает, что булева алгебра может передавать любые логические числовые отношения.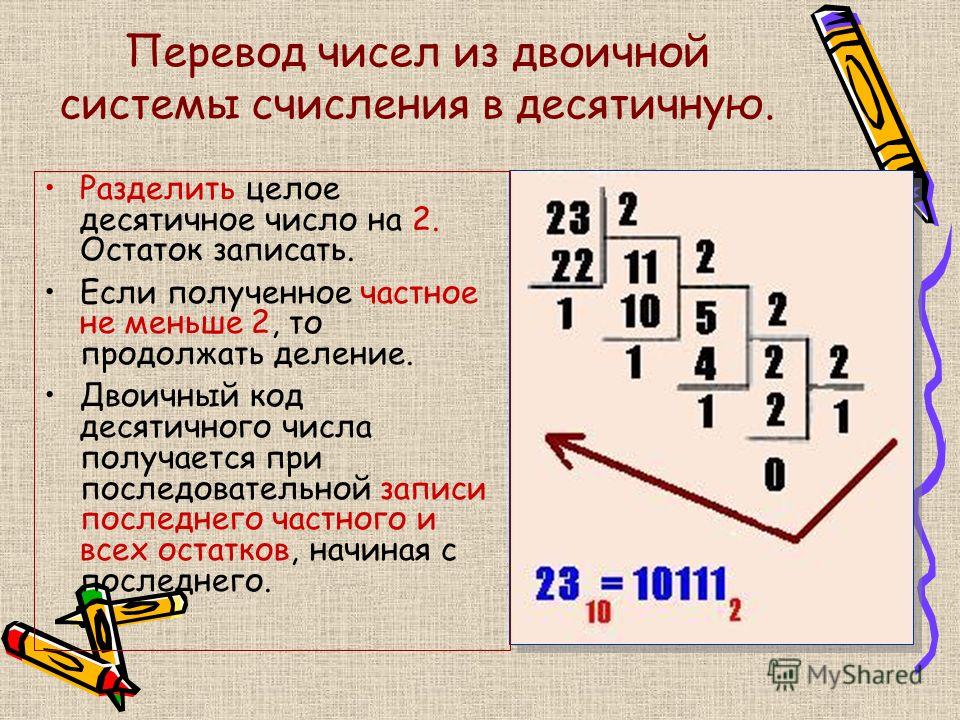
Что такое двоичный код?
Двоичная запись — это двухсимвольная система счета, способная сжимать сложные данные в длинную серию утверждений «да» или «нет». Все процессы, выполняемые компьютером, и все данные, сохраненные в нем, в конечном итоге переводятся в двоичный или машинный код для чтения компьютером.
В 1689 году Готфрид Либниц написал статью под названием Explication de l’Arithmetique , в которой объяснял важность и область применения двоичной системы счисления. В нем он описывает основные методы двоичного счета, объясняя при этом, как его гибкость может быть полезна для ряда различных приложений.
«Здесь одним взглядом становится очевидной причина знаменитого свойства геометрической прогрессии на двойки целых чисел, состоящего в том, что если иметь только одно из этих чисел для каждой степени, то из них можно составить все остальные целые числа. ниже двойника высшей степени.
Ибо здесь все равно, что сказать, например, что 111, или 7, есть сумма четырех, двух и одного, а 1101, или 13, есть сумма восьми, четырех и одного.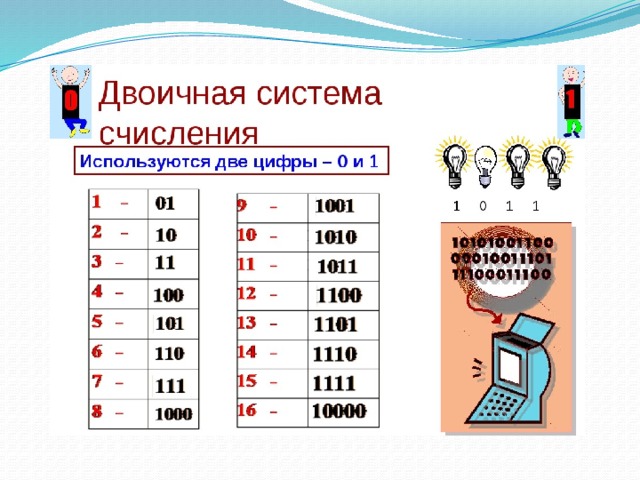
Это свойство позволяет оценщикам взвешивать все виды масс с небольшим весом и может использоваться при чеканке монет, чтобы получить несколько номиналов с помощью небольшого количества монет».
Здесь важно отметить, что с небольшим количеством монет, то есть с небольшим количеством символов, можно было бы производить удивительно сложные вычисления с минимальными ресурсами.
Как это работает?
Вместо использования системы счисления с основанием 10 (0–9) в двоичной системе счисления используется система счисления с основанием 2 (0–1). Это означает, что в десятичной системе счисления десять символов, а в двоичной — только два. В системе счисления с основанием 10 каждая добавленная цифра представляет значение, в десять раз превышающее предыдущую цифру, тогда как в системе счисления с основанием 2 каждая добавленная цифра представляет собой значение, в два раза превышающее предыдущее. Все это говорит о том, что 0, 1 и цифровая позиция этих двух символов — это все, что используется для определения значения конкретной строки чисел.
Но почему?
Физические ограничения компьютеров диктуют необходимость двоичного кодирования. Компьютеры в основном состоят из транзисторов, которые работают, получая небольшой электрический заряд. Большинство транзисторов работают, получая электрический заряд и включаясь или выключаясь подобно выключателю света. Сложите достаточное количество этих транзисторов вместе, и у нас есть основные компоненты схемы.
Хотя было бы сложно разработать схему, которая могла бы измерять градусов электрического заряда, относительно легче разработать компонент, который измеряет существование одного из них.
Все это приводит к риторическому вопросу:
«Что проще построить, выключатель или диммер?»
Транзисторы равны биту и, по сути, являются атомом или строительным блоком всех вычислений. В своей простейшей форме они могут только включаться или выключаться. На карте все переключатели, которые быстро включаются и выключаются в разной последовательности, определяют основные функции компьютера.
