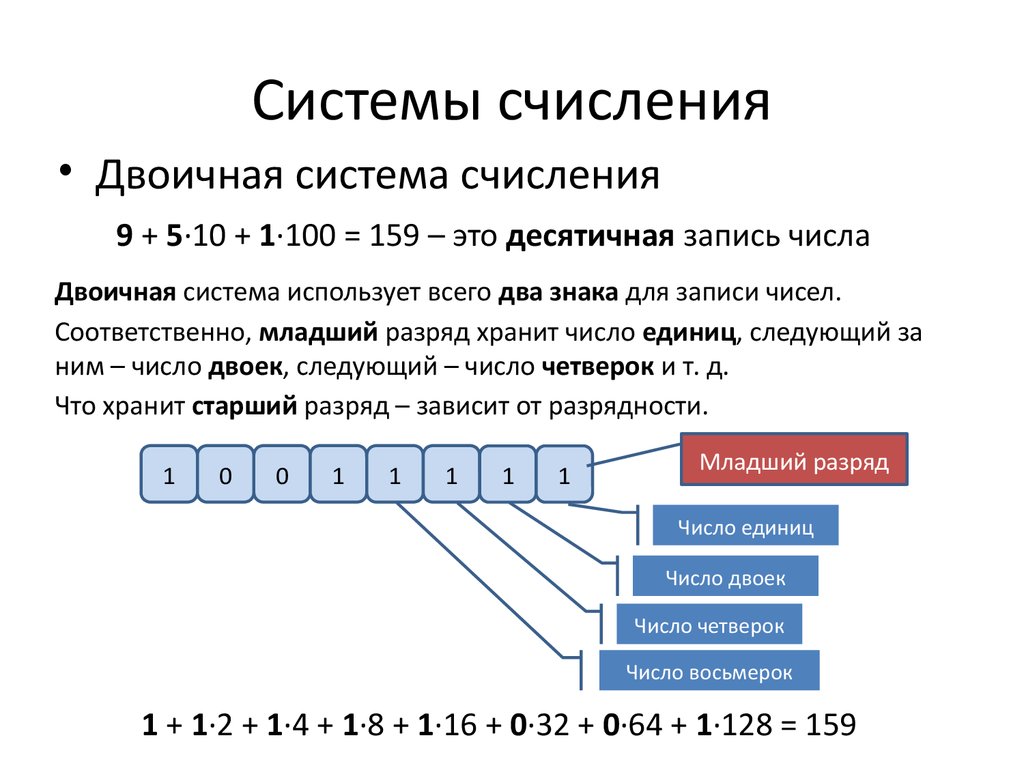
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 11 из 37Следующая ⇒ Показал полезность применения двоичной системы немецкий математик Г. Лейбниц в 1703 г. Однако лишь благодаря работам Дж. Фон Неймана, опубликованным в 1940-х гг., двоичная система получила практическое использование при создании компьютерных средств. Применение двоичной системы в вычислительной технике было обусловлено такими обстоятельствами, как двухпозиционный характер работы электронных элементов, высокая экономичность двоичной системы счисления и простота выполнения операций с двоичными числами. Как отмечалось в отчете Дж. Фон Неймана (1946 г.): «основное же преимущество двоичной системы по сравнению с десятичной состоит в том, что основная часть машины по своему характеру является не арифметической, а логической. Новая логика, будучи системой типа «да — нет», в основном двоична. В современной вычислительной технике, в устройствах автоматики и связи используется в основном двоичная система счисления, что обусловлено рядом преимуществ перед другими системами. Так, для ее реализации нужны технические устройства лишь с двумя устойчивыми состояниями, например материал намагничен или размагничен. Это обеспечивает более надежное и помехоустойчивое представление информации, дает возможность применения аппарата булевой алгебры для выполнения логических преобразований информации. Кроме того, арифметические операции в двоичной системе счисления выполняются наиболее просто. Недостаток двоичной системы – быстрый рост числа разрядов, необходимых для записи больших чисел. Этот недостаток имеет существенное значение. Если возникает необходимость кодировать информацию “вручную”, например при составлении программы на машинном языке, используют восьмеричную или шестнадцатеричную системы счисления. Примеры изображения чисел в данных системах счисления представлены в таблице 4.2. Таблица 4.2. Представление чисел в двоичной, восьмеричной и Шестнадцатеричной системах счисления
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления осуществляется путем замены каждой цифры эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр). Пример 4 . Переведем число 537,18 537,18 = 101 011 111, 0012 5 3 7 1 Пример 5 . Переведем число 1A3,F16 в двоичную систему счисления. 1A3,F16 = 1 1010 0011, 11112 1 A 3 F Чтобы перевести число из двоичной системы счисления в восьмеричную или шестнадцатеричную, его нужно разбить влево или вправо от запятой на триады ( для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной или шестнадцатеричной цифрой. Пример 6 . Переведем число 10101001,101112 в восьмеричную систему счисления. 10101001,101112 2 5 1 5 6 Пример 7. Переведем число 10101001,101112 в шестнадцатеричную систему счисления. 10101001,101112 = 1010 1001,1011 10002 = A9,В816 A 9 В 8
Выполнение арифметических операций в двоичной, восьмеричной и шестнадцатеричной системах счисления Правила выполнения арифметических операций сложения, вычитания, умножения и деления в 2-, 8- и 16-ичной системах счисления будут такими же, как и в десятичной системе, только надо пользоваться особыми для каждой системы таблицами сложения и умножения. Таблицы сложения для 2-ичной, 8-ичной и 16-ичной систем счисления представлены в таблицах 4.3-4.5. При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево. Таблица 4.3. Сложение в двоичной системе Таблица 4.4. Сложение в восьмеричной системе
Таблица 4.5. ⇐ Предыдущая6789101112131415Следующая ⇒ Читайте также: Техника прыжка в длину с разбега Тактические действия в защите История Олимпийских игр История развития права интеллектуальной собственности |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 2849; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Системы счисления, двоичная десятичная система счисления и числа
Системы счисления
Система счисления – одно из ключевых понятий в информатике, которое надо знать при изучении информационных технологий. Это основа, на базе которой строится всё остальное. Без понимания, что это такое, в будущем вам будет достаточно тяжело. Поэтому, самое время разобраться, что из себя представляет система счисления.
Что за зверь
Если говорить простыми словами, то система счисления – это способ записи чисел. Числа пишутся и
обозначаются через знаки. Эти знаки называются цифрами. Все мы их уже прекрасно
знаем – это 1, 2, 3, 4, 5 и так далее до бесконечности. Это арабские цифры, к
которым мы все привыкли. Но есть и римские. Чаще всего мы встречаем вот эти
римские цифры: I, V, X. Но есть ещё и вот такие: L, M. У нас они применяются, но гораздо
реже, чем арабские цифры. Отсюда мы делаем вывод, что числа систем счисления бывают двух видов:
Но есть и римские. Чаще всего мы встречаем вот эти
римские цифры: I, V, X. Но есть ещё и вот такие: L, M. У нас они применяются, но гораздо
реже, чем арабские цифры. Отсюда мы делаем вывод, что числа систем счисления бывают двух видов:
- Арабские;
- Римские.
Также бывает позиционная и непозиционная система счисления. В первой итоговое количество чисел зависит от позиции, где стоит цифра. В непозиционной такого правила нет. Приведём пример. Возьмём число 11 и II. В первом случае мы используем арабские цифры, во втором – римские. 11 – это позиционная система счисления, где первая 1-ца показывает десятки, а вторая – единицу. В конце мы получаем итоговое число – одиннадцать. То есть, итог у нас зависит от того, на какой позиции стояли цифры. Поэтому такая система и называется позиционной.
Читайте также статью единицы измерения информации
Что же с II?
Это пример непозиционной системы. Здесь мы видим, что I – это один.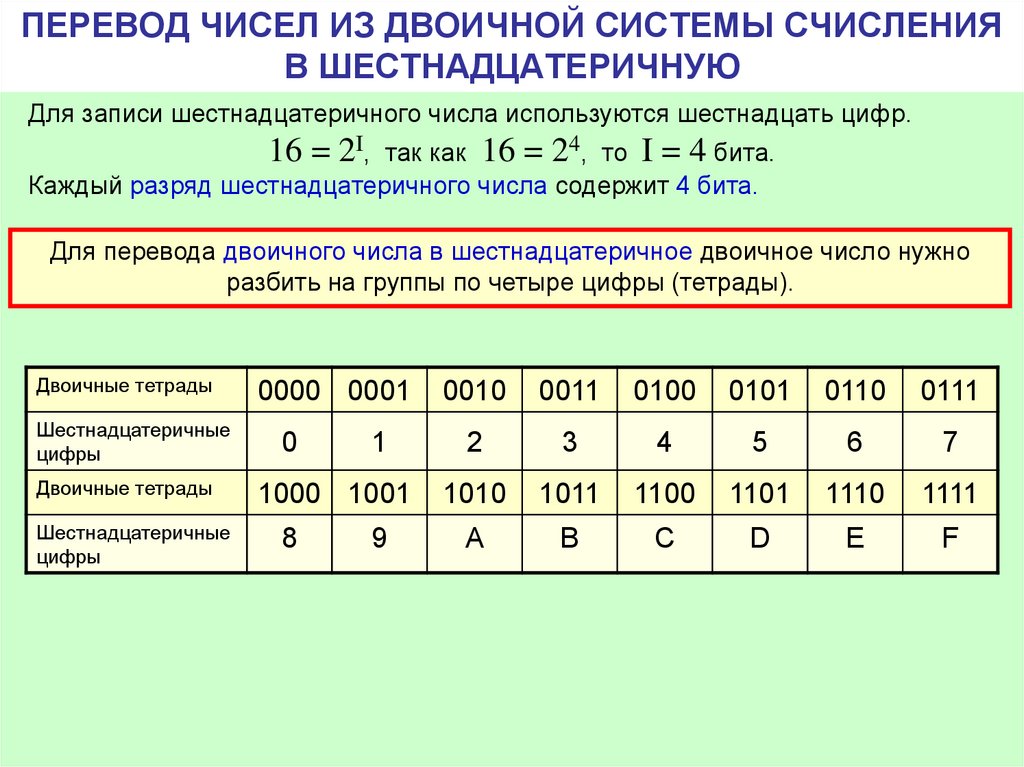 А II означает два, так как стоят
две «палочки» и итоговое значение не зависит от позиции цифры в числе. Поэтому
система непозиционная.
А II означает два, так как стоят
две «палочки» и итоговое значение не зависит от позиции цифры в числе. Поэтому
система непозиционная.
Надеемся, здесь всё понятно. Время перейти к примерам посложнее.
Возьмём числа 819, 595, 910. Рассматриваемой цифрой у нас будет девятка. В первом варианте 819 она стоит на последней позиции, а значит играет роль обычной девятки. В 595 девятка стоит на втором месте между пятёрками. Здесь она играет роль десятых (90), обозначая 95 – девяносто пять. В третьем числе 910 она стоит на первом месте, обозначая сотые (900), поэтому читается как «девять сот». Это ещё один пример позиционной системы счисления.
Возьмём непозиционную систему. Например, XXV, XVI, XIV. Рассматриваемое число – V. Посмотрите внимательно. Куда бы мы не поставили нашу V, она всегда будет обозначать пять единиц. А значит, итоговое значение не будет зависеть от позиции.
Возникает вопрос: как тогда удобнее
считать? Как вы заметили, при сложении, умножении, делении, вычитании, мы
применяем позиционные числа систем
счисления.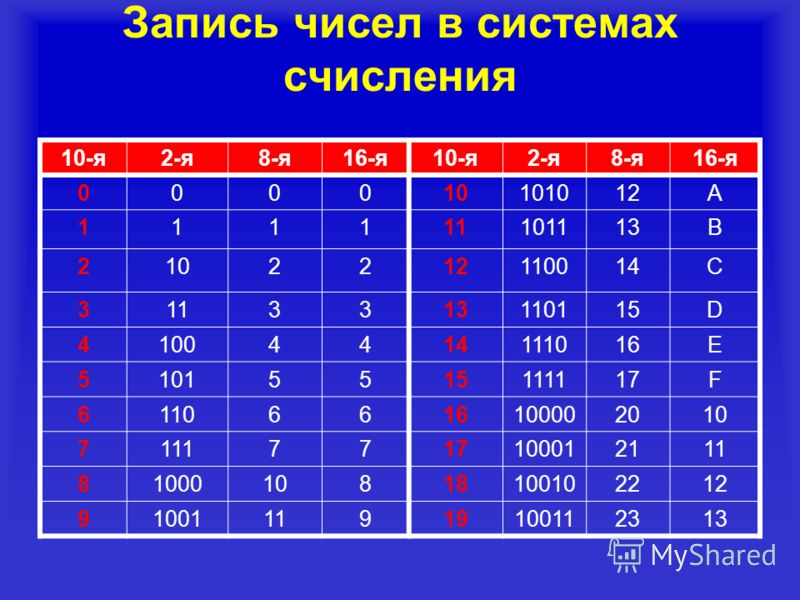 То есть, 12, 492,
3123 и так далее. Это неспроста. Выполнять математические операции с такими
числами гораздо проще. Можно складывать и умножать в столбик, так проще делать
операции деления и вычитания. С римскими гораздо тяжелее. По этой причине римские
числа чаще применяются для обозначения времени. Например, XV лет до нашей
эры. Тут можете просто заглянуть в учебник по истории, где римские цифры будут
почти в каждой теме.
То есть, 12, 492,
3123 и так далее. Это неспроста. Выполнять математические операции с такими
числами гораздо проще. Можно складывать и умножать в столбик, так проще делать
операции деления и вычитания. С римскими гораздо тяжелее. По этой причине римские
числа чаще применяются для обозначения времени. Например, XV лет до нашей
эры. Тут можете просто заглянуть в учебник по истории, где римские цифры будут
почти в каждой теме.
Слышал про разряд – что это такое
При работе с числами есть такое понятие, как разряд. Здесь
совсем всё просто. Разряд — это позиция цифры, которое оно занимается в числе.
А разрядность числа – то количество цифр, которые находятся в числе. Например,
48 – двухразрядное число, 987412 — шестиразрядное число, 127501750174 –
двенадцатиразрядное число. Как мы это определили? А вы посчитайте количество
цифр в числе и сами поймёте. В самих числах разряды считаются с правой стороны
налево. Например, число 841. Единица находится в первом разряде. Четвёрка – во
втором.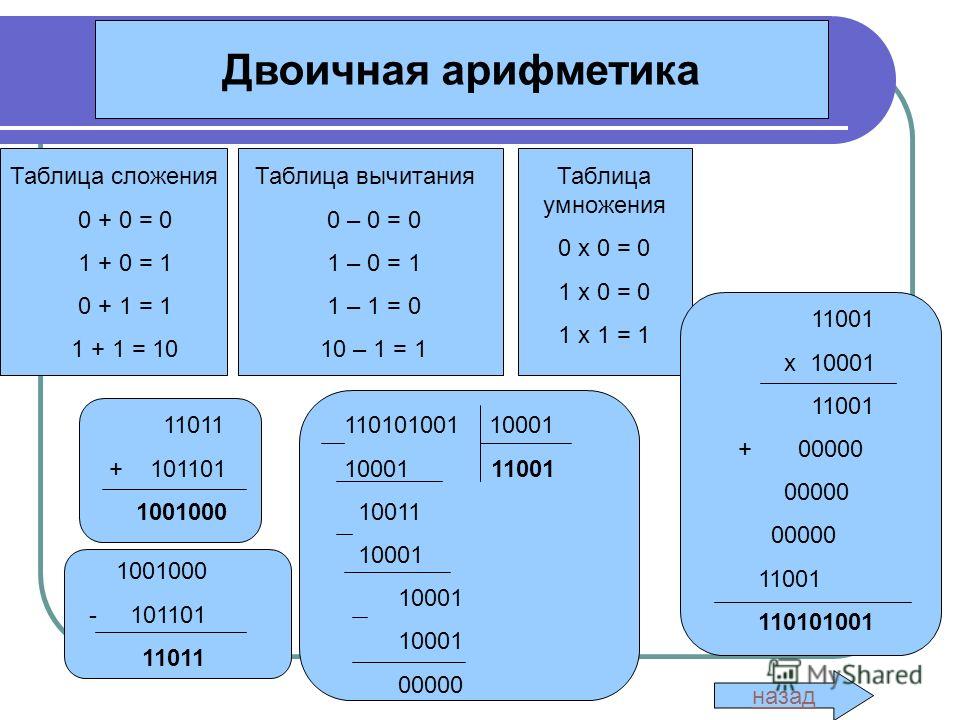 Восьмёрка – в третьем. Думаем, принцип вы поняли.
Восьмёрка – в третьем. Думаем, принцип вы поняли.
Двоичная система счисления – это система, в которой применяют только две цифры 0 (ноль) и 1 (единица). Двоичная система счисления во многом связана с десятичной системой счисления. Для простоты понимания двоичной системы, начнём с десятичной, так как в жизни мы используем её чаще всего.
В десятичной системе счисления мы применяем десять цифр. Это 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Когда мы доходим до последнего числа 9, то мы переходим на новый разряд – десяток. Счёт начинается с 10 и продолжается дальше 11, 12, 13 и так далее. Когда мы опять доходим до 9-ки в последнем числе разряда, в данном случае до 99, то мы переходим на сотни. Счёт начинается со ста – 100 и продолжается 101, 102, 103 и так далее. Снова доходим до последнего числа разряда сотен, 999, прибавляем 1 и начинается разряд тысяч – 1000, 1001, 1002 и далее. Так до бесконечности. Следовательно, последними цифрами в разряде десятка, сотни, тысячи являются 99, 999, 999 соответственно.
Так до бесконечности. Следовательно, последними цифрами в разряде десятка, сотни, тысячи являются 99, 999, 999 соответственно.
Что такое защита информации? Читайте лекцию на сайте!
Двоичная система счисления точно такая же, как десятичная. Отличие лишь в том, что в ней есть только два числа – 0 и 1. Других цифр в этой системе нет. В каждом разряде есть свой предел. Для простоты понимания и решения разных задач, часто двоичную систему переводят в десятичную. Это выгляди так:
| Двоичная система счисления | Десятичная система счисления |
| 0 | Ноль |
| 1 | Один |
| 10 | Два |
| 11 | Три |
| 100 | Четыре |
| 101 | Пять |
| 110 | Шесть |
| 111 | Семь |
| 1000 | Восемь |
| 1001 | Девять |
Двоичная система
счисления одна из самых распространённых в мире. Дело в том, что на ней
работают все компьютеры и любая техника, которая выполняет вычисление. Они
оперируют нулями и единицами. Почему не применяют десятичную систему? Это
гораздо труднее. Зачем делать вычисления с огромными числами, когда можно
создать систему для вычисления только двух чисел – нуля и единицы. По этой
причине двоичная система применяется в любой вычислительной технике.
Дело в том, что на ней
работают все компьютеры и любая техника, которая выполняет вычисление. Они
оперируют нулями и единицами. Почему не применяют десятичную систему? Это
гораздо труднее. Зачем делать вычисления с огромными числами, когда можно
создать систему для вычисления только двух чисел – нуля и единицы. По этой
причине двоичная система применяется в любой вычислительной технике.
Теперь вы знаете, какие бывают системы счисления, числа систем счисления, что такое двоичная система счисления и десятичная система счисления. Отметим, что также бывает восьмеричная и шестнадцатеричная система счисления. Но, об этом позже. Рекомендуем для начала разобраться в двоичной и десятичной системах, а потом можно пойти и дальше.
Удачи в изучении!
Как хорошо вы знаете эту тему? пройдите тест системы счисления !
Двоичная система счисления это в информатике
Двоичная система счисления — это позиционная система счисления с основанием 2.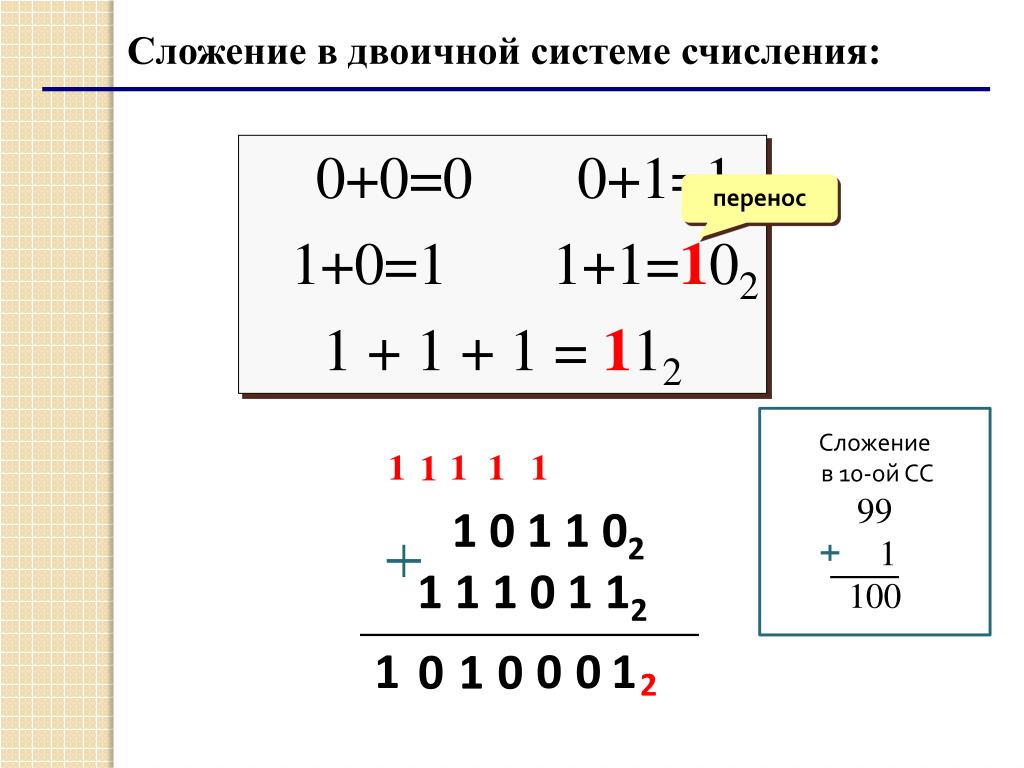 В этой системе счисления числа записываются с помощью двух символов: 0 и 1. Двоичную цифру называют битом. Двоичная система счисления является основной системой представления информации в памяти компьютера.
В этой системе счисления числа записываются с помощью двух символов: 0 и 1. Двоичную цифру называют битом. Двоичная система счисления является основной системой представления информации в памяти компьютера.
Сложение, вычитание и умножение двоичных чисел.
Пример: 1001 + 10 = 1011
Пример: 1111101 – 10001 = 1101100
Пример: 1111 · 1001 = 10000111
Перевод чисел.
Для перевода десятичного числа в двоичное надо разделить его на 2 и собрать остатки, начиная с последнего частного.
Для перевода двоичного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания двоичной системы счисления на соответствующие цифры в разрядах двоичного числа.
Пример: требуется перевести двоичное число 10110110 в десятичное. В этом числе 8 цифр и 8 разрядов ( разряды считаются, начиная с нулевого, которому соответствует младший бит). Представим его в виде суммы степеней с основанием 2: 101101102 = (1·2 7 )+(0·2 6 )+(1·2 5 )+(1·2 4 )+(0·2 3 )+(1·2 2 )+(1·2 1 )+(0·2 0 ) = 128+32+16+4+2 = 18210
В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)
Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)
Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.
В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.
Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.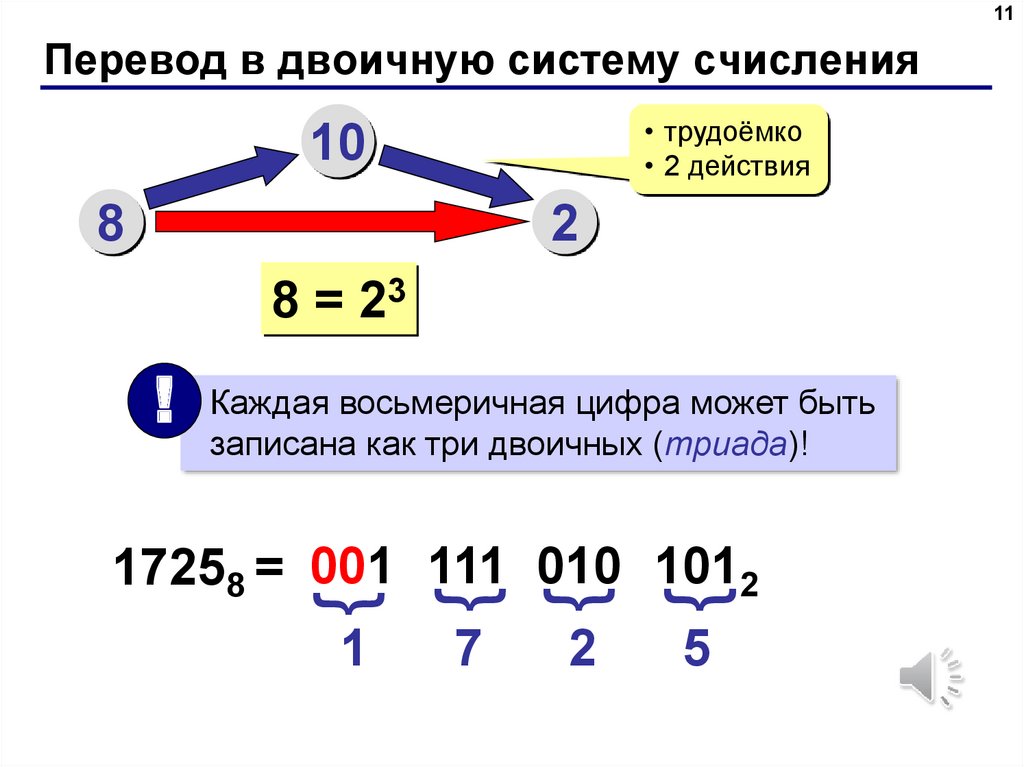 д.
д.
Перевод чисел из двоичной системы счисления в десятичную
Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:
1476 = 1000 + 400 + 70 + 6
Можно пойти еще дальше и разложить так:
1476 = 1 * 10 3 + 4 * 10 2 + 7 * 10 1 + 6 * 10 0
Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 – это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:
Только основание здесь будет 2:
10001001 = 1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0
Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:
1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:
Почему двоичная система счисления так распространена?
Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Перевод десятичного числа в двоичное
Может потребоваться перевести десятичное число в двоичное.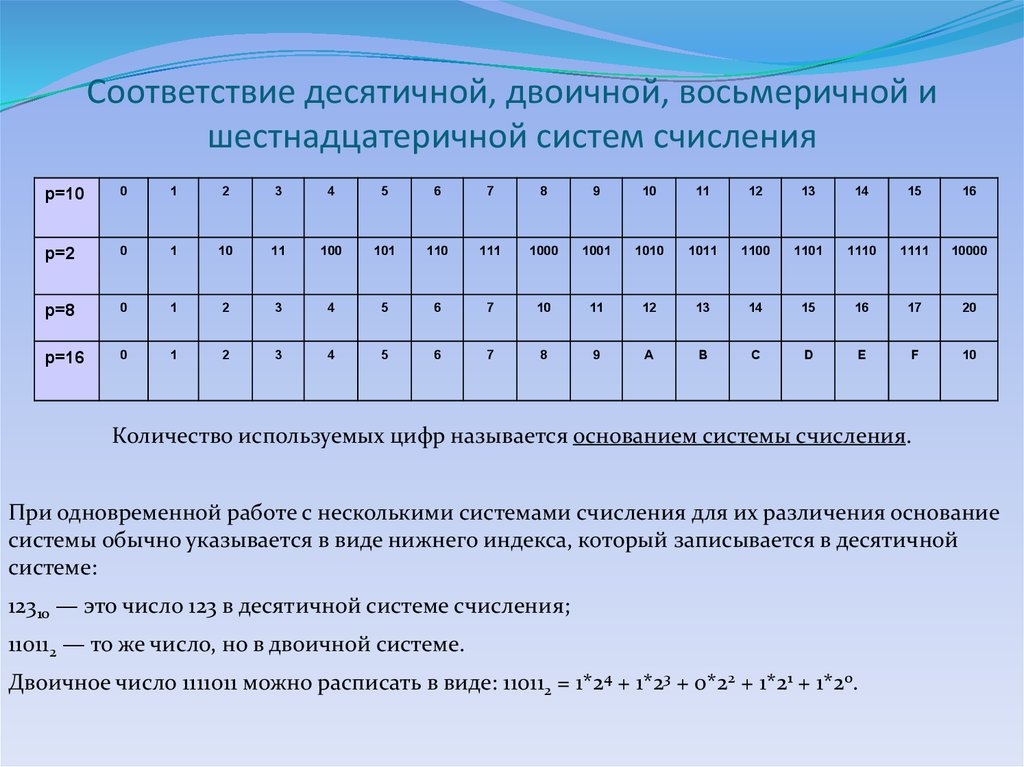 Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:
1001101 = 1*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 1*2 2 + 0*2 1 + 1*2 0 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
Тема: «Двоичная система счисления».
Цел урока:
- обобщить и закрепить знания об основных понятиях позиционных систем счисления на примере двоичной системы счисления;
- активизировать познавательную деятельность учащихся;
- показать применение игровых ситуаций на уроке;
1. Повторение и обобщение предыдущих знаний.
Повторение учащимися основных понятий позиционных систем счисления может быть организовано в виде игры по принципу «домино» (карточка делится пополам на вопрос-ответ, разрезаются и раздаются, дети ищут ответ на вопрос, образуя при этом пару для дальнейшей работы). Можно предложить следующие определения для контроля.
Можно предложить следующие определения для контроля.
Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Количество цифр, используемых в системе счисления для записи чисел, называется ее основанием.
Существуют позиционные и непозиционные системы счисления.
Непозиционной системой счисления называется система, в которой вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа.
Позиционной системой счисления называется система, в которой вес каждой цифры измеряется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Поскольку за основание системы счисления можно принять любое натуральное число, то существует бесчисленное множество позиционных систем счисления. Рассмотрим традиционные из них.
2. Мотивация рассмотрения двоичной системы счисления
Учитель. Люди предпочитают десятичную систему счисления вероятно потому, что с древних времен они считали по пальцам, а пальцев у людей по 10 на руках и ногах.
Десятичная система счисления пришла к нам из Индии.
Но не всегда и везде используют десятичную систему счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.
Для общения с ЭВМ используют, кроме десятичной, двоичную, восьмеричную и шестнадцатеричную системы счисления.
- Какие же цифры используют в двоичной системе счисления (восьмеричной, шестнадцатеричной) системе счисления?
- Как формируется натуральный ряд?
- Как записываются и читаются числа, и какие разряды чисел существуют в двоичной системе счисления?
Все это мы узнаем с вами на уроке, а помощницей нам будет известная десятичная система счисления.
Из всех систем счисления особенно проста и поэтому интересна для технической реализации в ЭВМ двоичная система счисления.
В ЭВМ используют двоичную систему, потому что она имеет ряд преимуществ перед другими системами:
- для ее реализации нужны технические элементы с двумя возможными состояниями (есть ток, нет тока; включено, выключено и т.
 д. Одному из состояний ставится в соответствие 1, другому – 0), а не десять, как в десятичной системе,
д. Одному из состояний ставится в соответствие 1, другому – 0), а не десять, как в десятичной системе, - представление информации посредством только двух состояний надежно и помехоустойчиво,
- упрощается выполнение арифметических действий,
- возможность использовать аппарат булевой алгебры для выполнения логической преобразований информации
Используя знания предыдущего урока заполним следующую таблицу «Сведения о двоичной системе» .
При заполнении таблицы учащиеся ориентируются на знания десятичной системы счисления и знания предыдущего урока. Каждый этап таблицы дополняется и разъясняется учителем, делаются выводы.
3. Попробуем составить таблицу первых 10 двоичных чисел.
Учитель: Сколько потребуется разрядов для записи цифры десятичного числа?
Ученики вычисляют: 2 3 = 8, 2 4 = 16. Значит для записи цифры десятичного числа достаточно 4 разрядов.
Учитель: составим таблицу первых десятичных чисел
При наличии времени (и более сильным учащимся) можно предложить продолжить данную таблицу, формируя натуральный ряд чисел двоичной системы счисления.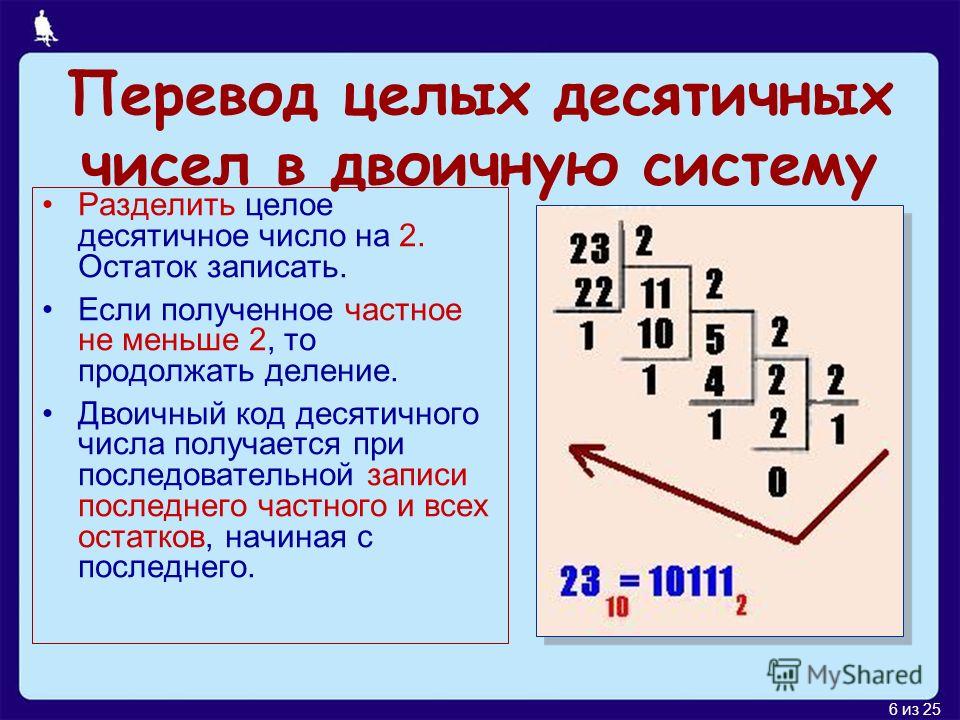
Вывод: недостаток двоичной системы – это быстрый рост числа разрядов, необходимых для записи чисел.
Учитель: оказывается, что мы с вами повторили открытие одного немецкого ученого математика Вильгельм Готфрид Лейбниц (1646-1716)
Медаль, нарисованная В.Г Лейбницем, поясняет соотношение между двоичной и десятичной системами счисления.
Начиная со студенческих лет и до конца жизни великий европеец, немецкий ученый Вильгельм Готфрид Лейбниц (1646-1716), занимался исследованием свойств двоичной системы счисления, ставшей в дальнейшем основной при создании компьютеров. Он придавал ей некий мистический смысл и считал, что на ее базе можно создать универсальный язык для объяснения явлений мира и использования во всех науках, в том числе в философии. Сохранилось изображение медали, нарисованное В. Лейбницем в 1697 г., поясняющее соотношение между двоичной и десятичной системами исчисления:
На ней была изображена табличка из двух столбцов, в одном числа от 0 до 17 в десятичной системе, а в другом – те же числа в двоичной системе счисления.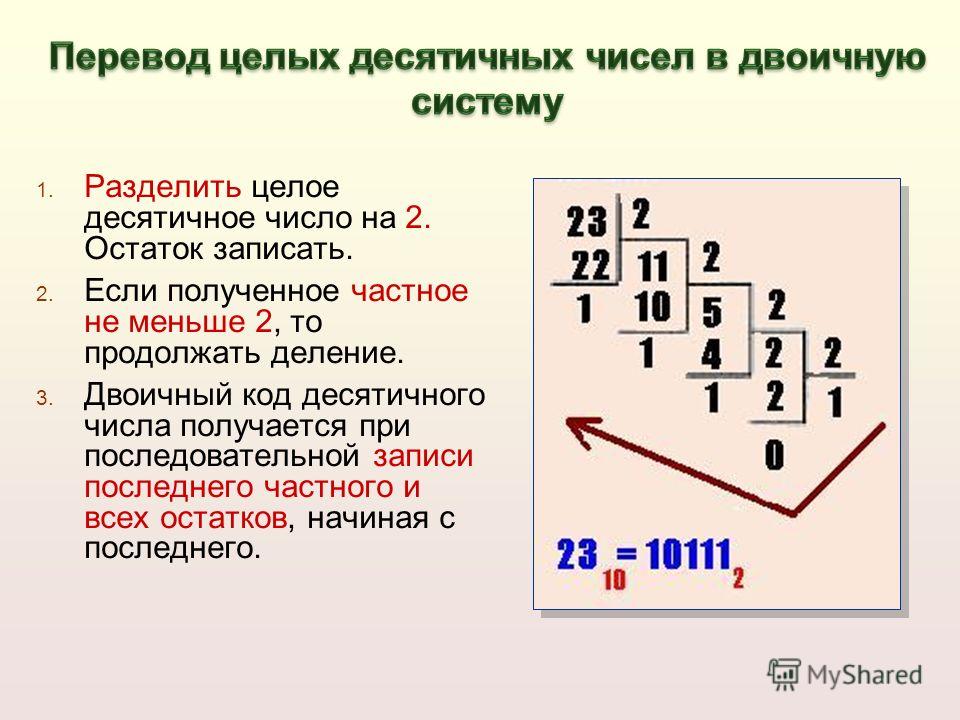 Вверху была надпись: «2,3,4,5 и т.д. Для получения их всех из нуля достаточно единицы». Внизу же гласила надпись: «Картина создания. Изобрёл ГГЛ. МDС XCYII».
Вверху была надпись: «2,3,4,5 и т.д. Для получения их всех из нуля достаточно единицы». Внизу же гласила надпись: «Картина создания. Изобрёл ГГЛ. МDС XCYII».
Учитель: постарались вы на славу, предлагаю отдохнуть. Выполним зарядку для рук. Будем показывать числа, которые мы только что перевели в двоичную систему счисления.
Если 0- загибаем палец, если 1 – оттопыриваем. Учитель сначала последовательно, затем в разбивку говорит числа в десятичной системе счисления, а учащиеся показывают их в двоичной системе на пальцах, и наоборот. Данное упражнение вносит эмоциональный характер, но требует внимания от учащихся.
5. Демонстрация решения задачи, связанной с переводом десятичного числа в двоичную систему счисления пальцевым методом.
Смысл перевода прост: нумеруем на одной руке (левой, ладонь к себе)от мизинца до большого пальца разряды от 0 до 4, что соответствует числам в десятичной системе 1,2, 4, 8,16. Считая, что 0- это согнутый палец, а 1 – оттопыренный, при решении задач, связанных с переводом целых чисел в двоичную из десятичной системы счисления требуется лишь сложить эти цифры, соответствующие загнутым пальцам.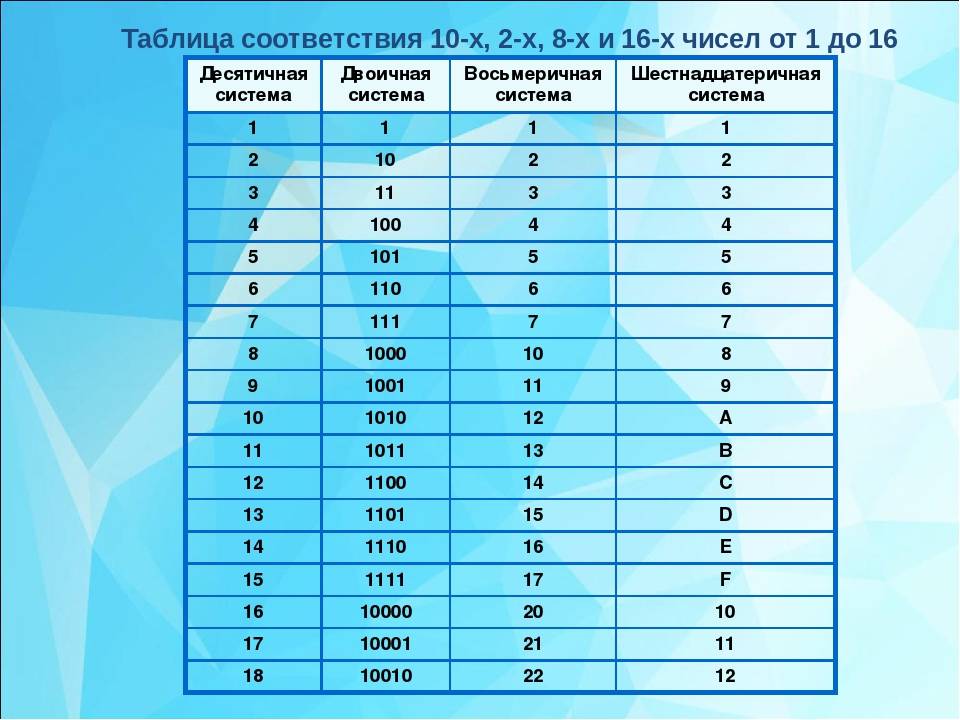 Данное упражнение, основанное на самом древнем способе- счете на пальцах, подразумевает развёрнутую форму записи числа в двоичной системе счисления. (Две руки можно использовать для перевода целых чисел до 512, так и для перевода дробных конечных чисел, где левая рука – целая часть числа, а правая – дробная). Учитель говорит число в десятичной системе (до 31 или 62), а школьники устно переводят число на пальцах в двоичную систему и записывают ответ. Для больших чисел приводится сам развёрнутый способ перевода числа из двоичной системы счисления в десятичную с примером.
Данное упражнение, основанное на самом древнем способе- счете на пальцах, подразумевает развёрнутую форму записи числа в двоичной системе счисления. (Две руки можно использовать для перевода целых чисел до 512, так и для перевода дробных конечных чисел, где левая рука – целая часть числа, а правая – дробная). Учитель говорит число в десятичной системе (до 31 или 62), а школьники устно переводят число на пальцах в двоичную систему и записывают ответ. Для больших чисел приводится сам развёрнутый способ перевода числа из двоичной системы счисления в десятичную с примером.
6. Затем учитель говорит, что существует и обратный способ перевода, предлагая алгоритм перевода десятичного целого числа в двоичную систему счисления.
Приводятся примеры. Сложность перевода для детей в том, что правило деления отличается от математического тем, что при делении чисел требуется определить частное сразу, а не поразрядно. Каждый этап комментируется учителем
Перевести 2310 в двоичную систему.
7. Решение упражнений
Затем предлагается самостоятельно перевести числа из десятичной системы в двоичную .
Например, перевести числа 18; 36; 47; 235 и др. из десятичной системы счисления в двоичную систему с помощью алгоритма (с записью в тетрадях).
8. Подведение итогов и задание на дом.
Для общения с компьютером нужна двоичная (восьмеричная, шестнадцатеричная) система счисления. В каких (кроме компьютера) приборах (и не только) применяется двоичная система счисления? Оправдано ли это применение (приведите аргументы в защиту).
Возможный ответ: http://www.compulenta.ru
Время в двоичной системе.
В Японии поступили в продажу необычные электронные часы, отображающие время в двоичной системе счисления. Выглядят часы также довольно необычно. Они заключены в круглый металлический корпус, однако вместо циферблата со стрелками или индикатора с цифрами под стеклом находится печатная плата зеленого цвета с резисторами, конденсаторами и расположенными в два ряда десятью светодиодами. Именно они и показывают время. Каждый из светодиодов соответствует двоичному разряду.В верхнем ряду имеются четыре диода, соответствующих числам от одного (20) до восьми (23) и показывающих часы. Нижний ряд из шести светодиодов (разряды от 1 до 32) показывает минуты. Чтобы получить нужное значение нужно сложить числа, соответствующие горящим светодиодам. Для удобства владельца рядом со светодиодами указаны числа, которым те соответствуют. Цена часов составляет 8900 иен или около 80 долларов США.
Именно они и показывают время. Каждый из светодиодов соответствует двоичному разряду.В верхнем ряду имеются четыре диода, соответствующих числам от одного (20) до восьми (23) и показывающих часы. Нижний ряд из шести светодиодов (разряды от 1 до 32) показывает минуты. Чтобы получить нужное значение нужно сложить числа, соответствующие горящим светодиодам. Для удобства владельца рядом со светодиодами указаны числа, которым те соответствуют. Цена часов составляет 8900 иен или около 80 долларов США.
Системы счисления. Двоичная система счисления как основа компьютерной техники. [Реферат №9808]
Содержание:
Введение
Система счисления — это способ записи (представления) чисел.
Что под этим подразумевается? Например, вы видите перед собой несколько деревьев. Ваша задача — их посчитать. Для этого можно — загибать пальцы, делать зарубки на камне (одно дерево — один палец\зарубка) или сопоставить 10 деревьям какой-нибудь предмет, например, камень, а единичному экземпляру — палочку и выкладывать их на землю по мере подсчета. В первом случае число представляется, как строка из загнутых пальцев или зарубок, во втором — композиция камней и палочек, где слева — камни, а справа — палочки
В первом случае число представляется, как строка из загнутых пальцев или зарубок, во втором — композиция камней и палочек, где слева — камни, а справа — палочки
Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные.
Двоичная система счисления имеет прямое отношение к математической теории чисел. Необходимость изучения данной темы связана с тем, что в нашей современной жизни трудно обойтись без компьютера, а все числа в памяти компьютера представлены в двоичной системе счисления. Данная тема вносит вклад в фундаментальное математическое школьное образование. Различные системы счисления используются тогда, когда появляется потребность в числовых расчетах, начиная с вычислений в начальной школе на бумаге и заканчивая вычислениями на суперкомпьютерах.
Теоретический раздел
Нашу жизнь нельзя представить без цифр. Температура воздуха, цены на продукты, номера телефонов, время и прочее. Везде мы используем цифры даже не замечая этого.
Число – это одно из фундаментальных и самых древних понятий математики. Первые числа появились вместе с речью. В древние времена счет считался математической деятельностью. Одним из первых существенных открытий являются представления о самом числе и изобретение основных четырех действий: сложение, вычитание, умножение и деление. Возникновение и развитие математики проходило благодаря египтянам и вавилонянам, примерно 3000 лет до нашей эры.
Счет был необходим для занятия торговлей и даже скотоводством, чтобы следить за количеством животных. Вначале для счета использовали части тела, например, пальцы рук. Число появилось сначала в связи со счетом отдельных предметов, а затем стало обозначать количественную меру. Это привело к идее о бесконечности натурального ряда чисел: 1, 2, 3, 4… и т.д. Для обычных обывателей такого определения достаточно, но математиками были разработаны и другие числа. В 19 веке была разработана теория действительных чисел. Новый импульс эта теория получила в связи с развитием компьютерных технологий.
Числовая ось бесконечна, потому что к каждому числу можно прибавить еще одну единицу и получить следующее число, с которым можно поступить так же. При этом придумывать какие-либо специальные обозначения (цифры) для любого элемента (числа) бесконечной числовой оси нереально. Поэтому для записи произвольного числа бесконечной числовой оси прибегают к помощи одной или нескольким систем счисления.
Понятие системы счисления и их виды
Система счисления – это способ представления любых чисел с помощью определенного количества знаков (цифр) по позиционному принципу. Количество знаков, которые обычно именуют «цифрами», всегда ограничено. И с помощью такого, ограниченного количества цифр (мы используем десять цифр) удается записывать произвольные числа, например, 23 456 или 1 000 123 456 789. Чтобы преодолеть это ограничение, используется особый способ записи, который называется «позиционным».
Позиционная система счисления состоит в использовании ограниченного числа цифр, при этом позиция каждой цифры в числе обеспечивает значимость (вес) этой цифры. Позиция цифры на математическом языке называется разрядом. Значение цифры «переменчиво» и зависит от ее позиции в числе. Например, в числе «11» две единицы имеют разное значение, это относится и к другим сочетаниям «единиц» — «111», «1111», «11 111» и далее. Не всякие числовые системы используют именно такой позиционный способ записи.
Позиция цифры на математическом языке называется разрядом. Значение цифры «переменчиво» и зависит от ее позиции в числе. Например, в числе «11» две единицы имеют разное значение, это относится и к другим сочетаниям «единиц» — «111», «1111», «11 111» и далее. Не всякие числовые системы используют именно такой позиционный способ записи.
Выбор количества цифр диктуется какими-либо потребностями реальной жизни, науки или удобствами обработки. Исторически этот выбор определялся привычками или традициями конкретного народа.
Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.
Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.
Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.
Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упомянутую ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9.
Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д.
Непозиционные системы
Как только люди научились считать — возникла потребность записи чисел. В начале все было просто — зарубка или черточка на какой-нибудь поверхности соответствовала одному предмету, например, одному фрукту.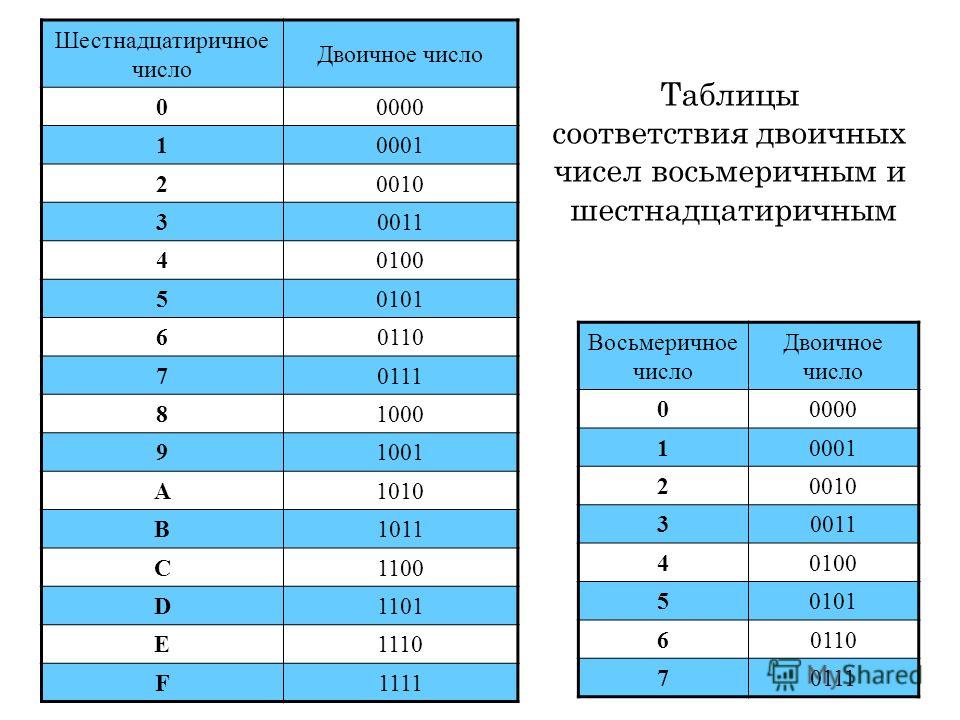 Так появилась первая система счисления — единичная.
Так появилась первая система счисления — единичная.
Единичная система счисления
Число в этой системе счисления представляет собой строку из черточек (палочек), количество которых равно значению данного числа. Таким образом, урожай из 100 фиников будет равен числу, состоящему из 100 черточек.
Но эта система обладает явными неудобствами — чем больше число — тем длиннее строка из палочек. Помимо этого, можно легко ошибиться при записи числа, добавив случайно лишнюю палочку или, наоборот, не дописав.
Для удобства, люди стали группировать палочки по 3, 5, 10 штук. При этом, каждой группе соответствовал определенный знак или предмет. Изначально для подсчета использовались пальцы рук, поэтому первые знаки появились для групп из 5 и 10 штук (единиц). Все это позволило создать более удобные системы записи чисел.
Группы систем счисления:
Анатомического происхождения:
Пятеричная система была распространена у некоторых африканских племен.
Десятичная система оказалась общепринятой по причине того, что десять пальцев рук — это самый первый аппарат для счета, которым человек пользовался с доисторических времен. По пальцам удобно считать от 1 до 10. Сосчитав до 10, естественно принять само число 10 за новую, более крупную единицу – единицу следующего разряда и т.д. Именно счет по пальцам рук положил начало той системе, которая кажется нам самой привычной.
По пальцам удобно считать от 1 до 10. Сосчитав до 10, естественно принять само число 10 за новую, более крупную единицу – единицу следующего разряда и т.д. Именно счет по пальцам рук положил начало той системе, которая кажется нам самой привычной.
Десятичная система счисления представляет собой систему, в которой, каждое целое положительное число представляется в виде суммы различных степеней числа 10 с коэффициентами, которые могут принимать значения от 0 до 9 включительно. Например, запись числа 3 756 означает, что рассматриваемое число содержит 6 единиц, 5 десятков, 7 сотен и 3 тысячи.
Десятичная система счисления не сразу заняла господствующее положение. В разные исторические периоды разные народы мира пользовались другими система счисления.
Двенадцатеричная система.
Широкое распространение имела двенадцатеричная система счисления. Ее происхождение тоже связано со счетом пальцев рук. Так как четыре пальца руки (кроме большого) имеют 12 фаланг, то по этим фалангам, перебирая их по очереди большим пальцем, и ведут счет от 1 до 12. Потом 12 принимается за единицу следующего разряда и т.д. Остатки двенадцатеричной системы сохранились до наших дней: вместо «двенадцать» говорят «дюжина». Многие предметы часто считают именно дюжинами (вилки, тарелки, ножи, носовые платки). А также число месяцев в году — 12. Остатки двенадцатеричной системы счисления имеются у англичан, например, в системе мер 1 фут = 12 дюймам или в денежной системе 1 шиллинг = 12 пенсам.
Потом 12 принимается за единицу следующего разряда и т.д. Остатки двенадцатеричной системы сохранились до наших дней: вместо «двенадцать» говорят «дюжина». Многие предметы часто считают именно дюжинами (вилки, тарелки, ножи, носовые платки). А также число месяцев в году — 12. Остатки двенадцатеричной системы счисления имеются у англичан, например, в системе мер 1 фут = 12 дюймам или в денежной системе 1 шиллинг = 12 пенсам.
С математической точки зрения, двенадцатеричная система имела некоторые преимущества перед десятичной, потому что число 12 делится на 2, 3, 4, 6 и 12, а число 10 только на 2, 5 и 10. А больший запас делителей у числа, служащего основанием системы счисления создает удобства в ее использовании.
Двадцатеричная система.
У ацтеков и майя — народов, населявших в течении многих столетий обширные области американского континента и создавших там высокую культуру – была принята двадцатеричная система. Она же была принята у кельтов, населявших Западную Европу, начиная со второго тысячелетия до нашей эры. Следы двадцатеричной системы кельтов сохранились и в современном французском языке, например, «восемьдесят» по-французски будет как «четырежды двадцать». Число 20 встречалось и во французской денежной системе: франк делится на 20 су.
Следы двадцатеричной системы кельтов сохранились и в современном французском языке, например, «восемьдесят» по-французски будет как «четырежды двадцать». Число 20 встречалось и во французской денежной системе: франк делится на 20 су.
Шестидесятеричная система.
В древнем Вавилоне существовала сложная шестидесятеричная система. Мнения историков по поводу происхождения данной системы расходятся. Но не смотря на недоказанность гипотез возникновения шестидесятеричной системы, сам факт её существования и широкого распространения в древнем Вавилоне установлен. Эта система сохранилась до наших дней, например, в часе 60 минут, а в минуте 60 секунд или в системе измерения углов: градус = 60 минутам, минута = 60 секундам.
Алфавитные:
Древнеармянская, древнегрузинская, древнегреческая, славянская.
Машинные:
Двоичная система – это позиционная система с основанием 2.
Двоичная система встречалась у некоторых племен Австралии и Полинезии.
Восьмеричная система — это позиционная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Для представления чисел в ней используются цифры от 0 до 7.
Восьмеричная система чаще всего используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно. Широко использовалась в программировании и компьютерной документации, однако позднее была почти полностью вытеснена шестнадцатеричной.
Шестнадцатеричная система — это позиционная система счисления по основанию 16. В качестве цифр этой системы счисления обычно используются цифры от 0 до 9 и латинские буквы от A до F. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510 соответственно.
Шестнадцатеричная система широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной адресуемой единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами.
Прочие системы счисления:
Римская система
Способ записи чисел с помощью римских цифр такой: если цифра расположена справа, то ее значение прибавляется к предыдущей, например, число «XI» означает «одиннадцать», а если слева, то значение вычитается, например, число «IX», состоящее из тех же цифр, уже означает «девять». Кроме того, в римской системе счисления в числе вес цифры X в любой позиции равен десяти, например, число XXXII (тридцать два). Римская система счисления не прижилась, потому что римские числа трудно складывать или умножать, не говоря уже о более сложных функциях.
Кроме того, в римской системе счисления в числе вес цифры X в любой позиции равен десяти, например, число XXXII (тридцать два). Римская система счисления не прижилась, потому что римские числа трудно складывать или умножать, не говоря уже о более сложных функциях.
Вавилонская, Египетская, Китайская и другие.
Неколичественная система счета (качество выступает в роли количества: «много», «мало») была у эскимосов.
Из всех вышеперечисленных систем счисления меня очень заинтересовала двоичная система счисления.
Двоичная система счисления
В двоичной системе счисления основание равно двум. В этой системе счисления используются всего два знака, две цифры – «0» и «1».
Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.
В десятичной системе счисления мы располагаем десятью знаками-цифрами от 0 до 9. Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то появляется третий разряд – сотни.
После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то появляется третий разряд – сотни.
Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две цифры: 0 и 1. Как только разряд достигает своего предела, т.е. единицы, появляется новый разряд, а старый обнуляется.
Перевод чисел из двоичной системы счисления в десятичную
В двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Необходимо уметь переводить двоичные числа в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д.
пример:
1365 = 1000 + 300 + 60 + 5 или
1365 = 1 * 103 + 3 * 102 + 6 * 101 + 5 * 100
Если посмотреть на эту запись внимательно мы увидим здесь цифры 1, 3, 6 и 5 — это набор цифр из которых состоит число 1365.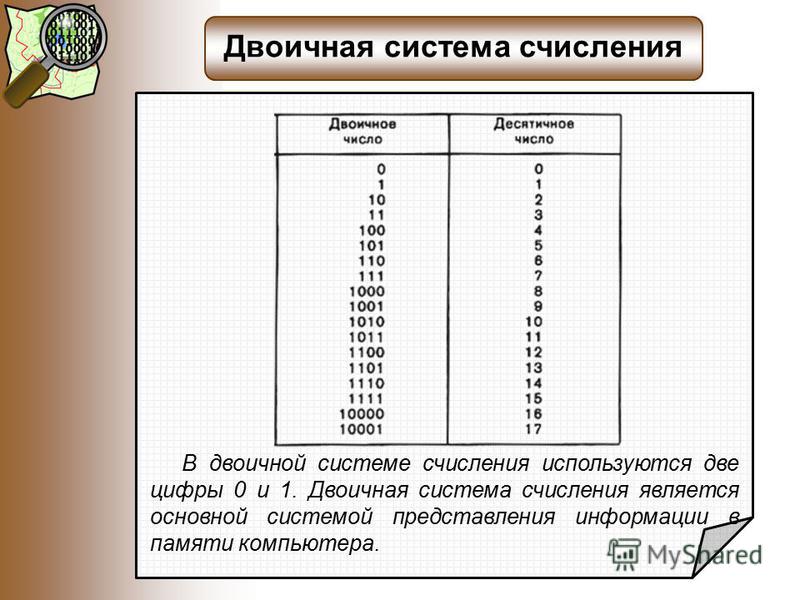 Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Аналогично можно разложить и любое двоичное число, только основание здесь будет 2.
Сложение в двоичной системе счисления
При сложении чисел в двоичной системе важно помнить, что она имеет всего два символа — 0 и 1. Никаких других символов в ней быть не может! Поэтому сложение двух единиц 1 + 1 дает не 2, как в десятичной системе, а 10, так как 10 – это следующее за единицей число в двоичной системе.
0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 10
Эти правила необходимы, чтобы складывать числа в двоичной системе в столбик. В случае прибавления единицы к единице, единица идет в следующий разряд. Прибавление нуля к любому двоичному числу не изменит это число. Большие двоичные числа удобно складывать в столбик. Правила в двоичной системе аналогичны сложению правилам сложения в столбик в десятичной системе.
Вычитание в двоичной системе счисления
Вычитать двоичные числа несколько сложнее, чем складывать, для этой цели есть два метода: вычитание с использованием дополнительного кода числа и вычитание в столбик.
Метод вычитания с использованием дополнительного кода приводит поставленную задачу к операции сложения путем преобразований над вычитаемым числом. Это преобразование называется дополнительным кодом (ДК). Определить его можно по следующему алгоритму: сначала значения всех позиций вычитаемого числа меняются на противоположные: нули на единицы, а единицы на нули. Потом к получившемуся промежуточному результату прибавляется двоичная единица, т.е. число, которое увеличивает его младший разряд на 1 в степени 4.
пример: найти разность чисел: 11001 – 1101
а) меняем значения всех позиций вычитаемого числа на
противоположные:
1 1 0 1 на
0 0 1 0
б) к получившемуся промежуточному результату прибавляем
двоичную единицу:
0 0 1 0
+ 0 0 0 1
= 0 0 1 1
в) складываем уменьшаемое число и число, полученное из 2-го
действия:
1 1 0 0 1
+ 0 0 1 1
= 1 1 1 0 0
г) завершающий этап данного метода – необходимо отбросить единицу,
стоящую в старшей позиции, т. е. 1 1 1 0 0 = 1 1 0 0.
е. 1 1 1 0 0 = 1 1 0 0.
Преимущества двоичной системы счисления:
— простота математических действий;
— возможность производить автоматическую обработку информации, используя только два состояния элементов компьютера;
— применение двоичной системы счисления для обработки информации на ЭВМ позволяет упростить построение аппаратуры и облегчить проектирование машин.
Недостатки двоичной системы счисления:
— быстрый рост числа разрядов в записи, представляющее двоичное число;
— трудность чтения значения числа, требующее определенного навыка;
— затруднительны расчеты, связанные с двоичным кодированием.
Применение двоичной системы счисления
Мы используем двоичную систему счисления в повседневной жизни. Такие значения как: да или нет, черное или белое, мужчина или женщина, правда или ложь можно описать двумя знаками – единица и ноль. Единица – это истина, ноль – это ложь.
На различных выключателях также присутствует двоичная система, 1 –включено, 0 – выключено. С помощью единиц и нулей можно описать любую ситуацию. В электронике также: есть сигнал – единица, нет сигнала – ноль.
С помощью единиц и нулей можно описать любую ситуацию. В электронике также: есть сигнал – единица, нет сигнала – ноль.
В современной технике примером применения двоичного кодирования является штрих-код. Его можно увидеть в любом магазине, на любом товаре. Он нужен для автоматического занесения информации о товаре в кассовый аппарат. Штрих-код состоит из 30 черных полос переменной толщины, разделенной промежутками переменной толщины. Толщина полос может принимать 4 значения, такую же толщину могут иметь и промежутки.
В век компьютерных технологий десятичная система счисления оказалась не удобной. Для вычисления одной десятичной операции необходимо иметь 10 различных потенциалов в цепи. Поэтому пришлось перейти на двоичную систему. В компьютерах все виды информации кодируются на машинном языке, в виде логических последовательностей нулей и единиц, потому что удалось создать надежно работающие технические устройства, которые могут со 100 процентной надежностью сохранять и распознавать не более двух различных состояний.
Один символ в двоичной системе называется бит (разряд). С помощью одного бита можно зашифровать две информации: ДА или НЕТ. Четыре бита – это полубайт, 8 бит – 1 байт, 16 бит – слово, 32 бита – двойное слово.
Сколько информации можно показать с помощью двух бит? Два бита – это два знака вместе в двоичной системе счисления. Простой пример:
У нас две руки – 2 бита. Сколько комбинаций рук мы можем применить:
Подняты две руки (11)
Обе руки опущены (00)
Правая рука поднята, левая опущена (01)
Левая рука поднята, правая опущена (10)
В итоге с помощью двух рук (2 битов) мы можем закодировать 4 информации. А теперь посмотрим сколько информации можно закодировать с помощью 3 битов.
Остались дома, играем, без друга (110)
Остались дома, делаем уроки, без друга (100)
Пошли в школу, играем, без друга (010)
Пошли в школу, делаем уроки, без друга (000)
Остались дома, играем, с другом (111)
Остались дома, делаем уроки, с другом (101)
Пошли в школу, играем, с другом (011)
Пошли в школу, делаем уроки, с другом (001)
Получается, что 000,001,011 и т. д. – это 3-х битная запись информации.
д. – это 3-х битная запись информации.
А сколько информации можно закодировать, используя 4 или более бит. Для этого есть простая формула:
Возможные варианты информации = 2 в степени N, где N – количество бит.
1.2. Двоичная система счисления и представление информации в компьютере.
Для представления информации в компьютере используется двоичная система счисления. Мы привыкли для записи чисел использовать десятичную систему счисления. На самом деле эта система счисления не единственная. В общем случае позиционной системой счисления называется способ представления чисел в виде последовательности цифр, при котором вклад цифры в величину числа зависит от положения цифры в записи числа.
Сначала разберемся
в том, что собой представляет десятичная
система счисления. Начнем с целых чисел.
Возьмем какое-либо число, записанное в
десятичной системе счисления, например,
397. В этом числе 7 единиц, 9 десятков и 3
сотни, т.е. величина числа равна
7*1+9*10+3*100 = 7*100+9*101+3*102. Аналогично устроена позиционная система
счисления по произвольному основанию.
В общем случае, пусть число X
записывается в системе счисления по
основанию M
в виде ANAN-1…A2A1A0 (число цифр в записи равно N+1).
Тогда величина числа вычисляется по
формуле X
= A0*M0 + A1*M1 + A2*M2 +…+ AN-1*MN-1 +
AN*MN.
Здесь A0,
A1,
A2,
…, AN-1,
AN – так называемые M-ричные
цифры, которые представляют значения
от 0 до M-1
включительно.
Аналогично устроена позиционная система
счисления по произвольному основанию.
В общем случае, пусть число X
записывается в системе счисления по
основанию M
в виде ANAN-1…A2A1A0 (число цифр в записи равно N+1).
Тогда величина числа вычисляется по
формуле X
= A0*M0 + A1*M1 + A2*M2 +…+ AN-1*MN-1 +
AN*MN.
Здесь A0,
A1,
A2,
…, AN-1,
AN – так называемые M-ричные
цифры, которые представляют значения
от 0 до M-1
включительно.
Например, записанное
в семиричной системе счисления число
236417 =
1+4*71+6*72+3*73+2*74 = 1+28+294+1029+4802
= 615410 .
Проще вычислить это значение с
использованием так называемой схемы
Горнера, которая заключается в расстановке
скобок в вышеприведенной сумме:
1+4*71+6*72+3*73+2*74 =
1+7*(4+7*(6+(7*(3+7*2) ) )= 1+7*(4+7*(6+7*17)
) = 1+7*(4+7*125) = 1+7*879 = 615410 .
Как вычислить цифры M-ричного представления числа? Для этого сначала посмотрим, как вычисляются цифры десятичного представления числа. Пусть X снова равно 397. При делении числа 397 на 10 получаем 39 и 7 в остатке. Остаток 7 выражает количество единиц в числе X. Теперь разделим 39 на 10. Получим частное 3 и 9 в остатке. Остаток 9 теперь представляет число лесятков. Наконец, делим 3 на 10 и получаем 0 и 3 в остатке. В результате этой операции получаем количество сотен – 3. Десятичная запись числа состоит из остатков 7, 9 и 3, но стоящих в обратном порядке.
По такой же схеме
вычисляются цифры в произвольной
M-ричной
системе счисления . Возьмем то же число
X=39710 (естественно, что величина числа не
зависит от той системы счисления, в
которой оно записано). Попробуем записать
его в пятиричной системе счисления. Для
этого разделим его на 5. Получим 79 и 2 в
остатке. Запомним первый остаток: A0 = 2. Далее разделим 79 на 5. Получим 15 и 4 в
остатке. Запомним второй остаток: A1 = 4. Теперь разделим на 5 число 15. Получим
3 и 0 в остатке. Следовательно, A2 = 0. Последнее деление 3 на 5 дает 0 и 3 в
остатке, то есть последняя полученная
цифра – это A3 = 3. Равенство частного нулю означает,
что процедуру следует завершить.
Полученные остатки следует записать в
обратном порядке. В результате проделанного
вычисления получаем, что 39710 = 30425.
Теперь разделим на 5 число 15. Получим
3 и 0 в остатке. Следовательно, A2 = 0. Последнее деление 3 на 5 дает 0 и 3 в
остатке, то есть последняя полученная
цифра – это A3 = 3. Равенство частного нулю означает,
что процедуру следует завершить.
Полученные остатки следует записать в
обратном порядке. В результате проделанного
вычисления получаем, что 39710 = 30425.
Для дробных чисел формула для вычисления величины числа слегка видоизменяется. Пусть число записано в системе счисления по основанию M в виде AnAn-1…A2A1A0, A-1A-2…A-h . Тогда его величина вычисляется по формуле
X = A-h*M-h +…+
A-2*M-2+A-1*M-1 + A0*M0 +
A1*M1 +
A2*M2 +…+An-1*Mn-1 +
An*Mn.
Так, число 1011,0112 представляет собой значение 2-3+2-2+20+21+23 = 11,37510 . Следует отметить, что в европейских языках для разделения целых и дробных разрядов числа вместо запятой используется точка.
В информатике
актуальны двоичная и шестнадцатиричная
системы счисления. В шестнадцатиричной
системе счисления требуется 16 цифр. В
качестве шестнадцатиричных цифр
используются 10 десятичных цифр от 0 до
9, а также шесть первых букв латинского
алфавита: A
(10), B
(11), C
(12), D
(13), E
(14) и F
(15). В двоичной системе счисления всего
две цифры: 0 и 1. В соответствии с общим
определением число, записанное в двоичной
системе счисления, является суммой
степеней двойки, соответствующих тем
местам в записи числа, на которых стоят
единицы. Например, число 10010111012 равно сумме
1+22+23+24+26+29 = 1+4+8+16+64+512 = 60510 .
Для хранения числа в памяти компьютера оно переводится в двоичную систему счисления. Каждая двоичная цифра соответствует одному разряду хранения информации в памяти компьютера – одному биту. В современных компютерах биты хранения информации объединяются в группы по восемь, которые называются байтами. Соответственно при хранении чисел двоичные цифры группируются по восемь. Например, для хранения числа 10011 100111012 требуется два байта. В первый байт записываются цифры 00010011, а во второй – цифры 10011101.
Шестнадцатиричная
и двоичная системы счисления связаны
между собой. Если в двоичной записи
числа сгруппировать двоичные цифры по
четыре (считая справа налево), а затем
заменить каждую четверку двоичных цифр
на шестнадцатиричную цифру, то получится
шестнадцатиричное представление числа.
Например, если в вышеприведенном примере
10011100111012 разбить
двоичные цифры на четыре группы 1 0011
1001 1101, то 12 = 116 , 00112 = 316 , 10012 =
916 , 11012 = D16 , и в результате получается представление
числа 10011100111012 в
шестнадцатиричной системе: 139D16 . Шестнадцатиричная
запись иногда используется, если
необходимо указать содержимое нескольких
байтов памяти компьютера (например, в
руководстве или учебном пособии).
Шестнадцатиричная
запись иногда используется, если
необходимо указать содержимое нескольких
байтов памяти компьютера (например, в
руководстве или учебном пособии).
Вся информация в
компьютере представляется в цифровой
форме. Это естественно для чисел. Для
нечисловой информации (например, текста)
используется стандартный прием:
всевозможные элементарные значения
нумеруются, и вместо самих значений
хранятся их номера (которые играют роль
кодов). Так, при представлении текстовой
информации все символы сводятся в
таблицу, а текст записывается номерами
символов. В любом случае коды нечисловых
данных, хранящиеся в компьютере, не
имеют содержания вне таблиц нумерации.
Количество двоичных разрядов, необходимых
для записи наибольшего номера объекта
данных, зависит от их общего объема.
Наибольшее число, которое в двоичной
системе счисления можно записать с
помощью N
цифр, состоит из N
единиц. Это число равно 1+2+4+…+2N-1 = 2N-1
. Например, с помощью восьми двоичных
цифр можно различать 28=256
символов текста.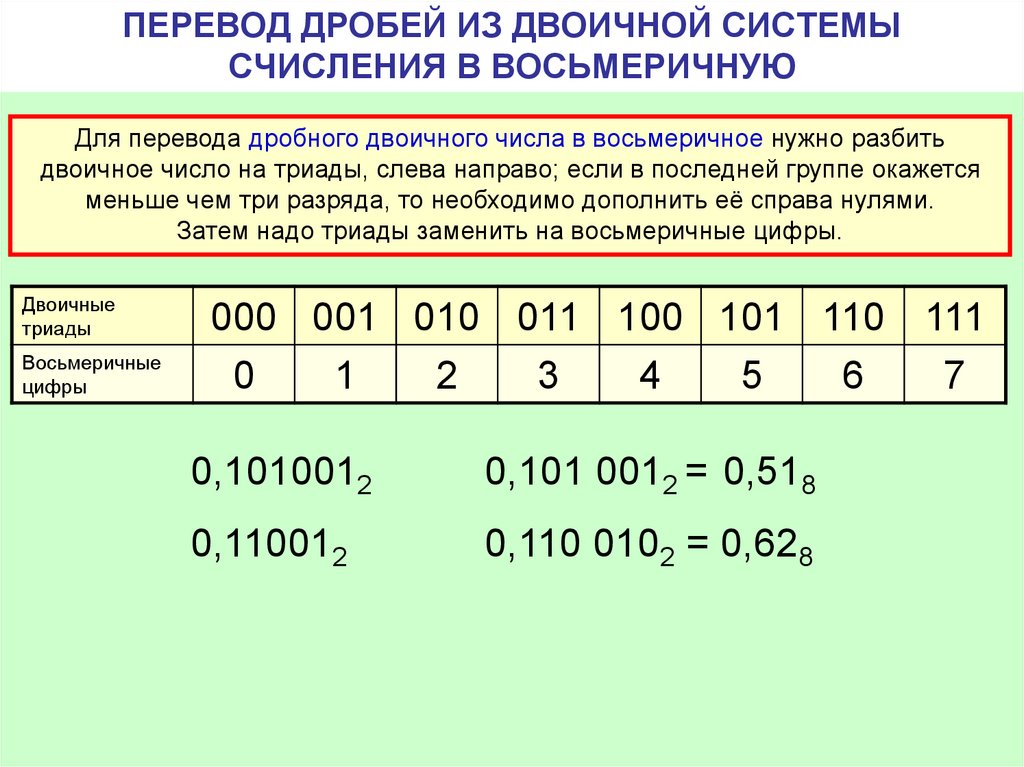
Это рассуждение настолько важно для всей идеологии хранения информации в двоичном коде, что в информатике принято измерять объем не в десятичной системе счисления, а в специальных единицах измерения, использующих степени двойки. Используя то обстоятельство, что 210=1024 не очень отличается от 103-1000, принято 1024 байт называть килобайтом (1Кб). Аналогично мегабайт – это 1024 килобайта (1Мг), а гигабайт – 1024 мегабайта (1Гб). Количество информации в современном мире столь велико, что приходится вводить еще одну единицу – терабайт, равную 1024 гигабайта (1Тб). Если не нужна особая точность, то можно считать, что:
1 терабайт = 1 000 гигабайт = 1 000 000 мегабайт = 1 000 000 000 килобайт = 1 000 000 000 000 байт.
То устройство
компьютера, в котором хранится информация,
называется оперативным запоминающим
устройством (ОЗУ) или оперативной
памятью. Если отвлечься от технических
деталей, оперативная память компьютера
представляет собой линейную
последовательность байтов.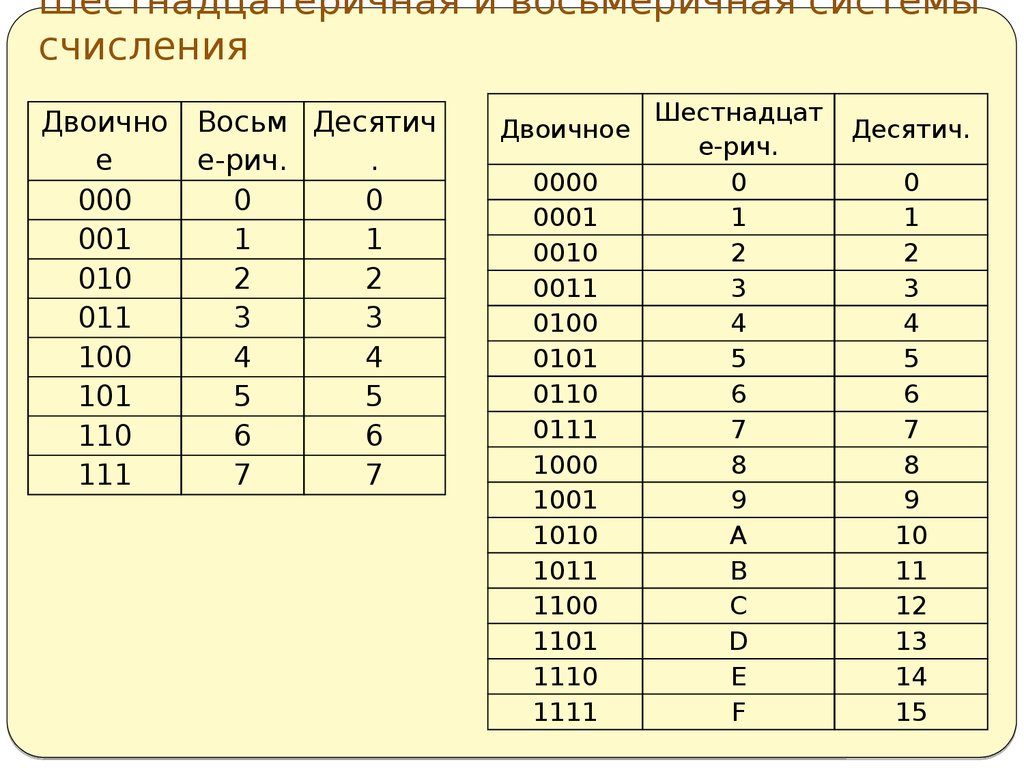 Длина этой
последовательности в современных
персональных компьютерах десятки сотни
мегабайт. Еще больше память суперкомпьютеров.
Для хранения чисел выделяется несколько
байтов (от одного до 10). Различают две
основных формы представления числа в
памяти компьютера. При первом способе
все разряды выделенных для хранения
числа байтов памяти последовательно
нумеруются, и двоичные цифры числа
непосредственно записываются в
соответствующие биты памяти. Один бит
выделяется для представления знака
числа (0 – плюс, 1 – минус). При втором
способе число представляется в так
называемой нормализованной (или
экспоненциальной) форме: X=M*10n,
где число М (называемое мантиссой)
заключено от 1 до 10, число n
(называемое порядком) — целое.
Длина этой
последовательности в современных
персональных компьютерах десятки сотни
мегабайт. Еще больше память суперкомпьютеров.
Для хранения чисел выделяется несколько
байтов (от одного до 10). Различают две
основных формы представления числа в
памяти компьютера. При первом способе
все разряды выделенных для хранения
числа байтов памяти последовательно
нумеруются, и двоичные цифры числа
непосредственно записываются в
соответствующие биты памяти. Один бит
выделяется для представления знака
числа (0 – плюс, 1 – минус). При втором
способе число представляется в так
называемой нормализованной (или
экспоненциальной) форме: X=M*10n,
где число М (называемое мантиссой)
заключено от 1 до 10, число n
(называемое порядком) — целое.
Используется
несколько форматов представления целых
и нормализованных чисел, которые
отличаются объемом и наличием или
отсутствием знакового бита. От этого
зависит диапазон чисел, которые могут
быть представлены в этом формате.
Например, если заранее известно, что
какая то целая величина положительна
и не может быть больше 255, то для ее
хранения достаточно одного байта. Для
хранения величин, изменяющихся в
диапазоне от -215 = –32768 до 215-1
= 32767, выделяется два байта. Если целое
число не вмещается в этот диапазон, то
для его хранения выделяется четыре
байта (диапазон от –231 до 231-1).
Для
хранения величин, изменяющихся в
диапазоне от -215 = –32768 до 215-1
= 32767, выделяется два байта. Если целое
число не вмещается в этот диапазон, то
для его хранения выделяется четыре
байта (диапазон от –231 до 231-1).
В принципе, подобный подход годится и для дробных чисел. В память компьютера заносятся цифры числа, но при этом считается, что на определенном месте этой записи стоит десятичная запятая. Такая форма записи называется представлением числа с фиксированной запятой. Максимальное число цифр в числе и конкретное положение запятой определяется форматом числа. Предусмотрено несколько вариантов формата представления чисел с фиксированной запятой в памяти компьютера.
Представление
нормализованных чисел называется
представлением числа с плавающей
запятой. Он используется для хранения
величин, которые могут принимать любые
значения. В памяти компьютера порядок
и мантисса хранятся отдельно в форме
двоичных целых чисел со знаком.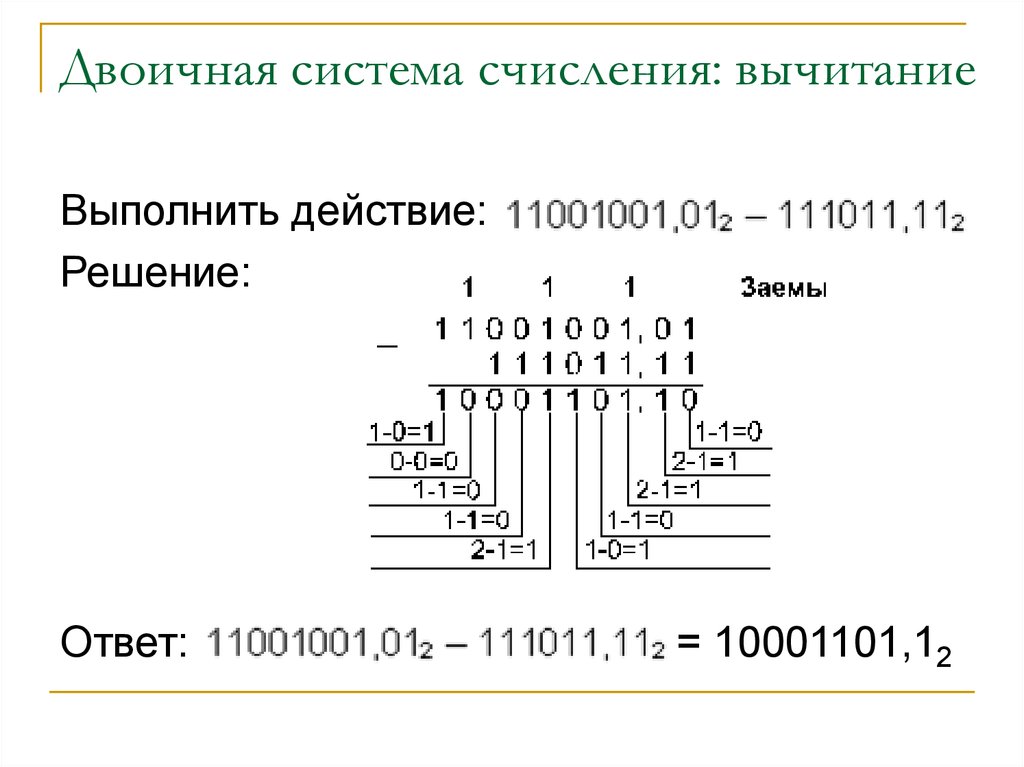 В
современных компьютерах используется
несколько форматов представления чисел
с плавающей запятой, которые отличаются
общим объемом представления чисел (6, 8
или 10 байтов), а также размерами памяти,
отводимой отдельно для мантиссы и
порядка. От этого зависят общий диапазон
возможных значений числовой величины
в компьютере и минимальная ошибка в
вычислениях, проистекающая из-за
невозможности запоминать в компьютере
большее количество знаков после запятой.
В
современных компьютерах используется
несколько форматов представления чисел
с плавающей запятой, которые отличаются
общим объемом представления чисел (6, 8
или 10 байтов), а также размерами памяти,
отводимой отдельно для мантиссы и
порядка. От этого зависят общий диапазон
возможных значений числовой величины
в компьютере и минимальная ошибка в
вычислениях, проистекающая из-за
невозможности запоминать в компьютере
большее количество знаков после запятой.
В реальной
действительности информация разнородна.
Обычно делят данные на числовую
информацию, текстовую информацию и
логическую информацию. Под текстовой
информацией понимается линейная
последовательность символов. Для
представления символа в памяти компьютера
используется следующая схема: фиксируется
множество допустимых символов текста
(обычно их 28 = 256 символов) и каждому символу
присваивается номер (от 0 до 255). После
этого последовательность символов
заменяется на последовательность
номеров, которые в памяти компьютера
записываются в виде целых двоичных
чисел (без знака). Один номер помещается
в одном байте памяти (именно поэтому
исторически сложилось разбиение памяти
на группы по восемь битов, так как
оказалось, что оптимальное количество
символов – 28,
а не, например, 29).
Один номер помещается
в одном байте памяти (именно поэтому
исторически сложилось разбиение памяти
на группы по восемь битов, так как
оказалось, что оптимальное количество
символов – 28,
а не, например, 29).
Множество допустимых
символов и их номера составляют таблицу
кодирования символов. Естественно, эта
таблица не должна зависеть от произвола
программиста или производителя
компьютеров, поскольку передача
информации в этом случае будет сильно
затруднена. В настоящее время существует
стандарт ASCII (American Standard Code for Informational
Interchange), содержащий набор и номера 128
основных символов (коды от 0 до 127) и набор
и номера 128 расширенных символов (коды
от 128 до 255). Поскольку в этот стандарт
не входят символы национальных алфавитов
(которых значительно больше, чем 128), в
каждой стране 128 кодов расширенных
символов (от 128 до 255) заменяются символами
национального алфавита. Другими словами,
каждый язык с алфавитом, отличным от
английского алфавита, устанавливает
свой стандарт. Осмысленный текст на
одном языке будет бессмысленным на
другом. Таким образом, для правильной
работы с текстом важна не только сама
информация, но и ее интерпретация.
Программа, которая правильно интерпретирует
колы символов в соответствии с таблицей
кодирования в определенном алфавите,
называется текстовым драйвером.
Осмысленный текст на
одном языке будет бессмысленным на
другом. Таким образом, для правильной
работы с текстом важна не только сама
информация, но и ее интерпретация.
Программа, которая правильно интерпретирует
колы символов в соответствии с таблицей
кодирования в определенном алфавите,
называется текстовым драйвером.
Логическая величина – это величина, которая может принимать всего два значения – true и false («истина» и «ложь»). Для хранения значения логической переменной достаточно одного бита. Обычно значение «ноль» бита памяти ассоциируется с истиной, значение «единица» – с ложью.
Для хранения в памяти
компьютера более сложных объектов,
таких как видеоизображения или звуки,
описания этих объектов преобразуются
в числовую форму. Способов кодирования
такого вида информации существует
достаточно много, но в конечном итоге
изображение или звук представляются в
виде последовательности нулей и единиц,
которые размещаются в битах памяти
компьютера и при необходимости извлекаются
оттуда и интерпретируются определенным
образом.
Контрольные вопросы по теме.
Переведите 134210 в семиричную систему счисления.
Переведите 13425 в десятичную систему счисления.
Переведите 134210 в двоичную систему счисления.
Переведите 100111010101102 в шестнадцатиричную систему счисления.
Что такое представление чисел с плавающей запятой и для чего оно используется?
Что такое ASCII-коды?
Почему в байте 8 битов?
Сколько книг поместится в 1Гб, если книги содержат 500 стр., а на странице примерно 2000 символов?
«Применение двоичной системы счисления в современности.»
Муниципальное общеобразовательное бюджетное учреждение
«Средняя общеобразовательная школа № 90»
Проект на тему:
Выполнил: ученик 8а класса
Шова Кирилл
Руководитель проекта
Прожерина А. Г
Г
Содержание:
Введение ……………………………………………………………………1
Глава I что, понимается под словом «число»?
1.1 Понятие числа
1.2 Язык чисел
Глава II Позиционные системы счисления
2.1 Двоичная система счисления
2.2 Системы счисления и их практическое применение
Глава III Практическая
3.1 Арифметические операции позиционных СС
3.2 Опрос учеников «Умеешь выполнять арифметические операции в двоичной, восьмеричной, шестнадцатеричных СС
4.Заключение………………………………………………………………..13
6.Литература……………………………………………………………………………………..14
Введение
В журнале «Юный ученый»
Прочитал. высказывание Пьер-Симона Лаплас (1749–1827): Мысль выражать все числа
немногими знаками, придавая им, кроме значения по форме, еще значение по месту,
настолько проста, что именно из-за этой простоты трудно оценить, насколько она
удивительна, Десятичная система счисления, которой мы пользуемся, кажется нам
единственно удобной и пригодной для вычислений. Но так ли это? Эту проблему я
решил выяснить. Задал себе вопрос, какие системы счисления существуют, и какое
применение находят различные системы счисления в практической деятельности
человека.
высказывание Пьер-Симона Лаплас (1749–1827): Мысль выражать все числа
немногими знаками, придавая им, кроме значения по форме, еще значение по месту,
настолько проста, что именно из-за этой простоты трудно оценить, насколько она
удивительна, Десятичная система счисления, которой мы пользуемся, кажется нам
единственно удобной и пригодной для вычислений. Но так ли это? Эту проблему я
решил выяснить. Задал себе вопрос, какие системы счисления существуют, и какое
применение находят различные системы счисления в практической деятельности
человека.
Тема «Применение двоичной системы счисления в современности»
Объект исследования: Двоичная система счисления.
Предмет исследования: Применение двоичной системы счисления
Проблема исследования: проблема применения арифметических операций систем счисления у подростков и найти ответ на вопрос «Является ли проблемой арифметические операции в позиционных систем счисления?»
Гипотеза: можно предположить, что Интернет-зависимость
проявляется в том, что люди утрачивают способность контролировать свое время в
сети, предпочитая виртуальную жизнь реальной.
Задачи исследования:
1. Узнать о позиционных системах счисления;
2. Узнать правила перевода позиционных системе счисления;
3. Провести социальный опрос учащихся «Знаешь в какой профессии используют двоичную систему»
4. предложить решение этой проблемы.
Методы исследования:
1. Анализ учебной литературы;
2. Методы практического исследования;
Поставил цель исследования. узнать, для чего нужна двоичная система счисления.
Для достижения поставленной цели сформулировали следующие
Задачи:
ü изучить литературу о позиционных системах счисления,
ü выяснить вопрос почему в ЭВМ информация представляется в двоичной системе счисления и чем она удобна,
ü Где еще применяется позиционные системы счисления.
В работе дается краткое описание
Позиционных систем
счисления они помогают во многих сферах нашей деятельности, связанной с
компьютером. Ученые используют компьютер для написания специальных программ,
которые позволяют выполнять различные сложные расчеты. На сегодняшний день
существует множество программ, которые способны выполнять те или иные
операции и в них конечно используются различные системы счисления. Но самая
актуальная система счисления, двоичная. В данной работе речь пойдет о двоичной
системе счисления. Это одна из наиболее часто используемых тем в школьном
курсе, для работы с компьютером. С приходом цифрового оборудования время
изменилось, и без компьютерных эффектов уже не обходится ни один эффект
электронного кода (двоичного). Учащиеся изучают тему «Системы счисления». В
изучение входит Двоичная система счисления. На уроках информатики А.Г
предлагает нам практические работы, цель обучиться арифметическим операциям в
двоичной системе счисления. Изучение данной темы приобретает особую актуальность,
потому что каждый день мы пользуемся счетом, о происхождении которого даже
многого не знаем. На ранних ступенях развития общества люди почти не умели
считать. Они отличали друг от друга совокупности двух и трех предметов, а
всякая совокупность, содержащая большее число предметов, объединялась в понятии
«много».
На сегодняшний день
существует множество программ, которые способны выполнять те или иные
операции и в них конечно используются различные системы счисления. Но самая
актуальная система счисления, двоичная. В данной работе речь пойдет о двоичной
системе счисления. Это одна из наиболее часто используемых тем в школьном
курсе, для работы с компьютером. С приходом цифрового оборудования время
изменилось, и без компьютерных эффектов уже не обходится ни один эффект
электронного кода (двоичного). Учащиеся изучают тему «Системы счисления». В
изучение входит Двоичная система счисления. На уроках информатики А.Г
предлагает нам практические работы, цель обучиться арифметическим операциям в
двоичной системе счисления. Изучение данной темы приобретает особую актуальность,
потому что каждый день мы пользуемся счетом, о происхождении которого даже
многого не знаем. На ранних ступенях развития общества люди почти не умели
считать. Они отличали друг от друга совокупности двух и трех предметов, а
всякая совокупность, содержащая большее число предметов, объединялась в понятии
«много». В наши дни, когда мы и не думаем о возникновении счета, в век
высоких технологий, значение данной работы трудно переоценить. Таким образом,
основная проблема исследовательской работы актуализируется на изучении арифметических
операциях позиционных систем счисления, их влиянии систем счисления на развитие
компьютеров.
В наши дни, когда мы и не думаем о возникновении счета, в век
высоких технологий, значение данной работы трудно переоценить. Таким образом,
основная проблема исследовательской работы актуализируется на изучении арифметических
операциях позиционных систем счисления, их влиянии систем счисления на развитие
компьютеров.
Глава I что понимается под словом «число»?
1.1 Понятие числа
Существует большое количество определению «Число» . О числах первый
начал рассуждать Пифагор. ПО высказыванию Пифагора «Все прекрасно благодаря
числу» По его учению число 2 означало гармонию, 5 цвет, 6 холод, 7 разум,
здоровье, 8 любовь, и дружбу Число — абстракция, используемая для количественной
характеристики объектов. Числа возникли еще в первобытном обществе в связи с
потребностью людей считать предметы. С течением времени по мере развития науки
число превратилось в важнейшее математическое понятие. Для решения задач и доказательства различных теорем необходимо
понимать, какие бывают виды чисел.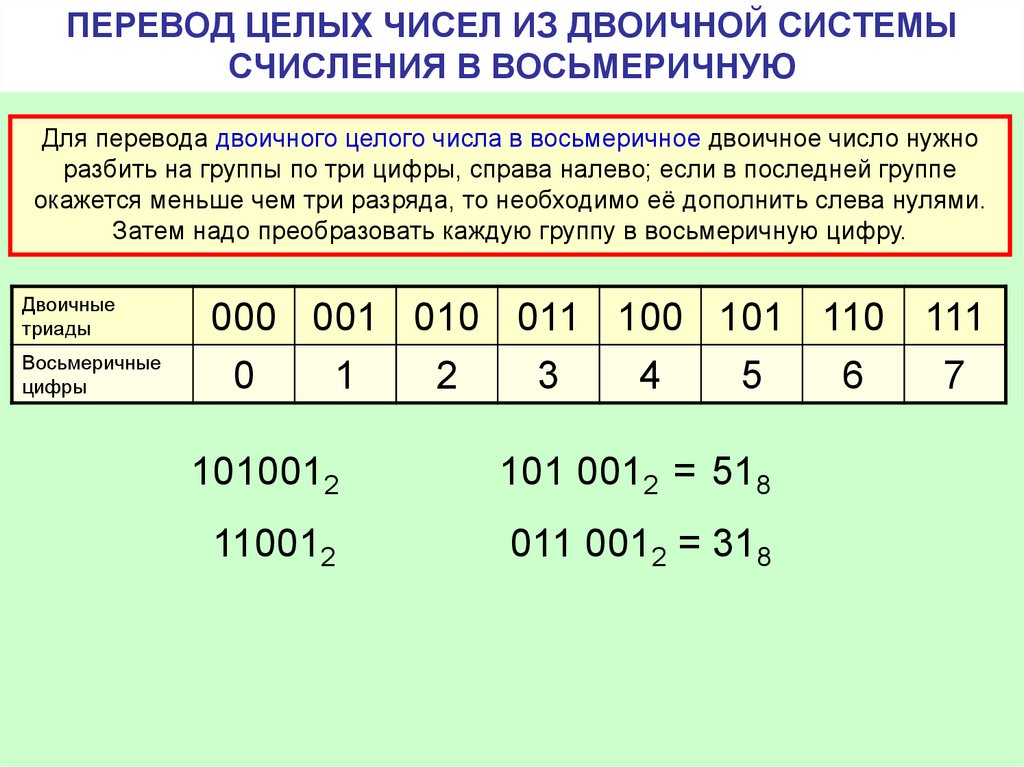 Основные виды чисел включают в себя:
натуральные числа, целые числа, рациональные числа, действительные числа. В журнале «Наука и жизнь просчитал» В повседневной
жизни мы, как правило, пользуемся десятичной системой счисления. Но это лишь
одна из многих систем, которая получила свое распространение, вероятно, по той
причине, что у человека на руках 10 пальцев. Однако эта система не всегда
удобна. Так, в вычислительной технике применяется двоичная система счисления.
Системой счисления называют совокупность приемов и правил наименования и
обозначения чисел, с помощью которых можно установить взаимно однозначное
соответствие между любым числом и его представлением в виде совокупности
конечного числа символов.
Основные виды чисел включают в себя:
натуральные числа, целые числа, рациональные числа, действительные числа. В журнале «Наука и жизнь просчитал» В повседневной
жизни мы, как правило, пользуемся десятичной системой счисления. Но это лишь
одна из многих систем, которая получила свое распространение, вероятно, по той
причине, что у человека на руках 10 пальцев. Однако эта система не всегда
удобна. Так, в вычислительной технике применяется двоичная система счисления.
Системой счисления называют совокупность приемов и правил наименования и
обозначения чисел, с помощью которых можно установить взаимно однозначное
соответствие между любым числом и его представлением в виде совокупности
конечного числа символов.
1.2 Язык чисел
В книге Иосиф Лазарев «Духовная
нумерология. Язык чисел», прочитал. Язык чисел – самый древний из всех существующих языков. Мало
того, числа древнее самого мира! Чтобы Бог мог создавать наш мир в первый день, второй,
третий и т. д., сначала должны были появиться числа.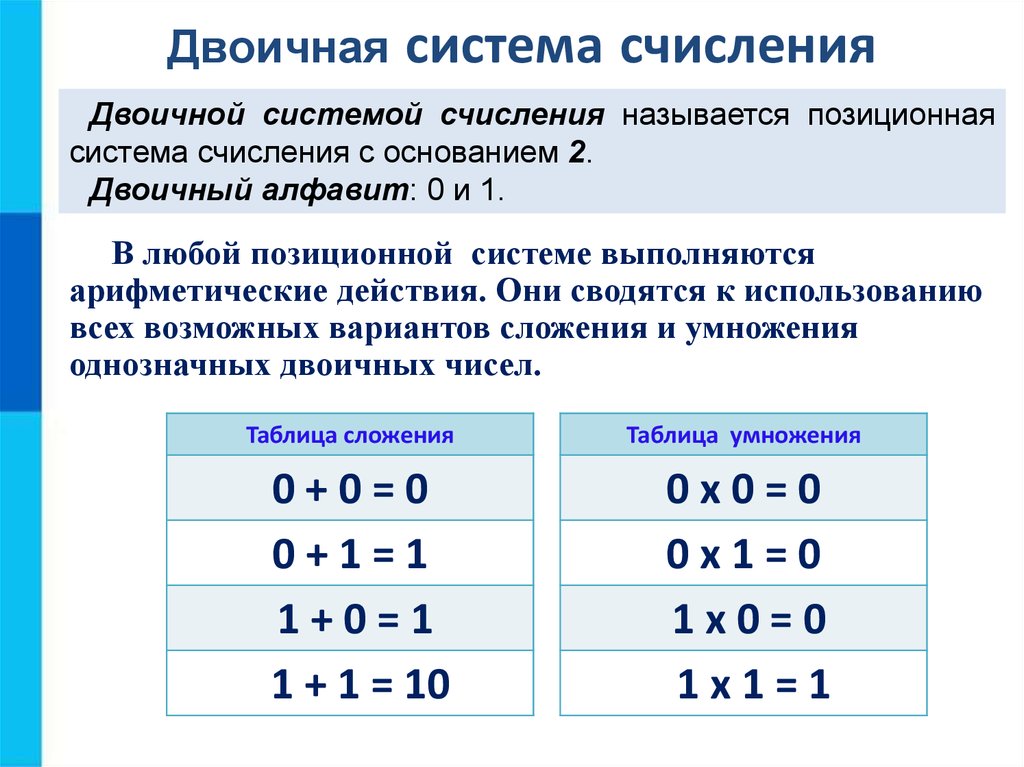 Существует
множество пособий по изучению разных языков. Но пособия по изучению языка чисел
до сих пор не существовало. Ведь невозможно считать ныне известные нумерологические
изыски учебниками по изучению языка чисел. Сплошь и рядом какие-то надуманные
методы, расчёты, многосложная терминология, от которой Ум либо окончательно
теряет способность отличать главное от второстепенного, либо вообще приходит в
отчаянье, словно студент, заваливший очередной экзамен. Все будто забыли о том,
что нумерология – это наука о смысле чисел, а не «трудная игра
в цифры». Действительно забыли или никогда не знали? Так или иначе, данная
книга представляет собой пособие именно по изучению языка чисел.
Существует
множество пособий по изучению разных языков. Но пособия по изучению языка чисел
до сих пор не существовало. Ведь невозможно считать ныне известные нумерологические
изыски учебниками по изучению языка чисел. Сплошь и рядом какие-то надуманные
методы, расчёты, многосложная терминология, от которой Ум либо окончательно
теряет способность отличать главное от второстепенного, либо вообще приходит в
отчаянье, словно студент, заваливший очередной экзамен. Все будто забыли о том,
что нумерология – это наука о смысле чисел, а не «трудная игра
в цифры». Действительно забыли или никогда не знали? Так или иначе, данная
книга представляет собой пособие именно по изучению языка чисел.
Глава II Позиционные системы счисления
2.1 В
журнале «Международный школьный научный вестник.» прочитал Система счисления – это способ
представления чисел и соответствующие ему правила действий над
числами. Система счисления – это знаковая система, в которой числа записываются
по определенным правилам с помощью символов некоторого алфавита, называемых
цифрами.
Двоичная система счисления
Главный редактор журнала «Международный школьный научный вестник.» кандидат медицинских наук Струкова Наталия Юрьевна журнала объяснила в статье по системам счисления пояснила: Примером позиционной системы счисления может служить система, в среде которой выполняются все операции по всему миру. Возникновение десятичной системы – это одно из самых важных событий в математике. Неудивительно, что история десятичной системы счисления занимает умы многих ученых. Существует несколько версий возникновения системы. Существует версия, что она зародилась в Китае. Есть также предположение, что ее изобрел Аль-Хорезми (узбекский математик). Но более распространенная версия состоит в том, что история возникновения десятичной системы началась в Индии. Сначала в этой системе счисления было всего девять цифр, ноль появился гораздо позднее.
Основоположником двоичной системы является немецкий философ
Лейбниц Готфрид Вильгельм. Двоичная система проста, так как для представления
информации в ней используются всего два состояния или две цифры. Такое
представление информации принято называть двоичным кодированием. Представление
информации в двоичной системе использовалось человеком с давних времен. Так,
жители островов Полинезии передавали необходимую информацию при помощи
барабанов: чередование звонких и глухих ударов (на подобии азбуки Морзе). С
точки зрения технической реализации использование двоичной системы счисления
для кодирования информации оказалось намного более простым, чем применение
других способов. Действительно, удобно кодировать информацию в виде последовательности
нулей и единиц: 0 – отсутствие электрического сигнала, 1 – наличие
электрического сигнала. Компьютеры используют двоичную систему потому, что она
имеет ряд преимуществ перед другими системами:
Такое
представление информации принято называть двоичным кодированием. Представление
информации в двоичной системе использовалось человеком с давних времен. Так,
жители островов Полинезии передавали необходимую информацию при помощи
барабанов: чередование звонких и глухих ударов (на подобии азбуки Морзе). С
точки зрения технической реализации использование двоичной системы счисления
для кодирования информации оказалось намного более простым, чем применение
других способов. Действительно, удобно кодировать информацию в виде последовательности
нулей и единиц: 0 – отсутствие электрического сигнала, 1 – наличие
электрического сигнала. Компьютеры используют двоичную систему потому, что она
имеет ряд преимуществ перед другими системами:
— для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток и нет тока, намагничен и не намагничен и т.п.), а не, например, с десятью, как в десятичной;
— представление информации посредством только двух состояний надежно и помехоустойчиво;
— двоичная арифметика намного проще десятичной.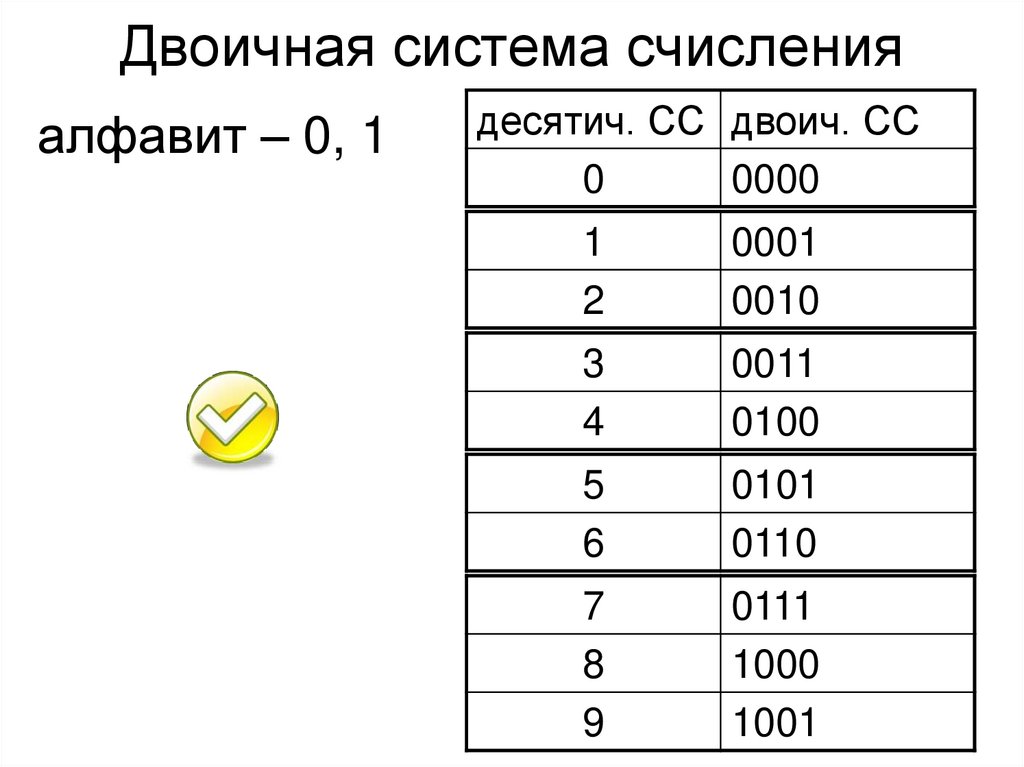
Но у двоичной системы есть один недостаток — быстрый рост числа разрядов, необходимых для записи чисел.
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи. Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Для программистов удобнее работать с более компактной записью.
В итоге было решено использовать альтернативные и более простые системы счисления: восьмеричную и шестнадцатеричную. Числа 8 и 16 являются степенями двойки (2 в третьей и 2 в четвёртой степени соответственно), поэтому выполнять преобразования из двоичной системы и, наоборот, гораздо легче, чем при десятичной системе счисления, которая не может похвастаться своей причастностью к степеням числа 2.
2.2 Системы счисления и их практическое применение
На сайте HintFoks.com прочитал: Развитие чисел тесно связано с потребностями общества в
измерениях, контроле, особенно в областях аграрной, промышленной и
налогообложения. Первые области применения чисел были связаны с созерцанием
звезд и земледелием. Изучение звездного неба позволило проложить торговые
морские пути, караванные дороги в новые районы и резко увеличить эффект
торговли между государствами. Обмен товарами приводил к обмену культурными
ценностями, к развитию толерантности как явления, лежащего в основе мирного
сосуществования различных рас и народов. Понятие числа всегда сопровождалось и
нечисловыми понятиями. Например, один, два, много. Эти нечисловые понятия
всегда ограждали числа. Числа придавали законченный вид всем наукам, где они
применялись.
Первые области применения чисел были связаны с созерцанием
звезд и земледелием. Изучение звездного неба позволило проложить торговые
морские пути, караванные дороги в новые районы и резко увеличить эффект
торговли между государствами. Обмен товарами приводил к обмену культурными
ценностями, к развитию толерантности как явления, лежащего в основе мирного
сосуществования различных рас и народов. Понятие числа всегда сопровождалось и
нечисловыми понятиями. Например, один, два, много. Эти нечисловые понятия
всегда ограждали числа. Числа придавали законченный вид всем наукам, где они
применялись.
Развитие чисел тесно связано с потребностями общества в
измерениях, контроле, особенно в областях аграрной, промышленной и
налогообложения. Первые области применения чисел были связаны с созерцанием звезд
и земледелием. Изучение звездного неба позволило проложить торговые морские
пути, караванные дороги в новые районы и резко увеличить эффект торговли между
государствами. Обмен товарами приводил к обмену культурными ценностями, к
развитию толерантности как явления, лежащего в основе мирного сосуществования
различных рас и народов.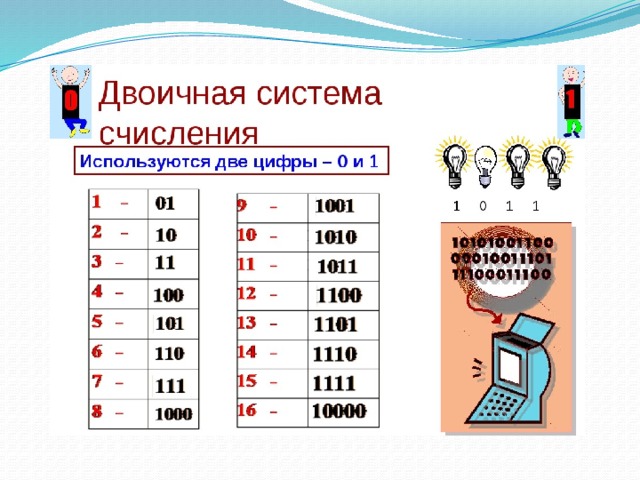 Понятие числа всегда сопровождалось и нечисловыми
понятиями. Например, один, два, много. Эти нечисловые понятия всегда ограждали
числа. Числа придавали законченный вид всем наукам, где они применялись.
Понятие числа всегда сопровождалось и нечисловыми
понятиями. Например, один, два, много. Эти нечисловые понятия всегда ограждали
числа. Числа придавали законченный вид всем наукам, где они применялись.
Для решения математических и физических задач, в которых трудно обойтись только целыми числами, используется представление чисел в форме с плавающей запятой.
В современных компьютерах, в зависимости от типа
операционной системы и конкретных прикладных программ, используются 8-разрядные
и 16-разрядные (Windows 95, 98, ХР) коды символов. Использование 8-разрядных
кодов позволяет закодировать 256 различных знаков, этого вполне достаточно для
представления многих символов, используемых на практике. При такой кодировке
для кода символа достаточно выделить в памяти один байт. Так и делают: каждый
символ представляют своим кодом, который записывают в один байт памяти. В
персональных компьютерах обычно используется система кодировки ASCII (American
standard Соде for Information Interchange) — американский стандартный код для
обмена информации. В этой системе не предусмотрены коды для русского алфавита,
поэтому в нашей стране используются варианты этой системы кодировки, в которые
включают буквы русского алфавита. Чаще всего используется вариант, известный
под названием «Альтернативная кодировка».
В этой системе не предусмотрены коды для русского алфавита,
поэтому в нашей стране используются варианты этой системы кодировки, в которые
включают буквы русского алфавита. Чаще всего используется вариант, известный
под названием «Альтернативная кодировка».
Компьютерные технологии постоянно совершенствуются, и в настоящее время все большее число программ начинает поддерживать шестнадцати битовый стандарт Unicode, который позволяет кодировать практически все языки и диалекты жителей Земли в силу того, что кодировка включает в себя 65 536 различных двоичных кодов.
Кроме того, числа в восьмеричной системе как минимум более приятны глазу и гораздо короче, чем их аналоги в двоичной системе.
Шестнадцатеричная система счисления так же, как и восьмеричная,
используется при составлении программ для более короткой и удобной записи
двоичных кодов — команд. Она наилучшим образом подходит для представления
данных и адресов в 8-ми, 16-ти и 32-разрядных ЭВМ(электронно вычислительная
машина). Байтовые значения удобно выражаются двумя символами, а 16 — и
32-разрядные величины легко поделить на байты.
Байтовые значения удобно выражаются двумя символами, а 16 — и
32-разрядные величины легко поделить на байты.
Учитывая, что спокойно сосуществуют разные системы счисления, вполне логично предположить, что между ними есть связь. Перевести число из одной системы счисления в другую довольно просто. Чтобы перевести из привычной нам десятичной системы в другую надо всего лишь использовать известное нам с начальной школы деление «уголочком» или столбиком. А так как из десятичной переводят делением, то обратно, что вполне логично, переводят умножением.
3.1 Арифметические операции позиционных СС
На цифровом образовательном ресурсе для школ, «Я класс». В основе проекта
лежит технологическая платформа Genexis, изначально написанная на языке C++ еще
в 1990-х гг. профессором российского Института информатизации образования Александром
Гуртовым. В
Информатике 8 класс. Узнал Арифметические операции во всех позиционных системах
счисления выполняются по одним и тем же хорошо известным правилам.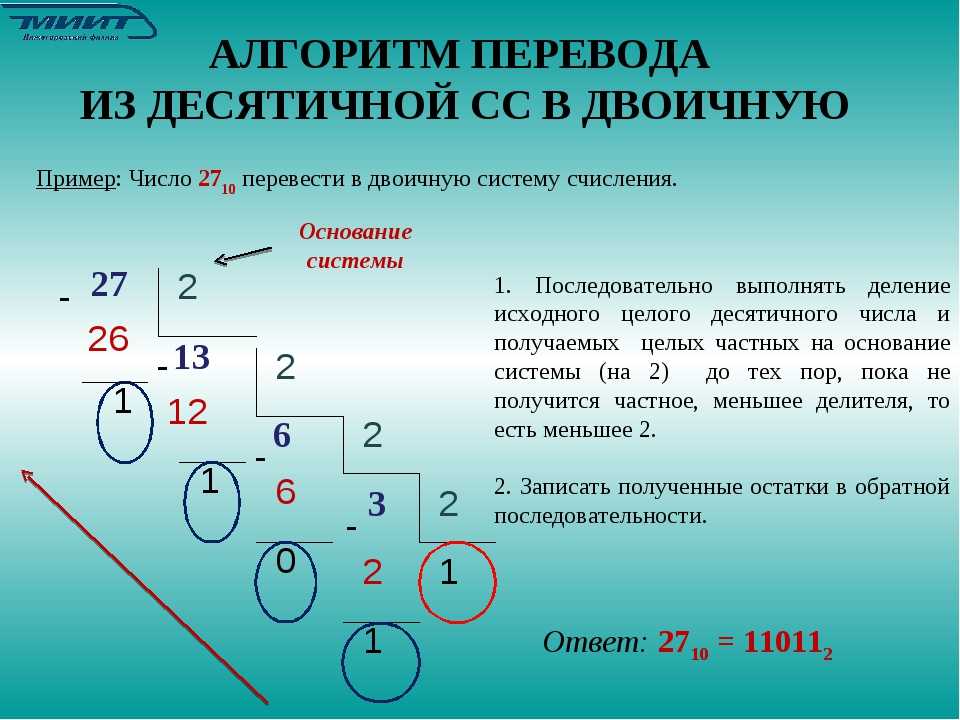
Правила выполнения арифметических операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление уголком. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
Таблицы сложения в любой позиционной системе счисления легко составить, используя правило счета:
Если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд.
Таблица сложения в двоичной системе:
Таблица сложения в восьмеричной системе:
Пример:
1) Сложим числа 15 и 6 в различных системах счисления.
Решение. Переведем числа 15 и 6 в двоичную и восьмеричную системы счисления и выполним сложение, используя таблицы сложения (см. выше).
Ответ: 15+6=2110=101012=258
2) Вычислим сумму чисел 438 и 5616.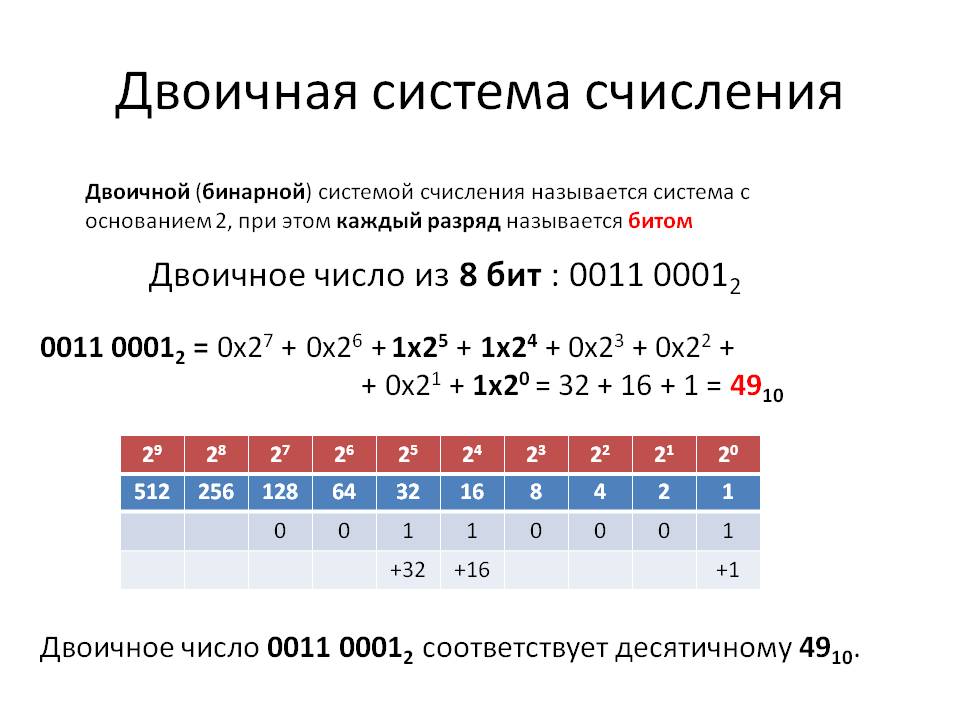 Результат представим в восьмеричной системе счисления.
Результат представим в восьмеричной системе счисления.
Решение: переведем число 5616 в восьмеричную систему счисления, используя поразрядный способ перевода разложением на тэтрады и триады:
Пользуясь правилами сложения в восьмеричной системе счисления, получаем:
Ответ: 438 + 5616 = 1718
Вычитание осуществляется по тем же правилам, что и в десятичной системе счисления.
При вычитании из меньшего числа большего производится заем из старшего разряда.
Пример:
Вычислим разность X−Y двоичных чисел, если X=10101002 и Y=10000102. Результат представим в двоичном виде.
Решение:
Ответ: 100102
Замечание. Если вам трудно складывать или
вычитать в системах счисления, отличных от десятичной, можете перевести числа в
десятичную систему счисления, выполнить арифметические действия, а затем
результат перевести в требуемую в ответе систему счисления.
Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
Таблица умножения в двоичной системе:
Таблица умножения в
восьмеричной системе: A
Умножение многоразрядных чисел в различных позиционных системах счисления происходит по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя.
Пример:
Перемножим числа 15 и 12.
Ответ: 15⋅12=18010=101101002=2648
Операция деления выполняется
по алгоритму, подобному алгоритму выполнения операции деления в десятичной
системе счисления. Следует только грамотно пользоваться теми цифрами,
которые входят в алфавит используемой системы счисления.
Следует только грамотно пользоваться теми цифрами,
которые входят в алфавит используемой системы счисления.
При выполнении любых арифметических операций над числами, представленными в разных системах счисления, следует предварительно перевести их в одну и ту же систему.
3.2 Опрос учеников «Умеешь выполнять арифметические операции в двоичной, восьмеричной, шестнадцатеричных СС
(СМ. ПРИЛОЖЕНИЕ РИС.1)
III. Заключение
Работая над этим проектом, я столкнулись с огромным количеством интересной информации. Я бы хотел бы закончить мое выступление словами немецкого философа Готфрида Вильгельма Лейбница: «Кто хочет ограничиться настоящим, без знания прошлого, тот никогда его не поймет…»
Приложение
рис.1
Анкета соц.опроса. (было опрошено 30 человек)
1. Умеешь выполнять арифметические операции в двоичной СС
2. Умеешь выполнять арифметические операции в восьмеричной СС?
3. Умеешь выполнять арифметические операции в шестнадцатеричной
СС?
Умеешь выполнять арифметические операции в шестнадцатеричной
СС?
4. Равно ли число, записанное в двоичной и в восьмеричной системах счисления ?
5. 11111112 сколько это будет в 1010
9.Список литературы.
1. Бендукидзе А.Д. О системах счисления // Квант — 1975 — №8 — с 59-61.
2. Вайман А.А. Шумеро-вавилонская математика. III — I тысячелетия до н.э. М.: Изд. вост. лит., 1961. — 278с.
3. Выгодский М.Я. Арифметика и алгебра в древнем мире. Изд. 2-е, испр. идоп. М.: Наука, 1967. — 367 с.
4. Глейзер Г.И. История арифметике в школе: IV — VI кл. Пособие для учителей. — М.: Просвещение, 1981. — 239 с.
5. Детская энциклопедия: [В 10-ти т.] Для среднего и старшего
возраста. Гл.ред. Маркушевич А.И. Т.2. — Мир небесных тел; Числа и фигуры. -М.:
Педагогика, 1972. — 480 с.
-М.:
Педагогика, 1972. — 480 с.
6. Подробнее см.: https://www.nkj.ru/archive/articles/5200/ (Наука и жизнь, СИСТЕМЫ СЧИСЛЕНИЯ)
Двоичная система счисления
— определение, преобразование, примеры
Двоичная система счисления — это один из четырех типов систем счисления, используемый для определения числа в двоичной системе. Двоичная система счисления представляет число только двумя цифрами, то есть 0 (ноль) и 1 (единица). В слове «двоичный» «би» означает «два». В результате это возвращает линию к представлению числа, используя только числа 0 и 1. Система счисления с основанием 2 используется для представления двоичных чисел. Например, (1101) 2 — двоичное число, где 2 — основание. Каждая цифра в двоичной системе счисления называется «бит».
Эта система счисления широко используется в компьютерах. Все входные данные, поступающие на компьютер, декодируются им в последовательность нулей или единиц перед дальнейшей обработкой, поскольку компьютер может понимать только двоичную информацию, которая представлена числами 0 или 1. Десятичное число просто преобразовать в числовое значение. двоичное число и наоборот. Обозначения для десятичных чисел и двоичных чисел различны. Например, десятичная дробь представлена как (15) 10 , где 10 — основание десятичного числа, а соответствующее двоичное число представлено как (1111) 2 , где 2 — основание двоичного числа.
Десятичное число просто преобразовать в числовое значение. двоичное число и наоборот. Обозначения для десятичных чисел и двоичных чисел различны. Например, десятичная дробь представлена как (15) 10 , где 10 — основание десятичного числа, а соответствующее двоичное число представлено как (1111) 2 , где 2 — основание двоичного числа.
Binary Number Table
Decimal Number | Binary Number | Decimal Number | Binary Number |
|---|---|---|---|
1 | 001 | 11 | 1011 |
2 | 010 | 12 | 1100 |
3 | 011 | 13 | 1101 |
4 | 100 | 14 | 1110 |
5 | |||
5 | |||
5 | |||
15 | 1111 | ||
6 | 110 | 16 | 10000 |
7 | 111 | 17 | 10001 |
8 | 1000 | 18 | 10010 | 110 | 9
9 | 1001 | 19 | 10011 |
10 | 1010 | 20 | 10100 |
Binary to Decimal Преобразование
Двоичное число преобразуется в десятичное число путем умножения каждой цифры двоичного числа на степень 1 или 0 до соответствующей степени 2. Предположим, что двоичное число имеет n цифр, B = a n-1 …a 3 a 2 a 1 a 0 . Теперь соответствующее десятичное число задается как D = (a n-1 × 2 n-1 ) +…+(a 3 × 2 3 ) + (a 2 × 2 2 ) + (а 1 × 2 1 ) + (а 0 × 2 0 ).
Предположим, что двоичное число имеет n цифр, B = a n-1 …a 3 a 2 a 1 a 0 . Теперь соответствующее десятичное число задается как D = (a n-1 × 2 n-1 ) +…+(a 3 × 2 3 ) + (a 2 × 2 2 ) + (а 1 × 2 1 ) + (а 0 × 2 0 ).
Давайте рассмотрим пример, чтобы лучше понять концепцию.
Пример: Преобразование (10011) 2 в десятичное число.
Решение:
Данное двоичное число равно (10011) 2 .
(10011) 2 = (1 х 2 4 ) + (0 х 2 3 ) + (0 х 2 2 ) + (1 х 2 1 ) + (1 х 2 1 ) + (1 х 9 2 ) 0 )
= 16 + 0 + 0 + 2 + 1 = (19)10
Следовательно, двоичное число (10011) 2 выражается как (19) 10 .
Преобразование десятичного числа в двоичное
Десятичное число преобразуется в двоичное путем непрерывного деления заданного десятичного числа на 2 до тех пор, пока мы не получим частное равное 1, и записываем числа снизу вверх.
Давайте рассмотрим пример, чтобы лучше понять концепцию.
Пример: Преобразуйте (28) 10 в двоичное число.
Решение:
Следовательно, (28) 10 выражается как (11100) 2 .
Арифметическая операция над двоичными числами
Двоичное сложение
Результат сложения двух двоичных чисел также является двоичным числом. Чтобы получить результат сложения двух двоичных чисел, мы должны сложить разряд двоичных чисел по разряду. Помните таблицу, приведенную ниже, при сложении двух двоичных чисел.
Binary number 1 | Binary number 2 | Addition | Carry |
|---|---|---|---|
0 | 0 | 0 | 0 |
0 | 1 | 1 | 0 |
1 | |||
1 0046 | 0 | 1 | 0 |
1 | 1 | 0 | 1 |
Binary Subtraction
The result вычитания двух двоичных чисел также является двоичным числом. Чтобы получить результат вычитания двух двоичных чисел, мы должны вычесть разряд двоичных чисел за разрядом. Вспомните таблицу, приведенную ниже, при вычитании двух двоичных чисел.
Чтобы получить результат вычитания двух двоичных чисел, мы должны вычесть разряд двоичных чисел за разрядом. Вспомните таблицу, приведенную ниже, при вычитании двух двоичных чисел.
Binary number 1 | Binary number 2 | Subtraction | Borrow |
|---|---|---|---|
0 | 0 | 0 | 0 |
0 | 1 | 1 | 1 |
1 | |||
1 0046 | 0 | 1 | 0 |
1 | 1 | 0 | 0 |
Binary Multiplication
The multiplication процесс двоичных чисел аналогичен умножению десятичных чисел.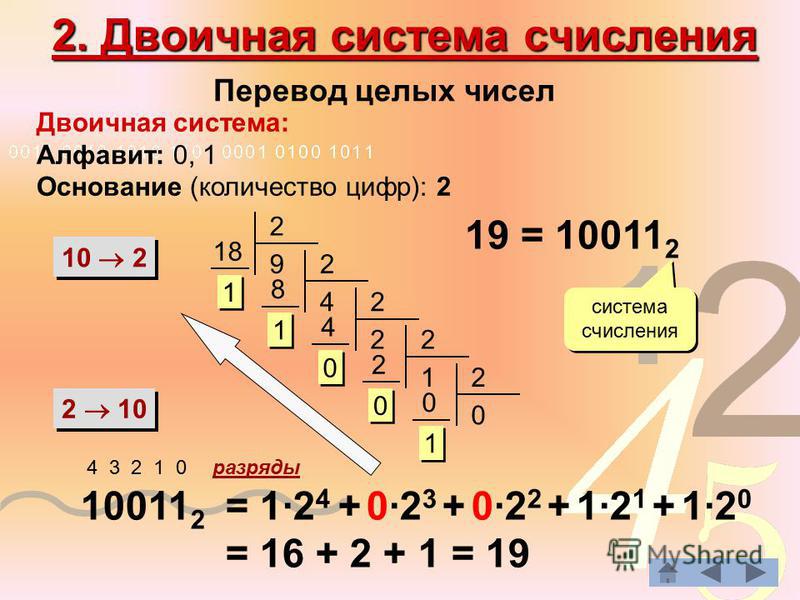 Правила умножения любых двух двоичных чисел следующие:
Правила умножения любых двух двоичных чисел следующие:
Binary number 1 | Binary number 2 | Multiplication |
|---|---|---|
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | |
1 | ||
1 |
Двоичное деление
Метод деления двоичных чисел аналогичен методу деления десятичных чисел.
Давайте рассмотрим пример, чтобы лучше понять концепцию.
Пример: Разделить (101101) 2 на (110) 2 .
Решение:
Дополнение 1 и 2 двоичного числа
- Дополнение до 1 двоичного числа получается путем инвертирования цифр двоичного числа.

Пример: Определить дополнение до 1 числа (10011) 2 .
Решение:
Данное двоичное число равно (10011)2.
Теперь, чтобы найти его дополнение до 1, мы должны инвертировать цифры данного числа.
Таким образом, дополнение (10011) 2 до 1 равно (01100) 2 .
- Дополнение до 2 двоичного числа получается путем инвертирования цифр двоичного числа, а затем добавления 1 к младшему значащему биту.
Пример: Определите дополнение до 2 (1011) 2 .
Решение:
Данное двоичное число равно (1011)2.
Чтобы найти дополнение до 2, сначала найдите его дополнение до 1, т. е. (0100) 2 .
Теперь, прибавив 1 к младшему значащему биту, мы получим (0101) 2 .
Следовательно, дополнение до 2 (1011) 2 равно (0101) 2 .
Задачи на основе двоичной системы счисления
Задача 1. Преобразование десятичного числа (98) 10 в двоичное.
Решение:
Чтобы получить двоичное число для 98, мы должны непрерывно разделить его на 2. .
Задача 2. Преобразование двоичного числа (1010101) 2 в десятичное число.
Решение:
Данный двоичный номер составляет (1011101) 2
= (1 × 2 0 ) + (0 × 2 1 ) + (1 × 2 2 ) 1 ) + (1 × 2 2 ) 1 ) + (1 × 2 2 ) + (1 × 2 2 ) + (1 × 2 2 + (0 × 2 3 ) + (1 × 2 4 ) + (0 × 2 5 ) + (1 × 2 6 )
= 1 + 0 + 4 + 0 + 16 + 0 + 64
= (85) 10
Таким образом, двоичное число 1010101 равно 85 в десятичном виде.
Задача 3: Разделить (11110) 2 на (101) 2 .
Решение:
Задача 4. Сложите (11011) 2 и (10100) 2 .
Решение:
Следовательно, (11011) 2 + (10100) 2 = (101111) 2 .
Задача 5: Вычесть (11010) 2 и (10110) 2 .
Решение:
Следовательно, (11010) 2 – (10110) 2 = (00100)
1 2 .
Задача 6: Умножьте (1110) 2 и (1001) 2 .
Решение:
Таким образом, (1110) 2 × (1001) 2 = (1111110)
1 2 .
Как Пингала создал двоичную систему счисления
«Физически разделены, но связаны цифровым способом!» должно быть нашим девизом в эти дни пандемии коронавируса. По правде говоря, цифровые технологии позволили нам пережить эти дни самоизоляции.
По правде говоря, цифровые технологии позволили нам пережить эти дни самоизоляции.
Знаете ли вы, на каком фундаментальном принципе работают современные цифровые технологии? Это двоичная система счисления.
Но знаете ли вы, что это дар древней индийской математики миру технологий. Древнеиндийский просодист и математик Пингала был первым, кто разработал и использовал двоичную систему счисления при изучении и анализе санскритских поэтических размеров (chandah / छन्द:) в своей работе Chandahshastra, составленной примерно в 3 веке до нашей эры.
Двоичная система счисления, как и десятичная система счисления, является позиционной системой. В десятичной системе счисления у вас есть десять цифр (от 0 и от 1 до 9). Точно так же в двоичной системе счисления у вас есть только две цифры, 0 и 1, которые называются битами. Бит — это сокращение от «Двоичная цифра».
Ачарья Пингала
Двоичная система счисления — это система счисления с основанием два. В десятичной системе счисления значение цифры зависит от ее положения, т. е. цифра, умноженная на степень десяти. В двоичной системе счисления значение цифры также зависит от ее положения, но здесь это цифра, умноженная на степень 2. 90) = 128 + 64 + 32 + 0 + 8 + 4 + 0 + 1 = 237
е. цифра, умноженная на степень десяти. В двоичной системе счисления значение цифры также зависит от ее положения, но здесь это цифра, умноженная на степень 2. 90) = 128 + 64 + 32 + 0 + 8 + 4 + 0 + 1 = 237
В таблице 1 приведены двоичные эквиваленты десятичных чисел от 0 до 31. Пожалуйста, обратите внимание на структуру битов двоичных чисел в этом стол.
Таблица 1
Теперь вам должно быть интересно, как Пингала разработал двоичную систему счисления? Чтобы понять это, давайте сначала разберемся с основами санскритской просодии.
Буквы на санскрите могут быть как длинными (гуру/गुरु स्वर), так и короткими (лагху/लघु स्वर) слогами. Эти два типа слогов являются основными строительными блоками санскритской просодии. Стих в классической санскритской литературе состоит из четырех четвертей или пад (पाद) в строфе. Размер стиха определяется количеством слогов и порядком их расположения в четверти.
Слог (अक्षर) — это гласный или гласный звук, которому предшествует один или несколько согласных.
Краткий слог — это тот, который заканчивается одной из кратких (храсва / ह्रस्व ) гласных, которыми являются a (अ), i (इ), u (उ), ṛ (ऋ) и ḷ (ऌ).
Даже краткий слог будет гуру, если за ним следует конъюнктивный согласный, анусвара или висарга.
Долгий слог определяется как слог с одной из долгих (диргха / दीर्घ) гласных, а именно ā (आ), ī (ई), ū (ऊ), ṝ (ॠ), e (ए), ai (ऐ ), о (ओ) и au (औ).
Последний слог метра считается гуру по выбору.
Давайте теперь разберем санскритский размер на примере. Ниже приведены первые две из восьми строф Бхавани аштакам (भवान्यष्टकम्), прекрасной композиции Ади Шанкарачарьи.
भवान्यष्टकम्
न तातो न माता न बनшить
न जाय|
Ни отца, ни матери; ни родственник, ни благодетель,
Ни сын, ни дочь; ни слуга, ни муж,
Ни жена, ни (мирское) знание; ни профессия,
Ты одна мое убежище, ты одна мое убежище, о Мать Бхавани.
भवाब्धावपा возможности
.
В бескрайнем океане мирского бытия я полон печали и сильно боюсь,
Я пал от чрезмерных желаний и жадности, опьяненный и опьяненный,
Всегда связанный узами этой жалкой сансары (мирского существования), 912 = 4096 различных расположений слогов Гуру и Лагху. Это означает, что у вас может быть 4096 различных метров с четвертью, состоящей из 12 букв.
Это означает, что у вас может быть 4096 различных метров с четвертью, состоящей из 12 букв.
Пингала разработал технику (пратьяй, प्रत्याय) или алгоритм под названием Прастаар (प्रस्तार, что означает разворачиваться или открываться) для зачисления всех возможных комбинаций слогов для четверти с длиной и буквами.
Таблица 2
Для метра, состоящего из 2 слогов:
На шаге 1 Пингала скопировала предыдущую матрицу непосредственно под собой. А на шаге 2 он заполнил верхнюю половину следующего столбца 2 G и нижнюю половину 2 L, как показано в Таблице 3.
Таблица 3
Для метра с 3 слогами:
На шаге 1 Пингала скопировала предыдущую матрицу непосредственно под собой. А на шаге 2 он заполнил верхнюю половину последнего столбца 4 G и нижнюю половину 4 L, как показано в Таблице 4.
1, пингала скопировала предыдущую матрицу сразу под себя. А на шаге 2 он заполнил верхнюю половину последней колонки 8 G и нижнюю половину 8 L, как показано в Таблице 5.
Таблица 5
Для счетчиков с большим количеством букв мы можем повторить эту технику рекурсивно. Если мы теперь заменим G на 0 и L на 1 в таблице 5, мы получим:
Таблица 6
двоичные эквиваленты чисел от 0 до 15. См. Таблицу 7.
Таблица 7
Вот как Пингала создал двоичную систему счисления. Это один из самых значительных вкладов Индии в мир математики.
Продолжение следует…
Отказ от ответственности: Мнения, высказанные в этой статье, принадлежат автору. Indic Today не несет ответственности за точность, полноту, пригодность или достоверность любой информации в статье.
Как это работает? Полное руководство 5, 6, 7, 8, 9.
Когда вы считаете числа, вы должны повторно использовать примитивные числа после достижения 9. Это связано с тем, что нет специальных символов для чисел после 9. Число после 9 равно 10, которое представляет собой комбинацию примитивных цифр 1 и 0
В двоичной системе есть только два простых числа: 0 и 1.
Когда вы считаете двоичными числами, вы достигаете предела отсутствия цифр намного быстрее. Это означает, что вы должны повторно использовать 0 и 1 уже после второго числа.
0 1 10 11 100 101 110 111
Это подробное руководство по двоичной системе счисления. Это руководство отвечает на такие вопросы, как:
- Что такое системы счисления, такие как десятичная или восьмеричная?
- Что такое двоичная система счисления?
- Как преобразовать двоичные числа в десятичные?
Начнем с традиционного подсчета чисел. Пожалуйста, не пропускайте этот этап, так как это важный первый шаг к пониманию двоичной системы.
Подсчет чисел
Десятичная система счисленияВ повседневной жизни вы привыкли использовать числа от 0 до 9.
Это называется десятичной системой счисления. В десятичной системе существует десять различных числовых символов. Это, конечно же:
В десятичной системе существует десять различных числовых символов. Это, конечно же:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Теперь, когда вы считаете числа в десятичной системе, вы сталкиваетесь с проблемой. Когда нужно подсчитать более 9 элементов, у вас закончатся числовые символы. Число 9 — последняя цифра, которую вы можете использовать.
Чтобы преодолеть это, вы начинаете повторно использовать номера. Для этого вы стратегически размещаете цифры рядом друг с другом, чтобы представить числа больше 9.
Например, число после 9 равно 10, что является комбинацией единицы и нуля. Невозможно представить число десять уникальным символом.
Когда вы продолжите считать с 10, вы столкнетесь с той же проблемой в 19. Еще раз, вы использовали все числа в десятичной системе и должны повторно использовать их для дальнейшего счета. Теперь пришло время поместить число 2 слева и запустить числа справа от 0 до 9..
Теперь пришло время поместить число 2 слева и запустить числа справа от 0 до 9..
Этот процесс продолжается до тех пор, пока вы не достигнете числа 99. Теперь оба числа полностью прошли десятичную систему. Невозможно выразить большее десятичное число двумя цифрами. В этом случае нужен третий. Теперь счетчик на 100.
Эта идея продолжается до бесконечности.
Очевидно, подсчет чисел происходит автоматически. Вам никогда не придется разбивать его таким образом, если только вы не хотите узнать, как работает двоичная система счисления.
Но чтобы понять, как работает двоичная система, нужно знать механизм повседневных чисел. В частности, вам нужно увидеть, как вы можете повторно использовать числа в системе для выражения больших чисел.
Системы счисления
В предыдущем разделе вы узнали, как работают «традиционные» десятичные числа. Но нет ничего особенного в наличии десяти чисел в системе счисления. На самом деле номеров может быть сколько угодно.
Естественно, наличие другой базовой системы влияет на способ выполнения вычислений.
Например, давайте создадим систему счисления с основанием восемь (также называемую восьмеричной системой счисления).
В системе с основанием восемь вы можете использовать только восемь простых чисел:
0, 1, 2, 3, 4, 5, 6, 7
Теперь давайте начнем считать так же, как вы это делали в предыдущем разделе. Но поскольку теперь у вас есть только восемь цифр на выбор, вам придется начать повторное использование цифр раньше.
Например, посчитаем до восьми в восьмеричной системе:
0 1 2 3 4 5 6 7 10
Как видите, число после 7 равно 10. Это потому, что в системе с основанием восемь последняя доступная цифра числа — 7. Таким образом, вы должны начать повторно использовать цифры точно так же, как раньше. Но вместо того, чтобы делать это после числа 9, вы должны сделать это после 7 в восьмеричной системе.
Это потому, что в системе с основанием восемь последняя доступная цифра числа — 7. Таким образом, вы должны начать повторно использовать цифры точно так же, как раньше. Но вместо того, чтобы делать это после числа 9, вы должны сделать это после 7 в восьмеричной системе.
В качестве другого примера, посчитаем от 0 до 20, используя одновременно десятичную и восьмеричную системы:
| Десятичное (с основанием 10) | Восьмеричное (по основанию 8) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | 13 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | 14 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | 15 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | 16 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | 17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | 20 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | 21 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | 22 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | 23 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | 24 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Binary | Decimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
| 10000 | 16 |
| 10001 | 17 |
| 10010 | 18 |
| 10011 | 19 |
| 10100 | 20 |
| 10101 | 21 |
| 10110 | 22 |
| 10111 | 23 |
| 11000 | 24 |
| 11001 | 25 |
| 11010 | 26 |
| 11011 | 27 |
| 11100 | 28 |
| 11101 | 29 |
| 11110 | 30 |
| 11111 | 31 |
Давайте рассмотрим двоичные числа. Существует четкая закономерность между двоичными числами и десятичными числами.
Существует четкая закономерность между двоичными числами и десятичными числами.
Всякий раз, когда за единицей следуют только нули, соответствующее десятичное число является степенью двойки.
Например:
- 1-> 1
- 10-> 2
- 100-> 4
- 1000-> 8
- 10000-> 16
Теперь, дайте Reb-WRITE. из двух:
- 1 —> 2⁰
- 10 —> 2¹
- 100 —> 2²
- 1000 —> 2³
- 10000 —> 2⁴ .
- .
- .
Это наблюдение поможет вам вручную преобразовать двоичные числа в десятичные числа.
На основании этого наблюдения мы можем создать таблицу для Powers от 0 до 7:
| 2⁷ = 128 | 2⁶ = 64 | 2⁵ = 32 | 2⁴ = 16 | 2³ = 8 | 3 2 2 2⁴ = 16 | 2³ = 8 | 3 2 2 2⁴ = 16 | 2³ = 8 | 23 2 2⁴ = 16 | 2. = 4 | 2¹ = 2 | 2⁰ = 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
This table represents an eight -значное двоичное число.
Теперь всякий раз, когда вы видите «1» в любом столбце, это означает, что в двоичном числе присутствует соответствующая степень двойки.
Таким образом, чтобы преобразовать двоичное число в десятичное, вы должны сложить все существующие числа в таблице наблюдений.
Позвольте мне показать вам, что я имею в виду.
Например, давайте преобразуем двоичное число 1101 в десятичное число.
Прежде всего, всякий раз, когда вы имеете дело с двоичными числами, вы можете добавлять столько нулей слева, сколько хотите.
Итак, когда мы говорим о 1101 , мы также можем записать его как 00001101 .
Теперь давайте вставим эти 0s и 1s этого числа в двоичную таблицу:
| 2⁷ = 128 | 2⁶ = 64 | 2⁵ = 32 | 2⁴ = 16 | 2= = 8 | 2 2⁴ = 16 | 2³ = 8 | 33 2 2⁴ = 16 | 2= = 8 | 2 4. 42¹ = 2 | 2⁰ = 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 9.1 |
Чтобы преобразовать число в десятичное, начнем справа.
- Присутствует один 2⁰ = 1.
- Нет 2¹ = 2.
- Имеется одно 2² = 4.
- Имеется один 2³ = 8.
- Нет 2⁴ = 16.
- Нет 2⁵ = 32.
- Нет 2⁶ = 64.
- Нет 2⁷ = 128.
Теперь давайте сложим значения, присутствующие в двоичном коде. Это дает нам 1 + 4 + 8 = 13. Таким образом, двоичное число 1101 равно 13 в десятичной системе счисления.
Подведение итогов
Сегодня вы узнали, как работает двоичная система счисления.
Короче говоря, в двоичной системе вы можете производить вычисления только с числами 0 и 1.
В «традиционной» системе счисления у вас есть десять чисел для выполнения вычислений. Когда вы считаете числа традиционным способом, вы должны повторно использовать цифры после числа 9.. Например, число 64 представляет собой комбинацию примитивных цифр 6 и 4.
В двоичной системе идея та же. Но поскольку можно использовать только два числа, повторное использование чисел происходит уже сразу после числа 1.
Например, число 3 в десятичной системе равно 11 в двоичной системе.
0 1 10 11
Спасибо за внимание!
Читайте также
Хотите узнать еще одну интересную систему счисления? Обязательно проверьте, какие шестнадцатеричные цвета. В этом руководстве рассказывается о шестнадцатеричной (16-базовой) системе счисления.
Разница между десятичной и двоичной системами счисления
В математике система, которая используется для представления чисел в различных формах, определяется как система счисления . Математическое значение, которое используется для подсчета, измерения и выполнения различных арифметических вычислений, называется числом. В зависимости от свойств числа подразделяются на различные типы, такие как натуральные числа, целые числа, дроби, рациональные и иррациональные числа и так далее. Точно так же у нас есть разные виды систем счисления, основанные на разных свойствах, такие как двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления. Мы можем преобразовать число из любой системы счисления в любую из трех других систем счисления.
В зависимости от свойств числа подразделяются на различные типы, такие как натуральные числа, целые числа, дроби, рациональные и иррациональные числа и так далее. Точно так же у нас есть разные виды систем счисления, основанные на разных свойствах, такие как двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления. Мы можем преобразовать число из любой системы счисления в любую из трех других систем счисления.
Десятичная система счисления
Система счисления, которая представляет число от 0 до 9 цифр, представляет собой десятичную систему счисления . Десятичная система счисления состоит из десяти цифр, т. е. 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Основание числа в этой системе равно 10. В десятичной системе счисления число выражается в терминах степеней 10, т. Е. Позиции последовательных цифр слева от десятичной точки представляют единицы, десятки, сотни, тысячи и так далее. Некоторые примеры чисел в десятичной системе счисления: (23) 10 , (123) 10 , (5547) 10 , (6531) 10 и так далее. В повседневной жизни мы чаще всего представляем числа в десятичной системе счисления.
В повседневной жизни мы чаще всего представляем числа в десятичной системе счисления.
Например, (123) 10 в степени 10 выражается как 1 × 10 2 + 2 × 10 1 + 3 × 10 0 . 1 в разряде сотен, 2 в разряде десятков и 3 в разряде единиц.
Двоичная система счисления
Система счисления, которая выражает число цифрами 0 и 1, представляет собой двоичная система счисления . Двоичная система имеет только две цифры, т. е. 0 и 1. Основание числа в этой системе равно 2. В двоичной системе счисления число выражается через степени двойки. Например, десятичное число 26 равно выражается как (11010) 2 в двоичной системе. Двоичные цифры 0 и 1 используются во всех компьютерных кодах и языках, таких как C, C++, Java и т. д., для написания программы и кодирования любых цифровых данных.
Двоичное число (1011) 2 выражается в степени двойки как (1 × 2 3 ) + (0 × 2 2 ) + (1 × 2 1 ) + (1 × 2 0 ).
Decimal number | Binary number |
|---|---|
1 | 01 |
2 | 10 |
3 | 11 |
4 | 100 |
5 | 101 |
6 | 110 |
7 | 111 |
8 | 1000 |
9 | 1001 |
10 | 1010 |
КОНТАРИ1008
Двоичные числа могут быть преобразованы в десятичные числа, а десятичные числа могут быть преобразованы обратно в двоичные числа с использованием следующих правил:
Преобразование двоичных чисел в десятичные
двоичная система счисления, тогда как десятичная система счисления представляет число от 0 до 9 цифр. Теперь, чтобы преобразовать двоичное число в десятичное, умножьте каждую цифру двоичного числа на степень 2.
Теперь, чтобы преобразовать двоичное число в десятичное, умножьте каждую цифру двоичного числа на степень 2.
Если B = a n-1 …a 3 a 2 a 1 a 0 — двоичное число, состоящее из n цифр, то соответствующее десятичное число будет
D = (
0 n-1 × 2 n-1 ) +…+(a 3 × 2 3 ) + (a 2 × 2 2 ) + (a 1 90 9 03 9 9 0 0 0 9 0 2 9 0 0 0 2 9 + (а 0 × 2 0 ).
Пример: Преобразование (11001) 2 в десятичное число.
Решение:
Данное двоичное число равно (11001) 2 .
(11001) 2 = (1 × 2 4 ) + (1 × 2 3 ) + (0 × 2 2 ) + (0 × 2 1 ) + (12 × 9 ) 0 )
= 16 + 8 + 0 + 0 + 1 = (25) 10
Следовательно, двоичное число (11001) 2 выражается как (25) 10 .
Преобразование десятичного числа в двоичное
Чтобы преобразовать десятичное число в двоичное, делите данное число на 2 непрерывно, пока не получите частное, равное 1. Обратите внимание, что мы должны записывать числа снизу вверх.
Пример: Преобразование (31) 10 в двоичное число.
Solution:
Therefore, (31) 10 is expressed as (11111) 2
Difference between the binary and decimal systems
Binary Number System | Десятичная система счисления | Система счисления, которая представляет число от 0 до 9 цифр, является десятичной системой счисления. |
|---|---|---|
| Двоичная система имеет только две цифры, т. е. 0 и 1. | Десятичная система счисления имеет десять цифр, т. е. 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. . | |
Основание числа в этой системе равно 2. | Основание числа в этой системе равно 10. | |
| В двоичной системе счисления число выражается в степени двойки. | В десятичной системе счисления число выражается в степени 10. | |
| Десятичное число 26 выражается как (11010) 2 в двоичной системе. | Двоичное число (11010) 2 равно 26 в десятичной системе счисления. |
Решенный пример преобразования двоичного числа в десятичное и обратно
Пример 1: Преобразование (65) 10 в двоичное число.
Решение:
Следовательно, (65) 10 выражается как (1000001) 2
Пример 2. Преобразование (10101) 2 десятичного числа в
Решение:
Данное двоичное число равно (10101) 2 .
(10101)2 = (1 × 2 4 ) + (0 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) )
= 16 + 0 + 4 + 0 + 1 = (21) 10
Следовательно, двоичное число (10101) 2 выражается как (21) 10 .
Пример 3: Преобразование (111001) 2 в десятичное число.
Решение:
Данное двоичное число равно (111001) 2 .
(10101)2 = (1 × 2 5 ) + (1 × 2 4 ) + (1 × 2 3 ) + (0 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )
= 32 + 16 + 8 + 0 + 0 + 1 = (57) 10
Следовательно, двоичное число (111001) 2 выражается как (57) 10 .
Пример 4: Преобразование (46) 10 в двоичное число.
Решение:
Следовательно, (46) 10 выражается как (101110) 2 .
Часто задаваемые вопросы о десятичной и двоичной системах счисления
Вопрос 1: Что такое двоичная и десятичная системы счисления?
Ответ:
Система счисления, которая выражает число цифрами 0 и 1, является двоичной системой счисления, тогда как десятичная система счисления представляет число цифрами от 0 до 9.
Вопрос 2: Как преобразовать двоичное число в десятичное?
Ответ:
Чтобы преобразовать двоичное число в десятичное, умножьте каждую цифру двоичного числа на степень 2. Если B = a n-1 …a 3 a 2 a 1 a 0 — двоичное число, состоящее из n цифр, тогда соответствующее десятичное число будет
D = (a n-1 2 n-1 ) +…+(а 3 × 2 3 ) + (а 2 × 2 2 ) + (а 1 × 2 0) (а 9024 0) × 2 0 ).
Вопрос 3: Как преобразовать десятичное число в двоичное?
Ответ:
Чтобы преобразовать десятичное число в двоичное, нужно непрерывно делить данное число на 2, пока не получится частное, равное 1. Обратите внимание, что мы должны записывать числа снизу вверх.
Вопрос 4: В чем разница между двоичной и десятичной системами счисления?
Ответ:
Система счисления, которая выражает число цифрами 0 и 1, является двоичной системой счисления, тогда как десятичная система счисления представляет число от 0 до 9.
цифры. В двоичной системе счисления число выражается в степени двойки, тогда как в десятичной системе счисления число выражается в степени 10.
Вопрос 5: Какое десятичное число эквивалентно двоичному номер 11010?
Ответ:
11010 = (1 × 2 4 ) + (1 × 2 3 ) + (0 × 2 2 0 ) + (1 × 2 2 0 ) + (1 × 2 2 0 ) + (093 + 2 9 ) × 2 0 )
= 16 + 8 + 0 + 2 + 0 = 26
Итак, (11010) 2 равно 26 в десятичной системе счисления.
Учебное пособие по двоичным числам — Понимание и работа с двоичными числами
Системы счисления!
Теория чисел и принцип работы двоичных чисел.
Введение
Числа окружают нас повсюду, и по большей части мы принимаем их как должное. Если бы я предложил вам 1337 долларов, вы были бы счастливы, потому что знаете, что это довольно разумная сумма. Система счисления — это средство представления количества вещей. Десятичная система счисления — это всего лишь одна из нескольких систем счисления, а другие, особенно двоичные, важны для понимания в различных областях, особенно в вычислительной технике.
Система счисления — это средство представления количества вещей. Десятичная система счисления — это всего лишь одна из нескольких систем счисления, а другие, особенно двоичные, важны для понимания в различных областях, особенно в вычислительной технике.
В нашем введении для начинающих в двоичные, шестнадцатеричные и восьмеричные числа вы изучите двоичные преобразования и арифметику с интерактивными демонстрациями и подробными объяснениями.
Схема
Этот двоичный учебник разделен на 3 раздела. В общем, я рекомендую вам работать с ними по порядку, но если вы пришли сюда только для того, чтобы узнать о конкретной теме, то кто я такой, чтобы замедлять вас, просто идите прямо дальше.
- Системы счисления. Читайте ниже, чтобы узнать о теории чисел.
- Преобразования — Как преобразовать между двоичным и десятичным, шестнадцатеричным и восьмеричным.
- Арифметика. Узнайте, как выполнять различные арифметические операции с двоичными числами.

- Отрицательные числа — узнайте, как работать с отрицательными числами в двоичном формате.
- Плавающая точка и дроби. Узнайте, как преобразовывать десятичные числа в двоичные дроби и числа с плавающей запятой.
Шаблоны и ярлыки
При работе с системами счисления есть много сокращений, которые можно использовать:
- облегчают работу с ними.
- помогите проверить вашу работу / выявить глупые ошибки, которые вы, возможно, сделали.
Я укажу на некоторые из них по мере работы с материалом, но вы всегда должны сами их искать (не только в работе с числами, но и в других областях).
В общем, вы хотите следить за шаблонами, а затем думать о том, как вы можете использовать эти шаблоны для своей выгоды. С практикой вы научитесь их замечать.
Десятичная система счисления
Десятичная система счисления нам наиболее знакома, мы используем ее каждый день. Десятичная система счисления — это то, что мы называем позиционной системой счисления. То есть положение цифр придает значение значению, которое они представляют. Другие системы счисления (двоичная, шестнадцатеричная и восьмеричная) также являются позиционными, поэтому, как только мы поймем основную теорию десятичной системы счисления, мы сможем легко применить ее для понимания других систем.
То есть положение цифр придает значение значению, которое они представляют. Другие системы счисления (двоичная, шестнадцатеричная и восьмеричная) также являются позиционными, поэтому, как только мы поймем основную теорию десятичной системы счисления, мы сможем легко применить ее для понимания других систем.
Рассмотрим пример:
Если у меня есть число 31415, то это на самом деле означает:
30 000 + 1 000 + 400 + 10 + 5
Или, точнее:
| 3 * 10 4 | 30 000 |
| 1 * 10 3 | 1000 |
| 4 * 10 2 | 400 |
| 1 * 10 1 | 10 |
| 5 * 10 0 | 5 |
Десятичное число равно по основанию 10 . Это означает, что у нас есть 10 символов для представления значений (0-9). По мере того, как мы перемещаемся по каждой позиции, мы умножаем это число на 10 в степени этой позиции (начиная с 0 в крайнем правом углу).
Помните: все, что в степени 0, всегда равно 1
Десятичная система удобна как система счисления, так как каждый раз, когда мы увеличиваем степень, все, что нам нужно сделать, это добавить еще один 0. К каждой цифре в числе добавить количество 0 требуется для позиции, и у вас есть ее позиционное значение. Затем каждая цифра естественным образом выстраивается в общее число.
Двоичный
Двоичный соответствует тому же образцу, что и Десятичный, за исключением того, что вместо 10 используется с основанием 2 . Вместо 10 символов для представления значений у нас есть два (0 и 1).
Итак, Decimal — это система счисления с основанием 10, у нас есть 10 символов и умножение на степени 10. Отсюда следует, что Binary — это система счисления с основанием 2, у нас есть два символа и умножение на степени 2.
Давайте посмотрим на пример:
Если у меня есть двоичное число 101010, это преобразуется в десятичное как:
32 + 0 + 8 + 0 + 2 + 0 = 42
Или:
| 1 * 2 5 | 32 |
| 0 * 2 4 | 0 |
| 1 * 2 3 | 8 |
| 0 * 2 2 | 0 |
| 1 * 2 1 | 2 |
| 0 * 2 0 | 0 |
Как видно из этого примера, двоичный код не так удобен для чтения и работы, как десятичный. Итак, вы можете спросить, зачем тогда возиться с двоичным кодом? Ответ заключается в том, что это более простой формат для работы с компьютерами. Его также можно использовать в других областях в качестве ярлыка для представления настроек.
Итак, вы можете спросить, зачем тогда возиться с двоичным кодом? Ответ заключается в том, что это более простой формат для работы с компьютерами. Его также можно использовать в других областях в качестве ярлыка для представления настроек.
Поскольку все степени двойки, кроме 0, дают четное число, единственный способ получить нечетное число — это использовать крайнюю правую цифру, равную 1. Это можно использовать в качестве быстрой проверки при выполнении преобразований, которые вы еще не выполняли. совершил глупую ошибку.
Шестнадцатеричная и восьмеричная
Две другие системы счисления, которые обычно используются в вычислениях, — шестнадцатеричная и восьмеричная. Обе они также являются базовыми системами счисления.
- Шестнадцатеричное основание 16
- Восьмеричное основание 8
Оба они тесно связаны с двоичным кодом. Вы заметите, что:
- 16 равно 2 4
- 8 равно 2 3
Это не относится к десятичным числам (нет степени двойки, равной 10). Это дает шестнадцатеричные и восьмеричные характеристики по отношению к двоичному, которых нет у десятичного. Мы рассмотрим их в следующем разделе, конверсии.
Это дает шестнадцатеричные и восьмеричные характеристики по отношению к двоичному, которых нет у десятичного. Мы рассмотрим их в следующем разделе, конверсии.
Для шестнадцатеричных чисел мы увеличиваем число до 15 (помните, что мы начинаем с 0). Как только мы доберемся до 9, мы добавим буквы алфавита от A до F, чтобы представить 10-15 (см. справочную таблицу ниже).
Возьмем десятичное число 27.
В шестнадцатеричном виде это будет 1B, что в десятичном виде будет:
1 * 16 1 + 11 * 16 0 = 16 + 11
1 В восьмеричном будет 33, что в десятичной форме означает:
3 * 8 1 + 3 * 8 0 = 24 + 3
Префиксы
Как видно из приведенных выше примеров, числа потенциально могут выглядеть одинаково независимо от того, являются ли они двоичными, десятичными, восьмеричными или шестнадцатеричными. Если бы я дал вам число 2F7, вы бы сразу поняли, что оно шестнадцатеричное, но если бы я дал вам число 101, то это:
- 101 в двоичном формате и 5 в десятичном
- 101 в десятичном формате
- 101 в шестнадцатеричном формате и 257 в десятичном формате
- 101 в восьмеричной и 65 в десятичной
??
Как видите, количество, которое представляет 101, сильно различается в зависимости от используемой базы. Чтобы избежать этой двусмысленности, мы добавляем префиксы к числам, чтобы идентифицировать их основу.
Чтобы избежать этой двусмысленности, мы добавляем префиксы к числам, чтобы идентифицировать их основу.
- Десятичное число не имеет префикса.
- Шестнадцатеричное число имеет префикс Ox, например: Ox1B
- Octal имеет префикс O, например: O421
- Двоичный файл имеет префикс Ob, например: Ob1101
Некоторые люди вместо этого используют суффикс, но они не так популярны:
- Десятичное число не имеет суффикса.
- Шестнадцатеричное число имеет суффикс H, например: 1BH
- Octal имеет суффикс O, например: 421O
- Двоичный файл имеет суффикс B, например: 1101B
Примечание: для префиксов и суффиксов выше это заглавная буква, а не ноль.
В большей части этого урока я не буду использовать префиксы, а укажу базу напрямую, чтобы было понятнее.
Справочная таблица
Вот справочная таблица для различных систем счисления.
| Десятичный | Двоичный | Окталь | Шестнадцатеричный |
|---|---|---|---|
| 0 | 0000 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | А |
| 11 | 1011 | 13 | Б |
| 12 | 1100 | 14 | С |
| 13 | 1101 | 15 | Д |
| 14 | 1110 | 16 | Е |
| 15 | 1111 | 17 | Ф |
Вы заметите, что в двоичном файле есть шаблон. Крайний правый столбец чередуется между 0 и единицей. Следующий столбец делает то же самое, но по 2 за раз. Третий столбец делает то же самое, но по 4 за раз. Крайний левый столбец делает то же самое, но по 8 за раз. Этот шаблон упрощает проверку правильности написания.
Крайний правый столбец чередуется между 0 и единицей. Следующий столбец делает то же самое, но по 2 за раз. Третий столбец делает то же самое, но по 4 за раз. Крайний левый столбец делает то же самое, но по 8 за раз. Этот шаблон упрощает проверку правильности написания.
Если вы сдаете экзамен по двоичному коду, вам часто не разрешают сдавать материал, но ничто не мешает вам самостоятельно нарисовать эту таблицу после начала экзамена. Это может быть хорошим справочным материалом, особенно для конверсий, которые мы рассмотрим в следующем разделе.
Консультация
Этот материал может быть немного сложным для понимания. Если чтение материала утомляет вас, вот что я предлагаю:
- Работайте с примерами на бумаге. Изучение двоичного кода похоже на езду на велосипеде. Лучший способ — просто сделать это.
- Оставьте это на день или два, затем вернитесь и попробуйте еще раз.
Двоичная система счисления: ее история, применение и преимущества
От простой механики до сложного квантового моделирования наш мир значительно изменился с течением времени. Единственное, что не изменилось, — это наша «воля» считаться. Примерно сто лет назад основной системой, которую люди использовали для вычислений, была десятичная система счисления. Но компьютеры и другие технологические достижения подпитывали потребность в более сложной и технологичной системе счисления. Это то, что вызвало рождение двоичной системы счисления. Здесь мы рассмотрим историю, применение и преимущества этой системы счисления!
Единственное, что не изменилось, — это наша «воля» считаться. Примерно сто лет назад основной системой, которую люди использовали для вычислений, была десятичная система счисления. Но компьютеры и другие технологические достижения подпитывали потребность в более сложной и технологичной системе счисления. Это то, что вызвало рождение двоичной системы счисления. Здесь мы рассмотрим историю, применение и преимущества этой системы счисления!
Реплика часов Audemars Piguet
Несколько сотен лет назад люди изобрели десятичную систему счисления. Какое-то время это служило цели, но развитие машины и неспособность этой системы выполнять сложные функции вынудили математиков разработать систему счисления, которая могла бы удовлетворить вышеупомянутые потребности. Проявление булевой логики, двоичная система счисления существует только в двух состояниях: Истина или Ложь. Это представлено 1 и 0. Более того, различные комбинации этих двух состояний определяют все остальные состояния.
Булева логика, впервые представленная в 1930-х годах Джорджем Булем, английским математиком, логиком и педагогом, стала заметным прорывом в мире электроники и компьютеров. С тех пор двоичная система счисления использовалась для ряда приложений. Это включает в себя обработку изображений, запись высококачественного звука и фильмов в формате HD, хранение миллионов введенных данных и обработку многочисленных приложений для цифровой обработки сигналов. Инструментом, который может обеспечить успех этих приложений, является двоичный преобразователь. Прежде чем мы обсудим области применения и преимущества двоичной системы счисления, давайте кратко рассмотрим ее историю.
С тех пор двоичная система счисления использовалась для ряда приложений. Это включает в себя обработку изображений, запись высококачественного звука и фильмов в формате HD, хранение миллионов введенных данных и обработку многочисленных приложений для цифровой обработки сигналов. Инструментом, который может обеспечить успех этих приложений, является двоичный преобразователь. Прежде чем мы обсудим области применения и преимущества двоичной системы счисления, давайте кратко рассмотрим ее историю.
Из всех позиционных систем двоичная система счисления кажется самой простой. 2 является основанием или основанием системы, а это означает, что в системе появляются только две цифры, представленные 0 и 1. Сегодня эта система счисления используется в каждом цифровом компьютере. Две цифры, 1 и 0, рассматриваются как два состояния (выключено/включено), и эти состояния используются для передачи инструкций и хранения данных в компьютерах. Как правило, этот элемент представляет собой только один бит, который называется двоичной цифрой.
Как правило, этот элемент представляет собой только один бит, который называется двоичной цифрой.
Теперь давайте кратко рассмотрим историю двоичной системы счисления — системы счисления, в которой используется двоичный преобразователь. Знаете ли вы о первом электронном цифровом компьютере? Семьдесят один год назад был изобретен первый электронный компьютер, созданный в Пенсильванском университете и получивший название «Электронный числовой интегратор и калькулятор» (ENAIC). Однако двоичная система счисления, которую он использовал, предшествовала ему почти на три столетия.
В 1701 году Готфрид Вильгельм Лейбниц, соавтор исчисления, написал о своем изобретении бумажное эссе D’une Nouvelle Science Des Nombres. Статья была представлена в Парижскую академию. Но потребовалось еще двадцать лет, чтобы открытие произошло точно так же, как несколько сотен лет потребовалось для разработки бинарного преобразователя. Согласно имеющейся литературе по этому вопросу, 1796 был первым случаем сообщения о двоичной арифметической записи. Итак, можно сказать, что двоичная система счисления родилась как раз перед началом 19 -го -го века.
Итак, можно сказать, что двоичная система счисления родилась как раз перед началом 19 -го -го века.
С помощью двух символов: 0 и 1 двоичная система счисления представляет числовые значения. Чтобы быть более конкретным, позиционное обозначение с основанием 2’ — это то, чем представлена типичная система с основанием 2. Слишком сложно понять? Нет проблем, вот более простое объяснение этого. Только две цифры: 0 и 1 используются для представления всех возможных значений в двоичной системе счисления. Здесь 1 представляет собой истинное состояние, а 0 — ложное состояние.
Хотя мы рассказали вам о формальном начале двоичной системы, нам еще предстоит раскрыть ее неформальное введение. Около 200 г. до н.э. Пингала, индийский писатель, ввел сложные математические концепции, описывающие метрику, и таким образом дал миру первое в истории описание двоичной системы счисления.
Когда мы используем десятичную систему счисления в нашей повседневной жизни, мы считаем предметы следующим образом. Вот десять различных символов, которые могут определять десять различных единиц. Цифры {0,1,2,3,4,5,6,7,8,9}. Все комплексные числа, такие как 100 или 1350, представляют собой не что иное, как комбинацию этих десяти первичных чисел. Позиция чисел увеличивается каждый раз, когда счетчик превышает набор из десяти первичных символов, и это дает нам новый набор еще из десяти возможных значений. Инструментом, который может помочь вам в расчетах, является двоичный преобразователь.
Вот десять различных символов, которые могут определять десять различных единиц. Цифры {0,1,2,3,4,5,6,7,8,9}. Все комплексные числа, такие как 100 или 1350, представляют собой не что иное, как комбинацию этих десяти первичных чисел. Позиция чисел увеличивается каждый раз, когда счетчик превышает набор из десяти первичных символов, и это дает нам новый набор еще из десяти возможных значений. Инструментом, который может помочь вам в расчетах, является двоичный преобразователь.
Возвращаясь к обсуждаемой теме, двоичная система имеет только два символа: 0 и 1 в первичном наборе. Это приводит к смещению десятичного разряда на 2n раз. Здесь n — представление двоичного разряда. Хотя двоичная система счисления может увеличиваться в значении, она легко понимается машинами, поскольку имеет только два основных состояния.
Краткий обзор булевой логики Теперь, когда мы хорошо разобрались в двоичной системе, пришло время взглянуть на логику, управляющую ею, и на то, как символы системы взаимодействуют друг с другом. Так работает булевская логика. Сравнение двух значений является основным принципом этой логики. Согласно Boolean, есть три основные логики. Это включает в себя логику И, ИЛИ и НЕ. Ниже приводится то, что представляет каждая логика.
Так работает булевская логика. Сравнение двух значений является основным принципом этой логики. Согласно Boolean, есть три основные логики. Это включает в себя логику И, ИЛИ и НЕ. Ниже приводится то, что представляет каждая логика.
И: Эта логика говорит, что если оба сравнительных значения имеют истинное значение (1), то результатом будет значение ИСТИНА (1)
ИЛИ: Эта логика говорит, что если какое-либо из сравнительных значений имеет истинное значение (1), то результатом будет значение ИСТИНА (1)
НЕ: Эта логика просто инвертирует заданное значение. Например, если заданное значение является значением True, то это значение инвертирует его в значение False, а если это значение False, то оно будет инвертировано в значение True
Из трех упомянутых выше логик для двух требуется как минимум две переменные и только НЕ может работать с одной переменной. В дополнение к вышеупомянутым первичным логикам существуют и некоторые другие логики, но они представляют собой лишь комбинацию трех первичных логик. После обсуждения булевой логики пришло время перейти к приложениям двоичной системы счисления и к тому, как использовать двоичный преобразователь.
После обсуждения булевой логики пришло время перейти к приложениям двоичной системы счисления и к тому, как использовать двоичный преобразователь.
Компьютерные технологии являются наиболее распространенным применением этой системы счисления. В конце концов, двузначная система счисления, используемая в цифровом кодировании, — это то, на чем основан весь компьютерный язык и программирование. Получение данных и их последующее отображение с помощью ограниченных битов информации — вот что составляет процесс цифрового кодирования. Ограниченная информация состоит из нулей и единиц двоичной системы. Примером этого являются изображения на экране вашего компьютера. Двоичная строка для каждого пикселя используется для кодирования этих изображений. 916. Кроме того, в разделе математики, известном как булева алгебра, вы найдете применение двоичной системы счисления. Логика и значения истинности — это то, с чем связана эта область математики. В этом приложении, в зависимости от того, истинны они или нет, утверждениям присваивается 0 или 1. Если вы ищете инструмент, который помогает в этом приложении, вы можете попробовать двоичный преобразователь.
Если вы ищете инструмент, который помогает в этом приложении, вы можете попробовать двоичный преобразователь.
Двоичная система счисления полезна для многих вещей. Например, чтобы сложить числа, компьютер щелкает переключателями. Добавляя в систему двоичные числа, вы можете стимулировать компьютерное добавление. Теперь есть две основные причины использовать эту систему счисления для компьютеров. Во-первых, он может обеспечить безопасный диапазон надежности. Второстепенное и, что наиболее важно, это помогает свести к минимуму количество необходимых схем. Это снижает требуемое пространство, потребляемую энергию и затраты.
Что ждет бинарную систему в будущем С появлением квантовой технологии бинарная система в будущем может устареть. Однако только время покажет, произойдет ли это на самом деле. На данный момент двоичная система счисления питает компьютерные системы по всему миру и при этом помогает миру оставаться на связи и выполнять сложные задачи через Интернет.


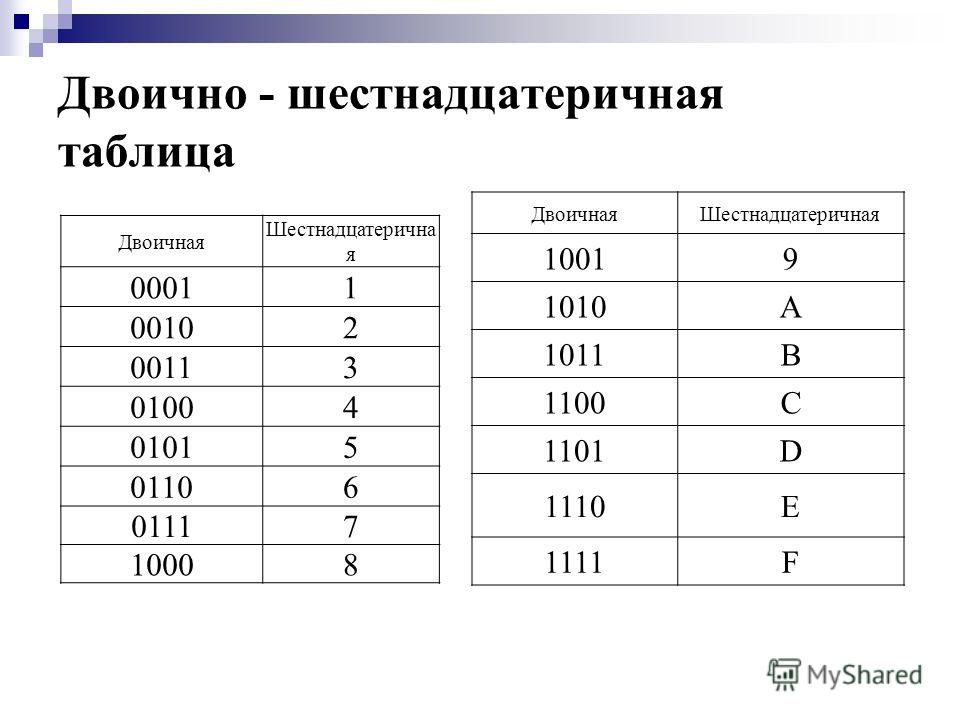



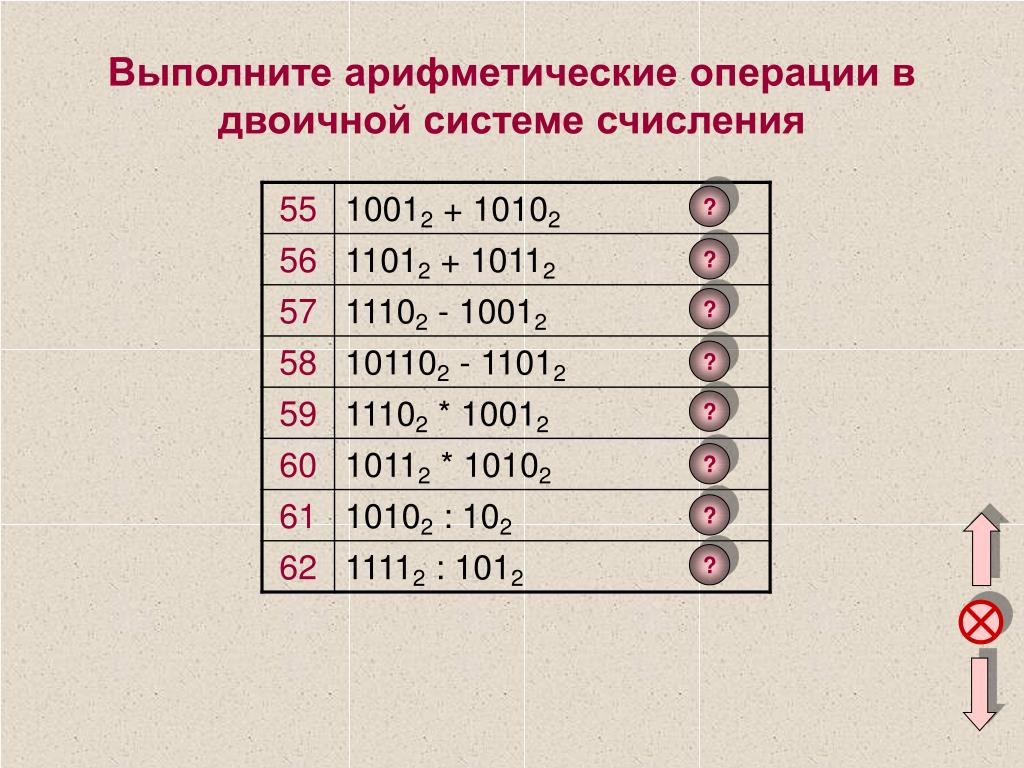 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.01 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.01 с.) д. Одному из состояний ставится в соответствие 1, другому – 0), а не десять, как в десятичной системе,
д. Одному из состояний ставится в соответствие 1, другому – 0), а не десять, как в десятичной системе,