Практическая работа №1. Метод координат. Работа с таблицами. Двоичное представление чисел
На этом уроке мы рассмотрим метод координат, научимся решать задачи с помощью таблиц, а также поговорим подробнее о двоичном представлении чисел.
Тема сегодняшнего урока – «Практическая работа №1. Метод координат. Работа с таблицами. Двоичное представление чисел». На предыдущем уроке мы обсудили способы кодирования информации, а также единицы измерения информации.
Сегодня мы займёмся рассмотрением метода координат, работы с таблицами и двоичного представления чисел. Эти практические задачи помогут нам разобраться более подробно с изученными ранее темами. Народная мудрость гласит: «Лучше один раз увидеть, чем сто раз услышать». Действительно, рисунки, схемы, чертежи способны заменить долгие разъяснения. Любая информация, в том числе и графическая, может быть представлена с помощью чисел. Сейчас мы познакомимся с таким способом представления графической информации, который называется «Метод координат» и научимся представлять графическую информацию с помощью чисел.
История возникновения системы координат описывается следующей легендой. Французский математик Рене Декарт пришёл в театр и не смог найти себе свободного места.

Рис. 1. Рене Декарт (Источник)
Дело в том, что ранее в театрах не нумеровали места, а просто продавали билеты по количеству мест в зале. В результате этой ошибки Декарту пришла в голову идея пронумеровать ряды и места.

Рис. 2. Ряды и места в зрительном зале (Источник)
Оказывается, это и есть прообраз первой системы координат. В честь своего создателя, система координат называется декартовой.
Чтобы связать числа и точки, используют системы координат.
Горизонтальная ось называется осью OX (ось абсцисс), вертикальная – осью OY (ось ординат).
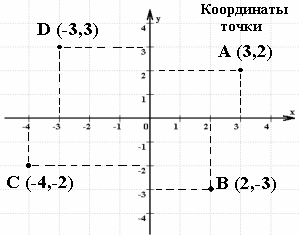
Место пересечения осей ОХ и ОY называется началом координат, которое также обозначают цифрой 0 («ноль»).
Каждая точка на координатной плоскости имеет свой точный адрес.
Это пара чисел: первое число по оси ОХ, второе – по оси ОY.
Эти числа называются координатами точки.
Например: А(3,2), B(2,-3), C(-4,-2), D
Двоичная система счисления — Информатика, информационные технологии
Двоичная система счисления была придумана математиками и философами ещё до появления компьютеров (XVII — XIX вв.). Выдающийся математик Лейбниц говорил: Вычисление с помощью двоек… является для науки основным и порождает новые открытия… При сведении чисел к простейшим началам, каковы 0 и 1, везде появляется чудесный порядок. Позже двоичная система была забыта, и только в 1936 — 1938 годах американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем. Рассмотрим пример представления числа в двоичной системе счисления:
Пример 2.1.1. Переведём число 2000 в двоичную систему.
1. Делим 2000 на основание новой системы счисления — 2:
2000:2=1000(0 — остаток),
1000:2=500(0),
500:2=250(0),
250:2=125(0),
125:2=62(1),
62:2=31(0),
31:2=15(1),
15:2=7(1),
7:2=3(1),
3:2=1(1)
2. Собираем последнее частное от деления (всегда равно 1) и остатки от деления и записываем их по порядку, начиная снизу :
200010==111110100002
Для проверки переведём полученное число в десятичную систему счисления, для этого:
1. Выделим двоичные разряды числа, то есть, степени числа 2, начиная с 0-й:
| 210 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 2′ | 2° |
2. Запишем сумму произведений 0 и 1 на соответствующую степень числа 2 (см. представление числа в р-ричной системе счисления):
0*20+0*21+0*22+0*23+l*24+0*25+l*26+l*27+l*28+l*29+l*210= 16+64+128+256+512+1024=2000
Существуют системы счисления, родственные двоичной. При работе с компьютерами иногда приходится иметь дело с двоичными числами, так как двоичные числа заложены в конструкцию компьютера. Двоичная система удобна для компьютера, но неудобна для человека — слишком длинные числа неудобно записывать и запоминать. На помощь приходят системы счисления, родственные двоичной — восьмеричная и шестнадцатеричная.
Например, в шестнадцатеричной системе для записи чисел предназначены 10 арабских цифр и буквы латинского алфавита {А, В, С, D, Е, F}. Чтобы записать число в этой системе счисления, удобно воспользоваться двоичным представлением числа. Возьмём для примера то же число — 2000 или 11111010000 в двоичной системе. Разобьём его на четвёрки знаков, двигаясь справа налево, в последней четвёрке слева припишем незначащий 0, чтобы количество знаков в триадах было по четыре: 0111 1101 0000. Начнём перевод — числу 0111 в двоичной системе соответствует число 7 в десятичной (710=1*20+1*21+1*22), в шестнадцатеричной системе счисления цифра 7 есть; числу 1101 в двоичной системе соответствует число 13 в десятичной (13=1*20 + 0*21 + 1*22 + 1*23), в шестнадцатеричной системе этому числу соответствует цифра D, и, наконец, число 0000 — в любой системе счисления 0. Запишем теперь результат: 111110100002 = 7D016.
Кодирование координат
Закодировать можно не только числа, но и другую информацию. Например, информацию о том, где находится некоторый объект. Величины, определяющие положение объекта в пространстве, называются координатами. В любойсистеме координат есть начало отсчёта, единица измерения, масштаб, направление отсчёта, или оси координат. Примеры систем координат — декартовы координаты, полярная система координат, шахматы, географические координаты.
Кодирование музыки
Как всякий звук, музыка является не чем иным, как звуковыми колебаниями, зарегистрировав которые достаточно точно, можно этот звук безошибочно воспроизвести. Нужно только непрерывный сигнал, которым является звук, преобразовать в последовательность нулей и единиц. С помощью микрофона звук можно превратить в электрические колебания, измерить амплитуду колебаний через равные промежутки времени (несколько десятков тысяч раз в секунду). Каждое измерение записывается в двоичном коде. Этот процесс называетсядискретизацией. Устройство для выполнения дискретизации — АЦП (аналогово-цифровой преобразователь). Воспроизведение такого звука ведётся при помощи ЦАП (цифро-аналогового преобразователя). Полученный ступенчатый сигнал сглаживается и преобразуется в звук при помощи усилителя и динамика. На качество воспроизведения влияютчастота дискретизации и разрешение(размер ячейки, отведённой под запись значения амплитуды). Например, при записи музыки на компакт-диски используются 16-разрядные значения и частота дискретизации 44 032 Гц. Понятно, что музыкальное произведение содержит в себе множество разных звуков, поэтому для того, чтобы хранить такой объём информации, нужно много места, такую запись трудно обрабатывать, так как в музыке ещё очень много оттенков. По этим причинам удобнее использовать для кодирования музыки нотную запись — своего рода алгоритм музыканту. В 1983 году ведущие производители электронных музыкальных инструментов и композиторов договорились о системе команд универсального синтезатора. Это соглашение — стандарт MIDI (Musical Instrument Digital Interface). При таком кодировании запись компактна, легко меняется инструмент исполнителя, тональность звучания, одна и та же запись воспроизводится как на синтезаторе, так и на компьютере.
Кодирование текста
Текст закодировать довольно просто. Для этого достаточно как-нибудь перенумеровать все буквы, цифры, знаки препинания и другие используемые при письме символы. Для хранения одного символа чаще всего используется восьмиразрядная ячейка — один байт, иногда два байта (иероглифы, например). В байт можно записать 256 различных чисел, значит, это позволит закодировать 256 различных символов. Соответствие символов и их кодов задаётся в специальной таблице. Коды записываются в шестнадцатеричной системе, так как для записи числа из восьми разрядов нужно всего две шестнадцатеричных цифры.
Кодирование изображений
Цифровые персональные компьютеры хорошо работают с числами, но не умеют обрабатывать непрерывные величины. Но человеческий глаз можно обмануть: изображение, составленное из большого числа отдельных мелких деталей, воспринимается как непрерывное. Если разбить картинку вертикальными и горизонтальными линиями на маленькие мозаичные квадратики, получим так называемыйрастр — двумерный массив квадратиков. Сами квадратики —элементы растра или пиксели (picture’s element) — элементы картинки. Цвет каждого пикселя кодируется числом, тогда, задав по порядку номера цветов (слева направо или сверху вниз), можно описать любую картинку. Часть информации неизбежно потеряется, но чем больше растр (мельче пиксели), тем точнее воспроизводится картинка.
Для описания черно-белых изображений используются оттенки серого цвета, то есть при кодировании учитывается только яркость. Она описывается одним числом, поэтому для кодирования одного пикселя требуется от 1 до 8 бит: чёрный цвет — 0, белый цвет — N=2k-l, где k — число разрядов, которые отводятся для кодирования цвета. Например, при длине ячейки в 8 бит это 256-1=255. Человеческий глаз в состоянии различить от 100 до 200 оттенков серого цвета, поэтому восьми разрядов вполне хватает.
Цветные изображения воспринимаются нами как сумма трёх основных цветов — красного, зелёного и синего. Например, сиреневый = красный + синий; жёлтый = красный + зелёный; оранжевый = красный + зелёный, но в другой пропорции. Поэтому достаточно закодировать цвет тремя числами — яркостью его красной, зелёной и синей составляющих. Этот способ кодирования называетсяRGB (Red—Green—Blue). Его используют в устройствах, способных излучать свет (мониторы). При рисовании на бумаге действуют другие правила, так как краски сами по себе не испускают свет, а только поглощают некоторые цвета спектра. Если смешать красную и зелёную краски, то получится коричневый, а не жёлтый цвет. Поэтому при печати цветных изображений используют метод CMY (Cyan—Magenta—Yellow) —голубой, сиреневый, жёлтый цвета. При таком кодировании красный = сиреневый + жёлтый; зелёный = голубой + жёлтый.
Кодирование фильмов
Фильм представляет собой последовательность быстро сменяющих друг друга кадров, на которых изображены последовательные фазы движения. Поскольку известны принципы кодирования отдельных кадров, то закодировать фильм как последовательность таких кадров ничего не стоит. Звук записывают независимо от изображения. При демонстрации фильма важно только добиться синхронизации звука и изображения (в кино для этого используют хлопушку — по щелчку хлопушки совмещаются звук и изображение).
Закодированный фильм несёт в себе информацию о размере кадра в пикселях и количество используемых цветов; частоте и разрешении для звука; способе записи звука (покадровый или непрерывный для всего фильма). После этого следует последовательность закодированных картинок и звуковых фрагментов.
Статьи к прочтению:
Просто о сложном: Двоичная система счисления
Похожие статьи:
Бинарные числа: двоичная система счисления
Бинарные числа — это числа из двоичной системы счисления, имеющей основание 2. Она непосредственно реализована в цифровой электронике, используется в большинстве современных вычислительных устройств, включая компьютеры, мобильные телефоны и разного рода датчики. Можно сказать, что все технологии нашего времени построены на бинарных числах.

Запись чисел
Любое число, сколь бы большим оно ни было, в двоичной системе записывается посредством двух символов: 0 и 1. Например цифра 5 из всем знакомой десятичной системы в двоичной будет представлено как 101. Бинарные числа могут быть обозначены префиксом 0b или амперсандом (&), например: &101.
Во всех системах счисления, исключая десятичную, символы читаются по одиночке, то есть взятое в пример 101 читается как «один ноль один».
Перевод из одной системы в другую
Программисты, постоянно работающие с двоичной системой счисления, на ходу могут перевести бинарное число в десятичное. Это действительно можно сделать и без всяких формул, особенно если человек имеет представление о том, как работает самая малая часть компьютерного «мозга» — бит.
Цифра ноль так же обозначает 0, а цифра один в двоичной системе тоже будет единицей, но что делать дальше, когда цифры закончились? Десятичная система «предложила» бы в таком случае ввести термин «десяток», а в бинарной системе это будет называться «двойка».

Если 0 это &0 (амперсанд — обозначение двоичной системы), 1 = &1, то 2 будет обозначаться как &10. Тройку тоже можно записать в двух разрядах, она будет иметь вид &11, то есть одна двойка и одна единица. Возможные комбинации исчерпаны, и в десятичной системе на этом этапе вводятся сотни, а в двоичной — «четверки». Четыре — это &100, пять — &101, шесть — &110, семь — &111. Следующая, более крупная единица счета — это восьмерка.
Можно заметить особенность: если в десятичной системе разряды умножаются на десять (1, 10, 100, 1000 и так далее), то в двоичной, соответственно, на два: 2, 4, 8, 16, 32. Это соответствует размеру флеш-карт и прочих накопителей, использующихся в компьютерах и других устройствах.
Что такое бинарный код
Числа, представленные в двоичной системе счисления, называются бинарными, однако в таком виде можно представить и не числовые значения (буквы и символы). Таким образом, в цифрах можно закодировать слова и тексты, правда вид они будут иметь не столь лаконичный, ведь для записи всего одной буквы потребуется несколько нолей и единиц.
Но каким образом компьютерам удается считывать такое количество информации? На самом деле все проще, чем кажется. Люди, привыкшие к десятичной системе счисления, сначала переводят двоичные числа в более привычные, и только потом производят с ними какие-либо манипуляции, а в основе компьютерной логики изначально лежит бинарная система чисел. Единице в технике соответствует высокое напряжение, а нулю — низкое, либо для единицы напряжение есть, а для ноля вообще отсутствует.

Бинарные числа в культуре
Ошибкой будет считать, что двоичная система счисления — это заслуга современных математиков. Хотя бинарные числа и являются основополагающими в технологиях нашего времени, использовались они уже очень давно, причем в разных уголках планеты. Используются длинная линия (единица) и прерывистая (ноль), кодирующие восемь символов, означающих восемь стихий: небо, землю, гром, воду, горы, ветер, огонь и водоем (массу воды). Этот аналог 3-битных цифр описывался в классическом тексте книги Перемен. Триграммы составляли 64 гексаграммы (6-битные цифры), порядок которых в книге Перемен был расположен в соответствии с двоичными цифрами от 0 до 63.
Этот порядок был составлен в одиннадцатом веке китайским ученым Шао Юном, хотя нет доказательств того, что он действительно понимал двоичную систему счисления в целом.
В Индии еще до нашей эры тоже применялись бинарные числа в математической основе для описания поэзии, составленные математиком Пингалой.
Узелковая письменность инков (кипу) считается прообразом современных баз данных. Именно они впервые применили не только бинарный код числа, но и не числовые записи в двоичной системе. Узелковое письмо кипу характерно не только первичными и дополнительными ключами, но и использованием позиционных чисел, кодированием с помощью цвета и сериями повторений данных (циклами). Инки впервые применили способ ведения бухгалтерского учета, называемый двойной записью.

Первый из программистов
Двоичную систему счисления, основанную на цифрах 0 и 1, описал и знаменитый ученый, физик и математик, Готфрид Вильгельм Лейбниц. Он увлекался древней китайской культурой и, изучая традиционные тексты книги Перемен, заметил соответствие гексаграмм бинарным числам от 0 до 111111. Он восхитился свидетельствам подобных достижений в философии и математике для того времени. Лейбница можно назвать первым из программистов и информационных теоретиков. Именно он обнаружил, что если записать группы двоичных чисел вертикально (одно под другим), то в получившихся вертикальных столбцах чисел будут регулярно повторяться ноли и единицы. Это позвонило ему предположить, что возможно существование совершенно новых математических законов.
Лейбниц понял и то, что бинарные числа оптимальны для применения в механике, основой которой должна быть смена пассивных и активных циклов. На дворе был 17 век, а этот великий ученый изобрел на бумаге вычислительную машину, работавшую на основе его новых открытий, однако быстро понял, что цивилизация еще не достигла такого технологического развития, и в его время создание такой машины будет невозможным.
Двоичная система счисления — это… Что такое Двоичная система счисления?
| Системы счисления в культуре | |
|---|---|
| Индо-арабская система счисления | |
| Арабская Индийские Тамильская Бирманская | Кхмерская Лаоская Монгольская Тайская |
| Восточноазиатские системы счисления | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные системы счисления | |
| Абджадия Армянская Ариабхата Кириллическая | Греческая Эфиопская Еврейская Катапаяди |
| Другие системы | |
| Вавилонская Египетская Этрусская Римская | Аттическая Кипу Майская |
| Позиционные системы счисления | |
| Десятичная система счисления (10) | |
| 2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60 | |
| Нега-позиционная система счисления | |
| Симметричная система счисления | |
| Смешанные системы счисления | |
| Фибоначчиева система счисления | |
| Непозиционные системы счисления | |
| Единичная (унарная) система счисления | |
| Список систем счисления | |
Двоичная система счисления — позиционная система счисления с основанием 2.
Двоичные цифры
В этой системе счисления числа записываются с помощью двух символов (0 и 1).
История
- В 1605 году Френсис Бэкон описал систему, буквы алфавита которой могут быть сведены к последовательностям двоичных цифр, которые в свою очередь могут быть закодированы как едва заметные изменения шрифта в любых случайных текстах. Важным шагом в становлении общей теории двоичного кодирования является замечание о том, что указанный метод может быть использован применительно к любым объектам.
- Современная двоичная система была полностью описана Лейбницем в XVII веке в работе Explication de l’Arithmétique Binaire[8]. В системе счисления Лейбница были использованы цифры 0 и 1, как и в современной двоичной системе. Как человек, увлекающийся китайской культурой, Лейбниц знал о книге Перемен и заметил, что гексаграммы соответствуют двоичным числам от 0 до 111111. Он восхищался тем, что это отображение является свидетельством крупных китайских достижений в философской математике того времени.
- В 1937 году Клод Шеннон представил к защите кандидатскую диссертацию Символический анализ релейных и переключательных схем в MIT, в которой булева алгебра и двоичная арифметика были использованы применительно к электронным реле и переключателям. На диссертации Шеннона по существу основана вся современная цифровая техника.
- В ноябре 1937 года Джордж Штибиц, впоследствии работавший в Bell Labs, создал на базе реле компьютер «Model K» (от англ. «Kitchen», кухня, где производилась сборка), который выполнял двоичное сложение. В конце 1938 года Bell Labs развернула исследовательскую программу во главе со Штибицом. Созданный под его руководством компьютер, завершённый 8 января 1940 года, умел выполнять операции с комплексными числами. Во время демонстрации на конференции American Mathematical Society в Дартмутском колледже 11 сентября 1940 года Штибиц продемонстрировал возможность посылки команд удалённому калькулятору комплексных чисел по телефонной линии с использованием телетайпа. Это была первая попытка использования удалённой вычислительной машины посредством телефонной линии. Среди участников конференции, бывших свидетелями демонстрации, были Джон фон Нейман, Джон Мокли и Норберт Винер, впоследствии писавшие об этом в своих мемуарах.
Запись двоичных чисел
Двоичная система счисления является комбинацией двоичной системы кодирования и показательной весовой функции с основанием равным 2. Положительные целые числа (без знака) записываются в виде:
где:
- — представляемое число, первый индекс — основание системы кодирования (размерность множества цифр a={0,1}), второй индекс — основание весовой показательной функции b (в двоично-десятичном кодировании b=10),
- — запись числа, строка цифровых знаков,
- — обозначение основания системы кодирования и основания системы счисления,
- — количество цифр (знаков) в числе x2,2,
- — порядковый номер цифры,
- — цифры числа
- — основание показательной весовой функции, основание системы счисления,
- — весовая показательная функция, создающая весовые коэффициенты.
Количество записываемых кодов (чисел) зависит от основания системы кодирования — c, определяется в комбинаторике и равно числу размещений с повторениями:
где:
Количество записываемых кодов (чисел) от основания показательной функции — b не зависит.
Основание показательной функции — b определяет диапазон представляемых числами x2,b величин и разреженность представляемых чисел на числовой оси.
Целые числа являются частными суммами степенного ряда:
в котором коэффициенты an берутся из множества R=a{0,1}, X=2, n=k, а верхний предел в частных суммах ограничен с до — n-1.
Целые числа со знаком записываются в виде:
где:
- — знак числа из множества z={+,-}, у положительных целых чисел знак зачастую опускается.
Дробные числа записываются в виде:
где:
- — число цифр дробной части числа,
- — весовые коэффициенты из множества ,
- основание системы кодирования равно 2,
- — основание показательной весовой функции, основание системы счисления.
Следует отметить, что число может быть записано в двоичном коде, а система счисления при этом может быть не двоичной, а с другим основанием. Пример: двоично-десятичное кодирование, в котором десятичные цифры записываются в двоичном виде, а система счисления — десятичная.
Сложение, вычитание и умножение двоичных чисел
Таблица сложения
Пример сложения «столбиком» (14 + 5 = 19):
| 1 | ↖ | ||||
|---|---|---|---|---|---|
| + | 1 | 1 | 1 | 0 | |
| 1 | 0 | 1 | |||
| 1 | 0 | 0 | 1 | 1 | |
Таблица вычитания
| — | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | (заём из старшего разряда) 1 | 0 |
Таблица умножения
Пример умножения «столбиком» (14 × 5 = 70):
| × | 1 | 1 | 1 | 0 | |||
| 1 | 0 | 1 | |||||
| + | 1 | 1 | 1 | 0 | |||
| 1 | 1 | 1 | 0 | ||||
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | |
Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1, называется двоичной точкой.
Преобразование двоичных чисел в десятичные
Допустим, вам дано двоичное число 110001. Для перевода в десятичное просто запишите его справа налево как сумму по разрядам следующим образом:
.Можно записать это в виде таблицы следующим образом:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | ||||
| +32 | +16 | +1 |
Точно так же, начиная с двоичной точки, двигайтесь справа налево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа.
Таким образом, двоичное число 110001 равнозначно десятичному 49.
Преобразование методом Горнера
Для того, чтобы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47. Перевод дробных чисел методом Горнера 1) 0,11012=0,X10 (рассматриваем цифры в обратном порядке)
1:2=0,5
0,5+0=0,5
0,5:2=0,25
0,25+1=1,25
1,25:2=0,625
0,625+1=1,625
1,625:2=0,8125
Ответ: 0,11012= 0,812510
2) 0,3568=0,X10 (рассматриваем цифры в обратном порядке)
6:8=0,75
0,75+5=5,75
5,75:8=0,71875
0,71875+3=3,71875
3,71875:8=0,46484375
Ответ: 0,3568=0,4648437510
3) 0,A6E16=0,X10 (рассматриваем цифры в обратном порядке)
14:16=0,875
0,875+6=6,875
6,875:16=0,4296875
0,4296875+10=10,4296875
10,4296875:16=0,65185546875
Ответ: 0,A6E16=0,6518554687510
Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
19 /2 = 9 с остатком 1 9 /2 = 4 c остатком 1 4 /2 = 2 без остатка 0 2 /2 = 1 без остатка 0 1 /2 = 0 с остатком 1
Итак, мы делим каждое частное на 2 и записываем остаток в конец двоичной записи. Продолжаем деление до тех пор, пока в частном не будет 0. Результат записываем справа налево. То есть нижнее число будет самым левым и.т.д. В результате получаем число 19 в двоичной записи: 10011.
Преобразование дробных двоичных чисел в десятичные
Нужно перевести число 1011010,101 в десятичную систему. Запишем это число следующим образом:
Или по таблице:
| 64 | 32 | 16 | 8 | 4 | 2 | 1 | 0.5 | 0.25 | 0.125 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0. | .1 | 0 | 1 |
| +64 | +16 | +8 | +2 | +0.5 | +0.125 |
Преобразование дробных десятичных чисел в двоичные
Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:
- Вначале переводится целая часть десятичной дроби в двоичную систему счисления;
- Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;
- В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;
- Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.
Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.
Перевод целой части дает 20610=110011102 по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:
0,116 • 2 = 0,232
0,232 • 2 = 0,464
0,464 • 2 = 0,928
0,928 • 2 = 1,856
0,856 • 2 = 1,712
0,712 • 2 = 1,424
0,424 • 2 = 0,848
0,848 • 2 = 1,696
0,696 • 2 = 1,392
0,392 • 2 = 0,784
и т. д.
Получим: 206,11610=11001110,00011101102
Применения
В цифровых устройствах
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:
- Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток (ток больше пороговой величины) — нет тока (ток меньше пороговой величины), индукция магнитного поля больше пороговой величины или нет (индукция магнитного поля меньше пороговой величины) и т. д.
- Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину напряжения, тока или индукции магнитного поля, потребуется ввести два пороговых значения и два компаратора, что не будет способствовать помехоустойчивости и надёжности хранения информации.[источник не указан 770 дней]
- Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.
В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует (очевидно) один двоичный разряд двоичного регистра, то есть двоичный триггер с двумя состояниями (0,1).
В английской системе мер
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 715/16″, 311/32″ и т. д.
Интересные факты
См. также
Примеры чисел-степеней двойки
| Степень | Значение |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
| 9 | 512 |
| 10 | 1024 |
| 11 | 2048 |
| 12 | 4096 |
| 13 | 8192 |
| 14 | 16384 |
| 15 | 32768 |
| 16 | 65536 |
| 17 | 131072 |
| 18 | 262144 |
| 19 | 524288 |
| 20 | 1048576 |
| 21 | 2097152 |
| 22 | 4194304 |
| 23 | 8388608 |
| 24 | 16777216 |
| 25 | 33554432 |
| 26 | 67108864 |
| 27 | 134217728 |
| 28 | 268435456 |
| 29 | 536870912 |
| 30 | 1073741824 |
| 31 | 2147483648 |
| 32 | 4294967296 |
| 33 | 8589934592 |
| 34 | 17179869184 |
| 35 | 34359738368 |
| 36 | 68719476736 |
| 37 | 137438953472 |
| 38 | 274877906944 |
| 39 | 549755813888 |
| 40 | 1099511627776 |
| 41 | 2199023255552 |
| 42 | 4398046511104 |
| 43 | 8796093022208 |
| 44 | 17592186044416 |
| 45 | 35184372088832 |
| 46 | 70368744177664 |
| 47 | 140737488355328 |
| 48 | 281474976710656 |
| 49 | 562949953421312 |
| 50 | 1125899906842624 |
| 51 | 2251799813685248 |
Примечания
- ↑ Sanchez, Julio & Canton, Maria P. (2007), «Microcontroller programming: the microchip PIC», Boca Raton, Florida: CRC Press, с. 37, ISBN 0-8493-7189-9
- ↑ W. S. Anglin and J. Lambek, The Heritage of Thales, Springer, 1995, ISBN 0-387-94544-X
- ↑ Ordish George, Hyams, Edward. The last of the Incas: the rise and fall of an American empire. — New York: Barnes & Noble, 1996. — С. 80. — ISBN 0-88029-595-3
- ↑ Experts ‘decipher’ Inca strings. Архивировано из первоисточника 18 августа 2011.
- ↑ Carlos Radicati di Primeglio, Gary Urton Estudios sobre los quipus. — P. 49.
- ↑ Dale Buckmaster (1974). «The Incan Quipu and the Jacobsen Hypothesis». Journal of Accounting Research 12 (1): 178-181. Проверено 2009-12-24.
- ↑ Bacon, Francis, «The Advancement of Learning», vol. 6, London, сс. Chapter 1, <http://home.hiwaay.net/~paul/bacon/advancement/book6ch2.html>
- ↑ http://www.leibniz-translations.com/binary.htm Leibniz Translation.com EXPLANATION OF BINARY ARITHMETIC
- ↑ Aiton, Eric J. (1985), «Leibniz: A Biography», Taylor & Francis, сс. 245–8, ISBN 0-85274-470-6
Ссылки
Двоичные числа — это… Что такое Двоичные числа?
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:
- Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток — нет тока, индукция магнитного поля больше пороговой величины или нет и т. д.
- Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину индукции магнитного поля, потребуется ввести два пороговых значения, что не будет способствовать помехоустойчивости и надёжности хранения информации.
- Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.
- Возможно применение аппарата алгебры логики для выполнения побитовых операций над числами.
В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).
1 + 0 = 1 1 + 1 = 10 10 + 10 = 100
Таблица умножения двоичных чисел
0 • 0 = 0 0 • 1 = 0 1 • 0 = 0 1 • 1 = 1
Использование двоичной системы при измерении дюймами
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 715/16″, 311/32″ и т. д.
Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1 называется двоичной точкой.
Преобразование двоичных чисел в десятичные
Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | ||||
| 32 | +16 | +2 | +1 |
Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Либо 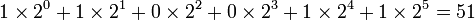 .
.
Преобразование методом Горнера
Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.
Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа
Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.
unsigned int to_deg_2(unsigned int num){
int i;
if ( num == 1 ) return 2;
for( num-=1,i=1; i < sizeof(unsigned int)*8; i*=2 ) num = num|(num>>i);
return num+1;
}
Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
19 /2 = 9 с остатком 1 9 /2 = 4 c остатком 1 4 /2 = 2 с остатком 0 2 /2 = 1 с остатком 0 1 /2 = 0 с остатком 1
Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.
Другие системы счисления
В статье «Системы счисления (продолжение)»[1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.
См. также
Ссылки
- ↑ http://potan.livejournal.com/91399.html Системы счисления (продолжение)
Wikimedia Foundation. 2010.
Система координат — Википедия
Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.
В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.
В географии координаты выбираются как (приближённо) сферическая система координат — широта, долгота и высота над известным общим уровнем (например, океана). См. Географические координаты.
В астрономии небесные координаты — упорядоченная пара угловых величин (например, прямое восхождение и склонение), с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой сферическую систему координат (без радиальной координаты) с соответствующим образом выбранной фундаментальной плоскостью и началом отсчёта. В зависимости от выбора фундаментальной плоскости система небесных координат называется горизонтальной (плоскость горизонта), экваториальной (плоскость экватора), эклиптической (плоскость эклиптики) или галактической (галактическая плоскость).
Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.
 Точка P и её координаты в трёхмерной системе координат (с осью Х, направленной к читателю)
Точка P и её координаты в трёхмерной системе координат (с осью Х, направленной к читателю)В этом разделе даются разъяснения к наиболее употребляемым системам координат в элементарной математике.
Декартовы координаты[править | править код]
Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел (x,y):{\displaystyle (x,y):}
- x{\displaystyle x} — расстояние от точки P до оси y с учетом знака
- y{\displaystyle y} — расстояние от точки P до оси x с учетом знака
В пространстве необходимы уже три координаты (x,y,z):{\displaystyle (x,y,z):}
- x{\displaystyle x} — расстояние от точки P до плоскости yz
- y{\displaystyle y} — расстояние от точки P до плоскости xz
- z{\displaystyle z} — расстояние от точки P до плоскости xy
Полярные координаты[править | править код]
 Полярные координаты.
Полярные координаты.В полярной системе координат, применяемой на плоскости, положение точки P определяется её расстоянием до начала координат r = |OP| и углом φ её радиус-вектора к оси Ox.
В пространстве применяются обобщения полярных координат — цилиндрические и сферические системы координат.
Цилиндрические координаты[править | править код]
 Цилиндрические координаты.
Цилиндрические координаты.Цилиндрические координаты — трёхмерный аналог полярных, в котором точка P представляется упорядоченной тройкой (r,φ,z).{\displaystyle (r,\varphi ,z).} В терминах декартовой системы координат,
- 0⩽r{\displaystyle 0\leqslant {r}} (радиус) — расстояние от оси z до точки P,
- 0⩽φ<360∘{\displaystyle 0\leqslant \varphi <360^{\circ }} (азимут или долгота) — угол между положительной («плюсовой») частью оси x и отрезком, проведённым от полюса до точки P и спроектированной на плоскость xy.
- z{\displaystyle z} (высота) равна декартовой z-координате точки P.
- Примечание: в литературе для первой (радиальной) координаты иногда используется обозначение ρ, для второй (угловой, или азимутальной) — обозначение θ, для третьей координаты — обозначение h.
Полярные координаты имеют один недостаток: значение φ не определено при r = 0.
Цилиндрические координаты полезны для изучения систем, симметричных относительно некоторой оси. Например, длинный цилиндр с радиусом R в декартовых координатах (с осью z, совпадающей с осью цилиндра) имеет уравнение x2+y2=R2,{\displaystyle x^{2}+y^{2}=R^{2},} тогда как в цилиндрических координатах оно выглядит гораздо проще, как r = R.
Сферические координаты[править | править код]
 Сферические координаты.
Сферические координаты.Сферические координаты — трёхмерный аналог полярных.
В сферической системе координат расположение точки P определяется тремя компонентами: (ρ,φ,θ).{\displaystyle (\rho ,\varphi ,\theta ).} В терминах декартовой системы координат,
- 0⩽ρ{\displaystyle 0\leqslant \rho } (радиус) — расстояние от точки P до полюса,
- 0⩽φ⩽360∘{\displaystyle 0\leqslant \varphi \leqslant 360^{\circ }} (азимут или долгота) — угол между положительной («плюсовой») полуосью x и проекцией отрезка, проведённого из полюса до точки P, на плоскость xy.
- 0⩽θ⩽180∘{\displaystyle 0\leqslant \theta \leqslant 180^{\circ }} (широта или полярный угол) — угол между положительной («плюсовой») полуосью z и отрезком, проведённым из полюса до точки P.
- Примечание: в литературе иногда азимут обозначается θ, а полярный угол — φ. Иногда для радиальной координаты используется r вместо ρ. Кроме того, диапазон углов для азимута может выбираться как (−180°, +180°] вместо диапазона [0°, +360°). Наконец, полярный угол может отсчитываться не от положительного направления оси z, а от плоскости xy; в этом случае он лежит в диапазоне [−90°, +90°], а не в диапазоне [0°, 180°]. Иногда порядок координат в тройке выбирается отличным от описанного; например, полярный и азимутальный углы могут быть переставлены.
Сферическая система координат также имеет недостаток: φ и θ не определены, если ρ = 0; угол φ не определён также и для граничных значений θ = 0 и θ = 180° (или для θ = ±90°, в случае принятия соответствующего диапазона для этого угла).
Для построения точки P по её сферическим координатам нужно от полюса вдоль положительной полуоси z отложить отрезок, равный ρ, повернуть его на угол θ вокруг оси y в направлении положительной полуоси x, и затем повернуть на угол θ вокруг оси z в направлении положительной полуоси y.
Сферические координаты полезны при изучении систем, симметричных относительно точки. Так, уравнение сферы с радиусом R в декартовых координатах с началом отсчёта в центре сферы выглядит как x2+y2+z2=R2,{\displaystyle x^{2}+y^{2}+z^{2}=R^{2},} тогда как в сферических координатах оно становится намного проще: ρ=R.{\displaystyle \rho =R.}
Другие распространённые системы координат[править | править код]
- Аффинная (косоугольная) система координат — прямолинейная система координат в аффинном пространстве. На плоскости задается точкой начала координат О и двумя упорядоченными неколлинеарными векторами, которые представляют собой аффинный базис. Осями координат в данном случае называются прямые, проходящие через точку начала координат параллельно векторам базиса, которые, в свою очередь, задают положительное направление осей. В трехмерном пространстве, соответственно, аффинная система координат задается тройкой линейно независимых векторов и точкой начала координат. Для определения координат некоторой точки М вычисляются коэффициенты разложения вектора ОМ по векторам базиса[1].
- Барицентрические координаты были впервые введены в 1827 году А. Мебиусом, решавшим вопрос о центре тяжести масс, расположенных на вершинах треугольника. Они аффинно инвариантны, представляют собой частный случай общих однородных координат. Точка с барицентрическими координатами расположена в n-мерном векторном пространстве En, а собственно координаты при этом относятся к фиксированной системе точек, которые не лежат в (n−1)-мерном подпространстве. Барицентрические координаты используются также и в алгебраической топологии применительно к точкам симплекса[2].
- Биангулярные координаты — частный случай бицентрических координат, система координат на плоскости, задаваемая двумя фиксированными точками С1 и С2, через которые проводится прямая, выступающая в качестве оси абсцисс. Позиция некоторой точки P, которая не лежит на этой прямой, определяется углами PC1C2 и PC2C1.
- Биполярные координаты [3] характеризуются тем, что в качестве координатных линий на плоскости в этом случае выступают два семейства окружностей с полюсами A и B, а также семейство окружностей, ортогональных к ним. Преобразование биполярных координат в декартовы прямоугольные осуществляется посредством специальных формул. Биполярные координаты в пространстве называются бисферическими; в этом случае координатными поверхностями являются сферы, поверхности, образуемые вращением дуг окружностей, а также полуплоскости, проходящие через ось Oz[4].
- Бицентрические координаты — всякая система координат, которая основана на двух фиксированных точках и в рамках которой положение некоторой другой точки определяется, как правило, степенью её удаления или вообще позицией относительно этих двух основных точек. Системы подобного рода могут быть довольно полезны в определённых сферах научных исследований[5][6].
- Бицилиндрические координаты — система координат, которая образуется в том случае, если система биполярных координат на плоскости Oxy параллельно переносится вдоль оси Oz. В качестве координатных поверхностей в этом случае выступают семейство пар круговых цилиндров, оси которых параллельны, семейство ортогональных к ним круговых цилиндров, а также плоскость. Для перевода бицилиндрических координат в декартовы прямоугольные для трехмерного пространства также применяются специальные формулы[7].
- Конические координаты — трехмерная ортогональная система координат, состоящая из концентрических сфер, которые описываются посредством их радиуса, и двух семейств перпендикулярных конусов, расположенных вдоль осей x и z[8].
- Координаты Риндлера используются преимущественно в рамках теории относительности и описывают ту часть плоского пространства-времени, которая обыкновенно называется пространством Минковского. В специальной теории относительности равномерно ускоряющаяся частица находится в гиперболическом движении, и для каждой такой частицы в координатах Риндлера может быть выбрана такая точка отсчёта, относительно которой она покоится.
- Параболические координаты — это двумерная ортогональная система координат, в которой координатными линиями является совокупность конфокальных парабол. Трехмерная модификация параболических координат строится путём вращения двумерной системы вокруг оси симметрии этих парабол. У параболических координат также имеется определенный спектр потенциальных практических приложений: в частности, они могут использоваться применительно к эффекту Штарка. Параболические координаты связаны определенным отношением с прямоугольными декартовыми[9].
- Проективные координаты существуют, согласно наименованию, в проективном пространстве Пn (К) и представляют собой взаимно однозначное соответствие между его элементами и классами конечных подмножеств элементов тела К, характеризующихся свойствами эквивалентности и упорядоченности. Для определения проективных координат проективных подпространств достаточно определить соответствующие координаты точек проективного пространства. В общем случае относительно некоторого базиса проективные координаты вводятся чисто проективными средствами[10].
- Тороидальная система координат — трехмерная ортогональная система координат, получаемая в результате вращения двумерной биполярной системы координат вокруг оси, разделяющей два её фокуса. Фокусы биполярной системы, соответственно, превращаются в кольцо с радиусом а, лежащее на плоскости xy тороидальной системы координат, в то время как ось z становится осью вращения системы. Фокальное кольцо также называют иногда базовой окружностью[11].
- Трилинейные координаты являются одним из образцов однородных координат и имеют своей основой заданный треугольник, так что положение некоторой точки определяется относительно сторон этого треугольника — главным образом степенью удаленности от них, хотя возможны и другие вариации. Трилинейные координаты могут быть относительно просто преобразованы в барицентрические; кроме того, они также конвертируемы в двумерные прямоугольные координаты, для чего используются соответствующие формулы[12].
- Цилиндрические параболические координаты — трехмерная ортогональная система координат, получаемая в результате пространственного преобразования двумерной параболической системы координат. Координатными поверхностями, соответственно, служат конфокальные параболические цилиндры. Цилиндрические параболические координаты связаны определенным отношением с прямоугольными, могут быть применены в ряде сфер научных исследований[13].
- Эллипсоидальные координаты — эллиптические координаты в пространстве. Координатными поверхностями в данном случае являются эллипсоиды, однополостные гиперболоиды, а также двуполостные гиперболоиды, центры которых расположены в начале координат. Система ортогональна. Каждой тройке чисел, являющихся эллипсоидальными координатами, соответствуют восемь точек, которые относительно плоскостей системы Oxyz симметричны друг другу[14].
Переход из одной системы координат в другую[править | править код]
Декартовы и полярные[править | править код]
- x=rcosφ,{\displaystyle x=r\,\cos \varphi ,}
- y=rsinφ,{\displaystyle y=r\,\sin \varphi ,}
- r=x2+y2,{\displaystyle r={\sqrt {x^{2}+y^{2}}},}
- φ=arctgyx+πu0(−x)sgny,{\displaystyle \varphi =\operatorname {arctg} {\frac {y}{x}}+\pi u_{0}(-x)\,\operatorname {sgn} y,}
где u0 — функция Хевисайда с u0(0)=0,{\displaystyle u_{0}(0)=0,} а sgn — функция signum. Здесь функции u0 и sgn используются как «логические» переключатели, аналогичные по значению операторам «если .. то» (if…else) в языках программирования. Некоторые языки программирования имеют специальную функцию atan2 (y, x), которая возвращает правильный φ в необходимом квадранте, определённом координатами x и y.
Декартовы и цилиндрические[править | править код]
- x=rcosφ,{\displaystyle x=r\,\cos \varphi ,}
- y=rsinφ,{\displaystyle y=r\,\sin \varphi ,}
- z=z.{\displaystyle z=z.\quad }
- r=x2+y2,{\displaystyle r={\sqrt {x^{2}+y^{2}}},}
- φ=arctgyx+πu0(−x)sgny,{\displaystyle \varphi =\operatorname {arctg} {\frac {y}{x}}+\pi u_{0}(-x)\,\operatorname {sgn} y,}
- z=z.{\displaystyle z=z.\quad }
- (dxdydz)=(rcosθ−rsinφ0rsinθrcosφ0001)⋅(drdφdz),{\displaystyle {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}={\begin{pmatrix}r\cos \theta &-r\sin \varphi &0\\r\sin \theta &r\cos \varphi &0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}},}
- (drdφdz)=(xx2+y2yx2+y20−yx2+y2xx2+y20001)⋅(dxdydz).{\displaystyle {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}}={\begin{pmatrix}{\frac {x}{\sqrt {x^{2}+y^{2}}}}&{\frac {y}{\sqrt {x^{2}+y^{2}}}}&0\\{\frac {-y}{\sqrt {x^{2}+y^{2}}}}&{\frac {x}{\sqrt {x^{2}+y^{2}}}}&0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}.}
Декартовы и сферические[править | править код]
- x=ρsinθcosφ,{\displaystyle {x}=\rho \,\sin \theta \,\cos \varphi ,\quad }
- y=ρsinθsinφ,{\displaystyle {y}=\rho \,\sin \theta \,\sin \varphi ,\quad }
- z=ρcosθ;{\displaystyle {z}=\rho \,\cos \theta ;\quad }
- ρ=x2+y2+z2,{\displaystyle {\rho }={\sqrt {x^{2}+y^{2}+z^{2}}},}
- θ=arccoszρ=arctgx2+y2z,{\displaystyle {\theta }=\arccos {\frac {z}{\rho }}=\operatorname {arctg} {\frac {\sqrt {x^{2}+y^{2}}}{z}},}
- φ=arctgyx+πu0(−x)sgny.{\displaystyle {\varphi }=\operatorname {arctg} {\frac {y}{x}}+\pi \,u_{0}(-x)\,\operatorname {sgn} y.}
- (dxdydz)=(sinθcosφρcosθcosφ−ρsinθsinφsinθsinφρcosθsinφρsinθcosφcosθ−ρsinθ0)⋅(dρdθdφ),{\displaystyle {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}={\begin{pmatrix}\sin \theta \cos \varphi &\rho \cos \theta \cos \varphi &-\rho \sin \theta \sin \varphi \\\sin \theta \sin \varphi &\rho \cos \theta \sin \varphi &\rho \sin \theta \cos \varphi \\\cos \theta &-\rho \sin \theta &0\end{pmatrix}}\cdot {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}},}
- (dρdθdφ)=(x/ρy/ρz/ρxzρ2×2+y2yzρ2×2+y2−(x2+y2)ρ2×2+y2−yx2+y2xx2+y20)⋅(dxdydz).{\displaystyle {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}}={\begin{pmatrix}x/\rho &y/\rho &z/\rho \\{\frac {xz}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {yz}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {-(x^{2}+y^{2})}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}\\{\frac {-y}{x^{2}+y^{2}}}&{\frac {x}{x^{2}+y^{2}}}&0\end{pmatrix}}\cdot {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}.}
Цилиндрические и сферические[править | править код]
- r=ρsinθ,{\displaystyle {r}=\rho \,\sin \theta ,}
- φ=φ,{\displaystyle {\varphi }=\varphi ,\quad }
- z=ρcosθ;{\displaystyle {z}=\rho \,\cos \theta ;}
- ρ=r2+z2,{\displaystyle {\rho }={\sqrt {r^{2}+z^{2}}},}
- θ=arctgzr+πu0(−r)sgnz,{\displaystyle {\theta }=\operatorname {arctg} {\frac {z}{r}}+\pi \,u_{0}(-r)\,\operatorname {sgn} z,}
- φ=φ.{\displaystyle {\varphi }=\varphi .\quad }
- (drdφdh)=(sinθρcosθ0001cosθ−ρsinθ0)⋅(dρdθdφ),{\displaystyle {\begin{pmatrix}dr\\d\varphi \\dh\end{pmatrix}}={\begin{pmatrix}\sin \theta &\rho \cos \theta &0\\0&0&1\\\cos \theta &-\rho \sin \theta &0\end{pmatrix}}\cdot {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}},}
- (dρdθdφ)=(rr2+z20zr2+z2−zr2+z20rr2+z2010)⋅(drdφdz).{\displaystyle {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}}={\begin{pmatrix}{\frac {r}{\sqrt {r^{2}+z^{2}}}}&0&{\frac {z}{\sqrt {r^{2}+z^{2}}}}\\{\frac {-z}{r^{2}+z^{2}}}&0&{\frac {r}{r^{2}+z^{2}}}\\0&1&0\end{pmatrix}}\cdot {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}}.}
Географическая система координат обеспечивает возможность идентификации любой точки на поверхности земного шара совокупностью цифробуквенных обозначений. Как правило, координаты назначаются таким образом, что один из указателей обозначает позицию по вертикали, а другой или совокупность других — по горизонтали. Традиционный набор географических координат — широта, долгота и высота[15]. Географическая система координат с использованием трёх перечисленных указателей является ортогональной.
Широта точки на поверхности Земли определяется как угол между плоскостью экватора и прямой, проходящей через эту точку в виде нормали к поверхности базового эллипсоида, примерно совпадающего по форме с Землей. Эта прямая обычно проходит в нескольких километрах от центра Земли, за исключением двух случаев: полюсов и экватора (в этих случаях она проходит непосредственно через центр). Линии, соединяющие точки одной широты, именуются параллелями. 0° широты соответствуют плоскости экватора, Северный полюс Земли соответствует 90° северной широты, Южный — соответственно, 90° южной широты. В свою очередь, долгота точки на поверхности Земли определяется как угол в восточном или западном направлении от основного меридиана к другому меридиану, проходящему через эту точку. Меридианы, соединяющие точки одной долготы, представляют собой полуэллипсы, сходящиеся на полюсах. Нулевым считается меридиан, проходящий через королевскую обсерваторию в Гринвиче, близ Лондона. Что касается высоты, то она отсчитывается от условной поверхности геоида, являющегося абстрактным пространственным представлением земного шара.
Новый взгляд на координаты точек. Перевод чисел из различных систем счисления в десятичную и обратно
Ещё один способ перевода чисел из десятичной системы счисления в двоичную систему заключается в подборе чисел, которые должны входить в состав ряда степеней двойки, и, просуммировав которые, мы получим заданное десятичное число.
Ещё раз запишем полученные результаты степень
двойки по возрастанию для лучшего визуального
восприятия данного ряда чисел:
1 2 4 8 16 32 64 128 256 512 1024
Рассмотрим этот способ перевода на конкретном примере: переведём число 567 из десятичной системы счисления в двоичную систему.
Видно, что первое значение, которое входит в ряд степеней двойки и меньше заданного числа 567, это 512. Записываем 1 для данного разряда и выполняем вычитание: 567512.
Получилось число 55. Следующее число, входящее в
заданный ряд и меньшее теперь уже числа 55 это 32:
в соответствующем данному числу разряде тоже
надо поставить 1. Но между 512 и числом 32
располагаются в записанном нами ряду степеней
двойки числа 64, 128, 256. Мы их не можем миновать
просто так и оставить без внимания: запишем в
соответствующих им разрядах нули. Итого, запись
нашего двоичного числа преобразуется уже в
следующий вид: 10001 (первая единица соответствует
512ти, нули 256, 128, 64, и последняя единица 32м)
Выполняем действие: 5532=23 . Следующее после 32
число 16 сразу подходит нам, так как оно меньше 23.
Следовательно, в разряде, соответствующем 16, мы
тоже записываем 1. Двоичное число приобретает
вид: 100011.
Вновь выполняем действие: 2316=7. Следующее, подходящее для результата число ряда это 4. В разряде, соответствующем числу 8 (которое мы миновали), мы ставим 0, а в разряде, соответствующем 4, пишем 1. Двоичное число приобретает вид: 10001101.
Вновь выполняем действие: 74=3. Следующее подходящее число 2 . Ставим в соответствующем разряде 1.
Выполняем действие: 32=1. Ставим последнюю единицу в разряде, соответствующем 1. Законченная запись числа приобретает вид: 1000110111.
Все объяснения можно было свести к следующей записи:
1 0 0 0 1 1 0 1 1 1
512 256 128 64 32 16 8 4 2 1
из которой явственно видно, суммированием каких чисел ряда степеней двойки можно получить заданное число 567. Над нужными числами стоят 1, над числами, не используемыми при суммировании, ставится 0.
Ну а теперь, для закрепления, переведём число 736 в двоичную систему счисления:
1 0 1 1 1 0 0 0 0 0
512 256 128 64 32 16 8 4 2 1
При изучении темы о переводе чисел различных систем счисления перед преподавателями возникает проблема как заинтересовать учащихся процессом перевода: ведь просто выполнять арифметические действия представляется малоинтересным. Можно предложить им задание на закрепление, суть которого заключается в переводе координат точек, представленных в недесятичных системах счисления, в их обычный десятичный вид записи числа. Затем эти координаты использовать при построении рисунка в графическом редакторе Microsoft Paint (на рис.1 представлена сетка для построения, которую учитель должен приготовить заранее).
Перевод чисел двоичной, восьмеричной, шестнадцатеричной систем счисления в десятичную систему (варианты заданий)
Вариант №1
Координаты точек представлены в недесятичной системе счисления. Выполните перевод координат в десятичную систему счисления и отметьте точки на координатной плоскости. Правильно сделав перевод и соединив последовательно все точки, получите некий рисунок.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
X |
100002 |
11102 |
11102 |
11002 |
11002 |
11012 |
11102 |
11102 |
1116 |
1416 |
1416 |
1516 |
Y |
1002 |
1002 |
102 |
102 |
10102 |
11002 |
10102 |
101102 |
1816 |
1616 |
А16 |
С16 |
продолжение таблицы
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
X |
1616 |
1616 |
1416 |
248 |
228 |
228 |
208 |
208 |
218 |
228 |
228 |
Y |
А16 |
216 |
216 |
48 |
48 |
28 |
28 |
128 |
148 |
128 |
48 |
Результат построения на рис.2
Вариант №2
Координаты точек представлены в недесятичной системе счисления. Выполните перевод координат в десятичную систему счисления и отметьте точки на координатной плоскости. Правильно сделав перевод и соединив последовательно все точки, получите некий рисунок.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
X |
10102 |
10002 |
100102 |
100102 |
11102 |
228 |
128 |
128 |
228 |
Y |
102 |
10002 |
1102 |
101102 |
101012 |
248 |
208 |
148 |
108 |
продолжение таблицы
10 |
11 |
12 |
13 |
14 |
15 |
|
X |
168 |
1216 |
1216 |
1С16 |
1А16 |
А16 |
Y |
168 |
1416 |
616 |
816 |
216 |
216 |
Результат построения на рис.3
Вариант №3
Координаты точек представлены в недесятичной системе счисления. Выполните перевод координат в десятичную систему счисления и отметьте точки на координатной плоскости. Правильно сделав перевод и соединив последовательно все точки, получите некий рисунок.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
X |
100002 |
100002 |
10102 |
100002 |
11002 |
208 |
168 |
228 |
Y |
102 |
1002 |
1002 |
10102 |
10102 |
168 |
168 |
248 |
продолжение таблицы
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
X |
268 |
248 |
1816 |
1416 |
1А16 |
1416 |
1416 |
1016 |
Y |
168 |
168 |
А16 |
А16 |
416 |
416 |
216 |
216 |
Результат построения на рис.4
Вариант №4
Координаты точек представлены в недесятичной системе счисления. Выполните перевод координат в десятичную систему счисления и отметьте точки на координатной плоскости. Правильно сделав перевод и соединив последовательно все точки, получите некий рисунок.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
X |
1102 |
10102 |
100002 |
100102 |
1416 |
1616 |
1416 |
1316 |
1A16 |
Y |
11102 |
100002 |
11102 |
11112 |
F16 |
E16 |
E16 |
D16 |
816 |
продолжение таблицы
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
X |
1D16 |
348 |
348 |
328 |
158 |
138 |
11002 |
10002 |
1102 |
Y |
916 |
78 |
48 |
68 |
118 |
108 |
10102 |
11002 |
11102 |
Результат построения на рис.5

