Курс Harvard CS50 — Лекция: Двоичная система счисления
Harvard CS50
0 уровень , 3 лекция
Открыта
У нас 10 пальцев, и система — десятичная. То есть, любое, сколь угодно большое число мы можем представить с помощью цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. В зависимости от того, где в числе стоит цифра, она может означать разное: если эта цифра последняя, то она расположена в разряде единиц, предпоследняя — разряд десятков, еще левее — разряд сотен и так далее. По сути, любое число можно расписать в виде суммы цифр, каждая из которых умножена на десять в определенной степени. В случае единиц, эта степень — нулевая.
Например,
1573 = 3*100 + 7*101 + 5*102 + 1*103.
Число, на степень которого умножаются цифры называется базой системы счисления. Для десятичной системы базой, логично, является десятка.
У компьютера пальцев нет, но есть два состояния: условно «ток идет» и «ток не идет», нулик и единичка.
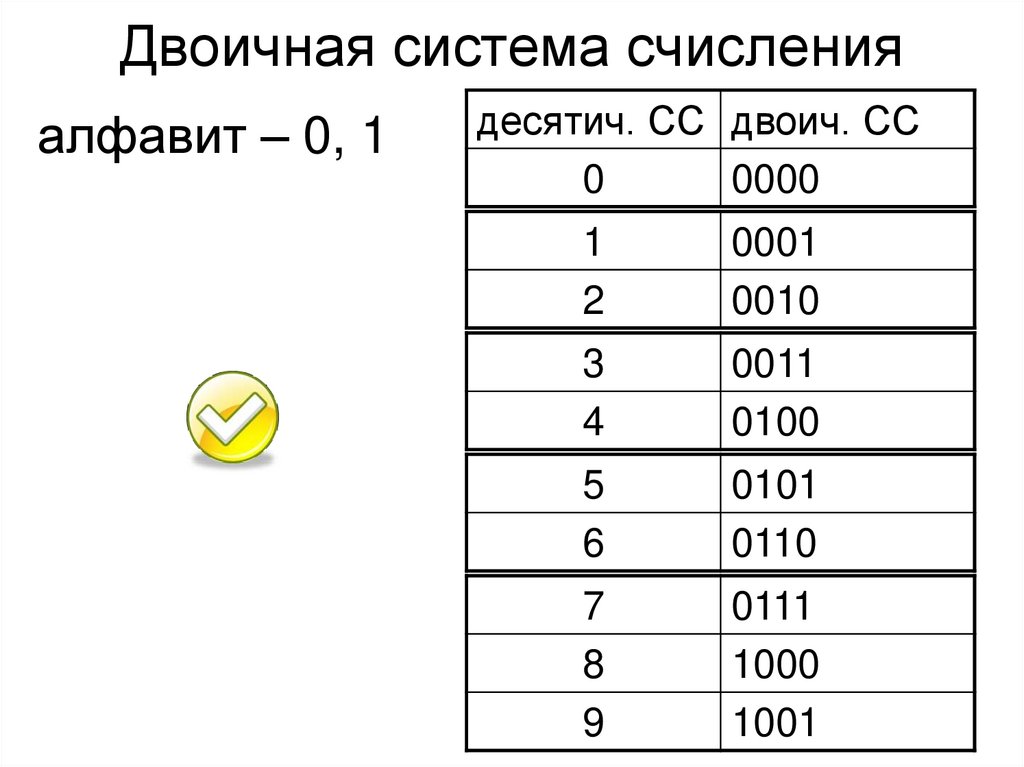
0 в двоичной системе = 0 1 в двоичной системе = 1 2 в двоичной системе = 10 710=1112
Научитесь переводить из двоичной системы в десятичую. Вы, наверное, уже поняли, как это делается — просто берем цифру числа начиная с самой правой и умножаем её на базу системы счисления в степени, соответствующей её разряду, так с каждым разрядом. Затем складываем все получившиеся таким образом числа.
Пример:
Давайте найдем десятичный аналог двоичного числа 1011012
- Самая правая единичка = 1*20
- Следующий нулик = 0*21
- Третья справа единичка = 1*22
- Четвертая = 1*23
- … и так далее
1011012 = 1*20 + 0*21 + 1*22 + 1*23 + 0*24 + 1*25 = 1 + 0 + 4 + 8 + 0 + 32 = 4510
Представьте восемь лампочек, выставленных в ряд.
У каждой из них — свой собственный выключатель.
Каждая из лампочек — это разряд. Да что представлять, вспомните самую первую лекцию (там есть такой агрегат) или вот вам виджет: cdn.cs50.net/2016/x/psets/0/pset0/bulbs.html
Поиграйтесь с ним, «прочувствуйте» двоичную систему.
Тут тоже всё просто, если понимать суть.
Пример:
У нас есть десятичное число 5710. Чтобы перевести его в двоичную систему, нужно определить, какая максимальная степень двойки не превосходит это число.
26 = 64. Это явно многовато. А вот 25 = 32.
Мы определили старший разряд. 3210 = 1000002. Теперь ищем следующий разряд. 57-32 = 25. Теперь для 25 ищем степень двойки, которая не превосходит 25. 2
32 + 16 + 8 = 5610 = 1110002. 57 - 56 = 1, то есть осталась только одна степень 20. Таким образом, 5710 = 1110012.
На этом все =) Переходите к следующей лекции!
Экскурс в двоичную систему счисления
Публикуем главу из книги математика Юджинии Ченг«Математический беспредел. От элементарной математики к возвышенным абстракциям» о том, почему некоторые числа невозможно сосчитать, а бесконечность + 1 не то же самое, что 1 + бесконечность. Перевод с английского А. Шмид.
Двоичная система счисления — это такое представление чисел, в котором вместо цифр 0, 1, 2, 3 и так далее до 9, которыми мы обычно пользуемся в десятичной системе счисления, используются только цифры 0 и 1. Удивительно, сколько информации можно хранить с помощью всего лишь двух цифр, 0 и 1. Компьютеры работают исключительно в этой системе, как будто все вокруг представляет собой лишь переключение с on на off, и таких переключений существуют миллионы и миллиарды.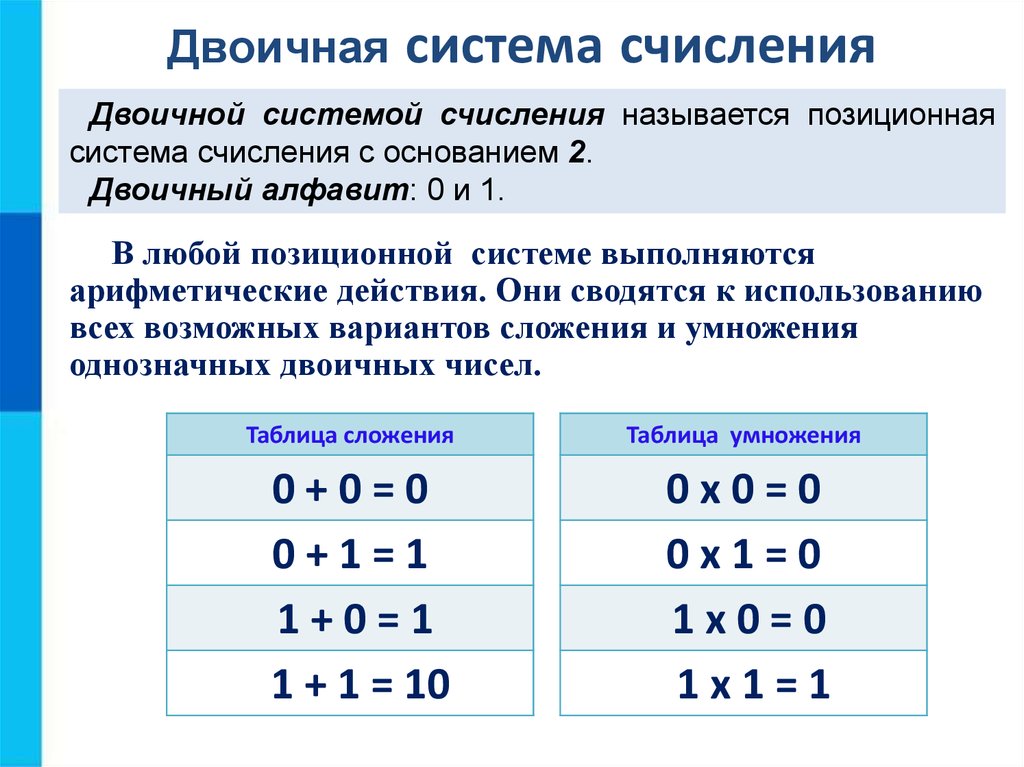
Вы можете получить очень много разных конфигураций, имея в своем распоряжении очень маленькое количество вариантов on/off переключений.
При наличии двух переключений вы можете получить четыре возможные конфигурации:
При наличии трех переключений вы получаете уже восемь конфигураций:
Это похоже на меню из двух или трех блюд. Дерево переключений будет выглядеть таким образом:
При наличии трех переключений каждая из восьми конечных точек дает нам одну из восьми конфигураций. Мы просто должны проследить сверху вниз по веткам до конечной точки, считывая по пути off и on.
Мы будем называть эти рисунки деревьями, потому что именно так они называются в математике. Это кажется глупым, ведь обычно деревья растут снизу вверх, но математические деревья часто растут так, потому что нам привычно читать сверху вниз. Хотя некоторые направляют математические деревья в сторону:
Думаю, вы понимаете, что не имеет никакого значения, в какую сторону мы направляем наше математическое дерево, потому что независимо от расположения схемы в ней зашифрована одна и та же информация.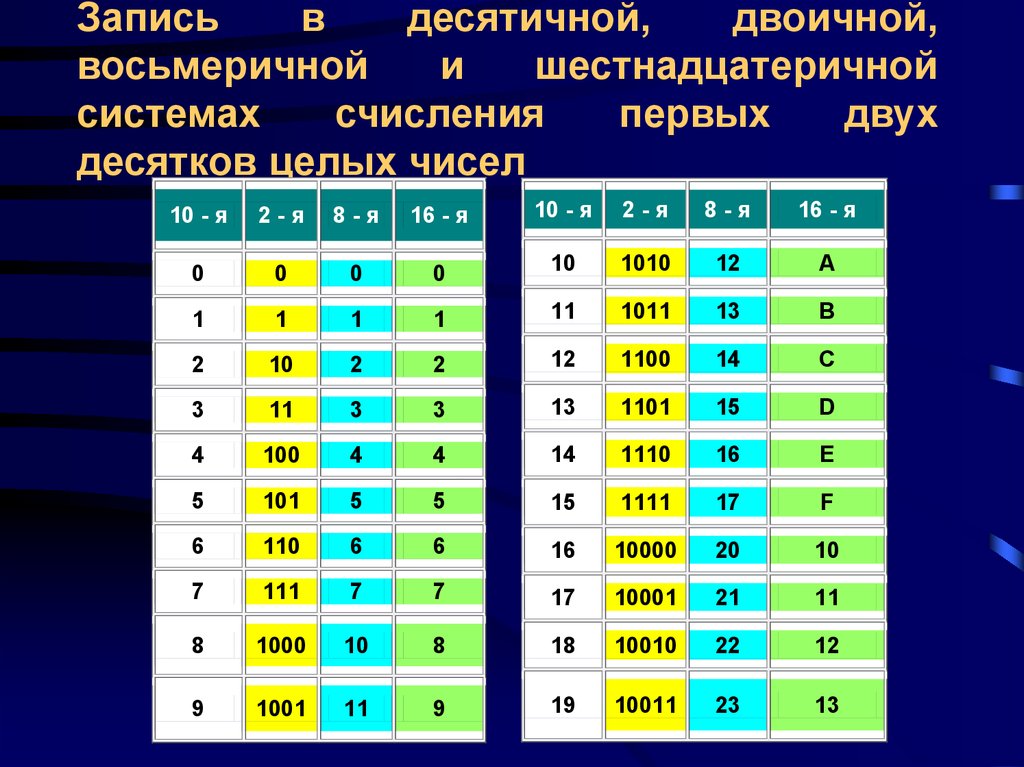
Мы можем также назвать такое дерево блок-схемой, так как оно демонстрирует абстрактные, а не физические отношения объектов друг к другу. По мере того как математика становится более абстрактной, в ней используются все более наглядные схемы, а абстрактные отношения объектов друг к другу становятся все более тонкими и все более значительными. Кроме того, схемы часто способны представить информацию гораздо более кратко, чем словесные объяснения. Вспомните, например, нашу схему эвакуации бесконечного отеля-небоскреба Гильберта.
В большинстве случаев базовая математика идет прямым путем. Например, вот такое сложение:
3 + 2 = 5.
Или вот такое уравнение:
2х + 3 = 7.
Символы радостно выстроились в ряд. Решение этого уравнения мы тоже будем записывать рядами:
2х = 7 – 3
2х = 4
х = 2.
Далее мы увидим, что по мере усложнения математика приобретет больше измерений. Если изучаемые нами объекты имеют форму, то у нас уже появляется больше способов скомпоновать их друг с другом.
n возможных конфигураций. Это похоже на то, как мы считали числа с n-м количеством десятичных знаков, только теперь у нас не десять, а два варианта выбора для каждого уровня, как в примере с меню.
Двоичная система счисления представляет собой различные наборы on/off переключений. Она похожа на десятичную систему счисления, но вместо единиц, десятков, сотен, тысяч и так далее у нас будут единицы, пары, четверки, восьмерки и так далее. Целые числа в двоичной системе счисления более популярны, чем дроби. Мы можем сравнить четырехзначное число в десятичной и в двоичной системе счисления, например, вот таким образом:
В десятичной системе счисления число 1101 можно разложить следующим образом:
(1 × 1 000) + (1 × 100) + (0 × 10) +1.
А двоичное число 1101 можно разложить на десятичные разряды следующим образом:
(1 × 8) + (1 × 4) + (0 × 2) + 1.
В то время как в десятичной системе это будет 13.
В десятичной системе четырехзначное число может выразить любое число до 9999, то есть 10^4 – 1.
4 – 1 = 15.
Может показаться, что двоичная система счисления слабовата, особенно при том, что в главе 5 я пообещала, что в двоичном мире мы сможем считать на пальцах до 1023. Но мы будем использовать принцип чередования. В двоичной системе вы можете зашифровать все, что угодно, с помощью простых on/off переключений, а в десятичной системе каждая «позиция» предполагает десять вариантов фрагмента информации, выраженные цифрами 0, 1 и далее до 9. Иногда у нас есть большое количество цифр, которые мы можем использовать, но мало позиций для них (скажем, в компьютере). Или, например, ISBN-код на книгах размещается на ограниченном пространстве, но каждая позиция может выражать множество разных вещей. Цветовой код HTML еще более компактный, он записывается в шестнадцатеричной системе счисления, то есть на базе 16. Это значит, каждая позиция имеет 16 возможных вариантов. Используются такие знаки, как 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, B, C, D, E, F.
Один из моих любимых вариантов использования двоичной системы счисления — это свечи на именинном пироге.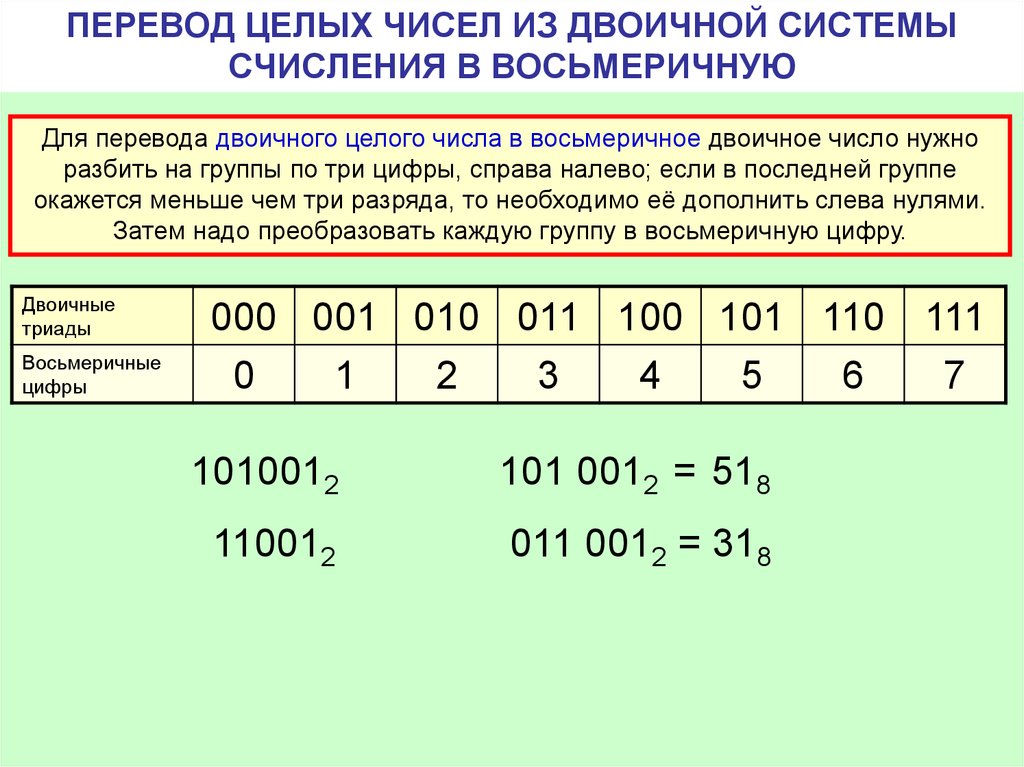
10 – 1. Вот как это делается. У каждого пальца есть два возможных положения. Он может быть выпрямленным, это будет 1, или загнутым, это будет 0. И вот у нас есть десять цифр (десять обычных цифр!), которые мы можем использовать в двоичной системе счисления, что позволит нам выразить числа от 0 до 1023. На рисунке ниже приведены числа от 0 до 31, которые мы можем показать с помощью одной руки.
А вот соответствующие цифры в пятизначной двоичной системе:
Это довольно занимательно, но требует некоторой концентрации внимания, гораздо большей, чем при обычном счете на пальцах до 10. К сожалению, маловероятно, что этот метод поможет нам высвободить ментальное пространство. Я не уверена, что у меня получится долго считать в двоичной системе и одновременно разговаривать с кем-нибудь. (Я только что попробовала сделать это, но дошла только до 10, а потом сбилась.)
Если вы умеете концентрироваться и хорошо владеете своими пальцами, то можете использовать их даже на базе 3.
Это означает, что у вас будет 3 возможных варианта для каждой позиции. Для этого вы должны уметь сгибать каждый палец наполовину, независимо от положения остальных пальцев, тогда каждый палец будет иметь 3 возможных положения, которые будут соответствовать 0, 1 и 2. Попробуйте выпрямить безымянный палец и одновременно согнуть средний палец наполовину, затем согните безымянный палец полностью. Есть ли разница между этими положениями? Тут требуется немало ловкости.
Это все о целых числах, но кроме них у нас есть дроби, которые мы точно так же можем использовать в двоичной системе счисления. Нужно просто вспомнить, что в действительности означают десятичные знаки, и превратить их в «двоичные знаки». Кроме того, мы никогда не должны использовать слово «десятичный», когда имеем в виду «дроби». (Мне всегда хочется сказать «двоичный десятичный», но с лингвистической точки зрения это не имеет смысла.)
Когда мы имеем дело с десятичными дробями, после запятой идут десятые, потом сотые, потом тысячные и так далее.
Например, число
0,3526
в действительности представляет собой
У двоичных дробей первый знак после запятой будет половина, следующий — четверти, потом восьмые доли и шестнадцатые доли. Так, двоичное число
0,1101
можно также записать как
Что в обычной десятичной системе счисления будет десятичной дробью 0,8125. Мы также можем изобразить все возможные двоичные дроби в виде дерева, точно так же, как мы рисовали все конфигурации переключений on/off.
На этом рисунке вместо ветвей off и on у нас будут ветви 0 и 1. Это похоже на то, как мы использовали зажженные и незажженные свечки на двоичном именинном пироге в качестве 0 и 1. Сейчас у нас есть только четыре цифры, и, значит, будет только четыре уровня разветвления. Мы могли бы использовать этот метод также для обычных десятичных дробей, но тогда нам понадобилось бы десять ветвей, выходящих из каждой конечной точки на каждом уровне. Такое дерево быстро нарисовать не получится.
Теперь каждый лист представляет собой двоичную дробь. Чтобы узнать, какую именно, нужно проследить по дереву сверху вниз, считывая по пути нули и единицы на каждой ветви. Так, первый лист будет 0,0000. Второй — 0,0001 и т. д. Вот они все:
Если у нас четыре цифры, то наше дерево будет иметь пять уровней, если у нас n цифр, то наше дерево будет иметь n-е количество уровней, а если у нас будут двоичные дроби с бесконечным количеством десятичных знаков, то это будет «дерево с бесконечным количеством уровней». Это немного странная концепция, потому что предполагается, что конечные точки дерева — листья — должны представлять собой итоговые числа. Но если дерево растет бесконечно, то не будет никаких конечных точек. По этой причине разумнее рассматривать числа как линии на дереве. Мы уже выяснили, что можем узнать, какое число выражает каждый листок, проследив за его линией по дереву сверху вниз. Даже если у дерева нет никаких конкретных конечных точек (потому что оно бесконечно), мы все равно можем проследить за его линиями, которые тоже будут продолжаться бесконечно.
n линий.
* По дереву с бесконечным количеством уровней проходит «два в бесконечной степени» линий.
До сих пор мы не рассматривали целую часть дроби. В следующей главе мы узнаем, почему эта часть дроби не имеет большого значения. Мы также выясним, почему целую часть дроби лучше рассматривать в двоичной системе счисления, а не в десятичной и почему сначала мы могли ее игнорировать.
Возможно, сейчас вы думаете, что мы все еще ничего не добились. Ведь мы так и застряли на вопросе: сколько будет два в бесконечной степени? В следующей главе мы соберемся с силами и справимся с этим вопросом. Но сначала увидим такой захватывающий пейзаж, какой мы только способны оценить. Мы уже знаем, как построить действительные числа из натуральных с помощью деревьев. Знаем, что именно так можно создать более большую бесконечность. Все, что нам теперь нужно, — это повторение, и так мы создадим иерархию бесконечностей. Это тема следующей главы.
Источник: https://postnauka.ru/longreads/89461
Двойные звездные системы: классификация и эволюция
В двойной системе J0806 два белых карлика вращаются вокруг друг друга каждые 321 секунду.
Более четырех пятых отдельных точек света, которые мы наблюдаем в ночном небе, на самом деле представляют собой две или более звезды, вращающиеся вместе. Наиболее распространенными из множественных звездных систем являются двойные звезды, системы, состоящие только из двух звезд вместе. Эти пары имеют множество конфигураций, которые помогают ученым классифицировать звезды и могут повлиять на развитие жизни. Некоторые люди даже думают, что Солнце является частью бинарной системы.
Классификация двойных
Двойные звезды — это две звезды, вращающиеся вокруг общего центра масс. Более яркая звезда официально классифицируется как главная звезда, а более тусклая из двух — второстепенная (классифицируется как A и B соответственно).
В случаях, когда звезды имеют одинаковую яркость, соблюдается обозначение, данное первооткрывателем.
Бинарные пары можно классифицировать на основе их орбиты. Широкие двойные системы — это звезды, орбиты которых удерживают их на расстоянии друг от друга. Эти звезды развиваются отдельно, практически не оказывая влияния на своих компаньонов. Возможно, когда-то они содержали третью звезду, которая вытолкнула далекого компаньона наружу, в то время как в конечном итоге они сами были выброшены.
Тесные двойные системы , с другой стороны, эволюционируют поблизости, способные передавать свою массу от одной к другой. Первичные звезды некоторых тесных двойных звезд поглощают материал своего компаньона, иногда оказывая гравитационное воздействие, достаточно сильное, чтобы полностью притянуть меньшую звезду. [Инфографика: Как планеты «Татуин» вращаются вокруг звезд-близнецов Kepler-47]
Пары также можно классифицировать на основе того, как они наблюдаются, система, которая имеет перекрывающиеся категории.
Визуальные двоичные файлы — это две звезды с достаточно большим расстоянием между ними, чтобы их можно было увидеть в телескоп или даже в бинокль. От 5 до 10 процентов видимых звезд являются визуально двойными.
Спектроскопические двойные объекты кажутся близкими даже при наблюдении в телескоп. Ученые должны измерить длины волн света, излучаемого звездами, и определить их двойную природу на основе особенностей этих измерений.
Затменные двойные звезды — это две звезды, орбиты которых расположены под таким углом, что от Земли одна проходит перед другой, вызывая затмение. Эта функция основана на линии прямой видимости, а не на какой-либо конкретной функции пары.
Астрометрические двойные звезды — это звезды, которые, кажется, танцуют вокруг пустого пространства; то есть их товарищей нельзя идентифицировать, а можно только предположить. Такой компаньон может быть слишком тусклым, чтобы его можно было увидеть, или может быть скрыт в ярком свете главной звезды.
Звезды, называемые двойными звездами , — это две звезды, которые визуально кажутся близкими друг к другу в небе, но не обязательно находятся где-то рядом друг с другом в космосе.
Открытие и эволюция
Первые наблюдаемые двойные звезды были визуально-двойными. В 1617 году по просьбе коллеги-ученого Галилео Галилей направил свой телескоп на вторую звезду от конца рукоятки Большой Медведицы, обнаружив, что одна звезда кажется двумя; в итоге оказалось шесть. В 1802 году сэр Уильям Гершель, каталогизировавший около 700 пар звезд, впервые использовал термин «двойные» по отношению к этим двойным звездам.
Звезды путешествуют по галактике, и иногда массивная звезда захватывает проходящую, создавая новую бинарную пару. Но это редкое событие. Чаще оболочка из газа и пыли, которая схлопывается сама по себе, образуя звезду, расщепляется и вместо этого образует две или более звезд. Эти звезды развиваются вместе, хотя и не обязательно одинаково.
Эволюция пары звезд зависит от их расстояния друг от друга. Широкие двойные системы очень мало влияют друг на друга, поэтому они часто эволюционируют так же, как одиночные звезды. Однако тесные двойные системы влияют на эволюцию друг друга, а перенос массы изменяет состав звезд. Если одна звезда в тесной двойной системе взрывается сверхновой или сбрасывает свои внешние слои и образует пульсар, компаньон часто разрушается. Если он выживает, он продолжает вращаться вокруг новообразованного тела, возможно, передавая больше своего материала.
Двойные звездные системы предоставляют ученым наилучшие средства для определения массы звезды. Поскольку пара притягивает друг друга, астрономы могут рассчитать размер и оттуда определить такие характеристики, как температура и радиус. Эти факторы помогают охарактеризовать отдельные звезды главной последовательности во Вселенной.
Звезды в нескольких системах могут иметь прямое влияние на жизнь. Уже обнаружено множество планет, вращающихся вокруг нескольких звезд.
Орбиты этих звезд могут влиять на эволюцию жизни, которая нуждается в относительно стабильной системе для развития. света, тепла и радиации, которые они получают, такие системы, как широкие двойные или тесные двойные, могут фактически создавать условия, при которых жизнь могла бы в конечном итоге развиваться. [9Экзопланеты, на которых может быть инопланетная жизнь]
В 2015 году астрофизик Пол Саттер — научный сотрудник Астрономической обсерватории Триеста — написал на Space.com, что существование жизни в большинстве бинарных систем кажется маловероятным.
«Хотя двойные системы, безусловно, имеют обитаемую зону, где жидкая вода потенциально может существовать на поверхности планеты, жизни может быть трудно закрепиться. Обращение вокруг двух звезд одновременно, как это делает наш друг Kepler-47c, делает жизнь очень эллиптична, время от времени вынося планету из зоны. Жизнь не слишком любезна, чтобы часто замерзать», — писал он.
«Обращаясь вокруг одной звезды в двойной системе? Ну, иногда у вас будет две звезды на небе одновременно, что может быть немного поджаренным.
А иногда у вас будет звезда на каждой стороне планеты, разрушая ночь. И не забывайте о двойных дозах УФ-излучения и солнечных вспышках. При такой нестабильности, беспорядочности и облучении трудно представить, что сложная жизнь развивается с той регулярностью, в которой она нуждается».
Ближайшая к Земле звездная система — Альфа Центавра — включает двойную пару звезд, Альфа Центавра A и Альфа Центавра B. Третья звезда, Проксима Центавра, находится примерно в одной пятой светового года от нас (примерно в 13 000 солнечных Земные расстояния; некоторые астрономы спорят о том, следует ли считать Проксиму Центавра частью той же системы.) Хотя в двойной звездной части Альфы Центавра не было обнаружено звезд в обитаемой зоне, планета Проксима Центавра b была объявлена в 2016 году обитаемой области своей звезды. Тем не менее, ученые расходятся во мнениях относительно того, имеет ли красный карлик, такой как Проксима Центавра, достаточно стабильную «космическую погоду», чтобы предотвратить радиационные или тепловые скачки, уменьшающие шансы на жизнь на соседней планете.
Является ли Солнце двойной звездой?
В 1980-х годах ученые предположили наличие Немезиды, второй звезды — коричневого карлика, тусклого красного карлика или белого карлика — в солнечной системе как причину периодических массовых вымираний, имевших место в истории Земли, которые некоторые палеонтологи предполагают, что они происходили с циклами в 26 миллионов лет, хотя циклическая природа обсуждается.
В 2010 году широкоугольный инфракрасный исследовательский центр НАСА (WISE) начал поиск коричневых карликов, хотя он не занимается поиском конкретно одного из них в Солнечной системе. Но если компаньон существует, WISE должен включить его. Ни WISE, ни двухмикронный обзор всего неба не обнаружили признаков компаньона, а в программе НАСА «Спросите астробиолога» Дэвид Моррисон, старший научный сотрудник астробиологии, заявил, что такой объект был бы четко обнаружен этими чувствительными телескопами.
Исследование, проведенное в 2017 году, показало, что почти у каждой звезды, подобной Солнцу, вероятно, был спутник при рождении. Исследование с использованием Очень большого массива в Нью-Мексико и телескопа Джеймса Клерка Максвелла на Гавайях изучило десятки систем и обнаружило, что более молодые обычно имеют широкое разделение, а более старые — узкое.
Моделирование показало, что большинство звезд формируются на некотором расстоянии друг от друга, а затем либо сближаются, либо расходятся, разрывая гравитационные связи. В случае с солнцем до сих пор неясно, существовала ли Немезида. Если бы это было так, родной брат Солнца, вероятно, удалился миллиарды лет назад.
Некоторые ученые предполагают, что существуют доказательства существования Немезиды. Доказательства, которые они приводят, включают далекую орбиту карликовой планеты Седна, четко очерченный край пояса Койпера (диск мусора в нашей Солнечной системе) и орбиты объектов в Облаке Оорта (ледяные скалы за пределами орбиты Плутона).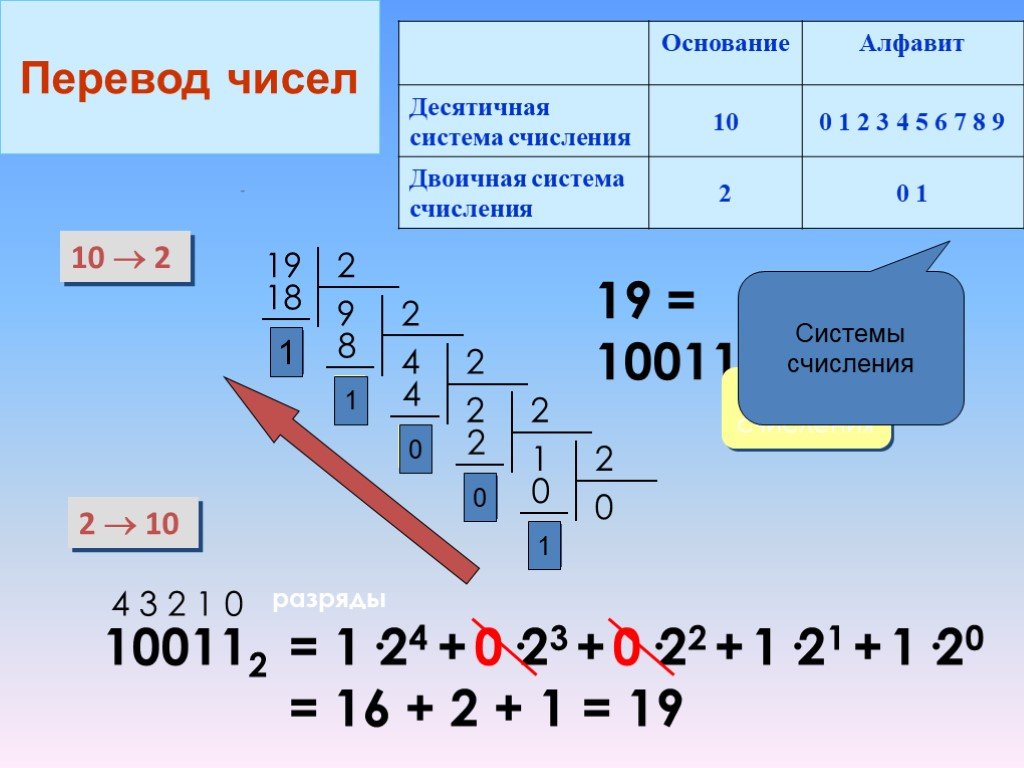
Отдельные исследовательские группы исследуют след предполагаемой «Планеты Девять» ледяной гигантской планеты, которая находится на краю нашей Солнечной системы. В 2016 году Константин Батыгин и Майк Браун (оба исследователи из Калифорнийского технологического института) заявили, что Девятая планета может изменять орбиты объектов в поясе Койпера.
Присоединяйтесь к нашим космическим форумам, чтобы продолжать обсуждать последние миссии, ночное небо и многое другое! А если у вас есть новость, исправление или комментарий, сообщите нам об этом по адресу: [email protected].
Space.com — главный источник новостей об исследованиях космоса, инновациях и астрономии, ведающий хроникой (и отмечающий) продолжающееся расширение человечества за последние рубежи. Первоначально основанный в 1999 году, Space.com всегда был и остается страстью писателей и редакторов, которые являются поклонниками космоса, а также обученными журналистами. Наша текущая команда новостей состоит из главного редактора Тарика Малика; Редактор Ханнеке Вейтеринг, старший космический писатель Майк Уолл; старший сценарист Меган Бартельс; Старший писатель Челси Год, старший писатель Тереза Пултарова и штатный писатель Александр Кокс, специализирующиеся на электронной коммерции.
Двоичный код — SparkFun Learn
Авторы: Джимблом
Избранное Любимый 50
Основание каждой системы счисления также называется основанием . Основание десятичного числа — десять, основание двоичного — два. Основание определяет, сколько различных символов требуется для конкретизации системы счисления. В нашей десятичной системе счисления у нас есть 10 числовых представлений значений от нуля до десяти с небольшим: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.. Каждый из этих символов представляет собой очень конкретное стандартизированное значение.
В двоичной системе разрешены только два символа: 0 и 1. Но с помощью этих двух символов мы можем создать любое число, которое может использовать десятичная система.
Счет в двоичной системе
Вы можете бесконечно считать в десятичной системе, даже во сне, но как бы вы считали в двоичной системе? Ноль и единица в базе два должны выглядеть довольно знакомо: 0 и 1. Отсюда все становится явно бинарным.
Помните, что у нас есть только эти две цифры, поэтому, как и в десятичном виде, когда у нас заканчиваются символы, мы должны сдвинуть один столбец влево, добавить 1 , и поверните все цифры вправо до 0. Таким образом, после 1 мы получим 10, затем 11, затем 100. Начнем считать…
| Десятичное число | Двоичное число 9024| Decimal | Binary | 0 | 0 | 16 | 10000 | 1 | 1 | 17 | 10001 | 2 | 10 | 18 | 10010 | 3 | 11 | 19 | 10011 | 4 | 100 | 20 | 10100 | 5 | 101 | 21 | 10101 | 6 | 110 | 22 | 10110 | 7 | 23 | 1000 | 24 | 11000 | 9 | 1001 | 25 | 11001 | 10 | 1010 | 26 | 11010 | 11 | 1011 | 27 | 11011 | 12 | 1100 | 28 | 11100 | 13 | 1101 | 29 | 11101 | 14 | 1110 | 30 | 11110 | 15 | 1111 | 31 | 11111 | |
Does that start to paint the picture? Давайте рассмотрим, как мы можем преобразовать эти двоичные числа в десятичные.
Преобразование двоичного числа в десятичное
Не существует единого способа преобразовать двоичное число в десятичное. Ниже мы опишем два метода: более «математический» и другой, более наглядный. Мы рассмотрим оба, но если в первом используется слишком много уродливой терминологии, переходите ко второму.
Метод 1
Есть удобная функция, которую мы можем использовать для преобразования любого двоичного числа в десятичное:
В этом уравнении есть четыре важных элемента:
Например, двоичное число, такое как 101, имеет длину 3, что-то большее, например 10011110, имеет длину 8.Давайте избавимся от этих n и показателей степени и выполним наше уравнение двоичной позиционной записи из восьми позиций:
Продолжая это, давайте подставим некоторые значения для цифр. Что, если бы у вас было двоичное число, например: 10011011? Это будет означать n значения:
Для целей этого руководства предположим, что самое правое значение всегда является наименее значащим . Наименее значащая цифра в числе — это цифра, которая оказывает наименьшее влияние на окончательное значение числа.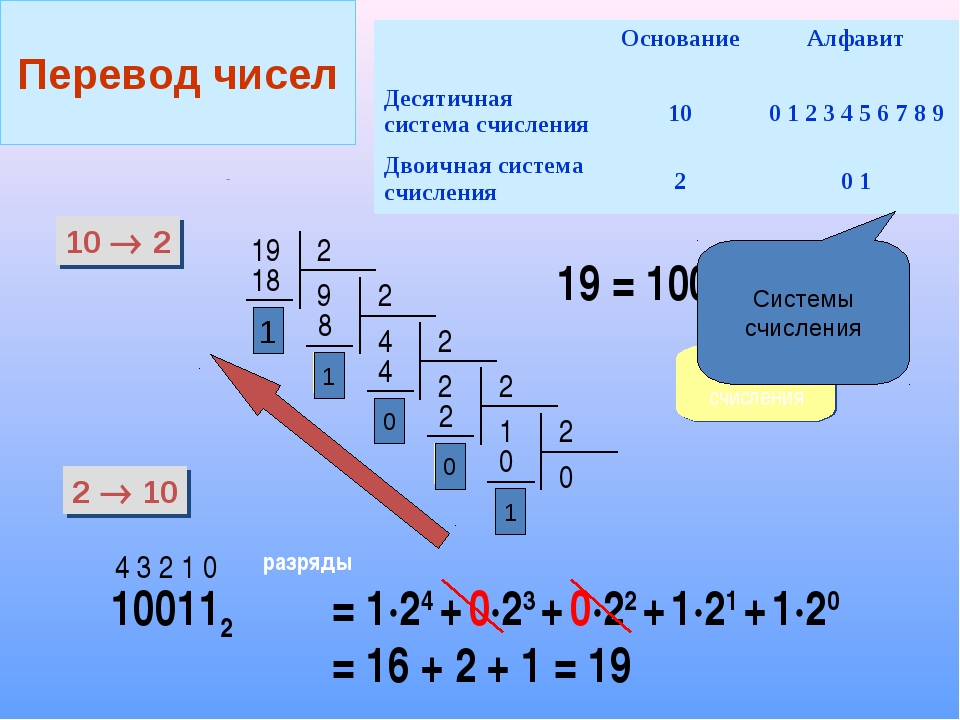
Значение цифр является произвольным — это часть соглашения , называемого endianness . Двоичное число может быть либо big -endian, где самая значащая цифра самая левая, либо little -endian, которые мы будем использовать в этом руководстве (обычно вы увидите двоичные числа, написанные таким образом ).
Теперь подставьте эти цифры в наше двоично-десятичное уравнение. Поскольку наше число имеет обратный порядок байтов, наименее значимое значение должно быть умножено на наименьший вес.
1 * 2 7 + 0 * 2 6 + 0 * 2 5 + 1 * 2 4 + 1 * 2 3 + 0 * 2 2 + 1 * * 2 1 4 1 4 1 1 + 0 * 2 2 + 1 * 2 + 0 * 2 2 . + 1 * 2 0
И мы можем упростить его, чтобы найти наше десятичное число:
= 1 * 128 + 0 * 64 + 0 * 32 + 1 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1 = 128 + 16 + 8 + 2 + 1 = 155
Вы быстро заметите, что для представления числа в двоичном формате требуется гораздо больше цифр, чем в десятичном, но все это делается всего двумя цифрами!
Метод 2
Другой, более наглядный способ преобразования двоичных чисел в десятичные состоит в том, чтобы начать с сортировки каждого числа 1 и 0 в ячейку.
Каждый бин имеет последовательную степень двойки, 1, 2, 4, 8, 16,… к которым мы привыкли. Выполнение восьми разрядов будет выглядеть примерно так:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
So, if we sorted our 10011011 binary number into those bins, it’d look like this:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
Для каждой ячейки, в которой есть двоичное значение 0 , просто зачеркните и удалите его.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
А затем сложите оставшиеся веса, чтобы получить свой номер!
Преобразование десятичного числа в двоичное
Как и в случае перехода из двоичного в десятичное, существует несколько способов преобразования десятичного числа в двоичное.
Первый использует деление и остаток, а второй использует вычитание. Попробуйте оба или придерживайтесь того, который вам удобен!
Способ 1
Не так просто преобразовать десятичное число в двоичное. Это преобразование требует многократного деления десятичного числа на 2, пока вы не уменьшите его до нуля. Каждый раз, когда вы делите остаток от деления становится цифрой в создаваемом вами двоичном числе.
Не помните, как делать остатки? Если это было давно, помните, что, поскольку мы делим на два, , если делимое равно , остаток будет 0; нечетный дивиденд означает остаток 1 .
Например, чтобы преобразовать 155 в двоичное число, выполните следующий процесс:
155 ÷ 2 = 77 R 1 (это крайняя правая цифра, 1-я позиция) 77 ÷ 2 = 38 Р 1 (2-я позиция) 38 ÷ 2 = 19Р 0 (3-я позиция) 19 ÷ 2 = 9 Р 1 9 ÷ 2 = 4 R 1 4 ÷ 2 = 2 R 0 2 ÷ 2 = 1 R 0 1 ÷ 2 = 0 R 1 (8-я позиция)
Первый остаток — это наименее значащая (самая правая) цифра, поэтому читаем сверху вниз, чтобы конкретизировать наше двоичное число справа налево: 10011011 .
Сопоставьте это с примером выше… это бинго!
Метод 2
Если деление и нахождение остатка вам не по душе, может существовать более простой способ преобразования десятичной дроби в двоичную. Начните с нахождения наибольшей степени двойки, которая все еще меньше вашего десятичного числа, и вычтите ее из десятичной дроби. Затем продолжайте вычитать в максимально возможной степени двойки, пока не дойдете до нуля. Каждое положение веса, которое было вычтено, получает двоичное число 9.0075 1 цифра; цифры, которые не были вычтены, получают 0 .
Continuing with our example, 155 can be subtracted by 128, producing 27:
| 155 — 128 = 27 | |||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | |||||||
Оба числа, 27 из этих 9, не могут быть вычтены из 4 или 3.
0075 0 . We can subtract by 16, producing 11.
| 27 — 16 = 11 | |||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | ||||
And 8 subtracts from 11, producing 3. After that, no such luck with 4.
| 11 — 8 = 3 | |||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | ||
Из 3 можно вычесть 2, получив 1. И, наконец, из 1 вычесть 1, получится 0. 0
У нас есть двоичное число!
Калькуляторы преобразования
К счастью, существует множество калькуляторов преобразования двоичных чисел в десятичные и наоборот.
