Двоичная система счисления: пресловутые нолики и единички
О чем речь? Можно с уверенностью назвать двоичную систему счисления одной из основных, которые используются в вычислительной технике. А значит, привычные нам компьютер и смартфон применяют 0 и 1 для расчетов.
На что обратить внимание? Стоит отметить, что такая «популярность» – это дань традиции, заложенной праотцом вычислительных машин Блезом Паскалем. И все же, порой, нужно переводить показатели двоичной системы в 10-ю или 16-ю. Как же это сделать?
В статье рассказывается:
- Общепринятые системы счисления
- Числа, используемые в двоичной системе счисления
- Сложение, вычитание и умножение в двоичной системе счисления
- Как переводить числа в двоичной системе счисления в десятичную
- Алгоритм перевода из двоичной системы счисления в шестнадцатеричную
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.
Бесплатно от Geekbrains
Общепринятые системы счисления
Человечество в ходе своего развития со временем стало нуждаться в способах подсчета. Нужно было считать, например, количество добычи или убитых врагов из других племен. И эта нужда у древних людей только возрастала. Поначалу пользовались абстрактными понятиями типа «нисколько», «один», «много». Затем в употребление вошла «пара», означающая два каких-то предмета. Уже одно это нововведение существенно упростило жизнь древнему человеку.
Общепринятые системы счисленияВ дальнейшем люди стали считать единицами, используя в качестве таковых пальцы на руках и ногах, зарубки на деревьях, кости зверей, узелки на веревках. Благодаря изобретению таких примитивных счетных машин человечество спустя тысячелетия смогло понять, что в древности люди умели не только считать, но также фиксировать результаты счета.
С течением времени возникла необходимость в символьном обозначении любого количества больше единицы.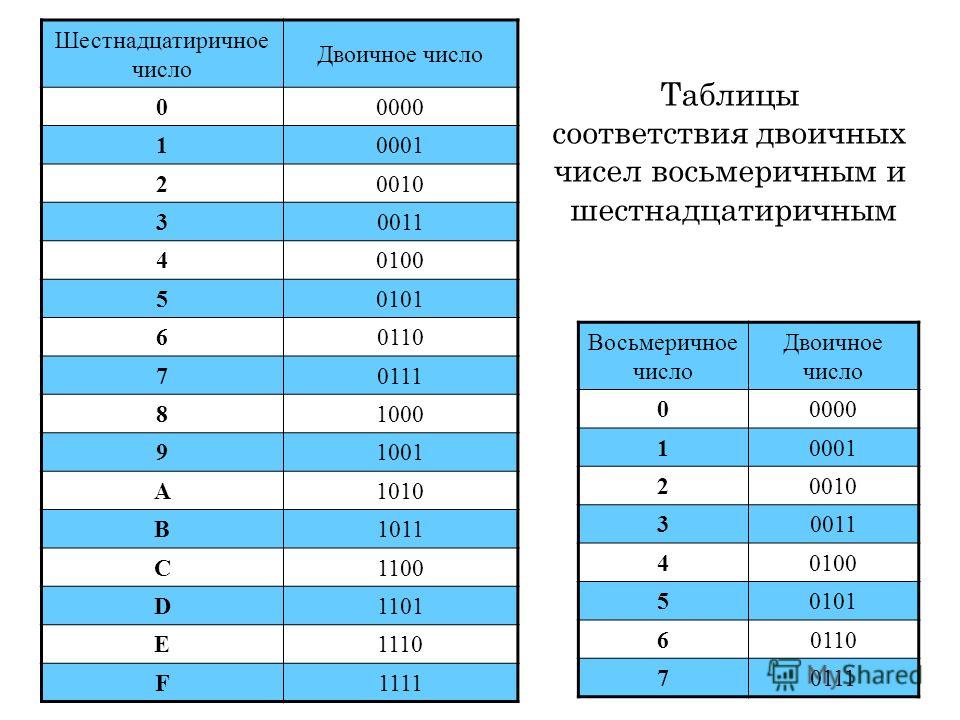
В итоге древними египтянами были впервые придуманы знаки, обозначающие 1, 5 и 10.
Система чисел, состоящая из определенных знаков (цифр), фактически и является системой счисления. Другими словами, это способ численного выражения с помощью принятых правил и специальных знаков, называемых цифрами.
Любая система счисления принадлежит к одной из двух категорий:
Позиционные СС
Конкретное значение числа определяется не только цифрами, но и их позицией. Сюда относят арабскую систему, где первый разряд справа отведен для единиц, второй разряд справа — для десятков, третий разряд справа — для сотен и т. д. Таким образом, для записи числа 475 необходимо в крайней правой позиции расположить пятерку (пять единиц), после нее — семерку (семь десятков) и затем — четверку (четыре сотни). Позиционными считаются также системы счисления с основаниями (2, 8, 16).
Непозиционные СС
Значение числа определяется только знаком (цифрой). Для обозначения единиц, десятков, сотен и тысяч используются отдельные символы.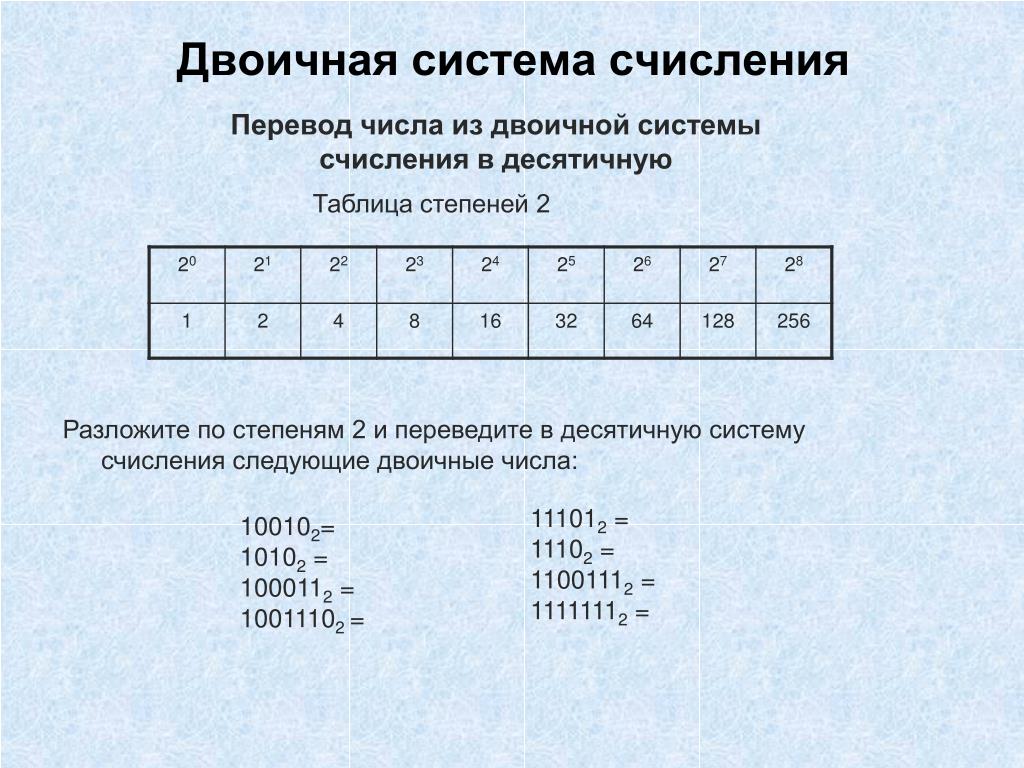
Наиболее показательным представителем данной группы является римская система счисления. Здесь имеется еще одна отличительная особенность. Для записи очень больших чисел необязательно использовать весь набор знаков — на такие случаи существуют функции сложения и вычитания.
К примеру, число 475 римскими цифрами может выглядеть как CCCCXXXXXXXIIIII либо, в сокращенном виде, как CDLXXV. В последнем варианте используются именно вычитание и прибавление. Значение цифры, стоящей слева от большего числа, отнимается соответственно от этого числа. Если эта цифра стоит справа, то значение прибавляется.
Впервые позиционная система счисления была введена в Вавилоне. Примечательно, что она была шестнадцатеричная. К 19 веку распространение получила двенадцатеричная система.
Прежде чем разбирать, как записывается двоичная система счисления, определимся с терминами. Алфавит любой СС состоит из знаков, обозначающих отдельные цифры. Основанием называют значение, равное количеству знаков для кодирования чисел и представляющее собой целое число от 2 и выше.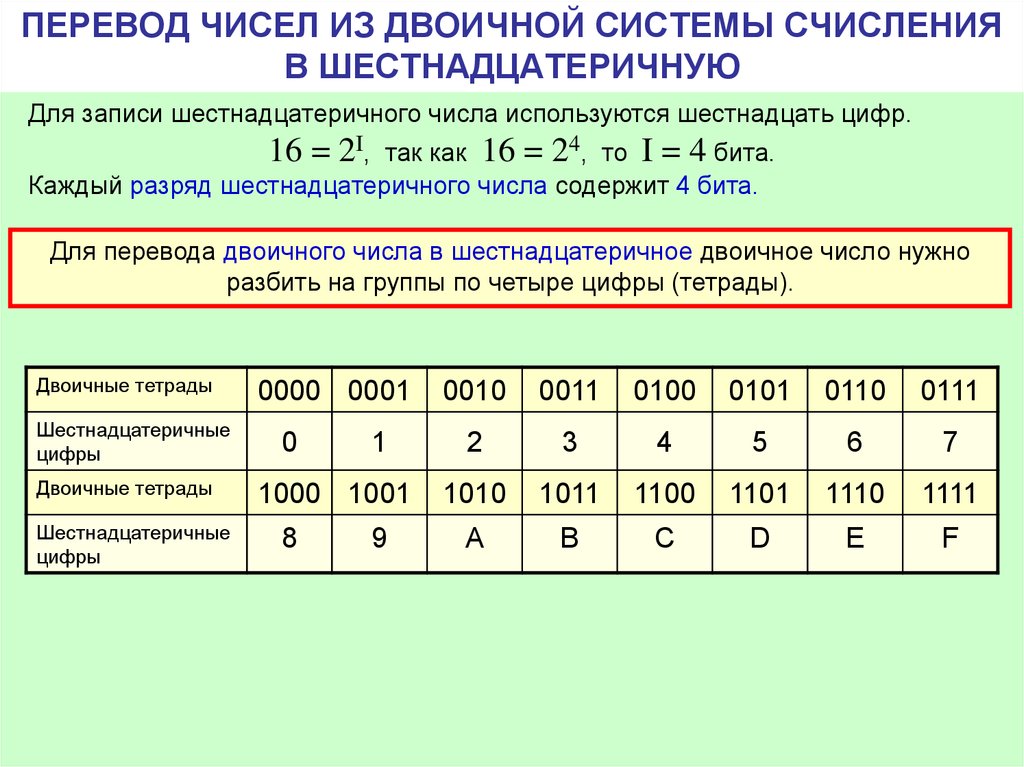
Когда рассматривается несколько разных СС, тип каждой из них обычно обозначается подстрочным знаком. По умолчанию, если не указано основание, число является десятичным. Позиция цифры в числе называется разрядом.
Числа, используемые в двоичной системе счисления
Состав двоичной системы счисления — цифры 0 и 1. Основание равно 2. В крайней правой позиции числа указывается количество единиц, левее — количество двоек, затем количество четверок и т. д.
Таким образом, любое натуральное число кодируется в последовательный ряд из нулей и единиц — это и будет являться двоичной системой счисления. Решение такой задачи покажем на примере ниже.
10112 = 1*23 + 0*2*2+1*21+1*20 =1*8 + 1*2+1=1110
Как известно, двоичная система счисления используется вычислительной техникой для хранения информации, а также для преобразования данных в графические изображения. В свою очередь обработка двоичного кода требует предварительного размещения каждой цифры внутри особой электронной схемы (триггера).
Отдельное число, состоящее из нескольких цифр, сохраняется группой триггеров — регистром. Оперативная память компьютера фактически является совокупностью таких регистров.
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
pdf 3,7mb
doc 1,7mb
Уже скачали 19763
С точки зрения вычислительной техники любое сохраняемое число представляет собой машинное слово, арифметические и логические операции над которым выполняет арифметико-логическое устройство (АЛУ). Чтобы компьютеру было проще работать с регистрами, они нумеруются (или наделяются адресами).
Так, для сложения двух чисел используются адреса регистров, где они расположены, а не сами эти числа. Данные записываются в восьмеричной и шестнадцатеричной системах для более быстрого и простого перевода чисел в двоичный формат.
Тем не менее, конечный пользователь видит всю числовую информацию в привычном ему десятичном виде. Почему так происходит? Изначально, нажимая на клавишу, пользователь передает компьютеру соответствующую последовательность электрических сигналов (нулей и единиц). Для каждого символа определен конкретный набор этих импульсов.
Специальные программы (драйверы клавиатуры и экрана) преобразуют эти сигналы в читаемый вид путем обращения к кодовой таблице. Например, стандарт Unicode позволяет закодировать таким образом 65536 символов. Именно так используется двоичная система счисления в информатике — нули и единицы преобразуются программным способом в текст и изображения на экране.
Далее приведем очевидные достоинства использования двоичного способа представления информации.
- От технических устройств требуется лишь два устойчивых состояния (например, наличие тока и отсутствие тока и т. д.).
- Вычислительной технике значительно проще выполнять операции с двоичными данными, чем с десятичными.
- Таблицы сложения и умножения в двоичной системе имеют гораздо меньший размер по сравнению с такими же таблицами для десятичной системы.
Недостатки:
- возможное превращение конечных десятичных дробей в бесконечные двоичные;
- большее количество занимаемых разрядов по сравнению с десятичной записью;
- сложность с восприятием записи чисел, поскольку двоичная система счисления — этопредставление только в виде нулей и единиц.
Сложение, вычитание и умножение в двоичной системе счисления
Для того, чтобы складывать числа, пользуются следующей таблицей:
| + | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 10 (переход в старший разряд) |
Таблица вычитания в двоичной системе счисления выглядит так:
| — | 0 | 1 |
| 0 | 0 | 1 |
| 1 | (взятие из старшего разряда) 1 | 0 |
Точный инструмент «Колесо компетенций»
Для детального самоанализа по выбору IT-профессии
Список грубых ошибок в IT, из-за которых сразу увольняют
Об этом мало кто рассказывает, но это должен знать каждый
Мини-тест из 11 вопросов от нашего личного психолога
Вы сразу поймете, что в данный момент тормозит ваш успех
Регистрируйтесь на бесплатный интенсив, чтобы за 3 часа начать разбираться в IT лучше 90% новичков.
Только до 2 марта
Осталось 17 мест
Умножение выполняется по следующей таблице:
| * | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
Как переводить числа в двоичной системе счисления в десятичную
Сперва приведем алфавиты трех используемых систем — двоичной, десятичной и шестнадцатеричной.
| Основание | Наименование системы | Алфавит |
| 2 | Двоичная | 0, 1 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| 16 | Шестнадцатеричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Как уже упоминалось, двоичная система счисления имеет основание 2. Чтобы перевести число в десятичный формат, можно воспользоваться такой таблицей степеней данного основания:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Здесь ряд начинается с единицы, а каждая последующая цифра является результатом умножения предыдущей на двойку.
После 1 ставится так называемая двоичная точка.
В качестве примера переведем число 1011011 двоичной системы счисления в 10-ный формат (число 91):
0*2+1=1>>1*2+0=2>>2*2+1=5>>5*2+1=11>>11*2+0=22>>22*2+1=45>> 45*2+1=91.
А конвертация 101111 в десятичную систему даст число 47:
0*2+1=1>>1*2+0=2>>2*2+1=5>>5*2+1=11>> 11*2+1=23 >> 23*2+1=47
НУЖНА КАРТИНКА
Таким же образом можно переводить и дробные числа. Для примера возьмем 1011010, 101 в двоичной системе счисления. Перевод чисел в десятичную можно осуществлять в таком виде:
1*26 + 0*25 + 1*24 + 1*2 + 0 *22 + 1 * 21 + 0 * 20 + 1 * 2-1 + 0 * 2-2 + 1 * 2-3 = 90,625
Иначе говоря, расчет будет следующим:
1*64+0*32+1*16+1*8+0*4+1*2+0*1+1*0,5+0*0,25+1*0,125 = 90,625
Полученное значение в десятичной системе также высчитывается по таблице:
| 64 | 32 | 16 | 8 | 4 | 2 | 1 | 0,5 | 0,25 | 0,125 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0. | .1 | 0 | 1 |
| +64 | +0 | +16 | +8 | +0 | +2 | +0 | +0.5 | +0 | +1.125 |
Алгоритм перевода из двоичной системы счисления в шестнадцатеричную
Здесь необходимо выполнить 2 шага:
- Перевод числа из двоичной системы в десятичную
- Преобразование полученного значения в шестнадцатеричный формат
К примеру, имеется число 1011101 в двоичной системе счисления. Запись чисел для выполнения первого шага осуществляется по формуле:
A2 = an-1 ∙ 2n-1 + an-2 ∙ 2n-2 + ∙∙∙ + a0 ∙ 20
Подставляем значения:
10111012=1 ∙ 26 + 0 ∙ 25 + 1 ∙ 24 + 1 ∙ 23 + 1 ∙ 22 + 0 ∙ 21 + 1 ∙ 20 = 1 ∙ 64 + 0 ∙ 32 + 1 ∙ 16 + 1 ∙ 8 + 1 ∙ 4 + 0 ∙ 2 + 1 ∙ 1 = 64 + 0 + 16 + 8 + 4 + 0 + 1 = 9310
Теперь полученное десятичное число необходимо преобразовать в шестнадцатеричное. Для этого 93 многократно последовательно делим на 16 до тех пор, пока остаток не станет меньше 16.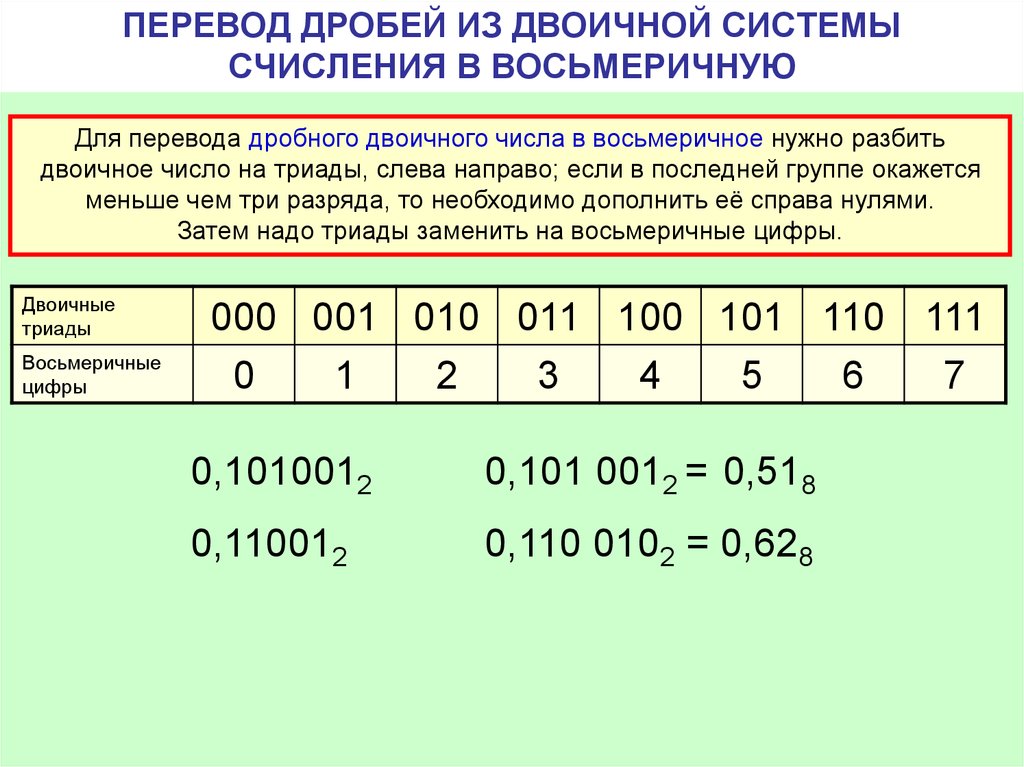
В процессе деления остатки нужно записывать в обратном порядке. Результатом всех операций будет число 9310=5D16.
НУЖНА КАРТИНКА
Перевод дробных чисел в шестнадцатеричный формат выполняется аналогичным образом — через промежуточный этап перевода в десятичную систему.
Вновь покажем это на примере. Преобразуем двоичное число 10001100.110 сначала в десятичную систему по формуле:
An = an-1 ∙ qn-1 + an-2 ∙ qn-2 + ∙∙∙ + a0 ∙ q0 + a-1 ∙ q-1 + ∙∙∙ + a-m ∙ q-m
Подставляем наши значения:
10001100.1102=1 ∙ 27 + 0 ∙ 26 + 0 ∙ 25 + 0 ∙ 24 + 1 ∙ 23 + 1 ∙ 22 + 0 ∙ 21 + 0 ∙ 20 + 1 ∙ 2-1 + 1 ∙ 2-2 + 0 ∙ 2-3 = 1 ∙ 128 + 0 ∙ 64 + 0 ∙ 32 + 0 ∙ 16 + 1 ∙ 8 + 1 ∙ 4 + 0 ∙ 2 + 0 ∙ 1 + 1 ∙ 0.5 + 1 ∙ 0.25 + 0 ∙ 0.125 = 128 + 0 + 0 + 0 + 8 + 4 + 0 + 0 + 0.5 + 0.25 + 0 = 140.7510
Следует отметить сильное сходство формул расчетов дробного и целого десятичных чисел. Тем не менее, отличия также имеются.
Вторым этапом переводим число 140,75 в шестнадцатеричный формат.
Это делается в два подэтапа:
- Перевод отдельно целой части числа.
- Перевод отдельно дробной части числа.
Итак, нам необходимо сначала преобразовать 140 в шестнадцатеричную систему счисления, последовательно деля это число на 16, пока остаток не станет меньше делителя.
После записи остатков в обратном порядке получаем результат: 14010=8C16
Операции с дробной частью отличаются тем, что мы многократно и последовательно умножаем ее, пока она не станет равной нулю (или значению в соответствии с заданной точностью).
В нашем случае это будет выглядеть так: 0.75 * 16 = 12.0 (C).
Поскольку после первого же умножения дробная часть обнулилась, дальнейшие итерации прекращаем. Итоговый результат: 0.12 (0.С) или, иначе, 0.75 ∙ 16 = 12.0 (C)
Остался последний этап — соединение преобразованных целой и дробной частей: 140.7510=8C.C16. Это и будет общим решением всей задачи.
Сперва может показаться, что изложенный здесь материал слишком сложен и запутан для простого обывателя.
На самом деле двоичная арифметика предельно логична и понятна. Пользование таблицами сложения и умножения не представляет сложности, если в них разобраться.
Рейтинг: 5
( голосов 1 )
Поделиться статьей
Системы исчисления [АйТи бубен]
Системы исчисления: двоичная, восьмеричная, десятичная, шестнадцатеричная.
Двоичная система счисления Материал из Википедии
Представление числовых данных в памяти ЭВМ
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов (1 и 0). Компьютер может различить только нулевое и единичное состояние бита, и работает компьютер в системе исчисления с основанием 2 или в двоичной системе.
Бит получил свое название от английского Binary digit (двоичная цифра).
Сочетанием двоичных цифр (битов) можно представить любое значение.
Значение двоичного числа определяется относительной позицией каждого бита и наличием единичных битов. Ниже показано восьмибитовое число, содержащее все единичные биты:
значения: 128 64 32 16 8 4 2 1 биты: 1 1 1 1 1 1 1 1
Самая правая цифра имеет весовое значение 1, следующая цифра влево — 2, следующая — 4 и т.д. Общая сумма для восьми единичных битов в данном случае составит 255:
(1+2+4+8+16+32+64+128=255)
Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
512 256 128 64 32 16 8 4 2 1
Начиная с цифры 1 все цифры умножаются на два.
Допустим, нам нужно перевести число 17 в двоичное. Согласно таблице степеней оснований (см. выше) 17=16+1. Значит на место значимых цифр 16 и 1 ставим 1 — остальные нули. Получаем 17=10001
512 256 128 64 32 16 8 4 2 1 0 0 0 0 0 1 0 0 0 1
Допустим, нам нужно перевести число 19 в двоичное.
Вы можете воспользоваться следующей процедурой :
19 /2 = 9 с остатком 1 9 /2 = 4 c остатком 1 4 /2 = 2 с остатком 0 2 /2 = 1 с остатком 0 1 /2 = 0 с остатком 1
Итак, мы делим каждое частное на 2 и записываем остаток в начало двоичной записи. Продолжаем делить на 2 частные от деления до тех пор, пока частное не станет равным 0. В результате получаем число 19 в двоичной записи: 10011.
В обратную сторону нужно десятичные сложить, основываясь на таблице степеней основания 2.
Арифметические действия в двоичном формате
Компьютер выполняет арифметические действия только в двоичном формате. Поэтому, необходимо знать правила сложения в двоичной системе исчисления. Напомним их:
0 + 0 = 0 1 + 0 = 1 1 + 1 = 10
Давайте рассмотрим использование этих правил на конкретном примере.
Пример: сложить числа 65 и 42, представленные в двоичной системе исчисления.
В десятичной системе исчисления все осуществляется достаточно просто: 65+42=107.
Для сложения этих чисел в двоичной системе исчисления нужно сначала перевести их в эту систему, например, как показано на рисунке:
Таким образом, получаем: 65 в 10-ой системе = 01000001 в 2-ой системе. Обратите внимание на то, что ведущий ноль в двоичном представлении числа добавлен для дополнения двоичного представления до восьми бит. Аналогично: 42 в 10 = 00101010 в 2. Выполним сложение этих чисел:
01000001 + 00101010 -------- 01101011
Можете перепроверить и убедиться, что 01101011 в 2=107 в 10:
0*27+1*26+1*25+0*24+1*23+0*22+1*21+1*20 = 64+32+8+2+1 = 107
Вычитание
Для выполнения операции вычитания последнее заменяется сложением, а в качестве второго слагаемого берется противоположное число. Например, пусть надо выполнить вычитание: 65 — 42. Заменим его сложением: 65 + (-42).
Двоичные числа имеют положительные значения, что обозначается нулевым значением самого левого, старшего разряда.
Отрицательные двоичные числа содержат единичный бит в старшем разряде.
27 /16 = 1 с остатком 11 11 /16 = 0 c остатком 1
И того получим 1B.
Остаток от деления на 16 всегда меньше 16. Это относится ко всем системам счисления.
Рассмотрим несколько простых примеров шестнадцатеричной арифметики. Следует помнить, что после шестнадцатеричного числа F следует шестнадцатеричное 10, что равно десятичному числу 16:
6+4=A 5+8=D F+1=10 F+F=1E 10+10=20 FF+1=100
Для чего использовалась двоичная система?
Двоичная система счисления лежит в основе всех вычислительных систем и операций. Он позволяет устройствам хранить, получать доступ и манипулировать всеми типами информации, направляемой в ЦП или память и из них .
Запрос на удаление |
Посмотреть полный ответ на techtarget.com
Для чего изначально использовался двоичный код?
Эти ранние компьютеры нуждались в ограниченном языке для управления их функциями, поэтому первые ученые-компьютерщики использовали двоичный код для представления включения и выключения или единиц и нулей.
По мере того, как компьютеры становились все более сложными, двоичный код стал наиболее используемым языком.
|
Посмотреть полный ответ на inverse.com
Почему была создана двоичная система?
Двоичные числа занимали центральное место в богословии Лейбница. Он считал, что двоичные числа символизируют христианскую идею creatio ex nihilo или создания из ничего. Лейбниц пытался найти систему, которая превращает логические вербальные утверждения в чисто математические.
Запрос на удаление |
Посмотреть полный ответ на en.wikipedia.org
Где используется двоичная система счисления?
Двоичная система счисления очень полезна в компьютерных технологиях, а языки компьютерного программирования также используют двоичную систему счисления, которая полезна при цифровом кодировании. Двоичная система счисления также может использоваться в булевой алгебре.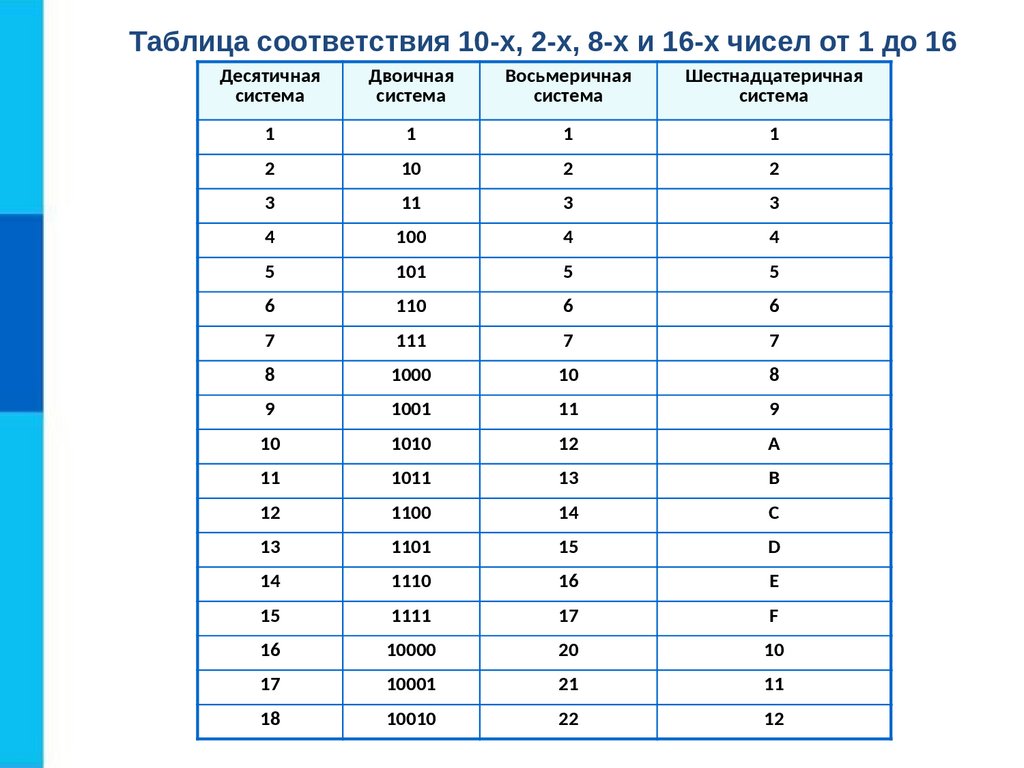
|
Посмотреть полный ответ на tutorialspoint.com
Когда использовался двоичный код?
Современная двоичная система счисления восходит к Готфриду Лейбницу, который в 17 веке предложил и развил ее в своей статье Explication de l’Arithmétique Binaire [1] . Лейбниц изобрел систему около 1679 г.но он опубликовал его в 1703 году.
Запрос на удаление |
Полный ответ см. на cs.cas.cz
Основы информатики: двоичный код
Как объяснить ребенку двоичный код?
Двоичный код — это то, как компьютеры говорят и представляют информацию.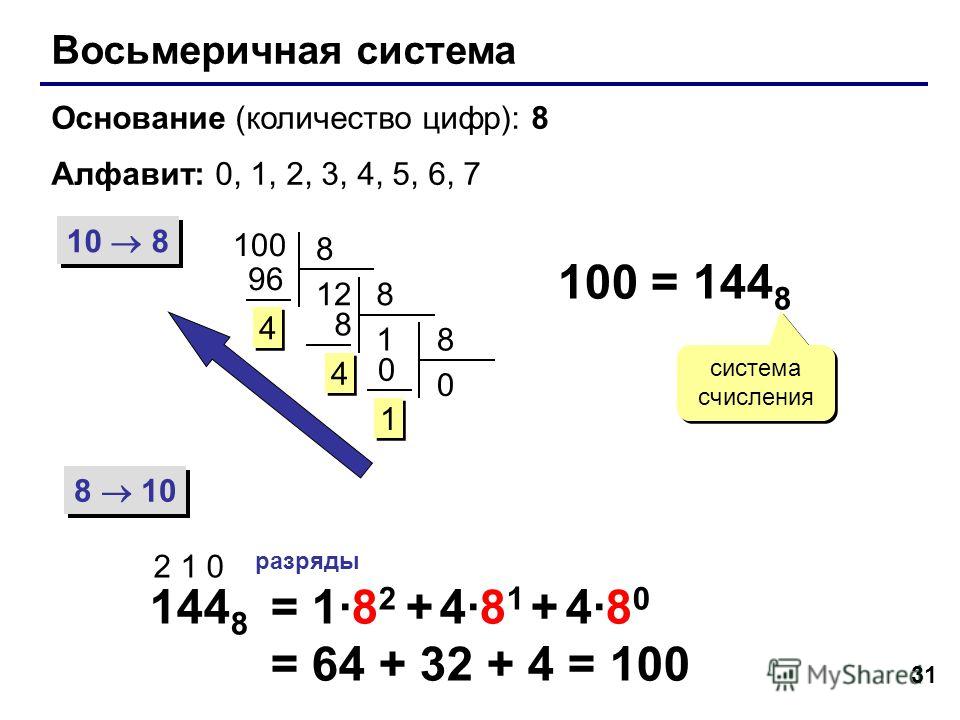
Буквы, цифры и картинки… в основном все, что вы видите на компьютере (включая этот пост), состоит из различных комбинаций 0 и 1.
|
Посмотреть полный ответ на Innovationkidslab.com
Кто создал двоичную систему?
Готфрид Вильгельм Лейбниц (1646-1716) является самопровозглашенным изобретателем двоичной системы и считается таковым большинством историков математики и/или математиков.
Запрос на удаление |
Посмотреть полный ответ на pubmed.ncbi.nlm.nih.gov
Что такое двоичная система счисления и объяснить?
Двоичная система счисления является одним из четырех типов системы счисления. В компьютерных приложениях, где двоичные числа представлены только двумя символами или цифрами, то есть 0 (ноль) и 1 (один). Двоичные числа здесь выражены в системе счисления с основанием 2. Например, (101) 2 — двоичное число.
|
Посмотреть полный ответ на byjus.com
Как поздороваться в двоичном коде?
01001000 01100101 01101100 01101100 01101111 00100001
Эти единицы и нули могут показаться вам ничем, но в двоичном коде числа на самом деле говорят «Привет!»
Запрос на удаление |
Посмотреть полный ответ на sciencefriday.com
Почему он называется бинарным?
Двоичная система счисления с основанием 2, изобретенная Готфридом Лейбницем, состоит только из двух чисел или цифр: 0 (ноль) и 1 (единица). Эта система нумерации является основой для всего двоичного кода, который используется для записи цифровых данных, таких как инструкции компьютерного процессора, используемые каждый день.
Запрос на удаление |
Посмотреть полный ответ на computerhope.com
Существовали ли бинарные файлы до появления компьютеров?
Новое исследование предполагает, что аборигены отдаленного полинезийского острова изобрели двоичную систему счисления, подобную той, которую используют компьютеры для расчетов, за столетия до того, как это сделали западные математики.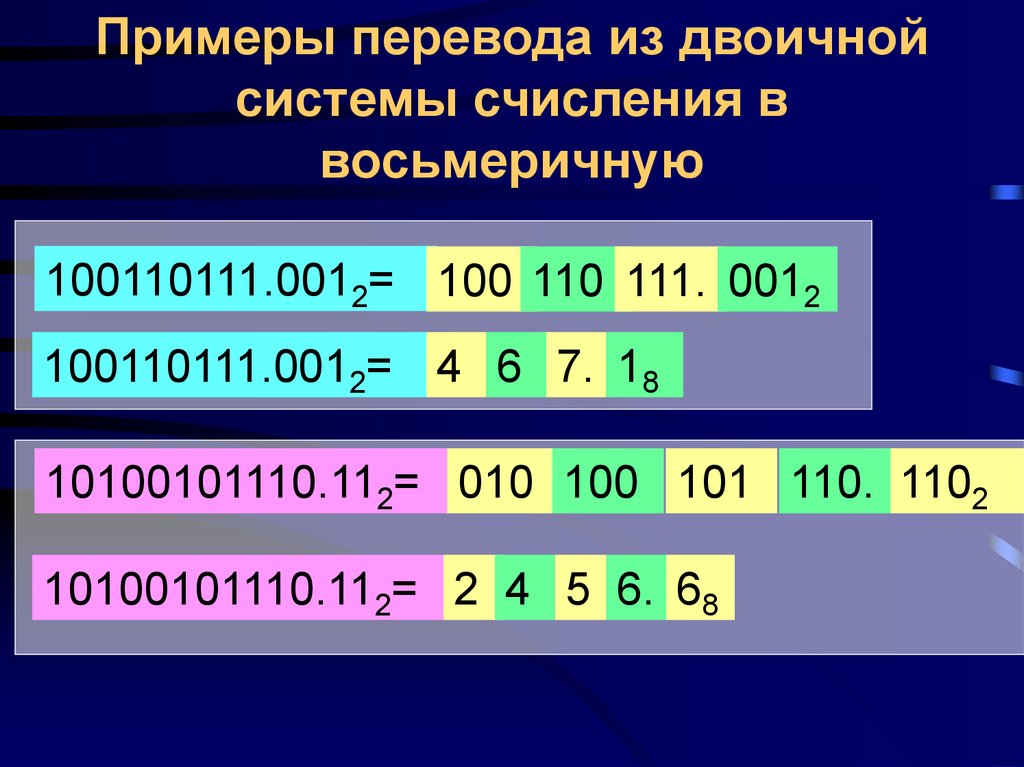
|
Посмотреть полный ответ на livecience.com
Люди когда-нибудь кодировали в двоичном коде?
Двоичный язык часто преподается как часть основ информатики, но это скорее введение в то, как работают компьютеры. Люди почти никогда не пишут двоичные файлы. Вместо этого они пишут на высокоуровневом или низкоуровневом языке программирования, структура которого ближе к естественным языкам и легче для понимания.
Запрос на удаление |
Посмотреть полный ответ на сайтеcarekarma.com
Почему люди мыслят бинарно?
Бинарное мышление помогает нам чувствовать уверенность. Неопределенность сложности может пугать и вызывать беспокойство, поэтому неудивительно, что люди впадают в бинарное мышление, особенно в такие неопределенные времена, как то, что мы переживаем сейчас.
Запрос на удаление |
Посмотреть полный ответ на lifehack.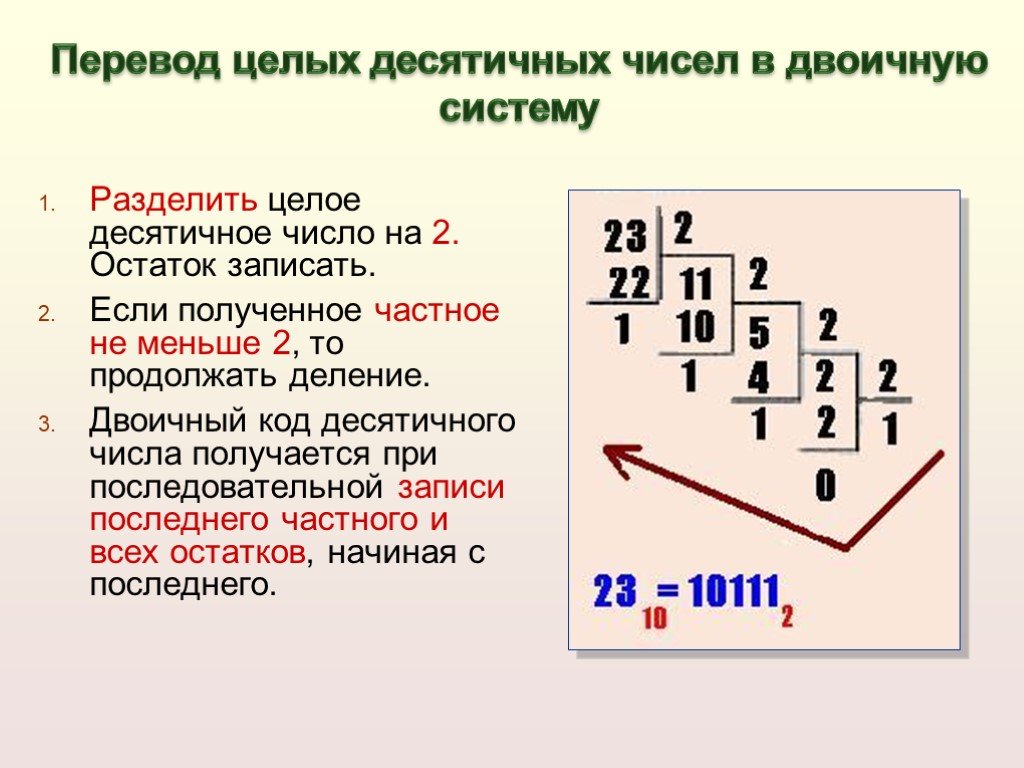
org
Кто изобрел небинарный пол?
Концепция неотождествления себя с назначенным полом не была официально задокументирована до 1910 года, когда немецкий сексолог доктор Магнус Хиршфельд ввел термин «трансвестит» в своей книге «Die Transvestitenin», создав один из первых современных терминов для описания трансгендеров.
Запрос на удаление |
Посмотреть полный ответ на pointfoundation.org
Что означает 11111111 в двоичном коде?
Следовательно, 255 в двоичном формате равно 11111111.
Запрос на удаление |
Посмотреть полный ответ на сайте Study.com
Что означает 0100100001101001 в двоичном формате?
Начальный кадр части 3 говорит: «0100100001101001», что в двоичном формате означает «привет» в ascii.
Запрос на удаление |
Посмотреть полный ответ на m.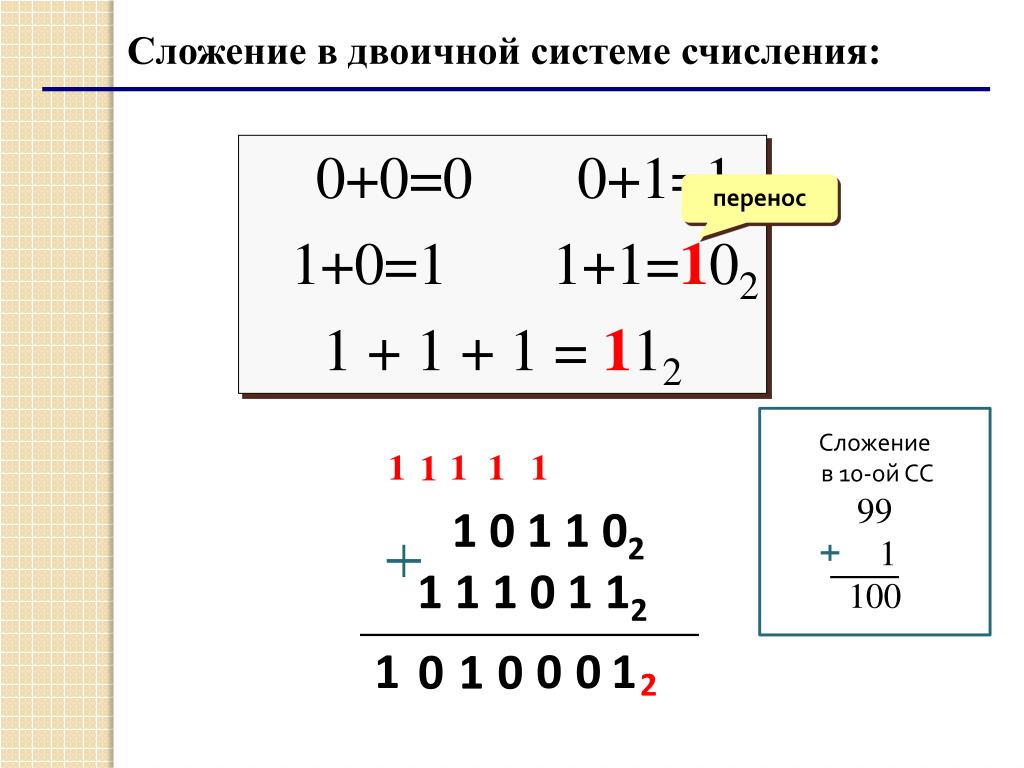
imdb.com
Что означает 1010101010 в двоичном коде?
Каждая шестнадцатеричная цифра представляет собой 4 двоичных разряда, называемых полубайтами, что упрощает представление больших двоичных чисел. Например, двоичное значение 1010101010 может быть представлено как 2AA в шестнадцатеричном формате.
Запрос на удаление |
Полный ответ см. на сайте calculate.net
. В чем важность двоичной системы счисления?
Использование двоичных чисел увеличило выразительную силу двоичных схем. Это можно использовать для снижения стоимости компьютера или для создания более мощного компьютера по той же цене. Это наш второй факт: использование двоичных чисел максимально увеличивает выразительную силу двоичных схем.
Запрос на удаление |
Посмотреть полный ответ на ccse.kennesaw.edu
Что является примером двоичного значения из повседневной жизни?
Что является примером двоичного значения из повседневной жизни? Двоичная цифра (или бит) имеет два возможных значения: 0 или 1.
Состояние включения и выключения простого переключателя является примером двух состояний, представленных битом.
|
Посмотреть полный ответ на quizlet.com
Что такое краткий ответ в двоичном коде?
двоичный код, код, используемый в цифровых компьютерах, основанный на двоичной системе счисления, в которой есть только два возможных состояния, выключено и включено, обычно обозначаемое 0 и 1.
Запрос на удаление |
Посмотреть полный ответ на britannica.com
Кто изобрел 1 и 0?
Около 773 г. н.э. математик Мохаммед ибн-Муса аль-Ховаризми первым начал работать над уравнениями, равными нулю (теперь известными как алгебра), хотя он называл это «сифр». К девятому веку ноль был частью арабской системы счисления и имел форму, аналогичную современному овалу, который мы используем сейчас.
Запрос на удаление |
Посмотреть полный ответ на blutick.
com
Как появился двоичный код?
Когда был изобретен двоичный код? Двоичный код, используемый в настоящее время в компьютерах и устройствах по всему миру, был изобретен, когда немецкий эрудит Готфрид Вильгельм Лейбниц (1646–1716) ввел систему использования только двоичных цифр 0 и 1 для выполнения арифметических операций.
Запрос на удаление |
Полный ответ см. на сайте study.com
Что делать, если мой ребенок небинарный?
Советы по поддержке небинарного ребенка
- Демонстрируйте принятие и любовь. Как только ваш ребенок откроется вам, убедитесь, что он знает, что вы принимаете и любите его. …
- Не называйте это фазой. …
- Используйте предпочтительные местоимения и/или имена. …
- Знайте, когда им нужна дополнительная поддержка. …
- 5 вещей, которые следует учитывать при планировании костюма на Хэллоуин.
|
Полный ответ см.
на geisinger.org
Как написать свой день рождения в двоичном формате?
Например, если ваш день рождения 11 июня 2013 года, это будет записано как 11.06.13. 2. Преобразуйте дату дня рождения в двоичный формат. Используя тот же пример, что и выше, число 11.06.13, переведенное в двоичный код, будет таким: 110/1011/1101.
Запрос на удаление |
Посмотреть полный ответ на raisingsmartgirls.com
← Предыдущий вопрос
Можно ли купить 2 отдельные дорожки Lightning?
Следующий вопрос →
Из какой части Африки живут ямайцы?
Система с основанием 2 и 8-битный байт
Причина, по которой компьютеры используют систему счисления по основанию 2, заключается в том, что это значительно упрощает их реализацию с помощью современных электронных технологий. Вы могли бы подключить и построить компьютеры, работающие с основанием 10, но сейчас они были бы чертовски дорогими.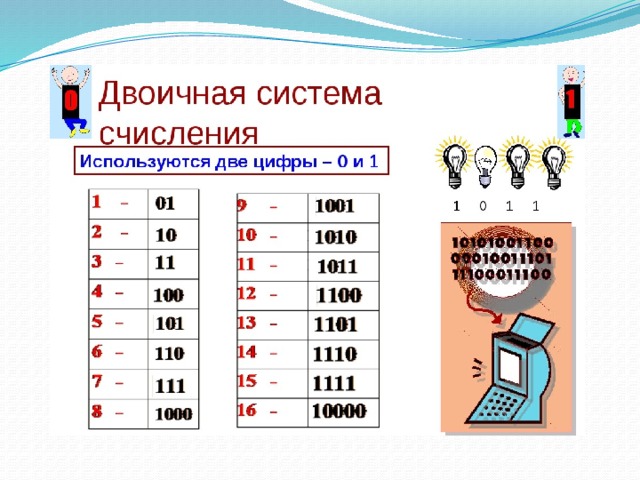
С другой стороны, компьютеры с основанием 2 относительно дешевы.
Таким образом, компьютеры используют двоичные числа и поэтому используют двоичных цифр вместо десятичных цифр. Слово 90) = 8 + 0 + 2 + 1 = 11
Как видите, в двоичных числах каждый бит содержит значение возрастающей степени двойки. Это делает двоичный счет довольно простым. Начиная с нуля и заканчивая 20, счет в десятичной и двоичной системе выглядит следующим образом:
0 = 0 1 = 1 2 = 10 3 = 11 4 = 100 5 = 101 6 = 110 7 = 111 8 = 1000 9 = 1001 10 = 1010 11 = 1011 12 = 1100 13 = 1101 14 = 1110 15 = 1111 16 = 10000 17 = 10001 18 = 10010 19 = 10011 20 = 10100
Если вы посмотрите на эту последовательность, 0 и 1 одинаковы для десятичной и двоичной систем счисления. Под номером 2 вы видите, что сначала перенос происходит в двоичной системе. Если бит равен 1, и вы добавляете к нему 1, бит становится 0, а следующий бит становится 1. При переходе от 15 к 16 этот эффект переходит через 4 бита, превращая 1111 в 10000.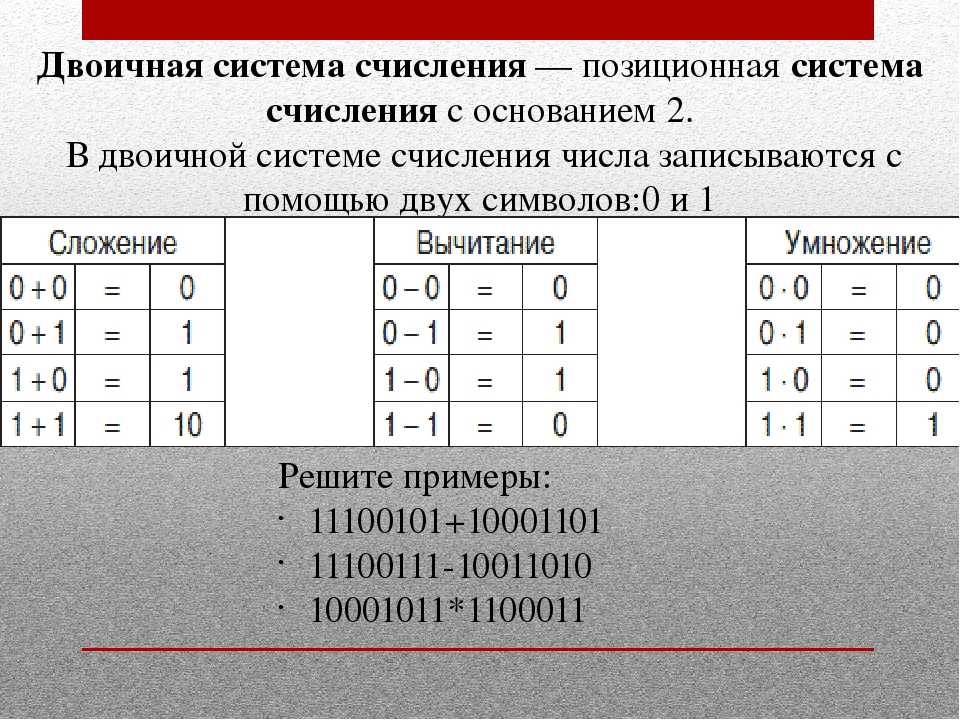
Биты встречаются редко один в компьютерах. Они почти всегда объединяются в 8-битные наборы, и эти наборы называются 9.0003 байта . Почему в байте 8 бит? Аналогичный вопрос: «Почему в дюжине 12 яиц?» 8-битный байт — это то, к чему люди пришли методом проб и ошибок за последние 50 лет.
С 8 битами в байте вы можете представить 256 значений в диапазоне от 0 до 255, как показано здесь:
0 = 00000000 1 = 00000001 2 = 00000010 ... 254 = 11111110 255 = 11111111
В статье Как работают компакт-диски вы узнаете, что компакт-диск использует 2 байта или 16 бит на семпл. Это дает каждой выборке диапазон от 0 до 65 535, например:
0 = 00000000000000000
1 = 0000000000000001
2 = 00000000000000010
...
65534 = 1111111111111110
65535 = 1111111111111111 Далее мы рассмотрим один из способов использования байтов.
Процитируйте это!
Пожалуйста, скопируйте/вставьте следующий текст, чтобы правильно цитировать эту статью HowStuffWorks.
