Site Loader
Posted on 16.01.2023

Двоичная система счисления

Содержание:
Что такое двоичная система счисления
Как перевести целое десятичное число в двоичную систему счисления
Как перевести десятичную дробь в двоичную систему счисления
Как перевести число из двоичной системы счисления в десятичную
Как перевести дробное двоичное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в двоичной системе счисления

Двоичная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа. Для записи числа в двоичной системе счисления используется две цифры 0 и 1. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления. Например, 10012 или 10001012

Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь калькулятором систем счисления с подробным решением онлайн.

Как перевести целое десятичное число в двоичную систему счисления

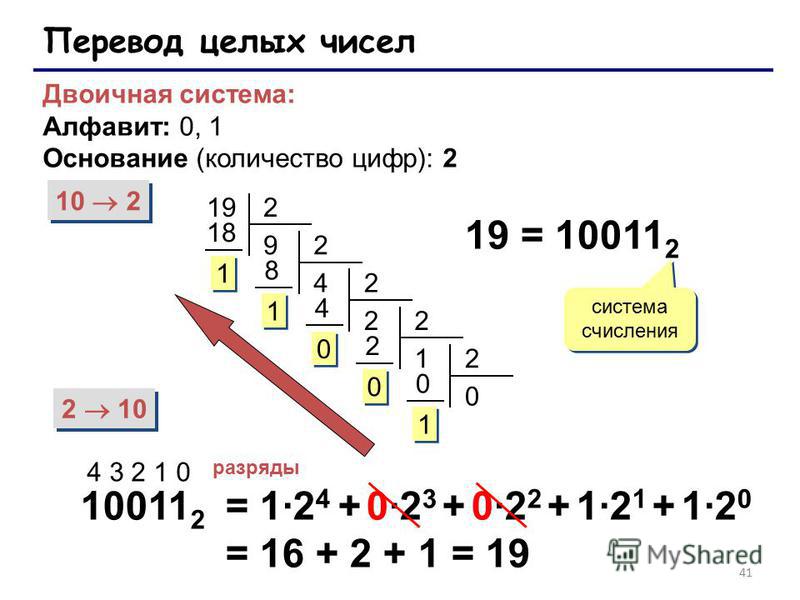
Для того, чтобы перевести целое десятичное число в двоичную систему счисления нужно десятичное число делить на 2 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.

Например, переведем число 17310 в двоичную систему счисления:

173 : 2 = 86 остаток: 1
86 : 2 = 43 остаток: 0
43 : 2 = 21 остаток: 1
21 : 2 = 10 остаток: 1

10 : 2 = 5 остаток: 0
5 : 2 = 2 остаток: 1
2 : 2 = 1 остаток: 0
1 : 2 = 0 остаток: 1

17310 = 101011012

Как перевести десятичную дробь в двоичную систему счисления

Для того чтобы перевести десятичную дробь в двоичную систему счисления необходимо сначала перевести целую часть десятичной дроби в двоичную систему счисления, а затем дробную часть, последовательно умножать на 2, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число) или не будет достигнуто необходимое количество знаков после запятой.

Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.

Например, переведем десятичное число 5.7410 в двоичную систему счисления:

Переведем целую часть

5 : 2 = 2 остаток: 1
2 : 2 = 1 остаток: 0
1 : 2 = 0 остаток: 1
510 = 1012

Переведем дробную часть

0.74 · 2 = 1.48
0.48 · 2 = 0.96
0.96 · 2 = 1.92
0.92 · 2 = 1.84
0.84 · 2 = 1.68

0.68 · 2 = 1.36
0.36 · 2 = 0.72
0.72 · 2 = 1.44
0.44 · 2 = 0.88
0.88 · 2 = 1.76

0.7410 = 0.10111101012
5.7410 = 101.10111101012

Двоичные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной двоичной. В данном примере получается бесконечная периодическая двоичная дробь, поэтому умножение на 2 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю. В данном случае десятичная дробь 5.74 не может быть точно представлена в двоичной системе счисления. К примеру, дробь 2.5

10 может быть представлена в двоичной системе счисления в виде конечной 2.510 = 10.12.

Как перевести число из двоичной системы счисления в десятичную

Для того, чтобы перевести число из двоичной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля. Каждая позиция цифры будет степенью числа 2, так как система счисления 2-ичная. Необходимо последовательно умножить каждое число на 2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.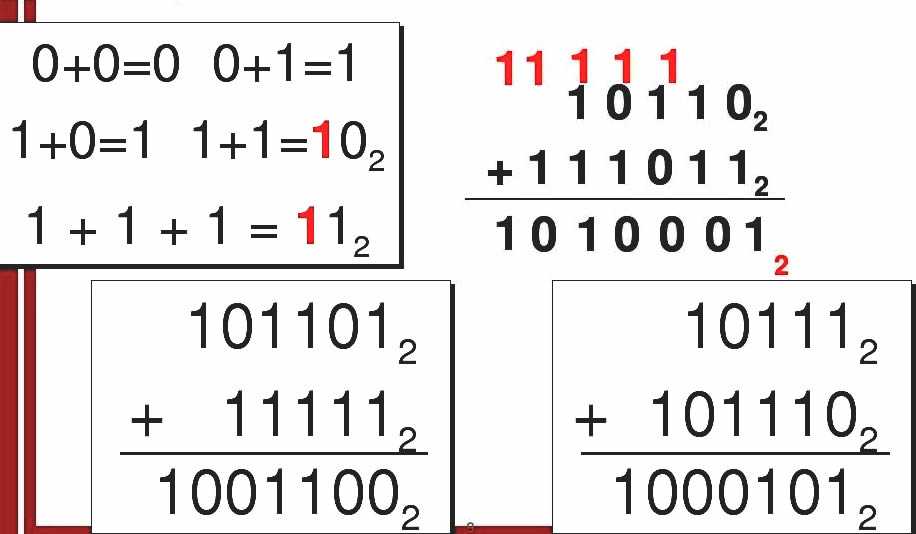

Например, переведем теперь обратно число 101011012 в десятичную систему счисления:

Позиция в числе76543210
Число10101101

101011012 = 1 ⋅ 27 + 0 ⋅ 26 + 1 ⋅ 25 + 0 ⋅ 24 + 1 ⋅ 23 + 1 ⋅ 22 + 0 ⋅ 21 + 1 ⋅ 2

0 = 17310

Как перевести дробное двоичное число в десятичное

Для того, чтобы перевести дробное двоичное число в десятичное, необходимо записать дробное двоичное число, убрав точку и затем сверху расставить индексы. Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию. Каждая позиция цифры (индекс) будет степенью числа 2, так как система счисления 2-ичная. Необходимо последовательно умножить каждое число на 2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.

Например, переведем дробное двоичное число 110.101 в десятичное:

Позиция в числе210-1-2-3
Число110101

110.1012 = 1 ⋅ 22 + 1 ⋅ 21 + 0 ⋅ 20 + 1 ⋅ 2-1 + 0 ⋅ 2-2 + 1 ⋅ 2-3 = 6.62510

Таблица значений десятичных чисел от 0 до 100 в двоичной системе счисления

Значение числа в десятичной системе счисленияЗначение числа в двоичной системе счисления
01002
11012
210102
310112
410
1002
5101012
6101102
7101112
81010002
91010012
101010102
111010112
121011002
131011012
141011102
151011112
1610		100002
1710100012
1810100102
1910100112
2010101002
2110
101012
2210101102
2310101112
2410110002
2510110012
2610110102
2710110112
2810111002
2910111012
3010111102
3110111112
32101000002
33101000012
34101000102
35101000112
36101001002
37101001012
38101001102
39101001112
40101010002
41101010012
42101010102
43101010112
44101011002
45101011012
46101011102
47101011112
48101100002
49101100012
50101100102

Значение числа в десятичной системе счисленияЗначение числа в двоичной системе счисления
51101100112
52101101002
53101101012
54101101102
55101101112
56101110002
57101110012
58101110102
59101110112
60101111002
61101111012
62101111102
63101111112
641010000002
651010000012
661010000102
671010000112
681010001002
691010001012
701010001102
711010001112
721010010002
731010010012
741010010102
751010010112
761010011002
771010011012
781010011102
791010011112
801010100002
811010100012
821010100102
831010100112
841010101002
851010101012
861010101102
871010101112
881010110002
891010110012
901010110102
911010110112
921010111002
931010111012
941010111102
951010111112
961011000002
971011000012
981011000102
991011000112
1001011001002

Электронный справочник по ИНФОРМАТИКЕ (Автор Панов В.

А.)


Двоичная система счисления

 

Введение

Перевод чисел

Дробные числа

Отрицательные числа

Двоичная арифметика

 

 

 

 

 

 

 

 

 

 

Двоичная система счисления является основной системой представления информации в памяти компьютера.

В этой системе счисления используются две цифры: 0 и 1.

Двоичную цифру называют битом.

Первое опубликованное обсуждение двоичной системы счисления принадлежит испанскому священнику Хуану Карамюэлю Лобковицу ( 1670 г .). Всеобщее внимание к этой системе привлекла статья немецкого математика Готфрида Вильгельма Лейбница, опубликованная в 1703 г . В ней пояснялись двоичные операции сложения, вычитания, умножения и деления. Лейбниц не рекомендовал использовать эту систему для практических вычислений, но подчёркивал её важность для теоретических исследований. Со временем двоичная система счисления становится хорошо известной и получает развитие. Большинство современных электронно-вычислительных машин используют в своей работе именно эту систему чисел.

 

Ей было тысяча сто лет.
Она в сто первый класс ходила,
В портфеле по сто книг носила —
Всё это правда, а не бред.
Когда пыля десятком ног,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий.
Она ловила каждый звук
Своими десятью ушами,
И десять загорелых рук
Портфель и поводок держали.
И десять тёмно-синих глаз
Рассматривали мир привычно…

Но станет всё совсем обычным,
Когда поймёте наш рассказ.

———————

С помощью двоичной системы кодирования можно зафиксировать любые данные и знания. Это легко понять, если вспомнить принцип кодирования и передачи информации с помощью азбуки Морзе.

Телеграфист, используя только два символа этой азбуки — точки и тире, может передать практически любой текст.

Объём памяти компьютера измеряется в байтах. Каждый байт может выражать букву, число, пробел, знак препинания или какой-либо другой символ. Количество символов, которые компьютер может хранить в оперативной памяти, меняется в широких пределах от вида компьютера и его модели.

Объём памяти, хотя он и измеряется в байтах, обычно выражается в килобайтах. Слово «килобайт», вообще говоря, означает «1000 байт». (Напомним, что приставка «кило» означает «тысяча».)

Фактически же килобайт равен 1024 байтам: 1 Кбайт = 1024 байт.

Компьютер с объёмом памяти в 64 К может хранить 64 х 1024 = 65536 символов.

Объём памяти первых микрокомпьютеров составлял всего лишь 2 Кб. Нынешние компьютеры имеют объём памяти 128, 256, 512, 1024 Мб и более

Объём памяти новейших компьютеров так велик, что она выражается в гигабайтах, т. е. в миллиардах байтов.

1 Мбайт = 1024 Кбайт = 1 048 576 байт.

Итак, каждый символ алфавитно-цифровой информации представляется в компьютере кодом из восьми двоичных цифр. Следовательно, каждый символ в компьютере имеет код объёмом 1 байт.

имеет в двоичной форме объём 25 байт: 23 буквы и 2 символа «пробел» по 1 байту.

Пример. Измерим в байтах объём текстовой информации в книге из 258 страниц, если на одной странице размещается в среднем 45 строк по 60 символов (включая пробелы). Один символ в двоичной форме содержит 1 байт. Строка будет содержать 61 байт, учитывая и служебный символ окончания строки. Тогда

61 байт * 45 строк = 2745 байт.

Так как в книге 258 страниц текста и на каждой странице в среднем по 2745 байт информации, то объём алфавитно-цифровой информации в книге

2745 байт * 258 страниц = 708210 байт » 692 Кбайт

Таким образом, текст книги имеет объём около 692 Кбайт.

 

Перевод чисел

Для перевода десятичного числа в двоичное надо разделить его на 2 и собрать остатки, начиная с последнего частного.

7310 = 10010012

А вот как происходит перевод двоичного числа в десятичное:

 

 

В любой системе счисления нужно уметь представлять не только целые числа, но и дробные. С математической точки зрения это ординарная задача, которая давно решена. Однако с точки зрения компьютерной техники это далеко не тривиальная проблема, во многом связанная с архитектурой компьютера. Ресурсы компьютеров не бесконечны, и основной трудностью является представление периодических и непериодических дробей. Следовательно, такие дроби следует округлять, задавать класс точности участвующих (и могущих появиться в результате вычислений!) чисел без потери точности вычислений, а также следить за тем, чтобы потеря точности не произошла при переводе чисел из одной системы счисления в другую. Особенно важно аккуратно производить вычисления при операциях с плавающей точкой.

Запишем формулу представления дробного числа в позиционной системе счисления:

 

Ap = an-1·pn-1+an-2·pn-2 + … + a1·p1+a0·p0 +a-1·p-1+a-2·p-2 + . .. + a-m·p-m,       

В случае десятичной системы счисления получим:

24,7310 = (2·101+4·100+7·10-1+3·10-2)10

Перевод дробного числа из двоичной системы счисления в десятичную производится по следующей схеме:

101101,1012 = (1·25+0·24+1·23+1·22+0·21+1·20+1·2-1+0·2-2+1·2-3)10=45,62510

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

·  Вначале переводится целая часть десятичной дроби в двоичную систему счисления;

·  Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;

·  В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;

·  Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений.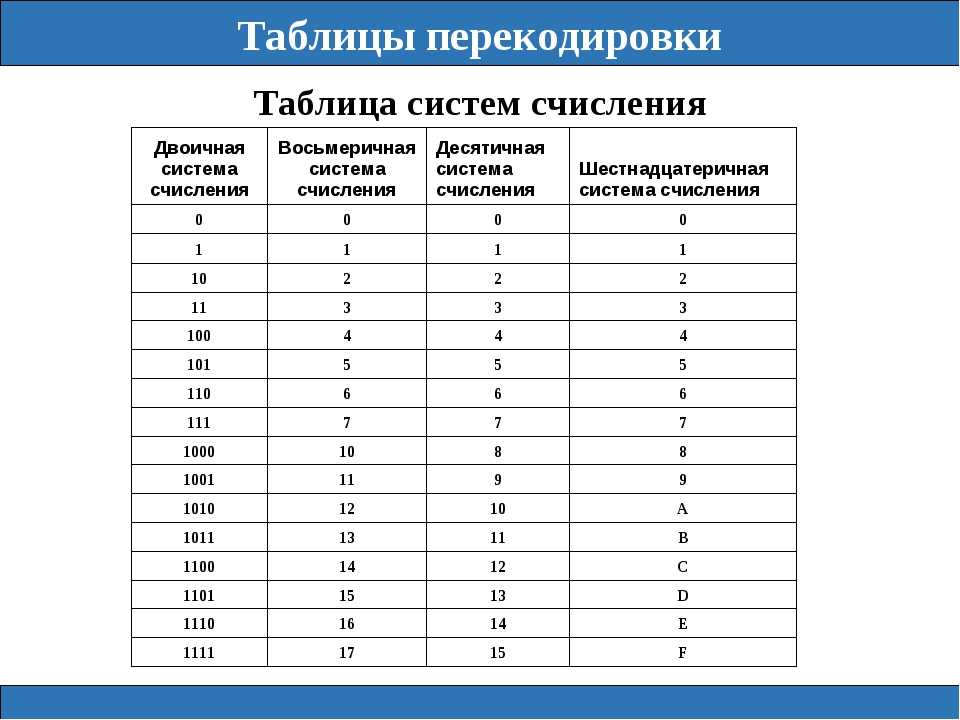 В противном случае вычисления продолжаются с предыдущего шага.

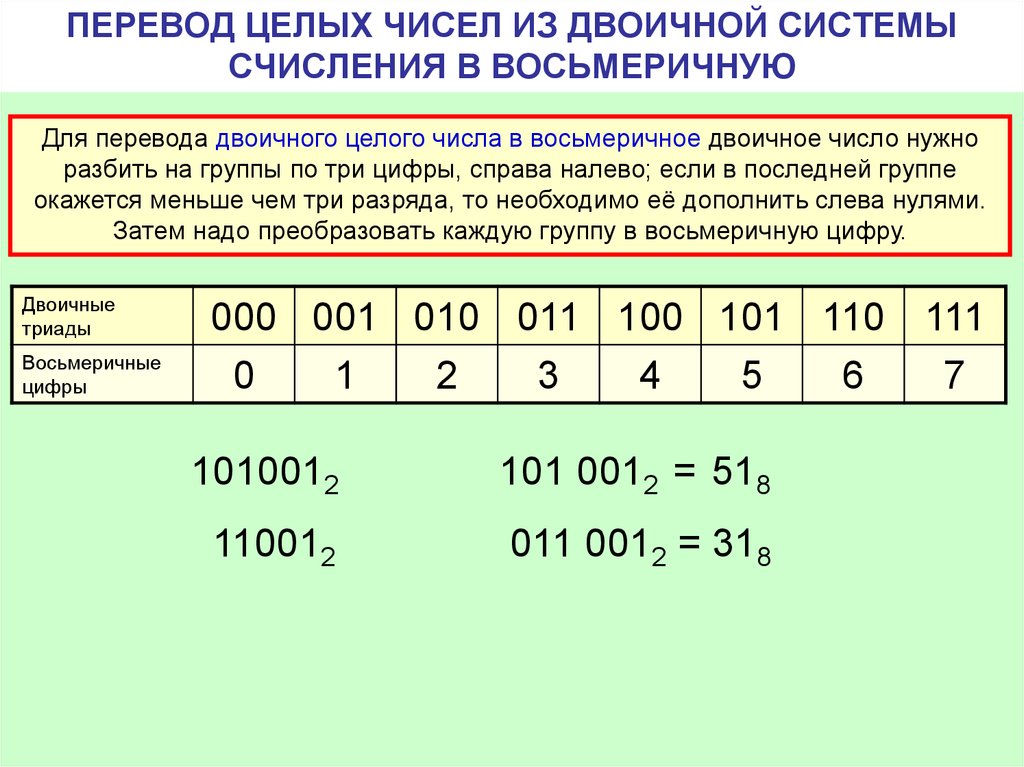
Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 20610=110011102 по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

 

.116 • 2 = 0.232

.232 • 2 = 0.464

.464 • 2 = 0.928

.928 • 2 = 1.856

.856 • 2 = 1.612

. 612 • 2 = 1.224

.224 • 2 = 0.448

.448 • 2 = 0.896

.896 • 2 =1.792

.792 • 2 = 1.584

и т.д.

Получим: 206,11610=11001110,00011100112

Таблицу степеней первых восьми отрицательных степеней двойки

 

Степень основания

2

8

16

0

1

1

1

1

2

8

16

2

4

64

256

3

8

512

4096

4

16

4096

65536

5

32

32768

1048576

6

64

262144

16777216

7

128

2097152

268435456

8

256

16777216

4294967296

9

512

134217728

68719476736

10

1024

1073741824

1099511627776

11

2048

8589934552

17592186044416

12

4096

68719476736

281474976710656

13

8192

549755813888

4503599627370496

14

16384

4398046511104

72057594037927936

15

32768

35184372088832

1152921504606846976

16

65536

281474976710756

18446744073709551616

 

Отрицательные числа

Перейдем теперь к вопросу представления отрицательных чисел. Для определенности рассмотрим тип byte, в котором любое число занимает ровно восемь бит. Из записи в двоичной системе счисления равенства (- 1) + 1 = 0 легко найти, какой вид должно иметь неизвестное нам пока двоичное представление xxxxxxxx числа — 1: 

    xxxxxxxx + 00000001 = 00000000

Ясно, что на месте символов xxxxxxxx должно быть расположено число 11111111. Правильным результатом при этом, конечно, следовало бы считать 100000000, а не 00000000, но ведь мы имеем дело с типом byte и, так как результат обязан разместиться в байте, единица <<исчезает>>.

Итак, число — 1 должно кодироваться как 11111111. Дальнейшее уже совсем просто: для получения — 2 нужно — 1 уменьшить на единицу, что даст 11111110; число — 3 представляется как 11111101 и т. д.

Отрицательные числа всегда имеют в своем двоичном представлении единицу в самом старшем разряде, который поэтому называют знаковым, а абсолютная величина кодируемого числа получается как двоичное дополнение остальных бит (нули нужно заменить на единицы и наоборот), увеличенное на один.

Легко видеть, что при этом самым маленьким отрицательным числом, которое принадлежит типу byte, является число — 128 (двоичное представление 10000000), а самым большим — число 127 (представление 01111111). Все представимыe числа (а их 256) в данном случае могут быть получены как пересечение двух множеств: множества Z всех целых чисел и отрезка [ — 128; 127 ].

Интересным является следующее наблюдение: если число 01111111 увеличить на единицу, то получится 10000000, что означает следующее:

127 + 1 = — 128 !!!

Итак, множество элементов типа byte можно представлять себе в виде свернутого в кольцо отрезка
[ — 128; 127 ].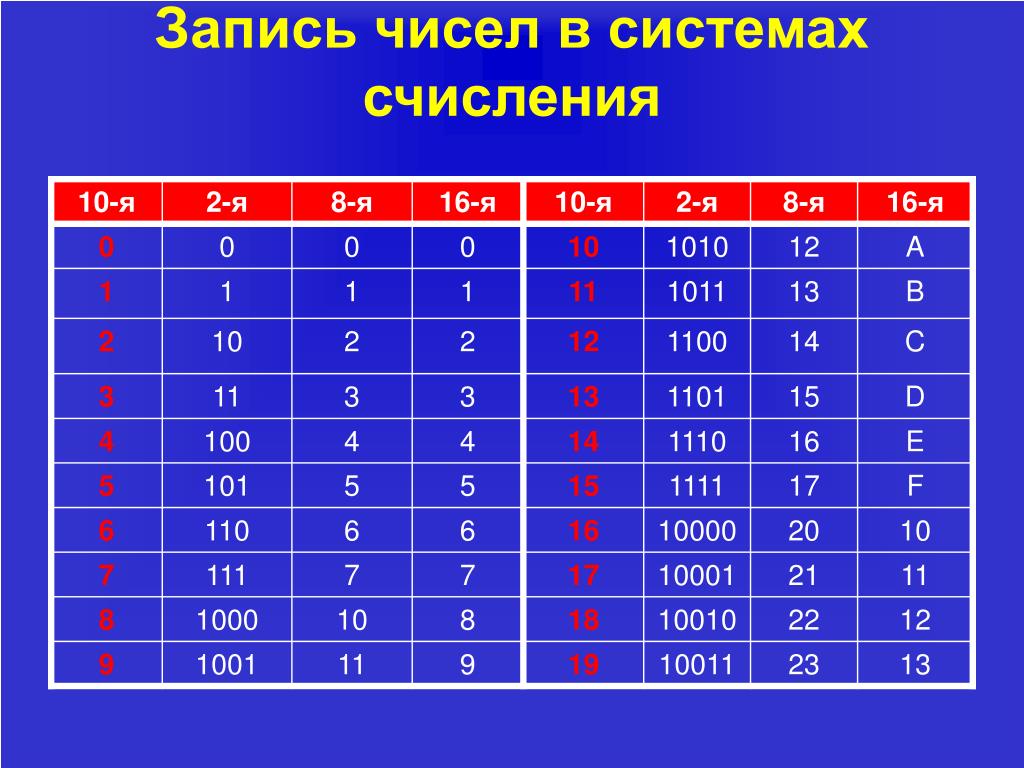

То, что для элементов множества , являющегося машинным аналогом Z, нарушено фундаментальное свойство целых чисел X + 1 > X, способно привести к различным невероятным на первый взгляд результатам, однако гораздо более странные вещи происходят при работе с вещественными числами.

 

 

Двоичная арифметика

Над числами в двоичной системе счисления можно выполнять арифметические действия.

При этом используются следующие таблицы:

Сложение

Вычитание

Умножение

0+0=0

0-0=0

0*0=0

1+0=1

1-0=1

1*0=0

0+1=1

1-1=0

0*1=0

1+1=10

10-1=1

1*1=1

Рассмотрим примеры:

1 1 0 1 0 12 + 1 1 0 1 12

 
1 1 0 1 12 — 1 1 0 12

 
1 1 0 1 12 * 1 0 12

Для деления в двоичной системе счисления нужно уметь сравнивать числа (определять, какое больше) и хорошо вычитать.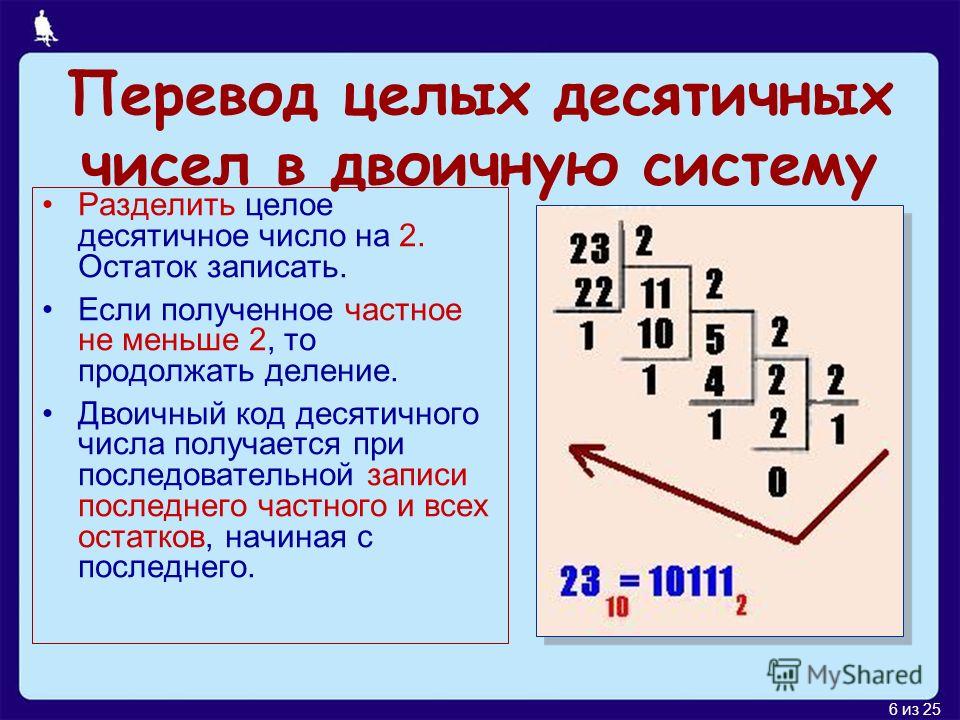 Посмотри деление на анимированном примере

Пример:

 

Еще несколько примеров:

 
Несколько примеров для тренировки:

 

CS101 — Системы счисления и двоичные числа

Вот несколько неформальных заметок о системах счисления и двоичных числах. См. также разделы 3.1–3.2 учебника.

Наша обычная система счисления — это позиционная система, в которой позиция (столбец) цифры представляет ее значение. Начиная справа, у нас есть столбец единиц, столбец десятков, сотни, тысячи и так далее. Таким образом, число 3724 означает три ТЫСЯЧИ, СЕМЬСОТ, две ДЕСЯТКИ (называемые двадцатью) и четыре ЕДИНИЦЫ.

Значения этих столбцов получаются из степеней десяти, которые затем называются по основанию системы счисления. Десятичная система счисления также называется десятичной .

В десятичной системе счисления нет ничего особенного, за исключением того, что это то, чему вы научились с юных лет. Позиционная система счисления может использовать любое количество в качестве основы. Возьмем, к примеру, основание пять. В базе пять столбцы представляют количества (справа налево) один, пять, двадцать пять и сто двадцать пять. Нам нужно использовать пять символов для обозначения количества от нуля до четырех. Для простоты давайте сохраним те же цифры, которые мы знаем: 0, 1, 2, 3 и 4.

Число, показанное на этом рисунке, 3104 по основанию пять, представляет то же самое количество, которое мы обычно записываем как 404 по основанию десять.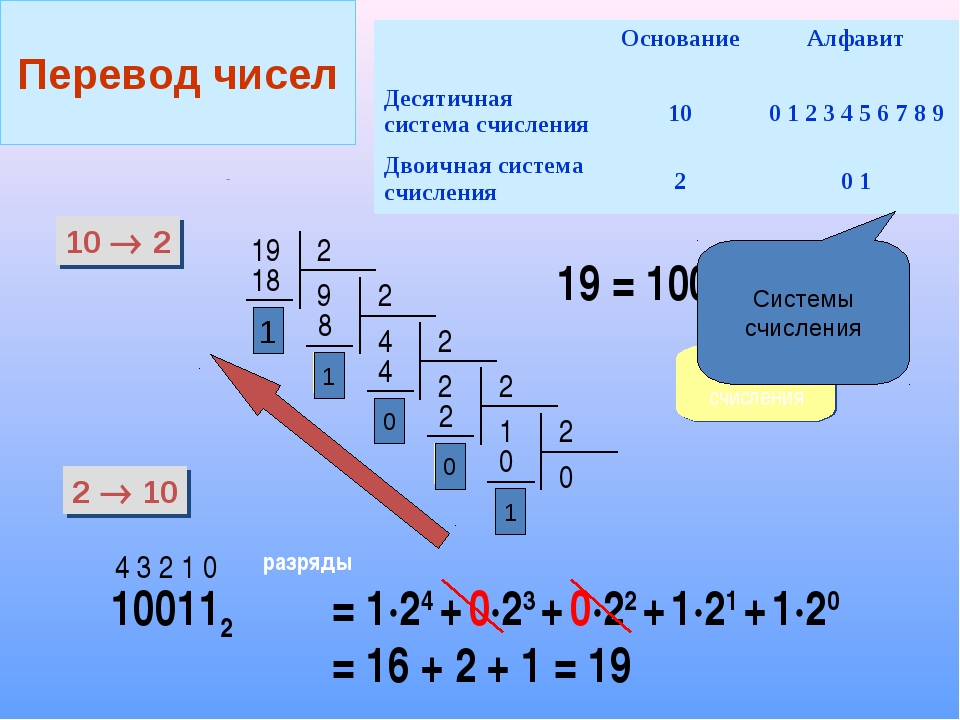 Это потому, что это три × сто двадцать пять (= 375), плюс один × двадцать пять (= 25) плюс четыре единицы (= 4), поэтому 375 + 25 + 4 = 404.

Вы можете посчитать прямо в основание пять; выглядит так: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30, 31, 32, 33, 34, 40, 41, 42 , 43, 44, 100. (Соответствуют количествам от нуля до двадцати пяти.)

Попробуйте считать и конвертировать между другими базами. Ниже представлен интересный видео обзор системы счисления дюжинальная (с основанием двенадцать).

Компьютерные системы используют двоичных чисел — это просто означает, что они находятся в базе два. Использование двух в качестве основы действительно удобно и гибко, потому что нам нужны только два «символа», и существует так много способов их представления: ноль/единица, вкл/выкл, вверх/вниз, высокий/низкий, положительный/отрицательный.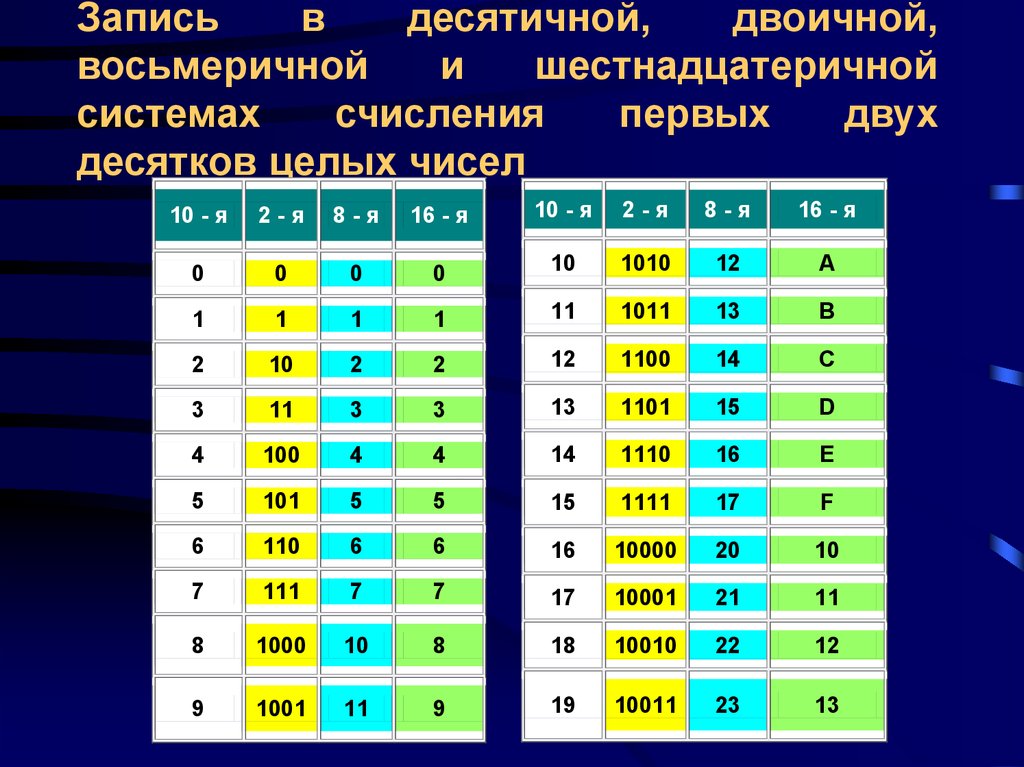 и т. д.

В двоичном формате столбцы (справа налево) 1, 2, 4, 8, 16, 32 и т. д. Использование нуля означает, что мы исключаем количество этого столбца, а единица означает, что мы его включаем.

Итак, двоичное число 10110 равно количеству 16 + 4 + 2 = 22. Каждая двоичная цифра (единица или ноль) называется битом . Самое большое пятиразрядное двоичное число, тогда 11111 = 16 + 8 + 4 + 2 + 1 = 31.

Стоит научиться считать в двоичном виде, хотя бы от нуля до пятнадцати:

 0000 = 0 0100 = 4 1000 = 8 1100 = 12
    0001 = 1 0101 = 5 1001 = 91101 = 13
    0010 = 2 0110 = 6 1010 = 10 1110 = 14
    0011 = 3 0111 = 7 1011 = 11 1111 = 15

Сравнительно легко складывать числа непосредственно в двоичном виде. Выровняйте столбцы, а затем действуйте справа налево, как обычно. Возможны только четыре случая:

  • Если в столбце нет единиц, ниже запишите ноль.
  • Если в столбце есть один, напишите один ниже.
  • Если в столбце две единицы, запишите ноль и перенесите единицу в следующий столбец (слева).
  • Наконец, если в столбце три единицы (возможно, из-за входящего переноса), запишите единицу и перенесите единицу в следующий столбец.

Ниже приведен пример сложения 10110 плюс 11100. Результат равен 110010, и вы можете видеть биты переноса над исходными числами оранжевым цветом.

При сложении таким способом всегда полезно проверить свою работу, преобразовав числа в десятичные числа и проверив сложение. В этом случае мы добавляем 22 (10110) к 28 (11100), чтобы получить 50 (110010).

Обычно мы располагаем числа вдоль линии, уходящей в бесконечность. Действительно, в двоичном формате мы всегда можем продолжить счет, добавляя все больше и больше столбцов, которые являются степенями двойки.

Однако в большинстве компьютерных систем и программ мы используем фиксированных чисел . То есть мы заранее решаем, сколько битов будет использовано для представления числа. Например, 32-разрядный компьютер представляет большинство своих чисел и адресов с помощью 32-разрядных чисел. Наибольшее такое число 2³²–1 = 4,29.4 967 295.

Если ваши числа имеют фиксированное количество битов, то нет числовой линии, уходящей в бесконечность. Вместо этого мы расставляем числа по кругу, как часы. Ниже приведено числовое колесо для 3-битных целых чисел. Наименьшее 3-битное целое число равно нулю, а наибольшее — семи. Затем, если вы попытаетесь продолжить счет, он просто снова вернется к нулю.

Когда вы выполняете арифметические действия с числами фиксированного размера, вы отбрасываете все лишние биты переноса; результат не может превышать обозначенный размер. Например, посмотрите, что произойдет, если мы попытаемся сложить 110 + 011, используя 3-битные целые числа:

В 3-битной арифметике 6 плюс 3 равно 1. Вы можете понять это на числовом колесе. Дополнение соответствует обходу колеса по часовой стрелке. Итак, начните с 6 и пройдите по часовой стрелке на 3. Вы получите 1, то есть 6+3.

Ниже видео о двоичных числах фиксированного размера в старых видеоиграх.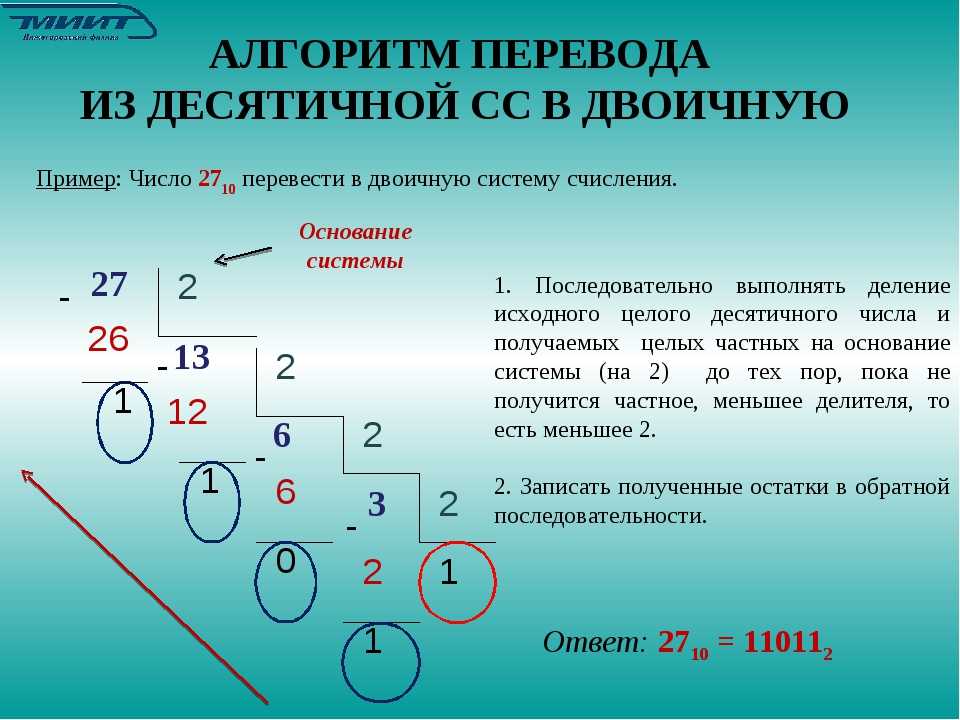

Теперь мы рассмотрим подписанных чисел — то есть числа, которые могут быть положительными или отрицательными. Существует два метода кодирования чисел со знаком. Первый называется величина со знаком. Сначала это кажется простым, но за этой простотой скрываются некоторые неуклюжие свойства.

Вот как это работает. Мы используем фиксированную ширину, а затем крайний левый бит представляет знак. Итак, 4-битная величина со знаком выглядит так:

 ___ ___ ___ ___
  sign 4 2 1

, где бит знака, установленный в «1», означает, что величина интерпретируется как отрицательная. Таким образом, 0110 равно +6 , тогда как 1110 равно -6 . В этой системе наибольшее положительное число равно 9.0087 0111 = +7 и самое отрицательное число 1111 = -7 .

Одним из неприятных эффектов этого представления является то, что есть два способа записать ноль: 0000 и также 1000 .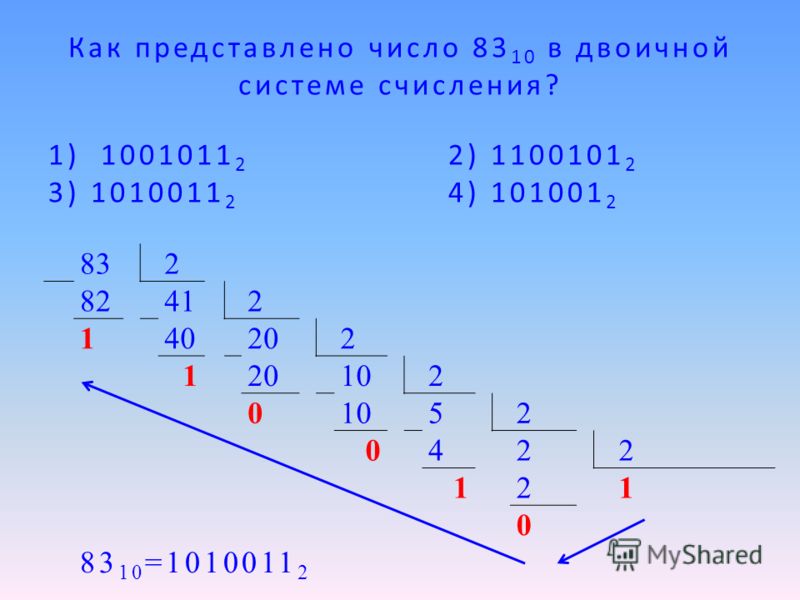 Нет такой вещи, как отрицательный ноль, так что это не имеет особого смысла.

Второй способ представления величин со знаком называется дополнением до двух. Хотя на первый взгляд это выглядит сложнее, на самом деле это работает очень хорошо. Ниже приведена интерпретация 4-битного дополнения до двух. Все, что нам нужно сделать по сравнению с обычными числами без знака, — это инвертировать значение самого левого бита.

 ___ ___ ___ ___
   -8 4 2 1

Таким образом, +6 — это 0110 , как и раньше, но как насчет -6 ? Нам нужно включить минус 8, а затем добавить два: 1010 . Чтобы представить -1 , вы включаете все биты: 1111 , потому что это дает -8+4+2+1 = -8+7 = -1 .

Преимущество дополнения до двух заключается в том, что вы можете сложить эти числа, и все получится. Давайте попробуем добавить 7 и -3 :

 0 1 1 1 = 7
   1 1 0 1 = -3
  --------- ----
   0 1 0 0 = 4

Также относительно легко инвертировать число, то есть перейти от +6 к -6 или от -3 к +3 . Вот шаги:

  1. Сначала переверните все биты. То есть все нули становятся единицами, а все единицы становятся нулями.

  2. Затем добавьте один.

Например, вот как мы производим -6 из +6 :

 0 1 1 0 = +6
   1 0 0 1 (перевернуть все биты)
       + 1 (добавить один)
  ---------
   1 0 1 0 = -6

Вам даже не нужно выполнять эти действия в обратном порядке, чтобы преобразовать обратно:

 1 0 1 0 = -6
   0 1 0 1 (перевернуть все биты)
       + 1 (добавить один)
  ---------
   0 1 1 0 = +6

Вот мультфильм от XKCD о том, как считать овец с помощью дополнения до двух!

Сколько битов использует этот человек?

Наконец, я хочу представить две системы счисления, которые очень полезны как 9.0007 аббревиатуры для двоичного кода. Они работают так хорошо, потому что их основания являются степенью двойки.

Восьмеричное число по основанию восемь, поэтому мы используем символы 0–7, а значения столбцов следующие:

 ___ ___ ___ ___
   512 64 8 1
    8³ 8² 8¹ 8⁰

Однако реальное значение восьмеричного числа состоит в том, что каждая восьмеричная цифра соответствует ровно трем двоичным цифрам. Таким образом, восьмеричное число, например 3714 , отображается следующим образом:

 3 7 1 4 восьмеричное число
  0 1 1 1 1 1 0 0 1 1 0 0 двоичное число
  
 (4 2 1 4 2 1 4 2 1 4 2 1)

Шестнадцатеричное число — это основание шестнадцать, поэтому мы используем символы 0–9, а затем А для обозначения десяти, В для одиннадцати и так далее до F для пятнадцати. Значения столбцов:

 ____ ____ ____ ____
4096 256 16 1
 16³ 16² 16¹ 16⁰

Таким образом, шестнадцатеричное число, такое как 2A5C , имеет значение 2×4096 + 10×256 + 5×16 + 12×1 = 10844 с основанием десять.

В шестнадцатеричном формате каждая цифра соответствует ровно четырем битам. Вот то самое число в двоичном формате:

 2 А 5 С
  0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 0
  
 (8 4 2 1 8 4 2 1 8 4 2 1 8 4 2 1)

Ниже приведены два отличных видеообзора шестнадцатеричных чисел. ( Обратите внимание на , когда вы смотрите это — британцы часто произносят ноль как «ноль». )

  1. Преобразуйте следующие десятичные числа в двоичные числа.

    1. 6
    2. 18
    3. 51
    4. 63

  2. Преобразуйте следующие двоичные числа без знака в десятичную систему счисления.

    1. 1010
    2. 1101
    3. 1000
    4. 10001

  3. Что общего у всех нечетных чисел, записанных в двоичном формате? (Подсказка: попробуйте записать числа 3, 5, 7, 9, 11 в двоичном формате.)

  4. Используя 7-битные знаковые (дополнение до двух) двоичные числа, какое наибольшее положительное число? Какое самое отрицательное число?

  5. Преобразуйте следующие 5-битные знаковые (дополнение до двух) двоичные числа в основание десяти.

    1. 01101
    2. 01111
    3. 10011
    4. 11111

  6. Преобразование следующего 16-разрядного двоичного числа в шестнадцатеричное, а затем в восьмеричное.

     0 1 1 1 1 1 1 1 0 0 1 1 1 0 1 0

  7. Преобразование следующих шестнадцатеричных чисел в двоичные:

    1. 9Д
    2. С4
    3. А17Е

  8. Добавьте и проверьте следующие беззнаковых двоичных чисел.

     1 0 1 1 1 1 1 1 0 1 1 1
+ 1 1 1 0 1 + 1 0 0 1 0 0
————————————— ——————————————

Решения здесь

@jaffathecake в Твиттере

Двоичные системы счисления

Двоичные системы счисления

Помпей Втрыскове дешевая обувь хуараче бомбы дешевые джорданы дешевый воздух макс дешевые кроссовки дешевые нфл трикотажные изделия дешевые Эйр Джорданс дешевая иорданская обувь дешевые оптовые Иордании

Дом История Проводка ввода/вывода Взаимодействие ввода/вывода Системы счисления Структура памяти Битовые инструкции Таймеры Счетчики Лаборатории ЛогиксПро Внешняя ссылка Карта сайта Страница цитирования

Двоичная система счисления

Вернуться к страницам с номерами | Десятичные числа | Двоичные числа | Шестнадцатеричные числа | Восьмеричные числа | Номер BCD | Отрицательные числа | Преобразование чисел

Двоичная система счисления используется всеми компьютерами, PLC/PAC и цифровое устройство.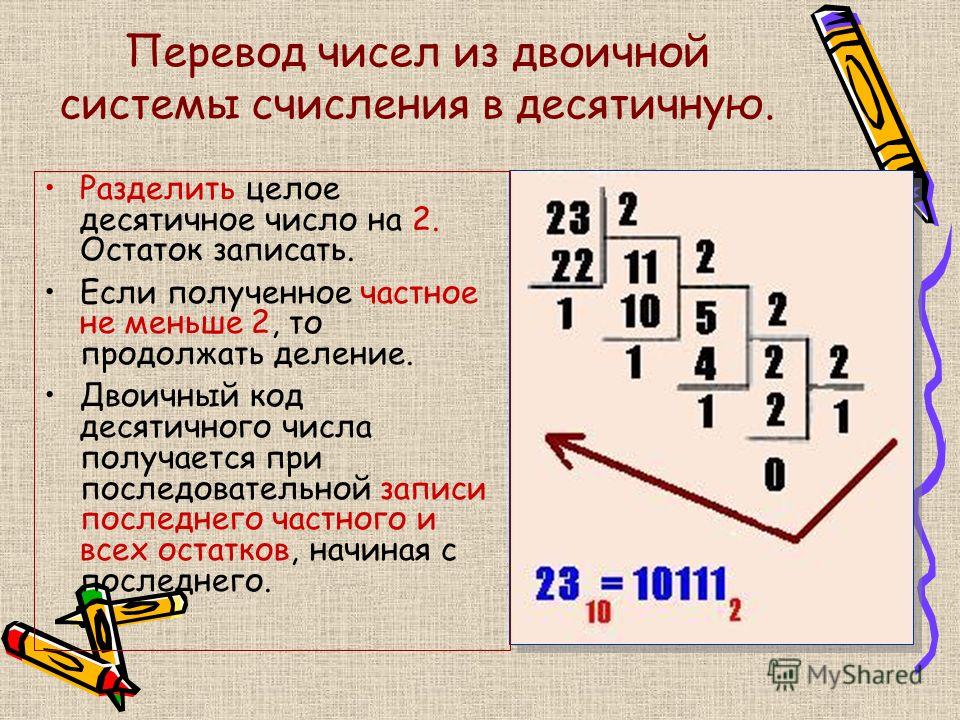

Двоичная система счисления — это система счисления с основанием 2, поэтому есть две допустимые цифры:

0 и 1

Одна цифра двоичного кода называется битом. Биты используются в группы для представления всех остальных чисел. Битовая группировка номиклатура выглядит следующим образом:

  • 1 двоичная цифра — это бит
  • 4 бита — это полубайт (термин используется нечасто)
  • 8 бит это байт
  • 16-битное слово
  • 32-битное двойное слово или DWORD
  • 64 бита — это четверное слово или QWORD

Двоичная система счисления используется в компьютерах и PLC/PAC. потому что легко использовать бит для представления уровней напряжения внутри компьютера или PLC/PAC.

alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *