4.4. Почему люди пользуются десятичной системой, а компьютеры — двоичной? 4.5. Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?

Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.

А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:

•  
  • для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
  • представление информации посредством только двух состояний надежно и помехоустойчиво;
  • возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
  • двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.4.5. Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно

в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).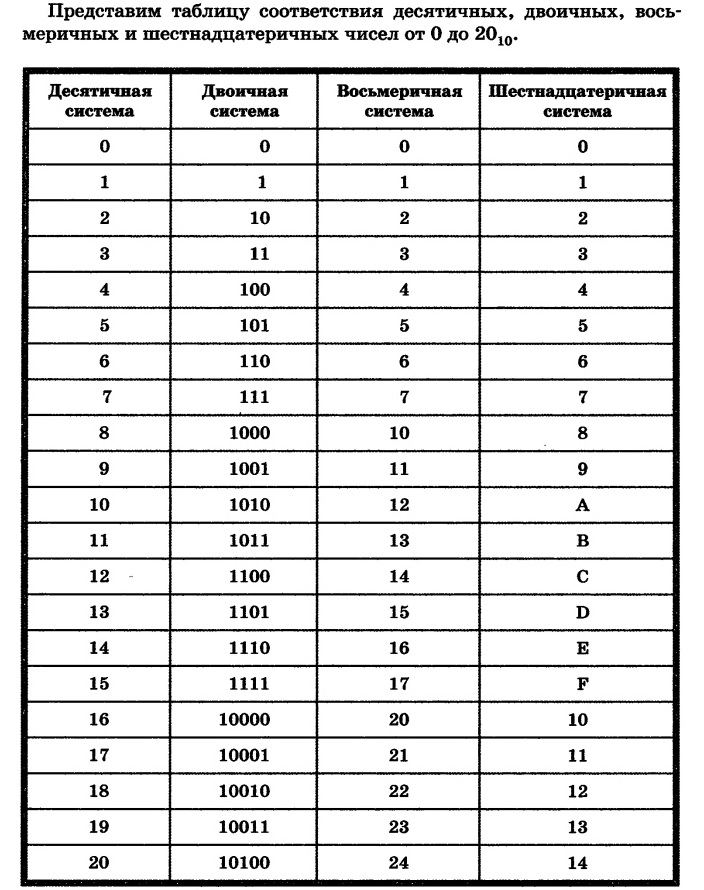

Например:

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответ-ствующей восьмеричной (шестнадцатеричной) цифрой.

Например,

Двоично-десятичная система счисления 📙 — Информатика

1. Обозначение смешанной системы счисления
2. Построение в двоично-десятичной системе
3. Для чего нужно использование двоично-десятичной системы счисления
4. Выгоды применения двоично-десятичной системы

В мире электронно-вычислительных технологий существуют различные системы счислений. Одним из классов систем счисления является класс смешанной системы счисления.

Смешанная система счисления — это такая система счисления, в которой числа одной системы с основанием Р, записываются цифрами другой системы с основанием Q, причем Q меньше Р.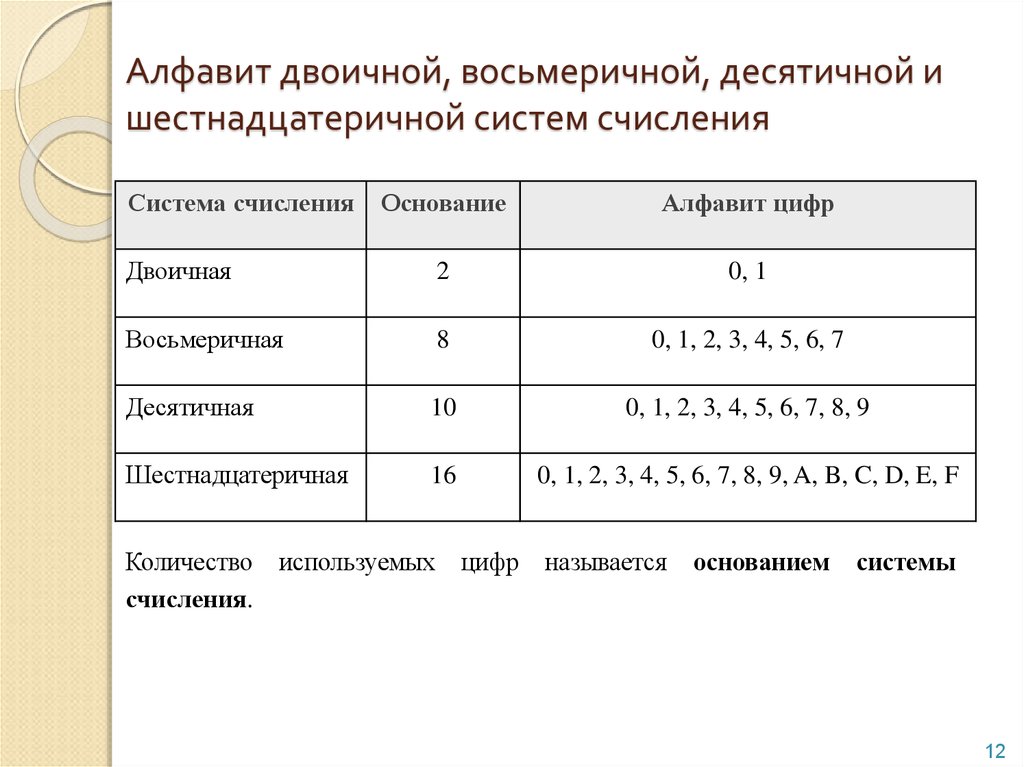 В данной системе Q считается младшим основанием, а Р — старшим, такая система называется Q-Р-ичной.

Таких систем существует несколько, одной из них является двоично-десятичная система счисления.

В двоично-десятичной системе счисления каждая десятичная цифра от 0 до 9 производится с помощью четырехразрядного числа, с использованием лишь элементарных цифр 0 и 1. А именно для записи цифры 0 используется код 0000, 1 — 0001, 2 — 0010, 3 — 0011,4 — 0100, 5 — 0101, 6 — 0110, 7 — 0111, 8 — 1000, 9  — 001. Для примера рассмотрим число десятичной системы счисления 925, в двоично-десятичной системе это число запишется как 1001 0010 0101. Формально это выглядит вот как:

925₁₀ = 10010010010_12-10.

В этой записи используются четверки цифр двоично-десятичной системы, которые последовательно отображают цифры 9, 2 и 5. Эти последовательные четверки цифр называются тетрадами.

В двоичной системе для изображения чисел также используются 0 и 1, но невзирая на это, изображения десятичного числа в двоично-десятичной системе отличается от его записи в двоичной системе счисления. К примеру, та же запись 100100100101 в этих двух системах будет обозначать разное десятичное число. Это выглядит так:

100100100101_2-10 = 925₁₀;
100100100101₂ = 2341₁₀.

Подобное изображение числа зачастую используется в качестве вспомогательного этапа при трансформации числа из двоичной в десятичную систему счисления и наоборот. В двоично-десятичной системе счисления алгоритмы арифметических вычислений многозначных чисел намного сложнее, чем в простых системах счисления, но тем не менее эта система счисления часто используется для этих операций в микросхемах компьютеров и калькуляторов.

При корректировке результатов элементарных арифметических операций с числами, записанными с помощью двоично-десятичных кодов, используют специальные команды для преобразования их в двоично-десятичную систему счисления. В данном случае применяется правило: для получения в результате простой арифметической операции сложения или вычитания число в тетраде, большее чем 9, к ней нужно прибавить число 6.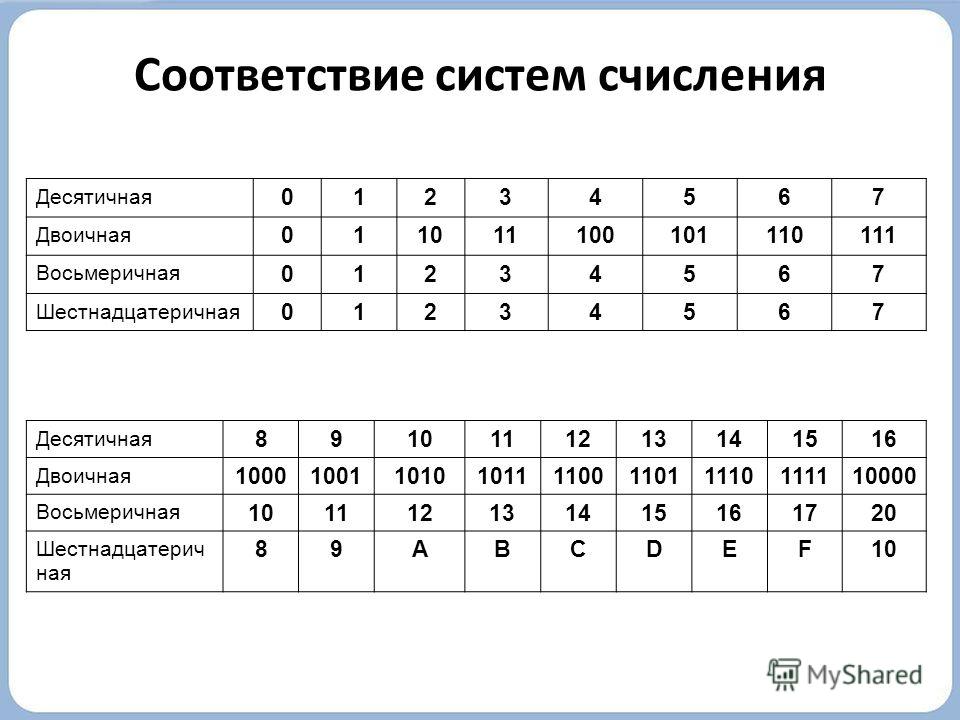

Такое уравновешивание по разрядам производится обычно с помощью двоично-десятичной системы счисления. При этом самым целесообразным является комплексное использование двоичной и двоично-десятичной систем счисления, так как при этом количество тактов уравновешивания намного меньшее, чем при использовании иных систем счисления.

Человеческому глазу понятна десятичная система изображения чисел, и мы используем ее практически в любой сфере жизни, где сталкиваемся с числами. Работа электроники построена на использовании двоичной системы вывода чисел. Поэтому вариант применения системы счисления с помощью двоично-десятичных кодов является компромиссным. Двоично-десятичные коды используется в тех микросхемах приборов, где есть потребность частого ввода и вывода десятичных чисел, к примеру, в электронных часах, калькуляторах, таймерах, дисплеях бытовой техники и прочих приборах, в которых нет смысла использовать универсальные микрокоды из-за ограниченного объема памяти.

В арифметических логических устройствах электронно-вычислительных машин есть специальные блоки арифметических вычислений, выполняющих операции на основании двоично-десятичной системы счисления. Во многих случаях это существенно повышает производительность электронно-вычислительных машин. Например, если рассмотреть системы автоматизированной обработки данных, в которых практически не используются арифметические вычисления, то процесс трансформации чисел из одной системы в другую занял бы длительный ресурс времени и памяти. Поэтому в микропроцессорах в таком случае применяются двоичные коды, но при этом они умеют распознавать команды трансформации в двоично-десятичные коды. В итоге результат изображается на дисплее в десятичной форме изображения числа, понятной человеку.

Применение двоично-десятичной системы счисления в комплексе с двоичной системой, которая является одной из основных, позволяет создавать на рынке высокопроизводительные электронно-вычислительные машины. Это становится возможным благодаря применению блока десятичных арифметических операций без необходимости программного трансформирования чисел в двоичную систему.

Трансформация чисел в двоично-десятичную систему из десятичной не требует громоздких арифметических вычислений, а является простой операцией с использованием четырехразрядных кодов тетрад, что производится автоматически при помощи элементарных алгоритмических программ.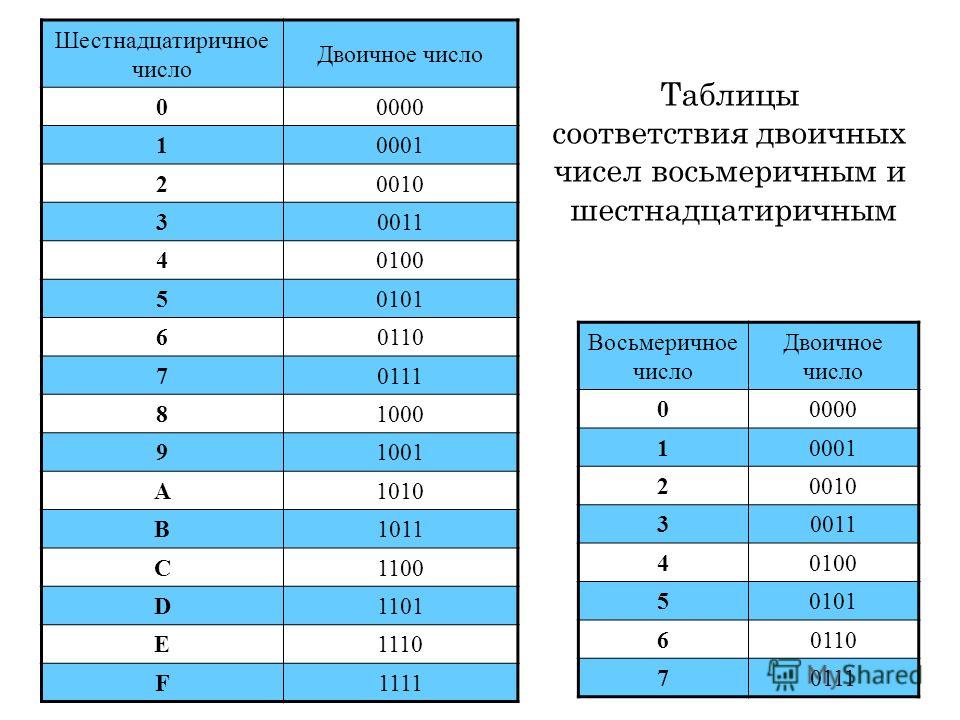

Так как две двоично-десятичные цифры в сумме занимают всего 1 байт памяти, то с его помощью можно записать любую десятичную цифру от 0 до 99. Таким образом, используя всего лишь 1 байт для изображения двух любых десятичных цифр, возможно записать любое количество двоично-десятичных чисел с необходимым количеством десятичных разрядов.

Десятичная и двоичная системы счисления

Сложите Содержание Десятичная и двоичная системы счисления Десятичная система счисления Двоичная система счисления

Прежде чем мы начнем изучать более сложные вопросы в разделе «Числовой анализ», мы должны сначала лучше понять десятичную систему счисления и двоичную систему счисления. Сначала мы закрепим основы десятичной системы счисления, с которой мы все слишком хорошо знакомы.

Десятичная система счисления

Определение: Десятичная система счисления — это система счисления, в которой каждое действительное число $x$ может быть записано десятью цифрами $0$, $1$, $2$, $3$, $4$, $5$, $6$, $7$, $8$ и $9$ как сумма степеней $10$. Говорят, что число в десятичной системе счисления имеет основание $10$, и чтобы указать это, мы присоединяем индекс $10$ к $x$, записывая $(x)_{10}$.

Мы укажем основание числа для остальной части этой страницы, а после этого мы будем указывать основание числа только тогда, когда контекст неясен. 9{-n} \right ) + … \end{align}

Двоичная система счисления

Мы больше всего привыкли использовать описанную выше десятичную систему счисления и связанную с ней основную арифметику, однако двоичная система счисления система также чрезвычайно важна, особенно в вычислительной технике. Мы формально определим двоичную систему счисления ниже. Обратите внимание на сходство с определением, данным для десятичной системы счисления.

Определение: Двоичная система счисления — это система счисления, в которой каждое действительное число $x$ может быть записано двумя цифрами $0$ и $1$ как сумма степеней $2$. Говорят, что число, записанное в двоичной системе счисления, имеет основание $2$, и чтобы указать это, мы присоединяем индекс $2$ к $x$, записываемому как $(x)_{2}$.

В двоичной системе счисления действительные числа $x$ могут представлять только цифры $0$ и $1$, а заполнители для каждой цифры соответствуют степеням $2$. Например, рассмотрим двоичное число $(1101)_2$. Отметим, что: 9{-4} \right ) = (5.3125)_{10} \end{align}

Десятичная и двоичная системы счисления. Сходства и различия между двоичной и десятичной системами?

8 декабря 2022 г. от schoolelectronic

Сходства между двоичной и десятичной системами

Различия между двоичной и десятичной системами

В этом посте мы проведем быстрое сравнение десятичной и двоичной систем счисления, выделив все сходства и различия между двумя системами счисления для лучшего понимания их варианта использования.

Мы знакомы с десятичной системой счисления или десятичной системой счисления, так как мы используем ее каждый день для оплаты счетов, покупки продуктов, банковских операций и т.д. В десятичной системе счисления мы представляем или выражаем заданное десятичное число в единицах, десятках, сотнях, тысячах и т. д.,

. С другой стороны, наши компьютеры и другие цифровые устройства, которые мы используем каждый день, используют двоичное число. система для общения, выполнения арифметических и логических операций.

Десятичное число использует 10 цифр для представления различных значений, тогда как двоичное число использует только 2 цифры (0 и 1) для представления любого двоичного числа.

Мы продолжим обсуждение и посмотрим, каковы основные сходства и различия между двоичной и десятичной системами.

Сходства между двоичной и десятичной системами

Во-первых, двоичная и десятичная системы могут одинаково представлять или выражать числа как целыми, так и дробными частями.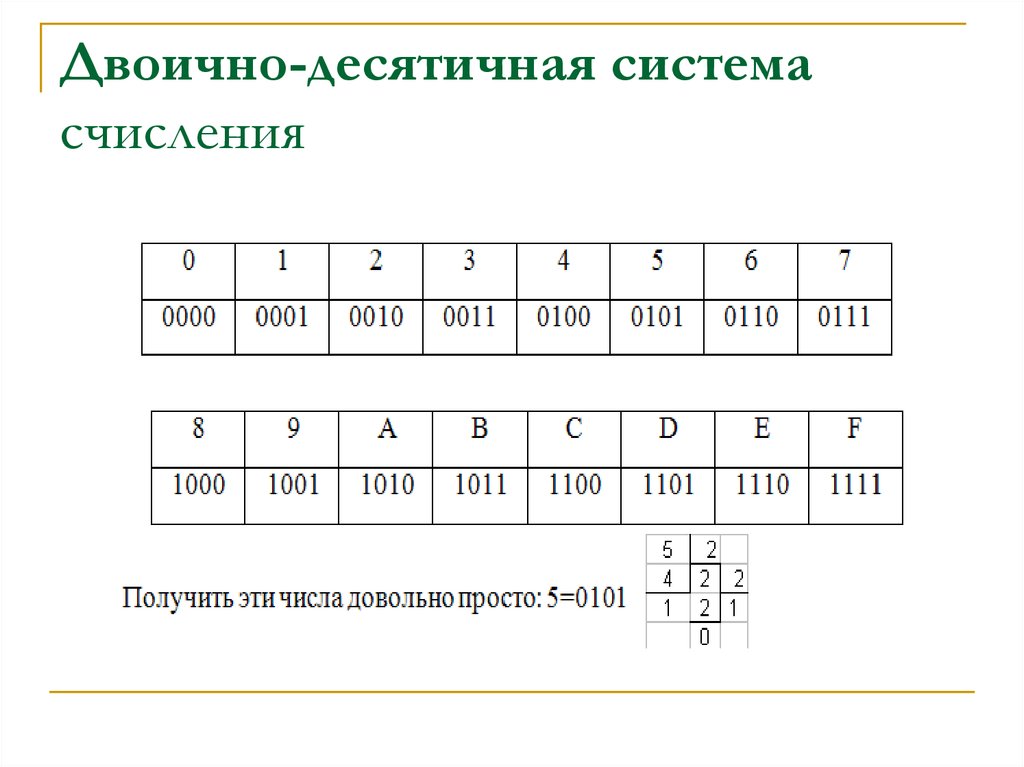 Таким образом, любое заданное число, например число 14, в десятичной системе равно (14) ₁₀ , а в двоичной системе выражается как (1110) ₂ . Здесь нижние индексы 10 и 2 являются основанием соответствующих систем счисления.

Другое важное сходство между двоичной и десятичной системами заключается в том, что значение данной цифры (в десятичном числе) или данного бита (в двоичном числе) определяется положением десятичной цифры от десятичной точки или положением двоичный бит из двоичной точки. Самая дальняя цифра или двоичный разряд от десятичной/двоичной точки имеет наибольший вес.

Пример для десятичной системы: 623,54 – самая левая цифра, начинающаяся с десятичной точки (1), имеет наибольший вес, а самая правая цифра с десятичной точки имеет наименьший вес или значение(4).

Пример для двоичной системы: 101.010 — самый левый бит, начинающийся с двоичной точки (1), имеет наибольший вес, а самый правый бит, начинающийся с двоичной точки вправо, имеет наименьший вес или значение (0).

В дополнение к этому сходство между двоичной и десятичной системами, которое стоит упомянуть, заключается в том, что двоичная система также способна выполнять все арифметические операции, такие как сложение, вычитание, умножение и деление, точно так же, как мы делаем в десятичной системе счисления.

Давайте перечислим все сходства между двоичной и десятичной системами в табличной форме, чтобы их было легко запомнить.

Двоичная система	Десятичная система
Двоичная система может представлять как целые двоичные числа, так и дробные двоичные числа.	Десятичная система может также представлять десятичные числа, содержащие как целые, так и дробные компоненты.
Значение или вес бита зависит от положения бита относительно точки счисления.	Значение/вес цифры в заданном десятичном числе также зависит от позиции цифры относительно десятичной точки.
Пример двоичного числа с целой и дробной частью: 101. 010 (пять и двадцать пять сотых)	Пример десятичного числа: 5.25 (пять и двадцать пять сотых)
Представление десятичного числа дроби и десятичного числа.	Представление двоичного числа и двоичной дроби.
Все арифметические операции, такие как сложение, вычитание, умножение и деление, могут выполняться над двоичными числами.	Арифметические операции сложения, вычитания, умножения и деления можно выполнять над десятичными числами.

Десятичная и двоичная системы счисления – сходства между двоичной и десятичной системами

Различия между двоичной и десятичной системами каждой системы. И двоичная, и десятичная системы различаются на разных уровнях.

Фундаментальное различие между двоичной и десятичной системами заключается в количестве цифр, используемых для представления любого заданного числа. Двоичная система использует только 2 цифры (0 и 1) для представления двоичных чисел, в то время как десятичная система использует 10 цифр от 0 до 9 (0,1,2,3,4,5,6,7,8,9) для представления. любое десятичное число целое или дробное.

Двоичная система, в которой используются только 2 цифры, также называется системой с основанием два, а десятичная система, использующая 10 цифр, известна как система с основанием десять.

Двоичная система счисления

Единицы двоичной системы счисления (0 и 1) известны как биты, более привычные в компьютерном мире. Единицы десятичной системы счисления (от 0 до 9) называются цифрами.

Десятичная система счисления

Основание, используемое в двоичной системе счисления, равно 2, основание, используемое в десятичной системе, равно 10. Другими словами, мы также можем сказать, что в двоичной системе значения или веса выражаются как степень 2 и в десятичной системе значения выражаются в степени 10.

Точка счисления в двоичной системе называется двоичной точкой, а точка счисления в десятичной системе называется десятичной точкой.

В двоичной системе самый левый бит, имеющий наибольший вес, называется старшим значащим битом (MSB), а самый правый бит двоичной точки, имеющий наименьший вес, называется значащим битом аренды ( младший разряд).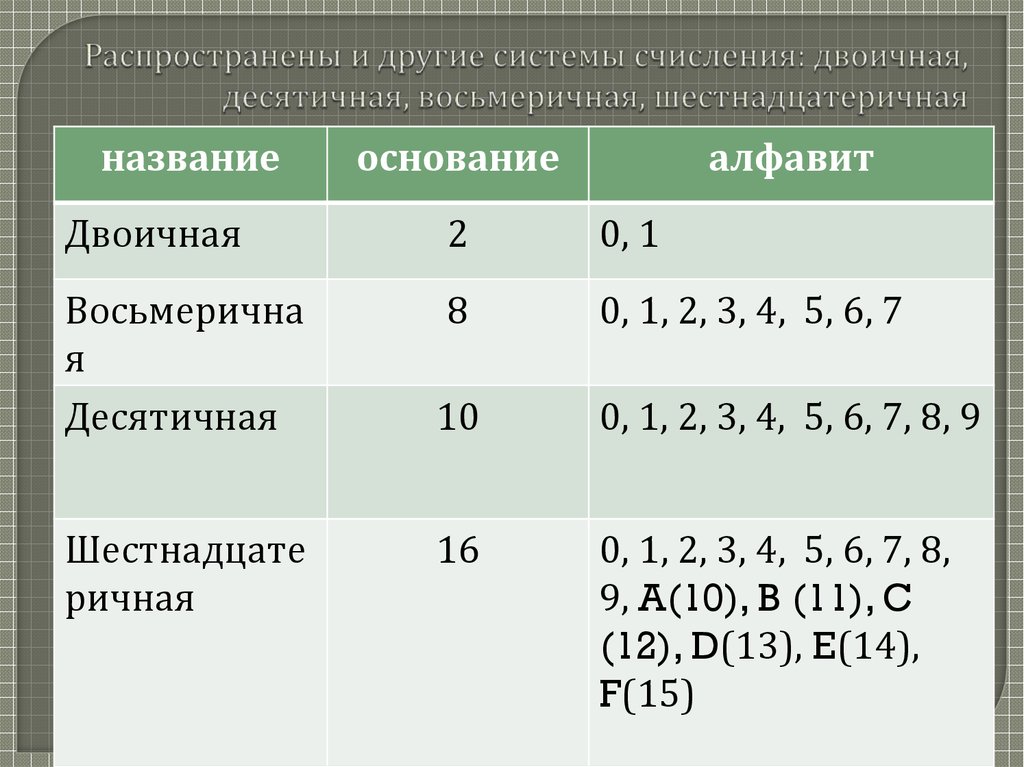 В десятичной системе крайняя левая цифра с наибольшим весом называется старшей значащей цифрой (MSD), а крайняя правая цифра с наименьшим весом называется наименьшей значащей цифрой (LSD).

Выучить различные арифметические и логические операции в двоичной системе проще, чем в десятичной, поскольку в двоичной системе всего 2 цифры (0 и 1).

Наоборот, запоминать и работать с большими двоичными числами становится утомительнее, чем с большими десятичными.

Пример: 65536 в десятичной системе легче запомнить, чем 100000000000000000 в двоичной системе.

Десятичные числа	Двоичные числа
Десятичные числа состоят из комбинации десяти цифр или значений от 0 до 9 (0,1,2,3,4,5,6,7,8,9).	Двоичные числа выражаются или представляются комбинацией только двух цифр или значений 0 (ноль) и 1 (единица).
Основание для десятичного числа равно 10, т. е. все цифры десятичного числа выражаются в степени 10.	Основание для двоичного числа равно 2, т. е. все цифры или значения в двоичном числа выражаются в степени числа 2.
Пример десятичного числа: 25 (двадцать пять)	Пример двоичного числа: 11001 (двадцать пять)
Представление десятичного числа и дроби десятичного числа.	Представление двоичного числа и двоичной дроби.
Легче представлять и работать с большими десятичными числами.	Запоминать большие двоичные числа и работать с ними довольно сложно, так как количество битов, необходимых для представления, резко возрастает по мере роста чисел.
Точка счисления называется десятичной точкой.	Точка счисления называется двоичной точкой.
В десятичной системе счисления у нас есть единицы, десятые, сотые, тысячные, обычно называемые десятичными единицами.	В двоичной системе счисления у нас есть биты. Группа из 4 бит называется полубайтом, Группа из 8 бит называется байтом Группа из 16 бит называется словом. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника