1.3.1 Движение в поле тяготения Земли.
Из закона всемирного тяготения следует, что у поверхности Земли все тела должны падать с одинаковым ускорением. В самом деле, по второму закону Ньютона ускорение, приобретаемое телом с массой m у поверхности Землиa=F/m, гдеF — сила, с которой тело притягивается земным шаром. По закону тяготения
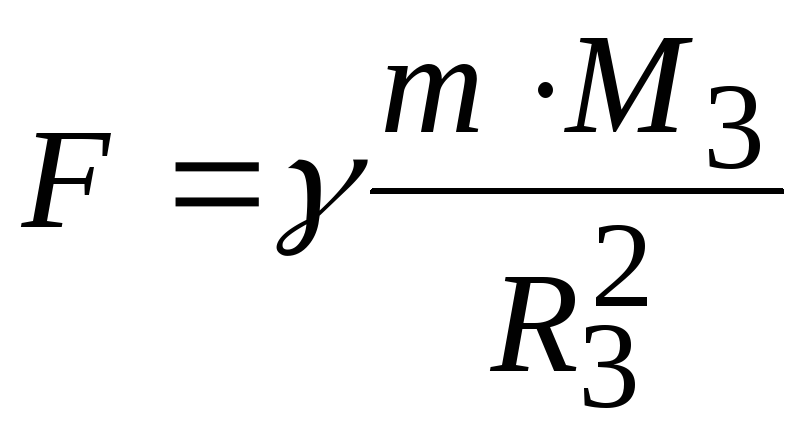 ,
(1.44)
,
(1.44)
M3— масса Земли и R3— радиус земного
шара. Отсюда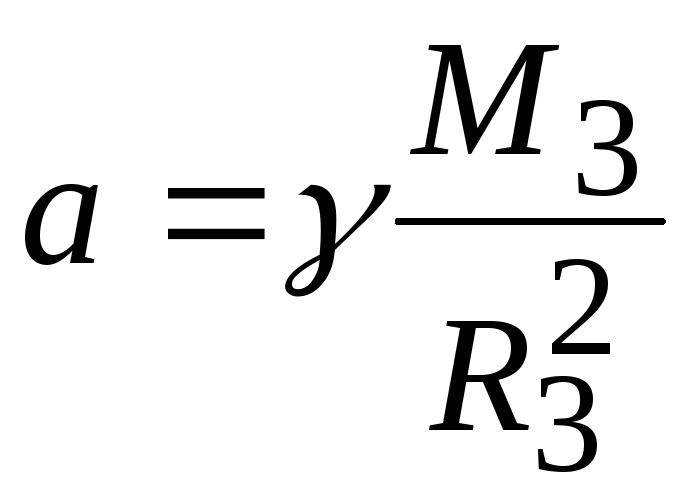
и не зависит от массы падающего тела. Таким образом, все тела у поверхности Земли независимо от их массы падают с одинаковым ускорением
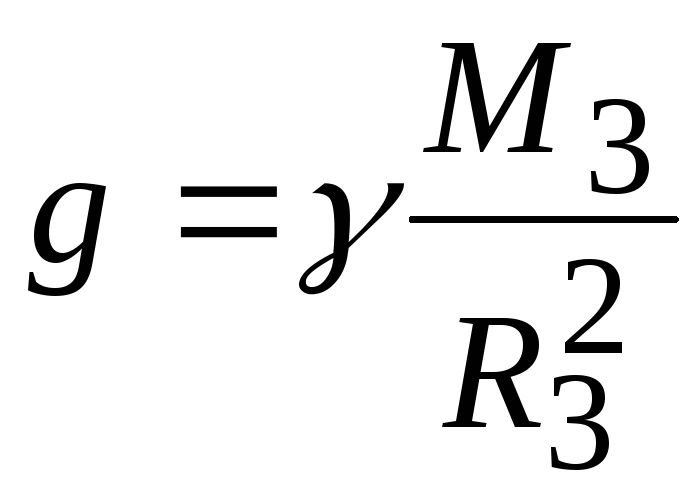 ,
(1.45)
,
(1.45)
которое называется ускорением свободного падения. Подставляя сюда известные значения констант, получим значение 9,8 м/c2. В действительности значенияg слегка различаются при учете сил сопротивления и реальной формы Земли. По второму закону Ньютона это означает, что в поле тяжести Земли все тела испытывают силу тяжести, равнуюmg. При перемещении массы с одной высоты на другую эта сила тяжести совершает работу, которую можно вычислить как изменение потенциальной энергии тела.
1.3.2 Космические скорости.
Определим скорость, которую необходимо иметь телу дли того, чтобы оно могло стать спутником Земли, т. е. первую космическую скорость. Величину этой скорости можно определить из условия равенства сил, действующих на тело при его вращении вокруг Земли. Сила притяжения должна быть уравновешена центробежной силой
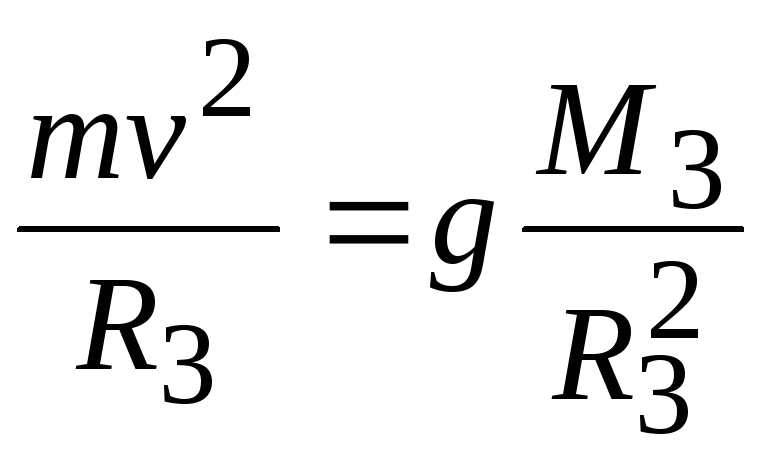 (1.46)
(1.46)
откуда находим значение первой космической скорости
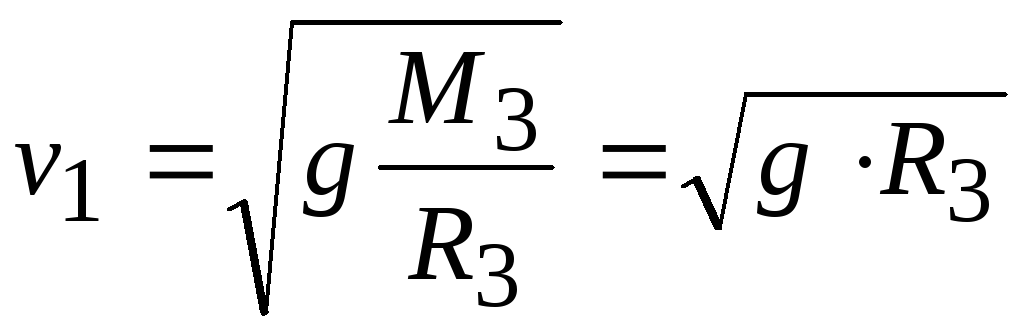 Подставляя
численные значения величин, получаемv1 = 8 км/с.
Подставляя
численные значения величин, получаемv1 = 8 км/с.
Вторая космическая скорость — это скорость, которую нужно сообщить телу для того, чтобы оно покинуло область земного притяжения. Для определения второй космической скорости следует вычислить работу, которую необходимо совершить против сил земного притяжения для удаления тела с поверхности Земли на бесконечность. Эта работа равна разности потенциальных энергий тела в начальном и в конечном положениях:
A = Uк ‑ Uн.
Потенциальная энергия тела в гравитационном поде Земли на ее поверхности согласно (1.41) имеет вид:
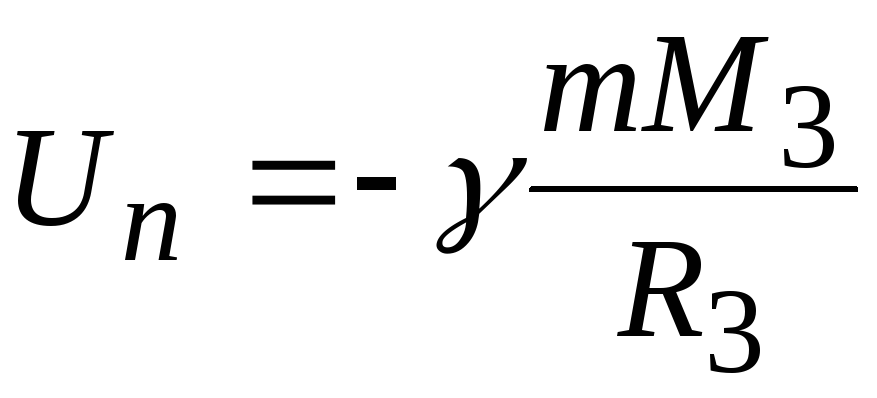
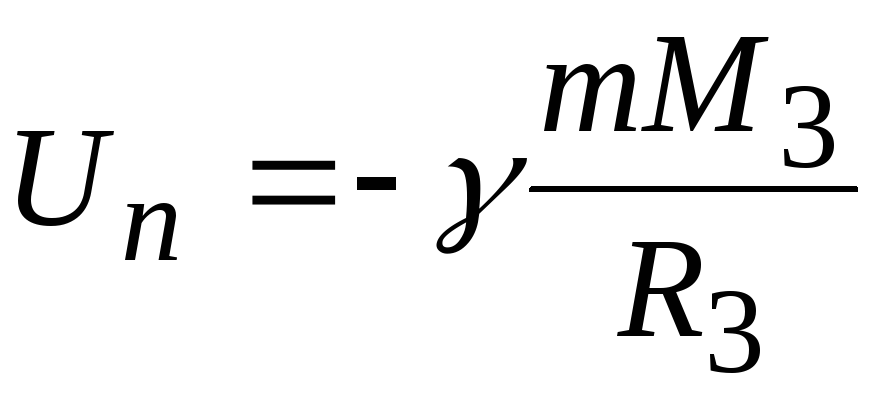 а на бесконечности
равна нулю. Таким образом,
а на бесконечности
равна нулю. Таким образом,
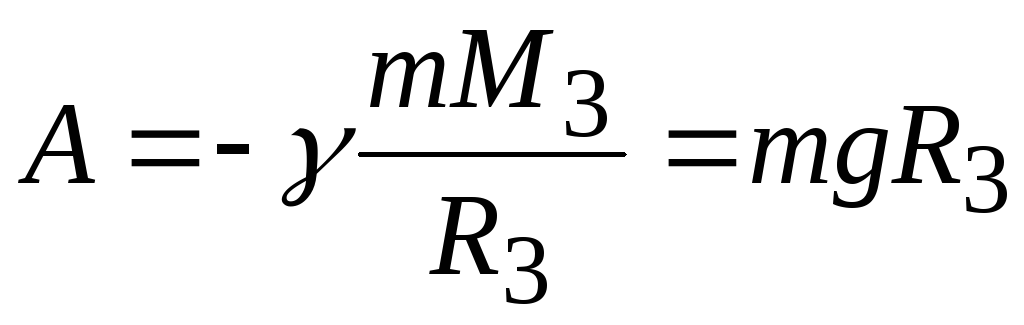
Величина
этой потенциальной энергии определяет
кинетическую энергию, которую должно
иметь тело для того, чтобы быть в состоянии
совершить указанную работу 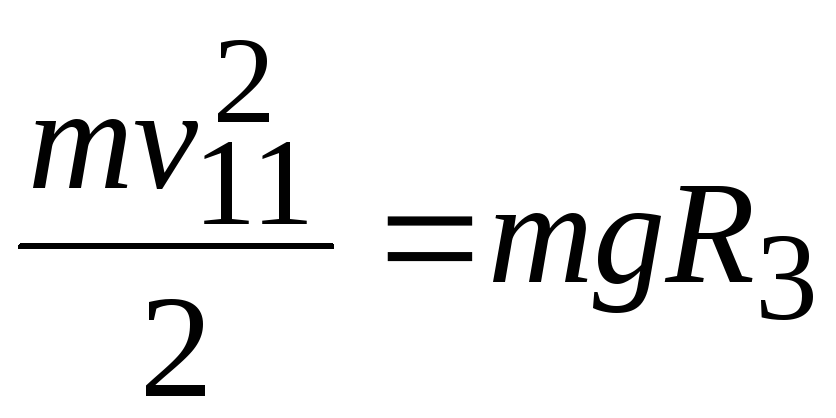
Отсюда вторая космическая скорость определяется выражением:
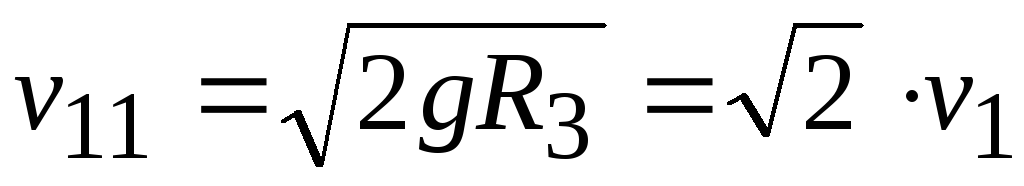 .
.
Ее численное значение приблизительно 11 км/с. Пусть перемещение происходит вдоль оси Z. При этом сила тяжести совершает работу
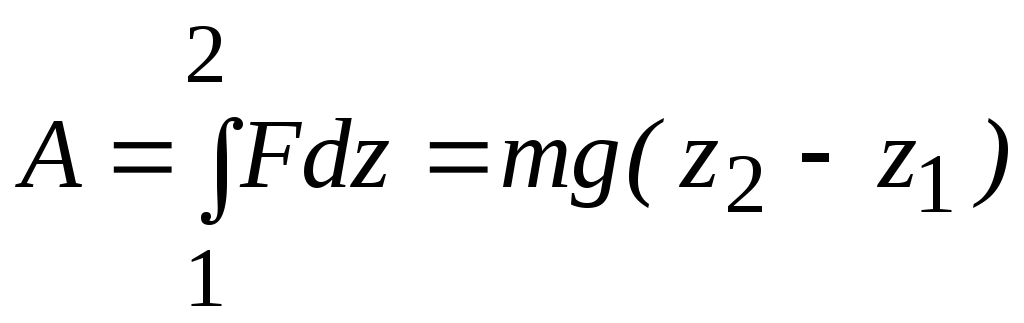
Согласно определению потенциальной энергии А = U1‑U2. Отсюда следует, что потенциальная энергия тела в поле силы тяжести Земли может быть записана в виде
U(z) = mgz + const, (1.48)
где постоянная связана с выбором начала отсчета энергии. Эту формулу можно получить и непосредственно из закона всемирного тяготения. Запишем его в виде
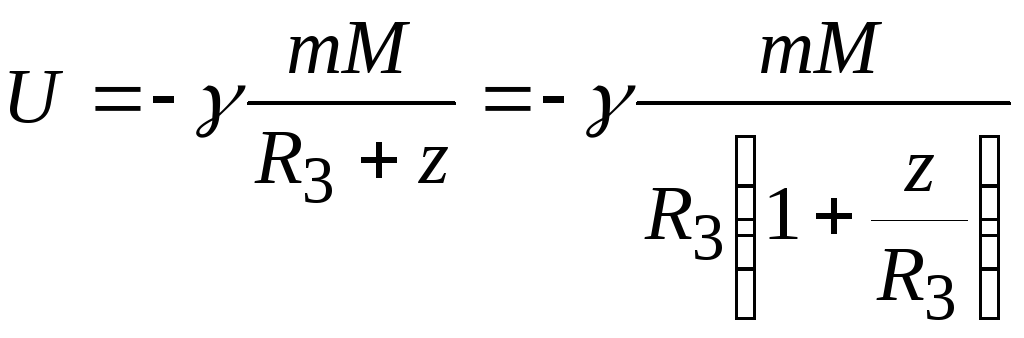 ,
,
где z— высота тела с массойm над поверхностью Земли. При малых
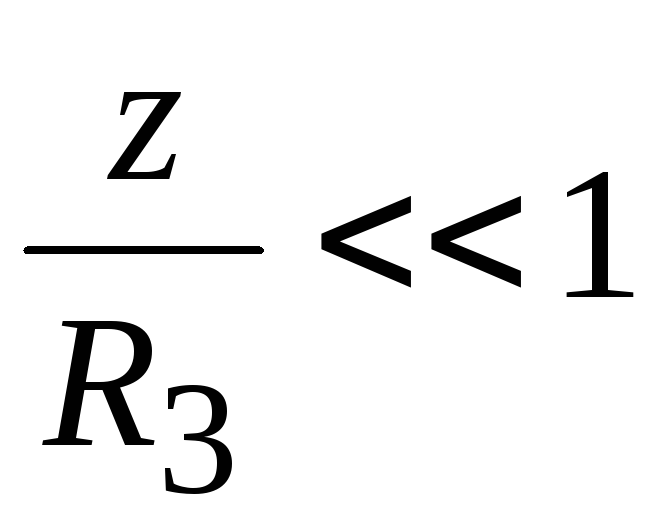

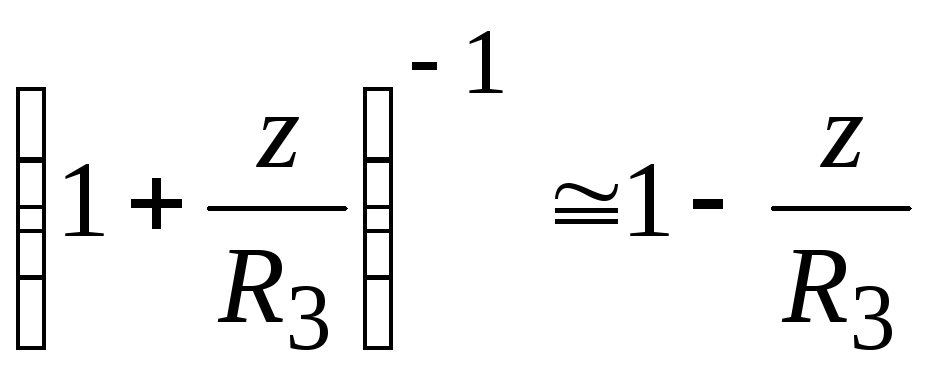 ,
откуда находимU =U0 +mgz =U(R3)
+mgz
,
откуда находимU =U0 +mgz =U(R3)
+mgz1.4. Силы инерции
Основным положением механики Ньютона является утверждение о том, что действие на тело со стороны других тел вызывает их ускорение. В системах координат, движущихся с ускорением относительно выбранной нами инерциальной системы, так называемых неинерциальных системах, формально справедливо и обратное — возникают силы, связанные не с реальным действием других тел, а с наличием указанных ускорений. Такие силы называют силами инерции. Рассмотрим несколько примеров.
1. Прямолинейное движение системы координат с ускорением a0 относительно инерциальной системы. В этом случае на тело с массойm в неинерциальной системе координат действует сила инерции, равная
fи = —ma0. (1.49)
2.
Центробежная сила инерции. Рассмотрим
движение тела во вращающейся системе
координат. Сначала рассмотрим вращение
тела в неподвижной системе. В ней тело
будет испытывать центростремительное
ускорение, которое, и будет заставлять
его вращаться. По третьему закону Ньютона
центростремительной силе соответствует
центробежная сила, приложенная к нити,
удерживающей вращающееся тело. Во
вращающейся системе координат тело
покоится, но центростремительное
ускорение по-прежнему отлично от нуля.
Это ускорение может быть связано теперь
с существованием центробежной силы 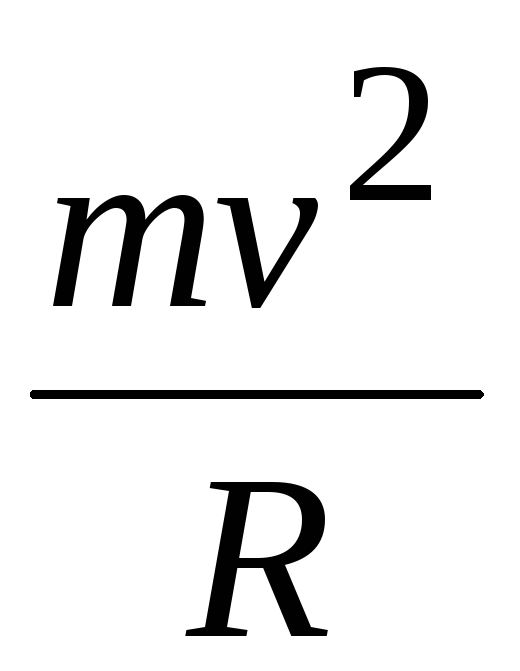
3. Свободно падающий лифт. Пусть ускорение свободно падающего лифта — неинерциальной системы отсчета — g. Сила инерции, действующая на материальную точку с массойm, в системе отсчета, связанной с лифтом, равнаmg. На тело в падающем лифте действуют, таким образом, две силы: — сила тяжести и сила инерции. Суммарная сила, действующая в свободно падающем лифте на материальную точку, равна нулю, т. е. сила инерции уравновешивает силу тяготения — в лифте возникает состояние невесомости. Аналогия между поведением тел в гравитационном поле и в неинерциальной системе отсчета составляет принцип эквивалентности сил тяготения и инерции: он используется в теории тяготения, основанной на теории относительности. В основе принципа эквивалентности лежит равенство инертной и гравитационной масс, о котором шла речь в начале данной главы.
Движение в поле тяготения Земли.
⇐ ПредыдущаяСтр 2 из 11Следующая ⇒Из закона всемирного тяготения следует, что у поверхности Земли все тела должны падать с одинаковым ускорением. В самом деле, по второму закону Ньютона ускорение, приобретаемое телом с массой
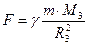 , (1.44)
, (1.44)
M3 — масса Земли и R3 — радиус земного шара. Отсюда
и не зависит от массы падающего тела. Таким образом, все тела у поверхности Земли независимо от их массы падают с одинаковым ускорением
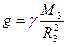 , (1.45)
, (1.45)
которое называется ускорением свободного падения. Подставляя сюда известные значения констант, получим значение 9,8 м/
Космические скорости.
Определим скорость, которую необходимо иметь телу дли того, чтобы оно могло стать спутником Земли, т. е. первую космическую скорость. Величину этой скорости можно определить из условия равенства сил, действующих на тело при его вращении вокруг Земли. Сила притяжения должна быть уравновешена центробежной силой
(1.46)
откуда находим значение первой космической скорости
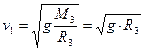
Подставляя численные значения величин, получаем v1= 8 км/с.
Вторая космическая скорость — это скорость, которую нужно сообщить телу для того, чтобы оно покинуло область земного притяжения. Для определения второй космической скорости следует вычислить работу, которую необходимо совершить против сил земного притяжения для удаления тела с поверхности Земли на бесконечность. Эта работа равна разности потенциальных энергий тела в начальном и в конечном положениях:
A = Uк ‑ Uн.
Потенциальная энергия тела в гравитационном поде Земли на ее поверхности согласно (1.41) имеет вид:
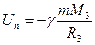
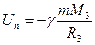 а на бесконечности равна нулю. Таким образом,
а на бесконечности равна нулю. Таким образом,
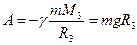 (1.47)
(1.47)
Величина этой потенциальной энергии определяет кинетическую энергию, которую должно иметь тело для того, чтобы быть в состоянии совершить указанную работу 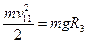 .
.
Отсюда вторая космическая скорость определяется выражением: 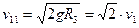 .
.
Ее численное значение приблизительно 11 км/с. Пусть перемещение происходит вдоль оси Z. При этом сила тяжести совершает работу
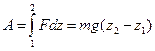 .
.
Согласно определению потенциальной энергии А = U1‑U2. Отсюда следует, что потенциальная энергия тела в поле силы тяжести Земли может быть записана в виде
U(z) = mgz + const, (1.48)
где постоянная связана с выбором начала отсчета энергии. Эту формулу можно получить и непосредственно из закона всемирного тяготения. Запишем его в виде
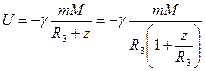 ,
,
где z— высота тела с массой m над поверхностью Земли. При малых
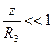 ,
, 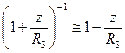 , откуда находим U =U0+ mgz = U(R3) +mgz
, откуда находим U =U0+ mgz = U(R3) +mgz
Силы инерции
Основным положением механики Ньютона является утверждение о том, что действие на тело со стороны других тел вызывает их ускорение. В системах координат, движущихся с ускорением относительно выбранной нами инерциальной системы, так называемых неинерциальных системах, формально справедливо и обратное — возникают силы, связанные не с реальным действием других тел, а с наличием указанных ускорений. Такие силы называют силами инерции. Рассмотрим несколько примеров.
1. Прямолинейное движение системы координат с ускорением a0относительно инерциальной системы. В этом случае на тело с массой m в неинерциальной системе координат действует сила инерции, равная
fи= —ma0. (1.49)
2. Центробежная сила инерции. Рассмотрим движение тела во вращающейся системе координат. Сначала рассмотрим вращение тела в неподвижной системе. В ней тело будет испытывать центростремительное ускорение, которое, и будет заставлять его вращаться. По третьему закону Ньютона центростремительной силе соответствует центробежная сила, приложенная к нити, удерживающей вращающееся тело. Во вращающейся системе координат тело покоится, но центростремительное ускорение по-прежнему отлично от нуля. Это ускорение может быть связано теперь с существованием центробежной силы 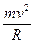 , направленной от центра вращения.
, направленной от центра вращения.
3. Свободно падающий лифт. Пусть ускорение свободно падающего лифта — неинерциальной системы отсчета — g. Сила инерции, действующая на материальную точку с массой m, в системе отсчета, связанной с лифтом, равна mg. На тело в падающем лифте действуют, таким образом, две силы: — сила тяжести и сила инерции. Суммарная сила, действующая в свободно падающем лифте на материальную точку, равна нулю, т. е. сила инерции уравновешивает силу тяготения — в лифте возникает состояние невесомости. Аналогия между поведением тел в гравитационном поле и в неинерциальной системе отсчета составляет принцип эквивалентности сил тяготения и инерции: он используется в теории тяготения, основанной на теории относительности. В основе принципа эквивалентности лежит равенство инертной и гравитационной масс, о котором шла речь в начале данной главы.
1.3.1 Движение в поле тяготения Земли.
Из закона всемирного тяготения следует, что у поверхности Земли все тела должны падать с одинаковым ускорением. В самом деле, по второму закону Ньютона ускорение, приобретаемое телом с массой m у поверхности Землиa=F/m, гдеF — сила, с которой тело притягивается земным шаром. По закону тяготения
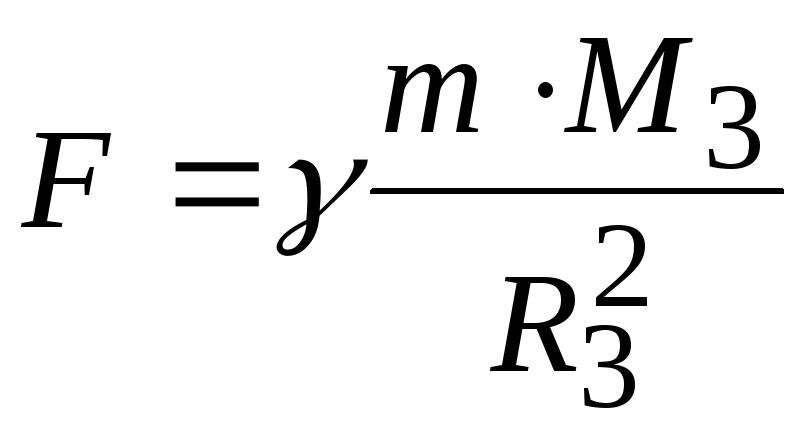 ,
(1.44)
,
(1.44)
M3— масса Земли и R3— радиус земного
шара. Отсюда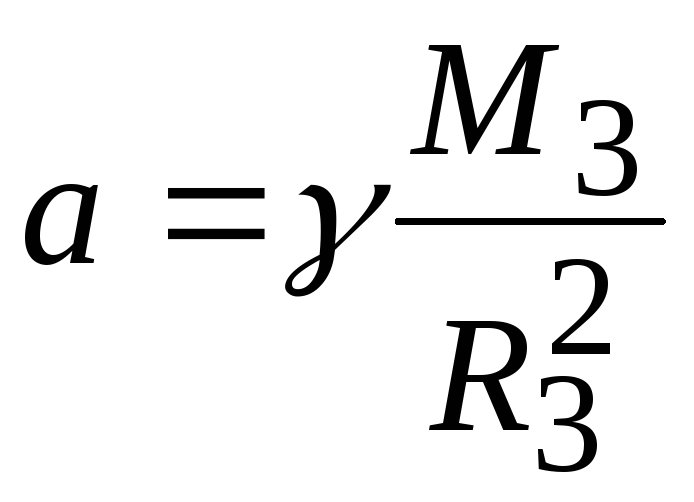
и не зависит от массы падающего тела. Таким образом, все тела у поверхности Земли независимо от их массы падают с одинаковым ускорением
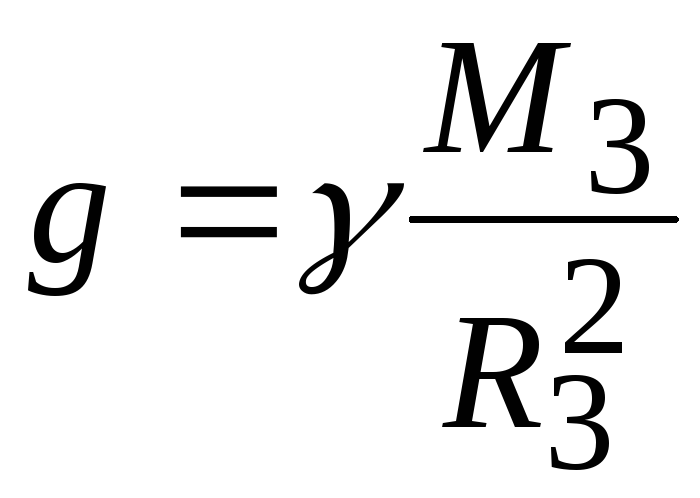 ,
(1.45)
,
(1.45)
которое называется ускорением свободного падения. Подставляя сюда известные значения констант, получим значение 9,8 м/c2. В действительности значенияg слегка различаются при учете сил сопротивления и реальной формы Земли. По второму закону Ньютона это означает, что в поле тяжести Земли все тела испытывают силу тяжести, равнуюmg. При перемещении массы с одной высоты на другую эта сила тяжести совершает работу, которую можно вычислить как изменение потенциальной энергии тела.
1.3.2 Космические скорости.
Определим скорость, которую необходимо иметь телу дли того, чтобы оно могло стать спутником Земли, т. е. первую космическую скорость. Величину этой скорости можно определить из условия равенства сил, действующих на тело при его вращении вокруг Земли. Сила притяжения должна быть уравновешена центробежной силой mv2/R. Таким образом,
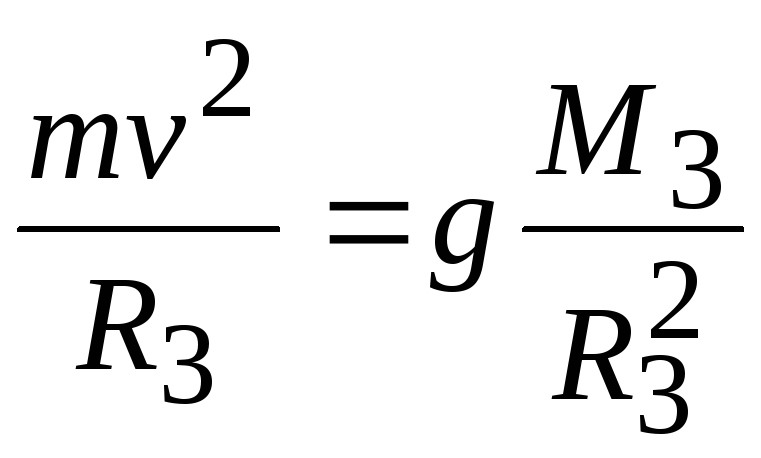 (1.46)
(1.46)
откуда находим значение первой космической скорости
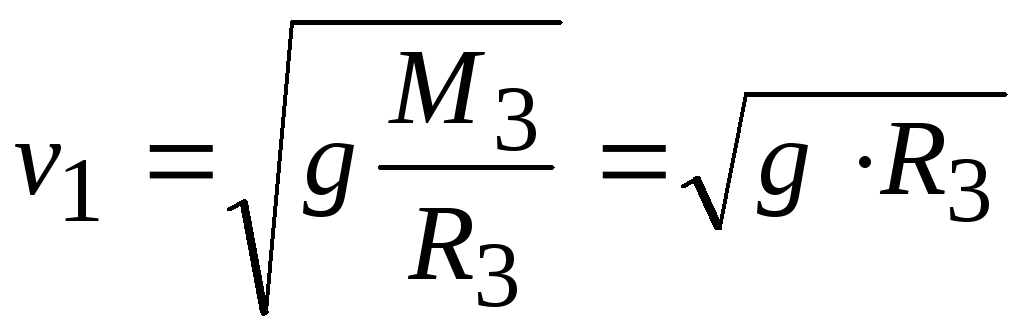 Подставляя
численные значения величин, получаемv1 = 8 км/с.
Подставляя
численные значения величин, получаемv1 = 8 км/с.
Вторая космическая скорость — это скорость, которую нужно сообщить телу для того, чтобы оно покинуло область земного притяжения. Для определения второй космической скорости следует вычислить работу, которую необходимо совершить против сил земного притяжения для удаления тела с поверхности Земли на бесконечность. Эта работа равна разности потенциальных энергий тела в начальном и в конечном положениях:
A = Uк ‑ Uн.
Потенциальная энергия тела в гравитационном поде Земли на ее поверхности согласно (1.41) имеет вид:
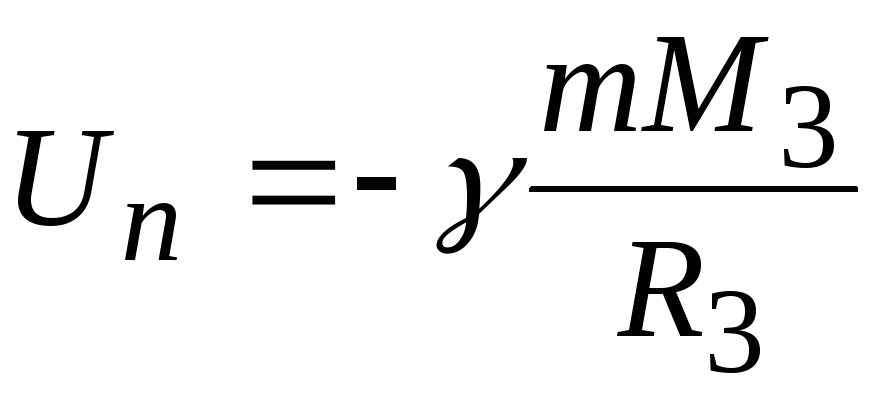
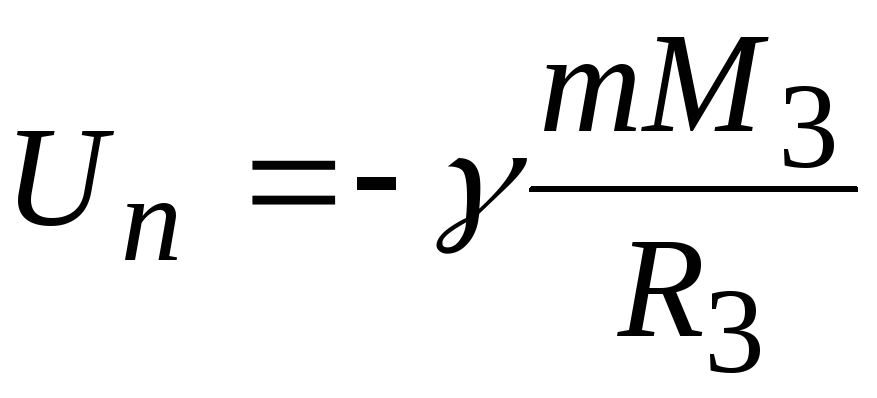 а на бесконечности
равна нулю. Таким образом,
а на бесконечности
равна нулю. Таким образом,
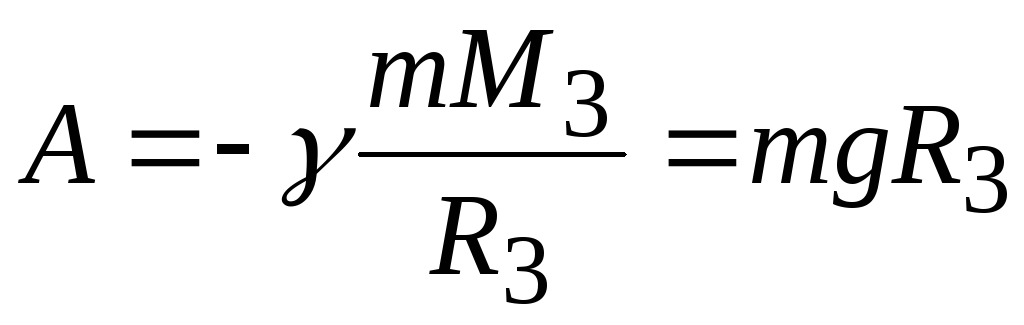 (1.47)
(1.47)
Величина
этой потенциальной энергии определяет
кинетическую энергию, которую должно
иметь тело для того, чтобы быть в состоянии
совершить указанную работу 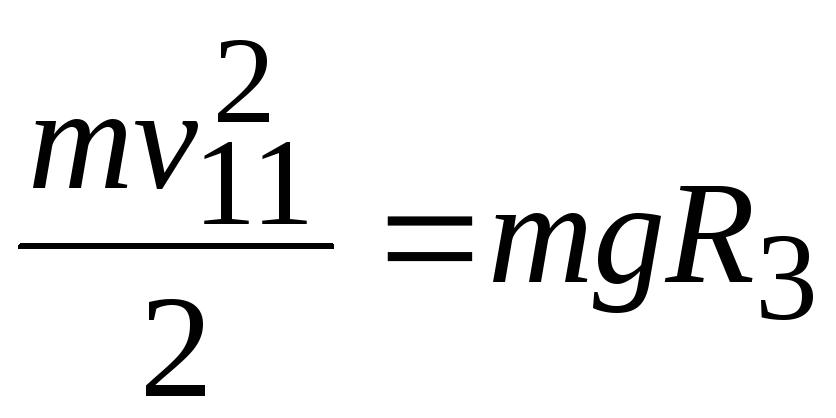
Отсюда вторая космическая скорость определяется выражением:
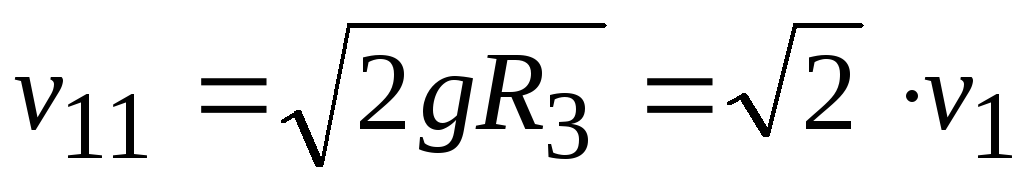 .
.
Ее численное значение приблизительно 11 км/с. Пусть перемещение происходит вдоль оси Z. При этом сила тяжести совершает работу
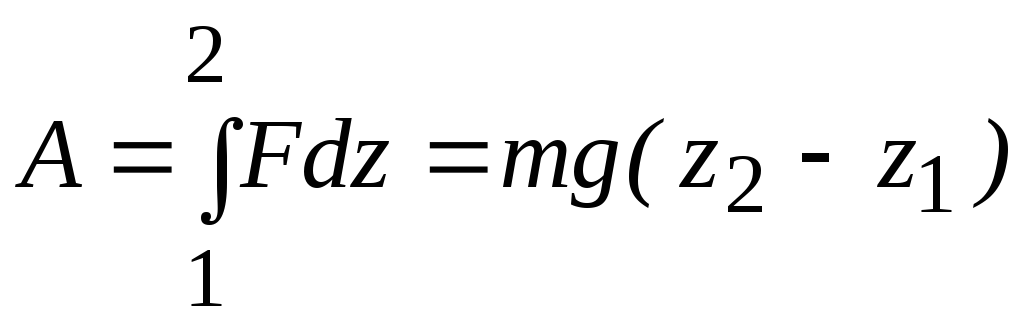 .
.
Согласно определению потенциальной энергии А = U1‑U2. Отсюда следует, что потенциальная энергия тела в поле силы тяжести Земли может быть записана в виде
U(z) = mgz + const, (1.48)
где постоянная связана с выбором начала отсчета энергии. Эту формулу можно получить и непосредственно из закона всемирного тяготения. Запишем его в виде
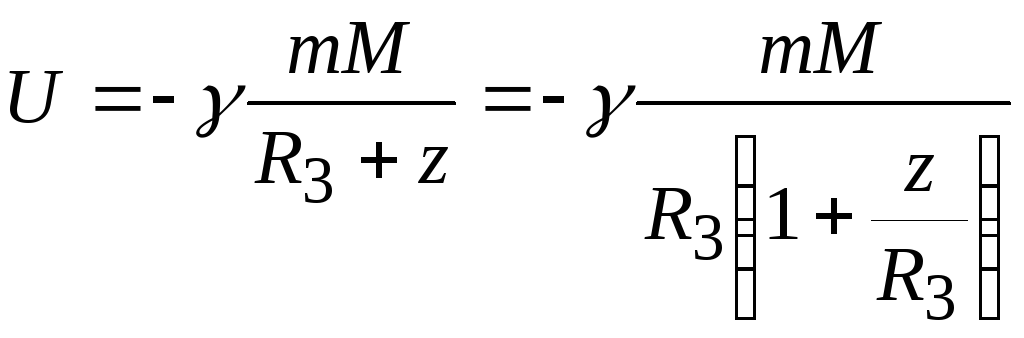 ,
,
где z— высота тела с массойm над поверхностью Земли. При малых
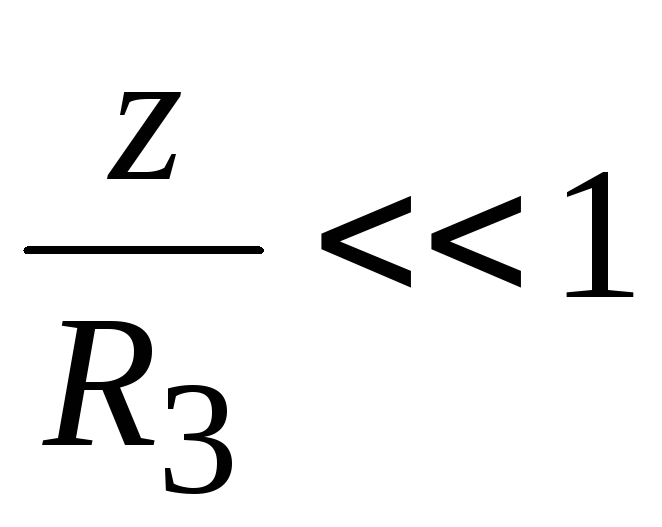 ,
, 
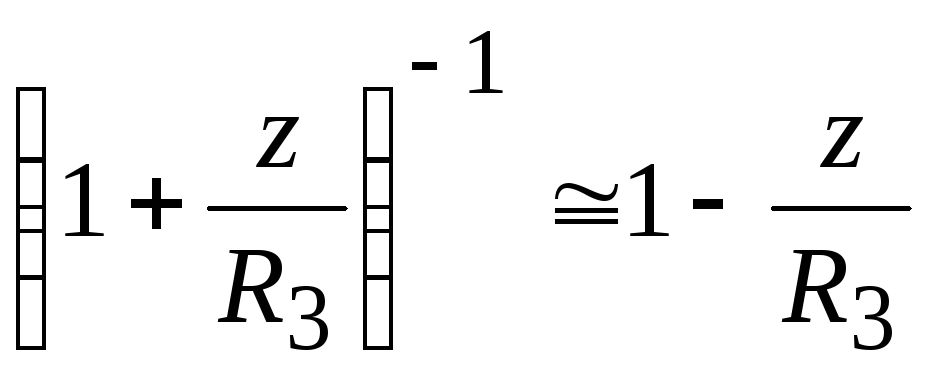 ,
откуда находимU =U0 +mgz =U(R3)
+mgz
,
откуда находимU =U0 +mgz =U(R3)
+mgz
1.4. Силы инерции
Основным положением механики Ньютона является утверждение о том, что действие на тело со стороны других тел вызывает их ускорение. В системах координат, движущихся с ускорением относительно выбранной нами инерциальной системы, так называемых неинерциальных системах, формально справедливо и обратное — возникают силы, связанные не с реальным действием других тел, а с наличием указанных ускорений. Такие силы называют силами инерции. Рассмотрим несколько примеров.
1. Прямолинейное движение системы координат с ускорением a0 относительно инерциальной системы. В этом случае на тело с массойm в неинерциальной системе координат действует сила инерции, равная
fи = —ma0. (1.49)
2.
Центробежная сила инерции. Рассмотрим
движение тела во вращающейся системе
координат. Сначала рассмотрим вращение
тела в неподвижной системе. В ней тело
будет испытывать центростремительное
ускорение, которое, и будет заставлять
его вращаться. По третьему закону Ньютона
центростремительной силе соответствует
центробежная сила, приложенная к нити,
удерживающей вращающееся тело. Во
вращающейся системе координат тело
покоится, но центростремительное
ускорение по-прежнему отлично от нуля.
Это ускорение может быть связано теперь
с существованием центробежной силы 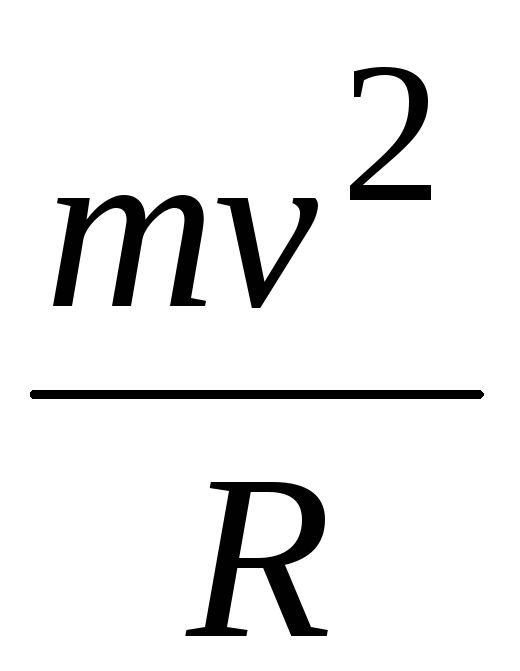 ,
направленной от центра вращения.
,
направленной от центра вращения.
3. Свободно падающий лифт. Пусть ускорение свободно падающего лифта — неинерциальной системы отсчета — g. Сила инерции, действующая на материальную точку с массойm, в системе отсчета, связанной с лифтом, равнаmg. На тело в падающем лифте действуют, таким образом, две силы: — сила тяжести и сила инерции. Суммарная сила, действующая в свободно падающем лифте на материальную точку, равна нулю, т. е. сила инерции уравновешивает силу тяготения — в лифте возникает состояние невесомости. Аналогия между поведением тел в гравитационном поле и в неинерциальной системе отсчета составляет принцип эквивалентности сил тяготения и инерции: он используется в теории тяготения, основанной на теории относительности. В основе принципа эквивалентности лежит равенство инертной и гравитационной масс, о котором шла речь в начале данной главы.
Закон всемирного тяготения. Гравитационное поле. Гравитационная энергия. Гравитационный радиус. “Черные дыры”. Движение в поле тяготения Земли. Космические скорости.
Считается, что законы Кеплера послужили экспериментальной основой ля вывода закона тяготения.
Законы Кеплера:
1) все планеты движутся по эллиптическим траекториям, в одном из фокусов которого Солнце.
2) за любые равные промежутки времени радиус-вектор планеты описывает одинаковую площадь,
то есть
3) отношение квадратов периода вращения планет к кубу длин больших полуосей одинаков для всех планет: 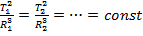 .
.
Покажем, что законы Кеплера могут быть использованы для вывода закона всемирного тяготения.
Предположим, что все орбиты круговые и так как вектор направлен то касательной к траектории, то 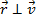 .
. 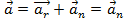 , где
, где 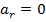 , так как движение равномерное.
, так как движение равномерное.
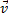 |
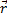 |
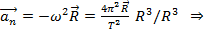
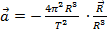 , где
, где 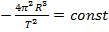
согласно третьему закону Кеплера.
Таким образом 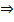
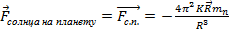 . По третьему закону Ньютона:
. По третьему закону Ньютона: 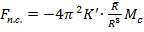 . Следовательно
. Следовательно 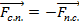 . Таким образом,
. Таким образом, 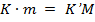 =>
=>
Ньютон предположил, что 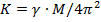 , где — гравитационная постоянная.
, где — гравитационная постоянная.
Таким образом, 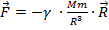 – закон тяготения между планетами солнца. Ньютон также предположил, что все тела во вселенной испытывают притяжения друг к другу. Для точечных тел закон всемирного тяготенияимеет вид:
– закон тяготения между планетами солнца. Ньютон также предположил, что все тела во вселенной испытывают притяжения друг к другу. Для точечных тел закон всемирного тяготенияимеет вид: 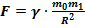
Эта сила прямо пропорциональна произведению их масс точечных тел и обратно пропорциональна квадрату расстояний между ними.
Особенности: 1) Силы тяготения всегда силы притяжения;
2) не зависят от физической (химической) природы тела;
3)в силу малости гравитационной постоянной 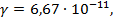 гравитационные силы имеют значимое значение для больших масс.
гравитационные силы имеют значимое значение для больших масс. 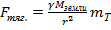 =g
=g 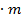 . где
. где 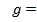
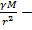 ускорение силы тяжести. Таким образом, для небольших высот
ускорение силы тяжести. Таким образом, для небольших высот 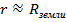 , тогда , ускорение силы тяжести Земли одинаково для всех тел. (Закон справедлив и для тел сферической формы).
, тогда , ускорение силы тяжести Земли одинаково для всех тел. (Закон справедлив и для тел сферической формы).
4) Сравним закон тяготения со вторым законом Ньютона: , 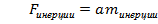
Одинакова ли масса гравитационная и инерционная? Было показано с точностью 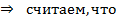
Принцип эквивалентности:
Если есть система, движущаяся с ускорением 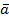 и находящаяся в гравитационном поле, то исследователь, находящийся в этой системе, не может определить, какая часть сил обусловлена гравитационными силами , а какая – ускоренным движением системы.
и находящаяся в гравитационном поле, то исследователь, находящийся в этой системе, не может определить, какая часть сил обусловлена гравитационными силами , а какая – ускоренным движением системы.
Ньютон не стал давать объяснения физической природы гравитационных сил, назвав их силами дальнодествия. Соврененая теория- это теория полевого взаимодествия материальных тел.
Полевая теория
Любое тело создает вокруг себя поле – гравитационное поле.
Свойства гравитационного поля:
1) Оно непрерывно распределено в пространстве, проникает в другие поля и вещества.
2) Это поле действует с некоторой силой на все тела, помещенные в это поле.
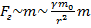
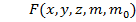 – сила тяготения зависит не только от выбора точки поля (x,y,z) и массы тела, создающего поле (
– сила тяготения зависит не только от выбора точки поля (x,y,z) и массы тела, создающего поле ( 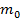 ,) , но и от массы «пробного» тела (m), что крайне не удобно для характеристики поля. Поэтому введем другую величину.
,) , но и от массы «пробного» тела (m), что крайне не удобно для характеристики поля. Поэтому введем другую величину.
Напряженность гравитационного поля 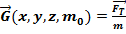 — -численно равна силе, дейсвующей на единичную массу, помещённую в данную точку поля. Тогда закон примет вид:
— -численно равна силе, дейсвующей на единичную массу, помещённую в данную точку поля. Тогда закон примет вид:
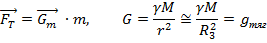
1) Поле 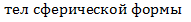 имеет точно такую же структуру, что и точечное тело такой же массs M, помещенной в центре сферы. (для
имеет точно такую же структуру, что и точечное тело такой же массs M, помещенной в центре сферы. (для 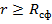 )
)
2) Это поле цетральное (поле центробежных сил.)
То есть поле потенциально, то:
1) работа сил поля A зависит только от начальной и конечной точки, а не от траектории.
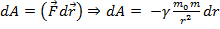 Знак минус т.к. угол между силой и радиус-вектором
Знак минус т.к. угол между силой и радиус-вектором 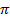 Тогда
Тогда 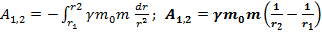
2) Так как работа равна изменению энергии,то имеет смысл разность потенциальных энергий
тела в двух точках поля:
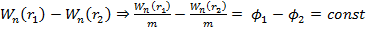 Найдём эту энергию через работу
Найдём эту энергию через работу
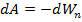
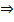
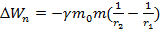 . Тогда
. Тогда 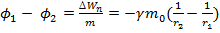 -разность потенциалов двух точек гравитационного поля: численно равна работе сил поля по перемещению единичной массы из первой точки во вторую.
-разность потенциалов двух точек гравитационного поля: численно равна работе сил поля по перемещению единичной массы из первой точки во вторую.
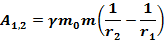
1. Если 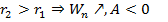 Тело удаляется, работа совершается против сил поля (притяжения). Работа отрицательна, потенциальная энергия растет.
Тело удаляется, работа совершается против сил поля (притяжения). Работа отрицательна, потенциальная энергия растет.
2. Если 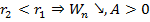 . Тела сближаются силами поля, работа положительна, потенциальная энергия уменьшается.
. Тела сближаются силами поля, работа положительна, потенциальная энергия уменьшается.
3. Если принять: Здесь 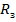 -радиус Земли.
-радиус Земли.
Так как 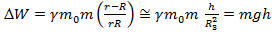 .
.
4. = 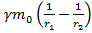
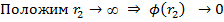 Тогда потенциал произвольной точки поля :
Тогда потенциал произвольной точки поля :
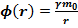 –относительно бесконечности: численно равен работе, которую нужно совершить, чтобы единичную массу перенести из данной точки в бесконечность.
–относительно бесконечности: численно равен работе, которую нужно совершить, чтобы единичную массу перенести из данной точки в бесконечность.
Определим энергии гравитационного поля 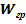 .
.
Пусть имеем шар массы 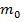 и радиусом-R. Энергию гравитационного поля шара можно определить как работу по переносу всей массы тела в бесконечность. Так как потенциал поверхности будет меняться с изменением размеров шара (и его массы), то следует переносить массу б.малыми порциями dm. Тогда -текущее значение потенциала поверхности шара. Выразим m(r):
и радиусом-R. Энергию гравитационного поля шара можно определить как работу по переносу всей массы тела в бесконечность. Так как потенциал поверхности будет меняться с изменением размеров шара (и его массы), то следует переносить массу б.малыми порциями dm. Тогда -текущее значение потенциала поверхности шара. Выразим m(r): 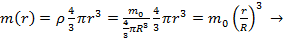
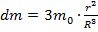 dr и можно записать в явном виде: .
dr и можно записать в явном виде: .
Подставляя в выражение для работы: => Таким образом 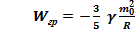 ,
, 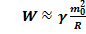
Примеры
1. Считая, что полная энергия электрона равна его гравитационной, получим: 
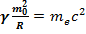
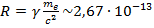 см – совпадает с другими методами вычислений. 2..Применим последнюю формулу к произвольному гравитационному объекту:
см – совпадает с другими методами вычислений. 2..Применим последнюю формулу к произвольному гравитационному объекту:
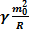 = Это гравитационный радиус объекта.
= Это гравитационный радиус объекта.
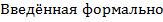 величина оказалась чрезвычайно информативной и важной.
величина оказалась чрезвычайно информативной и важной.
1) Можно оценить гравитационную энергию объекта. 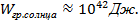 (Посчитав плотность энергии, излучаемой Солнцем , учёные пришли к выводу о наличии еще каких- то источников энергии , в частности, энергию термоядерной реакции.
(Посчитав плотность энергии, излучаемой Солнцем , учёные пришли к выводу о наличии еще каких- то источников энергии , в частности, энергию термоядерной реакции.
2) Если сравнить истинный радиус планеты и её гравитационный радиус, то при 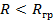 , с планеты нельзя излучать никакие виды энергии ( в том числе и свет). То есть, мы эту планету не увидим. Следовательно, возникает ЧЁРНАЯ ДЫРА.
, с планеты нельзя излучать никакие виды энергии ( в том числе и свет). То есть, мы эту планету не увидим. Следовательно, возникает ЧЁРНАЯ ДЫРА.
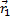 |
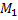 |
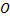 |
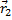 |
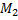 |
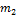 . Одно движется в
. Одно движется вгравитационном поле другого от точки отсчета проведены радиус-векторы.
, где 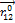 — единичный вектор.
— единичный вектор.
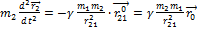
Начальные условия: 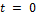 , , еще наложить условия
, , еще наложить условия
Вычтем: 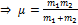 – приведённая масса, тогда
– приведённая масса, тогда
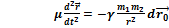 — уравнение движения одного тела, относительно другого.
— уравнение движения одного тела, относительно другого.
Решение этого уравнения достаточно сложное. Для качественных оценок можно использовать
законы сохранения:
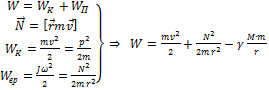 Здесь два последних слагаемых есть функции координат (r) т.е потенциальная энергия- ,(Так как N = const по закону сохранения момента импульса
Здесь два последних слагаемых есть функции координат (r) т.е потенциальная энергия- ,(Так как N = const по закону сохранения момента импульса
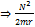 функция от r)
функция от r) 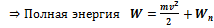
Замечания Качественный анализ.
1) 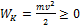 кинетическая энергия тела может быть только положительной
кинетическая энергия тела может быть только положительной
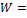 :
:  но полное не может быть меньше
но полное не может быть меньше
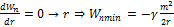
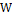
1. 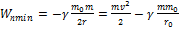 — для частицы с массой m.
— для частицы с массой m.
Единственное решение 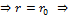 движение строго по окружности с
движение строго по окружности с 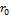 . r
. r
2. , то 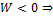 существует два решения в некотором интервале
существует два решения в некотором интервале 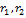
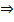 движение по эллипсу.
движение по эллипсу.
3. 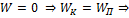 движение по параболе (разомкнута относительно
движение по параболе (разомкнута относительно 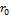 ).
).
4. 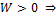 движение по гиперболе (разомкнута вообще).
движение по гиперболе (разомкнута вообще).
1.3.1 Движение в поле тяготения Земли.
Из закона всемирного тяготения следует, что у поверхности Земли все тела должны падать с одинаковым ускорением. В самом деле, по второму закону Ньютона ускорение, приобретаемое телом с массой m у поверхности Землиa=F/m, гдеF — сила, с которой тело притягивается земным шаром. По закону тяготения
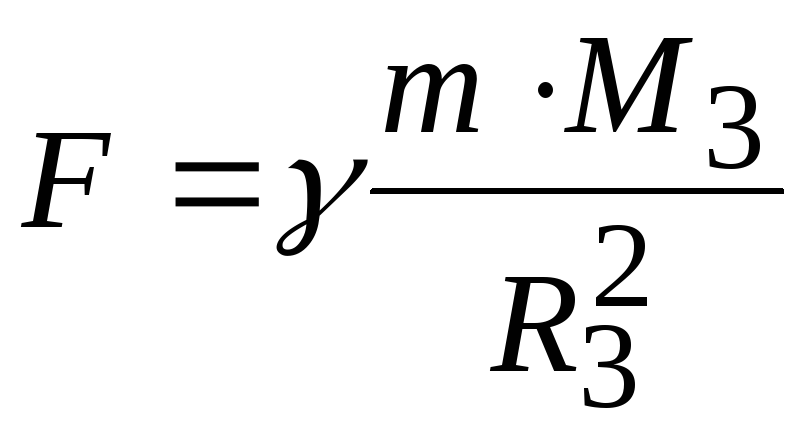 ,
(1.44)
,
(1.44)
M3— масса
Земли и R3— радиус земного шара.
Отсюда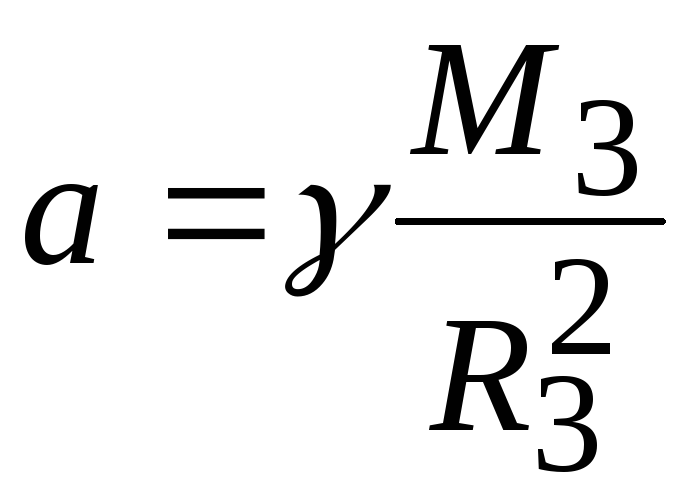
и не зависит от массы падающего тела. Таким образом, все тела у поверхности Земли независимо от их массы падают с одинаковым ускорением
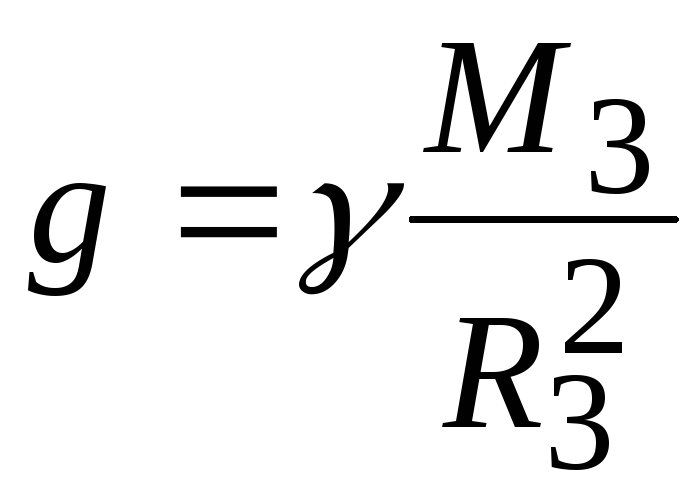 ,
(1.45)
,
(1.45)
которое называется ускорением свободного падения. Подставляя сюда известные значения констант, получим значение 9,8 м/c2. В действительности значенияg слегка различаются при учете сил сопротивления и реальной формы Земли. По второму закону Ньютона это означает, что в поле тяжести Земли все тела испытывают силу тяжести, равнуюmg. При перемещении массы с одной высоты на другую эта сила тяжести совершает работу, которую можно вычислить как изменение потенциальной энергии тела.
1.3.2 Космические скорости.
Определим скорость, которую необходимо иметь телу дли того, чтобы оно могло стать спутником Земли, т. е. первую космическую скорость. Величину этой скорости можно определить из условия равенства сил, действующих на тело при его вращении вокруг Земли. Сила притяжения должна быть уравновешена центробежной силой mv2/R. Таким образом,
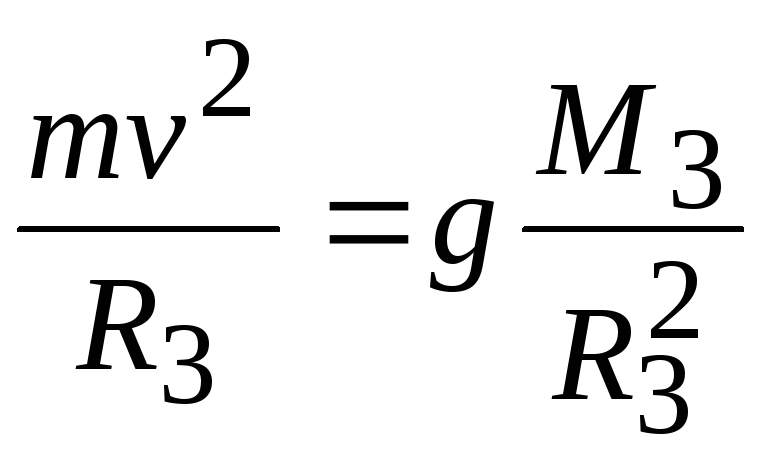 (1.46)
(1.46)
откуда находим значение первой космической скорости
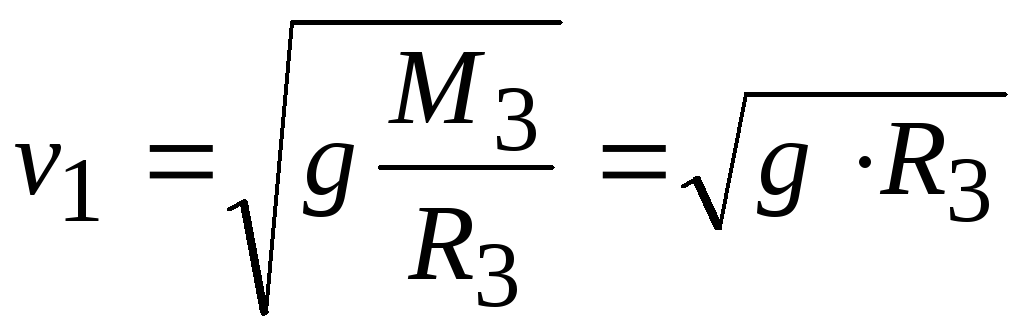 Подставляя
численные значения величин, получаемv1 = 8 км/с.
Подставляя
численные значения величин, получаемv1 = 8 км/с.
Вторая космическая скорость — это скорость, которую нужно сообщить телу для того, чтобы оно покинуло область земного притяжения. Для определения второй космической скорости следует вычислить работу, которую необходимо совершить против сил земного притяжения для удаления тела с поверхности Земли на бесконечность. Эта работа равна разности потенциальных энергий тела в начальном и в конечном положениях:
A =Uк ‑Uн.
Потенциальная энергия тела в гравитационном поде Земли на ее поверхности согласно (1.41) имеет вид:
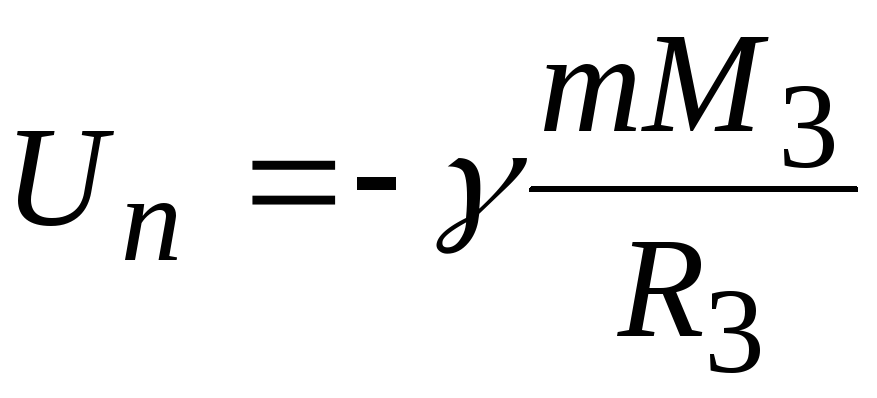
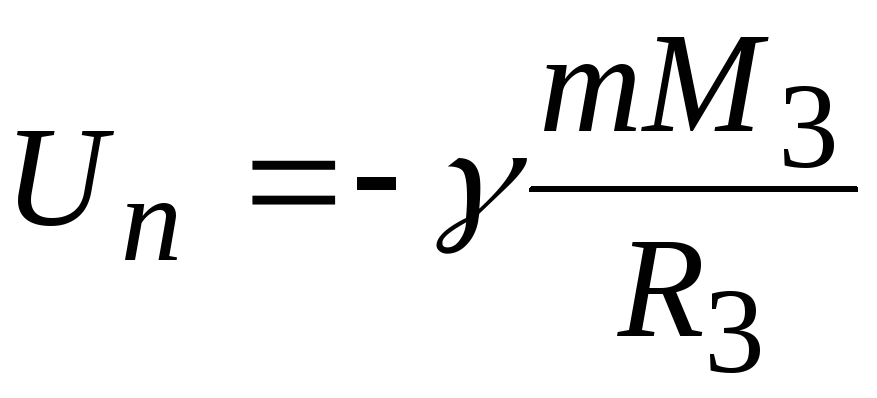 а на бесконечности
равна нулю. Таким образом,
а на бесконечности
равна нулю. Таким образом,
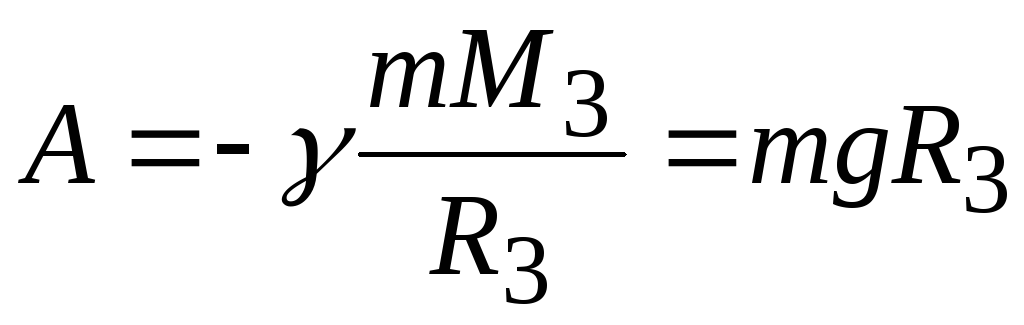 (1.47)
(1.47)
Величина этой потенциальной энергии определяет кинетическую энергию, которую должно иметь тело для того, чтобы быть в состоянии совершить указанную работу
Отсюда вторая космическая скорость определяется выражением:
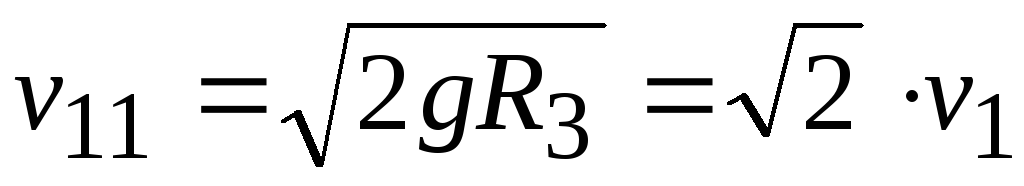 .
.
Ее численное значение приблизительно 11 км/с. Пусть перемещение происходит вдоль оси Z. При этом сила тяжести совершает работу
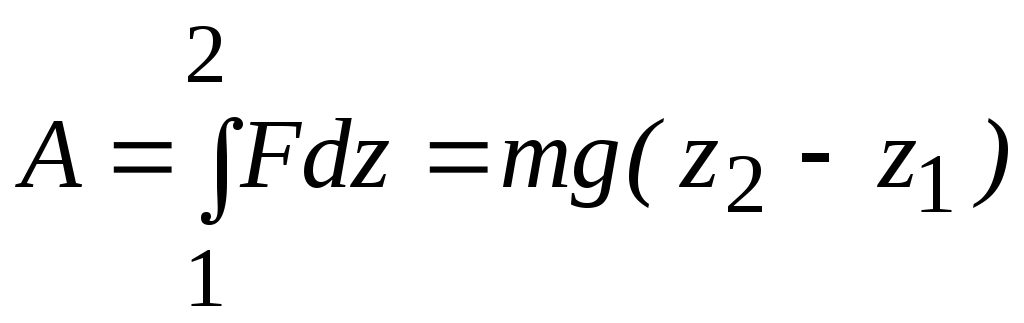 .
.
Согласно определению потенциальной энергии А = U1‑U2. Отсюда следует, что потенциальная энергия тела в поле силы тяжести Земли может быть записана в виде
U(z) =mgz +const, (1.48)
где постоянная связана с выбором начала отсчета энергии. Эту формулу можно получить и непосредственно из закона всемирного тяготения. Запишем его в виде
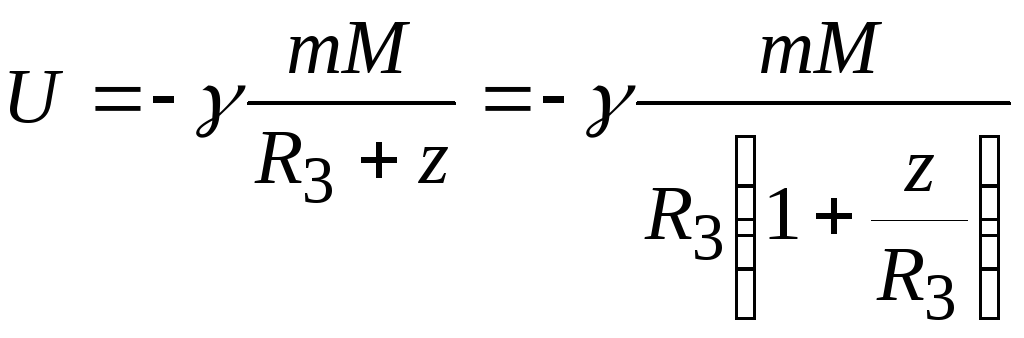 ,
,
где z— высота тела с массойm над поверхностью Земли. При малых
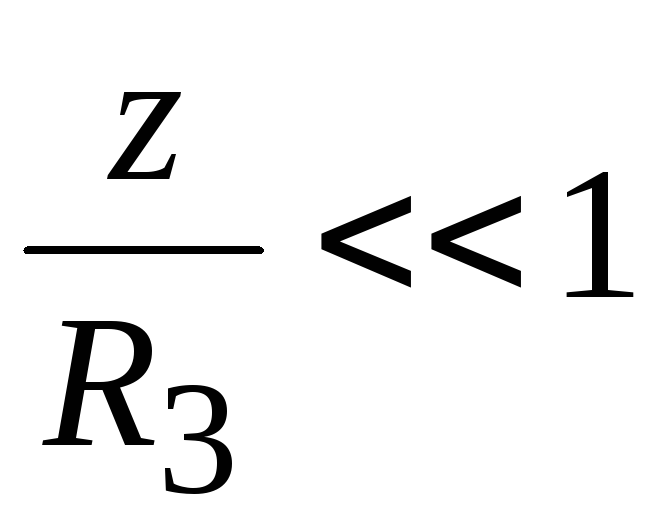 ,
, 
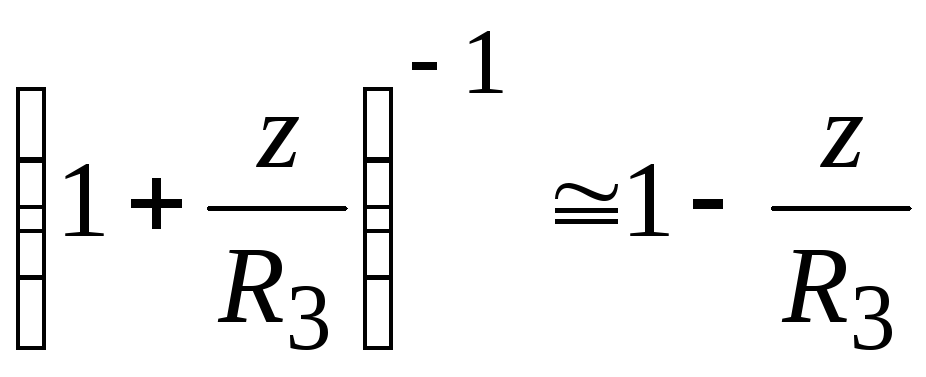 ,
откуда находимU =U0 +mgz =U(R3)
+mgz
,
откуда находимU =U0 +mgz =U(R3)
+mgz
1.4. Силы инерции
Основным положением механики Ньютона является утверждение о том, что действие на тело со стороны других тел вызывает их ускорение. В системах координат, движущихся с ускорением относительно выбранной нами инерциальной системы, так называемых неинерциальных системах, формально справедливо и обратное — возникают силы, связанные не с реальным действием других тел, а с наличием указанных ускорений. Такие силы называют силами инерции. Рассмотрим несколько примеров.
1. Прямолинейное движение системы координат с ускорением a0 относительно инерциальной системы. В этом случае на тело с массойm в неинерциальной системе координат действует сила инерции, равная
fи = —ma0. (1.49)
2. Центробежная
сила инерции. Рассмотрим движение тела
во вращающейся системе координат.
Сначала рассмотрим вращение тела в
неподвижной системе. В ней тело будет
испытывать центростремительное
ускорение, которое, и будет заставлять
его вращаться. По третьему закону Ньютона
центростремительной силе соответствует
центробежная сила, приложенная к нити,
удерживающей вращающееся тело. Во
вращающейся системе координат тело
покоится, но центростремительное
ускорение по-прежнему отлично от нуля.
Это ускорение может быть связано теперь
с существованием центробежной силы 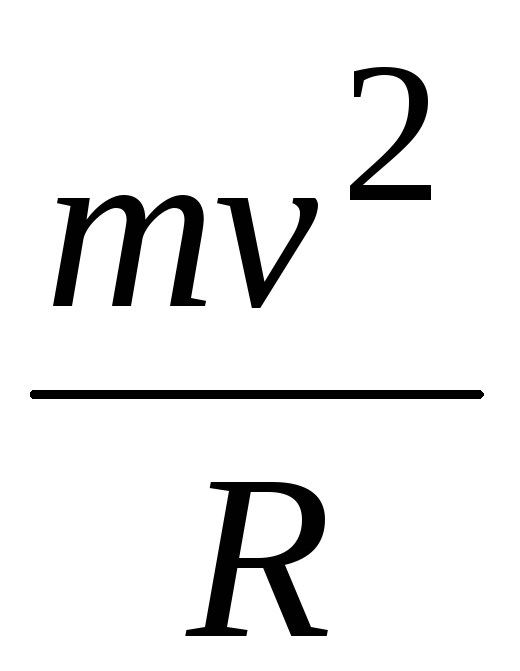 ,
направленной от центра вращения.
,
направленной от центра вращения.
3. Свободно падающий лифт. Пусть ускорение свободно падающего лифта — неинерциальной системы отсчета — g. Сила инерции, действующая на материальную точку с массойm, в системе отсчета, связанной с лифтом, равнаmg. На тело в падающем лифте действуют, таким образом, две силы: — сила тяжести и сила инерции. Суммарная сила, действующая в свободно падающем лифте на материальную точку, равна нулю, т. е. сила инерции уравновешивает силу тяготения — в лифте возникает состояние невесомости. Аналогия между поведением тел в гравитационном поле и в неинерциальной системе отсчета составляет принцип эквивалентности сил тяготения и инерции: он используется в теории тяготения, основанной на теории относительности. В основе принципа эквивалентности лежит равенство инертной и гравитационной масс, о котором шла речь в начале данной главы.
1.3.1 Движение в поле тяготения Земли.
Из закона всемирного тяготения следует, что у поверхности Земли все тела должны падать с одинаковым ускорением. В самом деле, по второму закону Ньютона ускорение, приобретаемое телом с массой m у поверхности Землиa=F/m, гдеF — сила, с которой тело притягивается земным шаром. По закону тяготения
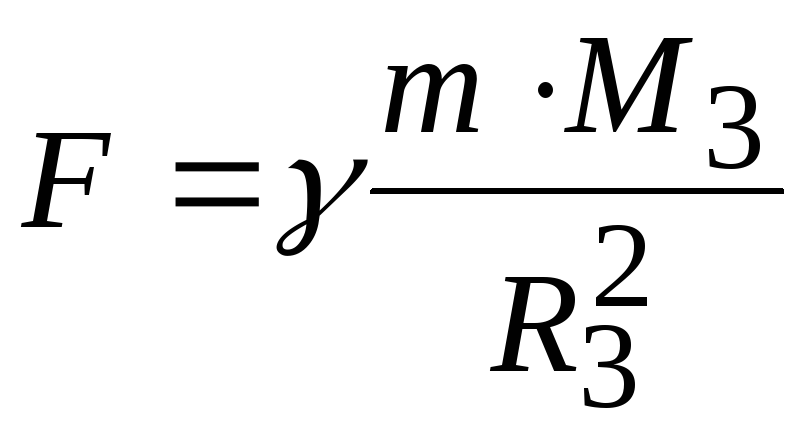 ,
(1.44)
,
(1.44)
M3— масса
Земли и R3— радиус земного шара.
Отсюда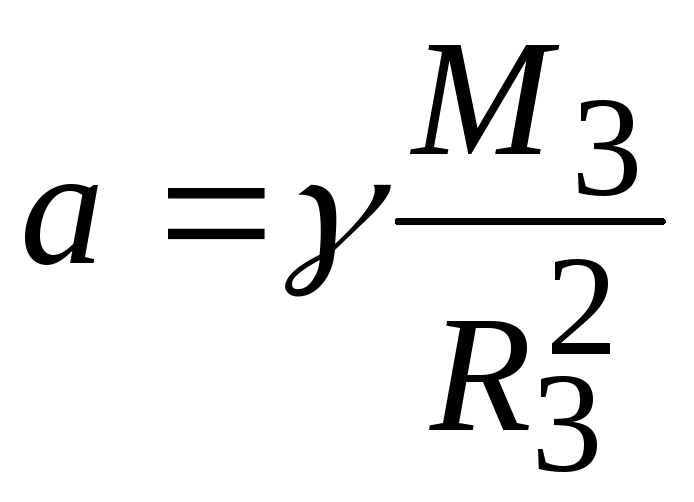
и не зависит от массы падающего тела. Таким образом, все тела у поверхности Земли независимо от их массы падают с одинаковым ускорением
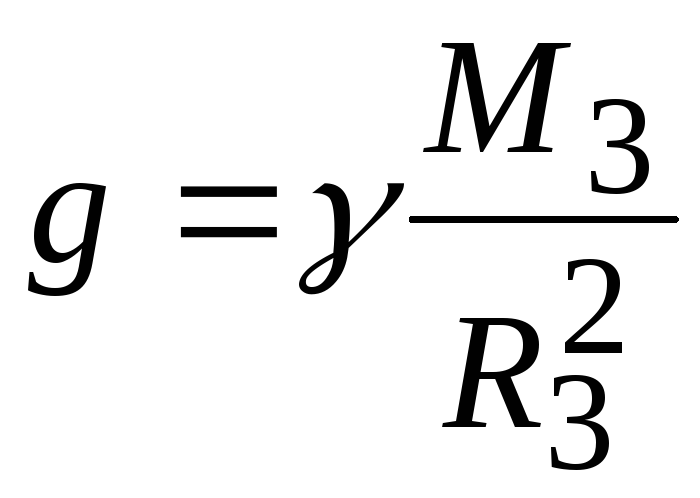 ,
(1.45)
,
(1.45)
которое называется ускорением свободного падения. Подставляя сюда известные значения констант, получим значение 9,8 м/c2. В действительности значенияg слегка различаются при учете сил сопротивления и реальной формы Земли. По второму закону Ньютона это означает, что в поле тяжести Земли все тела испытывают силу тяжести, равнуюmg. При перемещении массы с одной высоты на другую эта сила тяжести совершает работу, которую можно вычислить как изменение потенциальной энергии тела.
1.3.2 Космические скорости.
Определим скорость, которую необходимо иметь телу дли того, чтобы оно могло стать спутником Земли, т. е. первую космическую скорость. Величину этой скорости можно определить из условия равенства сил, действующих на тело при его вращении вокруг Земли. Сила притяжения должна быть уравновешена центробежной силой mv2/R. Таким образом,
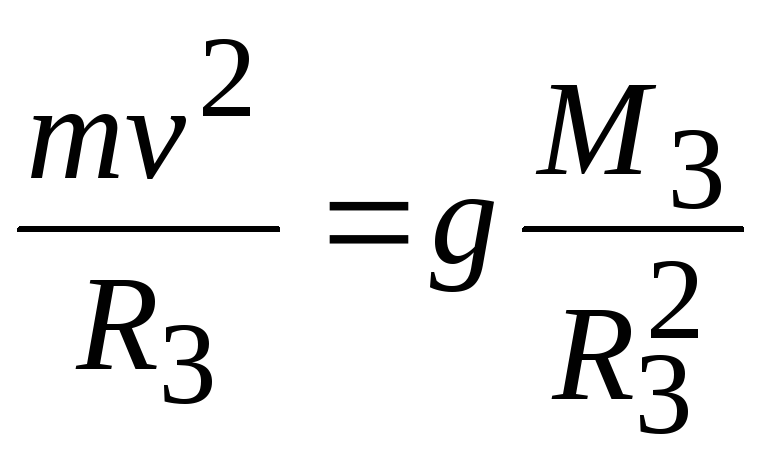 (1.46)
(1.46)
откуда находим значение первой космической скорости
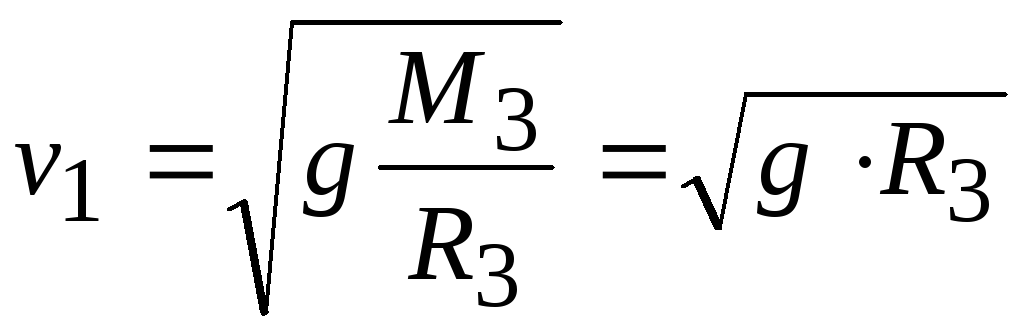 Подставляя
численные значения величин, получаемv1 = 8 км/с.
Подставляя
численные значения величин, получаемv1 = 8 км/с.
Вторая космическая скорость — это скорость, которую нужно сообщить телу для того, чтобы оно покинуло область земного притяжения. Для определения второй космической скорости следует вычислить работу, которую необходимо совершить против сил земного притяжения для удаления тела с поверхности Земли на бесконечность. Эта работа равна разности потенциальных энергий тела в начальном и в конечном положениях:
A = Uк ‑ Uн.
Потенциальная энергия тела в гравитационном поде Земли на ее поверхности согласно (1.41) имеет вид:
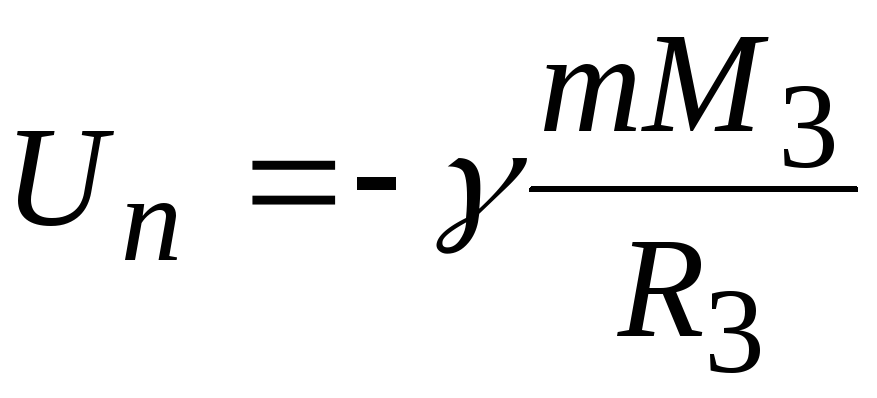
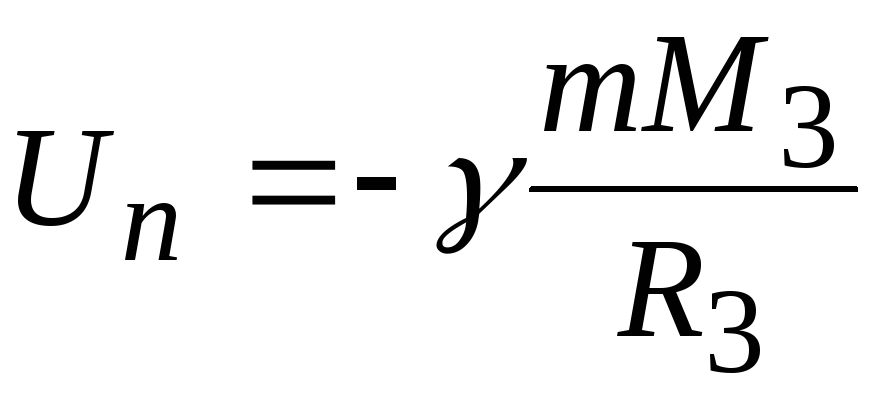 а на бесконечности
равна нулю. Таким образом,
а на бесконечности
равна нулю. Таким образом,
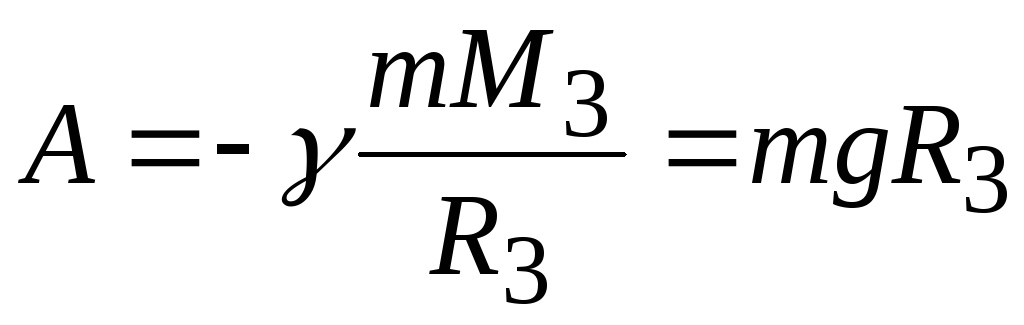 (1.47)
(1.47)
Величина этой
потенциальной энергии определяет
кинетическую энергию, которую должно
иметь тело для того, чтобы быть в состоянии
совершить указанную работу 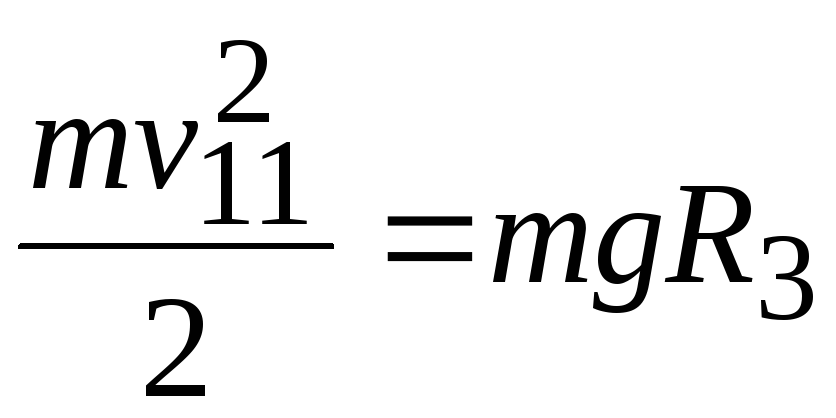
Отсюда вторая космическая скорость определяется выражением:
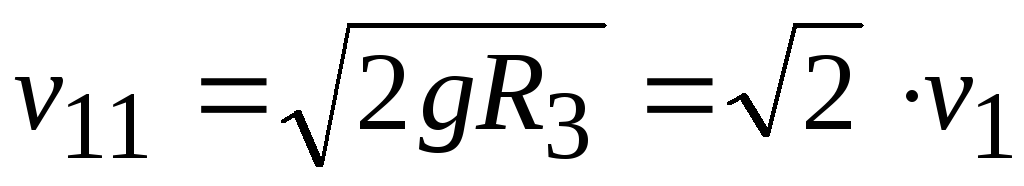 .
.
Ее численное значение приблизительно 11 км/с. Пусть перемещение происходит вдоль оси Z. При этом сила тяжести совершает работу
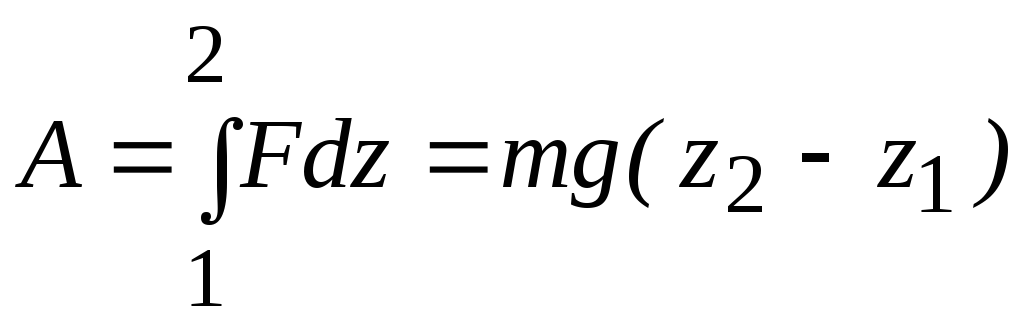 .
.
Согласно определению потенциальной энергии А = U1‑U2. Отсюда следует, что потенциальная энергия тела в поле силы тяжести Земли может быть записана в виде
U(z) = mgz + const, (1.48)
где постоянная связана с выбором начала отсчета энергии. Эту формулу можно получить и непосредственно из закона всемирного тяготения. Запишем его в виде
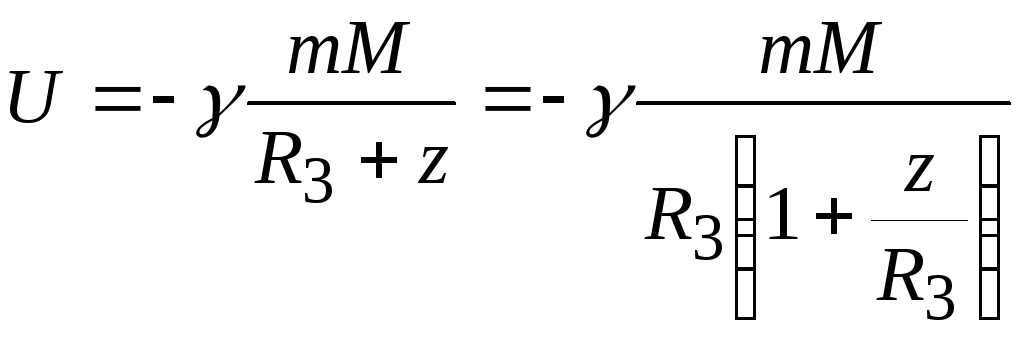 ,
,
где z— высота тела с массойm над поверхностью Земли. При малых
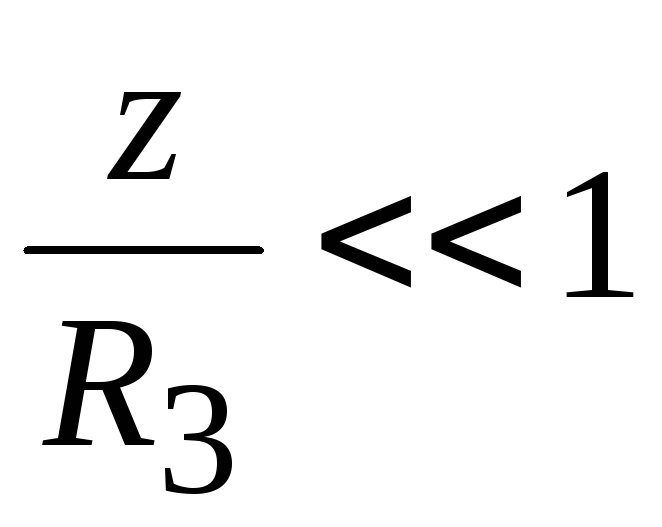 ,
, 
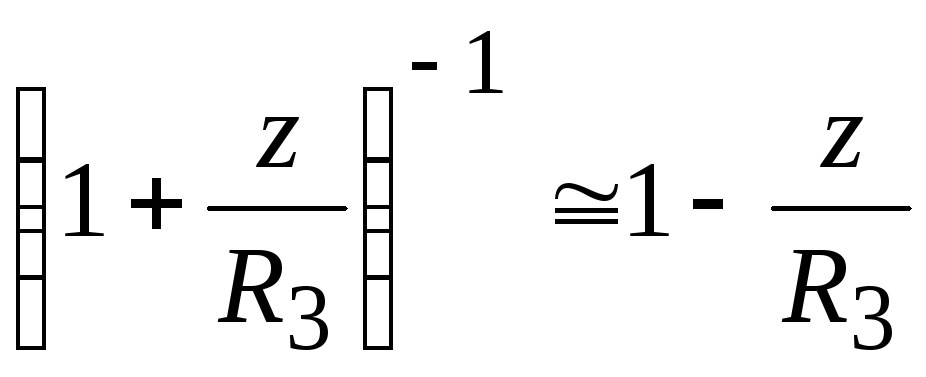 ,
откуда находимU =U0 +mgz =U(R3)
+mgz
,
откуда находимU =U0 +mgz =U(R3)
+mgz
1.4. Силы инерции
Основным положением механики Ньютона является утверждение о том, что действие на тело со стороны других тел вызывает их ускорение. В системах координат, движущихся с ускорением относительно выбранной нами инерциальной системы, так называемых неинерциальных системах, формально справедливо и обратное — возникают силы, связанные не с реальным действием других тел, а с наличием указанных ускорений. Такие силы называют силами инерции. Рассмотрим несколько примеров.
1. Прямолинейное движение системы координат с ускорением a0 относительно инерциальной системы. В этом случае на тело с массойm в неинерциальной системе координат действует сила инерции, равная
fи = —ma0. (1.49)
2. Центробежная
сила инерции. Рассмотрим движение тела
во вращающейся системе координат.
Сначала рассмотрим вращение тела в
неподвижной системе. В ней тело будет
испытывать центростремительное
ускорение, которое, и будет заставлять
его вращаться. По третьему закону Ньютона
центростремительной силе соответствует
центробежная сила, приложенная к нити,
удерживающей вращающееся тело. Во
вращающейся системе координат тело
покоится, но центростремительное
ускорение по-прежнему отлично от нуля.
Это ускорение может быть связано теперь
с существованием центробежной силы 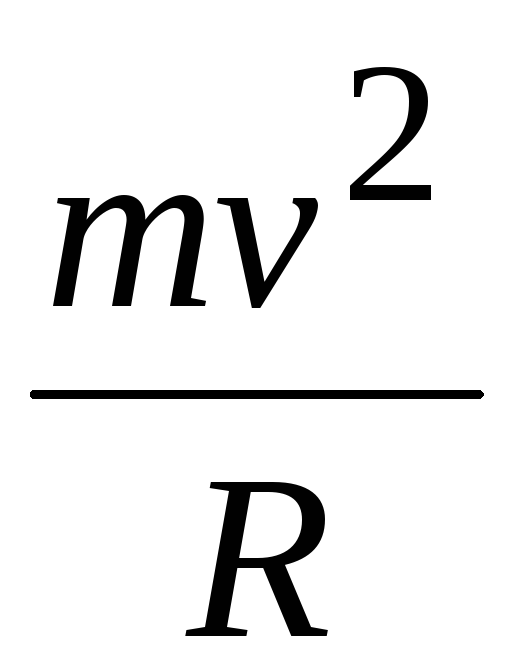 ,
направленной от центра вращения.
,
направленной от центра вращения.
3. Свободно падающий лифт. Пусть ускорение свободно падающего лифта — неинерциальной системы отсчета — g. Сила инерции, действующая на материальную точку с массойm, в системе отсчета, связанной с лифтом, равнаmg. На тело в падающем лифте действуют, таким образом, две силы: — сила тяжести и сила инерции. Суммарная сила, действующая в свободно падающем лифте на материальную точку, равна нулю, т. е. сила инерции уравновешивает силу тяготения — в лифте возникает состояние невесомости. Аналогия между поведением тел в гравитационном поле и в неинерциальной системе отсчета составляет принцип эквивалентности сил тяготения и инерции: он используется в теории тяготения, основанной на теории относительности. В основе принципа эквивалентности лежит равенство инертной и гравитационной масс, о котором шла речь в начале данной главы.
1.3 Движение в гравитационном поле.
ствующей с полем сил.
Подставим соотношение (1.35) в (1.33) и опять проинтегрируем вдоль траектории от точки 1 до точки 2. Получим
T2 — T1 +const(φ2 — φ1) = 0,
т.е. величина T2 +const·φ2 = T1 +const·φ1
остается постоянной при движении вдоль траектории. Таким образом, для частицы в потенциальном поле внешней силы сохраняется, т. е. является интегралом движения, величина
E = T+const·φ(r). | (1.36) |
Величина U = const·φ(r) называется потенциальной энергией частицы в поле φ(r), а выражение (1.36) представляет собой полную механическую энергию частицы
1.2.3 Равновесие механической системы
Из выражения (1.37) следует, что при постоянной величине полной энергии кинетическая энергия частицы может возрастать только за счет уменьшения потенциальной энергии. Поэтому, если потенциальная энергия имеет минимальное значение, кинетическая энергия не может измениться без внешнего воздействия. Таким образом, условием механического равновесия системы является минимум ее потенциальной энергии
dU | = 0 , | (1.38) |
| ||
dr |
|
|
что эквивалентно равенству нулю сил, действующих на части-
цу.
В1687 г. Ньютон на основании уже обнаруженных к тому времени на опыте законов движения планет установил, что всякие два тела притягиваются друг к другу с силой, прямо пропорциональной квадрату расстояния между ними. Например, материальная точка с массой m, находящаяся на расстоянии r от другой материальной точки с массой M, будет притягиваться последней с силой
F =γ | Mm | , | (1.39) |
| r2 |
|
|
где γ— размерная постоянная, необходимая для того, чтобы величина F имела размерность силы. В случае наличия тел сложной формы, когда их нельзя рассматривать как материальные точки, формула (1.39) видоизменяется, но основной характер взаимодействия сохраняется. Постоянная в уравнении (1.39) была впервые определена в 1798г. английским физиком Кавендишем в поразительном по точности опыте. Ее численное значение очень мало γ = 6,6∙10-11 н∙м2/кг2 — это значит, что с силой столь малой величины притягиваются друг к другу две массы в 1 кг каждая на расстоянии в 1 м. Огромное значение, которое имеют силы гравитации в природе, обусловлено с одной стороны, большими массами небесных тел, а с другой — отсутствием сил иного происхождения.
Соотношение (1.39) носит название закона всемирного тяготения. Оно хорошо описывает движение тяготеющих масс.
С физической точки зрения соотношение (1.39) описывает взаимодействие массы m с полем тяготения, или, как принято говорить, с гравитационным полем, создаваемым в пространстве массой M. Хотя способ передачи гравитационного взаимодействия нам неизвестен, опыт показывает, что с каждой массой в пространстве связано гравитационное поле.
Гравитационное поле, создаваемое в пространстве массой M, будем характеризовать потенциалом
ϕ = −γ | M . | (1.40) |
| r |
|
Потенциальная энергия, приобретенная телом с массой в этом поле, согласно результатам предыдущего раздела, может быть записана в виде
U = −γ | mM | , | (1.41) |
| r |
|
|
т. е. потенциальная энергия поля в гравитационном поле равна потенциалу поля в точке нахождения тела, умноженному на массу тела.
Сила притяжения (1.39) может быть найдена по формуле (1.35):
| dU |
| d 1 |
|
| r | mM |
| ||||||
F = − |
| =γ m M |
|
|
| = −γ m M |
|
| = −γ |
| 2 er | (1.42) | ||
r | 3 | r | ||||||||||||
| dr |
| dr r |
|
|
|
|
|
| |||||
( er | = | r | — единичный вектор в направлении радиус-вектора r). | |||||||||||
r | ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||
Зная потенциал поля, можно вычислить работу, совершаемую силами поля над телом с массой т при перемещении его из положения 1 в положение 2. Эта работа может быть выражена через разность значений потенциала поля в указанных точках
2 |
|
| 2 | dU |
| −ϕ2 ) (1.43) |
A = ∫Fdr = −∫ |
| dr =U(1) −U(2) = m(ϕ1 | ||||
1 |
|
| 1 | dr |
|
|
Отсюда видно, что работа в поле сил тяготения не зависит от пути, т. е. от того, каким образом тело было перемещено из положения 1 в 2.
Массы, фигурирующие в законе всемирного тяготения, характеризуют способность тел создавать поле тяготения и в свою очередь испытывать на себе их действие. Поэтому масса, о которой идет здесь речь, может быть названа тяготеющей, или гравитационной, массой, в отличие от инертной массы, фигурирующей во втором законе Ньютона. Хотя их физический смысл различен и ниоткуда не следует их равенство, тем не менее они все же тождественны. Невозможность различить обе массы является следствием большого числа самых совершенных опытов. Таким образом, во втором законе Ньютона и в законе тяготения проявляются различные свойства одной и той же величины — физической массы.
1.3.1 Движение в поле тяготения Земли.
Из закона всемирного тяготения следует, что у поверхности Земли все тела должны падать с одинаковым ускорением. В самом деле, по второму закону Ньютона ускорение, приобретаемое телом с массой m у поверхности Земли a = F/m, где F — сила, с которой тело притягивается земным шаром. По закону тяготения
F =γ | m M 3 | , | (1.44) |
| R32 |
|
|
M3 — масса Земли и R3 — радиус земного шара. Отсюда
a =γ M23 R3
и не зависит от массы падающего тела. Таким образом, все тела у поверхности Земли независимо от их массы падают с одинаковым ускорением
g =γ | M 3 | , | (1.45) | |
R32 | ||||
|
|
|
которое называется ускорением свободного падения. Подставляя сюда известные значения констант, получим значение 9,8 м/c2. В действительности значения g слегка различаются при учете сил сопротивления и реальной формы Земли. По второму закону Ньютона это означает, что в поле тяжести Земли все тела испытывают силу тяжести, равную mg. При перемещении массы с одной высоты на другую эта сила тяжести совершает работу, которую можно вычислить как изменение потенциальной энергии тела.
1.3.2 Космические скорости.
Определим скорость, которую необходимо иметь телу дли того, чтобы оно могло стать спутником Земли, т. е. первую космическую скорость. Величину этой скорости можно определить из условия равенства сил, действующих на тело при его вращении вокруг Земли. Сила притяжения должна быть уравновешена центробежной силой mv2/R. Таким образом,
mv2 | =γ | mM3 | (1.46) |
R | R2 | ||
3 |
| 3 |
|
откуда находим значение первой космической скорости
v | = | γ M3 | = |
|
g R | ||||
1 |
| R3 | 3 | |
|
|
| ||
Подставляя численные значения величин, получаем v1 = 8 км/с. Вторая космическая скорость — это скорость, которую нужно сообщить телу для того, чтобы оно покинуло область земного притяжения. Для определения второй космической скорости следует
вычислить работу, которую необходимо совершить против сил земного притяжения для удаления тела с поверхности Земли на бесконечность. Эта работа равна разности потенциальных энергий тела в начальном и в конечном положениях:
A = Uк — Uн.
Потенциальная энергия тела в гравитационном поде Земли на ее поверхности согласно (1.41) имеет вид:
Un = −γ mM 3
R3
Un = −γ mM 3 а на бесконечности равна нулю. Таким образом,
R3
A = −γ | mM 3 = mgR3 | (1.47) |
| R3 |
|
Величина этой потенциальной энергии определяет кинетическую энергию, которую должно иметь тело для того, чтобы быть в состоянии совершить указанную работу
mv2112 = mgR3 .
Отсюда вторая космическая скорость определяется выражением:
v11 = 2gR3 = 2 v1 .
Ее численное значение приблизительно 11 км/с. Пусть перемещение происходит вдоль оси Z. При этом сила тяжести совершает работу
2
A = ∫Fdz = mg(z2 − z1 ) .
1
Согласно определению потенциальной энергии A = U1-U2. Отсюда следует, что потенциальная энергия тела в поле силы тяжести Земли может быть записана в виде
U(z) = mgz + const, (1.48)
где постоянная связана с выбором начала отсчета энергии. Эту

