1.3.1 Движение в поле тяготения Земли.
Из закона всемирного тяготения следует, что у поверхности Земли все тела должны падать с одинаковым ускорением. В самом деле, по второму закону Ньютона ускорение, приобретаемое телом с массой m у поверхности Землиa=F/m, гдеF — сила, с которой тело притягивается земным шаром. По закону тяготения
, (1.44)
M3— масса Земли и R3— радиус земного шара. Отсюда
и не зависит от массы падающего тела. Таким образом, все тела у поверхности Земли независимо от их массы падают с одинаковым ускорением
, (1.45)
которое
называется ускорением свободного
падения. Подставляя сюда известные
значения констант, получим значение
9,8 м/c2.
В действительности значенияg слегка различаются при учете сил
сопротивления и реальной формы Земли.
По второму закону Ньютона это означает,
что в поле тяжести Земли все тела
испытывают силу тяжести, равнуюmg.
1.3.2 Космические скорости.
Определим скорость, которую необходимо иметь телу дли того, чтобы оно могло стать спутником Земли, т. е. первую космическую скорость. Величину этой скорости можно определить из условия равенства сил, действующих на тело при его вращении вокруг Земли. Сила притяжения должна быть уравновешена центробежной силой mv2/R. Таким образом,
(1.46)
откуда находим значение первой космической скорости
Подставляя численные значения величин, получаемv1 = 8 км/с.
Вторая
космическая скорость — это скорость,
которую нужно сообщить телу для того,
чтобы оно покинуло область земного
притяжения. Для определения второй
космической скорости следует вычислить
работу, которую необходимо совершить
против сил земного притяжения для
удаления тела с поверхности Земли на
бесконечность.
A = Uк ‑ Uн.
Потенциальная энергия тела в гравитационном поде Земли на ее поверхности согласно (1.41) имеет вид:
(1.47)
Величина этой потенциальной энергии определяет кинетическую энергию, которую должно иметь тело для того, чтобы быть в состоянии совершить указанную работу
Отсюда вторая космическая скорость определяется выражением:
.
Ее численное значение приблизительно 11 км/с. Пусть перемещение происходит вдоль оси Z. При этом сила тяжести совершает работу
.
Согласно определению потенциальной энергии А = U1‑U2. Отсюда следует, что потенциальная энергия тела в поле силы тяжести Земли может быть записана в виде
U(z) =
 48)
48)где постоянная связана с выбором начала отсчета энергии. Эту формулу можно получить и непосредственно из закона всемирного тяготения. Запишем его в виде
,
где z— высота тела с массойm над поверхностью Земли. При малых
, , откуда находимU =U0 +mgz =U(R3) +mgz
1.4. Силы инерции
Основным положением механики Ньютона является утверждение о том, что действие на тело со стороны других тел вызывает их ускорение. В системах координат, движущихся с ускорением относительно выбранной нами инерциальной системы, так называемых неинерциальных системах, формально справедливо и обратное — возникают силы, связанные не с реальным действием других тел, а с наличием указанных ускорений. Такие силы называют силами инерции. Рассмотрим несколько примеров.
1.
Прямолинейное движение системы координат
с ускорением a0 относительно инерциальной системы. В этом случае на тело с массойm в неинерциальной системе координат
действует сила инерции, равная
В этом случае на тело с массойm в неинерциальной системе координат
действует сила инерции, равная
fи = —ma0. (1.49)
2. Центробежная сила инерции. Рассмотрим движение тела во вращающейся системе координат. Сначала рассмотрим вращение тела в неподвижной системе. В ней тело будет испытывать центростремительное ускорение, которое, и будет заставлять его вращаться. По третьему закону Ньютона центростремительной силе соответствует центробежная сила, приложенная к нити, удерживающей вращающееся тело. Во вращающейся системе координат тело покоится, но центростремительное ускорение по-прежнему отлично от нуля. Это ускорение может быть связано теперь с существованием центробежной силы , направленной от центра вращения.
3. Свободно падающий лифт. Пусть ускорение свободно падающего лифта — неинерциальной системы отсчета — g. Сила инерции, действующая на материальную точку с массой
 На тело в
падающем лифте действуют, таким образом,
две силы: — сила тяжести и сила инерции.
Суммарная сила, действующая в свободно
падающем лифте на материальную точку,
равна нулю, т. е. сила инерции уравновешивает
силу тяготения — в лифте возникает
состояние невесомости. Аналогия между
поведением тел в гравитационном поле
и в неинерциальной системе отсчета
составляет принцип эквивалентности
сил тяготения и инерции: он используется
в теории тяготения, основанной на теории
относительности. В основе принципа
эквивалентности лежит равенство инертной
и гравитационной масс, о котором шла
речь в начале данной главы.
На тело в
падающем лифте действуют, таким образом,
две силы: — сила тяжести и сила инерции.
Суммарная сила, действующая в свободно
падающем лифте на материальную точку,
равна нулю, т. е. сила инерции уравновешивает
силу тяготения — в лифте возникает
состояние невесомости. Аналогия между
поведением тел в гравитационном поле
и в неинерциальной системе отсчета
составляет принцип эквивалентности
сил тяготения и инерции: он используется
в теории тяготения, основанной на теории
относительности. В основе принципа
эквивалентности лежит равенство инертной
и гравитационной масс, о котором шла
речь в начале данной главы.
Между координатами получилась квадратичная зависимость. Значит траектория — парабола.
Движение снаряда в воздухе
вязкость воздуха; Вязкость воздуха объясняется наличием внутреннего сцепления между частицами воздуха. При движении снаряда частицы воздуха, непосредственно примыкающие к снаряду, вследствие сцепления с его поверхностью, движутся со скоростью снаряда.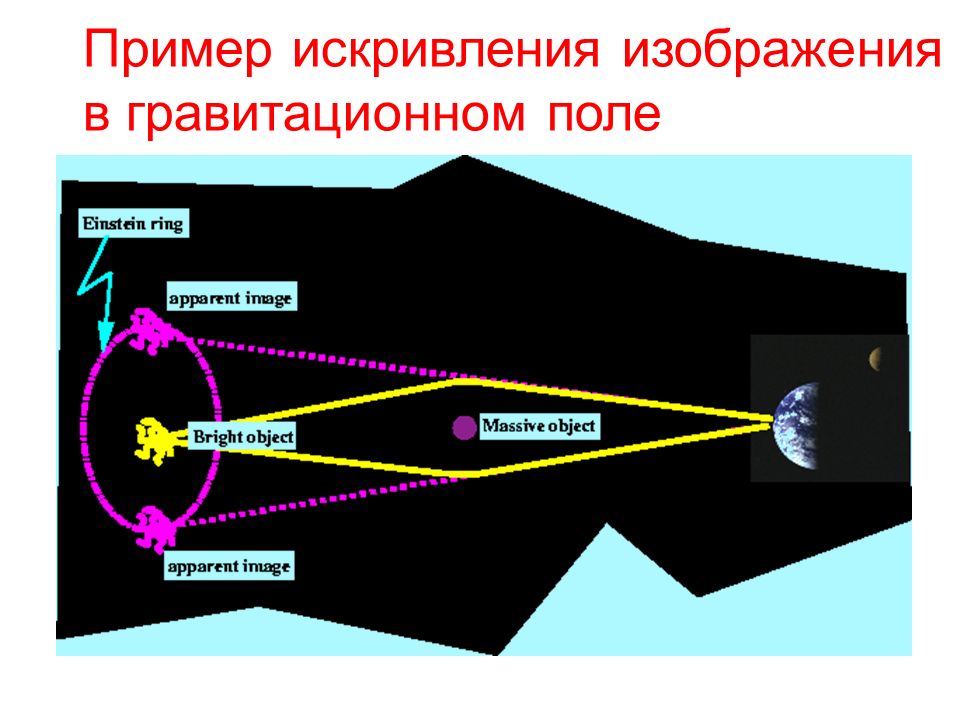
При всяком колебании и движении тел в воздухе создаются бесконечно малые уплотнения, которые распространяются со скоростью звука. Если частота этих колебаний находится в пределах 20-20000 колебаний в секунду, мы воспринимаем их как звук.
При скорости снаряда, равной скорости звука, эти уплотнения накладываются одно на другое у головной части, создавая уже значительно плотный слой. Образуется баллистическая волна. Давление на фронте этой волны может достигать 8 — 10 атмосфер.
Ветер оказывает значительное влияние на полёт снарядов. Это влияние тем больше, чем больше скорость ветра и меньше вес и скорость снарядов. В зависимости от скорости ветра различают:При стрельбе из артиллерийских орудий, особенно на средние и большие дальности, существенное влияние на дальность полёта снаряда оказывает продольный ветер.
Плотность воздуха увеличивает или уменьшает сопротивление воздуха.
С увеличением атмосферного давления плотность воздуха увеличивается, и, следовательно, увеличивается сила сопротивления воздуха.
Величина силы сопротивления воздуха может значительно превосходить силу тяжести. Эта разница тем больше, чем меньше вес снаряда и больше скорость его полёта. Величина силы сопротивления возрастает особенно резко при движении снарядов со скоростями, превышающими скорость звука.
Из повседневной практики известно, что поток газа действует на тело, помещенное в этот поток, с некоторой силой, названной силой лобового сопротивления.
Fсопр = Сx r V2 Sмид/ 2.
Пусть составляющие силы сопротивления
m∙ax = — Fсопр x, где Fсопр x = Fсопр∙cosβ;
Каталог: files -> file жүктеу/скачать 445 b. Достарыңызбен бөлісу: |
Использование теоретических знаний по теме: Движение тела в поле тяготения Земли в военной науке баллистике.
Государственное образовательное учреждение
дополнительного профессионального образования
(повышения квалификации)
Московской области
ПЕДАГОГИЧЕСКАЯ АКАДЕМИЯ ПОСЛЕДИПЛОМНОГО ОБРАЗОВАНИЯ
Факультет профессиональной подготовки педагогических работников
Кафедра естественнонаучных дисциплин
Инвариантный кафедральный модуль
«Актуальные проблемы проведения физики»
МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЯ
по теме:
«Использование теоретических знаний по теме:
Движение тела в поле тяготения Земли в военной науке баллистике»
В 10 КЛАССЕ (С УГЛУБЛЕННЫМ ИЗУЧЕНИЕМ ФИЗИКИ)
Выполнил:
Заматаев Сергей Александрович
учитель физики
МОУ Поведниковская СОШ
Мытищинского района
Руководитель:
к. п.н., доцент Ковалёва С.Я.
п.н., доцент Ковалёва С.Я.
г.Москва
2010
Содержание.
1. Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
- История возникновения баллистического движения . . . . . . . . . . . . . . . . . . 4
- Баллистика как наука . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4
- Краткая биография Исаака Ньютона . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
- История открытия закона Всемирного тяготения . . . . . . . . . . . . . . . . . . . .10
- Закон Всемирного тяготения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .15
- Из биографии Генри Кавендиша . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .19
- Опыт Генри Кавендиша . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21
- Скорость при баллистическом движении .
 . . . . . . . . . . . . . . . . . . . . . . . . . 22
. . . . . . . . . . . . . . . . . . . . . . . . . 22 - Траектория движения тела в поле силы тяжести . . . . . . . . . . . . . . . . . . . .24
- Траектория баллистического движения . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
- Применение балистического движения на практике . . . . . . . . . . . . . . . . .27
- Применение теоретических расчетов к управлению баллистическими ракетами . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
а) Траектория баллистической ракеты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
б) Траектории управляемых снарядов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
в) Координаты, определяющие положение ракеты в пространстве . . . . . 32
Введение.
Механика является наукой о движении, а движение охватывает все происходящее во Вселенной, начиная от простого перемещения и кончая мышлением. По образному выражению академика А. Ю. Ишлинского, «механика — это основа познания природы и база творений техники».
По образному выражению академика А. Ю. Ишлинского, «механика — это основа познания природы и база творений техники».
На всем протяжении истории науки механика была, есть и будет фундаментом физики, наиболее тесно связанной с окружающим нас миром.
Механика является тем разделом физики, который благодаря строгости и логичности своего построения в сильной степени способствует развитию мышления учащихся. От его усвоения зависит успешность изучения всех разделов курса физики.
Что касается опытов, то опыты в механике предназначены для того, чтобы облегчить учащимся освоение основных понятий, связать эти понятия с реальными движениями. Кроме того, и это не менее важно, цель ряда опытов заключается в том, чтобы показать принципиальную возможность измерения основных величин.
Изучая баллистику, учащиеся повторяют основные теоретические положения и законы кинематики, а также исследуют и выводят новые закономерности, которые можно и даже необходимо проверять на опыте.
Лабораторные работы дают возможность глубоко исследовать баллистическое движение и основные физические величины его характеризующие, а также мотивируют учащихся к более детальному исследованию аспектов этой и других тем.
Работы предусматривают не только измерение основных величин и подтверждение теории на основе эксперимента, но также и привитие экспериментальных умений. К ним относят не только умения, связанные непосредственно с выполнением эксперимента, но и умения высказывать и обосновывать гипотезы, совместно решать проблемы, выбирать и конструировать способ деятельности, оценивать результаты собственной и
коллективной деятельности .
Изучение баллистического движения (движения тела под углом к горизонту) на уроках физики у меня вызвало большой интерес. Но к сожалению эта тема в учебнике нам дана поверхностно и я в серьёз решил заинтересоваться ей. Я хотел бы рассказать про баллистику как науку, показать баллистическое движение (дижение тела под углом к горизонту) в практической части.
История возникновения баллистического движения.
В многочисленных войнах на протяжении всей истории человечества враждующие стороны, доказывая своё превосходство, использовали сначала камни, копья , и стрелы, а затем ядра, пули, снаряды, и бомбы. Успех сражения во многом определялся точностью попадания в цель. При этом точный бросок камня, поражение противника летящим копьём или стрелой фиксировались воином визуально. Это позволяло при соответствующей тренировке повторять свой успех в следующем сражении. Значительно возросшая с развитием техники скорость и дальность полёта снарядов и пуль сделали возможным дистанционные сражения. Однако навыки война, разрешающей способности его глаза было недостаточно для точного попадания в цель артиллерийской дуэли первым. Желание побеждать стимулировало появление баллистики (от греческого слова ballo-бросаю).
Успех сражения во многом определялся точностью попадания в цель. При этом точный бросок камня, поражение противника летящим копьём или стрелой фиксировались воином визуально. Это позволяло при соответствующей тренировке повторять свой успех в следующем сражении. Значительно возросшая с развитием техники скорость и дальность полёта снарядов и пуль сделали возможным дистанционные сражения. Однако навыки война, разрешающей способности его глаза было недостаточно для точного попадания в цель артиллерийской дуэли первым. Желание побеждать стимулировало появление баллистики (от греческого слова ballo-бросаю).
Баллистика как наука.
Возникновение баллистики относится к 16 в. Баллистика — наука о движении снарядов, мин, пуль, неуправляемых ракет при стрельбе (пуске). Основные разделы баллистики: внутренняя баллистика и внешняя баллистика. Исследованием реальных процессов, происходящих при горении пороха, движении снарядов, ракет (или их моделей) и т. д., занимается эксперимент баллистики. Внешняя баллистика изучает движение снарядов, мин, пуль,
Внешняя баллистика изучает движение снарядов, мин, пуль,
неуправляемых ракет и др. после прекращения их силового взаимодействия со стволом оружия (пусковой установкой), а также факторы, влияющие на это движение. Основные разделы внешней баллистики: изучение сил и моментов, действующих на снаряд в полёте; изучение движения центра масс снаряда для расчета элементов траектории, а также движение снаряда относительно центра масс с целью определения его устойчивости и характеристик рассеивания. Разделами внешней баллистики являются также теория поправок, разработка методов получения данных для составления таблиц стрельбы и внешнебаллистическое проектирование. Движение снарядов в особых случаях изучается специальными разделами внешней баллистики, авиационной баллистикой, подводной баллистикой и др.
Внутренняя баллистика изучает движение снарядов, мин, пуль и др. в канале ствола оружия под действием пороховых газов, а также другие процессы, происходящие при выстреле в канале или камере пороховой ракеты. Основные разделы внутренней баллистики: пиростатика, изучающая закономерности горения пороха и газообразования в постоянном объёме; пиродинамика, исследующая процессы в канале ствола при выстреле и устанавливающая связь между ними, конструктивными характеристиками канала ствола и условиями заряжания; баллистическое проектирование орудий, ракет, стрелкового оружия. Баллистика (изучает процессы периода последствия) и внутренняя баллистика пороховых ракет (исследует закономерности горения топлива в камере и истечения газов через сопла, а также возникновение сил, действий на неуправляемые ракеты).
Основные разделы внутренней баллистики: пиростатика, изучающая закономерности горения пороха и газообразования в постоянном объёме; пиродинамика, исследующая процессы в канале ствола при выстреле и устанавливающая связь между ними, конструктивными характеристиками канала ствола и условиями заряжания; баллистическое проектирование орудий, ракет, стрелкового оружия. Баллистика (изучает процессы периода последствия) и внутренняя баллистика пороховых ракет (исследует закономерности горения топлива в камере и истечения газов через сопла, а также возникновение сил, действий на неуправляемые ракеты).
Баллистическая гибкость оружия — это свойство огнестрельного оружия, позволяющее расширять его боевые возможности повышать эффективность действия за счёт изменения баллистических характеристик. Достигается путем изменения баллистического коэффициента (направлением, введением тормозных колец) и начальной скорости снаряда (применением переменных
зарядов). В сочетании с изменением угла возвышения это позволяет получать большие углы падения и меньшее рассеивание снарядов на промежуточные дальности.
Баллистическая ракета, ракета, полет которой, за исключением относительно небольшого участка, совершается по траектории свободно брошенного тела. В отличие от крылатой ракеты баллистическая ракета не имеет несущих поверхностей для создания подъёмной силы при полёте в атмосфере. Аэродинамическая устойчивость полёта некоторых баллистических ракет обеспечивается стабилизаторами. К баллистическим ракетам относят ракеты различного назначения, ракеты-носители космических аппаратов и др. Они бывают одно- и многоступенчатыми, управляемые и неуправляемыми. Первые боевые баллистические ракеты ФАУ-2 были применены фашисткой Германией в конце мировой войны. Баллистические ракеты с дальностью полёта свыше 5500 км (по иностранной классификации — свыше 6500 км) называются межконтинентальными баллистическими ракетами (МБР). Современные МБР имеют дальность полёта до 11500 км (направленные, американские «Минитмен»-11500 км, «Титан -2» окло 11000 км, «Трайдер-1» около 7400 км). Их пуск производят с наземных (шахтных) пусковых установок или подводных лодок (из надводного или подводного положения). МБР выполняются многоступенчатыми, с жидкостными или твердотопливными двигательными установками, могут оснащаться моноблочными или многозарядными ядерными головными частями.
МБР выполняются многоступенчатыми, с жидкостными или твердотопливными двигательными установками, могут оснащаться моноблочными или многозарядными ядерными головными частями.
Баллистическая трасса — это специальный оборудованный на артилеристическом полигоне участок местности для эксперимента, изучения движения артилеристических снарядов, мин и др. На баллистической трассе устанавливаются соответственные баллистические приборы и баллистические мишени, с помощью которых на основе опытных стрельб определяются функция (закон) сопротивления воздуха, аэродинамические характеристики,
параметры поступательного и колебательного движения, начальные условия вылета и характеристики рассеивания снарядов.
Баллистические условия стрельбы, совокупность баллистических характеристик, оказывающих наибольшее влияние на полёт снаряда (пули). Нормальными, или табличными, баллистическими условиями стрельбы считаются условия, при которых масса и начальная скорость снаряда (пули) равны расчётной (табличной), температура зарядов 15°С, а форма снаряда (пули) соответствует установленному чертежу.
Баллистические характеристики, основные данные, определяющие закономерности развития процесса выстрела и движения снаряда (мины, гранаты, пули) в канале ствола (внутрибаллистические) или на траектории (внешнебаллистические). Основные внутрибаллистические характеристики: калибр оружия, объём зарядной каморы, плотность заряжания, длина пути снаряда в канале ствола, относительная масса заряда (отношение её к массе снаряда), сила пороха, максимальное давление, давление форсирования, характеристики прогрессивности горения пороха и др. К основным внешнебаллистическим характеристикам относятся: начальная скорость, баллистический коэффициент, углы бросания и вылета, срединные отклонения и др.
Баллистический вычислитель, электронный прибор стрельбы (как правило, прямой наводкой) из танков, БМП (боевая машина пехоты), малокалиберных зенитных пушек и др. Баллистический вычислитель учитывает сведения о координатах и скорости цели и своего объекта, ветре, температуре и давлении воздуха, начальной скорости и углах вылета снаряда и др.
Баллистический спуск, неуправляемое движение спускаемого космического аппарата (капсулы) с момента схода с орбиты до достижения заданной относительно поверхности планеты.
Баллистическое подобие, свойство артиллерийных орудий, заключающееся
в сходстве зависимостей, характеризующих процесс горения порохового заряда при выстреле в каналах стволов различных артиллерийных систем. Условия баллистического подобия изучаются теорией подобия, основу которой составляют уравнения внутренней баллистики. На основании этой теории составляются баллистические таблицы, используемые при баллистическом проектировании.
Баллистический коэффициент (С), одна из основных внешнебаллистических характеристик снаряда (ракеты), отражающая влияние его коэффициент формы (i), калибра (d), и массы (q) на способность преодолевать сопротивление воздуха в полёте. Определяется по формуле С=(id/q)1000, где d в м, a q в кг. Чем меньше баллистический коэффициент, тем легче снаряд преодолевает сопротивление воздуха.
Баллистическая фотокамера — это специальное устройство для фотографирования явления выстрела и сопровождающих его процессов внутри канала ствола и на траектории с целью определения качественных и количественных баллистических характеристик оружия. Позволяет осуществлять мгновенное одноразовое фотографирование к.-л. фазы изучаемого процесса или последовательное скоростное фотографирование (более 10 тыс. кадров/с) различных фаз. По способу получения экспозиции балистически фотокамеры бывают искровые, с газосветными лампами, с электрооптическими затворами и рентгенографичные.
Краткая биография Исаака Ньютона.
Исаак Ньютон (1642 — 1727) – великий ученый, сделавший большой вклад в развитие физики, математики, астрологии. Родился в местечке Вулсторп в Англии.
После школы образование Ньютона было получено в колледже святой Троицы при Кембриджском университете. Под влиянием физиков, Ньютон еще в студенчестве сделал несколько открытий, в большей степени математических.
В период с 1664 по 1666 год он вывел формулу бинома Ньютона, формулу Ньютона – Лейбница, вывел закон Всемирного тяготения. В 1668 году в биографии Исаака Ньютона получена степень магистра, в 1669 году – профессора математических наук. Благодаря созданному Ньютоном телескопу (рефлектору) были сделаны значительные открытия в астрономии. Ученый был членом Королевского двора (с 1703 года — президент), смотрителем Монетного.
Законы Ньютона являют собой основы классической механики. Первый закон Ньютона объясняет сохранение скорости тела при скомпенсированных внешних воздействиях. Второй закон Ньютона описывает зависимость ускорения тела от приложенной силы. Из 3-х законов Ньютона могут быть выведены другие законы механики.
Любовь Ньютона к математике обусловила величайших ряд его открытий в данной науке. Так он описал интегральное, дифференциальное исчисление, метод разностей, метод поиска корней уравнения (метод Ньютона).
История открытия закона Всемирного тяготения.
Огромный рост числа молодых энергичных работников, подвизающихся на научной ниве, есть счастливое следствие расширения научных исследований в нашей стране, поощряемых и лелеемых Федеральным правительством. Измотанные и задерганные научные руководители бросают этих неофитов на произвол судьбы, и они часто остаются без лоцмана, который мог бы провести их среди подводных камней государственного субсидирования. По счастью, они могут вдохновляться историей сэра Исаака Ньютона, открывшего закон Всемирного тяготения. Вот как это произошло.
В 1665 году молодой Ньютон стал профессором математики в Кембриджском университете. Он был влюблён в работу, и способности его как преподавателя не вызывали сомнений. Однако нужно заметить, что это ни в коей мере не был человек не от мира сего или же непрактичный обитатель башни из слоновой кости. Его работа в колледже не ограничивалась только аудиторными занятиями: он был деятельным членом Комиссии по Составлению Расписаний, заседал в управлении университетского отделения Ассоциации Молодых Христиан Благородного Происхождения, подвизался в Комитете Содействия Декану, в Комиссии по Публикациям и прочих и прочих комиссиях, которые были необходимы для надлежащего управления колледжем в далёком 17 веке. Тщательные исторические изыскания показывают, что всего за пять лет Ньютон заседал в 379 комиссиях, которые занимались изучением 7924 проблем университетской жизни, из коих решена 31 проблема.
Тщательные исторические изыскания показывают, что всего за пять лет Ньютон заседал в 379 комиссиях, которые занимались изучением 7924 проблем университетской жизни, из коих решена 31 проблема.
Однажды (а было это в 1680 году) после очень напряжённого дня заседание комиссии, назначенное на одиннадцать часов вечера, раньше времени не было, не собрало необходимого кворума, ибо один из старейших членов комиссии внезапно скончался от нервного истощения. Каждое мгновение сознательной жизни Ньютона было тщательно распланировано, а тут вдруг оказалось, что в этот вечер ему нечего делать, так как начало заседания
следующей комиссии было назначено только на полночь. Поэтому он решил немного пройтись. Эта коротенькая прогулка изменила мировую историю.
Была осень. В садах многих добрых граждан, живших по соседству со скромным домиком Ньютона, деревья ломились под тяжестью спелых яблок. Всё было готово к сбору урожая. Ньютон увидел, как на землю упало очень аппетитное яблоко. Немедленной реакцией Ньютона на это событие, типичной для человеческой стороны великого гения, было перелезть через садовую изгородь и сунуть яблоко в карман. Отойдя на приличное расстояние от сада, он с наслаждением надкусил сочный плод. Вот тут его и осенило. Без обдумывания, без предварительных логических рассуждений в мозгу его блеснула мысль, что падение яблока и движение планет по своим орбитам должны подчиняться одному и тому же универсальному закону. Не успел он доесть яблоко и выбросить огрызок, как формулировка гипотезы о законе Всемирного тяготения была уже готова. До полуночи оставалось три минуты, и Ньютон поспешил на заседание Комиссии по Борьбе с Курением Опиума Среди Студентов Неблагородного Происхождения. В последующие недели мысли Ньютона все снова и снова возвращались к этой гипотезе. Редкие свободные минуты между двумя заседаниями он посвящал планам её проверки.
Отойдя на приличное расстояние от сада, он с наслаждением надкусил сочный плод. Вот тут его и осенило. Без обдумывания, без предварительных логических рассуждений в мозгу его блеснула мысль, что падение яблока и движение планет по своим орбитам должны подчиняться одному и тому же универсальному закону. Не успел он доесть яблоко и выбросить огрызок, как формулировка гипотезы о законе Всемирного тяготения была уже готова. До полуночи оставалось три минуты, и Ньютон поспешил на заседание Комиссии по Борьбе с Курением Опиума Среди Студентов Неблагородного Происхождения. В последующие недели мысли Ньютона все снова и снова возвращались к этой гипотезе. Редкие свободные минуты между двумя заседаниями он посвящал планам её проверки.
Прошло несколько лет, в течение которых, как показывают тщательные подсчёты, он уделил обдумыванию этих планов 63 минуты 28 секунд. Ньютон понял, что для проверки его предположения нужно больше свободного времени, чем то, на которое он может рассчитывать. Ведь требовалось определить с большой точностью длину одного градуса широты на земной поверхности и изобрести дифференциальное исчисление.
Не имея ещё опыта в таких делах, он выбрал простую процедуру и написал краткое письмо из 22 слов королю Карлу, в котором изложил свою гипотезу и указал на то, какие великие возможности она сулит, если подтвердится. Видел ли король это письмо, неизвестно, вполне возможно, что и не видел, так как он
ведь был перегружен государственными проблемами и планами грядущих войн. Однако нет никакого сомнения в том, что письмо, пройдя по соответствующим каналам, побывало у всех начальников отделов, их заместителей и заместителей их заместителей, которые имели полную возможность высказать свои соображения и рекомендации.
В конце концов письмо Ньютона, вместе с объёмистой папкой комментариев, которыми оно успело обрасти по дороге, достигло кабинета секретаря ПКЕВИР/КИНИ/ППАБИ (Плановая Комиссия Его Величества по Исследованиям и Развитию, Комитет по Изучению Новых Идей, Подкомитет по Подавлению Антибританских Идей). Секретарь сразу же осознал важность вопроса и вынес его на заседание Подкомитета, который проголосовал за предоставление Ньютону возможности дать показания на заседании Комитета. Этому решению предшествовало краткое обсуждение идеи Ньютона на предмет выяснения, нет ли в его намерениях чего-нибудь антибританского, но запись этой дискуссии, заполнившая несколько томов in quarto, с полной ясностью показывает, что серьёзного подозрения на него так и не упало.
Этому решению предшествовало краткое обсуждение идеи Ньютона на предмет выяснения, нет ли в его намерениях чего-нибудь антибританского, но запись этой дискуссии, заполнившая несколько томов in quarto, с полной ясностью показывает, что серьёзного подозрения на него так и не упало.
Показания Ньютона перед ПКЕВИР/КИНИ следует рекомендовать для прочтения всем молодым учёным, ещё не знающим, как вести себя, когда придёт их час. Колледж проявил деликатность, предоставив ему на период заседаний Комитета двухмесячный отпуск без сохранения содержания, а зам. декана по научно-исследовательской работе проводил его шутливым напутственным пожеланием не возвращаться без »жирного» контракта. Заседание Комитета проходило при открытых дверях, и публики набилось довольно много, но впоследствии оказалось, что большинство присутствующих ошиблось дверью, стремясь попасть на заседание КЕВОРСПВО (Комиссии Его Величества по Обличению Разврата Среди Представителей Высшего Общества).
После того как Ньютон был приведён к присяге и торжественно заявил, что
он не является членом Лояльной Его Величества Оппозиции, никогда не писал безнравственных книг, не ездил в Россию и не совращал молочниц, его попросили кратко изложить суть дела. В блестящей, простой, кристально ясной десятиминутной речи, произнесённой экспромтом, Ньютон изложил законы Кеплера и свою собственную гипотезу, родившуюся при виде падающего яблока. В этот момент один из членов Комитета, импозантный и динамичный мужчина, настоящий человек действия, пожелал узнать, какие средства может предложить Ньютон для улучшения постановки дела по выращиванию яблок в Англии. Ньютон начал объяснять, что яблоко не является существенной частью его гипотезы, но был прерван сразу несколькими членами Комитета, которые дружно высказались в поддержку проекта по улучшению английских яблок. Обсуждение продолжалось несколько недель, в течение которых Ньютон с характерным для него спокойствием и достоинством сидел и ждал, когда Комитет пожелает с ним проконсультироваться. Однажды он опоздал на несколько минут к началу заседания и нашёл дверь запертой. Он осторожно постучал, не желая мешать размышлениям членов Комитета. Дверь приотворилась, и привратник, прошептав, что мест нет, отправил его обратно.
В блестящей, простой, кристально ясной десятиминутной речи, произнесённой экспромтом, Ньютон изложил законы Кеплера и свою собственную гипотезу, родившуюся при виде падающего яблока. В этот момент один из членов Комитета, импозантный и динамичный мужчина, настоящий человек действия, пожелал узнать, какие средства может предложить Ньютон для улучшения постановки дела по выращиванию яблок в Англии. Ньютон начал объяснять, что яблоко не является существенной частью его гипотезы, но был прерван сразу несколькими членами Комитета, которые дружно высказались в поддержку проекта по улучшению английских яблок. Обсуждение продолжалось несколько недель, в течение которых Ньютон с характерным для него спокойствием и достоинством сидел и ждал, когда Комитет пожелает с ним проконсультироваться. Однажды он опоздал на несколько минут к началу заседания и нашёл дверь запертой. Он осторожно постучал, не желая мешать размышлениям членов Комитета. Дверь приотворилась, и привратник, прошептав, что мест нет, отправил его обратно. Ньютон, всегда отличавшийся логичностью мышления, пришёл к заключению, что Комитет не нуждается более в его советах, а посему вернулся в свой колледж, где его ждала работа в различных комиссиях.
Ньютон, всегда отличавшийся логичностью мышления, пришёл к заключению, что Комитет не нуждается более в его советах, а посему вернулся в свой колледж, где его ждала работа в различных комиссиях.
Спустя несколько месяцев Ньютон был удивлён, получив объемистый пакет из ПКЕВИР/КИНИ. Открыв его, он обнаружил, что содержимое состоит из многочисленных правительственных анкет, в пяти экземплярах каждая. Природное любопытство, главная черта всякого истинного учёного, заставило его внимательно изучить эти анкеты. Затратив на это изучение определённое время, он понял, что его приглашают подать прошение о заключении контракта на постановку научного исследования для выяснения связи между способом выращивания яблок, их качеством и скоростью падения на землю. Конечной
целью проекта, как он понял, было выведение сорта яблок, которые не только имели бы хороший вкус, но и падали бы на землю мягко, не повреждая кожуры. Это, конечно, было не совсем то, что Ньютон имел в виду, когда писал письмо королю. Но он был человеком практичным и понял, что, работая над предлагаемой проблемой, сможет попутно проверить и свою гипотезу. Так он соблюдет интересы короля и позанимается немножко наукой, за те же деньги. Приняв такое решение, Ньютон принялся заполнять анкеты без дальнейших колебаний.
Но он был человеком практичным и понял, что, работая над предлагаемой проблемой, сможет попутно проверить и свою гипотезу. Так он соблюдет интересы короля и позанимается немножко наукой, за те же деньги. Приняв такое решение, Ньютон принялся заполнять анкеты без дальнейших колебаний.
Однажды в 1865 году точный распорядок дня Ньютона был нарушен. В четверг после обеда он готовился принять комиссию вице-президентов компаний, входивших во фруктовый синдикат, когда пришло повергшее Ньютона в ужас и всю Британию в скорбь известие о гибели всего состава комиссии во время страшного столкновения почтовых дилижансов. У Ньютона, как это уже было однажды, образовалось ничем не занятое »окно», и он принял решение прогуляться. Во время этой прогулки ему пришла (он сам не знает как) мысль о новом, совершенно революционном математическом подходе, с помощью которого можно решить задачу о притяжении вблизи большой сферы. Ньютон понял, что решение этой задачи позволит проверить его гипотезу с наибольшей точностью, и тут же, не прибегая ни к чернилам, ни к бумаге, в уме доказал, что гипотеза подтверждается. Легко можно себе представить, в какой восторг он пришёл от столь блестящего открытия.
Легко можно себе представить, в какой восторг он пришёл от столь блестящего открытия.
Вот так правительство Его Величества поддерживало и воодушевляло Ньютона в эти напряженные годы работы над теорией. Мы не будем распространяться о попытках Ньютона опубликовать своё доказательство, о недоразумениях с редакцией »Журнала садоводов» и о том, как его статью отвергли журналы »Астроном-любитель» и »Физика для домашних хозяек». Достаточно сказать, что Ньютон основал свой собственный журнал, чтобы иметь возможность напечатать без сокращений и искажений сообщение о своём
открытии.
Закон Всемирного тяготения.
Чтобы в полной мере оценить весь блеск этого прозрения, давайте ненадолго вернемся к его предыстории. Когда великие предшественники Ньютона, в частности Галилей, изучали Равноускоренное движение тел, падающих на поверхность Земли, они были уверены, что наблюдают явление чисто земной природы, существующее только недалеко от поверхности нашей планеты. Когда другие ученые, например Иоганн Кеплер (см. Законы Кеплера), изучали движение небесных тел, они полагали что в небесных сферах действуют совсем иные законы движения, нежели законы, управляющие движением здесь, на Земле. История науки свидетельствует, что практически все аргументы, касающиеся движения небесных тел, до Ньютона сводились в основном к тому, что небесные тела, будучи совершенными, движутся по круговым орбитам в силу своего совершенства, поскольку окружность — суть идеальная геометрическая фигура. Таким образом, выражаясь современным языком, считалось, что имеются два типа гравитации, и это представление устойчиво закрепилось в сознании людей того времени. Все считали, что есть земная гравитация, действующая на несовершенной Земле, и есть гравитация небесная, действующая на совершенных небесах.
Законы Кеплера), изучали движение небесных тел, они полагали что в небесных сферах действуют совсем иные законы движения, нежели законы, управляющие движением здесь, на Земле. История науки свидетельствует, что практически все аргументы, касающиеся движения небесных тел, до Ньютона сводились в основном к тому, что небесные тела, будучи совершенными, движутся по круговым орбитам в силу своего совершенства, поскольку окружность — суть идеальная геометрическая фигура. Таким образом, выражаясь современным языком, считалось, что имеются два типа гравитации, и это представление устойчиво закрепилось в сознании людей того времени. Все считали, что есть земная гравитация, действующая на несовершенной Земле, и есть гравитация небесная, действующая на совершенных небесах.
Прозрение же Ньютона как раз и заключалось в том, что он объединил эти два типа гравитации в своем сознании. С этого исторического момента искусственное и ложное разделение Земли и остальной Вселенной прекратило свое существование.
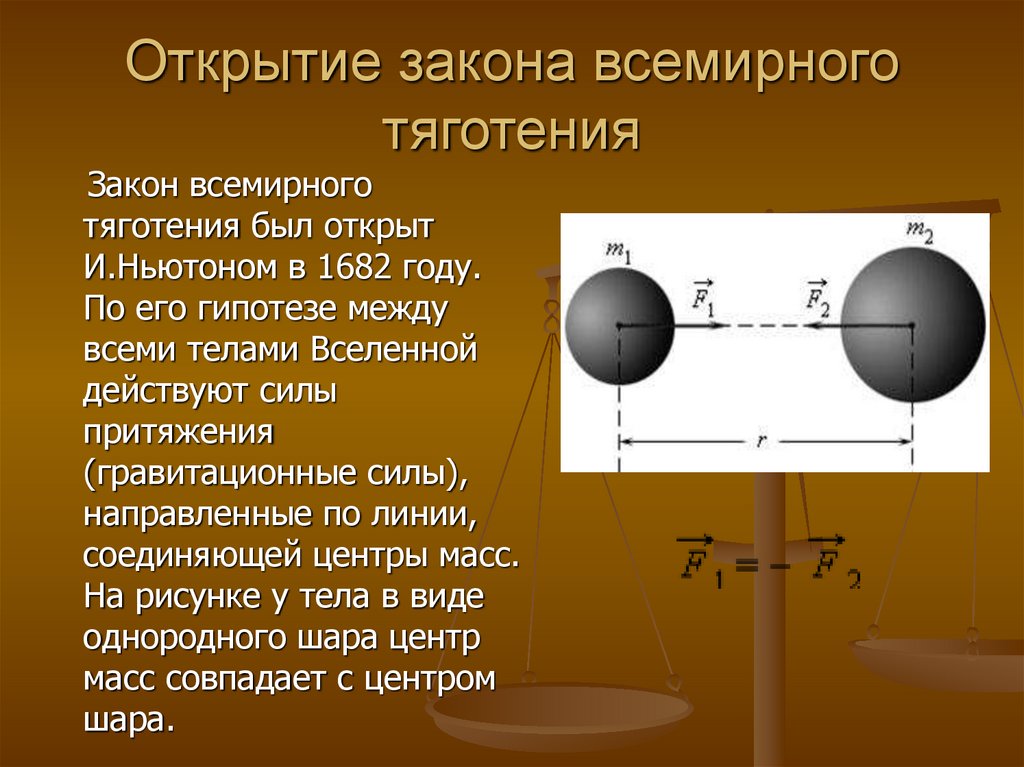
Результаты ньютоновских расчетов теперь называют Законом Всемирного тяготения Ньютона. Согласно этому закону между любой парой тел во Вселенной действует сила взаимного притяжения. Как и все физические законы, он облечен в форму математического уравнения. Если M и m — массы
двух тел, а R — расстояние между ними, тогда сила F взаимного гравитационного притяжения между ними равна:
F=GMm/R2
где G — гравитационная константа, определяемая экспериментально. В единицах СИ ее значение составляет приблизительно 6,67×10–11 (Н·м2)/кг2.
Относительно этого закона нужно сделать несколько важных замечаний. Во-первых, его действие в явной форме распространяется на все без исключения физические материальные тела во Вселенной. В частности, сейчас вы и эта книга испытываете равные по величине и противоположные по направлению силы взаимного гравитационного притяжения. Конечно же, эти силы настолько малы, что их не зафиксируют даже самые точные из современных приборов, — но они реально существуют, и их можно рассчитать. Точно так же вы испытываете взаимное притяжение и с далеким квазаром, удаленным от вас на десятки миллиардов световых лет. Опять же, силы этого притяжения слишком малы, чтобы их инструментально зарегистрировать и измерить.
Точно так же вы испытываете взаимное притяжение и с далеким квазаром, удаленным от вас на десятки миллиардов световых лет. Опять же, силы этого притяжения слишком малы, чтобы их инструментально зарегистрировать и измерить.
Второй момент заключается в том, что сила притяжения Земли у ее поверхности в равной мере воздействует на все материальные тела, находящиеся в любой точке земного шара. Прямо сейчас на нас действует сила земного притяжения, рассчитываемая по вышеприведенной формуле, и мы ее реально ощущаем как свой вес. Если мы что-нибудь уроним, оно, под действием всё той же силы, равноускоренно устремится к земле. Галилею первому удалось экспериментально измерить приблизительную величину ускорения свободного падения (см. Уравнения равноускоренного движения) вблизи поверхности Земли. Это ускорение обозначают буквой g.
Для Галилея g было просто экспериментально измеряемой константой. По Ньютону же ускорение свободного падения можно вычислить, подставив в формулу закона всемирного тяготения массу Земли M и радиус Земли R, помня
при этом, что, согласно Второму закону механики Ньютона, сила, действующая на тело, равняется его массе, умноженной на ускорение. Тем самым то, что для Галилея было просто предметом измерения, для Ньютона становится предметом математических расчетов или прогнозов.
Тем самым то, что для Галилея было просто предметом измерения, для Ньютона становится предметом математических расчетов или прогнозов.
Наконец, закон Всемирного тяготения объясняет механическое устройство Солнечной системы, и законы Кеплера, описывающие траектории движения планет, могут быть выведены из него. Для Кеплера его законы носили чисто описательный характер, ученый просто обобщил свои наблюдения в математической форме, не подведя под формулы никаких теоретических оснований. В великой же системе мироустройства по Ньютону, законы Кеплера становятся прямым следствием универсальных законов механики и закона Всемирного тяготения. То есть, мы опять наблюдаем, как эмпирические заключения, полученные на одном уровне, превращаются в строго обоснованные логические выводы при переходе на следующую ступень углубления наших знаний о мире.
Картину устройства солнечной системы, вытекающую из этих уравнений и объединяющую земную и небесную гравитацию, можно понять на простом примере. Предположим, вы стоите у края отвесной скалы, рядом с вами пушка и горка пушечных ядер. Если просто сбросить ядро с края обрыва по вертикали, оно начнет падать вниз отвесно и равноускоренно. Его движение будет описываться законами Ньютона для равноускоренного движения тела с ускорением g. Если теперь выпустить ядро из пушки в направлении горизонта, оно полетит и будет падать по дуге. И в этом случае его движение будет описываться законами Ньютона, только теперь они применяются к телу, движущемуся под воздействием силы тяжести и обладающему некой начальной скоростью в горизонтальной плоскости. Теперь, раз за разом заряжая в пушку всё более тяжелое ядро и стреляя, вы обнаружите, что, поскольку каждое следующее ядро вылетает из ствола с большей начальной скоростью, ядра
Предположим, вы стоите у края отвесной скалы, рядом с вами пушка и горка пушечных ядер. Если просто сбросить ядро с края обрыва по вертикали, оно начнет падать вниз отвесно и равноускоренно. Его движение будет описываться законами Ньютона для равноускоренного движения тела с ускорением g. Если теперь выпустить ядро из пушки в направлении горизонта, оно полетит и будет падать по дуге. И в этом случае его движение будет описываться законами Ньютона, только теперь они применяются к телу, движущемуся под воздействием силы тяжести и обладающему некой начальной скоростью в горизонтальной плоскости. Теперь, раз за разом заряжая в пушку всё более тяжелое ядро и стреляя, вы обнаружите, что, поскольку каждое следующее ядро вылетает из ствола с большей начальной скоростью, ядра
падают всё дальше и дальше от подножия скалы.
Теперь представьте, что вы забили в пушку столько пороха, что скорости ядра хватает, чтобы облететь вокруг земного шара. Если пренебречь сопротивлением воздуха, ядро, облетев вокруг Земли, вернется в исходную точку точно с той же скоростью, с какой оно изначально вылетело из пушки. Что будет дальше, понятно: ядро на этом не остановится и будет продолжать наматывать круг за кругом вокруг планеты. Иными словами, мы получим искусственный спутник, обращающийся вокруг Земли по орбите, подобно естественному спутнику — Луне. Так мы поэтапно перешли от описания движения тела, падающего исключительно под воздействием «земной» гравитации (ньютоновского яблока), к описанию движения спутника (Луны) по орбите, не изменяя при этом природы гравитационного воздействия с «земной» на «небесную». Вот это-то прозрение и позволило Ньютону связать воедино считавшиеся до него различными по своей природе две силы гравитационного притяжения.
Что будет дальше, понятно: ядро на этом не остановится и будет продолжать наматывать круг за кругом вокруг планеты. Иными словами, мы получим искусственный спутник, обращающийся вокруг Земли по орбите, подобно естественному спутнику — Луне. Так мы поэтапно перешли от описания движения тела, падающего исключительно под воздействием «земной» гравитации (ньютоновского яблока), к описанию движения спутника (Луны) по орбите, не изменяя при этом природы гравитационного воздействия с «земной» на «небесную». Вот это-то прозрение и позволило Ньютону связать воедино считавшиеся до него различными по своей природе две силы гравитационного притяжения.
Остается последний вопрос: правду ли рассказывал на склоне своих дней Ньютон? Действительно ли всё произошло именно так? Никаких документальных свидетельств того, что Ньютон действительно занимался проблемой гравитации в тот период, к которому он сам относит свое открытие, сегодня нет, но документам свойственно теряться. С другой стороны, общеизвестно, что Ньютон был человеком малоприятным и крайне дотошным во всем, что касалось закрепления за ним приоритетов в науке, и это было бы очень в его характере — затемнить истину, если он вдруг почувствовал, что его научному приоритету хоть что-то угрожает. Датируя это открытие 1666-м годом, в то время как реально ученый сформулировал, записал и опубликовал этот закон лишь в 1687 году, Ньютон, с точки зрения приоритета, выгадал для себя преимущество больше чем в два десятка лет.
Датируя это открытие 1666-м годом, в то время как реально ученый сформулировал, записал и опубликовал этот закон лишь в 1687 году, Ньютон, с точки зрения приоритета, выгадал для себя преимущество больше чем в два десятка лет.
Я допускаю, что кого-то из историков от моей версии хватит удар, но на
самом деле меня этот вопрос мало беспокоит. Как бы то ни было, яблоко Ньютона остается красивой, притчей и блестящей метафорой, описывающей непредсказуемость и таинство творческого познания природы человеком. А является ли этот рассказ исторически достоверным — это уже вопрос вторичный.
Из биографии Генри Кавендиша.
(10 октября 1731 г. – 24 февраля 1810 г.).
Английский физик и химик Генри Кавендиш родился в Ницце; второй сын лорда Чарлза Кавендиша, герцога Девонширского. В 1749–1753 гг. обучался в Кембриджском университете, где заинтересовался естественными науками (надо отметить, что отец Кавендиша довольно успешно занимался метеорологией). В 1860 г. Кавендиш стал членом Лондонского королевского общества, а в 1802 г. был избран в Парижскую академию наук. Унаследовав в 1773 г. от своего дяди крупное состояние, Кавендиш тратил почти все доходы на проведение экспериментов; в своем доме в Лондоне он устроил лабораторию, где собрал лучшие приборы и инструменты того времени. Один из биографов Кавендиша, французский физик Жан Батист Био, назвал его самым учёным среди богачей и самым богатым среди учёных. В то же время Кавендиш вёл очень скромный и уединённый образ жизни. В частной жизни Кавендиш слыл чудаком и оригиналом; со своими домашними он объяснялся исключительно знаками, раз навсегда выработанными, дабы не терять напрасно времени и слов, и охотно беседовал только с коллегами по науке.
В 1860 г. Кавендиш стал членом Лондонского королевского общества, а в 1802 г. был избран в Парижскую академию наук. Унаследовав в 1773 г. от своего дяди крупное состояние, Кавендиш тратил почти все доходы на проведение экспериментов; в своем доме в Лондоне он устроил лабораторию, где собрал лучшие приборы и инструменты того времени. Один из биографов Кавендиша, французский физик Жан Батист Био, назвал его самым учёным среди богачей и самым богатым среди учёных. В то же время Кавендиш вёл очень скромный и уединённый образ жизни. В частной жизни Кавендиш слыл чудаком и оригиналом; со своими домашними он объяснялся исключительно знаками, раз навсегда выработанными, дабы не терять напрасно времени и слов, и охотно беседовал только с коллегами по науке.
Основные труды Кавендиша относятся к химии газов и различным разделам экспериментальной физики. В 1766 г. Кавендиш опубликовал первую важную работу по химии – «Искусственный воздух», где сообщалось об открытии «горючего воздуха» (водорода). Он разработал методику собирания,
Он разработал методику собирания,
очистки и изучения газов, с помощью которой в 1766 г. ему удалось получить в чистом виде водород и углекислый газ, установить их удельный вес и другие свойства. В 1781 г. Кавендиш определил состав воздуха, а в 1784 г., сжигая водород, установил химический состав воды, опровергнув представления об её элементарности. Оставаясь твёрдым приверженцем теории флогистона, он тем не менее не оспаривал взгляды своего современника Антуана Лавуазье, допуская, что его кислородная теория имеет право на существование.
В 1772 г. одновременно с Даниилом Резерфордом Кавендиш открыл азот, однако опубликовал свои результаты с большим опозданием. В 1785 г. с помощью электрической искры он получил оксиды азота и исследовал их свойства. Он показал, что при пропускании электрического разряда через воздух над поверхностью воды азот реагирует с кислородом с образованием азотной кислоты. При этом Кавендиш обратил внимание на то, что 1/120 часть первоначального объема воздуха не вступает в реакцию. Вследствие несовершенства методов анализа и приборов Кавендиш не смог обнаружить в непрореагировавшем остатке новый элемент – аргон, который был открыт в 1894 г. Уильямом Рамзаем.
Вследствие несовершенства методов анализа и приборов Кавендиш не смог обнаружить в непрореагировавшем остатке новый элемент – аргон, который был открыт в 1894 г. Уильямом Рамзаем.
Большинство работ Кавендиша в области теплоты и электричества были опубликованы лишь через много лет после его смерти (труды по электричеству – в 1879 г. Джеймсом Максвеллом, собрание трудов – в 1921г.). Кавендиш ввёл в науку понятие электрического потенциала, исследовал зависимость ёмкости электрического конденсатора от среды, изучал взаимодействие электрических зарядов, предвосхитив закон Ш. Кулона. Он впервые сформулировал понятие теплоёмкости. В 1790 г. Кавендиш сконструировал крутильные весы и измерил с их помощью силу притяжения двух сфер, подтвердив закон Всемирного тяготения, а также определил гравитационную постоянную, массу и среднюю плотность Земли. Именем Кавендиша названа организованная Максвеллом в 1874 г. физическая лаборатория в Кембриджском университете.
Опыт Генри Кавендиша.
Установление Ньютоном закона Всемирного тяготения явилось важнейшим событием в истории физики. Его значение определяется прежде всего универсальностью гравитационного взаимодействия. На законе всемирного тяготения основывается один из центральных разделов астрономии — небесная механика. Мы ощущаем силу притяжения к Земле, однако притяжение малых тел друг к другу неощутимо. Требовалось экспериментально доказать справедливость закона всемирного тяготения и для обычных тел. Именно это и сделал Г.Кавендиш, попутно определив среднюю плотность Земли.
Его значение определяется прежде всего универсальностью гравитационного взаимодействия. На законе всемирного тяготения основывается один из центральных разделов астрономии — небесная механика. Мы ощущаем силу притяжения к Земле, однако притяжение малых тел друг к другу неощутимо. Требовалось экспериментально доказать справедливость закона всемирного тяготения и для обычных тел. Именно это и сделал Г.Кавендиш, попутно определив среднюю плотность Земли.
где m1 и m2 — массы материальных точек, R — расстояние между ними, a F — сила взаимодействия между ними. До начала XIX века G в закон всемирного тяготения не вводилось, так как для всех расчетов в небесной механике достаточно использовать постоянные GM, имеющие кинематическую размерность. Постоянная G появилась впервые, по-видимому, только после унификации единиц и перехода к единой метрической системе мер в конце XVIII века. Первоначально эксперимент был предложен Джоном Мичеллом. Именно он сконструировал главную деталь в экспериментальной установке — крутильные весы, однако умер в 1793 году так и не поставив опыта. После его смерти экспериментальная установка перешла к Генри Кавендишу. Кавендиш модифицировал установку, провёл опыты и описал их в Philosophical Transactions в 1798 году.
После его смерти экспериментальная установка перешла к Генри Кавендишу. Кавендиш модифицировал установку, провёл опыты и описал их в Philosophical Transactions в 1798 году.
Установка представляет собой деревянное коромысло с прикреплёнными к его концам небольшими свинцовыми шарами. Оно подвешено на нити из посеребрённой меди длиной 1 м. К шарам подносят шары большего размера массой 159 кг, сделанные также из свинца. В результате действия гравитационных сил коромысло закручивается на некий угол. Жёсткость нити была такой, что коромысло делало одно колебание за 15 минут. Угол поворота коромысла определялся с помощью луча света, пущенного на зеркальце на коромысле, и отражённого в микроскоп. Зная упругие свойства нити, а также угол поворота коромысла, можно вычислить гравитационную постоянную. Для предотвращения конвекционных потоков установка была заключена в ветрозащитную камеру. Угол отклонения измерялся при помощи телескопа. Списав закручивание нити на магнитное взаимодейстивие железного стержня и свинцовых шаров, Кавендиш заменил его медным, получив те же результаты.
Скорость при баллистическом движении.
Для расчёта скорости υ снаряда произвольной точке траектории, а также для определения угла β, который образует вектор скорости с горизонталью, достаточно знать проекции скорости на оси X и Y:
Если υх и υу известны, по теореме Пифагора можно найти скорость: υ=√υх2+υу2. Отношение катета υу, противолежащего углу β, к катету υх, принадлежащему к этому углу, определяет tg β и соответственно угол β: tg β =υу/υх. При равномерном движении по оси X проекция скорости движения υх
остаётся неизменной и равной проекции начальной скорости υ0х : υх= υо cos2 α. Зависимость υу(t) определяется формулой: υу= υ0у+ ау t, в которую следует подставить: υ0у= υ0 sin α, aу= -g. Тогда υу = υ0 sin α — gt.
Графики зависимости проекций скорости υх, υу от времени приведены ниже:
В любой точке траектории проекция скорости на ось X остается постоянной. По мере подъема снаряда проекция скорости на ось У уменьшается по линейному закону. При t=0 она равна υу= υ0 sinα. Найдем промежуток времени, через который проекция этой скорости станет равна нулю:
При t=0 она равна υу= υ0 sinα. Найдем промежуток времени, через который проекция этой скорости станет равна нулю:
0 = υ0 sin α — gt , t =(υ0sin α)/g
Полученный результат совпадает со временем подъема снаряда на
максимальную высоту. В верхней точке траектории вертикальная компонента скорости равна нулю.
Следовательно, тело больше не поднимается. При t > tmax проекция скорости υу становится отрицательной. Значит, эта составляющая скорости направлена противоположно оси Y, т. е. тело начинает падать вниз.
Так как в верхней точке траектории υ=0, то скорость снаряда равна:
υ = υх= υ0 cos α
Траектория движения тела в поле силы тяжести.
Рассмотрим основные параметры траектории снаряда, вылетающего с начальной скоростью υ0 из орудия, направленного под углом α к горизонту.
Движение снаряда происходит в вертикальной плоскости XY, содержащей υ0.
Выберем начало отсчёта в точке вылета снаряда. В евклидовом физическом пространстве перемещения тела по координатным осям X и Y можно рассматривать независимо.
Ускорение свободного падения g направлено вертикально вниз, поэтому по оси X движение будет равномерным. Это означает, что проекция скорости υх остаётся постоянной, равной её значению в начальный момент времени υ0х. Закон равномерного движения снаряда по оси X имеет вид: x= x0+ υ0х t. (1) По оси Y движение является равномерным, так как вектор ускорения свободного
падения g постоянен. Закон равнопеременного движения снаряда по оси Y можно представить в следующем виде: y = y0+v0у t + (ауt2)/2. (2) Криволинейное баллистическое движение тела можно рассматривать как результат сложения двух прямолинейных движений равномерного движения по оси X и равнопеременного движения по оси Y.
В выбранной системе координат:
x0=0 y0=0
υ0х= υ0 cos α υ0у= υ0 sin α
Ускорение свободного падения направлено противоположно оси Y, поэтому: ау= -g. Подставляя x0, y0, υ0х,υ0у, и ау в уровнения (1) и (2), получаем закон баллистического движения в координатной форме, в виде системы двух уравнений:
(3)
Уравнение траектории снаряда, или зависимость y(x), можно получить, исключая из уравнений системы время. Для этого из первого уравнения системы найдём: t=х/(υ0 cos α). Подставляя это значение во второе уравнение системы, получаем: y = υ0 sin α х/(υ0 cos α) — gx2/(2υ02cos2α) . Сокращая υ0 в первом слагаемом и учитывая, что sin α/cos α=tg α, получаем уравнение траектории снаряда: y = x tg α – gx2/(2υ02cos2α) (4).
Для этого из первого уравнения системы найдём: t=х/(υ0 cos α). Подставляя это значение во второе уравнение системы, получаем: y = υ0 sin α х/(υ0 cos α) — gx2/(2υ02cos2α) . Сокращая υ0 в первом слагаемом и учитывая, что sin α/cos α=tg α, получаем уравнение траектории снаряда: y = x tg α – gx2/(2υ02cos2α) (4).
Траектория баллистического движения.
Построим баллистическую траекторию. Графиком квадратичной функции, как известно, является парабола. В рассматриваемом случае парабола проходит
через начало координат, так как из (4) следует, что у=0 при х=0. Ветви параболы направлены вниз, так как коэффициент ( — g/(2υ02cos2α) ) при x2 меньше нуля.
Определим основные параметры баллистического движения: время подъема на максимальную высоту, максимальную высоту, время и дальность полета. Вследствие независимости движений по координатным осям подъем снаряда по вертикали определяется только проекцией начальной скорости υ0у на ось Y. В соответствии с формулой: tmax=υ0/g, полученной для тела, брошенного вверх с начальной скоростью υ0, время подъема снаряда на максимальную высоту равно: tmax=υ0у/g=(υ0 sin α)/g.
Максимальная высота подъема может быть рассчитана по формуле: уmax=υ02, если υ0у подставить вместо υ0: уmax = υ0у2/g = (υ02 sin2α)/2g.
На последнем рисунке сопоставляется вертикальное и криволинейное движение с одинаковой начальной скоростью по оси Y. В любой момент времени тело, брошенное вертикально вверх, и тело, брошенное под углом к горизонту с той же вертикальной проекцией скорости, движутся по оси Y синхронно.
Так как парабола симметрична относительно вершины, то время полета tn снаряда в 2 раза больше времени его подъема на максимальную высоту: tn=2tmax=(2υ0 sin α)/g. Подставляя время полета в закон движения по оси X, получаем максимальную дальность полета: xmax=(υ0 cos α)·(2υ0 sin α)/g. Так как
2 sin α cos α = sin 2α, то: xmax=(υ02/g)·sin2α.
Применение баллистического движения на практике.
Представим себе, что из одной точки выпустили несколько снарядов, под различными углами. Например, первый снаряд под углом 30°, второй под углом 40°, третий под углом 60°,а четвертый под углом 75°
1) На рисунке зеленым цветом изображен график снаряда выпущенного под углом 30°, белым под углом 45°, фиолетовым под углом 60°, а красным под углом 75°. А теперь посмотрим на графики полёта снарядов и сравним их.(начальная скорость одинакова, и равна 20 км/ч).
А теперь посмотрим на графики полёта снарядов и сравним их.(начальная скорость одинакова, и равна 20 км/ч).
Сравнивая эти графики можно вывести некоторую закономерность: с увеличением угла вылета снаряда, при одинаковой начальной скорости, дальность полёта уменьшается, а высота увеличивается.
2) Теперь рассмотрим другой случай, связанный с различной начальной
скоростью, при одинаковом угле вылета. На следующем рисунке зеленым цветом изображен график снаряда выпущенного с начальной скоростью 18 км/ч, белым со скоростью 20 км/ч, фиолетовым со скоростью 22 км/ч, а красным со скоростью 25 км/ч. А теперь посмотрим на графики полёта снарядов и сравним их (угол полёта одинаков и равен 30°). Сравнивая эти графики можно вывести некоторую закономерность: с увеличением начальной скорости вылета снаряда, при одинаковом угле вылета, дальность и высота полёта снаряда увеличиваются.
Из выше перечисленных примеров напрашивается следующий вывод: с увеличением угла вылета снаряда, при одинаковой начальной скорости, дальность полёта уменьшается, а высота увеличивается, а с увеличением
начальной скорости вылета снаряда, при одинаковом угле вылета, дальность и
высота полёта снаряда увеличиваются.
Применение теоретических расчётов к управлению баллистическими ракетами.
а) траектория баллистической ракеты.
Наиболее существенной чертой, отличающей баллистические ракеты от ракет других классов, является характер их траектории. Траектория баллистической ракеты состоит из двух участков – активного и пассивного. На активном участке ракета движется с ускорением под действием силы тяги двигателей. При этом ракета запасает кинетическую энергию. В конце активного участка траектории, когда ракета приобретёт скорость, имеющую заданную величину
и направление, двигательная установка выключается. После этого головная часть ракеты отделяется от её корпуса и дальше летит за счёт запасённой кинетической энергии.
Второй участок траектории (после выключения двигателя) называют участком свободного полёта ракеты, или пассивным участком траектории. Ниже для краткости будем обычно говорить о траектории свободного полёта ракеты, подразумевая при этом траекторию не всей ракеты, а только её головной части.
Баллистические ракеты стартуют с пусковых установок вертикально вверх. Вертикальный пуск позволяет построить наиболее простые пусковые установки и обеспечивает благоприятные условия управления ракетой сразу же после старта. Кроме того, вертикальный пуск позволяет снизить требования к жёсткости корпуса ракеты и, следовательно, уменьшить вес её конструкции.
Управление ракетой осуществляется так, что через несколько секунд после старта она, продолжая подъём вверх, начинает постепенно наклоняться в сторону цели, описывая в пространстве дугу. Угол между продольной осью ракеты и горизонтом (угол тангажа) изменяется при этом на 90º до расчетного
конечного значения. Требуемый закон изменения (программа) угла тангажа
задается программным механизмом, входящим в бортовую аппаратуру ракеты. На завершающем отрезке активного участка траектории угол тангажа выдерживается постоянным и ракета летит прямолинейно, а когда скорость достигает расчетной величины, двигательную установку выключают. Кроме величины скорости, на завершающем отрезке активного участка траектории устанавливают с высокой степенью точности также и заданное направление полёта ракеты (направление вектора её скорости). Скорость движения в конце активного участка траектории достигает значительных величин, но ракета набирает эту скорость постепенно. Пока ракета находится в плотных слоях атмосферы, скорость её мала, что позволяет снизить потери энергии на преодоление сопротивления среды.
Кроме величины скорости, на завершающем отрезке активного участка траектории устанавливают с высокой степенью точности также и заданное направление полёта ракеты (направление вектора её скорости). Скорость движения в конце активного участка траектории достигает значительных величин, но ракета набирает эту скорость постепенно. Пока ракета находится в плотных слоях атмосферы, скорость её мала, что позволяет снизить потери энергии на преодоление сопротивления среды.
Момент выключения двигательной установки разделяет траекторию баллистической ракеты на активный и пассивный участки. Поэтому точку траектории, в которой выключаются двигатели, называют граничной точкой. В этой точке управление ракетой обычно заканчивается и весь дальнейший путь к цели она совершает в свободном движении. Дальность полёта баллистических ракет вдоль поверхности Земли, соответствующая активному участку траектории, равна не более чем 4-10% общей дальности. Основную часть траектории баллистических ракет составляет участок свободного полёта.
Для существенного увеличения дальности нужно применять многоступенчатые ракеты. Многоступенчатые ракеты состоят из отдельных блоков-ступеней, каждая из которых имеет свои двигатели. Ракета стартует с работающей двигательной установкой первой ступени. Когда топливо первой ступени израсходуется, включается двигатель второй ступени, а первая ступень сбрасывается. После сброса первой ступени сила тяги двигателя должна сообщить ускорение меньшей массе, что приводит к значительному возрастанию скорости υн в конце активного участка траектории по сравнению с
одноступенчатой ракетой, имеющей ту же начальную массу.
Расчеты показывают, что уже при двух ступенях можно получить начальную скорость, достаточную для полёта головной части ракеты на межконтинентальные расстояния.
Идею применения многоступенчатых ракет для получения больших начальных скоростей и, следовательно, больших дальностей полёта, выдвинул К.Э. Циолковский. Эту идею используют при создании межконтинентальных баллистических ракет и ракет-носителей для запуска космических объектов.
б) траектории управляемых снарядов.
Траектория ракеты – это линия, которую в пространстве описывает её центр тяжести. Управляемый снаряд – это беспилотный летательный аппарат, обладающий средствами управления, с помощью которых можно влиять на движение аппарата на всей траектории или на одном из участков полёта. Управление снарядом на траектории потребовалось для того, чтобы поразить цель, оставаясь на безопасном от неё расстоянии. Существуют два главных класса целей: подвижные и неподвижные. В свою очередь реактивный снаряд может запускаться с неподвижного стартового устройства или с подвижного (например, с самолёта). При неподвижных целях и стартовых устройствах данные, необходимые для поражения цели, получаются из известного относительного расположения места старта и цели. При этом траектория движения реактивного снаряда может быть заранее рассчитана, а снаряд снабжен устройствами, обеспечивающими его движение по определённой рассчитанной программе.
В других случаях относительное расположение места старта и цели непрерывно меняется. Для поражения цели в этих случаях необходимо иметь устройства, следящие за целью и непрерывно определяющие взаимное положение снаряда и цели. Сведения, получаемые от этих устройств,
Для поражения цели в этих случаях необходимо иметь устройства, следящие за целью и непрерывно определяющие взаимное положение снаряда и цели. Сведения, получаемые от этих устройств,
используются для управления движением снаряда. Управление должно
обеспечивать движение ракеты к цели по наивыгоднейшей траектории.
Для того чтобы полностью охарактеризовать полёт ракеты, недостаточно знать только такие элементы её движения, как траектория, дальность, высота, скорость полёта и другие величины, характеризующие движение центра тяжести ракеты. Ракета может занимать в пространстве различные положения относительно своего центра тяжести.
Ракета представляет собой тело значительных размеров, состоящее из множества узлов и деталей, изготовленных с известной степенью точности. В процессе движения она испытывает различные возмущения, связанные с неспокойным состоянием атмосферы, неточностью работы силовой установки, различного рода помехи и т. п. Совокупность этих погрешностей, не предусмотренных расчётом, приводит к тому, что фактическое движение сильно отличается от идеального. Поэтому для эффективного управления ракетой необходимо устранить нежелательное влияние случайных возмущающих воздействий, или, как говорят, обеспечить устойчивость движения ракеты.
Поэтому для эффективного управления ракетой необходимо устранить нежелательное влияние случайных возмущающих воздействий, или, как говорят, обеспечить устойчивость движения ракеты.
в) координаты, определяющие положение ракеты в пространстве.
Изучение разнообразных и сложных движений, совершаемых ракетой может быть значительно упрощено, если движение ракеты представить как сумму поступательного движения её центра тяжести и вращательного движения относительно центра тяжести. Примеры, приведенные выше, наглядно показывают, что для обеспечения устойчивости движения ракеты чрезвычайно важно иметь её устойчивость относительно центра тяжести, т. е. угловую стабилизацию ракеты. Вращение ракеты относительно центра тяжести можно представить как сумму вращательных движений относительно трёх перпендикулярных осей, имеющих определённую ориентацию в пространстве. Ниже, на рисунке изображена идеальная оперенная ракета, летящая по
рассчитанной траектории. Начало систем координат, относительно которой мы
будем стабилизировать ракету, поместим в центр тяжести ракеты. Ось X направим по касательной к траектории в сторону движения ракеты. Ось Y проведём в плоскости траектории перпендикулярно к оси X, а ось Z -перпендикулярно к первым двум осям, как показано на приведенном ниже рисунке. С ракетой свяжем прямоугольную систему координат X’, Y’, Z’, аналогичную первой, причём ось X’ должна совпадать с осью симметрии ракеты. В идеально стабилизированной ракете оси X’ ,Y’ ,Z’ совпадают с осями X, Y, Z, что показано все на том же, ниже рисунке.
Ось X направим по касательной к траектории в сторону движения ракеты. Ось Y проведём в плоскости траектории перпендикулярно к оси X, а ось Z -перпендикулярно к первым двум осям, как показано на приведенном ниже рисунке. С ракетой свяжем прямоугольную систему координат X’, Y’, Z’, аналогичную первой, причём ось X’ должна совпадать с осью симметрии ракеты. В идеально стабилизированной ракете оси X’ ,Y’ ,Z’ совпадают с осями X, Y, Z, что показано все на том же, ниже рисунке.
Под действием возмущений ракета может поворачиваться вокруг каждой из ориентированных осей X, Y, Z. Поворот ракеты вокруг оси X называют креном ракеты. Угол крена γ лежит в плоскости YOZ. Его можно определить, измерив в этой плоскости угол между осями Z и Z’ или Y и Y’. Поворот вокруг оси Y называют рысканием ракеты. Угол рыскания φ находится в плоскости XOZ как угол между осями X и X’ или Z и Z’. Угол поворота вокруг оси Z называют углом тангажа φ’. Он определяется углом между осями X,X’ и Y,Y’, лежащими в плоскости траектории.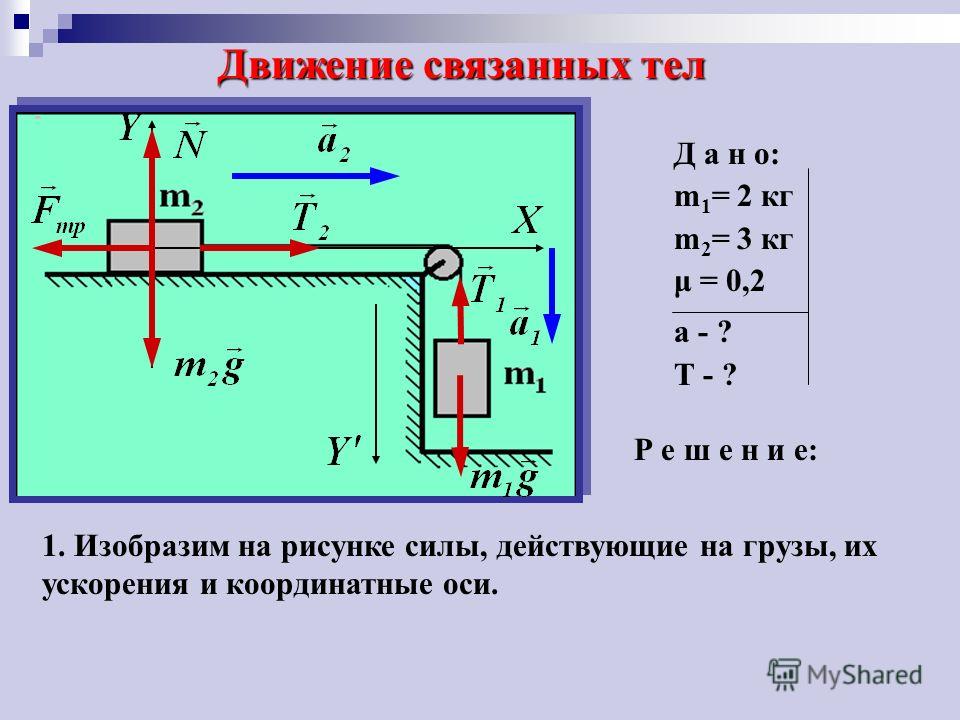
Автоматические устройства стабилизации ракеты должны придавать ей такое положение, когда φ’=0 или φ’=α, φ=0, γ=0 . Для этого на ракете должны находиться чувствительные устройства, способные изменить её угловое
положение. Траектория ракеты в пространстве определяется текущими
координатами X0, Y0, Z0 её центра тяжести. За начало отсчёта берут точку старта ракеты. Для ракет дальнего действия за ось X0 принимают прямую, касательную к дуге большого круга, соединяющего старт с целью. Ось Y0 направляют при этом вверх, а ось Z0 — перпендикулярно к двум первым осям. Эта система координат называется земной.
Расчётная траектория баллистических ракет лежит в плоскости X0OY0, называемой плоскостью стрельбы, и определяется двумя координатами X0 и Y0.
С помощью этой работы можно многое рассказать ученикам о баллистике, баллистическом движении тел, о полете ракет, а также нахождении их координат в пространстве.
Дополнительные источники и литература.
- Управление ракетами — Петров В.
 П., Сочивко А.А., Москва: изд-во
П., Сочивко А.А., Москва: изд-во
«Воениздат.»-1959 г.
- Управление баллистическими ракетами и космическими объектами — Жаков А.М., Москва: изд-во «Воениздат»-1974 г.
- Ксомонавтика сегодня и завтра — Уманский С.П., Москва: изд-во «Просвещение»-1986 г.
- Военный энциклопедический словарь — Огарков Н.В., изд-во «Воениздат»-1984 г.
- Сайт «Википедия. Свободная энциклопедия», //http://ru.wikipedia.org/wiki/Isaac_Newton
- Сайт «Южный Федеральный университет», //http://www.physchem.chimfak.rsu.ru/Source/History/Persones/Cavendish.html
Виртуальные лабораторные работы по физике
Виртуальные лабораторные работы по физике
Announcements
Виртуальные интерактивные лабораторные работы по физике
Virtual laboratory assignments in physics
Электронные интерактивные экспериментальные задачи по физике
Interactive experimental electronic problems in physics
Электронный демонстрационный эксперимент по физике
Electronic demo-experiment in physics
Более 200 виртуальных лабораторных работ, экспериментальных задач и демонстраций по всем разделам физики
More than 200 virtual laboratory assignments, experimental tasks and demos in all sections of physics
Работа виртуальных лабораторных работ, экспериментальных задач и электронных демонстраций в режиме реального времени.
Implementation of virtual laboratory assignments, experimental tasks and virtual demos in real time. Non-stationary and stationary interactive electronic physical models
Виртуальные экспериментальные задачи для подготовки к олимпиадам школьников
Virtual experimental tasks helping prepare for school Olympiads
«Виртуальная лабораторная работа по физике.
«Виртуальные лабораторные работы по физике.
«Виртуальные лабораторные работы по физике.
«Виртуальная лабораторная работа по физике.
Форум для пользователей сайта Forum
1. Виртуальные лабораторные работы по механике Page
2. Виртуальные лабораторные работы по молекулярной физике и термодинамике Page
3.
 Виртуальные лабораторные работы по электричеству и магнетизму Page
Виртуальные лабораторные работы по электричеству и магнетизму Page4. Виртуальные лабораторные работы по изучению физики колебаний и волн Page
Интерактивные модели — иллюстрации по всем разделам физики Page
Apps on Physics (Приложения по физике) URL
Skip available courses
Available courses
Документы
Документы
Course
Физика МГОК
Физика МГОК
Course
Астрономия МГОК
Астрономия МГОК
Course
Виртуальные лабораторные работы
Виртуальные лабораторные работы
Course
Молекулярная физика и основы термодинамики
Молекулярная физика и основы термодинамики
Course
1.
 Механика
Механика1. Механика
Курс «Физический практикум по курсу «Механика»» предназначен для уч…
Course
2. Молекулярная физика
2. Молекулярная физика
Курс «Физический практикум по курсу «Молекулярная физика и основы т…
Course
3. Электричество и магнетизм
3. Электричество и магнетизм
Курс «Физический практикум по курсу «Электричество и магнетизм» пре…
Course
4. Колебания и волны
4. Колебания и волны
Курс «Физический практикум по курсу «Механические колебания и волны…
Course
5. Оптика
5. Оптика
Course
6.
 Квантовая и атомная физика
Квантовая и атомная физика6. Квантовая и атомная физика
Course
Экспериментальные задачи 2018/11
Экспериментальные задачи 2018/11
Экспериментальные задачи
Course
Экспериментальные задачи 2019/10
Экспериментальные задачи 2019/10
Экспериментальные задачи «Физпрактикум 2019/10»
Course
Мякишев
Мякишев
Course
Колебания и волны
Колебания и волны
Курс «Колебания и волны» предназначен для учащихся школ профильных …
Course
Виртуальные лабораторные работы для всех разделов физики
Виртуальные лабораторные работы для всех разделов физики
Course
VirtualLab
VirtualLab
Course
1.
 Тематические задачи и правила дорожного движения — категории ABM
Тематические задачи и правила дорожного движения — категории ABM1. Тематические задачи и правила дорожного движения — категории ABM
Курс содержит вопросы экзаменационных билетов по ПДД распределенных…
Course
2. Правила дорожного движения по задачам — категории АВМ
2. Правила дорожного движения по задачам — категории АВМ
Курс содержит тесты по правилам дорожного движения, задачи которых …
Course
3. Марафоны по задачам ПДД — категории АВМ
3. Марафоны по задачам ПДД — категории АВМ
Курс содержит тесты сгруппированные по одинаковым темам правил доро…
Course
4. Экзаменационные билеты по ПДД — категории АВМ
4. Экзаменационные билеты по ПДД — категории АВМ
Курс содержит официальные экзаменационные билеты по правилам дорожн. ..
..
Course
5. Контроль (зачеты и экзамены) — категории ABM
5. Контроль (зачеты и экзамены) — категории ABM
Курс предназначен для проведения внутренних зачетов и экзаменов в а…
Course
ЕГЭ Физика 2022
ЕГЭ Физика 2022
Course
Физика ЕГЭ
Физика ЕГЭ
Course
Физика ОГЭ
Физика ОГЭ
Course
Математика ЕГЭ
Математика ЕГЭ
Course
Электронный учебник «Колебания и волны»
Электронный учебник «Колебания и волны»
Course
Общий физический практикум (Атомная физика)
Общий физический практикум (Атомная физика)
Course
Элементарная физика
Элементарная физика
Раздел курса физики «Элементарная физика» для студентов заочного от. ..
..
Course
Macromedia Flash
Macromedia Flash
Course
Skip новости сайта
Новости сайта
Виртуальная лабораторная работа МЭШ по физике «Определение КПД тепловой установки при превращении льда в пар»
Приложение моделирует эксперимент по превращению льда в пар. Целью работы является определение коэффициента полезного действия тепловой установки. Виртуальная лабораторная установка …
Read the rest of this topic
(115 words)
Виртуальная лабораторная работа МЭШ по физике «Экспериментальное нахождение массы воды в мокром снеге». В приложении представлена интерактивная модель экспериментальной установки для нахождения массы воды в мокром снеге. Для нахождения искомой величины требуется поместить мокрый снег в …
Read the rest of this topic
(45 words)
Виртуальная лабораторная работа МЭШ по физике «Определение длины световой волны с помощью дифракционной решетки». В приложении представлена виртуальная лабораторная установка для определения длины световой волны с помощью дифракционной решетки. Приложение может быть использовано в качестве …
В приложении представлена виртуальная лабораторная установка для определения длины световой волны с помощью дифракционной решетки. Приложение может быть использовано в качестве …
Read the rest of this topic
(51 words)
Виртуальная лабораторная работа по физике «Определение удельной теплоты плавления льда». В приложении представлена модель лабораторной работы по физике «Определение удельной теплоты плавления льда». Установка работает в режиме реального времени под управлением электронного блока. Порядок …
Read the rest of this topic
(129 words)
Виртуальная лабораторная работа по физике «Определение удельной теплоемкости жидкостей методом электрокалориметра». Приложение моделирует эксперимент по определению удельной теплоемкости жидкостей методом электрокалориметра. Виртуальная лабораторная установка работает в режиме реального …
Read the rest of this topic
(32 words)
Виртуальная лабораторная работа МЭШ по физике «Градуирование пружины и измерение сил динамометром». Представленное приложение моделирует одноименную лабораторную установку, описанную в учебнике физики за 7 класс под авторством Перышкина А.В.
Представленное приложение моделирует одноименную лабораторную установку, описанную в учебнике физики за 7 класс под авторством Перышкина А.В.
Виртуальная лабораторная работа МЭШ по физике «Определение удельной теплоемкости металлов». Приложение моделирует эксперимент по определению удельной теплоемкости металлов. Виртуальная лабораторная установка работает в режиме реального времени и является интерактивной.
Виртуальная лабораторная работа МЭШ по физике «Определение удельной теплоты парообразования воды». Приложение моделирует эксперимент по определению удельной теплоты парообразования воды. Виртуальная лабораторная установка работает в режиме реального времени и является интерактивной.
Виртуальная лабораторная работа МЭШ по физике «Определение постоянной Больцмана».
Приложение моделирует реальный эксперимент по определению постоянной Больцмана. Виртуальная лабораторная установка работает в режиме реального времени и является многовариантной.
Виртуальная лабораторная работа по физике «Сравнение количеств теплоты при смешивании воды разной температуры».
Приложение моделирует одноименную лабораторную работу по физике за 8 класс под авторством Перышкина А.В. Виртуальная лабораторная установка работает в режиме реального времени и …
Read the rest of this topic
(66 words)
Older topics …
Skip Main menu
Новости сайта Forum
Create new account
Lost password?
Skip LoginCreate new account
Lost password?
Skip Calendar| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
No online users (last 5 minutes)
lissazhuДвижение тела в поле тяготения Земли в военной науке баллистике.
 доклад, проект
доклад, проект- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Использование теоретических знаний по теме: Движение тела в поле тяготения Земли в военной науке баллистике. , предмет презентации: Физика. Этот материал в формате pptx (PowerPoint) содержит 16 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
, предмет презентации: Физика. Этот материал в формате pptx (PowerPoint) содержит 16 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Использование теоретических знаний по теме:
Движение тела в поле тяготения Земли в военной науке баллистике.
Выполнил:
Учитель физики
МБОУ Поведниковской СОШ
Мытищинского района
Заматаев Сергей Александрович
Содержание
Понятие – баллистики.
История возникновения баллистики .
Основные законы баллистического движения.
Исследование баллистического движения на практике
Исследовательская работа с использованием баллистического пистолета. Исследовательская работа с использованием программы «Открытая физика»
Исследовательская работа с использованием программы «Открытая физика»
Задача (скорость тела направлена горизонтально)
Приложение1 (Что такое парашют, его история возникновения, первые практические прыжки, парашютизм как спорт)
Баллистика-раздел механики,изучающий движение тел в поле тяжести Земли.
Баллистика-наука о движении снарядов, мин, пуль, неуправляемых ракет при стрельбе (пуске). Основные разделы баллистики: внутренняя баллистика и внешняя баллистика. Исследованием реальных процессов, происходящих при горении пороха, движении снарядов, ракет (или их моделей) и т. д., занимается эксперимент баллистики. Внешняя баллистика изучает движение снарядов, мин, пуль, неуправляемых ракет и др. после прекращения их силового взаимодействия со стволом оружия (пусковой установкой), а также факторы, влияющие на это движение. Основные разделы внешней баллистики: изучение сил и моментов, действующих на снаряд в полёте; изучение движения центра масс снаряда для расчета элементов траектории, а также движение снаряда относительно центра масс с целью определения его устойчивости и характеристик рассеивания.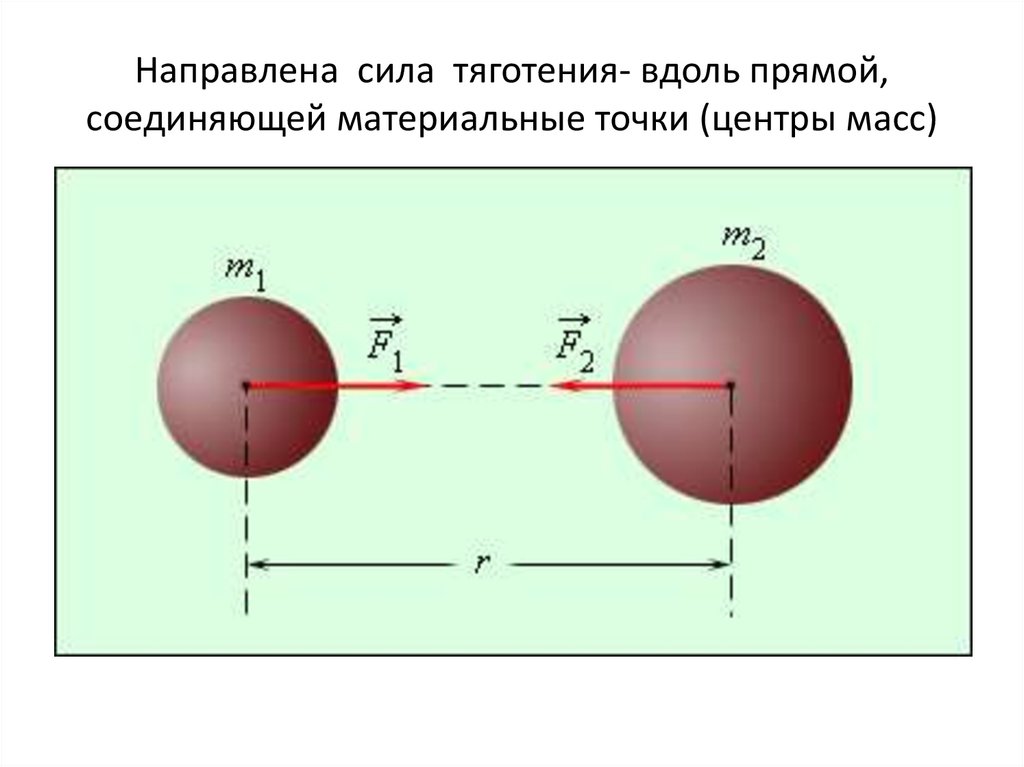 Разделами внешней баллистики являются также теория поправок, разработка методов получения данных для составления таблиц стрельбы и внешнебаллистическое проектирование.
Разделами внешней баллистики являются также теория поправок, разработка методов получения данных для составления таблиц стрельбы и внешнебаллистическое проектирование.
История возникновения баллистики.
Возникновение баллистики относится к 16 в. В многочисленных войнах на протяжении всей истории человечества враждующие стороны, доказывая своё превосходство, использовали сначала камни, копья , и стрелы, а затем ядра, пули, снаряды, и бомбы. Успех сражения во многом определялся точностью попадания в цель. При этом точный бросок камня, поражение противника летящим копьём или стрелой фиксировались воином визуально. Это позволяло при соответствующей тренировке повторять свой успех в следующем сражении. Значительно возросшая с развитием техники (скорость и соответственно дальность полета) снарядов и пуль сделали возможными дистанционные сражения. Однако навыка воина, разрешающей способности его глаза было недостаточно для точного попадания в цель в артиллерийской дуэли первым.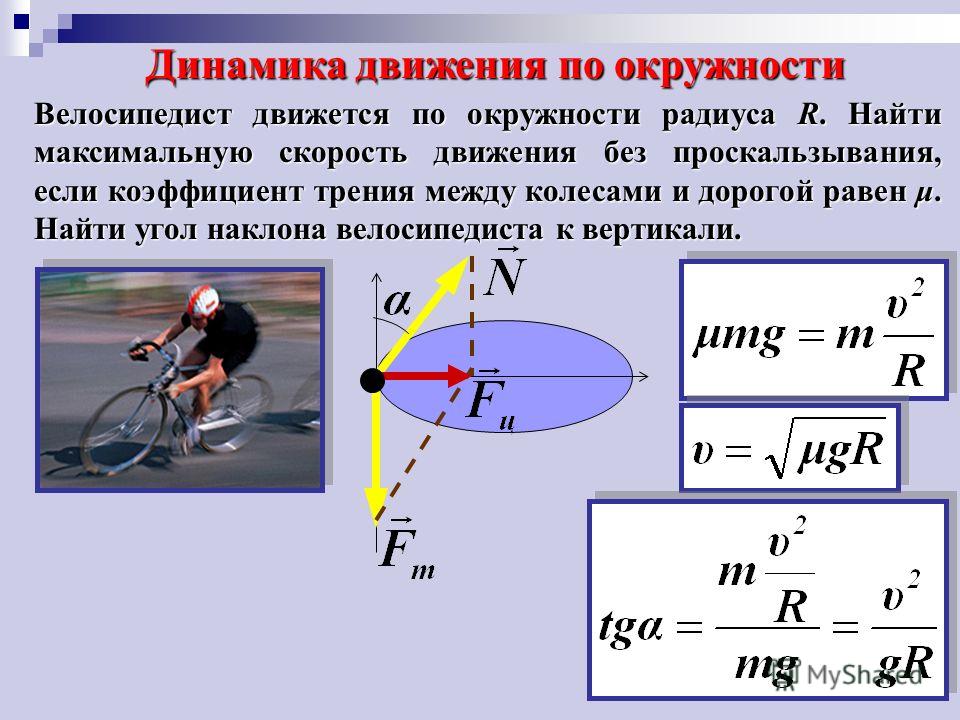 Желание побеждать стимулировало появление баллистики (от греч. ballo — бросаю).
Желание побеждать стимулировало появление баллистики (от греч. ballo — бросаю).
Скорость при баллистическом движении.
Для расчёта скорости v снаряда произвольной точке траектории, а также для определения угла , который образует вектор скорости с горизонталью, достаточно знать проекции скорости на оси X и Y.
Если Vx и Vy известны, то по теореме Пифагора можно найти скорость
υ=√υх2+υу2
Закон равномерного движения снаряда по оси Х имеет вид: х=х0+υ0хt
Закон равнопеременного движения снаряда по оси У можно представить в виде: у=у0+υ0уt+aуt2/2
Уравнение траектории снаряда:
Дальность полета тела при одной и той же начальной скорости зависит от угла, под которым тело брошено к горизонту L=x·tgα-gx2/(2υ02 cos2α)
Баллистическое движение:
1. Исследовательская работа
Исследовательская работа
Программа «Открытая физика».
Цель исследования: определить, от каких величин зависит дальность полета тела, брошенного под углом к горизонту.
Вывод: Проведя исследовательскую работу, устанавливаем: что дальность полёта тела зависит от его начальной скорости , чем она выше, тем дальность полёта тела больше.
Вывод: Проведя исследовательскую работу, выясняем, что дальность полёта тела при одной и той же начальной скорости зависит от угла, под которым тело брошено к горизонту. Максимальная дальность полёта наблюдается при 45 градусах. (При выбросе в 90 градусов, тело останется на месте.)
2)
Формулы:
Вычисление дальности полета:
L =
Вычисление максимальной высоты подъема:
Н =
Вычисление времени полета
t =
Вывод: проведя исследовательскую работу, мы убеждаемся в том, что дальность полёта тела зависит от его начальной скорости и от угла, под которым тело брошено к горизонту .
Исследование законов баллистики на практике
Метание гранаты на уроке физкультуры
Условие:
С самолёта, летящего в горизонтальном направлении со скоростью , на высоте над землёй сброшен груз. Как далеко от места сбрасывния груз упадёт на землю?
Решение:
За начало отсчёта координат примем точку, где груз был сброшен, а за начало отсчёта времени – момент сбрасывания. Ось X направим горизонтально, а ось Y – вертикально вверх.
Движение груза описывается известными уравнениями:
(1)
В нашей задаче и, значит, и . Тогда уравнения (1) примут вид:
Задача. (скорость направлена горизонтально)
В момент приземления груза ,а дальность полёта . Из уравнения (3) находим время полёта:
(2)
(3)
Подставив это выражение в уравнение (2), получаем:
Ответ:
Спасибо за внимание!
Скачать презентацию
 ru?
ru?Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Область досягаемости в задаче о свободном движении тела в поле тяготения Земли
В работе рассматривается простое решение задачи определения характеристик траектории тела, брошенного под углом к горизонту с заданной высоты, без учёта сопротивления среды. Вводится понятие области досягаемости как совокупности точек пространства, которые могут быть достигнуты при всех возможных углах бросания, и определяются её границы.
Ключевые слова: свободное падение, характеристики траектории движения тела, брошенного под углом к горизонту, область досягаемости.
Задача о свободном падении тела вблизи поверхности Земли изучена довольно основательно. Это движение в вакууме описано, например, в [1–4]. Традиционно при рассмотрении этой темы в школе основное внимание уделяется проблемам определения вида траектории движения, расчёта дальности полёта, получения аналитического выражения для необходимого угла бросания. При этом, к сожалению, не рассматривается проблема определения той области в плоскости движения тела, которая содержала бы в себе все точки пространства, которые могут быть достигнуты в процессе свободного движения тела, брошенного под различными углами к горизонту при заданной начальной высоте и известной начальной скорости.
Решение этой актуальной задачи представляет интерес как учебно-методический при изучении темы в школе, так, возможно, и практический при предварительной оценке тактико-технических характеристик артиллерийских систем и стрелкового оружия.
- Уравнение траектории в относительных переменных
Траектория движения изображена на рис.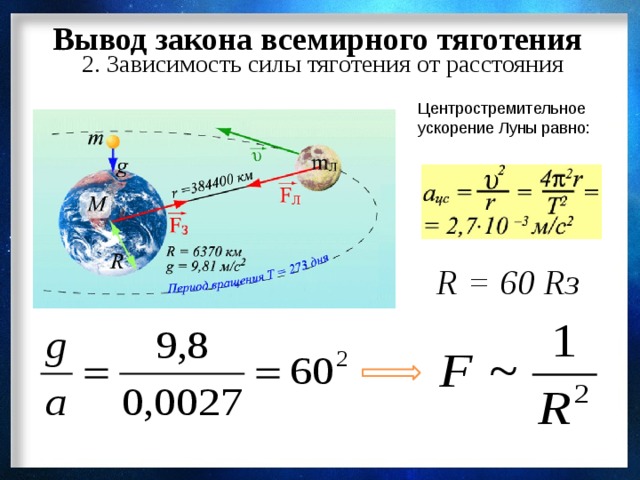 1, где x и y — соответственно, горизонтальная и вертикальная координаты тела, v0 — начальная скорость, h — начальная высота, α — угол бросания, D — дальность полёта.
1, где x и y — соответственно, горизонтальная и вертикальная координаты тела, v0 — начальная скорость, h — начальная высота, α — угол бросания, D — дальность полёта.
Рис. 1. Схема движения
В [1–4] для этой траектории получено следующее уравнение:
y = h + tg α ּ x — (1 + tg2 α ּ) x2. (1)
Для упрощения последующего анализа перейдём в этом выражении к безразмерным относительным величинам с помощью следующих обозначений [3]:
= H, = X, = Y, = a.
Физический смысл нормирующего множителя H состоит в том, что его значение равно максимальной высоте подъёма ymaxпри начальной скорости v0, направленной вертикально вверх (при h = 0 и α = ). В безразмерных величинах X и Y уравнение траектории (1) принимает вид [3]:
Y = a + tg α ּ X — (1 + tg2 α) ּ .
Оно упрощается, если обозначить tg α = z:
Y = — (1 + ) ּ + z ּ X + a. (2)
Уравнение (2) является квадратным как относительно горизонтальной координаты X, так и относительно тангенса угла бросания z. Целесообразно в (2) сделать замену переменной = s, чтобы получить уравнение траектории в виде
Y = ּ + ּ X + a, (3)
обеспечивающем затем в пунктах 4 и 5 довольно простое определение максимальной дальности полёта.
- Геометрическое место вершин траекторий
Выражение (2) представляет собой уравнение параболы, известное из школьного курса математики как y=a+ bx + c. Также из программы по математике известно, как можно найти координаты и вершины параболы: = , = y (). Воспользуемся этими простыми формулами для того, чтобы найти координаты XВ и YВ вершин парабол, определяемых уравнением (2). Получим:
Воспользуемся этими простыми формулами для того, чтобы найти координаты XВ и YВ вершин парабол, определяемых уравнением (2). Получим:
Xв = 2. (4)
Подставив это выражение в (2), получаем значение ординаты вершины параболы:
Yв = + a. (5)
Пара выражений (4) и (5) представляет собой в неявном виде уравнение той линии, на которой находятсявсевершины парабол — высшие точки всевозможных траекторий. Эта линия схематически изображена на рис. 2.
Рис. 2. Схема геометрического места вершин траекторий
Уравнение (4) — (5) получено в параметрической форме, в качестве параметра в нём выступает величина z. Желательно получить это уравнение в явном виде, а для этого из выражений (4) и (5) нужно исключить параметрz. Удобно сделать это, если из (5) выразить как функцию от Yв иподставить его в (4). Но в (4), кроме , есть ещё и z в первой степени, поэтому, чтобы не вводить в преобразования квадратный корень, вначале возведём в квадрат левую и правую части равенства (4). После несложных преобразований получаем уравнение геометрического места вершин траекторий уже в явном виде:
После несложных преобразований получаем уравнение геометрического места вершин траекторий уже в явном виде:
+ (1 + 2a) Yв + a + a2 = 0. (6)
Геометрическим образом уравнения (6) является эллипс, показанный на рис. 3 для случая нулевой начальной высоты (h = 0).
Рис. 3. Геометрическое место вершин траекторий в координатах X и Y при h = 0
При изменении начальной высоты h эллипс, изображённый на рис. 3, перемещается по оси ординат на величину , причём при положительном значении h — вверх, а при отрицательном — вниз.
Уравнение эллипса (6) можно привести к более простому виду, если выполнить масштабирование по оси X, то есть если перейти к новой переменной X1 по правилу X1 = 0,5 Xв. В получившемся уравнении в переменных X1 и Yв можно выделить полный квадрат и получить окончательно:
X12 + (Yв — (0,5 + a))2 = 0,52. (7)
(7)
Из школьного курса математики известно, что (7) — это уравнение окружности с центром в точке (0,5; 0,5 + a) и радиусом, равным 0,5.
Таким образом, в координатах X1 и Yв вершины траекторий находятся на полуокружности с радиусом, равным 0,5, и центром, находящимся на оси ординат в точке 0,5 + a (рис. 4).
Рис. 4. Полуокружности вершин траекторий (1 — при a = 0; 2 — при a = 0,25; 3 — при a = — 0,25)
Линия 1 на рис. 4 соответствует нулевому значению начальной высоты (h = 0). Из выражения (7) следует, что изменение начальной высоты h приводит только к перемещению центра окружности по оси ординат на величину , причём при положительном значении h — вверх (окружность 2 на рис. 4), а при отрицательном — вниз (окружность 3 на рис. 4). Величина радиуса полуокружности (0,5) при изменении начальной высоты не изменяется.
Для случая нулевой начальной высоты на рис.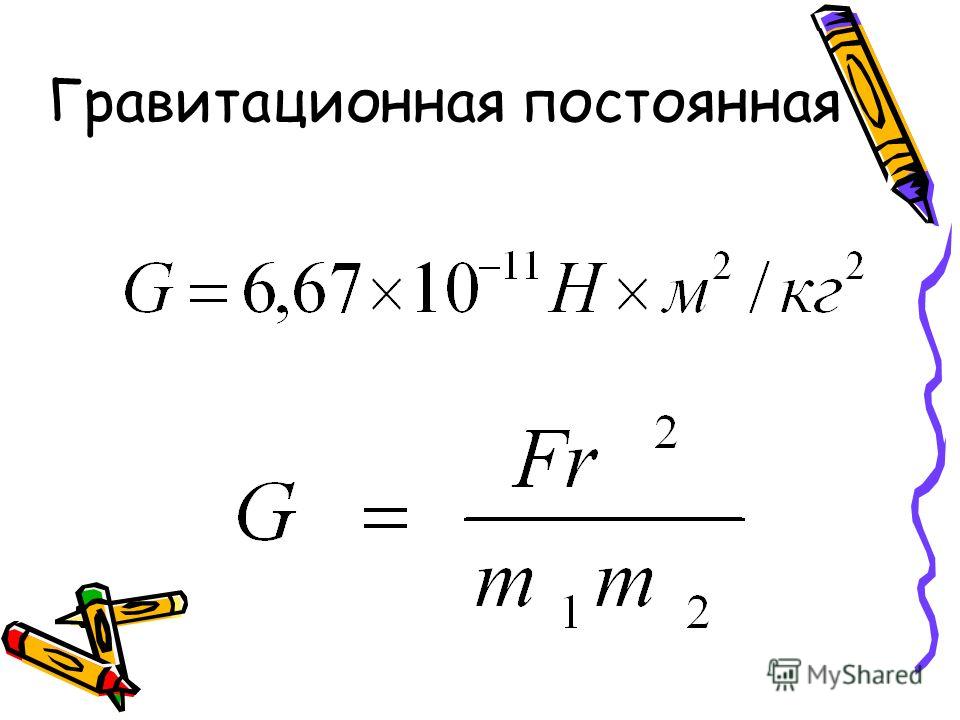 4 отмечены также точки, соответствующие углам бросания α, равным 300, 450 и 600. Из рисунка 4 видно, что нижняя часть полуокружности соответствует настильным (невысоким) траекториям, при которых α450, а верхняя часть — навесным (высоким) траекториям, для которых α>450.
4 отмечены также точки, соответствующие углам бросания α, равным 300, 450 и 600. Из рисунка 4 видно, что нижняя часть полуокружности соответствует настильным (невысоким) траекториям, при которых α450, а верхняя часть — навесным (высоким) траекториям, для которых α>450.
Поскольку вершины парабол являются самыми верхними точками траекторий движения, вполне естественным было бы предположить, что при X ≤ 1 верхняя часть полуокружностей, изображённых на рисунке 4, и является верхней границей для искомой области досягаемости. Однако в пункт 6.1 мы покажем, что это не так.
Ещё одной характеристикой, определяющей размер искомой области досягаемости в другом направлении — в горизонтальном, является дальность полёта. Поэтому далее в пунктах 4 и 5 получим явные выражения для дальности полёта в зависимости от величины угла бросания (α), выясним ограничения на α и a, а также исследуем зависимость максимальной дальности полёта и угла, обеспечивающего максимальную дальность, от начальной высоты (как положительной, так и отрицательной).
- Дальность полёта
Из выражения (3) при Y = 0, то есть при падении тела на землю, получаем:
4 d — 4 s a = 0. (8)
Здесь через d обозначено значение безразмерной горизонтальной координаты X при Y = 0: d = . Решив относительно переменной d квадратное уравнение (8), получаем значение дальности полёта:
d = 2 ( + ). (9)
Важно отметить, что это выражение — алгебраическое и получено оно — в отличие от аналогичного выражения (10) в работе [3] — без привлечения тригонометрических формул, которые к моменту изучения школьниками темы «Движение тела, брошенного под углом к горизонту» освоены ими ещё не достаточно полно. При этом в выражении (9) нет знаменателя и в нём не три корня, как в выражении (15) работы [3], а только два. Это значительно упрощает в дальнейшем вычисление производной от дальности d.
Из выражения (9) видно, что дальность полёта зависит от величины s (от угла бросания) и от начальной высоты (a). Эту зависимость и будем анализировать далее. При этом начальная высота (a) и угол бросания (α) не могут быть произвольными. Из (9) следует, что подкоренное выражение в нём должно быть неотрицательным, то есть a ≥ s . Соответствующая область допустимых значений a и s показана на рисунке 5 в виде заштрихованной зоны.
Эту зависимость и будем анализировать далее. При этом начальная высота (a) и угол бросания (α) не могут быть произвольными. Из (9) следует, что подкоренное выражение в нём должно быть неотрицательным, то есть a ≥ s . Соответствующая область допустимых значений a и s показана на рисунке 5 в виде заштрихованной зоны.
Рис. 5. Область допустимых значений для a и s
- Максимальная дальность полёта
Из выражения (9) следует, что при нулевой начальной высоте (a = 0) дальность полёта определяется выражением d (a = 0) = 4, то есть зависит только от величины угла бросания (α). Эту зависимость можно представить в виде d (a = 0) = 2 sin (2 α), из чего следует известный вывод, что при нулевой начальной высоте максимальная дальность (dm), равная двум, достигается при угле бросания α, равном 450. Однако при начальной высоте h, отличной от нуля, величина максимальной дальности уже зависит от высоты старта, а необходимый угол бросания отличается от 450 иопределяется параметром a. В статье [3, с. 35] утверждается, что угол αm, обеспечивающий максимальную дальность полёта, не превышает 450. Далее мы докажем, что этот угол может быть как меньше, так и больше, чем 450, в зависимости от начальной высоты. Для этого рассмотрим в выражении (9) дальность полёта d как функцию независимой переменной s, считая при этом переменную a параметром задачи.
Однако при начальной высоте h, отличной от нуля, величина максимальной дальности уже зависит от высоты старта, а необходимый угол бросания отличается от 450 иопределяется параметром a. В статье [3, с. 35] утверждается, что угол αm, обеспечивающий максимальную дальность полёта, не превышает 450. Далее мы докажем, что этот угол может быть как меньше, так и больше, чем 450, в зависимости от начальной высоты. Для этого рассмотрим в выражении (9) дальность полёта d как функцию независимой переменной s, считая при этом переменную a параметром задачи.
Для определения экстремума функции d (s) записываем производную d по s (для этого необходимо знать формулу производной только от степенной функции) и приравниваем её нулю:
= .
После возведения в квадрат левой и правой частей этого равенства получаем для переменной s, обеспечивающей максимальную дальность dm, следующее выражение:
sm = . (10)
(10)
Если теперь с помощью замен переменных вернуться к исходной переменной α, то для угла бросания αm, обеспечивающего максимальную дальность полёта, получаем его явное выражение в зависимости от безразмерной начальной высоты (a):
sin αm = . (11)
Графически зависимость (11) представлена на рисунке 6.
Рис. 6. Угол бросания (αm), обеспечивающий максимальную дальность, в зависимости от начальной высоты a
Из рисунка 6 и из выражения (11) видно, что в зависимости от начальной высоты угол αm, обеспечивающий максимальную дальность dm, может быть как меньше, так и больше, чем 450.
Теперь, имея явное выражение для угла бросания, который обеспечивает максимальную дальность, получим явное выражение и для самой максимальной дальности dm в зависимости от начальной высоты. Для этого подставим sm из (10) в (9) вместо s и получим:
dm= 2. (12)
(12)
Графически эта зависимость показана на рисунке 7.
Рис. 7. Максимальная дальность (dm) в зависимости от начальной высоты a
При произвольной начальной высоте (a) выражение (12) определяет крайнюю точку на оси X для области досягаемости.
Отметим, что выражение (12) для максимальной дальности полёта dmфактически совпадает с аналогичным выражением (12), приведённым в работе [4] в других переменных, но получено оно проще, чем в [4], поскольку для этого не использовались тригонометрические формулы.
Отметим также, что выражения (10) и (12) получены нами выше с помощью хоть и простого, но всё же дифференцирования, которое школьниками в момент изучения ими темы «Баллистическое движение» ещё не знакомо. Поэтому желательно попытаться получить те же выражения, но не используя для этого производные. Далее покажем, что это действительно возможно. Для этого, обозначив в выражении (9) 1 — s = u, запишем его в виде
d(u) = 2 ( + ).
Возведём его левую и правую части в квадрат, чтобы остался только один корень:
= 8 (1 — u) (u + ) + ).
Разделив на 8, получаем функцию, график которой уже можно построить. Например, при a = 0,2 и a = 0,5 можно убедиться в том, что максимального значения эта функция достигает при значениях u, равных . А тогда из замены переменной 1 — sm = umнаходим, что sm = . Это значение совпадает со значением (10), полученным выше с использованием производной. А это и доказывает, что справедливость формул (11) и (12), по которым определяется максимальная дальность полёта, можно установить и без привлечения для этого производных.
- Область досягаемости
5.1. Из изложенного в пунктах 3–5 следует, что при a = 0 искомой области досягаемости принадлежат следующие две подобласти в системе отсчёта XOY (рис.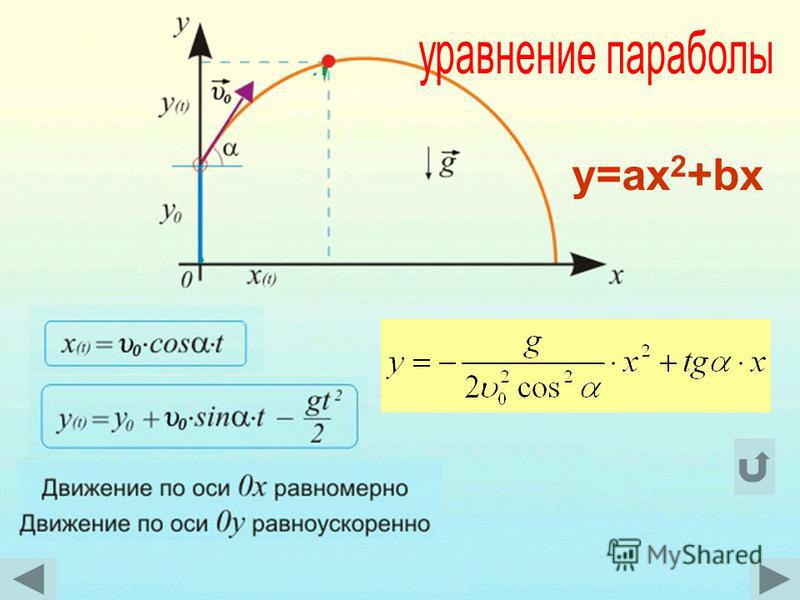 8):
8):
– подобласть 1, находящаяся под дугой эллипса между точками (0; 1) и (1; 0,5),
– подобласть 2 под параболой, соответствующей углу α в 450, между точками (1; 0,5) и (2; 0).
Рис. 8. Область досягаемости
5.2. Докажем, что над подобластью 1 есть некоторая подобласть области досягаемости. Ординаты траекторий (Y) определяются выражением (2), а ординаты вершин парабол (Yв) — выражением
Yв= (),
которое получаем при 0≤ X≤1 в результате решения квадратного уравнения (6) относительно Yв. Запишем разность этих ординат:
R1 = Y — Yв = — (1 + ) X2 + zX — (1 + ).
Эта разность не зависит от начальной высоты a, а зависит только от X и z. Для того чтобы доказать, что над подобластью 1 существует и ещё одна подобласть значений X и Y, достаточно указать хотя бы одну пару чисел X и z, при которых разность R1 положительна. Разность R1 больше нуля, например, при X = 0,9 и z = 2, а это и доказывает, что над подобластью 1 при 0≤ X≤1 есть и ещё одна подобласть (назовём её подобластью 3 — рис. 8) достижимых точек в плоскости XOY.
Разность R1 больше нуля, например, при X = 0,9 и z = 2, а это и доказывает, что над подобластью 1 при 0≤ X≤1 есть и ещё одна подобласть (назовём её подобластью 3 — рис. 8) достижимых точек в плоскости XOY.
- Докажем, что и над подобластью 2 находится некоторая подобласть области досягаемости.
Ордината Yптраектории, соответствующей углу бросания в 450, определяется выражением
Yп = — X2 + X. (13)
Запишем разность ординат траекторий, определяемых выражениями (2) и (13) и, поскольку для дальнейшего важен только знак этой разности, умножим её на . Тогда при a = 0 и 1X≤2 получим: R2 = 4 — (1 + z) X. Графически зависимость R2 от X представлена на рисунке 9.
Рис. 9. Разность ординат (R2) в зависимости от X
Из рисунка 9 видно, что при 1zR2 положительна.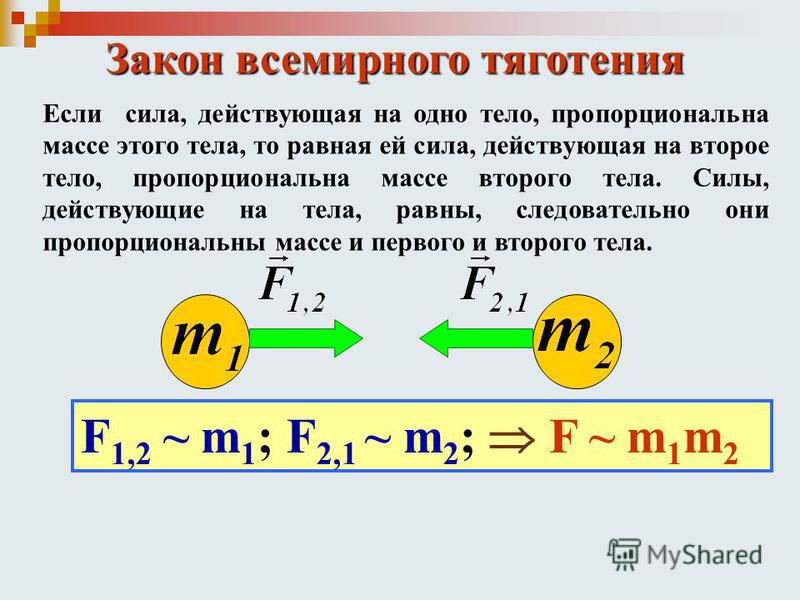 Следовательно, ординаты траекторий выше, чем парабола, соответствующая углу в 450, причём при увеличении X от 1 до 2 размер подобласти 4 уменьшается до нуля (рис. 8).
Следовательно, ординаты траекторий выше, чем парабола, соответствующая углу в 450, причём при увеличении X от 1 до 2 размер подобласти 4 уменьшается до нуля (рис. 8).
Таким образом, область досягаемости представляет собой сумму (объединение) четырёх подобластей (рис. 8), и теперь необходимо найти верхнюю границу этой области.
- Верхняя граница области досягаемости
Получим аналитическое выражение для верхней границы области досягаемости. Для этого выражение (2) представим как уравнение параболы относительно переменной z:
Y = — + ּX z — X2 + a. (14)
Из школьного курса алгебры известно, что наибольшее значение параболы y=a+ bx + c достигается при x = . Воспользовавшись этим простым правилом, найдём для каждого из значений X то значение переменной z, при котором получается максимальное значение для Y: z = .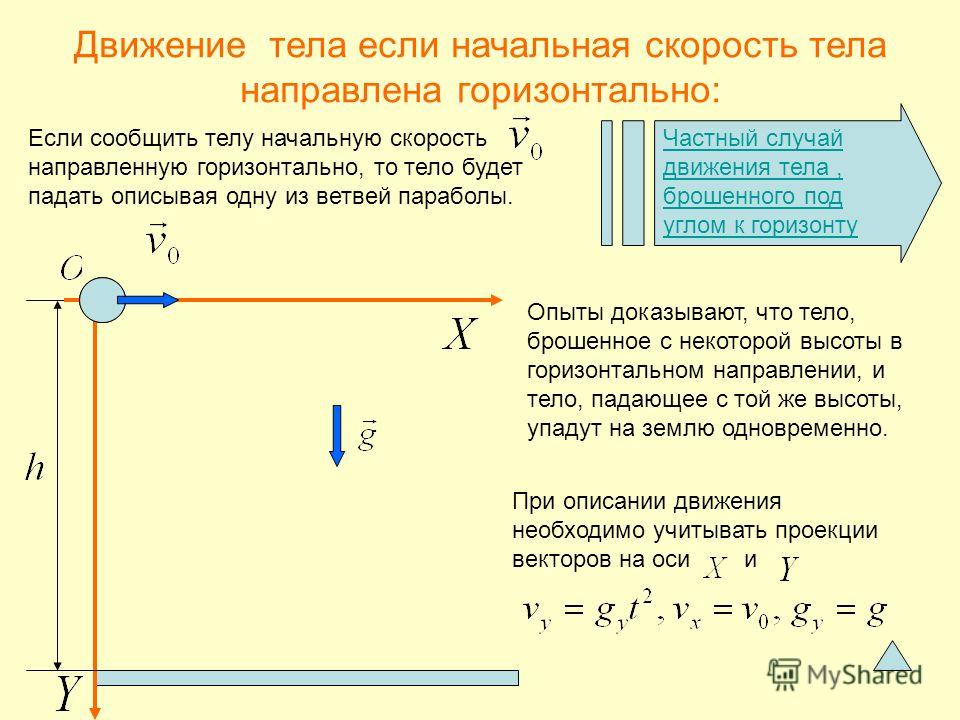 Подставив это значение в (14), получаем:
Подставив это значение в (14), получаем:
Y = 1–0,25 X2 + a.
Это и есть уравнение верхней границы области досягаемости. Эта линия ограничивает область досягаемости сверху. Слева и снизу при нулевой начальной высоте эта область ограничена, соответственно, осью ординат и осью абсцисс. При изменении начальной высоты верхняя граница области досягаемости перемещается по оси Y на величину, равную a, причём при положительных значениях a — вверх, а при отрицательных — вниз.
- Заключение
Предложено простое, доступное учащимся среднего уровня подготовленности, решение задачи анализа свободного движения тела, брошенного под углом к горизонту. Упрощение анализа особенностей задачи достигнуто в результате того, что всё исследование выполнено в безразмерных относительных величинах, а также вследствие перехода к переменным, в которых уравнения имеют более простой вид. При этом удалось обойтись практически без тригонометрических формул, которые к моменту изучения школьниками темы «Движение тела, брошенного под углом к горизонту» освоены ими ещё не в полной мере, а также без нахождения производных от сложных функций.
При этом удалось обойтись практически без тригонометрических формул, которые к моменту изучения школьниками темы «Движение тела, брошенного под углом к горизонту» освоены ими ещё не в полной мере, а также без нахождения производных от сложных функций.
Введено понятие области досягаемости как множества точек в плоскости движения, которые могут быть достигнуты при заданной начальной скорости, известной начальной высоте и всевозможных углах бросания. Определены границы области досягаемости.
Изложение материала, приведённое в этой работе, может быть полезным как учащимся, так и преподавателям физики в школе.
Следуя одному из основных дидактических принципов образования — доступность и преемственность с тем содержанием, которое осваивается в школе [5, с. 59], — анализ задачи, представленный в настоящей статье, рассчитан на учащихся с базовым уровнем знаний по физике и математике. Поэтому этот анализ основывается исключительно на средствах и приёмах, доступных этой категории учащихся, и тем самым он предоставляет всем школьникам равные возможности для решения ими творческих задач.
Литература:
- Касьянов В. А. Физика. 10 класс. Профильный уровень. — М.: Дрофа, 2013–428 с.
- М. М. Балашов, А. И. Гомонова, А. Б. Долицкий и др. Физика: Механика. 10 класс: Учебник для углублённого изучения физики/ Под ред. Г. Я. Мякишева. — М.: Дрофа, 2004–496 с.
- Бобылев Ю. В., Грибков А. И., Романов Р. В. «Кидай дальше», или Четыре способа решения одной известной физической задачи/ Физика в школе — 2018 — № 3 — С. 33–38.
- Бобылев Ю. В., Грибков А. И., Романов Р. В. Нестандартное нахождение траектории тела при свободном падении и её анализ/ Физика в школе — 2019 — № 2 — С. 31–35.
- Казакова Ю. В., Петрова Е. В. Размышления учителя физики о состоянии и перспективах развития исследовательской деятельности учащихся/ Физика в школе — 2015 — № 1 — С. 53–60.
Основные термины (генерируются автоматически): начальная высота, выражение, угол бросания, максимальная дальность, зависимость, область досягаемости, XOY, геометрическое место вершин траекторий, нулевая начальная высота, правая часть.
Движение в гравитационном поле
Сделать 4 мин чтения 1 мин видео
Движение в гравитационном поле
Из закона всемирного тяготения Ньютона мы знаем, что на объект в гравитационном поле Земли действует сила, притягивающая его к центру Земля. Если это единственная сила, действующая на объект, то объект будет ускоряться по направлению к центру Земли.
Человек, стоящий на поверхности Земли, интерпретирует это ускорение как объекты, всегда падающие вниз. 9{-2}$}\).
Важно:
В действительности, если вы уйдете очень далеко от поверхности Земли, величина \(\vec{g}\) изменится, но для повседневных задач мы можем смело считать ее постоянной. Мы также игнорируем любые эффекты, которые может иметь сопротивление воздуха (сопротивление).
В оставшейся части этого урока мы будем иметь дело только со случаем, когда сила гравитации является единственной силой, действующей на падающий снаряд. Любой снаряд можно описать как падающий, даже если изначально он движется вверх.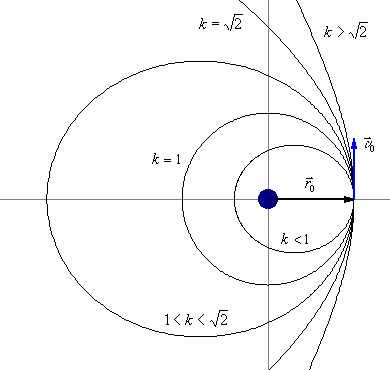
Начальная скорость, \(\vec{v}_i\), которую имеет объект, и ускорение, которое он испытывает, являются двумя разными величинами. Очень важно помнить, что гравитационное ускорение всегда направлено к центру Земли и постоянно, независимо от направления или величины скорости.
Совет:
Снаряды, движущиеся вверх или вниз в гравитационном поле Земли, всегда ускоряются вниз с постоянным ускорением \(\vec{g}\). Примечание: ненулевое ускорение означает, что скорость равна изменение .
Объекты, движущиеся вверх или вниз в гравитационном поле Земли, всегда ускоряются по направлению к центру Земли. Для человека, стоящего на поверхности Земли, это выглядит как нисходящее ускорение. Мы не рисуем оба вектора на объекте, потому что мы смешиваем скорость и ускорение, которые являются двумя различными физическими величинами.
Это означает, что если объект движется вверх с некоторой начальной скоростью в вертикальном направлении, модуль скорости в вертикальном направлении уменьшается до тех пор, пока не остановится (\(v=0\) \(\text{м·с $ ^{-1}$}\)) на мгновение.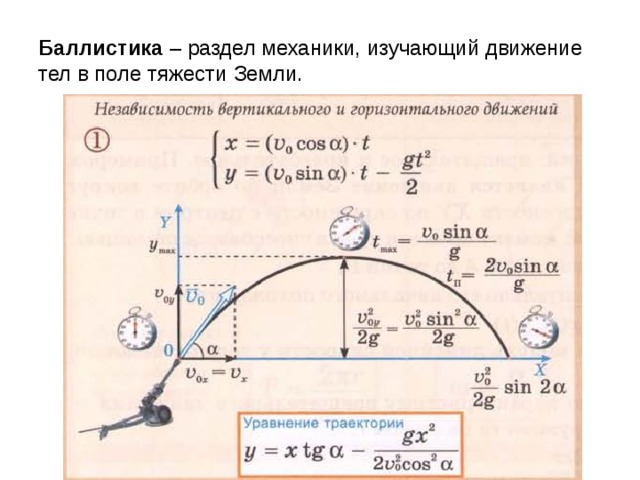 Точка, в которой скорость уменьшается до нуля, соответствует максимальной высоте \(h_{max}\), которую достигает объект. После этого объект начинает падать. Очень важно помнить, что ускорение постоянно, но вектор скорости изменился по величине и направлению. На максимальной высоте, где скорость равна нулю, ускорение равно \(\vec{g}\).
Точка, в которой скорость уменьшается до нуля, соответствует максимальной высоте \(h_{max}\), которую достигает объект. После этого объект начинает падать. Очень важно помнить, что ускорение постоянно, но вектор скорости изменился по величине и направлению. На максимальной высоте, где скорость равна нулю, ускорение равно \(\vec{g}\).
Совет:
Снаряды, которые имеют начальную скорость вверх, будут иметь нулевую скорость на максимальной высоте, \(h_{max}\). Ускорение по-прежнему \(\vec{g}\).
(a) Предмет брошен вверх с высоты \({h}_{i}\). Через время \({t}_{m}\) объект достигает максимальной высоты и начинает падать вниз. Через время \(2{t}_{m}\) объект возвращается на высоту \({h}_{i}\).
Рассмотрим предмет, брошенный вверх с вертикальной высоты \({h}_{i}\). Мы сказали, что объект будет двигаться вверх с уменьшающейся вертикальной скоростью, пока не остановится, а затем начнет двигаться вертикально вниз. Время, которое требуется объекту, чтобы упасть обратно на высоту \({h}_{i}\), равно времени, которое требуется объекту, чтобы достичь максимальной высоты с высоты \({h}_{i }\).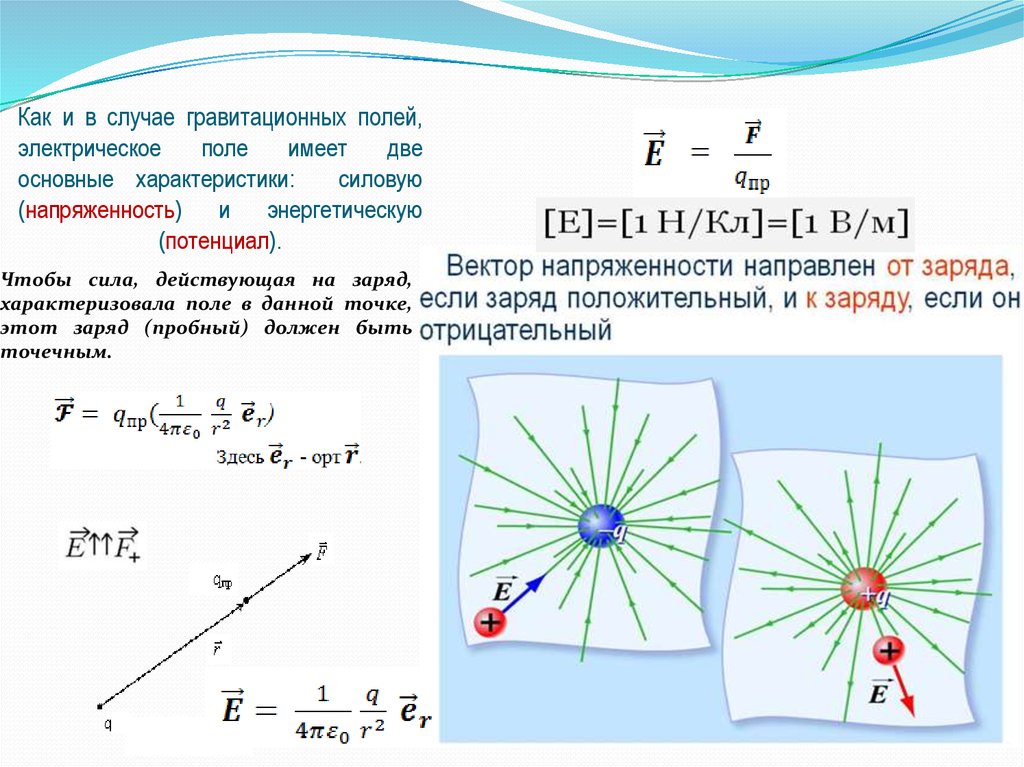 Это известно как временная симметрия . Это следствие равномерного ускорения снаряда.
Это известно как временная симметрия . Это следствие равномерного ускорения снаряда.
Это имеет два значения для снарядов, которые проходят через точку как на восходящей, так и на нисходящей части своего движения в свободном падении: то же самое, например, для подъема из исходного положения на максимальную высоту потребуется столько же времени, сколько и для возврата в исходное положение. Это относится к любой точке, как показано розовой точкой на рисунке выше. Интервал времени между прохождением снаряда точки и нахождением на максимальной высоте одинаков, \(\Delta t\).
Это очень полезно при решении задач, потому что, если у вас есть какая-либо информация о восходящем движении, вы также можете узнать что-то о нисходящем движении и наоборот.



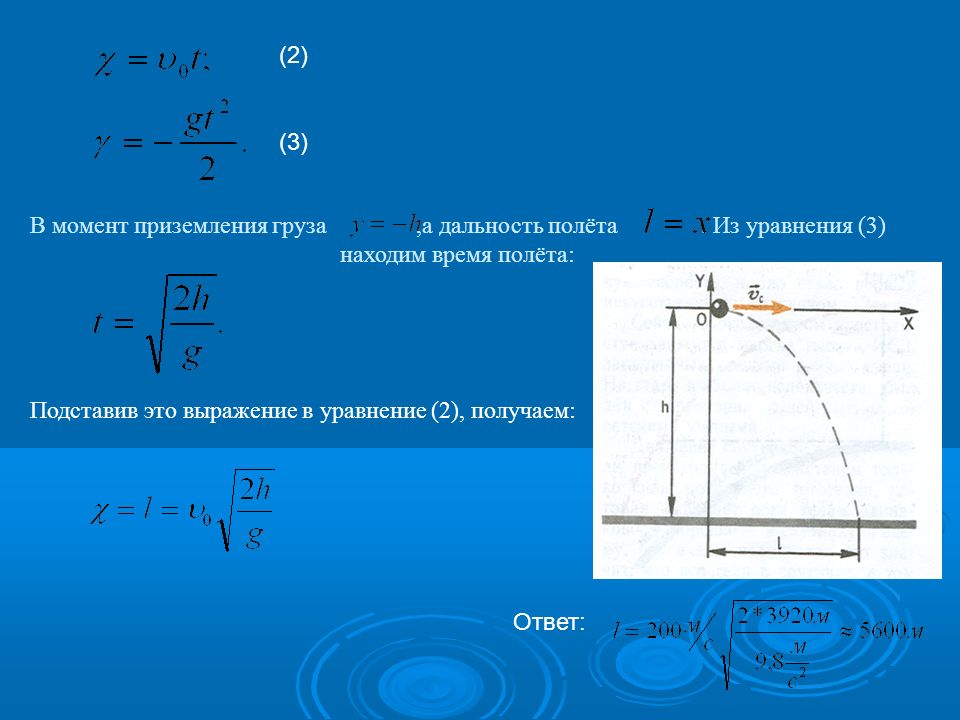
 Если частота этих колебаний находится в пределах 20-20000 колебаний в секунду, мы воспринимаем их как звук.
Если частота этих колебаний находится в пределах 20-20000 колебаний в секунду, мы воспринимаем их как звук.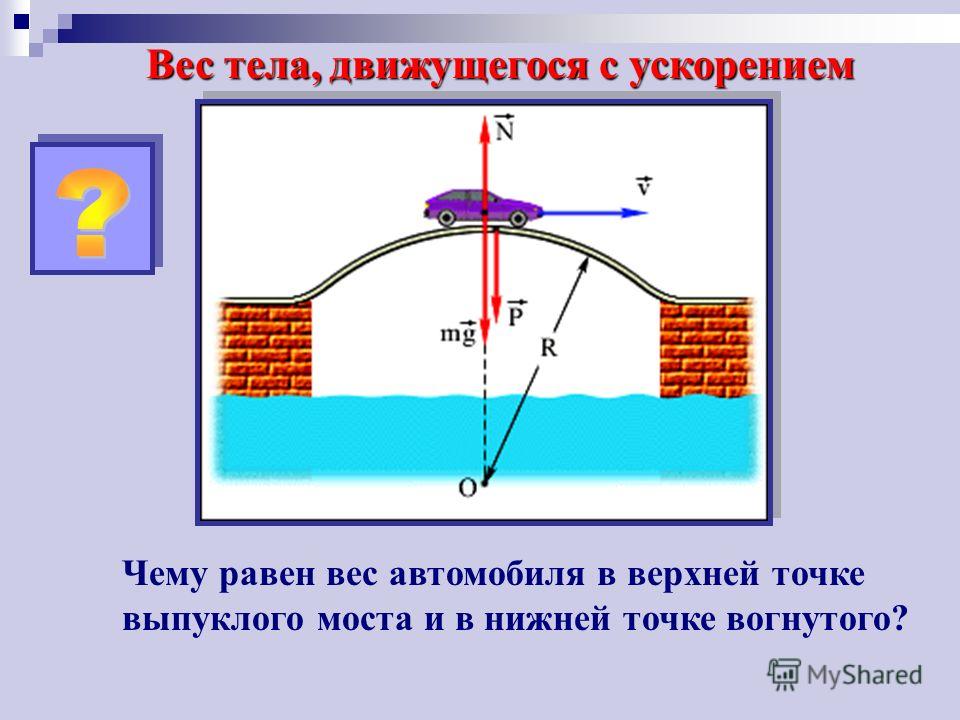
 Боковой ветер отклоняет снаряды в сторону от плоскости стрельбы, причём отклонения могут достигать даже при умеренном ветре значительных величин.
Боковой ветер отклоняет снаряды в сторону от плоскости стрельбы, причём отклонения могут достигать даже при умеренном ветре значительных величин.


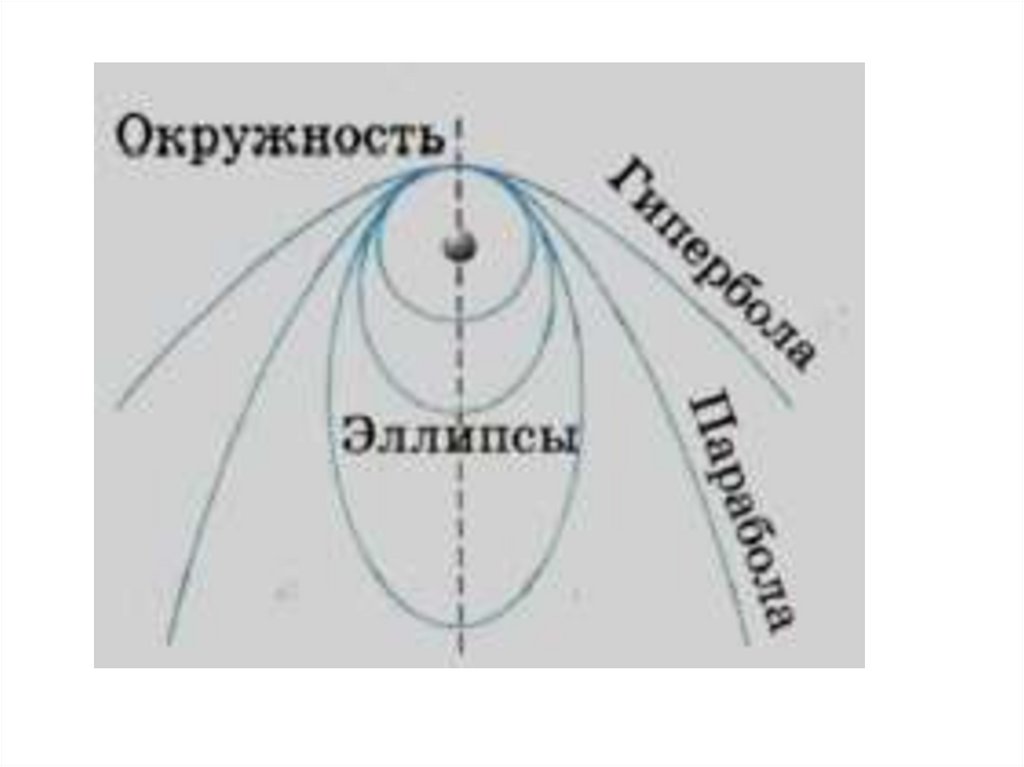

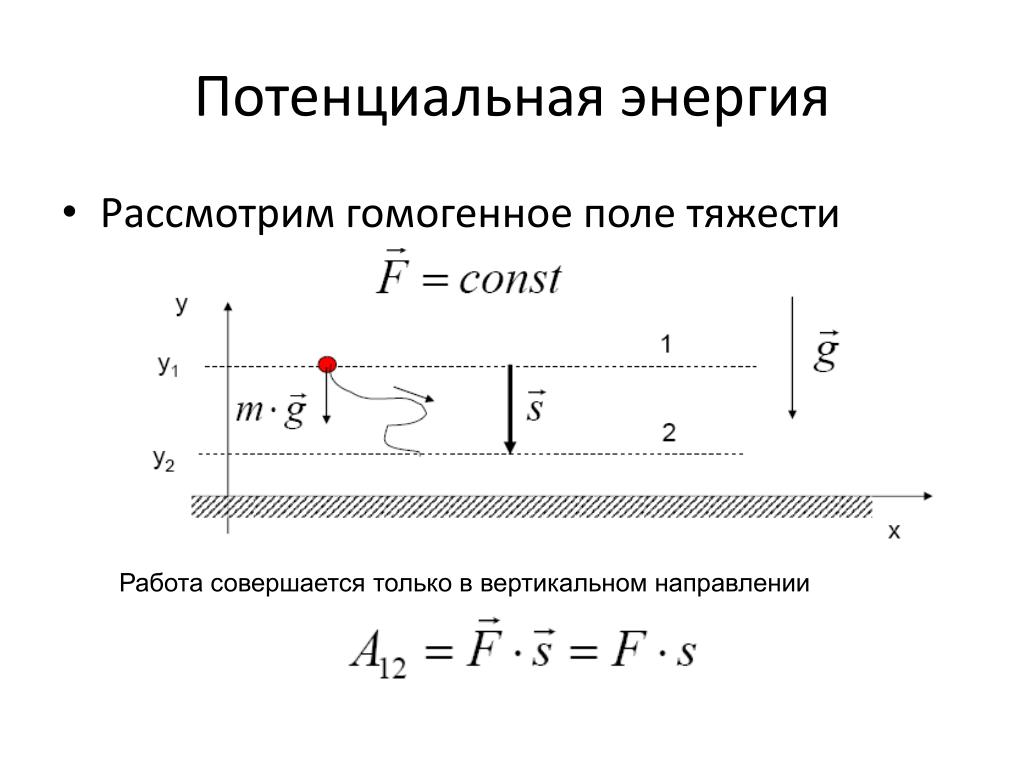
 . . . . . . . . . . . . . . . . . . . . . . . . . 22
. . . . . . . . . . . . . . . . . . . . . . . . . 22 П., Сочивко А.А., Москва: изд-во
П., Сочивко А.А., Москва: изд-во Виртуальные лабораторные работы по электричеству и магнетизму Page
Виртуальные лабораторные работы по электричеству и магнетизму Page