Движение тела под действием силы тяжести.

Глава 1. Движение тела под действием силы тяжести. Если на тело действует только сила тяжести, то тело совершает свободное падение. Вид траектории движения зависит от направления и модуля начальной скорости. При этом возможны следующие случаи движения тела: 1) Тело может двигаться по круговой или эллиптической орбите вокруг планеты. 2) Если начальная скорость тела равна нулю или параллельна силе тяжести, тело совершает прямолинейное свободное падение. 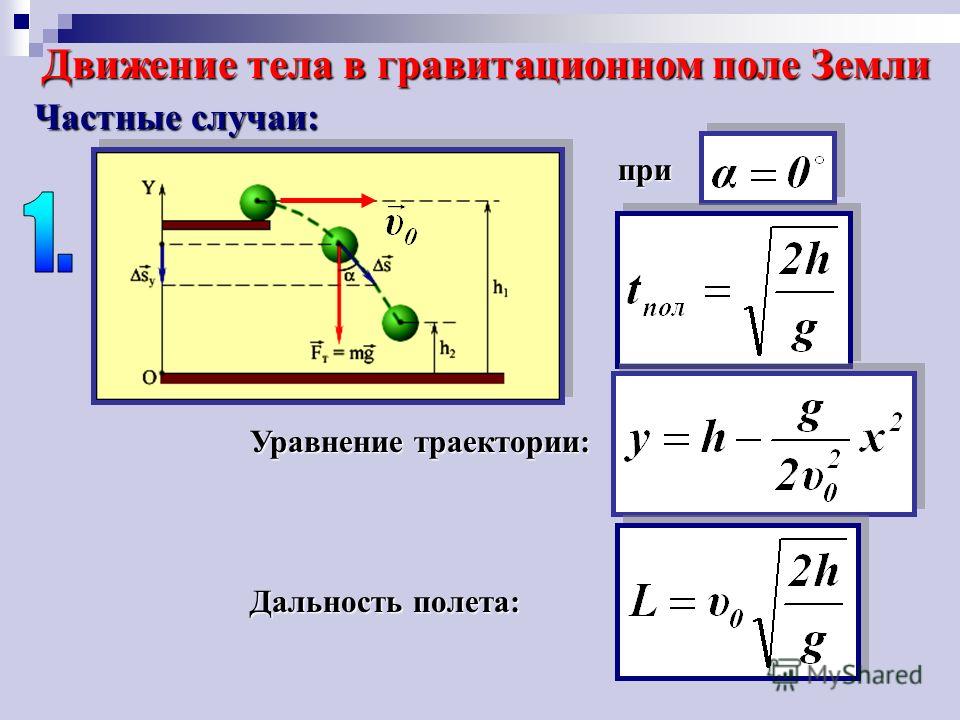3) Если начальная скорость тела направлена под углом к силе тяжести, то тело будет двигаться по параболе, либо по ветви параболы. 1.1 Движение тела по круговой или эллиптической орбите вокруг планеты. 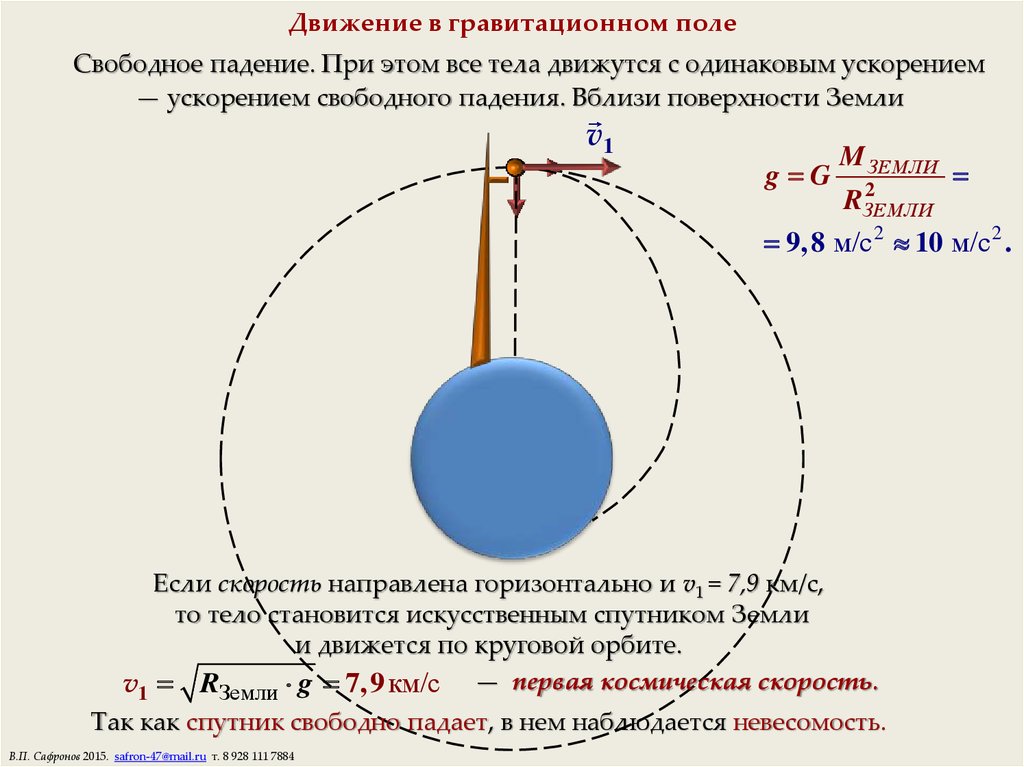Рассмотрим теперь вопрос об искусственных спутниках Земли. Искусственные спутники движутся за пределами земной атмосферы, и на них действуют только силы тяготения со стороны Земли. В зависимости от начальной скорости траектория космического тела может быть различной.

Мы рассмотрим здесь только случай движения искусственного спутника по круговой околоземной орбите. Такие спутники летают на высотах порядка 200-300 км, и можно приближенно принять расстояние до центра Земли равным ее радиусу RЗ. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Обозначим скорость спутника на околоземной орбите через х1. Эту скорость называют первой космической скоростью. Используя кинематическую формулу для центростремительного ускорения, получим: Двигаясь с такой скоростью, спутник облетал бы Землю за время На самом деле период обращения спутника по круговой орбите вблизи поверхности Земли несколько превышает указанное значение из-за отличия между радиусом реальной орбиты и радиусом Земли. Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли.

Для спутников, движущихся по круговым траекториям на значительном удалении от Земли, земное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Скорость спутника х находится из условия Таким образом, на высоких орбитах скорость движения спутников меньше, чем на околоземной орбите. Период T обращения такого спутника равен Здесь T1 — период обращения спутника на околоземной орбите. Период обращения спутника растет с увеличением радиуса орбиты. Нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6RЗ, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6Rо называется геостационарной. 1.2 Движение тела под действием силы тяжести в вертикальной плоскости Если начальная скорость тела равна нулю или параллельна силе тяжести, тело совершает прямолинейное свободное падение. Основной задачей механики, является определение положения тела в любой момент времени. Решением задачи для частиц, движущихся в поле тяжести Земли, являются уравнения, в проекциях на оси OX и OY: Этих формул достаточно, чтобы решить любую задачу о движении тела под действием силы тяжести. Тело брошено вертикально вверх В этом случае v0x = 0, gx = 0, v0y = v0, gy = -g. , Движение тела в этом случае будет происходить по прямой линии, причем сначала вертикально вверх до точки, в которой скорость обратится в нуль, а затем вертикально вниз. Рис.4.Движение тела, брошенного вверх. При движении тела с ускорением в поле тяготения изменяется вес тела. Весом тела называется сила, с которой тело действует на неподвижную относительно него опору или подвес. Вес тела возникает вследствие его деформации, вызванной действием силы со стороны опоры (силы реакции) или подвеса (силы натяжения) Вес существенно отличается от силы тяжести: Это силы разной природы: сила тяжести — гравитационная сила, вес — упругая сила (электромагнитной природы). Они приложены к разным телам: сила тяжести — к телу, вес — к опоре. Рис.5. Точки приложения силы тяжести и веса тела. Направление веса тела не обязательно совпадает с отвесным направлением. Сила тяжести тела в данном месте Земли постоянная и не зависит от характера движения тела; вес зависит от ускорения, с которым движется тело. Рассмотрим, как изменяется вес тела, движущегося в вертикальном направлении вместе с опорой. На тело действуют сила тяжести и сила реакции опоры. Рис.5. Изменение веса тела при движении с ускорением. Основное уравнение динамики: В проекции на ось Оу: а) По третьему закону Ньютона модули сил Np1 = P1. Следовательно, вес тела P1 = mg б) Значит , (тело испытывает перегрузки). в) Следовательно, вес тела Если a = g, то P = 0 Таким образом, вес тела при вертикальном движении может быть в общем случае выражен формулой. Мысленно разобьем неподвижное тело на горизонтальные слои.

На каждый из этих слоев действует сила тяжести и вес вышележащей части тела. Этот вес будет становиться тем больше, чем ниже лежит слой. Поэтому под влиянием веса вышележащих частей тела каждый слой деформируется и в нем возникают упругие напряжения, которые возрастают по мере перехода от верхней части тела к нижней. Рис.6.Тело, разбитое на горизонтальные слои. Если тело свободно падает (a = g), то его вес равен нулю, в теле исчезают всякие деформации и, несмотря на сохраняющееся действие силы тяжести, верхние слои не будут давить на нижние. Состояние, при котором в свободно движущемся теле исчезают деформации и взаимные давления, называется невесомостью. Причина невесомости заключается в том, что сила всемирного тяготения сообщает телу и его опоре одинаковое ускорение. Движение тела, если начальная скорость направлена под углом к силе тяжести Тело брошено горизонтально, т.е. под прямым углом к направлению силы тяжести. При этом v0x = v0 , gx = 0, v0y = 0, gy = — g , х0 = 0, и, следовательно, Чтобы определить вид траектории, по которой тело будет двигаться в этом случае, выразим время t из первого уравнения и подставим его во второе уравнение. В результате мы получим квадратичную зависимость у от х: Это означает, что тело при этом будет двигаться по ветви параболы. Рис.7. Движение тела, брошенного под углом к горизонту. Движение тела, брошенного с некоторой начальной скоростью хо под углом б к горизонту, тоже представляет собой сложное движение: равномерное по горизонтальному направлению и одновременно происходящее под действием силы тяжести равноускоренное движение в вертикальном направлении. Так движется лыжник при прыжке с трамплина, струя воды из брандспойта и т.д. Рис.8. Струя воды из брандспойта. Изучение особенностей такого движения началось довольно давно, еще в XVI веке и было связано с появлением и совершенствованием артиллерийских орудий. Представления о траектории движения артиллерийских снарядов в те времена были довольно забавными. Считалось, что траектория эта состоит из трех участков: А — насильственного движения, В — смешанного движения и С — естественного движения, при котором ядро падает на солдат противника сверху. Рис.9. Траектория движения артиллерийского снаряда. Законы полета метательных снарядов не привлекали особого внимания ученых до тех пор, пока не были изобретены дальнобойные орудия, которые посылали снаряд через холмы или деревья — так, что стреляющий не видел их полета. Сверхдальняя стрельба из таких орудий на первых порах использовалась в основном для деморализации и устрашения противника, а точность стрельбы не играла вначале особенно важной роли. Близко к правильному решению о полете пушечных ядер подошел итальянский математик Тарталья, он сумел показать, что наибольшей дальности полета снарядов можно достичь при направлении выстрела под углом 45° к горизонту. В его книге «Новая наука» были сформулированы правила стрельбы, которыми артиллеристы руководствовались до середины ХVII века. Однако, полное решение проблем, связанных с движением тел брошенных горизонтально или под углом к горизонту, осуществил все тот же Галилей. В своих рассуждениях он исходил из двух основных идей: тела, движущиеся горизонтально и не подвергающиеся воздействию других сил будут сохранять свою скорость; появление внешних воздействий изменит скорость движущегося тела независимо от того, покоилось или двигалось оно до начала их действия.

Галилей показал, что траектории снарядов, если пренебречь сопротивлением воздуха, представляют собой параболы. Галилей указывал, что при реальном движении снарядов, вследствие сопротивления воздуха, их траектория уже не будет напоминать параболу: нисходящая ветвь траектории будет идти несколько круче, чем расчетная кривая. Ньютон и другие ученые разрабатывали и совершенствовали новую теорию стрельбы, с учетом возросшего влияния на движение артиллерийских снарядов сил сопротивления воздуха. Появилась и новая наука — баллистика. Прошло много-много лет, и теперь снаряды движутся столь быстро, что даже простое сравнение вида траекторий их движения подтверждает возросшее влияние сопротивления воздуха. Рис.10. Идеальная и действительная траектории движения снаряда. На нашем рисунке идеальная траектория движения тяжелого снаряда, вылетевшего из ствола пушки с большой начальной скоростью, показана пунктиром, а сплошной линией — действительная траектория полета снаряда при тех же условиях выстрела. В современной баллистике для решения подобных задач используется электронно-вычислительная техника — компьютеры, а мы пока ограничимся простым случаем — изучением такого движения, при котором сопротивлением воздуха можно пренебречь. Это позволит нам повторить рассуждения Галилея почти без всяких изменений. Полет пуль и снарядов представляет собой пример движения тел, брошенных под углом к горизонту. Точное описание характера такого движения возможно только при рассмотрении некоторой идеальной ситуации. Посмотрим, как меняется скорость тела, брошенного под углом б к горизонту, в отсутствие сопротивления воздуха. В течение всего времени полета на тело действует сила тяжести. На первом участке траектории по направлению. Рис 11. Изменение скорости вдоль траектории. В наивысшей точке траектории — в точке С — скорость движения тела будет наименьшей, она направлена горизонтально, под углом 90° к линии действия силы тяжести. На второй части траектории полет тела происходит аналогично движению тела, брошенному горизонтально. Время движения от точки А до точки С будет равно времени движения по второй части траектории в отсутствие сил сопротивления воздуха. Если точки «бросания» и «приземления» лежат на одной горизонтали, что то же самое можно сказать и о скоростях «бросания» и «приземления». Углы между поверхностью Земли и направлением скорости движения в точках «бросания» и «приземления» будут в этом случае тоже равны. Дальность полета АВ тела, брошенного под углом к горизонту, зависит от величины начальной скорости и угла бросания. При неизменной скорости бросания V0 с увеличением угла, между направлением скорости бросания и горизонтальной поверхностью от 0 до 45°, дальность полета возрастает, а при дальнейшем росте угла бросания — уменьшается. В этом легко убедиться, направляя струю воды под разными углами к горизонту или следя за движением шарика, выпущенного из пружинного «пистолета» (такие опыты легко проделать самому). Траектория такого движения симметрична относительно наивысшей точки полета и при небольших начальных скоростях, как уже говорилось раньше, представляет собой параболу. Максимальная дальность полета при данной скорости вылета достигается при угле бросания 45°. Когда угол бросания составляет 30° или 60°, то дальность полета тел для обоих углов оказывается одинаковой. Для углов бросания 75° и 15° дальность полета будет опять одна и та же, но меньше, чем при углах бросания 30° и 60°. Значит, наиболее «выгодным» для дальнего броска углом является угол в 45°, при любых других значениях угла бросания дальность полета будет меньше. Если бросить тело с некоторой начальной скоростью vо под углом 45° к горизонту, то его дальность полета будет в два раза больше максимальной высоты подъема тела, брошенного вертикально вверх с такой же начальной скоростью.

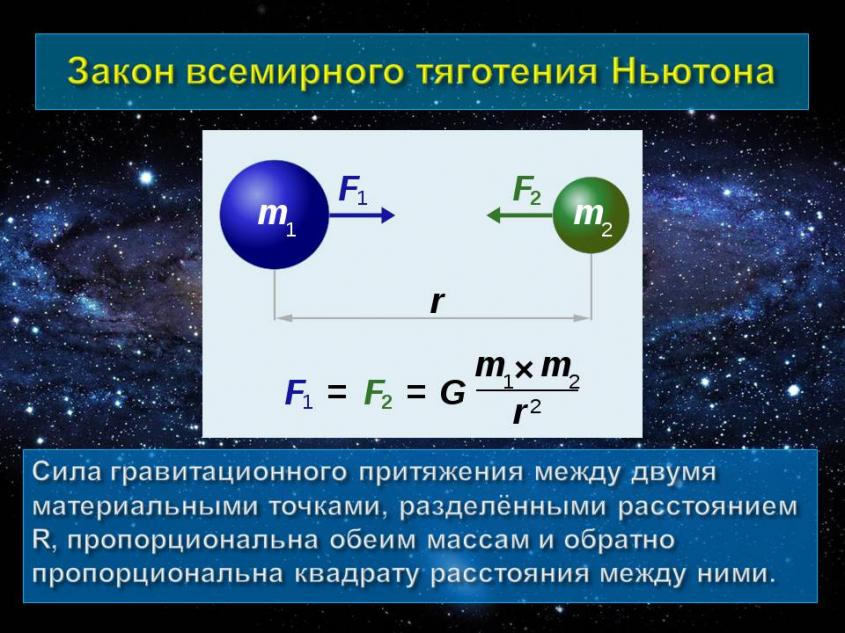
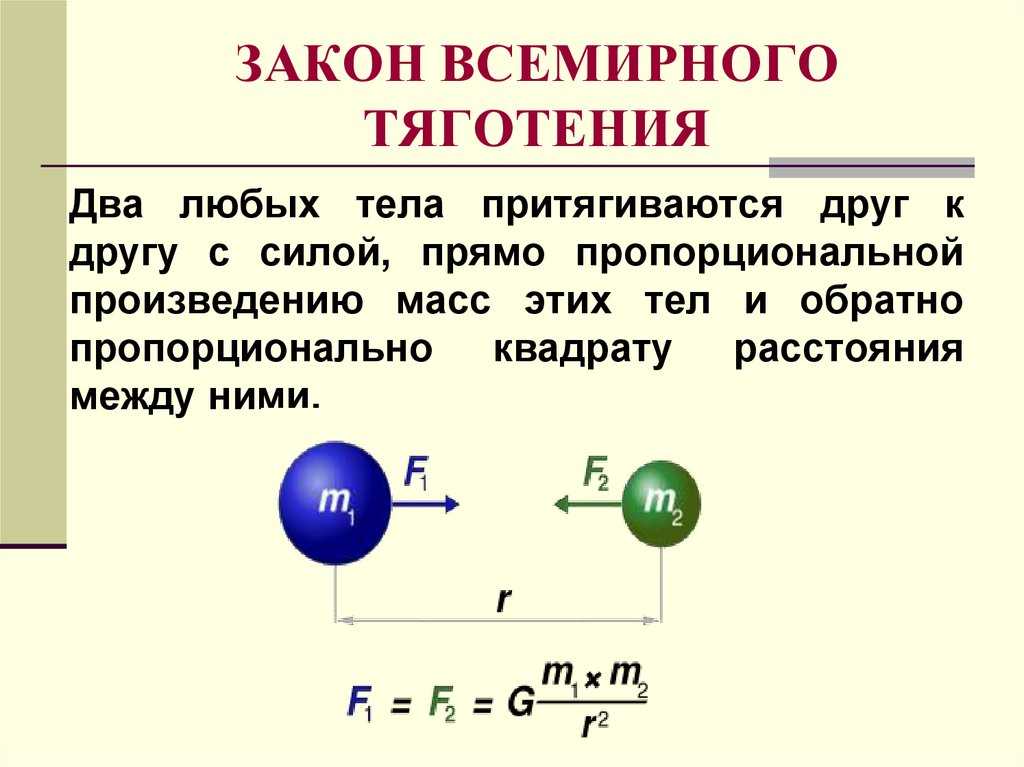
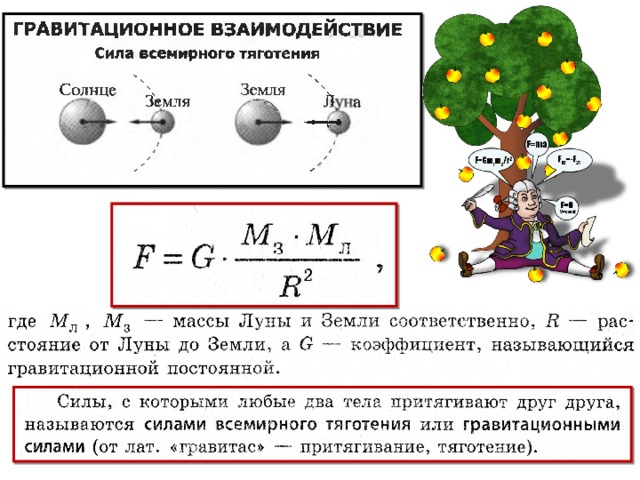
Движение под действием гравитационных сил

Ньютону удалось доказать, что гравитационные силы зависят от масс обоих взаимодействующих сил и от расстояния между ними.

В физике движение под действием гравитационных сил разделяют на небесную механика и баллистику.

В 18 веке бурно начала развиваться небесная механика. Небесная механика — раздел астрофизики, изучающий движение небесных тел.Небесные тела подразделяются на естественные (планеты, кометы, астероиды, звезды, метеоры) и искусственные (спутники).

Законы небесной механики были открыты Иоганном Кеплером для планет. Впоследствии они разрабатывались для описания движения любых небесных тел.Обратите внимание. Небесная механика изучает движение только тех тел, которые не имеют собственного движения.

1 закон КеплераПланета движется по эллипсу, в одном из фокусов которого находится Солнце.

Границы применимости 1 закона Кеплера Закон сформулирован для планет солнечной системы, но распространяется на любые небесные тела.

Следствия закона:

• Ближайшая к солнцу точка орбиты Земли наименьшее расстояние от земли до солнца называется перигелий.
• Самая дальняя точка называется апогелием.Для спутников Земли такие точки Перигей и Апогей соответственно.

Для спутников Луны — Периселений и Апоселений.

2 закон Кеплера За одинаковые промежутки времени радиус-вектор планеты описывает равные площади. Границы применения 2 закона Кеплера:Закон сформулирован для планет солнечной системы, но также распространяется и на другие небесные тела.

Следствия закона:

• При приближении планеты к Солнцу орбитальная скорость планеты увеличивается.
• При отдалении планеты от Солнца орбитальная скорость планеты уменьшается.Самую высокую скорость Земля имеет в начале января, а самую низкую — в начале июля.Обратите внимание.

3 закон  квадратов периодов обращения планет вокруг Солнца равно отношению кубов больших полуосей орбит этих планет.

Формула закона: T1²/T2²=R1³/R2³

Границы применимости закона:

Закон сформулирован для планет солнечной системы, но распространяется на любые небесные тела. Закон позволяет рассчитать среднее расстояние планеты от Солнца.

1 космическая скорость — минимальная скорость, при которой тело становится спутником планеты.Определение. Спутник — тело, обращающееся вокруг другого тела, точнее вокруг точки называемой общим центром масс.

Впервые это понял Исаак Ньютон и рассчитал значение первой космической скорости до Земли.

Не учитывая сопротивления воздуха для поверхности Земли 1 космическая скорость составляет около 7,9 км/с.2 космическая скорость — минимальная скорость, при которой тело может покинуть планету.

Для Земли 2 космическая скорость составляет около 11,2 км/с3 космическая скорость — минимальная скорость, при которой тело может покинуть солнечную систему.

Для солнечной системы 3 космическая скорость — около 40 км/с.Баллистика

Обратите внимание. Баллистика появилась во время первых артиллерийских стрельб и изучала движение снарядов в воздухе.

Баллистика — наука о движении тел в гравитационном поле планеты.

Баллистика делится на внутреннюю и внешнюю.

Внутренняя изучает движение пуль внутри ствола.

Внешняя изучает движение пуль после вылета из ствола.

Сила тяжести — равнодействующая сила гравитационного притяжения к планете и центростремительной силы, возникшей из-за движения планеты. Для Земли часто пренебрегают вторым компонентов, но для быстро-вращающихся небесных тел типо Юпитера им пренебрегать нельзя.

Движение тела, брошенного под углом к горизонту — это движение по параболе.Вывод. Механика и баллистика требуют знаний математики, так как кроме гравитационных сил на тела действуют ещё и сопротивление атмосферы, центростремительные и электростатические силы.

Поделиться статьей в соцсетях

Остались вопросы?
Наши репетиторы помогут

Остались вопросы?

Свободное падение и сопротивление воздуха

В предыдущем разделе было сказано, что все объекты ( вне зависимости от их массы ) свободно падают с одинаковым ускорением — 9,8 м/с/с. Это конкретное значение ускорения настолько важно в физике, что у него есть свое особое название — ускорение свободного падения — и свой особый символ — г . Но почему все объекты свободно падают с одинаковым ускорением независимо от их массы? Это потому, что они все весят одинаково? . .. потому что они все имеют ту же гравитацию, что и ? …потому что сопротивление воздуха у всех одинаковое? Почему? Эти вопросы будут рассмотрены в этом разделе урока 3.

В дополнение к исследованию свободного падения будет также анализироваться движение объектов, встречающих сопротивление воздуха. В частности, будут изучены два вопроса:

• Почему объекты, встречающие сопротивление воздуха, в конце концов достигают предельной скорости?
• Почему в ситуациях, когда есть сопротивление воздуха, более массивные предметы падают быстрее, чем менее массивные?

Чтобы ответить на поставленные выше вопросы, второй закон движения Ньютона (F _net = m•a) будет применен для анализа движения тел, падающих под действием единственной силы тяжести (свободное падение) и под двойным влиянием силы тяжести и сопротивления воздуха.

 

 

Движение свободного падения

Как вы узнали из предыдущего раздела, свободное падение — это особый тип движения, при котором единственной силой, действующей на объект, является гравитация. Объекты, о которых говорят, что они подвергаются свободное падение , не встречающие значительной силы сопротивления воздуха; они падают только под действием силы тяжести. В таких условиях все объекты будут падать с одинаковым ускорением независимо от их массы. Но почему? Рассмотрим свободное падение 1000-килограммового слоненка и 1-килограммовой мыши-переростка.

Если применить второй закон Ньютона к их падению и построить диаграмму свободного тела, то можно увидеть, что 1000-килограммовый слоненок будет испытывать большую силу тяжести. Эта большая сила тяжести будет иметь прямое влияние на ускорение слона; таким образом, основываясь только на силе, он 9Можно подумать, что 0007 означает, что 1000-килограммовый слоненок будет ускоряться быстрее. Но ускорение зависит от двух факторов: силы и массы. 1000-килограммовый слоненок явно имеет большую массу (или инерцию). Эта увеличенная масса оказывает обратное влияние на ускорение слона. Таким образом, прямое воздействие большей силы на 1000-килограммового слона равно компенсируется обратным действием большей массы 1000-килограммового слона; и поэтому каждый объект ускоряется с одинаковой скоростью — примерно 10 м/с/с. Отношение силы к массе (F _нетто /м) одинакова для слона и мыши в условиях свободного падения.

Это отношение (F _нетто /м) иногда называют силой гравитационного поля и выражается как 9,8 Н/кг (для местоположения на поверхности Земли). Сила гравитационного поля является свойством местоположения в гравитационном поле Земли, а не свойством слоненка или мыши. Все объекты, расположенные на поверхности Земли, будут испытывать такую ​​силу (9.8 Н) на каждый 1 кг массы объекта. Будучи свойством местоположения в гравитационном поле Земли, а не свойством самого свободно падающего объекта, все объекты на поверхности Земли будут испытывать такое количество силы на единицу массы. Таким образом, все объекты свободно падают с одинаковой скоростью независимо от их массы. Поскольку гравитационное поле 9,8 Н/кг на поверхности Земли вызывает ускорение любого объекта, помещенного на нее, на 9,8 м/с/с, мы часто называем это соотношение ускорением свободного падения. (Гравитационные силы будут обсуждаться более подробно в одном из следующих разделов учебника «Класс физики».)

 

 

 

Посмотри!

Величина напряженности гравитационного поля ( г ) различна в разных гравитационных средах. Используйте Значение g виджета ниже, чтобы узнать силу гравитационного поля на других планетах. Выберите местоположение из выпадающего меню; затем нажмите Кнопка Отправить .

Расследуй!

Даже на поверхности Земли существуют локальные вариации значения g. Эти вариации обусловлены широтой (Земля не идеальная сфера, она имеет выпуклость посередине), высотой и местной геологической структурой региона. Используйте виджет Gravitational Fields ниже, чтобы исследовать, как местоположение влияет на значение g.

 

Падение с сопротивлением воздуха

Когда объект падает в воздухе, он обычно сталкивается с некоторым сопротивлением воздуха. Сопротивление воздуха возникает в результате столкновений передней поверхности объекта с молекулами воздуха. Фактическая величина сопротивления воздуха, с которым сталкивается объект, зависит от множества факторов. Чтобы не усложнять тему, можно сказать, что двумя наиболее распространенными факторами, оказывающими прямое влияние на величину сопротивления воздуха, являются скорость объекта и площадь поперечного сечения объекта . Увеличение скорости приводит к увеличению сопротивления воздуха. Увеличение площади поперечного сечения приводит к увеличению сопротивления воздуха.

 

 

 

Почему объект, встречающий сопротивление воздуха, в конце концов достигает предельной скорости? Чтобы ответить на эти вопросы, применим второй закон Ньютона к движению падающего парашютиста.

На приведенных ниже диаграммах показаны диаграммы свободного тела, показывающие силы, действующие на 85-килограммового парашютиста (включая снаряжение). Для каждого случая используйте диаграммы, чтобы определить результирующую силу и ускорение парашютиста в каждый момент времени. Затем используйте кнопку для просмотра ответов.

 

 

 

Приведенные выше диаграммы иллюстрируют ключевой принцип. Когда объект падает, он набирает скорость. Увеличение скорости приводит к увеличению величины сопротивления воздуха. В конце концов, сила сопротивления воздуха становится достаточно большой, чтобы уравновесить силу тяжести. В этот момент времени результирующая сила равна 0 ньютонов; объект перестанет ускоряться. Говорят, что объект достиг конечной скорости . Изменение скорости прекращается в результате баланса сил. Скорость, при которой это происходит, называется конечной скоростью.

В ситуациях, когда есть сопротивление воздуха, более массивные предметы падают быстрее, чем менее массивные. Но почему? Чтобы ответить на вопрос почему , необходимо рассмотреть диаграммы свободного тела для объектов разной массы. Рассмотрим падение двух парашютистов: одного массой 100 кг (парашютист плюс парашют), а другого — 150 кг (парашютист плюс парашют). Диаграммы свободного тела показаны ниже для момента времени, когда они достигли предельной скорости.

Как было сказано выше, величина сопротивления воздуха зависит от скорости объекта. Падающий объект будет продолжать ускоряться до более высоких скоростей, пока не встретит сопротивление воздуха, равное его весу. Поскольку парашютист весом 150 кг весит больше (испытывает большую силу тяжести), он будет разгоняться до более высоких скоростей, прежде чем достигнет конечной скорости. Таким образом, более массивные объекты падают быстрее, чем менее массивные объекты, потому что на них действует большая сила тяжести; по этой причине они разгоняются до более высоких скоростей, пока сила сопротивления воздуха не сравняется с силой тяжести.

 

Расследуй!

Величина сопротивления воздуха, которое испытывает объект, зависит от его скорости, площади поперечного сечения, формы и плотности воздуха. Плотность воздуха зависит от высоты над уровнем моря, температуры и влажности. Тем не менее, 1,29 кг/м ³ — вполне разумное значение. Форма объекта влияет на коэффициент сопротивления ( C _d ). Значения для различных форм можно найти здесь. Используйте Какая дрянь! ниже, чтобы изучить зависимость силы сопротивления воздуха от этих четырех переменных.

 

Мы хотели бы предложить …

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактива «Прыжки с парашютом» и/или нашего интерактива «Падение тел — 1D». Вы можете найти их в разделе Physics Interactives на нашем сайте. Skydiving Interactive позволяет учащимся изучить влияние массы, размера парашюта и начальной высоты на опыт парашютиста.

Посетите:  Прыжки с парашютом || Падающие тела — 1D

 

Следующий раздел:

Перейти к следующему уроку:

Уравнение, формула, примеры [Примечания GATE]

Серия испытаний

Автор Deepak Yadav|Обновлено: 6 октября 2022 г. тяжести. Когда объект поднимается или отодвигается от земли, к объекту прикладывается направленная вниз сила. Эта сила называется гравитацией. Гравитация Земли толкает объект к себе с ускорением, известным как ускорение свободного падения. Эта сила является результатом гравитационного притяжения Земли и связана с идеей гравитационных сил.

Здесь мы даем краткое объяснение концепции движения под действием силы тяжести. Он охватывает такие темы, как вертикальное движение под действием силы тяжести, уравнение движения под действием силы тяжести, формулу и несколько примеров.

Скачать формулы для GATE Машиностроение-Инженерная механика

Содержание

• 1. Определение движения под действием силы тяжести
• 2. Уравнение движения под действием силы тяжести
• 3. Скорость тела, совершающего движение под действием силы тяжести
• 4. Движение под действием силы тяжести Примеры

Прочитать статью полностью

Определение движения под действием силы тяжести

Движение объекта, вертикальное движение которого изменяется под действием силы тяжести, называется движением под действием силы тяжести. ГРАВИТАЦИЯ — это сила, которая тянет предметы вниз.

Движение под действием силы тяжести PDF

В действительности гравитация притягивает объекты к центру Земли. Сила гравитационной силы определяется массой объекта и гравитационной постоянной.

Формула движения под действием силы тяжести

Основная формула тела с некоторым весом, на которое действует сила гравитации:

Вес = масса × сила тяжести

(w=mg)

в ньютонах. Гравитация измеряется в метрах в секунду (м/с ² ), а масса в килограммах (кг). Гравитация оценивается в 9,8 м/с ² для объектов относительно близко к поверхности Земли.

Скачать формулы для машиностроения GATE — TOM & Vibrations

Уравнение движения под действием силы тяжести

Когда объект движется под действием силы тяжести, существуют определенные стандартные уравнения движения, которые используются для анализа движения объекта. Уравнение движения для нормальных горизонтальных сил совпадает с уравнением движения для гравитации, которое показано ниже.

v = u + gt

h = ut + (1/2)gt ²

v ² = u ² + 2gh

следует во всех приведенных уравнениях, относящихся к понятию уравнений движения под действием силы тяжести. Он интерпретируется как подходящий для движения вниз и отрицательный для движения вверх.

Скорость тела, движущегося под действием силы тяжести

Когда объект падает с заданной высоты, это обозначается как «h». Поскольку объект изначально находится в состоянии покоя, а затем падает с этой высоты, его начальная скорость равна нулю. Должна быть некоторая конечная скорость тела, когда объект достигает земли.

В результате обсуждаемое уравнение движения выглядит следующим образом:

v ² = u ² + 2gh

Значение «g» будет интерпретироваться как положительное, что означает перемещение объекта. вниз.

v ² = (0) ² + 2gh

v ² = 2gh

v = √2gh

Движение под действием силы тяжести Примеры

2 :

• Каждый раз, когда мяч подбрасывается вверх, сила тяжести заставляет мяч падать обратно на землю.
• Движение человека по земле будет вызвано исключительно силой гравитации, удерживающей человека на месте.
• Силы гравитации регулируют приливы с точки зрения их кратковременного периодического движения, вызванного подъемом и опусканием воды в водоемах.
• Прыжки, скольжение, ходьба, бег трусцой, танцы и другие обычные повседневные действия управляются силами гравитации.
• Гравитационные силы управляют движением небесных тел вокруг Солнца, чтобы обеспечить правильное выравнивание и вращение вокруг их осей.

Загрузить формулы для машиностроения GATE — механика жидкостей и машин

Часто задаваемые вопросы о движении под действием силы тяжести

• Какие движения вызываются гравитацией?

  Гравитация также может привести к тому, что объект, подброшенный в воздух, изменит направление, замедлится и упадет обратно на поверхность Земли. Луна удерживается на орбите силой земного притяжения; гравитация заставляет Луну постоянно менять курс.

• Как объекты двигаются под действием силы тяжести?

  Гравитация заставляет объекты ускоряться, когда они падают на землю. Скорость — это мера скорости и направления движения, а ускорение — это изменение скорости. Чем дольше объект находится в свободном падении, тем быстрее он опускается к земле под действием силы тяжести.

• Сила тяжести или ускорение?

  Сила гравитации часто выражается в терминах ускорения, обеспечиваемого силой гравитации при падении объекта.