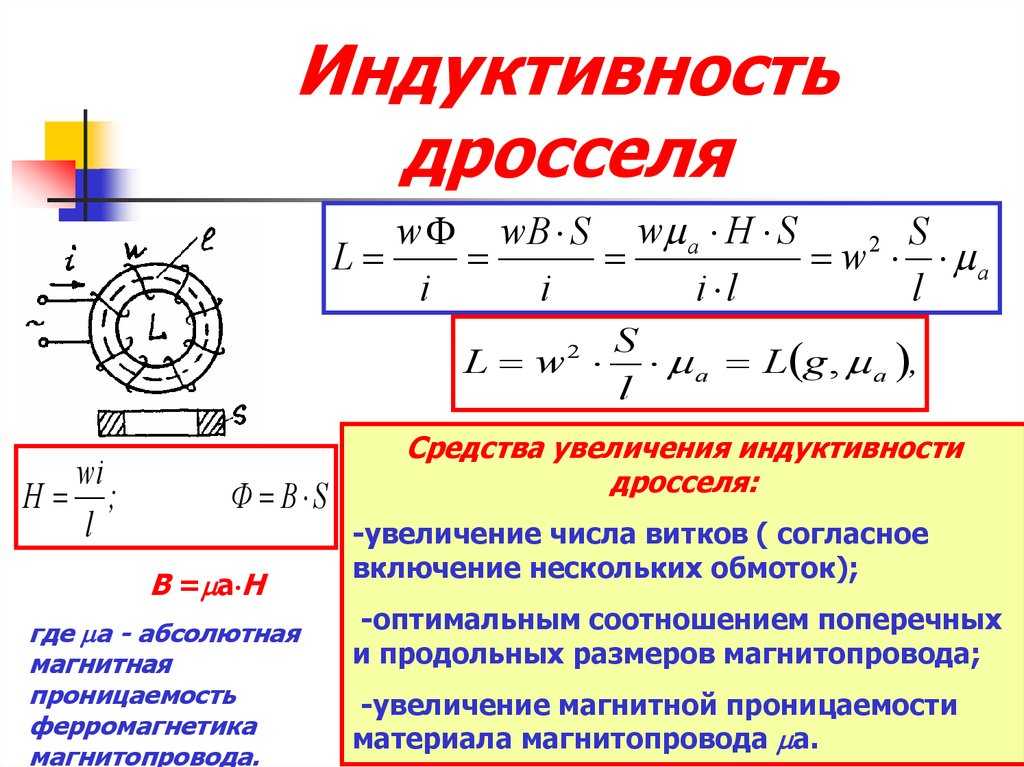
2.4.3 Добротность катушки q

Добротность катушки определяет резонансные свойства и кпд колебательных контуров, поэтому для сравнения этих параметров различных колебательных контуров используют именно этот параметр. На рисунке10 представлены типовые резонансные кривые контуров, катушки которых имеют разные добротности.

Рисунок 10 — Резонансные кривые контуров с катушками разных добротностей

Добротность катушки Q в общем виде представляет собой отношение мощности реактивной энергии электромагнитного поля, накоп­ленного в катушке, к мощности актив­ных потерь , рассеиваемых в катушке в виде тепла

. (4.6)

Формула (4.6) неудобна для практических расчетов. Воспользовавшись упрощенной эквивалентной схемой (рисунок 4) высокочастотной катушки, представляющую последовательно включенные идеальную катушку индуктивности с начальной индуктивностью и сопротивление потерь, выражение (4.

6) для добротности катушки можно записать в виде

,

где – частота переменного тока i, протекающего через катушку, рад/c;

– обобщенное сопротивление активных потерь в катушке, Ом.

Следовательно, добротность высокочастотной катушки индуктивности рассчитывается как отношение реактивного сопротивления катушки переменному току высокой частоты к обобщенному сопротивлению активных потерь в катушке.

Такое же определение добротности дается в ГОСТ 20718-75. Добротность катушки индуктивности — отношение индуктивного сопротивления катушки индуктивности к ее активному сопротивлению. Этим же стандартом предусмотрена номинальная добротность катушки индуктивности – это добротность при номинальном значении индуктивности, являющееся исходным для отсчета отклонений. Чем выше добротность, тем меньше величина потерь в катушке и выше ее качество.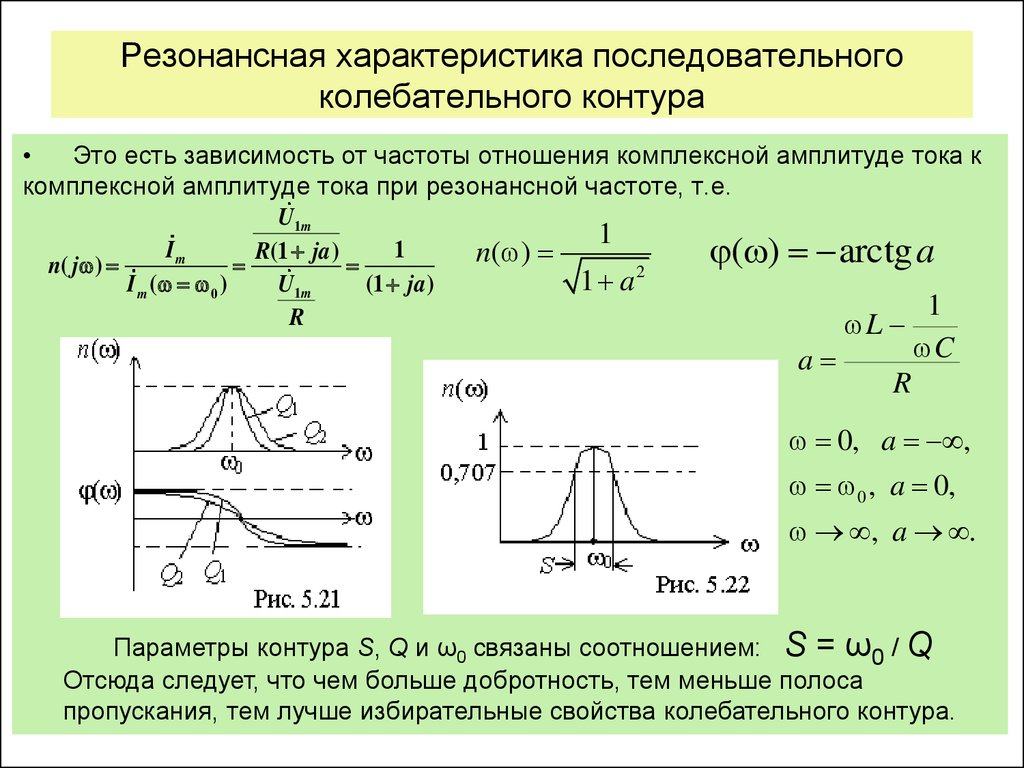

Значение Q определяется выбором типа обмотки, материала каркаса, конструкцией катушки и влиянием окружающих катушку других деталей при ее монтаже в аппаратуре.

Максимальное значение добротности высокочастотных катушек индуктивности обычно не превышает значение от 300 до 400 единиц.

Добротность катушки пропорциональна ее размерам. Для получения малогабаритных катушек с достаточно вы­сокой добротностью применяют магнитные сердечники. Катушки с сердечниками имеют меньшее число витков при заданной индуктивности, меньшее сопротивление провода и меньшие размеры. Запас добротности позволяет уменьшить размеры катушки и приблизить к ней экраны, т. е. получить малога­баритную катушку с добротностью до 150—250 и выше. Цен­ным свойством катушек с сердечниками является возможность подстройки, т. е. изменения индуктивности в небольших пре­делах, осуществляемого перемещением сердечника. Если бы в сердечнике не было потерь, то добротность катушки с сердечником также увеличилась бы в раз.

Однако из-за наличия потерь в сердечнике это увеличение не­сколько меньше. Приближенно можно считать, что доброт­ность катушки с сердечником в раз больше добротности катушки с такой же индуктивностью, но без сердечника. От­ношение добротности катушки с сердечником к добротности этой же катушки, но без сердечника, характеризует потери, вносимые сердечником в катушку. Это отношение зависит от коэффициента использования магнитных свойств материала, от его коэффициентов потерь и очень сильно — от частоты. С увеличением частоты потери в сердечнике возрастают, а про­ницаемость падает; это приводит к падению добротности. Отно­шение добротности катушки с сердечником к добротности той же катушки без сердечника может служить мерой для определения диапазона рабочих частот. Верхней границей ра­бочего диапазона является частота, при которой это отноше­ние достигает единицы, хотя допустимо применение сердеч­ника для регулировки индуктивности и при несколько более высоких частотах.

Добротность экранированной катушки оказывается ниже добротности той же катушки при отсутствии экрана.

Влияние экрана на параметры катушки проявляется тем сильнее, чем ближе его стенки расположены к обмотке.

Для того чтобы индуктивность и добротность катушки падали не более чем на 10%, рекомендуются следующие соотношения между диаметрами экрана и катушки: для однослойных катушек равно от 1,6 до 2,5, причем для ко­ротких катушек равно от 1,5 до 1,8. Эти соотношения при­годны и для многослойных катушек, если заменить на Для стабильных катушек рекомендуется брать больше 2,5. С повышением частоты эти соотношения можно умень­шать.

Добротность катушки индуктивности, как изготовить высокодобротную катушку, выбор каркаса и диаметра провода

Это нужно знать Весь перечень знаний находится на этой странице

Необузданные гонки за всё более высокими параметрами добротности колебательных контуров не так просты, как могли бы показаться на первый взгляд. На предыдущей странице, мы определились, что добротность контура в первую очередь определяется добротностью катушки индуктивности, а она в свою очередь напрямую связана с сопротивлением потерь и описывается формулой Q=2πfL/Rпот. Сопротивление потерь — это параметр, связанный не только с потерями в проводах, но и учитывающий потери в диэлектрике, сердечнике и экране. — Потери в сердечнике складываются из потерь на вихревые токи и потерь на гистерезис, связанных с перемагничивание материала в течение периода. — Потери в диэлектрике обусловлены как паразитной межвитковой ёмкостью между соседними витками катушки, так и магнитными свойствами диэлектрика каркаса катушки (эти потери аналогичны потерям в сердечнике). — Потери в экране вызываются индуцированием переменным магнитным полем вихревых ЭДС в окружающих проводниках. Точный расчёт всех перечисленных параметров — дело весьма затруднительное, поэтому, с целью упрощения задачи, обычно учитываются только потери в проводах, как вносящие основной вклад в общую сумму потерь. При этом применяются специальные меры по минимизации неучтённых потерь – керамические, или ребристые каркасы, бескаркасные катушки (с «воздушным» каркасом), отказ от использования сердечника. А теперь, что касается выбора параметра индуктивности катушки для достижения максимальной добротности. Глядя на формулу, описывающую величину добротности Q=2πfL/Rпот, а так же приведённую на рисунке, можно сделать преждевременный вывод — добротность катушки линейно растёт с ростом частоты и достигает максимума на частоте собственного резонанса, когда С минимальна и равна собственной паразитной ёмкости катушки и паразитных емкостей источника, нагрузки и монтажа. Однако, не всё так просто! Оказывается, что для достижения максимальной добротности на определённой частоте существует оптимальная величина индуктивности катушки. При понижении частоты добротность уменьшается, но не линейно, а несколько медленнее, за счёт снижения влияния действия скин эффекта, гуляющего внутри провода, а при повышении — тоже плавно уменьшается из-за проявляющейся зависимости совокупных паразитных ёмкостей от частоты (варикапный эффект). К тому же эти паразитные ёмкости начинают доминировать в общей ёмкости колебательного контура, а образованный ими конденсатор, как известно, обладает далеко не самым выдающимся параметром добротности. И в заключение нашего теоретического экскурса, всё же не воздержусь и приведу основные факторы, определяющие сопротивление потерь в проводах катушек на высоких частотах: 1. Омическое (активное) сопротивление проводника постоянному току — классика жанра, рассчитать можно по длине и диаметру провода на странице    ссылка на страницу. 2. Поверхностный эффект, скин-эффект — эффект роста сопротивления провода с ростом частоты. Суть эффекта состоит в вытеснении тока в поверхностные слои провода, в связи с чем уменьшается полезное сечение проводника и, как следствие, растёт его сопротивление. 3. Эффект близости, суть которого состоит в вытеснении тока под воздействием вихревых токов и магнитного поля к части провода, прилегающей к каркасу. В результате сечение, по которому протекает ток, принимает серповидную форму, что ведёт к дополнительному возрастанию сопротивления проводника. Думаю, на этом хватит! Переходим к опытно-практической части дипломной работы: Приготовим закуски и коктейли, накроем стол… Итак, какой должна быть высокодобротная катушка? 1. Очевидно, что из металла! Ладно, посмеялись — и будет. Нам нужен металл с минимальным удельным сопротивлением и с максимально возможным (в пределах разумного) диаметром проводника. На начальном уровне — медь, на продвинутом — медь с серебряным напылением. 2. Катушка должна быть большой! Опять же, как и в первом пункте — излишний фанатизм не приветствуется. Однако, помимо размеров катушки, пристальное внимание следует обратить и на форм-фактор — отношение длины к диаметру металлоизделия. Опытными мотальщиками было продемонстрировано, что оптимальная по добротности катушка имеет отношение длины к диаметру L/D ≈ 1, причём изменение этого отношения в пару раз в ту, или иную сторону — к существенному изменению добротности не приводит. 3. Желание минимизировать эффект близости и уменьшить собственную ёмкость катушки сподвигло специалистов к следующему постулату: оптимальное отношение шага намотки (расстояние между центрами соседних витков) к диаметру провода равно ≈2. 4. И вот теперь главный вопрос радиолюбительства: Сколько мотать витков в оптимизированной катушке для достижения максимальной добротности? На вопрос викторины отвечает М. Филатов, досконально изучивший этот предмет в 1976 г. на кафедре конструирования РЭА ФРиС РПИ.    Диапазон       Параметры катушки       D каркаса       L, мкГн       расчётные       20 мм       30 мм       40 мм      10 м   1,5   L нам. (мм)   10   15   20   n (вит.)   8,5   7   6   d пров.(мм)   0,84   1,5   2,4   Q   472   708   945   14 м   2,0   L нам. (мм)   12   18   24   n (вит.)   10,3   8,4   7,3   d пров.(мм)   0,8   1,46   2,2   Q   439   660   879   20 м   3,0   L нам. (мм)   12   18   24   n (вит.)   18,7   10,3   9   d пров.(мм)   0,67   1,2   1,8   Q   359   538   718   40 м   6,0   L нам. (мм)   14   21   28   n (вит.)   18,7   15,2   13,2   d пров.(мм)   0,53   0,66   1,46   Q   270   406   542   80 м   12,0   L нам. (мм)   14   21   28   n (вит.)   26,4   21,5   18,6   d пров.(мм)   0,37   0,66   1,0   Q   191   287   382   160 м   24,0   L нам. (мм)   16   24   32   n (вит.)   39   32   27,5   d пров.(мм)   0,31   0,53   0,8   Q   144   216   288 Данная таблица дошла до наших взоров благодаря стараниям латвийского радиолюбителя Юрия Балтина (YL2DX), опубликовавшим её в далёком 2003 году на своём сайте http://dx. ardi.lv, за что ему большое человеческое спасибо! Таблица эта — не догма и не абсолютная истина в последней инстанции, однако она позволяет достаточно наглядно пронаблюдать зависимость параметра добротности катушки индуктивности от диаметра каркаса и толщины провода, а заодно и оценить оптимальное значение индуктивности для того или иного частотного диапазона. Поэтому, если Вы всё-таки озадачились намоткой высокодобротного изделия, вооружайтесь информацией, изложенной на этой странице, доступным каркасом, или оправкой для бескаркасной катушки и бодро шагайте на сайт coil32.ru, где вы найдёте бесплатную, но очень хорошую программу для расчёта катушек индуктивности, а заодно и массу полезной теоретической информации по всему, что касается разнообразных намоточных изделий. А на следующей странице будем мотать высокодобротные катушки на ферритовых кольцах, а также на кольцах из распылённого железа.

Как добротность или добротность влияют на характеристики индуктора

Индуктивности являются наиболее доминирующим элементом в любых преобразователях силовой электроники, сетях фильтров и системах связи, где они в основном используются в резонансных сетях. Если вы совершенно не знакомы с катушками индуктивности, ознакомьтесь со статьей о катушках индуктивности, чтобы понять основы. На практике существует много типов индукторов, но ни один из них не является идеальным индуктором, то есть они не являются чистыми индукторами. Таким образом, при выборе катушки индуктивности для конкретного приложения, помимо значений индуктивности, некоторые другие параметры, такие как сопротивление постоянному току, сопротивление переменному току и паразитная емкость, также будут связаны с катушкой индуктивности, и это необходимо учитывать для удовлетворения проектных требований и улучшения. надежность.

 

После расчета значения индуктивности для выбранного приложения необходимо выбрать соответствующий практический компонент на основе технических данных производителя и карт линейки продуктов. В некоторых приложениях, особенно для радиочастотных приложений, важно учитывать коэффициент качества катушки индуктивности вместе со значением индуктивности. Но почему?

 

Почему важна добротность катушки индуктивности?

Как было сказано ранее, на практике идеального элемента не бывает. Катушки индуктивности изготавливаются путем намотки катушек на различные магнитные материалы, называемые сердечниками. Значение индуктивности любого практического индуктора определяется на основе количества витков, проницаемости материала сердечника, плотности потока, площади сердечника и т. д. При использовании этих индукторов в практических приложениях значение индуктивности может изменяться в зависимости от приложенного тока, сигнала частота, факторы старения, температурные условия эксплуатации и т. д.

 

Но надежная спецификация конструкции требует стабильной работы в широком диапазоне частот, входных и температурных условий. Таким образом, чтобы обеспечить постоянство производительности продукта, измеряются определенные параметры, чтобы обеспечить производительность индуктора. Одним из таких параметров является добротность катушки или добротность катушки индуктивности.

 

Что такое добротность?

В идеальном чистом индукторе индуктор будет иметь только значение индуктивности. Но в практической катушке индуктивности наряду с этим номинальным значением индуктивности также будут присутствовать постоянное и переменное сопротивление и паразитная емкость, которые ухудшат характеристики индуктивности. Коэффициент добротности или добротность используется для расчета производительности катушки индуктивности путем включения этого значения паразитного сопротивления и емкости. Q – фактор – это параметр измерения согласованности, который определяет «Качество индуктора» относительно его потерь и эффективности при практическом применении. Давайте подробно обсудим это паразитное сопротивление и емкость.

 

Сопротивление постоянному току (DCR или R _DC ):

При производстве индуктора катушки, намотанные на материал магнитного сердечника, имеют некоторое внутреннее сопротивление, которое вводит «сопротивление постоянному току» наряду с номинальным значением индуктивности. В паспорте производителя разработчики могут получить эти данные сопротивления в «DCR» или «R 9».0038 DC ”столбец. Значение сопротивления постоянному току индуктора зависит от длины провода и размера провода, используемого для намотки. Если требуемое значение индуктивности выше, то больше не требуется. необходимо намотать витков и использовать более длинный провод, что приводит к увеличению сопротивления постоянному току (на рис. 1 приведены данные о значении сопротивления для проводов разного размера и длины). Катушки индуктивности изготавливаются на основе рабочего тока, и соответствующие размеры катушек используются для определенных приложений. Значения сопротивления также зависят от размера провода. Использование катушек большего диаметра дает более низкое сопротивление постоянному току, чем катушки меньшего диаметра, но частотно-зависимые параметры играют важную роль при замене катушки меньшего диаметра катушкой большего диаметра.

 

Сопротивление переменному току (R _ac ) из-за скин-эффекта:

Сопротивление переменному току играет наиболее важную роль в увеличении сопротивления провода, когда система используется в диапазоне частот примерно выше 50 кГц. Этот эффект известен как « Skin Effect ». При подаче сигналов более высокой частоты (свыше 50 кГц) через проводники ток будет проходить через поверхность проводов, а не через всю площадь поперечного сечения проводника. Из-за неиспользования всей площади катушки сопротивление увеличивается, и это значение сопротивления изменяется в зависимости от увеличения частоты.

 

Сопротивление переменному току (R _ac ) из-за эффекта гистерезиса сердечника: 

В идеальном сердечнике изменение плотности потока будет следовать за изменением магнитного поля 0(0H0). Но в практических сердечниках из-за свойств материала будут небольшие различия. Плотность потока не будет равна нулю для приложенного нулевого поля H из-за остаточного магнетизма, и после определенного поля H плотность потока становится насыщенной. Дополнительная коэрцитивная сила должна быть приложена в обратном направлении, чтобы снизить остаточный магнетизм Br до нуля. В отрицательном цикле также следует использовать тот же метод, чтобы заставить систему работать между положительными и отрицательными областями 9.0007 Кривая ЧД . Кривая BH и остаточный магнетизм также варьировались в зависимости от приложенной частоты, гистерезисные потери увеличиваются с увеличением частоты. При формировании катушки индуктивности к целевому значению индуктивности добавляются гистерезисные потери в виде сопротивления переменному току.

 

Сопротивление изоляции (Rd):

В материале сердечника и катушек обмотки используется изоляция, чтобы избежать внутренних коротких замыканий. Диэлектрические материалы, используемые в изоляционных материалах, имеют собственное сопротивление, а к компоненту с потерями добавляется полезное значение индуктивности. Эта часть отвечает за ток утечки, а за счет диэлектрических материалов образовалась межпроводная емкость.

 

В практических индукторах указанные выше значения сопротивления присутствуют вместе с номинальными значениями индуктивности. Значение общего сопротивления, отличное от номинальной индуктивности, определяется приведенным ниже соотношением.

R  Total  = R  dc  + R  ac  +  Rd  

 

Коэффициент добротности (добротность) дает подробную информацию о соотношении между компонентами индуктивной реакции и резистора, которые вызывают потери в индукторе во время его работы. Коэффициент качества Формула приведена ниже.

Q = (2 * ᴫ * f * L) / (R  dc  + R  ac  +  Rd  ) 

 

Кроме того, коэффициент добротности может быть выражен в терминах зависимости мощности. Как упоминалось ранее, компоненты сопротивления добавляются к номинальной индуктивности из-за внешних параметров. Эти резисторы добавляют потери в катушку индуктивности, что снижает эффективность катушки индуктивности.

Q = 2 * ᴫ (Сохраненная_Энергия) / (Рассеиваемая_Энергия_за_Цикл)
 

 

Основываясь на двух приведенных выше соотношениях, мы можем определить, что если значения постоянного, переменного и диэлектрического сопротивления высоки, потери мощности также выше, а значение добротности снижается. Это приведет к снижению эффективности. Таким образом, коэффициент добротности даст подробную информацию о качестве индуктора. Если значение добротности высокое, пользователь может сделать вывод, что выбранный индуктор имеет более низкие значения сопротивления переменному и постоянному току и, следовательно, имеет низкие потери мощности по сравнению с более низкой добротностью. Значение индуктора. Отсюда и Значение добротности катушки индуктивности должно быть высоким , чтобы получить от нее оптимальную производительность.

 

Как добротность катушки индуктивности влияет на ее работу в цепи?

В практических схемах фильтров добротность играет доминирующую роль в запасе полосы пропускания фильтра . Для приложений с узкой полосой пропускания радиочастот, таких как система связи общественной безопасности, системы беспроводной связи полиции, данные, передаваемые с помощью узкополосной связи, и фильтры, используемые для этих приложений, должны требовать более узкой полосы пропускания, а фильтр должен иметь максимальную способность ослаблять сигналы вне области полосы пропускания.

Для некоторых других приложений требуется более широкая полоса пропускания, и фильтр должен пропускать более широкий диапазон частот сигналов. На рисунке ниже показана характеристика фильтра для разных значений добротности . Катушка индуктивности с более высоким коэффициентом добротности, показанная красным цветом, обеспечивает очень узкую полосу пропускания с более высоким коэффициентом усиления. Таким образом, фильтр обеспечивает эффективную фильтрацию для интересующей более узкой частоты, а все остальные частоты сигнала ослабляются. Катушка индуктивности с низким коэффициентом качества, показанная зеленым цветом, обеспечивает меньший коэффициент усиления по напряжению с увеличенной полосой пропускания. Таким образом, разработчик может выбрать оптимальные значения добротности, исходя из требований к конструкции и эффективности.

Coil32 — О расчете добротности

Детали

Опубликовано: 17 января 2015 г.

Просмотров: 17044

Расчет добротности катушки индуктивности довольно сложен. В конечном итоге добротность зависит от многих факторов — потерь в проводах, в сердечнике, в экране. Точный учет всего этого очень сложен. Однако можно упростить задачу, если учесть только потери в проводе. Во-первых, они вносят основной вклад в общую сумму потерь, а во-вторых оценивают добротность интересующей нас катушки при создании более добротных цепей. В этом случае мы применяем специальные меры по минимизации потерь путем реализации ребристого сердечника или катушки индуктивности с воздушным сердечником.

Напоминаю, что добротность катушки индуктивности это отношение реактивного сопротивления катушки ( 2πƒL ) к ее сопротивлению потерь ESR. Определить реактивное сопротивление катушки несложно. Но оценка потерь в проводе не так проста, и мы рассмотрим ее подробно…

Поиск решения привел на сайт G3YNH — Dr. David W Knight. Он провел расширенные теоретические исследования по расчету импеданса на высоких частотах, расчету катушек индуктивности, выбору формул, аппроксимирующих экспериментальные измерения. Их можно найти в разделе сайта — «От Передатчик к антенне ». Статья посвященная расчету катушек здесь. Эти исследования легли в основу метода расчета добротности в Coil32. Особая благодарность Д. Найту.

Одним из первых, кто попытался учесть потери в катушках индуктивности на радиочастотах, был С.Баттерворт, в работе: « Эффективное сопротивление катушек индуктивности на радиочастотах, 1926 «. Он более известен как разработчик широко известных «фильтров Баттерворта». Но метод Баттерворта с высокой точностью рассчитывает потери в проводе на ВЧ только для бесконечно длинного соленоида.

Потери в проводнике на высоких частотах складываются из трех факторов:

1. Прежде всего, в зависимости от материала провода . Очевидно, что провод из металла с большим удельным сопротивлением будет иметь большие потери. Как известно, сопротивление провода постоянному току можно рассчитать как:

   R DC = ρl/A . где А = πr 2

   [1]

   • R _DC – Сопротивление DC [Ом]
   • ρ – удельное сопротивление металла [Ом·м] (например, серебро = 1,59·10 ^-8 Ом-м)
   • l – длина провода [м]
   • A – сечение проводника [м ² ]
   • r – радиус провода [м]
   Можно утверждать, что это основные потери в проводе и потери на высоких частотах не могут быть меньше потерь на постоянном токе.
2. Явление скин-эффекта заключается в том, что переменный ток, протекающий по поверхности провода, экранирует внутренние слои и избегает прохождения к центру проводника, в результате чего почти весь ток концентрируется в тонком поверхностном слое, толщина определяется следующим выражением:

   δi = √[ ρ / ( π f μ )]

   [2]

   • δi – глубина скин-слоя [м], глубина, на которой плотность тока уменьшается в e раз (e = 2,71 – число Эйлера)
   • ρ – удельное сопротивление металла [Ом·м]
   • f – частота [Гц]
   • µ = µ ₀ *µ _r , µ ₀ = 4π · 10-7 — абсолютная магнитная проницаемость, µ _r — относительная магнитная проницаемость металла (близкая к единице)
   Очевидно, что импеданс для переменного тока увеличивается с частотой по мере уменьшения толщины скин-слоя. Для удобства логичности расчетов введем понятие коэффициента скин-эффекта — Ξ . Это будет коэффициент, показывающий, во сколько раз сопротивление проводника для переменного тока данной частоты выше сопротивления постоянному току.

   СОЭ = R DC · Ξ

   [3]

   Классический метод вычисляет площадь кольца от поверхности до глубины скин-слоя Aeff = π (2rδi — δi2) и подставляет ее в формулу [1], вычисляя сопротивление переменному току вместо постоянного. Скин-фактор в этом случае выражается как:

   Ξ = r²/( 2rδi — δi²)

   [4]

   Физически эту формулу можно выразить как отношение проводимости постоянного тока (пропорциональной r ² ) к проводимости переменного тока (пропорциональной r и δi ). Дэвид Найт усовершенствовал этот метод для получения более точных формул сопротивления переменному току. См. ссылку ниже…
3. Наличие эффекта близости явление . Эффект заключается в том, что магнитное поле от соседних витков катушки с проволокой индуцирует вихревые токи. Наложение этих токов на токи от скин-эффекта приводит к тому, что плотность тока фрагмента проводника, расположенного во внутренней части соленоида, выше, а скин не похож на кольцо и напоминает полумесяц.

   Очевидно, импеданс по переменному току под действием эффекта близости еще больше увеличивается. Эффект уменьшается с уменьшением близости, т.е. с увеличением зазора между витками. Следует иметь в виду, что как эффект близости, так и скин-эффект — это две стороны одного и того же явления — взаимодействия ВЧ-тока с магнитным полем.

   Из-за чрезвычайной сложности описания электромагнитного поля, связанного с радиочастотными катушками, не существует простых теоретически обоснованных приближенных формул для расчета эффекта близости в радиочастотной катушке произвольной конструкции. Мы можем использовать компьютерную модель в электромагнитных симуляторах, использующих метод конечных элементов — COMSOL Multiphysics , FEMM , ANSYS и т.д. Но для упрощения расчетов можно использовать психоаналитические методы расчета с использованием таблиц, составленных на основе экспериментальных измерений. . Мы спускаемся туда.

   По аналогии со скин-фактором введем понятие фактора близости — Ψ , тогда:

   СОЭ = R DC · Ξ · Ψ

   [5]

   Эффект близости отсутствует в прямом проводнике, и в этом случае Ψ = 1.

   В 1947 г. радиоинженер Р.Г.Медхерст — сотрудник научно-исследовательской лаборатории «Дженерал Электрик Ко.Лтд.» опубликовал ряд работ, связанных с экспериментальными исследованиями индукторов, в том числе исследованиями эффекта близости. Результаты этих исследований актуальны и по сей день. Из измерений параметров реальных катушек Медхерст пришел к выводу, что метод Баттерворта не работает для коротких катушек. Термин «короткий» относится к катушкам с отношением l/D <7 и шагом намотки менее чем в два раза больше диаметра провода. (т.е. именно те, которые чаще всего используются на практике).
   Нас интересуют экспериментальные данные по Ψ. Медхерст приводит их в виде таблицы в зависимости от отношения длины витка к диаметру (l/D) и шага намотки к диаметру провода (p/d). Желтым отмечено совпадение эксперимента и теории Баттерворта при ошибке менее 3%:

   р/д → л/д ↓	1	1.111	1,25	1,429	1,667	2	2,5	3.333	5	10
   0	5,31	3,73	2,74	2.12	1,74	1,44	1,20	1,16	1,07	1,02
   0,2	5,45	3,84	2,83	2,20	1,77	1,48	1,29	1,19	1,08	1,02
   0,4	5,65	3,99	2,97	2,28	1,83	1,54	1,33	1,21	1,08	1,03
   0,6	5,80	4. 11	3.10	2,38	1,89	1,60	1,38	1,22	1,10	1,03
   0,8	5,80	4.17	3,20	2,44	1,92	1,64	1,42	1,23	1,10	1,03
   1	5,55	4.10	3,17	2,47	1,94	1,67	1,45	1,24	1,10	1,03
   2	4.10	3,36	2,74	2,32	1,98	1,74	1,50	1,28	1,13	1,04
   4	3,54	3,05	2,60	2,27	2. 01	1,78	1,54	1,32	1,15	1,04
   6	3,31	2,92	2,60	2,29	2,03	1,80	1,56	1,34	1,16	1,04
   8	3,20	2,90	2,62	2,34	2,08	1,81	1,57	1,34	1,165	1,04
   10	3,23	2,93	2,65	2,27	2.10	1,83	1,58	1,35	1,17	1,04
   ∞	3,41	3.11	2,815	2,51	2,22	1,93	1,65	1,395	1,19	1,05

   Эту таблицу можно представить в виде массива данных, а промежуточные данные получить методом линейной интерполяции. Это было сделано в онлайн-калькуляторе ON4AA — http://hamwaves.com/antennas/inductance.html. Пожалуй, это единственный калькулятор, правильно считающий добротность. В Coil64_v2.1.25 используется метод из работы: «Сопротивление однослойных катушек индуктивности с круглым проводом по A.H.M.Arnold, D.Eng., Associate Member 1951». Тот же метод используется в Android-версии Coil32. Метод основан на формулах Баттерворта и списках с поправочными коэффициентами для коротких витков и вычисляет коэффициент эффекта близости с точностью ± 10 %. При этом учитывается рабочая частота, количество витков катушки, материал провода и то, что невозможно сделать напрямую по таблице Медхерста. В программе есть возможность выбрать материал провода. В реальной конструкции катушки индуктивности с воздушным сердечником отклонение расчета от измерения может достигать 20-30%.

Существует оптимальное соотношение шага намотки к диаметру провода в зависимости от форм-фактора катушки. Medhurst дает эту зависимость в виде графика.

Если учесть, что наибольшая добротность катушки достигается при l/D ≈ 1 , то в этом случае оптимальное отношение шага намотки катушки к диаметру p/d ≈ 2 , т.е. мы можем однозначно определить оптимальный диаметр проволоки, зная геометрию катушки. При этом катушка с таким же форм-фактором (l/D ≈ 1) имеет минимальную паразитную емкость. Это и понятно, ведь катушка с такой геометрией намотки имеет минимальную длину провода при максимальной индуктивности. Такие оптимальные катушки геометрически подобны, т.е. все размеры катушки, включая диаметр провода, можно увеличить, а ее собственная резонансная частота уменьшится, примерно так же, как это принято в антенной технике. Но добротность этих катушек не будет разной.

Ссылки:

1. Практические непрерывные функции для внутреннего импеданса сплошных цилиндрических проводников — © D.