=a→·npa→b→=b→·npb→a→ показывает, что npb→a→ — это числовая проекция a→ на b→, npa→a→- проекция b→ на a→ соостветсвенно.

Сформулируем определение произведения для двух векторов:

Скалярное произведение двух векторов a→ на b→ называют произведение длины вектора a→ на проекцию b→ на направление a→ или произведение длины b→ на проекцию a→ соответственно.

Скалярное произведение в координатах

Вычисление скалярного произведения можно производить через координаты векторов в заданной плоскости или в пространстве.

Скаларное произведение двух векторов на плоскости, в трехмерном простарнстве называют сумму координат заданных векторов a→ и b→.

При вычислении на плоскости скаларного произведения заданных векторов a→=(ax,ay), b→=(bx,by) в декартовой системе используют:

a→,b→=ax·bx+ay·by,

для трехмерного пространства применимо выражение:

a→,b→=ax·bx+ay·by+az·bz.

Фактически это является третьим определением скалярного произведения.

Докажем это.

)==ax·bx+ay·by+az·bz

– соответственно для векторов трехмерного пространства.

Скалярное произведение векторов с координатами говорит о том, что скалярный квадрат вектора равен сумме квадратов его координат в пространстве и на плоскости соответственно. a→=(ax,ay,az), b→=(bx,by,bz) и (a→,a→)=ax2+ay2.

Скалярное произведение и его свойства

Существуют свойства скалярного произведения, которые применимы для a→,b→ и c→:

1. коммутативность (a→,b→)=(b→,a→);
2. дистрибутивность(a→+b→,c→)=(a→,c→)+(b→,c→), (a→+b→,c→)=(a→,b→)+(a→,c→);
3. сочетательное свойство (λ·a→,b→)=λ·(a→,b→),(a→,λ·b→)=λ·(a→,b→), λ — любое число;
4. скалярный квадрат всегда больше нуля (a→,a→)≥0, где (a→,a→)=0 в том случае, когда a→ нулевой.

Пример 1

Свойства объяснимы благодаря определению скалярного произведения на плоскости и свойствам при сложении и умножении действительных чисел.

Доказать свойство коммутативности (a→,b→)=(b→,a→). Из определения имеем, что (a→,b→)=ay·by+ay·by и (b→,a→)=bx·ax+by·ay. )=3·7·cos60°=3·7·12=212

Ответ:(a→,b→)=212.

Пример 3

Заданны векторы a→=(1,-1,2-3), b→=(0,2,2+3). Чему равно скалярной произведение.

Решение

В данном примере рассматривается формула вычисления по координатам, так как они заданы в условии задачи:

(a→,b→)=ax·bx+ay·by+az·bz==1·0+(-1)·2+(2+3)·(2+3)==0-2+(2-9)=-9

Ответ: (a→,b→)=-9

Пример 4

Найти скалярное произведение AB→ и AC→. На координатной плоскости заданы точки A(1,-3), B(5,4), C(1,1).

Решение

Для начала вычисляются координаты векторов, так как по условию даны координаты точек:

AB→=(5-1,4-(-3))=(4,7)AC→=(1-1,1-(-3))=(0,4)

Подставив в формулу с использованием координат, получим:

(AB→,AC→)=4·0+7·4=0+28=28.

Ответ: (AB→,AC→)=28.

Пример 5

Заданы векторы a→=7·m→+3·n→ и b→=5·m→+8·n→, найти их произведение.m→ равен 3 и n→ равен 2 единицам, они перпендикулярные.

Решение

(a→,b→)=(7·m→+3·n→, 5·m→+8·n→). Применив свойство дистрибутивности, получим:

(7·m→+3·n→, 5·m→+8·n→)==(7·m→, 5·m→)+(7·m→, 8·n→)+(3·n→, 5·m→)+(3·n→, 8·n→)

Выносим коэффициент за знак произведения и получим:

(7·m→, 5·m→)+(7·m→, 8·n→)+(3·n→, 5·m→)+(3·n→, 8·n→)==7·5·(m→,m→)+7·8·(m→,n→)+3·5·(n→,m→)+3·8·(n→,n→)==35·(m→,m→)+56·(m→,n→)+15·(n→,m→)+24·(n→,n→)

По свойству коммутативности преобразуем:

35·(m→,m→)+56·(m→,n→)+15·(n→,m→)+24·(n→,n→)==35·(m→,m→)+56·(m→,n→)+15·(m→,n→)+24·(n→,n→)==35·(m→,m→)+71·(m→,n→)+24·(n→,n→)

В итоге получим:

(a→,b→)=35·(m→,m→)+71·(m→,n→)+24·(n→,n→). )+24·n→2==35·32+71·3·2·cosπ2+24·22=411.

Ответ: (a→,b→)=411

Если имеется числовая проекция.

Пример 6

Найти скалярное произведение a→и b→. Вектор a→ имеет координаты a→=(9,3,-3), проекция b→ с координатами (-3,-1,1).

Решение

По условию векторы a→ и проекция b→ противоположно направленные, потому что a→=-13·npa→b→→, значит проекция b→ соответствует длине npa→b→→, при чем со знаком «-»:

npa→b→→=-npa→b→→=-(-3)2+(-1)2+12=-11,

Подставив в формулу, получим выражение:

(a→,b→)=a→·npa→b→→=92+32+(-3)2·(-11)=-33.

Ответ: (a→,b→)=-33.

Задачи при известном скалярном произведении, где необходимо отыскать длину вектора или числовую проекцию.

Пример 7

Какое значение должна принять λ при заданном скалярном произведении a→=(1,0,λ+1) и b→=(λ,1,λ) будет равным -1.

Решение

Из формулы видно, что необходимо найти сумму произведений координат:

(a→,b→)=1·λ+0·1+(λ+1)·λ=λ2+2·λ.

В дано имеем (a→,b→)=-1. )=5·3·cos(45°)=1522.

Ответ: A=1522.

Пример 9

Материальная точка, перемещаясь из M(2,-1,-3) в N(5,3λ-2,4) под силой F→=(3,1,2), совершила работа равную 13 Дж. Вычислить длину перемещения.

Решение

При заданных координатах вектора MN→ имеем MN→=(5-2, 3λ-2-(-1), 4-(-3))=(3, 3λ-1,7).

По формуле нахождения работы с векторами F→=(3,1,2) и MN→=(3, 3λ-1,7) получим A=(F⇒, MN→)=3·3+1·(3λ-1)+2·7=22+3λ.

По условию дано, что A=13Дж, значит 22+3λ=13. Отсюда следует λ=-3, значит и MN→=(3,3λ-1,7)=(3,-10,7).

Чтобы найти длину перемещения MN→ , применим формулу и подставим значения:

MN→=32+(-10)2+72=158.

Ответ: 158.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р.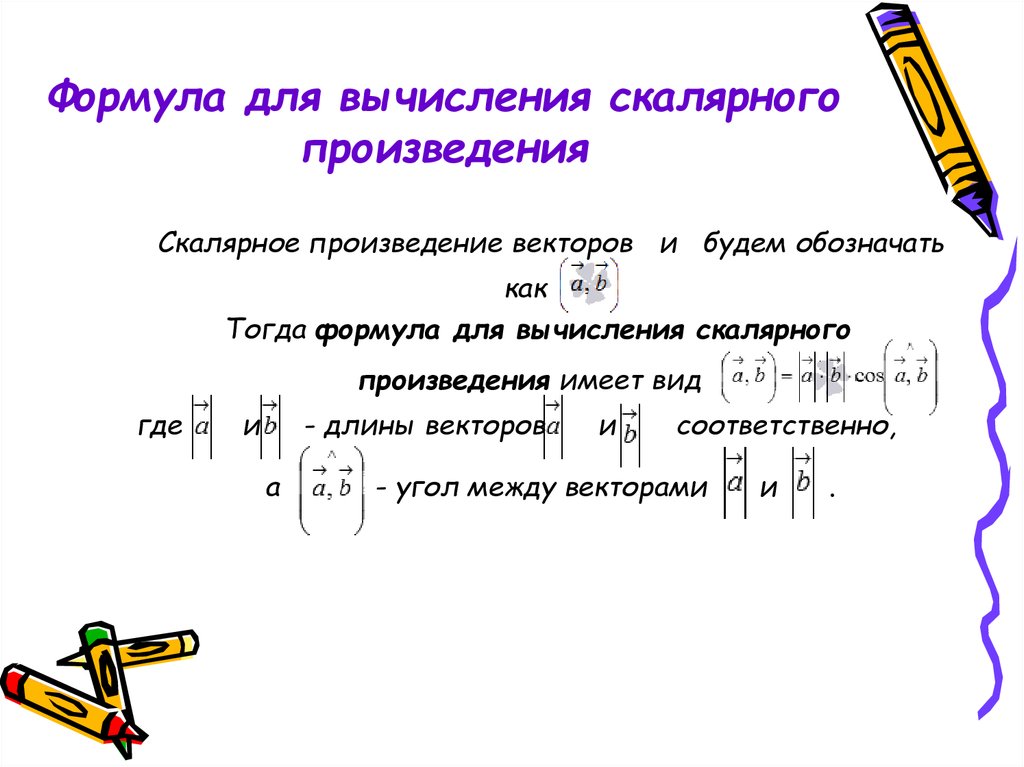

Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

40. Скалярное произведение векторов.

Определение 14.

Скалярным произведением двух векторов и называется число, равное произведению длин этих векторов на косинус угла между ними.

Таким образом, если , – вектора, то скалярное произведение обозначается и

.

Свойства скалярного произведения.

1) Коммутативность: .

Действительно, (так как , то есть четная функция, то ) .

2) Скалярное произведение двух векторов равно длине одного вектора умноженной на проекцию другого на направление первого.

Действительно, .

Отсюда видно, что если , то .

Следовательно, проекция вектора на ось равна скалярному произведению этого вектора на направляющий вектор оси.

3) .

Действительно, .

4) .

Действительно, .

5) Для того, что бы два ненулевых вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю.

Пусть     .

Пусть  , так как ,    .

6) Пусть  , т.е.  скалярный квадрат вектора равен квадрату длины вектора  .

Из последнего свойства следует, что – отдельная строка.

7) Пусть в пространстве геометрических векторов задан ортонормированный базис т.е. Тогда

Если вектора заданы своими координатами , то

т.е. в прямоугольной декартовой системе координат скалярное произведение векторов равно сумме произведений соответствующих координат.

Из свойства 7) вытекают некоторые метрические формулы:

1)  

2) Если , то , , .

Таким образом, прямоугольные координаты вектора есть его ортогональные проекции на оси прямоугольной системы координат.

3. Пусть , 

.

Таким образом,   .

Из формулы косинуса угла между векторами легко найти углы , , , которые вектор образует с осями координат. Эти углы называются направляющими углами.

Имеем:

, , .

, , называются направляющими косинусами вектора . Они связаны соотношением

.

Следовательно, вектор есть координаты вектора , то есть вектора и .

.

Определение 15. Упорядоченная тройка некомпланарных векторов называется правоориентированной или просто правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае тройка называется левоориентированной или левой.

Рис. 10. Ориентированные тройки векторов

а) Правая тройка б) Левая тройка

Определение 16. Векторным произведением двух векторов и называется вектор , удовлетворяющий условиям:

1. .

2. вектор ортогонален векторам и .

3. вектора образуют правую тройку векторов.

Обозначение:

Свойства векторного произведения

1. Длина вектора численно равна площади параллелограмма, построенного на векторах и .

Доказательство следует из определения 16.

2. Векторное произведение векторов равно нулю тогда и только тогда, когда сомножители коллинеарны.

Доказательство аналогично свойству 5 скалярного произведения.

3. Векторное произведение антикоммутативно, т.е.

Доказательство.

Тройка – правая, – левая. Тройка будет правой, если изменить направление , т.е. ∎

Пример. Если – правая тройка, то

Далее базис всегда будем рассматривать правый.

4. .

Докажем первое равенство.

1. В начале покажем равенство модулей.

.

2. Так как ||, то .

3. Покажем, что . Рассмотрим случай и .

Отсюда вытекает доказываемое свойство.

Определение 17. Смешанным произведением векторов называется число

Обозначение:

Свойства смешанного произведения

1. Смешанное произведение некомпланарных векторов по модулю равно объему параллелепипеда, построенного на сомножителях. Оно положительно, если тройка правая, и отрицательно, если она левая.

Доказательство.

Действительно, объем параллелепипеда, построенного на векторах равен произведению площади основания на высоту где – угол между и

Поэтому

Знак смешанного произведения совпадает со знаком и поэтому, смешанное произведение положительно, когда направлен с в одну сторону от плоскости векторов т.е. тройка – правая. Аналогично, смешанное произведение левой тройки векторов отрицательно. ∎

2. Три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.

Доказательство. Если один из векторов нулевой, то свойство очевидно.

Пусть , ,  0.

Пусть , , – компланарны. Тогда .

Пусть  либо , либо .

В первом случае это означает, что вектор  векторам , ,  , , – компланарны. Во втором случае – ||  и – линейно зависимы  , , – компланарны.

3. Смешанное произведение не зависит от группировки сомножителей, т.е. .

Доказательство. Тройки , , и , , ориентированы одинаково, значит знак смешанного произведения одинаковый. Модуль так же одинаковый в силу свойства 1.

Обозначение. Смешанное произведение векторов , , обозначается .

4. .

Следует из свойства циклической перестановки ориентированных векторов.

5. , .

Следует из свойств скалярного произведения.

Теорема 5 (линейность векторного произведения). Для любых векторов и любых чисел  и  имеет место равенство:

Доказательство. Воспользуемся линейностью смешанного произведения по второму сомножителю:

Выбирая вместо вектора ортонормированного базиса, можно видеть, что координаты векторов и равны, а значит, равны эти вектора. ∎

Свойства скалярного произведения векторов

Скалярное произведение двух векторов.

В физике работа А постоянной силы F при прямолинейном движении материальной точки из положения В в положение С (рис. 52) вычисляется по формуле

Эта формула вектору силы F и вектору перемещения ВС ставит в соответствие скалярную величину — работу. Величину А называют скалярным произведением векторов F и \(\overrightarrow{BC}\). Скалярное произведение может быть определено для любых двух векторов. Оно широко используется в физике и в математике.

Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Если из двух векторов хотя бы один нулевой, то скалярное произведение этих векторов принимается равным нулю.

Скалярное произведение векторов а и b обозначается а • b. Итак, по определению

а • b = | а | • | b | cos\(\widehat{(a; b)}\). (1)

Если а = b, то скалярное произведение принимает вид а • a и называется скалярным квадратом вектора а и обозначается символом a². Очевидно, что a² = а • a = |а|².

Как известно, проекция вектора b на ось, направление которой совпадает с направлением вектора а, выражается формулой

пр_ab = | b | cos\(\widehat{(a; b)}\). (2)

Используя формулы (1) и (2), можно записать

а • b = | а | np_ab. (3)

Таким образом, скалярное произведение двух векторов равно произведению длины одного из них и проекции второго вектора на направление первого.

Аналогично получается формула а • b = | b | np_ba.

Задача 1. Известно, что | а | = 2, | b | = ¹/₃ , \(\widehat{(a; b)}\) = 150°. Найти а • b .

По формуле (1) находим

а • b = | а | • | b | cos\(\widehat{(a; b)}\) = 2 • ¹/₃ • 150°

Задача 2. Найти всевозможные скалярные произведения базисных векторов i и j прямоугольной декартовой системы координат на плоскости.

По определению скалярного произведения

i • j = | i | • | j | cos 90° = 1 • 1 • 0 = 0,

i² = i • i = | i | • | i | cos 0° = 1 • 1 • 1 = 1.

Аналогично j • i = 0, j² = 1.

Задача 3. Какой знак имеет скалярное произведение векторов а и b, если
90° < \(\widehat{(a; b)}\) < 180°?

Так как в формуле а • b = | а | • | b | cos \(\widehat{(a; b)}\) числа | а | и | b | неотрицательны, знак а • b зависит от знака косинуса.

В промежутке ] 90°; 180°] cos \(\widehat{(a; b)}\) < 0, поэтому а • b < 0.

Задача 4. В каком промежутке находится величина угла между векторами а и b, если а • b > 0?

Так как а • b > 0, то | а | =/= 0, | b | =/= 0 и cos \(\widehat{(a; b)}\) > 0. Отсюда \(\widehat{(a; b)}\) \(\in\) [0°; 90° [.

Свойства скалярного произведения векторов

1. Скалярное умножение векторов обладает переместительным свойством:

а Х b = b Х а. (1)

Так как

\(\widehat{(a; b)}\) = \(\widehat{(b; a)}\) и | а | Х | b | = | b | Х | а |,

то

а Х b = | а | Х | b | cos \(\widehat{(a; b)}\) = | b | Х | а | cos\(\widehat{(b; a)}\) = b Х а.

Если а = 0 или b = 0, то по определению скалярного произведения а Х b = 0 и b Х а = 0, т. е. а Х b = b Х а

2. Скалярное умножение векторов обладает сочетательным свойством по отношению к умножению вектора на число:

(ka) Х b = k (а Х b). (2)

Обозначим \(\widehat{(a; b)}\) = φ и \(\widehat{(ka; b)}\) = φ₁.

Если k > 0, то \(\widehat{(a; b)}\) = \(\widehat{(ka; b)}\), т. е. φ = φ₁ и тогда

(ka) Х b = | kа | Х | b | cos φ₁ = k | а | Х | b | cos φ = k (а Х b).

Если k < 0, то ka \(\uparrow\downarrow\) a и φ₁ = 180° Ч φ, и тогда

(ka) Х b = | kа | Х | b | cos φ₁ = | k | Х | а | Х | b | cos (180° Ч φ) =
= Ч k Х | а | Х | b |(Ч cos φ) =

= k | а | Х | b | cos φ = k (а Х b)

Если k = 0 или a = 0, или b = 0, то

(ka) Х b = 0 и k (а Х b) = 0, и поэтому (ka) Х b =k (а Х b).

3. Скалярное умножение векторов обладает распределительным свойством относительно сложения векторов

а Х (b + с) = а Х b + а Х c. (3)

Если a = 0, то свойство (3) очевидно.

Пусть a =/= 0. Тогда

а Х (b + с) = | a | Х np_a(b + c) = | a | Х (np_ab + np_ac) =
= | a | Х np_ab + | a | Х np_ac = а Х b + а Х c.

В ходе доказательства были использованы известные свойства проекции вектора на ось.

Заметим, что из (1) и (3) следует формула

(a + b) Х c = a Х c + b Х c. (4)

Сходство свойств скалярного произведения векторов со свойствами произведения действительных чисел позволяет легко производить вычисления и преобразования со скалярными произведениями.

Задача. Доказать тождество

(a + b) ² = а² + 2a Х b + b².

Используя свойства (1) и (4) скалярного произведения, получаем

(a + b) ² = (a + b) Х (a + b) = (a + b) Х а + (a + b) Х b =
= aХa + bХa + aХb + bХb = а² + aХb + aХb + b² =

= а² + 2a Х b + b²

Теорема. Для того чтобы два ненулевых вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю:

(а =/= 0, b =/= 0, a Х b = 0 ) <==> a ⊥ b. (5)

Необходимость.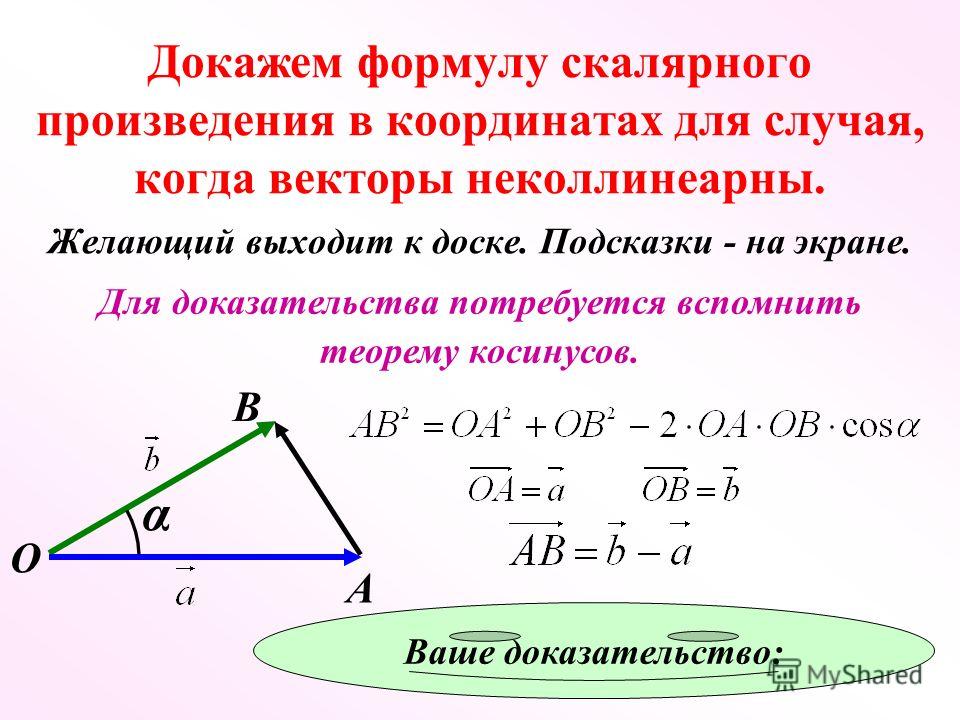 Пусть a ⊥ b. Тогда

φ = \(\widehat{(a; b)}\) = 90° и a Х b = | а | Х | b | Х cos 90° = 0.

Достаточность. Пусть a Х b = 0 , а =/= 0, b =/= 0.

Так как а =/= 0, b =/= 0, то | а | =/= 0, | b | =/= 0, а так как | а | Х | b | Х cos φ = 0, то cos φ = 0 и, следовательно, φ = 90°, т. е. a ⊥ b.

Скалярное произведение векторов, заданных своими координатами

Пусть на плоскости имеется некоторая прямоугольная декартова система координат и пусть заданы векторы а = (x₁ ; y₁ ) и b = (x₂ ; y₂). Так как

a = x₁i + y₁ j, b = x₂i + y₂ j,

то, используя соответствующие свойства скалярного умножения векторов, получаем

а • b = (x₁ + y₁ j) • (x₂i + y₂ j) = (x₁x₂) i ² + (x₁y₂) i • j + (y₁x₂) j • i+ (y₁y₂) j ².

Очевидно, что i ² = j ² = 1 и i • j = j • i = 0, поэтому

а • b = x₁x₂ + y₁y₂. (1)

Пусть теперь в пространстве имеется некоторая прямоугольная декартова система координат и заданы векторы

а = (x₁ ; y₁ ; z₁) , b = (x₂ ; y₂; z₂).

Аналогично предыдущему получим

а • b = x₁x₂ + y₁y₂+ z₁z₂. (2)

Итак, скалярное произведение двух векторов равно сумме произведений одноименных координат этих векторов.

Задача 1. Вычислить а • b , если а = 2i + 3j, b = — 5i + j.

а • b = (2i + 3j) • (- 5i + j) = 2 • (-5) + 3 • l = — 7.

Задача 2. Вычислить а • b, если а = (2; -3; 4), b = (5; 7;-1).

а • b = 2 • 5 + (-3) • 7 + 4 • (- 1) = — 15.

Задача 3. Найти длину вектора а = (х; у; z).

Применяя формулу (2) при b = a, получим

а² = а • а = хх + уу + zz = х² + у² + z².

С другой стороны, согласно определению скалярного произведения получаем

а² = а • а = | а | • | а | cos 0 = | а | ²

Следовательно,

$$ |a| = \sqrt{x^2 + y^2 + z^2} $$

Скалярное произведение векторов и его свойства с примерами решения и образцами выполнения

Оглавление:

Определение скалярного произведения:

Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.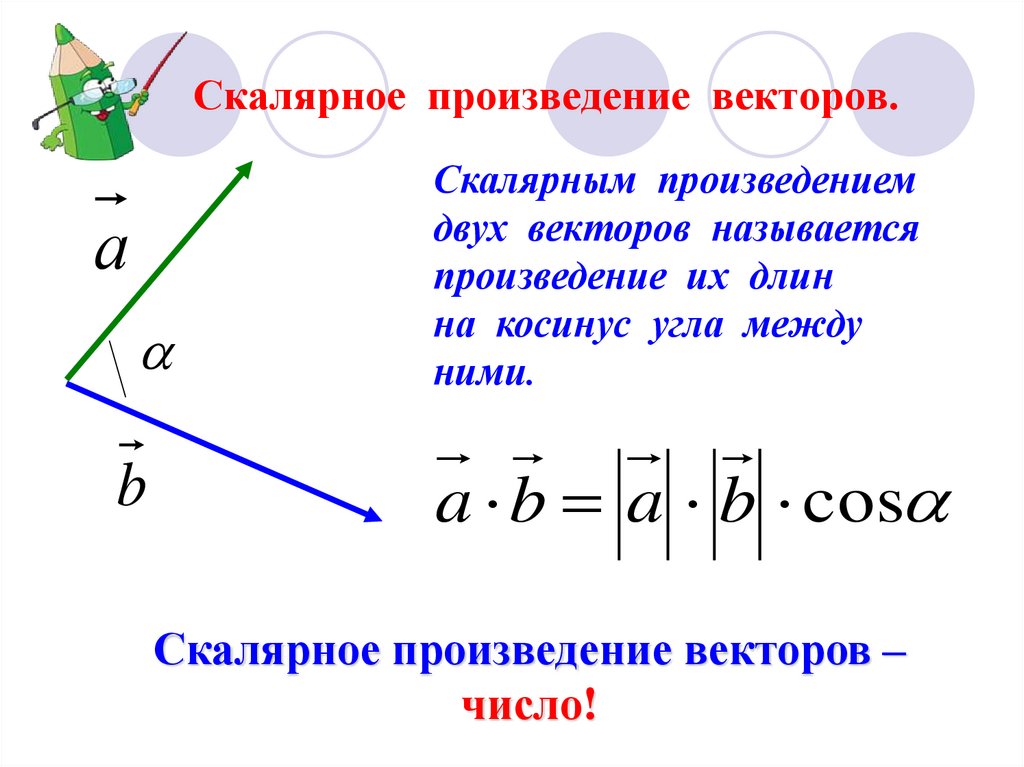

Обозначается (или ). Итак, по определению,

где

Формуле (6.1) можно придать иной вид. Так как (см. рис. 14), то получаем:

т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

Свойства скалярного произведения

1.Скалярное произведение обладает переместительным свойством:

И так как как произведение чисел и

2.Скалярное произведение обладает сочетательным свойством относительно скалярного множителя:

3.Скалярное произведение обладает распределительным свойством:

4.Скалярный квадрат вектора равен квадрату его длины:

В частности:

Если вектор возвести скалярно в квадрат и затем извлечь корень, то получим не первоначальный вектор, а его модуль , т. е.

Пример:

Найти длину вектора

Решение:

5.Если векторы (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если Справедливо и обратное утверждение: если

Так как

Следовательно,

Отсюда В частности:

Выражение скалярного произведения через координаты

Пусть заданы два вектора

Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:

т. e.

Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

Пример:

Доказать, что диагонали четырехугольника, заданного координатами вершин A(-4;- 4; 4), В(-3;2;2), С(2;5;1), D(3; -2; 2), взаимно перпендикулярны.

Решение:

Составим вектора лежащие на диагоналях данного четырехугольника. Имеем: Найдем скалярное произведение этих векторов:

Отсюда следует, что Диагонали четырехугольника ABCD взаимно перпендикулярны.

Некоторые приложения скалярного произведения

Угол между векторами

Определение угла ( между ненулевыми векторами

Отсюда следует условие перпендикулярности ненулевых векторов

Проекция вектора на заданное направление

Нахождение проекции вектора на направление, заданное вектором , может осуществляться по формуле

Работа постоянной силы

Пусть материальная точка перемещается прямолинейно из положения А в положение В под действием постоянной силы , образующей угол с перемещением (см. рис. 15).

Из физики известно, что работа силы при перемещении равна

Таким образом, работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.

Пример:

Вычислить работу, произведенную силой =(3; 2; 4), если точка ее приложения перемещается прямолинейно из положения A(2; 4; 6) в положение В (4; 2; 7). Под каким углом к АВ направлена сила ?

Решение: Находим Стало быть,

(ед. работы).

Угол между и находим по формуле т. е.

Скалярное произведение векторов

Смотрите также:

Предмет высшая математика

Решение заданий и задач по предметам:

• Математика
• Высшая математика
• Математический анализ
• Линейная алгебра

Дополнительные лекции по высшей математике:

1. Тождественные преобразования алгебраических выражений
2. Функции и графики
3. Преобразования графиков функций
4. Квадратная функция и её графики
5. Алгебраические неравенства
6. Неравенства
7. Неравенства с переменными
8. Прогрессии в математике
9. Арифметическая прогрессия
10. Геометрическая прогрессия
11. Показатели в математике
12. Логарифмы в математике
13. Исследование уравнений
14. Уравнения высших степеней
15. Уравнения высших степеней с одним неизвестным
16. Комплексные числа
17. Непрерывная дробь (цепная дробь)
18. Алгебраические уравнения
19. Неопределенные уравнения
20. Соединения
21. Бином Ньютона
22. Число е
23. Непрерывные дроби
24. Функция
25. Исследование функций
26. Предел
27. Интеграл
28. Двойной интеграл
29. Тройной интеграл
30. Интегрирование
31. Неопределённый интеграл
32. Определенный интеграл
33. Криволинейные интегралы
34. Поверхностные интегралы
35. Несобственные интегралы
36. Кратные интегралы
37. Интегралы, зависящие от параметра
38. Квадратный трехчлен
39. Производная
40. Применение производной к исследованию функций
41. Приложения производной
42. Дифференциал функции
43. Дифференцирование в математике
44. Формулы и правила дифференцирования
45. Дифференциальное исчисление
46. Дифференциальные уравнения
47. Дифференциальные уравнения первого порядка
48. Дифференциальные уравнения высших порядков
49. Дифференциальные уравнения в частных производных
50. Тригонометрические функции
51. Тригонометрические уравнения и неравенства
52. Показательная функция
53. Показательные уравнения
54. Обобщенная степень
55. Взаимно обратные функции
56. Логарифмическая функция
57. Уравнения и неравенства
58. Положительные и отрицательные числа
59. Алгебраические выражения
60. Иррациональные алгебраические выражения
61. Преобразование алгебраических выражений
62. Преобразование дробных алгебраических выражений
63. Разложение многочленов на множители
64. Многочлены от одного переменного
65. Алгебраические дроби
66. Пропорции
67. Уравнения
68. Системы уравнений
69. Системы уравнений высших степеней
70. Системы алгебраических уравнений
71. Системы линейных уравнений
72. Системы дифференциальных уравнений
73. Арифметический квадратный корень
74. Квадратные и кубические корни
75. Извлечение квадратного корня
76. Рациональные числа
77. Иррациональные числа
78. Арифметический корень
79. Квадратные уравнения
80. Иррациональные уравнения
81. Последовательность
82. Ряды сходящиеся и расходящиеся
83. Тригонометрические функции произвольного угла
84. Тригонометрические формулы
85. Обратные тригонометрические функции
86. Теорема Безу
87. Математическая индукция
88. Показатель степени
89. Показательные функции и логарифмы
90. Множество
91. Множество действительных чисел
92. Числовые множества
93. Преобразование рациональных выражений
94. Преобразование иррациональных выражений
95. Геометрия
96. Действительные числа
97. Степени и корни
98. Степень с рациональным показателем
99. Тригонометрические функции угла
100. Тригонометрические функции числового аргумента
101. Тригонометрические выражения и их преобразования
102. Преобразование тригонометрических выражений
103. Комбинаторика
104. Вычислительная математика
105. Прямая линия на плоскости и ее уравнения
106. Прямая и плоскость
107. Линии и уравнения
108. Прямая линия
109. Уравнения прямой и плоскости в пространстве
110. Кривые второго порядка
111. Кривые и поверхности второго порядка
112. Числовые ряды
113. Степенные ряды
114. Ряды Фурье
115. Преобразование Фурье
116. Функциональные ряды
117. Функции многих переменных
118. Метод координат
119. Гармонический анализ
120. Вещественные числа
121. Предел последовательности
122. Аналитическая геометрия
123. Аналитическая геометрия на плоскости
124. Аналитическая геометрия в пространстве
125. Функции одной переменной
126. Высшая алгебра
127. Векторная алгебра
128. Векторный анализ
129. Векторы
130. Векторное произведение векторов
131. Смешанное произведение векторов
132. Операции над векторами
133. Непрерывность функций
134. Предел и непрерывность функций нескольких переменных
135. Предел и непрерывность функции одной переменной
136. Производные и дифференциалы функции одной переменной
137. Частные производные и дифференцируемость функций нескольких переменных
138. Дифференциальное исчисление функции одной переменной
139. Матрицы
140. Линейные и евклидовы пространства
141. Линейные отображения
142. Дифференциальные теоремы о среднем
143. Теория устойчивости дифференциальных уравнений
144. Функции комплексного переменного
145. Преобразование Лапласа
146. Теории поля
147. Операционное исчисление
148. Системы координат
149. Рациональная функция
150. Интегральное исчисление
151. Интегральное исчисление функций одной переменной
152. Дифференциальное исчисление функций нескольких переменных
153. Отношение в математике
154. Математическая логика
155. Графы в математике
156. Линейные пространства
157. Первообразная и неопределенный интеграл
158. Линейная функция
159. Выпуклые множества точек
160. Система координат

Скалярное произведение векторов — справочник для студентов и школьников

Определение

Скалярное произведение двух ненулевых векторов \(\ \overline{a} \) и \(\ \overline{b} \) представляет собой число, равное произведению длин этих векторов и косинуса угла между ними:

\(\ \overline{a} \overline{b}=\overline{a} \cdot \overline{b}=(\overline{a}, \overline{b})=|\overline{a}||\overline{b}| \cos (\overline{a}, \overline{b}) \)

Пример

Задание. {2} \) и называется скалярным квадратом.

3. Если \(\ \overline{a} \neq \overline{0} \) , то \(\ (\overline{a}, \overline{b})=|\overline{a}| \cdot \Pi p_{\overline{a}} \overline{b} \)

4. Если \(\ \overline{a} \neq \overline{0} \) и \(\ \overline{b} \neq \overline{0} \) и \(\ (\overline{a}, \overline{b})=0 \), то \(\ \overline{a} \perp \overline{b} \). Обратное также верно.

5. \(\ (\overline{a}+\overline{b}, \overline{c})=(\overline{a}, \overline{c})+(\overline{b}, \overline{c}) \)

6. \(\ (\lambda \overline{a}, \overline{b})=\lambda(\overline{a}, \overline{b}) \)

7. \(\ (\alpha \overline{a}+\beta \overline{b}, \gamma \overline{c}+\delta \overline{d})=\alpha \gamma(\tilde{a}, \overline{c})+\alpha \delta(\overline{a}, \overline{d})+\beta \gamma(\overline{b}, \overline{c})+\beta \delta(\overline{b}, \overline{d}) \)

Если векторы \(\ \overline{a} \) и \(\ \overline{b} \) задаются своими координатами: \(\ \overline{a}=\left(a_{1} ; a_{2} ; a_{3}\right), \overline{b}=\left(b_{1} ; b_{2} ; b_{3}\right) \) , то их скалярное произведение вычисляется по формуле:

\(\ (\overline{a}, \overline{b})=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3} \)

Определение

Скалярное произведение векторов, заданное его координатами, равно сумме произведений соответствующих координат. {\circ} \)

Физика

166

Реклама и PR

31

Педагогика

80

Психология

72

Социология

7

Астрономия

9

Биология

30

Культурология

86

Экология

8

Право и юриспруденция

36

Политология

13

Экономика

49

Финансы

9

История

16

Философия

8

Информатика

20

Право

35

Информационные технологии

6

Экономическая теория

7

Менеджент

719

Математика

338

Химия

20

Микро- и макроэкономика

1

Медицина

5

Государственное и муниципальное управление

2

География

542

Информационная безопасность

2

Аудит

11

Безопасность жизнедеятельности

3

Архитектура и строительство

1

Банковское дело

1

Рынок ценных бумаг

6

Менеджмент организации

2

Маркетинг

238

Кредит

3

Инвестиции

2

Журналистика

1

Конфликтология

15

Этика

9

Формулы дифференцирования Угол между векторами Длина (модуль) вектора Координаты вектора. Направляющие косинусы Проекция вектора на ось

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю  Политику  конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Скалярное произведение векторов — Энциклопедия по экономике

Тогда стоимость потребительской корзины описывается скалярным произведением векторов Р и X.  [c.95]
Вектор ОР есть ортогональная проекция вектора Y на вектор S. Из векторной алгебры известно, что длина такого вектора равна отношению скалярного произведения векторов Y и S к длине вектора S, т. е.  [c.77]

Евклидовым пространством называется векторное (линейное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее следующим свойствам  [c.271]

Дюрация портфеля равна скалярному произведению векторов долей вложений в обли-  [c.34]

Этот результат немедленно вытекает из формулы (2.6) с учетом линейности скалярного произведения векторов пространства Ят.  [c.66]

Объясните связь между скалярным произведением векторов и векторами включенного угла.  [c.133]

Доказательство заметим, что скалярное произведение векторов-столбцов а и b может быть записано в виде произведения матриц либо как аТЬ, либо как Ъта. На этом основании можно записать  [c.263]

Скалярным произведением векторов х и у называется число, равное сумме произведений соответствующих компонент этих В.  [c.42]

Когда в пространстве введено понятие скалярного произведения векторов, можно определить и понятие К., двойственного к данному. Пусть С— выпуклый К., тогда множество С, состоящее из векторов, скалярные произведения которых с любым вектором, принадлежащим С, — отрицательны, называется двойственным конусом.  [c.153]

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ  [c.330]

Скалярное произведение векторов 42, 330  [c.488]

П — вычисление скалярного произведения векторов ху = 2х,у,  [c.47]

Различие между векторами и и и2 приводит к появлению движущих сил Xjj каждая из которых определяется только u j и t/2j, удовлетворяет условиям, аналогичным (2.1), и имеет тот же знак, что и поток Jj. Производство энтропии, характеризующее необратимость процесса, равно среднему значению скалярного произведения вектора потоков на вектор движущих сил  [c.54]

Требуемую меру Р строим так же, как и в (15) и (14), понимая под an(u>)Xn(ui) (в формуле (14)) скалярное произведение векторов ап(о>) кХп(ш).  [c.52]

Ограничение, которое в текущей точке выполняется как равенство, называют активным. Множество номеров активных ограничений в точке х будем обозначать как I(x ). В примере, изображенном на рис. 2.5, I(x(q)) = l, 3 . Также из рисунка видно, что все допустимые направления, исходящие из точки х должны образовывать тупые углы с векторами градиентов функций, задающих активные ограничения в данной точке. Последнее условие может быть выражено через задание ограничений на значения скалярных произведений вектора направления s на градиенты функции ограничений  [c.96]

Для упрощения обозначений скалярное произведение векторов 7 и Sn будем обозначать так же, как и произведение чисел, а именно,  [c.21]

Гипотеза, лежащая в основе модели поведения производителя заключается в том, что производитель выбирает технологически допустимый вектор чистых выпусков, максимизирующий прибыль. В терминах чистых выпусков прибыль есть скалярное произведение вектора чистых выпусков у е Y на вектор цен ру. Таким образом, если производитель, приобретая факторы производства и продавая производимые блага на рынках с совершенной конкуренцией блага, сталкивается с некоторым вектором цен р, то его выбор оказывается решением следующей задачи на экстремум  [c.125]

Скалярное произведение векторов . 15  [c.3]

Откуда ху = х 11 у os ф, т. е. скалярное произведение векторов х и у равно произведению длин этих векторов на косинус угла между ними.  [c.43]

Кроме того, определено скалярное произведение двух векторов  [c.32]

Условием перпендикулярности пары векторов является равенство нулю их скалярного произведения (11.27)  [c.77]

Скалярным произведением двух векторов х = (х, х2,…, х ) и  [c.270]

Два вектора называются ортогональными, если их скалярное произведение равно нулю.  [c.271]

Каждый узел многослойной сети проектирует свой входной вектор на вектор весов посредством скалярного произведения. Таким  [c.24]

В другом варианте победителем считается элемент, весовой вектор которого имеет наибольшее скалярное произведение с входным вектором. Эта величина также является некоторой мерой близости, потому что скалярное произведение — это проектирование входного вектора на вектор весов. Очевидно, такая проекция будет наибольшей, если векторы имеют близкие направления. При этом методе, однако, оба вектора — весовой и входной — должны быть нормированы по длине, например, быть равными единице. Напротив, евклидово расстояние позволяет работать с векторами произвольной длины.  [c.43]

Напомним, что символ (о, b) для ш-мерных векторов а и Ь означает п(.  [c.62]

Скалярное произведение и линейная (не-) зависимость векторов  [c.133]

На рис. 3.1, а два вектора включают в себя угол, который меньше 90 градусов. Это приводит к тому, что скалярное произведение этих двух векторов положительно. Векторы, расположенные друг к другу перпендикулярно, называются ортогональными (рис. 3.1, в). Их скалярное произведение равно нулю. Векторы, которые образуют друг с другом угол, превышающий 90 градусов, имеют отрицательное скалярное произведение (рис. 3.1, б). Если обозначить включенный угол символом а, то мы можем обобщенно записать  [c.134]

С помощью двумерных векторов можно сформировать скалярные произведения  [c.134]

Лишь vi и v3 расположены перпендикулярно друг к другу. Проверка скалярных произведений трехмерных векторов дает  [c.134]

Перрона следует, что существует неотрицательный вектор р, такой, что Ар = ЛАр. Выше было доказано, что неотрицательный собственный вектор положительной матрицы является положительным. Поэтому в действительности р >0. Рассмотрим скалярное произведение (р,Ау). Имеем  [c.264]

Доказательство. Достаточно учесть знак скалярного произведения (b, N/s(T)) при всех возможных положениях векторов NIS(T) в ОД /х.  [c.79]

В этой таблице /-е строки отражают виды КПТ, а /-е столбцы — соответствующие отрасли промышленности и народного хозяйства (см. п. 4.4.1). При этом каждому /(/=1,. .., 10) соответствуют три соседних столбца, из которых средний х) служит для представления переменных х) при меняющемся /, а крайние — соответствующих ограничений из условий (4. 53). Таким образом, переменная х) отображается клеткой на пересечении своих /-й строки и /-го столбца. При этом левая часть условия (4.51) отображается суммой значений х) во всех заполненных клетках /-й строки, а значение х) из правой части условия (4.51) представлено на пересечении /-й строки и столбца 5 и определяется при решении подзадач, реализующих модели 01, 02, 04 и 06. В этих моделях задаются и ограничения из. условий (4.55). Левая часть условий (4.52) формально представима как скалярное произведение соответствующих векторов, представленных столбцами 7 и x) i. Значение х пт из правой части условия (4.52) в других моделях не определялось. Оно заносится после расчета в 0-ю строку табл. 4.2 как выходного документа над столбцом ху ,. В две соседние клетки этой строки могут быть априорно занесены ограничения из условий (4.54), которые ранее также не вводились.  [c.104]

Пусть х= Xj — система п случайных величин с ограниченными дисперсиями и ограниченными математическими ожиданиями. Обозначим через Htn определяемое. случайным вектором х гильбертово пространство. Скалярное произведение в Н п  [c.20]

Гиперплоскость Н = х е EJ (с, х) = h (см. Гиперпрострапство, Гиперплоскость, а также Скалярное произведение векторов) называется опорной по отношению к множеству М в его граничной точке х ), если удовлетворяются следующие условия (с, х) [c.241]

Векторы х и у называются ортогональными, если их скалярное произведение равно нулю. Равенство В. — компонентное, т. е. два В. равны, если равны их соответствующие компоненты. Вектор 0 — (0,. .., 0) нулевой и-мерный В. — положительный (х > 0), если все его компоненты х больше нуля, неотрицательный (х > 0), если все его компоненты х. больше 0 или равны нулю, т. е. х. > 0 и полуположительный, если при этом хотя бы одна компонента х > 0 (обозначение х > 0) если В. имеют равное количество компонент, возможно их упорядочение (полное или частичное), т. е. введение на множестве векторов бинарного отношения «>» х > у, х > у, х > у в зависимости от того, положительна, полуположительна или неотрицательна разность х — у.  [c.42]

Lagrangian] — вспомогательная функция, применяемая при решении задач математического программирования, в частности линейного программирования. Образуется путем прибавления к целевой функции скалярного произведения двух векторов вектора разностей между константами ограничений и функциями ограничений и вектора (неизвестных) множителей, называемых множителями Лагранжа  [c.166]

Объяснение урока: Скалярное произведение в 3D

В этом объяснении мы узнаем, как найти скалярное произведение двух векторов в 3D.

Скалярное произведение, также называемое скалярным произведением, поскольку оно дает скалярную величину, не вектор, это один из способов перемножения векторов.

Возможно, вы уже знакомы с нахождением скалярного произведения на плоскости. (2Д). Возможно, вы узнали, что скалярное произведение ⃑𝐴 и ⃑𝐵 определяется как ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖×‖‖⃑𝐵‖‖×𝜃cos, где 𝜃 — угол между двумя векторами ⃑𝐴 и ⃑𝐵.

Приложив немного геометрии, можно показать, что его можно вычислить из компоненты обоих векторов: ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵, где 𝐴 и 𝐵 — 𝑥-компоненты ⃑𝐴 и ⃑𝐵, а 𝐴 и 𝐵 — их 𝑦-компоненты.

Рассмотрим два вектора ⃑𝐴 и ⃑𝐵, которые образуют углы 𝜃 и 𝜃 с положительное направление оси 𝑥 соответственно.

Тогда угол между ними равен 𝜃=𝜃−𝜃. При условии 𝐴 = ‖⃑𝐴⃑𝐴⃑𝐴⃑𝐴𝜃, 𝐴 = ‖⃑𝐴⃑𝐴⃑𝐴⃑𝐴, 𝐵 = ‖⃑𝐵⃑𝐵⃑𝐵⃑𝐵, 𝐵 = ‖⃑𝐵⃑𝐵⃑𝐵⃑𝐵, cossincossin мы находим, что 𝐴𝐵+𝐴𝐵 = ‖⃑𝐴⃑𝐴⃑𝐴‖⋅ ‖⃑𝐵⃑𝐵⃑𝐵𝜃𝜃𝜃𝜃+‖⃑𝐴⃑𝐴⃑𝐴⋅ ⋅ ‖⃑𝐵⃑𝐵𝜃𝜃 = ‖⃑𝐴⃑𝐴‖⋅‖⃑𝐵⃑𝐵⃑𝐵 коскоссинскоскоссинсин

Используя тригонометрическое тождество вычитания coscoscossinsin(𝛼−𝛽)=𝛼𝛽+𝛼𝛽, находим, заменив 𝛼 на 𝜃 и 𝛽 с 𝜃, что coscoscossinsincoscossinsin(𝜃−𝜃)=𝜃𝜃+𝜃𝜃=𝜃𝜃+𝜃𝜃.

Поскольку 𝜃=𝜃−𝜃 𝐴𝐵+𝐴𝐵=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖𝜃=⃑𝐴⋅⃑𝐵.cos

Переходя к 3D-векторам, определение скалярного произведения не изменилось.

Определение: скалярное произведение двух трехмерных векторов где 𝜃 — угол между ⃑𝐴 и ⃑𝐵.

Давайте посмотрим на наш первый пример и применим определение скалярного произведения.

Пример 1. Нахождение скалярного произведения двух векторов по данным Норма одного из них, составные части другого и Угол между ними

Допустим ⃑𝐴=(−1,2,7), ‖‖⃑𝐵‖‖=13, а угол между двумя векторов составляет 135∘. Найдите ⃑𝐴⋅⃑𝐵 с точностью до сотых.

Ответить

Мы знаем, что ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖𝜃cos. Мы уже знаем ‖‖⃑𝐵‖‖ и угол 𝜃. Поэтому нам нужно найти ‖‖⃑𝐴‖‖ используя компоненты ⃑𝐴: ‖‖⃑𝐴‖‖=𝐴+𝐴+𝐴=√(−1)+2+7=√54.

Теперь, подставив это значение в наше уравнение для ⃑𝐴⋅⃑𝐵, мы нашли ⃑𝐴⋅⃑𝐵=√54⋅13⋅135≃−67.55.cos∘

Практическое руководство. Вычисление скалярного произведения с использованием компонентов вектора

Скалярное произведение трехмерных векторов вычисляется с использованием компонентов вектора так же, как и в 2D, а именно, ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵+𝐴𝐵, где индексы 𝑥, 𝑦 и 𝑧 обозначим компоненты вдоль 𝑥-, 𝑦-, и 𝑧-оси.

Применим этот метод на следующем примере.

Пример 2. Нахождение скалярного произведения двух заданных векторов Их компоненты

Учитывая, что ⃑𝐴=(−6,−3,5) и ⃑𝐵=(7,−4,−1), определить ⃑𝐴⋅⃑𝐵.

Ответ

Здесь мы вычисляем скалярный продукт, используя ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵+𝐴𝐵, где индексы 𝑥, 𝑦 и 𝑧 обозначим компоненты вдоль 𝑥-, 𝑦-, и 𝑧-оси. Таким образом, мы имеем ⃑𝐴⋅⃑𝐵=(−6)⋅7+(−3)⋅(−4)+5⋅(−1)=−42+12+(−5)=−35.

Теперь, когда мы знаем, как определяется скалярный продукт и как его вычислить, используя компонентов векторов, давайте посмотрим на свойства скалярного произведения.

Поскольку скалярное произведение является произведением величин векторов, умноженных косинусом угла между ними, он равен нулю, когда косинус угла между обоими векторами равен нулю. Это происходит, когда угол между ними 90∘ или −90∘ (или 270∘), то есть, когда они перпендикулярны.

Свойство: Скалярное произведение двух перпендикулярных векторов

Скалярное произведение двух перпендикулярных векторов равно нулю. И наоборот, когда скалярное произведение двух векторов равно нулю, то эти два вектора перпендикулярны.

Чтобы вспомнить, у каких углов косинус равен нулю, вы можете визуализировать единичный круг, помня, что косинус — это 𝑥-координата точки P, связанная с угол 𝜃.

Мы собираемся использовать это свойство в следующих двух примерах.

Пример 3. Поиск недостающих компонентов ортогональных векторов

Для какого значения 𝑘 являются векторами ⃑𝐴=(7,−7𝑘,−6) и ⃑𝐵=(7,−3,𝑘) перпендикуляр?

Ответ

Если два вектора перпендикулярны, то угол между ними равен 90∘ или −90∘ (или 270∘). В обоих случаях косинус угла между ними равен нуль. Следовательно, скалярное произведение двух векторов равно нулю. В этом вопрос, значит ⃑𝐴⋅⃑𝐵=0; то есть, 𝐴𝐵+𝐴𝐵+𝐴𝐵=0.

Следовательно, имеем 7⋅7+(−7𝑘)⋅(−3)+(−6)⋅𝑘=049+21𝑘−6𝑘=0𝑘=-4915.

Пример 4. Определение перпендикулярных и параллельных векторов

Что из следующего верно для векторов ⃑𝐴=(−3,7,−8) и ⃑𝐵=(−6,−1,−1)?

1. Они параллельны.
2. Они перпендикулярны.
3. Они не параллельны и не перпендикулярны.

Ответ

Если ⃑𝐴 и ⃑𝐵 параллельны, то существует число 𝑘 такое, что ⃑𝐴=𝑘⃑𝐵. Мы было бы −3=−6𝑘7=−𝑘−8=−𝑘.

Очевидно, нет значения 𝑘, которое бы подтверждало три уравнения, поскольку мы получить три различных решения для каждого из них 12,−7,8а. Следовательно, ⃑𝐴 и ⃑𝐵 не параллельны.

Если ⃑𝐴 и ⃑𝐵 перпендикулярны, то их скалярное произведение равно нулю. Давайте работать их точечный продукт: ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵+𝐴𝐵=(−3)⋅(−6)+7⋅(−1)+(−8)⋅(−1)=18+(−7)+8=19. 

Их скалярное произведение не равно нулю; следовательно, ⃑𝐴 и ⃑𝐵 не перпендикулярны .

Правильный ответ: ⃑𝐴 и ⃑𝐵 не параллельны и не перпендикулярны.

Другие свойства скалярного произведения возникают из-за того, что косинус угол между двумя векторами является одним из его факторов. Например, учитывая, что функция косинуса четная с периодом 360∘, это означает, что не имеет значения, если берем угол от ⃑𝐴 к ⃑𝐵 или с ⃑𝐵 на ⃑𝐴, потому что coscoscos𝜃=(−𝜃)=(360−𝜃).

Следовательно, скалярное произведение коммутативно: ⃑𝐴⋅⃑𝐵=⃑𝐵⋅⃑𝐴.

Кроме того, скалярное произведение двух коллинеарных векторов равно плюс или минус произведению их величины. Действительно, рассмотрим сначала два коллинеарных вектора ⃑𝐴 и ⃑𝐵, угол между которыми равен нулю: ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖⋅0=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖, потому что поскольку cos0=1.

Теперь рассмотрим два коллинеарных вектора ⃑𝐴 и ⃑𝐵, причем угол между ними 180∘ (т. е. два вектора указывают в противоположных направлениях): ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖⋅180=−‖‖⃑𝐴‖‖⋅‖‖⃑𝐵‖‖, cos∘ поскольку cos180=−1∘.

Отсюда следует, что скалярное произведение вектора на самого себя дает квадрат его величины. Это можно легко проверить с помощью того, как мы вычисляем скалярное произведение: ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵+𝐴𝐵, так ⃑𝐴om⃑𝐴 = 𝐴𝐴+𝐴𝐴+𝐴𝐴 = 𝐴+𝐴+𝐴.

, так как ‖⃑𝐴⃑𝐴⃑𝐴 = 𝐴+𝐴+𝐴, мы находим, что ⃑𝐴⋅⃑𝐴=‖‖⃑𝐴‖‖.

Как и умножение, скалярное произведение является дистрибутивным: (⃑𝐴+⃑𝐵)⋅⃑𝐶=⃑𝐴⋅⃑𝐶+⃑𝐴⋅⃑𝐶.

Кроме того, у нас есть (𝑘⃑𝐴)⋅⃑𝐵=⃑𝐴⋅(𝑘⃑𝐵)=𝑘⃑𝐴⋅⃑𝐵.

Воспользуемся этими свойствами, чтобы ответить на следующий вопрос.

Пример 5: Использование распределения скалярного произведения

Если ⃑𝐴 и ⃑𝐵 — два перпендикулярных единичных вектора, найти (3⃑𝐴−⃑𝐵)⋅(−2⃑𝐴+⃑𝐵).

Ответ

Во фразе «⃑𝐴» есть две части информации и ⃑𝐵 два перпендикулярные единичные векторы». Во-первых, векторы перпендикулярны, что означает, что их скалярное произведение равно нулю. Второй что они являются единичными векторами, что означает, что они имеют величину 1. Теперь, используя распределительное свойство скалярного произведения, мы находим, что (3⃑𝐴−⃑𝐵)⋅(−2⃑𝐴+⃑𝐵)=−6⃑𝐴⋅⃑𝐴+3⃑𝐴⋅⃑𝐵+2⃑𝐵⋅⃑𝐴−⃑𝐵⋅⃑𝐵.

Поскольку векторы перпендикулярны, члены 3⃑𝐴⋅⃑𝐵 и 2⃑𝐵⋅⃑𝐴 равны нулю.

Также мы знаем, что ⃑𝐴⋅⃑𝐴=‖‖⃑𝐴‖‖=1 так как ⃑𝐴 является единичным вектором. То же самое относится к ⃑𝐵. Следовательно, мы находим, что (3⃑𝐴−⃑𝐵)⋅(−2⃑𝐴+⃑𝐵)=−6−1=−7.

Ключевые точки

• Скалярное произведение векторов ⃑𝐴 и ⃑𝐵 определяется как ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖×‖‖⃑𝐵‖‖×𝜃, потому что где 𝜃 — угол между двумя векторами ⃑𝐴 и ⃑𝐵.
• Скалярное произведение 3D-векторов можно рассчитать с помощью векторов составные части: ⃑𝐴⋅⃑𝐵=𝐴𝐵+𝐴𝐵+𝐴𝐵.
• Продукт DOT обладает следующими свойствами:
  • ⃑𝐴⋅⃑𝐵 = ⃑𝐵⋅⃑𝐴 (коммутативность),
  • ⃑𝐴⋅⃑𝐴 = ‖⃑𝐴⃑𝐴⃑𝐴,
  • ⃑𝐴⋅⃑𝐵 = 0, если и только если ⃑𝐴 и ⃑𝐵 перпендикулярно,
  • (⃑𝐴+⃑𝐵) ⋅⃑𝐶 = ⃑𝐴om⃑𝐶+⃑𝐴om⃑𝐶 (распределение),
  • (𝑘⃑𝐴) ⋅⃑𝐵 = ⃑𝐴om (𝑘⃑𝐵) = 𝑘⃑𝐴om⃑𝐵, где 𝑘 реальное число.

систем отсчета. Учитывая два вектора (без общей точки), возможно ли скалярное произведение между ними?

Ответить на этот вопрос можно по-разному, но наиболее естественным для целей физики является дифференциальная геометрия. Немного предыстории:

(1) Каждый вектор живет в некотором векторном пространстве . Векторное пространство — это набор векторов, подчиняющихся определенным аксиомам. Сложение двух векторов дает другой вектор, вы можете умножать векторы на скаляры (числа) и т. д. Они должны быть относительно знакомы любому старшекурснику по физике, даже если у вас не было формального обучения линейной алгебре. В частности, каждое векторное пространство содержит нулевой вектор , который определяет уникальное «начало».

(2) Скалярное произведение двух векторов является примером 92$, двумерное евклидово пространство, в котором каждой точке многообразия ставится в соответствие координата $(x,y)$. Обратите внимание, что многообразие не обязательно является векторным пространством и вообще не имеет начала координат. В этом смысле многообразие несколько больше похоже на аффинное пространство . Точки многообразия не являются векторами! Вы не можете складывать их или умножать на скаляры.

(4) (действительная) функция на многообразии — это карта, которая ставит в соответствие вещественное число каждой точке некоторой области ( 91$, вещественная линия, с натуральной координатой $x$, присваивающей каждой точке соответствующее действительное число. Функция $f(x)$, такая как $f(x) = \sin(x)$ или $f(x) = \tan(x)$, сопоставляет каждой точке некоторого подмножества многообразия действительное число. Заметим, что во втором случае функция не везде определена. Обратите внимание, что эти функции дифференцируемы везде, где они определены.

(5) Рассмотрим точку $p$ в многообразии. Рассмотрим некоторую последовательность точек $\gamma(s)$ ( кривая ), проходящих через $p$, параметризованную некоторым вещественным числом $s$. 3$, то видно, что касательные векторы вообще не лежат на сфере! В каждой точке сферы находится касательное векторное пространство , которое является плоскостью, касательной к сфере.

Таким образом, векторы естественным образом живут в касательных пространствах в каждой точке. На изображении, которое вы нарисовали, два вектора живут в 90 171 различных 90 172 касательных пространствах. В общем, на этом простом уровне нет априорного способа определить, как следует сравнивать векторы в разных касательных пространствах. Можно определить его в терминах координат, но это будет зависеть от используемых нами координат.

Итак, это все фон. Я не буду вдаваться в подробности, но урок в том, что 92$, которые вы рассматриваете, у нас на самом деле тайно уже есть естественная связь, плоская связь. По сути, эта связь говорит нам, что мы можем просто взять любые два вектора, которые нам нравятся (выраженные в одной и той же декартовой системе координат), и свободно взять их скалярное произведение (скалярное произведение).

Другой способ сказать, что метрика плоская. Метрика, как следует из ее названия, говорит нам, как мы должны «измерять» векторы. Точнее говоря, он определяет уникальный внутренний продукт в каждом касательном пространстве таким образом, чтобы он плавно менялся при движении по многообразию. Это также говорит нам, как 92$, как показано на изображении ниже. Параллельное перемещение вектора по замкнутому контуру обратно в его исходное касательное пространство фактически изменяет вектор, и именно так мы измеряем кривизну! Перемещение вектора по любой произвольной кривой между двумя разными касательными пространствами обычно приводит к разным результатам. Параллельный перенос — это перенос по геодезической многообразия, кривой кратчайшего пути. Кривые кратчайшего расстояния в евклидовом пространстве — это прямые линии, которые всегда параллельны и никогда не пересекаются, и именно поэтому мы можем свободно перемещать векторы в любом направлении, не меняя их компонентов.

Скалярный продукт и перекрестный продукт: в чем разница?

При изучении технических предметов, таких как физика или математика, один из наиболее частых вопросов, которые мы задаем: «Зачем нам это изучать и как это поможет нам в будущем?»

Я хотел бы ответить на этот вопрос для вас. Правда в том, что каждый аспект предметов, которые вы изучаете, имеет то или иное применение в вашей реальной жизни, будь то навыки, содержание или просто получение атрибута.

Обычная тема, которую каждый студент не хотел бы изучать, это векторная алгебра. Хотя на первый взгляд это может показаться сложным, в этой статье мы рассмотрим разницу между перекрестным произведением и скалярным произведением. Прежде чем мы углубимся в это, давайте разберемся, что такое векторная алгебра и как ее изучение может быть полезным.

Векторная алгебра, как следует из названия, имеет дело с векторами. Большинство величин являются либо скалярами, либо векторами. У скаляров есть только величина, тогда как у векторов есть и величина, и направление.

Теперь, когда мы поняли важность векторной алгебры, давайте перейдем конкретно к скалярному произведению и перекрестному произведению .

Разница между перекрестным произведением и скалярным произведением

1. Основным атрибутом, который разделяет обе операции по определению, является то, что скалярное произведение является произведением величины векторов и косинуса углов между ними, тогда как перекрестное произведение  является произведением величины векторов и синус углов между ними.

2. Хотя это словарное определение того, что означают обе операции, есть одна важная характеристика, которая разделяет их обе. Эту разницу можно отметить с точки зрения векторной алгебры. Результатом скалярного произведения является скалярная величина с величиной в целом, однако результатом перекрестного произведения является векторная величина как с величиной, так и с направлением.

Это два основных отличия, которые вы должны принять во внимание, чтобы понять концепции на первый взгляд.
Давайте применим математический подход, чтобы познакомиться с ним поближе:

Скалярный продукт представлен следующим образом:

а . б = ||а|| ||б|| соз (θ)

Здесь A и B — векторы и угол между обоими векторами.

а . б = ||а|| ||б|| sin (θ) n

Здесь A и B — векторы, а — угол между ними. N — единичный вектор, перпендикулярный плоскости, в которой А и В входят в состав.

ТОЧЕЧНОЕ ПРОИЗВЕДЕНИЕ И ПЕРЕКРЕСТНОЕ ПРОИЗВЕДЕНИЕ (табличная форма)

Это даст вам общее представление о различиях между обеими операциями, если говорить простыми словами.

Что это означает теоретически?

Дополнительный продукт:

Из-за наличия только величины и отсутствия направления оба вектора в операции скалярного произведения выравниваются одинаково. Берется косинус угла между этими векторами. Произведение оказывается скалярным. Он также известен как внутренний продукт или проекционный продукт.
Произведение имеет 4 различных свойства, известных как коммутативность, дистрибутивность, ортогональность или свойство, соответствующее скалярному закону умножения.

Применение скалярного произведения:
Операция используется для определения длины между двумя точками на плоскости с известными координатами.

Перекрестный продукт:

Из-за наличия как величины, так и направления, величина векторов берется вместе с синусом угла между ними. В результате произведение оказывается векторной величиной. Важно отметить, что конечный результат операции векторного произведения должен быть перпендикулярен обоим векторам или, другими словами, плоскости, на которой лежат оба вектора.

Таким образом, для определения направления можно использовать правило большого пальца правой руки. В этом случае два пальца представляют векторы, а большой палец определяет произведение. Перекрестное произведение также известно как направленное произведение площади.

Как и скалярное произведение, перекрестное произведение имеет 4 различных свойства. Он некоммутативен, дистрибутивен, ортогонален и совместим со скалярным законом умножения.

Применение перекрестного произведения:
В основном применяется в вычислительной геометрии для нахождения или определения расстояния между двумя наклонными линиями. Перекрестное произведение также можно использовать, чтобы предположить, являются ли два вектора компланарными или нет.

Заключение:

Векторная алгебра, охватывающая точечные и перекрестные произведения, является полезной темой для начинающих врачей и математиков, поскольку она дает представление об основах геометрии и тригонометрии, которые можно применять в реальных ситуациях. В математике сложение, вычитание и умножение векторов можно выполнять для понимания характера плана или траектории, тогда как в физике такие векторы, как расстояние, смещение, скорость и ускорение, используются для понимания более экстремальных предметов.

Векторы Евклида используются уже несколько сотен лет, внося большой вклад в математику и физику. Они были проанализированы, оценены и переработаны после того, как несколько ученых и математиков разработали концепцию, внося изменения и инновации по мере поступления новой информации.

Когда вы поймете, векторы могут стать интересной темой для дальнейшего изучения, а также применения в вашей жизни. Мы надеемся, что эта статья о точечных и перекрестных произведениях помогла вам понять основные различия с точки зрения формул, свойств и приложений!

1.4 Скалярный продукт – инженерная механика: статика

Перейти к содержимому

Глава 1: Основные понятия

Скалярное произведение дает одно число для описания произведения двух векторов. Если вы еще не изучали линейную алгебру, это может быть новой концепцией. Это форма умножения, используемая для вычисления работы, единичных векторов и нахождения угла между двумя векторами.

[латекс]\vec A\cdot \vec B=|\vec A||\vec B|\cos\theta[/latex]

 

Вектор можно умножить на другой вектор, но нельзя разделить на другой вектор. Есть два вида произведений векторов, широко используемых в физике и технике. Одним из видов умножения является скалярное умножение двух векторов . Скалярное произведение двух векторов приводит к числу (скаляру), как следует из его названия. Скалярные произведения используются для определения соотношения работы и энергии. Например, работа, которую сила (вектор) совершает над объектом, вызывая его перемещение (вектор), определяется как скалярное произведение вектора силы на вектор смещения. Совсем другой вид умножения — это 9.0171 векторное умножение векторов . Взятие векторного произведения двух векторов возвращает в результате вектор, как следует из его названия. Векторные произведения используются для определения других производных векторных величин. Например, при описании поворотов векторная величина, называемая крутящий момент , определяется как векторное произведение приложенной силы (вектор) и ее расстояния от оси вращения до силы (вектор). Важно различать эти два вида умножения векторов, потому что скалярное произведение — это скалярная величина, а векторное произведение — векторная величина.

Скалярное умножение двух векторов дает скалярное произведение.

Скалярное произведение

Скалярное произведение [latex]\vec A\cdot \vec B[/latex] двух векторов [latex]\vec A \text{ и } \vec B[/latex ] — число, определяемое уравнением:

[латекс]\vec A\cdot \vec B=|\vec A||\vec B| \cos \phi[/latex]

, где ϕ — угол между векторами. Скалярное произведение также называют точечным произведением из-за точечной записи, которая указывает на него.

Когда векторы даны в форме их векторных компонентов:

$$\vec A=A_x\underline{\hat{i}}+A_y\underline{\hat{j}}+A_z\underline{\hat{ k}}\text{  и  }\vec B=B_x\underline{\шляпа{i}}+B_y\underline{\шляпа{j}}+B_z\underline{\шляпа{k}}$$

мы можем вычислить их скалярное произведение следующим образом:

$$\vec A\cdot\vec B=(A_x\underline{\шляпа{i}}+A_y\underline{\шляпа{j}}+A_z\underline{\шляпа{ k}}) \ cdot (B_x \ underline {\ hat {i}} + B_y \ underline {\ hat {j}} + B_z \ underline {\ hat {k}}) \\ = A_xB_x \ underline {\ hat { i}} \ cdot \ underline {\ hat {i}} + A_xB_y \ underline {\ hat {i}} \ cdot \ underline {\ hat {j}} + A_xB_z \ underline {\ hat {i}} \ cdot \ подчеркивание {\ шляпа {k}} \\+ A_yB_x \ подчеркивание {\ шляпа {j}} \ cdot \ подчеркивание {\ шляпа {i}} + A_yB_y \ подчеркивание {\ шляпа {j}} \ cdot \ подчеркивание {\ шляпа {j}} + A_yB_z \ underline {\ hat {j}} \ cdot \ underline {\ hat {k}} \\+ A_zB_x \ underline {\ hat {k}} \ cdot \ underline {\ hat {i}} +A_zB_y\underline{\шляпа{k}}\cdot\underline{\шляпа{j}}+A_zB_z\underline{\шляпа{k}}\cdot\underline{\шляпа{k}}$ $

Поскольку скалярные произведения двух различных единичных векторов осей дают ноль, а скалярные произведения единичных векторов сами на себя дают единицу, в этом выражении всего три ненулевых члена. Таким образом, скалярное произведение упрощается до:

[латекс]\vec A\cdot\vec B=A_xB_x+A_yB_y+A_zB_z[/latex]

Мы можем использовать приведенное ниже уравнение, чтобы найти угол между двумя векторами. Когда мы делим [латекс]\vec A\cdot\vec B=|\vec A||\vec B| \cos\phi[/latex] от [latex]|\vec A || \vec B|[/latex] , получаем уравнение для cos(ϕ), в которое подставляем уравнение сверху:

$$\cos\phi=\frac{\vec A\cdot\vec B}{|\vec A||\vec B| }=\frac{A_xB_x+A_yB_y+A_zB_z}{|\vec A||\vec B| }$$

Угол ϕ между векторами [latex]\vec A \text{ и }\vec B[/latex] получается путем взятия арккосинуса выражения выше.

 

Источник: University Physics Volume 1, OpenStax CNX, https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/2-4-products-of-vectors (много примеров на этой странице).

 

Но что ЕСТЬ это?

Скалярное произведение представляет собой компонент вектора A вдоль B ( |A| cos Θ ), умноженный на величину (размер B). ИЛИ это составляющая B на A, умноженная на величину A. Визуально это видно на рисунке. ^[1]

На странице 169 «Физики, основанной на исчислении» есть прекрасное математическое доказательство.

Одна замечательная особенность скалярного произведения заключается в том, что A • B = B • A

Примером скалярного произведения является солнечная панель. Для максимальной эффективности лучи, исходящие от солнца, должны быть перпендикулярны панелям, то есть прямо на них. Вы можете использовать скалярное произведение между вектором солнечных лучей (желтый на изображении ниже) и единичным вектором, перпендикулярным поверхности (зеленый на изображении), чтобы вычислить, какая часть луча, падающего под углом, производит энергию.

 

Стрелки добавлены к фотографии из источника: https://www.pxfuel.com/en/free-photo-ouswv

В основном: Скалярное произведение — это метод нахождения числа, являющегося произведением двух векторов.

Применение: Две веревки, прикрепленные к знаку, тянут в разные стороны. Чтобы найти угол между ними, используйте скалярное произведение двух векторов.

Забегая вперед: Мы будем использовать скалярное произведение в разделе 2.3, посвященном уравнениям равновесия частиц (и в следующем семестре в динамике).

 

---

1. Источник: https://en.wikipedia.org/wiki/Dot_product#/media/File:Dot_Product.svg ↵

Лицензия

Инженерная механика: Статика Либби (Элизабет) Осгуд; Гейла Кэмерон; и Эмма Кристенсен находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, если не указано иное.

Поделиться этой книгой

Поделиться в Твиттере

Точечное и перекрестное произведение

Точечное и кросс-произведение

Скалярный продукт

Определение Определим скалярное произведение двух векторов v = a i + b j и w = c i + d j  в . w = ac + bd

Обратите внимание, что скалярное произведение двух векторов — это число, а не вектор. Для трехмерных векторов скалярное произведение определяется аналогично:

Скалярное произведение в R 3   Если v = а i + b j + c k и w = d i + e j + ф к затем v . w = объявление + быть + ср

Примеры:

Если 

        v = 2 i + 4 j  

и 

        w = i + 5 j

, затем

         против ^. с = (2)(1) + (4)(5) = 22

Упражнение

Найдите скалярное произведение

2 и + и — к     и      и + 2 и

---

Угол между двумя векторами

Определим угол тета между двумя векторами v и w по формуле

против ^. с
потому что q =                  
|| против || || с ||

так что
   

против . ш = || в| | || с || cos Q

Два вектора называются ортогональными , если их угол прямой.

Мы видим, что углы ортогональны тогда и только тогда, когда 

        v ^. с =  0

Пример  

Чтобы найти угол между

        v = 2i + 3j + k

и 

        w = 4i + j + 2k

вычисляем:

и

и

         v ^. с = 8 + 3 + 2 = 13

Отсюда

---

Углы направления

Определение направляющих косинусов Пусть            v = a i + b j + c k будет вектором, тогда мы определим косинусы направления быть следующим: cos a  =            || против || б cos b  =            || против || с cos g  =            || против ||

---

Выступы и компоненты Предположим, что автомобиль остановился на крутом холме, и пусть g будет силой сила тяжести, действующая на него. Мы можем разбить вектор g на компонент который толкает машину по дороге, и компонент, который толкает машину на дорогу. Мы определяем

Определение Пусть u и v — векторы. затем и можно разделить на два компонента, р и с такие что r параллельно v и s перпендикулярно против .   р называется проекция ты на против и s называется компонентом u перпендикулярно против .

Мы видим, что

|| и || || против || ||проект _v и ||
у ^. против =  || и || || против || cos q   =                                   
||у||

=  || против || ||проект _v и ||

следовательно 

ты . против ||проект v и || знак равно || против ||

Мы можем вычислить проекцию u на v по формуле:          

и . против проект v u = против   || против || 2

Обратите внимание, что это работает, поскольку, если мы возьмем величины обеих сторон, мы получим что

и ^. против
| |продж _в у|| = ||в||  
|| против || ²  

а правая часть упрощается до приведенной выше формулы. Направление верно, так как правая часть формулы есть постоянное кратное v , поэтому вектор проекции находится в направление v по мере необходимости.

Чтобы найти вектор s , обратите внимание на диаграмму, что

проект _v u + s = у

так что

с   = у — проект _v у

---

Работа

Работа, совершаемая постоянной силой F вдоль PQ, определяется выражением

Вт = F . PQ

Пример

Найдите работу, совершенную против силы тяжести, чтобы переместить груз массой 10 кг. ребенка из точки (2,3) в точку (5,7)?

Решение

Имеем, что вектор силы равен

Ф =  m a   =  (10)(-9,8 j )  =  -98 j

а вектор смещения равен

против = (5 — 2) i + (7 — 3) j   =  3 i + 4 и

Работа — это точечный продукт

W =  F ^. v   =  (-98 j ) ^. (3 и + 4 и )

= (0)(3) + (-98)(4) = -392

Обратите внимание, что отрицательный знак подтверждает, что работа выполняется против силы тяжести. Следовательно, чтобы сдвинуть ребенка с места, требуется 392 Дж работы.

---

Крутящий момент

Предположим, вы катаетесь на лыжах и ужасно падаете. Ваше тело вращается вокруг и лыжи остаются на месте (не пытайтесь повторить это дома). С правильными креплениями ваши крепления будут отпустите, и ваша лыжа оторвется. Привязки признают, что сила был применен. Эта сила называется крутящим моментом. Чтобы вычислить это мы используем перекрестное произведение двух векторов, которое не только дает крутящий момент, но также создает направление, перпендикулярное как силе, так и направление ноги.

---

Перекрестное произведение двух векторов

Определение Пусть u = a i + b j + c k и v = d i + e j + f k — векторы, тогда мы определяем перекрестное произведение v x w на определитель матрицы:

Мы можем вычислить этот определитель как

     =  (bf – ce) и + (кд — аф) и + (аэ — бд) к

Пример

Найдите векторное произведение и х против , если

u =  2 i + j — 3 k v = 4 j + 5 k

Решение

Мы рассчитываем

= 17 i — 10 j + 8 k

Если вам нужна дополнительная помощь, см. конспекты лекций по математике 103 B по матрицам.

Упражнения

Найти u x v когда

1. u = 3 i + j — 2 k ,      v = i — к
   

2. u = 2 i — 4 j — k ,      v = 3 i —   дж + 2 к
   

Обратите внимание, что с момента изменения порядка двух строк определителя знак определителя, имеем

         u x v   = — и х и

---

Геометрия и векторное произведение

Пусть и и v — векторы, и рассмотрим параллелограмм, который два вектора составляют. Затем

|| u x v || = Площадь параллелограмма

а направление u x v является прямым углом к ​​параллелограмму что следует правилу правой руки

Примечание.    Для i x j величина равна 1 и направление k , следовательно, i x j = k .

Упражнение

Найти j x k и i x к

---

Новый взгляд на крутящий момент

Определим крутящий момент (или момент M силы F относительно точки Q) как

М = PQ x F

 

Пример

Гаечный ключ на 20 дюймов расположен под углом 30 градусов с земля. Сила в 40 фунтов, которая составляет и угол 45 градусов с гаечным ключом поворачивает гаечный ключ. Найдите крутящий момент.

Решение  

Мы можем записать ключ как вектор

20 cos 30  i   + 20 sin 30 j = 17,3 i + 10 j

и сила как

-40 cos 75 i — 40 sin 75 j = -10,3 i — 38,6 j

следовательно, крутящий момент равен величине их векторного произведения:

       

= -564 дюйм фунты

---

Параллелепипеды

Чтобы найти объем параллелепипеда, натянутого на три вектора и , v и w находим тройное произведение:

Объем = u . ( v x w )

Это можно найти, вычислив определитель трех векторов:

   

Пример

Найти объем параллелепипеда, натянутого на векторы

u   =  <1,0,2>        v =  <0,2,3>         w  = <0,1,3>

Решение

Мы найти

---

---

Назад на векторную страницу

Назад на домашнюю страницу Math 107

Назад на домашнюю страницу математического факультета

электронная почта Вопросы и предложения

Скалярный продукт — исчисление 3

Все ресурсы исчисления 3

6 Диагностические тесты 373 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 6 7 8 9 … 17 18 Следующая →

Исчисление 3 Помощь » Векторы и векторные операции » Скалярный продукт

Вычислите скалярный продукт между , и .

Возможные ответы:

Правильный ответ:

Объяснение:

Все, что нам нужно сделать, это умножить подобные компоненты.

Сообщить об ошибке

Оценить скалярное произведение , и .

Возможные ответы:

Правильный ответ:

Объяснение:

Все, что нам нужно сделать, это перемножить одинаковые компоненты и сложить их вместе.

Сообщить об ошибке

Найдите скалярное произведение следующих векторов:

Возможные ответы:

Правильный ответ:

Объяснение:

, чтобы найти точечный продукт между двумя векторами

Мы рассчитываем

Таким образом, для

Мы имеем

Отчет о ошибке

Что на длину по длине по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли вектор.

?

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем вычислить длину вектора, взяв квадратный корень из скалярного произведения и , поэтому длина  равна:

Сообщить об ошибке

Найдите скалярное произведение следующих векторов:

Возможные ответы:

Правильный ответ:

Объяснение:

, чтобы найти точечный продукт между двумя векторами

Мы рассчитываем

Таким образом, для

Мы имеем

Отчет о ошибке

Что на длину по длине по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли по доли вектор.

?

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем вычислить длину вектора, взяв квадратный корень из скалярного произведения и , поэтому длина  равна:

Сообщить об ошибке

Какое из следующих утверждений нельзя использовать в качестве определения скалярное произведение двух векторов с действительным знаком?

Возможные ответы:

Все они могут быть использованы

, где  это угол между .

Правильный ответ:

Объяснение:

 неверно. Это говорит о том, что нужно сложить вместе все компоненты двух векторов. Два других определения обычно используются при вычислении углов между векторами и другими объектами, а также могут быть получены друг из друга.

Сообщить об ошибке

Что из следующего верно относительно скалярного произведения двух векторов?

Возможные ответы:

 определен корректно, если каждый вектор имеет одинаковую размерность

Ни одно из других утверждений не верно.

Скалярное произведение двух векторов никогда не бывает отрицательным.

 тогда и только тогда, когда   ортогональны.

Скалярное произведение двух векторов никогда не является скаляром.

Правильный ответ:

тогда и только тогда, когда ортогональны.

Объяснение:

Это утверждение верно; его можно получить из определения, установив острый угол между векторами равным  ; требование ортогональности. Кроме того, если любой из векторов имеет длину, векторы по-прежнему называются ортогональными.

Сообщить об ошибке

Что такое скалярное произведение векторов  и ?

Возможные ответы:

Правильный ответ:

Объяснение:

Пусть вектор  представлен как   , а вектор   представлен как  .