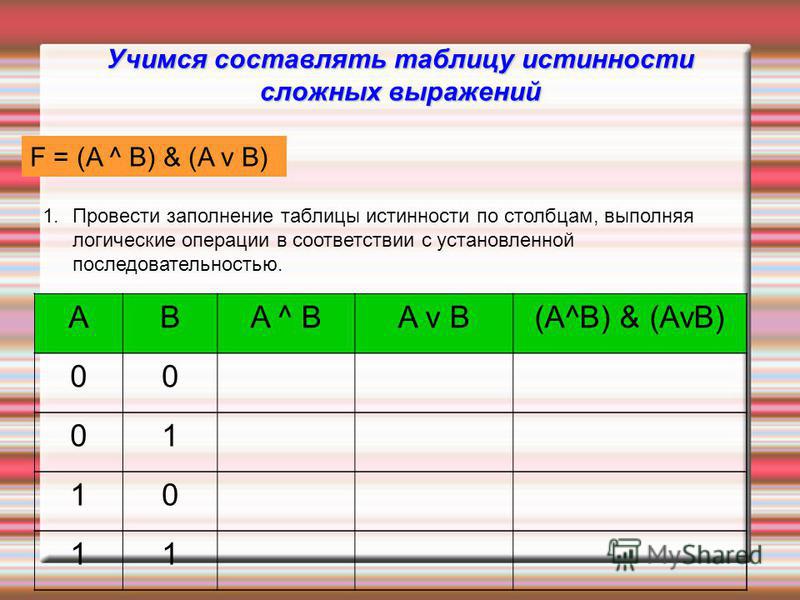
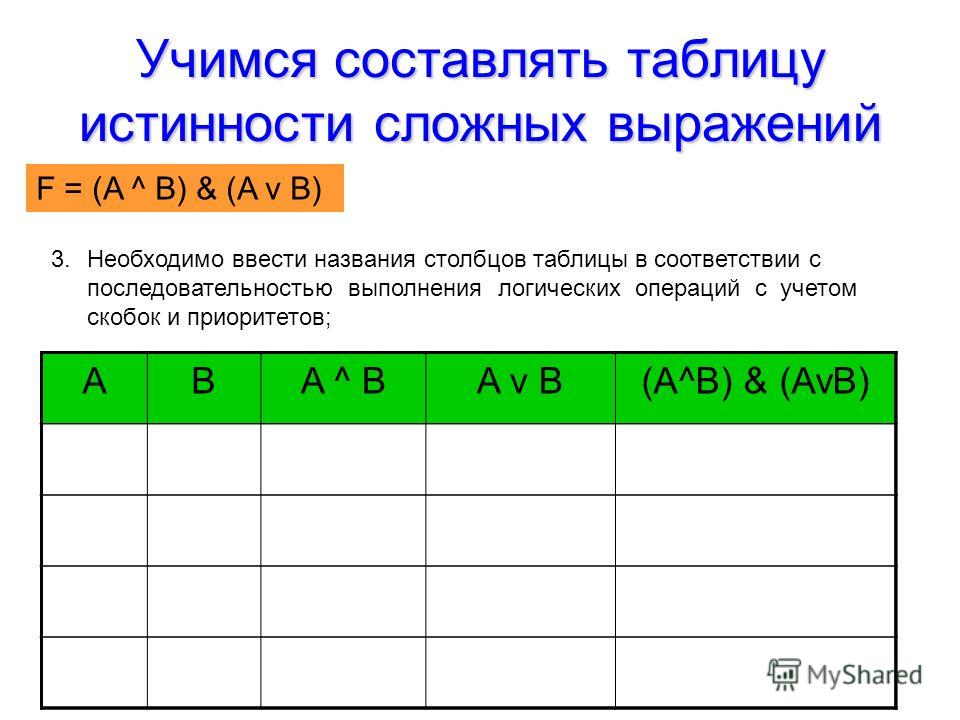
1. Частично заполненные таблицы истинности логических выражений
1. Частично заполненные таблицы истинности логических выражений
|
Сборка заданий. ЕГЭ по информатике
ЕГЭ задания 2
Задание 1. Для таблицы истинности функции F известны значения только некоторых ячеек.
x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
1 | 0 | 1 | |||||
0 | 0 | 0 | |||||
0 | 1 | 0 |
Каким выражением может быть F?
1) x1 ∧ x2 ∧ x3 ∧ x4 ∧ x5 ∧ x6 ∧ ¬x7
2) ¬x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ x5 ∧ ¬x6 ∧ x7
4) x1 ∨ x2 ∨ ¬ x3 ∨ ¬x4 ∨ x5 ∨ ¬x6 ∨ x7
Задание 2 . Миша заполнял таблицу истинности для выражения F. Он успел заполнить лишь небольшой фрагмент таблицы
Миша заполнял таблицу истинности для выражения F. Он успел заполнить лишь небольшой фрагмент таблицы
x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
1 | 0 | 1 | |||||
0 | 0 | 0 | |||||
0 | 1 | 0 |
Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ x4 ∧ x5 ∧ x6 ∧ ¬x7
2) ¬x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ x5 ∧ ¬x6 ∧ x7
4) x1 ∨ (x2 → ¬x3) ∨ ¬x4 ∨ x5 ∨ ¬x6 ∨ x7
Задание 3.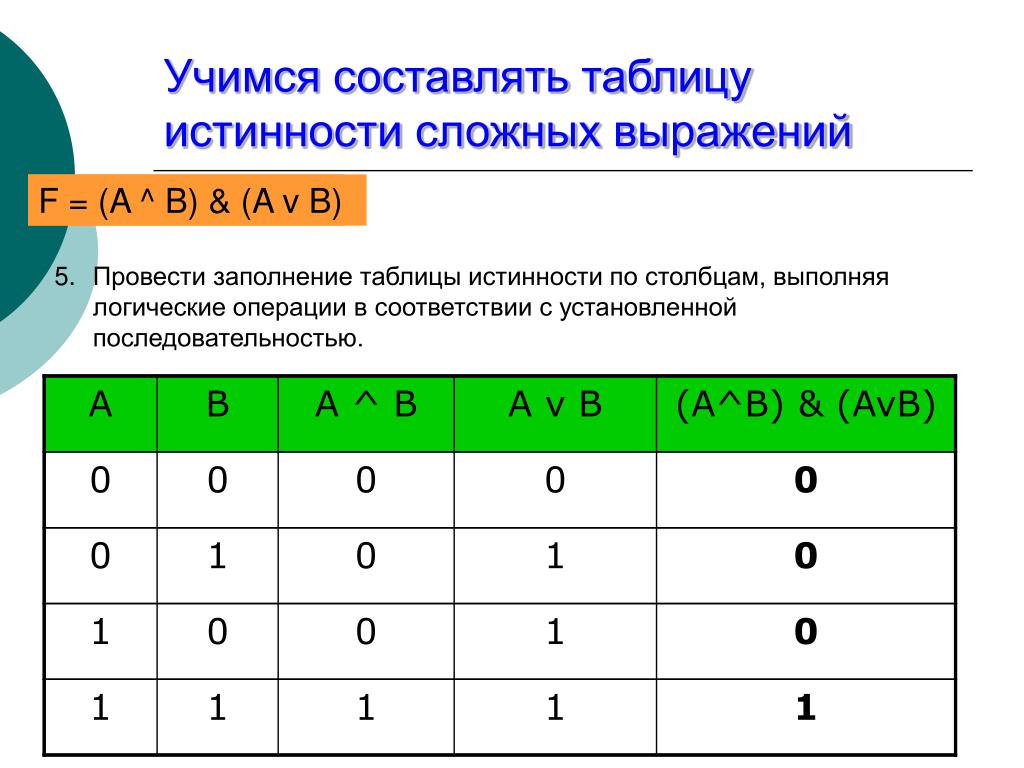 Логическая функция F задаётся выражением:
Логическая функция F задаётся выражением:
(¬x ∧ y ∧ z) ∨ (¬x ∧ ¬y ∧ z) ∨ (¬x ∧ ¬y ∧ ¬z).
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
Перем. 1 | Перем. 2 | Перем. 3 | Функция |
??? | ??? | ??? | F |
0 | 0 | 0 | 1 |
1 | 0 | 0 | 1 |
1 | 0 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу, затем – буква, соответствующая второму столбцу, и т.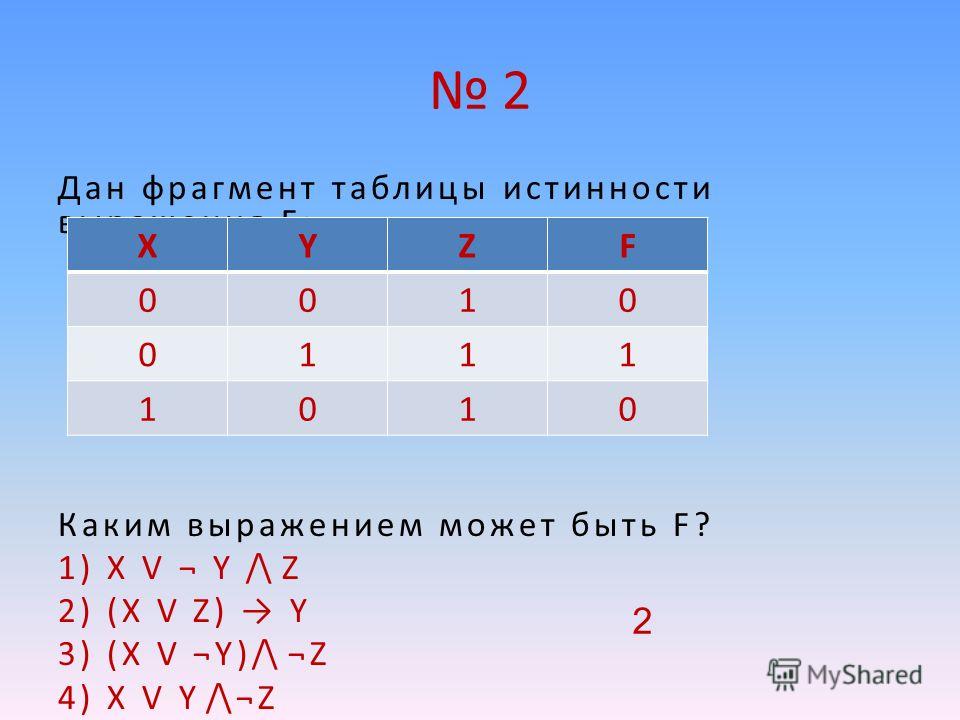 д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и таблица истинности:
Перем. 1 | Перем. 2 | Функция |
??? | ??? | F |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 1 |
1 | 1 | 1 |
Тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x.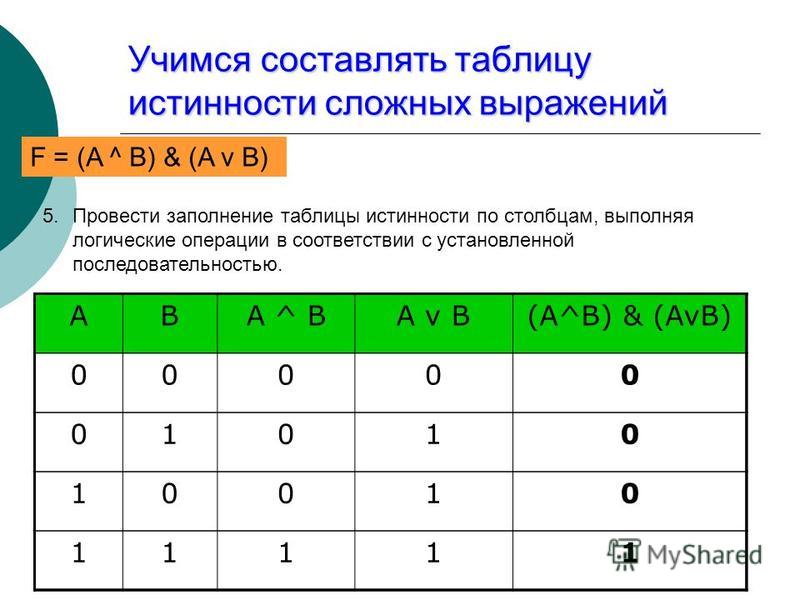 В ответе нужно написать: yx.
В ответе нужно написать: yx.
Задание 4. Логическая функция F задаётся выражением (¬z)∧x ∨ x∧y. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
Перем. 1 | Перем. 2 | Перем. 3 | Функция |
??? | ??? | ??? | F |
0 | 0 | 0 | 0 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 0 |
0 | 1 | 1 | 1 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу; затем – буква, соответствующая 2-му столбцу; затем – буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и таблица истинности:
Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и таблица истинности:
Перем. 1 | Перем. 2 | Функция |
??? | ??? | F |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 1 |
1 | 1 | 1 |
Тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x.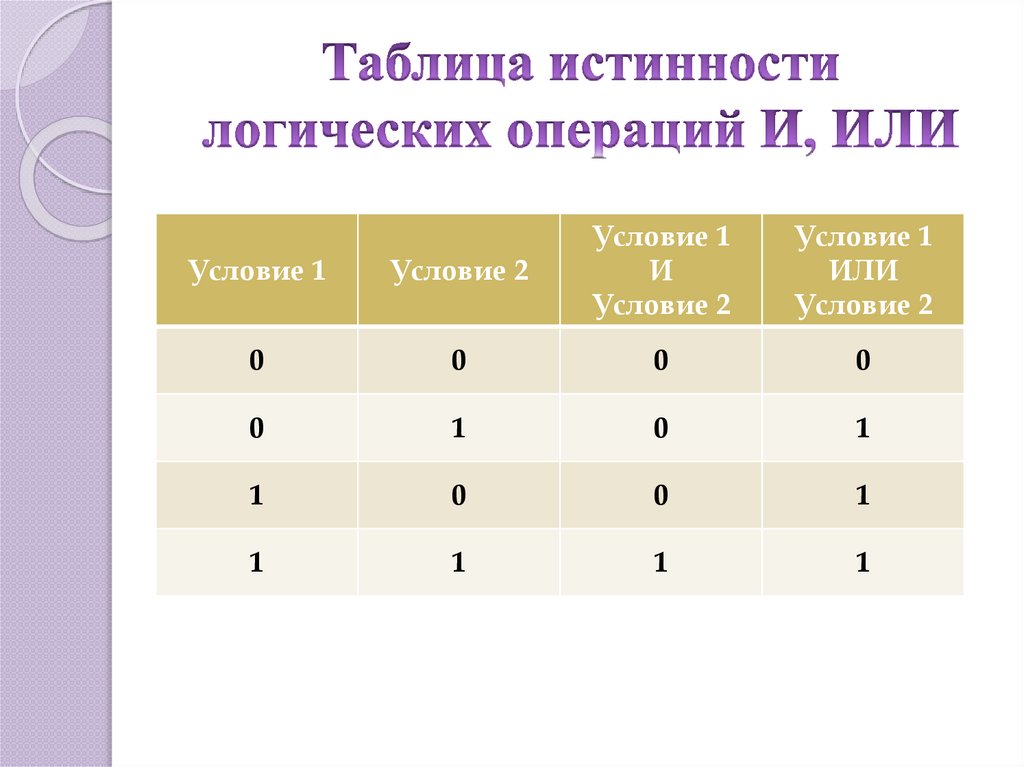 В ответе нужно написать: yx.
В ответе нужно написать: yx.
Задание 5. Дано логическое выражение, зависящее от 5 логических переменных:
z1 ∧ ¬z2 ∧ ¬z3 ∧ ¬z4 ∧ z5
Сколько существует различных наборов значений переменных, при которых выражение ложно?
1) 1
2) 2
3) 31
4) 32
Задание 6. Дан фрагмент таблицы истинности выражения F:
x1 | x2 | x3 | x4 | x5 | x6 | F |
1 | 1 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | 0 | 0 | 1 | 0 |
1 | 0 | 0 | 1 | 0 | 0 | 0 |
Каким выражением может быть F?
1) (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)
2) (x1 ∧ x3) ∨ (x3 ∧ x5) ∨ (x5 ∧ x1)
3) (x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2)
4) (x1 ∧ x4) ∨ (x2 ∧ x5) ∨ (x3 ∧ x6)
Задание 7.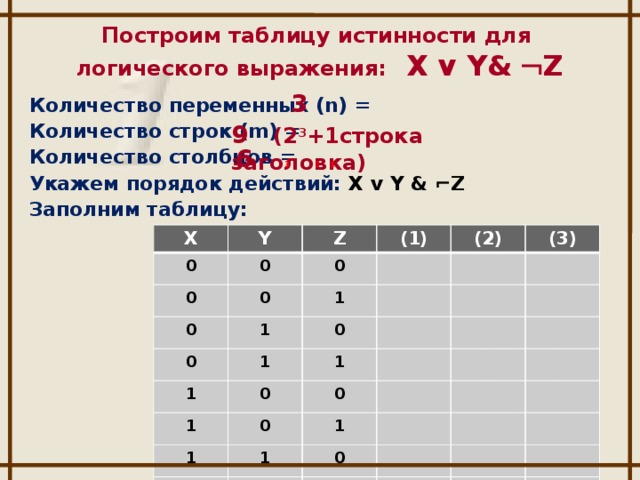 Дан фрагмент таблицы истинности выражения F.
Дан фрагмент таблицы истинности выражения F.
x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | F |
1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
Каким из приведённых ниже выражений может быть F?
1) (х1 —> х2) ∧ ¬хЗ ∧ х4 ∧ ¬х5 ∧ хб ∧ ¬х7 ∧ х8
2) (х1 —> х2) ∨ ¬хЗ ∨ х4 ∨ ¬х5 ∨ хб ∨ ¬х7 ∨ х8
3) ¬(х1 —> х2) ∨ хЗ ∨ ¬х4 ∨ х5 ∨ ¬хб ∨ х7 ∨ ¬х8
4) ¬(х1 —> х2) ∧ хЗ ∧ ¬х4 ∧ х5 ∧ ¬хб ∧ х7 ∧ ¬х8
Задание 8. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
X | Y | Z | F |
1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 |
0 | 0 | 1 | 1 |
Какое выражение соответствует F?
1) (0 ∧ Z) ∧ (X ≡ Y)
2) (0 ∨ ¬Z) ∧ (X ≡ Y)
3) (1 ∧ Z) ∧ (X ≡ Y)
4) ( ¬1 ∧ Z) ∧ (X ≡ Y)
Задание 9.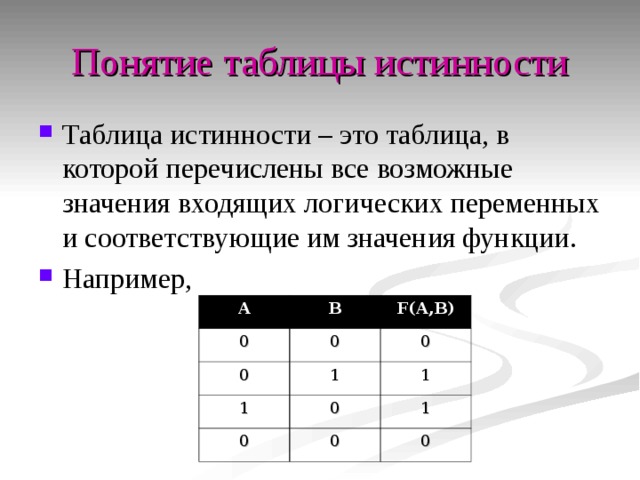 Символом F обозначено одно из указанных ниже логических выражений от трёх аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
Символом F обозначено одно из указанных ниже логических выражений от трёх аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
X | Y | Z | F |
0 | 0 | 0 | 1 |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 1 |
Какое выражение соответствует F?
1) X ∨ Y → Z
2) ¬X ∨ Y → Z
3) ¬X ∧ Z → Y
4) X ∨ ¬Z → Y
Моделирование
Моделирование- Конструктивные представления и проектные спецификации:
- Технические характеристики конструкции описать дизайн с точки зрения его результатов.

- Дизайнерские модели описать структуру и поведение проекта.
- На любом заданном уровне проект может быть описан с помощью уравнений, таблиц или HDL.
- Использует Расширение Шеннон :
- Повторное обращение к функции ф приводит к ДНФ функции.
- остаток функции для x я = 1 это его значение при x я установлен на 1.
- Например:
- Функции переключения (частный случай булевых функций) используются в TPG.
- Например, чтобы наблюдать застрявшую ошибку, ответ исправной цепи Р , должно отличаться от неисправного контура, Р ф .

- Для узлов х я у ИП, Р и Р ф являются остатками функции w.r.t. х я .
- Переписав приведенное выше выражение как Логическая разница относительно кси :
- Приравнивание этого к 1 определяет значения переменных, которые позволяют наблюдать неисправность на узле . х я на ПО.
- х я = 0 требуется для обнаружения
- Например:
- Учитывать неисправности на PI, х 2 .

- что означает, что х 1 = 1 и х 3 = 0,
- Для СА1 тест, установите продукт х 2 и логическая разница до 1.
- Для СА0 тесты поставили продукт х 2 и логическая разница до 1.
- К сожалению, этот метод неэффективен в вычислительном отношении для TPG.
- Формально выражается как шестикратный туплет (I, S, д, S 0 , О, л )
- I и O — входной/выходной алфавит. тип=диск>
- S 0 (начальные состояния) , являются подмножеством S. тип=диск>
- д: S X I -> S (функция следующего состояния),
- Табличное представление автомата.

- Асинхронные последовательные схемы (без часов), представленные таблицей потоков.

Состояние/ввод x | 0 | 1 |
|---|---|---|
1 | 2,1 | 3,0 |
2 | 2,1 | 4,0 |
3 | 1,0 | 4,0 |
4 | 3,1 | 3,0 |
00 | 01 | 11 | 10 | |
|---|---|---|---|---|
1 | 1,0 | 5,1 | 2,0 | 1,0 |
2 | 1,0 | 2,0 | 2,0 | 5,1 |
3 | 3,1 | 2,0 | 4,0 | 3,0 |
4 | 3,1 | 5,1 | 4,0 | 4,0 |
5 | 3,1 | 5,1 | 4,0 | 5,1 |
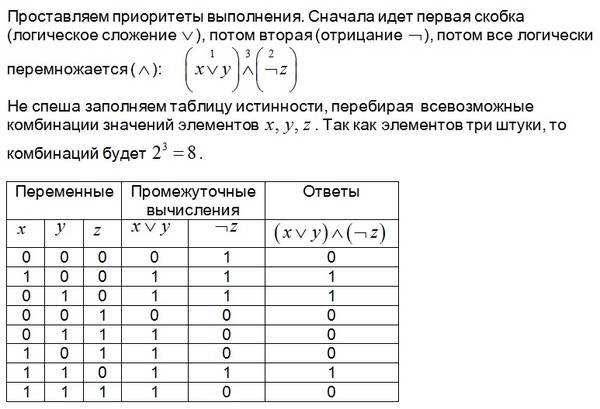
- Самый простой способ представить комбинационную схему — это ее таблица истинности :
- Структура данных, представляющая таблицу истинности, обычно представляет собой массив .
 В размера 2 номер , причем входы расположены в возрастающем двоичном порядке.
В размера 2 номер , причем входы расположены в возрастающем двоичном порядке. - Простой способ найти значение Z заключается в объединении входных значений.
х1 | х2 | х3 | Z |
|---|---|---|---|
0 | 0 | 0 | 1 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 0 |
0 | 1 | 1 | 1 |
1 | 0 | 0 | 1 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 |
1 | 1 | 1 | 0 |
- Таблица истинности, показанная ранее, может быть представлена в компактном представлении через Примитивные кубы.
- Кубическая запись для первых двух строк таблицы истинности равна . 00x|1 .
- подразумеваемый г из Z (х 1 , х 2 , х 3 ) преобразуется в куб ( v 1 v 2 v 3 | v Z ) по:
- Настройка v я до 1(0) , если х я ( х я ) появляется в г .
 тип=диск>
тип=диск> - Настройка v я до х , если ни х я ни х я появляется в г . тип=диск>
- Настройка v Z до 1 для v Z = Z (v 1 , в 2 , в 3 ). тип=диск>
- Например, импликант х1х2 преобразуется в 00x|1 .
- Если куб д можно получить из куба стр путем замены одного или нескольких х значения в стр по 0 или 1 , мы говорим стр охватывает д .

- Например куб 00x|1 крышки кубики 000|1 и 001|1 .
- Куб, представляющий главная импликанта из Z или Z называется примитивный куб .
- Затем мы можем использовать представление примитивного куба, чтобы определить значение входной комбинации, найдя запись, которая ее покрывает: .
- Например, ( v 1 v 2 v 3 ) = 010 соответствует примитивному кубу х10|0 .
- Следовательно, Z (010) = 0 .
- Операция сопоставления реализована с помощью перекресток оператор:
- Перекресток 0 и 1 это непоследовательный .

- Пересечение двух кубов согласовано если все соответствующие значения последовательный или совместимый .
&& | 0 | 1 | х |
|---|---|---|---|
0 | 0 | пустой | 0 |
1 | пустой | 1 | 1 |
х | 0 | 1 | х |
- Примитивные кубы обеспечивают компактное представление и могут помочь в TPG.
- Например, если мы ищем Z = 1 , нам нужно либо x 2 = 0 или х 1 х 3 = 01 .
- График Г ( В , Е , Вт ) определяется как:
- В : вершины или узлы тип=диск>
- Е : края тип=диск>
- Вт : вес тип=диск>
- направленный край е ( ты , v ) используется в ориентированном графе.

- Другие стандартные определения:
- неориентированный граф является симметричным ориентированным графом.
- А путь представляет собой последовательность ребер.
- А связный граф если существует путь от одного ребра до любого другого ребра.
- А цикл представляет собой замкнутый путь некоторой длины.
- А полный граф имеет ребро между каждой парой узлов.
- Двоичные диаграммы принятия решений (BDD):
- Это ориентированные ациклические графы (DAG).
- вершины разделены на три набора:
- Корень ( степень = 0, вне степени = 2) тип=диск>
- Внутренние узлы ( степень = 1, вне степени = 2) тип=диск>
- Оба они представляют переменные функции.

- Листья ( степень = 2, вне степени = 0) тип=диск>
- Значения конечных вершин равны 0 и 1.
- края графика представляют буквальные альтернативы (0 или 1) для этих переменных.
- Вычисление выражения включает обход графа.
- Поиск всех путей к 1 дает произведение ф .
- BDD могут быть разработаны путем рекурсивного применения расширения Шеннона.
- Начнем с переменной х 1 с f(x1,x2) = х 1 х 2
- преемники из х 1 — остатки ф за х 1 = 0 и х 1 = 1
- В этом случае функция симметрична и такая же диаграмма получается, если х 2 была начальной переменной.

- Однако в целом диаграмма чувствительна к порядку рассмотрения переменных.
- Алгоритмы генерации BDD имеют порядок O(2 N /Н).
- Приложение TPG:
- Выход исправной схемы равен 0 (1), а неисправной схемы — 1 (0).
- Процедура : трассировка от корня до каждого из 0 и 1 конечных узлов.
- Правила : Узлы общие на обеих трассах должно быть одинаковое значение .
- Соответствующие значения переменных составляют тест.
- RTL предоставляют модели для систем на уровне регистров и наборов инструкций.
- Данные хранятся в:
- Регистры тип=диск>
регистр IR[0->7]
- Память организована как массивы регистров тип=диск>
память MEM[0->256; 0->15]
- Модели RTL характеризуются как поведенческие (предоставляют только некоторую структурную информацию).

- Примитивные операторы («+» и «=») используются для преобразования и передачи данных.
С = А + В
- Также определены условные операторы.
если X, то C = A + B
если (ЧАСЫ и (AREG < BREG)) то AREG = BREG
- Также доступны языковые конструкции более высокого уровня, такие как if…then…else и операторы case.
тест (ИК[0->3])
случай 0: операция0
случай 1: операция1
…
случай 15: операция15
тестенд
- RTL также предоставляют компактные конструкции для адресации памяти.
ПАМЯТЬ [БАСЭРЕГ + ПК]
- Комбинационные функции могут быть непосредственно описаны булевыми операторами.
Z = (А и В) или С
- Другие примитивные операторы включают сдвиг и счет.

shift_right(AREG, 2, 0)
вкл (ПК)
- Некоторые RTL позволяют ссылаться на прошлые значения переменных, например, для моделирования нарастающего фронта тактового сигнала, . Х .
если (X(-1)=0 и X=1), то …
- Моделирование конечных автоматов.
состояние S1, S2, S3
S1: если X, то
начало
Р = Q + R
перейти на S2
конец
еще
Р = Q — R
перейти на S3
S2: …
- Есть две категории, в зависимости от трактовки концепции времени.
- Процедурные языки тип=диск>
- Подобно обычным языкам программирования, в которых операторы выполняются последовательно, например, . С получает новое значение А .

А = В
С = А
- Непроцедурные языки тип=диск>
- Операторы выполняются параллельно, например, обмены А и Б .
А = В
Б = А
- Процедурные RTL обычно используются для описания системы на уровне . набор инструкций уровень абстракции, который использует неявный на основе цикла модель ГРМ, например,
- Выборка, декодирование, выполнение фаз.
- Информация о времени может быть указана в модели поведения.
С = А + В, задержка = 100
- Некоторые RTL допускают сочетание процедурных и непроцедурных конструкций.
- Читать текстовое описание списков соединений и HDL (verilog и VHDL).

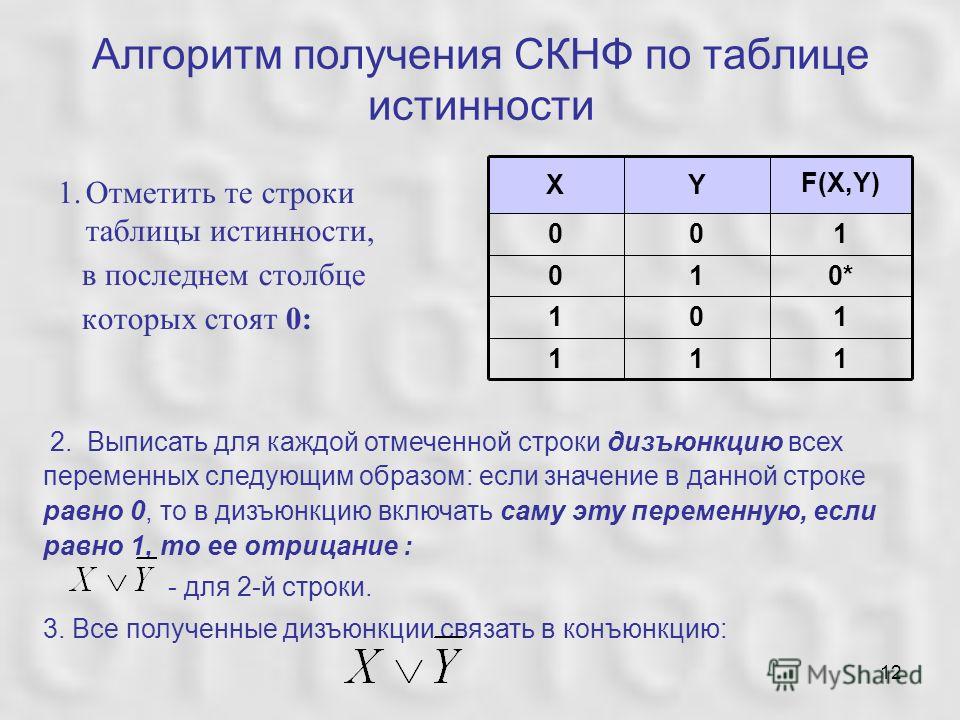
- Заметим, что эти представления ( таблицы истинности , таблицы состояний или BDD ) являются структурами данных, интерпретируемыми модельно-независимый программы.
- Альтернатива на основе кода модель ( модель скомпилированного кода) .
- Для скорости схема может быть смоделирована программой напрямую.
Что такое таблица истинности? — Определение из WhatIs.com
По
- Участник TechTarget
Таблица истинности представляет собой разбивку логической функции путем перечисления всех возможных значений, которые может получить функция. Такая таблица обычно содержит несколько строк и столбцов, причем верхняя строка представляет собой логические переменные и их комбинации, по возрастающей сложности ведущие к конечной функции.
Такая таблица обычно содержит несколько строк и столбцов, причем верхняя строка представляет собой логические переменные и их комбинации, по возрастающей сложности ведущие к конечной функции.
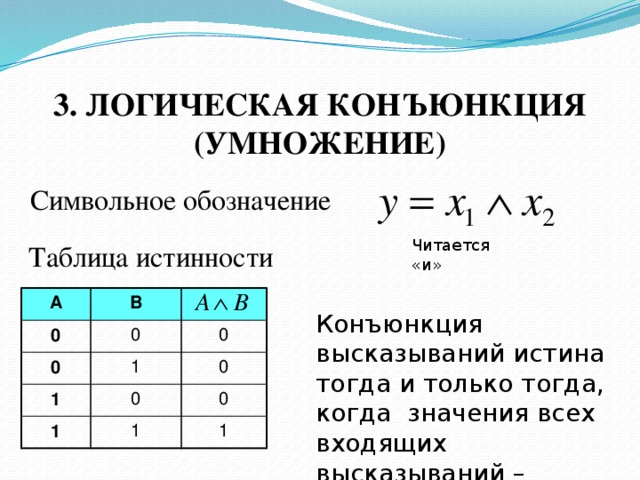
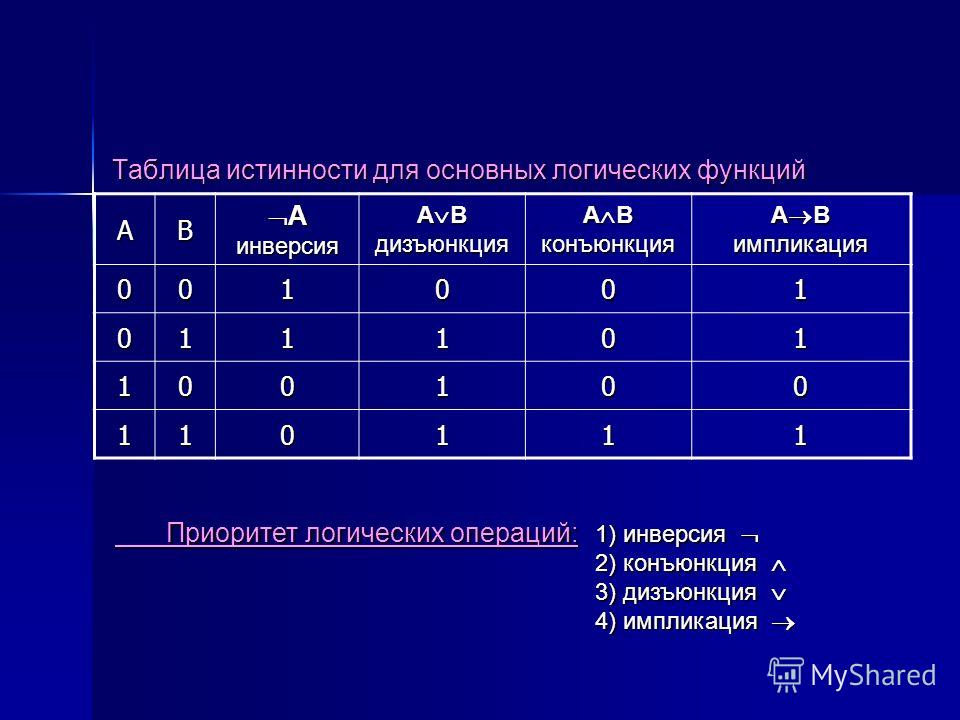
В логической функции есть три основные операции: НЕ (также называемая инверсией или отрицанием и обозначаемая символом -), ИЛИ (также называемая дизъюнкцией или сложением и обозначаемая символом +) и И (также называемая конъюнкцией или умножением и обозначаемая символом *). Значения функций обычно назначаются как логический 0 = ложь и логическая 1 = истина. Таким образом, применяются следующие правила:
Если A = 0, то -A = 1
Если A = 1, то -A = 0
A+B = 1, за исключением случаев, когда A = 0 и B = 0
A+B = 0, если A = 0 и B = 0
A*B = 0, за исключением случаев, когда A = 1 и B = 1
A*B = 1, если A = 1 и B = 1
В следующих таблицах показан процесс оценки значений логической функции -(A+B) * -(A*B), определяемый путем разбиения ее на составные функции.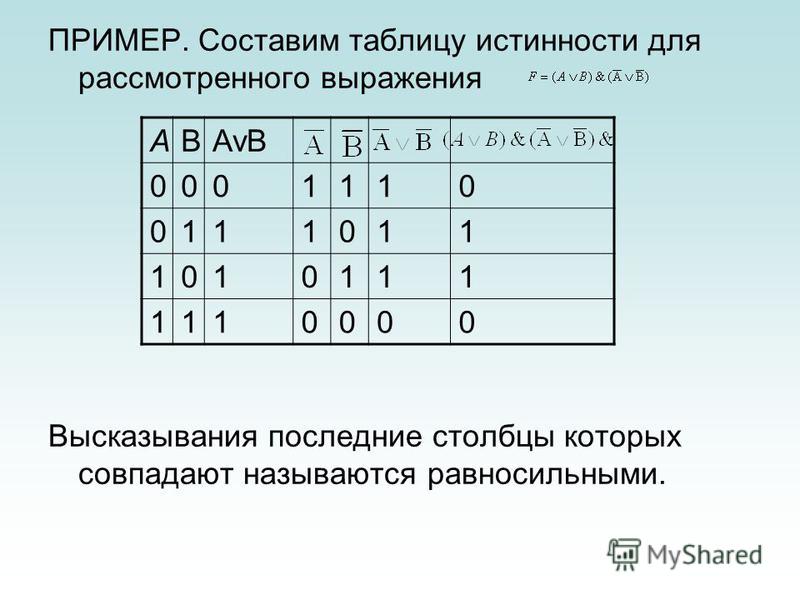 Две логические переменные, A и B, перечислены вверху первых двух столбцов. Все возможные комбинации значений для A и B перечислены в этих столбцах путем подсчета в двоичном порядке: 00, 01, 10, 11. Крайний правый (в данном случае седьмой) столбец содержит функцию, которую нужно вычислить (последняя функция).
Две логические переменные, A и B, перечислены вверху первых двух столбцов. Все возможные комбинации значений для A и B перечислены в этих столбцах путем подсчета в двоичном порядке: 00, 01, 10, 11. Крайний правый (в данном случае седьмой) столбец содержит функцию, которую нужно вычислить (последняя функция).
| А | Б | А+В | А*В | -(А+В) | -(А*В) | -(А+В) * -(А*В) |
| ? | ? | ? | ? | ? | ||
| 1 | ? | ? | ? | ? | ? | |
| 1 | ? | ? | ? | ? | ? | |
| 1 | 1 | ? | ? | ? | ? | ? |
После настройки этой структуры значения в третьем и четвертом столбцах определяются простыми правилами сложения и умножения:
| А | Б | А+В | А*В | -(А+В) | -(А*В) | -(А+В) * -(А*В) |
| ? | ? | ? | ||||
| 1 | 1 | ? | ? | ? | ||
| 1 | 1 | ? | ? | ? | ||
| 1 | 1 | 1 | 1 | ? | ? | ? |
Затем значения в пятом и шестом столбцах определяются путем инвертирования значений в третьем и четвертом столбцах:
| А | Б | А+В | А*В | -(А+В) | -(А*В) | -(А+В) * -(А*В) |
| 1 | 1 | ? | ||||
| 1 | 1 | 1 | ? | |||
| 1 | 1 | 1 | ? | |||
| 1 | 1 | 1 | 1 | ? |
Наконец, значения оцениваемой функции определяются путем умножения значений пятого и шестого столбцов:
| А | Б | А+В | А*В | -(А+В) | -(А*В) | -(А+В) * -(А*В) |
| 1 | 1 | 1 | ||||
| 1 | 1 | 1 | ||||
| 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 |
Это простая логическая функция. Некоторые функции имеют много входных переменных и состоят из многих составных функций. Это может привести к таблице с сотнями строк и столбцов. Компьютеры используются для создания таблиц истинности для очень сложных логических функций.
Некоторые функции имеют много входных переменных и состоят из многих составных функций. Это может привести к таблице с сотнями строк и столбцов. Компьютеры используются для создания таблиц истинности для очень сложных логических функций.
Альтернативой таблице истинности является использование булевых теорем. Этот метод, называемый булевой алгеброй, используется инженерами для поиска простейшей схемы, которая будет выполнять желаемую логическую функцию. Это оптимизирует эффективность системы за счет минимизации количества операций, которые необходимо выполнить для выполнения данной задачи.
Последнее обновление: сентябрь 2005 г.
прием данных
Прием данных — это процесс получения и импорта данных для немедленного использования или хранения в базе данных.
ПоискСеть
- беспроводная ячеистая сеть (WMN)
Беспроводная ячеистая сеть (WMN) — это ячеистая сеть, созданная путем соединения узлов беспроводной точки доступа (WAP), установленных в .
 ..
.. - Wi-Fi 7
Wi-Fi 7 — это ожидаемый стандарт 802.11be, разрабатываемый IEEE.
- сетевая безопасность
Сетевая безопасность охватывает все шаги, предпринятые для защиты целостности компьютерной сети и данных в ней.
ПоискБезопасность
- Что такое модель безопасности с нулевым доверием?
Модель безопасности с нулевым доверием — это подход к кибербезопасности, который по умолчанию запрещает доступ к цифровым ресурсам предприятия и …
- RAT (троянец удаленного доступа)
RAT (троян удаленного доступа) — это вредоносное ПО, которое злоумышленник использует для получения полных административных привилегий и удаленного управления целью …
- атака на цепочку поставок
Атака на цепочку поставок — это тип кибератаки, нацеленной на организации путем сосредоточения внимания на более слабых звеньях в организации .
 ..
..
ПоискCIO
- Пользовательский опыт
Дизайн взаимодействия с пользователем (UX) — это процесс и практика, используемые для разработки и внедрения продукта, который обеспечит позитивное и …
- соблюдение конфиденциальности
Соблюдение конфиденциальности — это соблюдение компанией установленных правил защиты личной информации, спецификаций или …
- контингент рабочей силы
Временная рабочая сила — это трудовой резерв, члены которого нанимаются организацией по запросу.
SearchHRSoftware
- Поиск талантов
Привлечение талантов — это стратегический процесс, который работодатели используют для анализа своих долгосрочных потребностей в талантах в контексте бизнеса …
- удержание сотрудников
Удержание сотрудников — организационная цель сохранения продуктивных и талантливых работников и снижения текучести кадров за счет стимулирования .




 Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и таблица истинности:
Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и таблица истинности: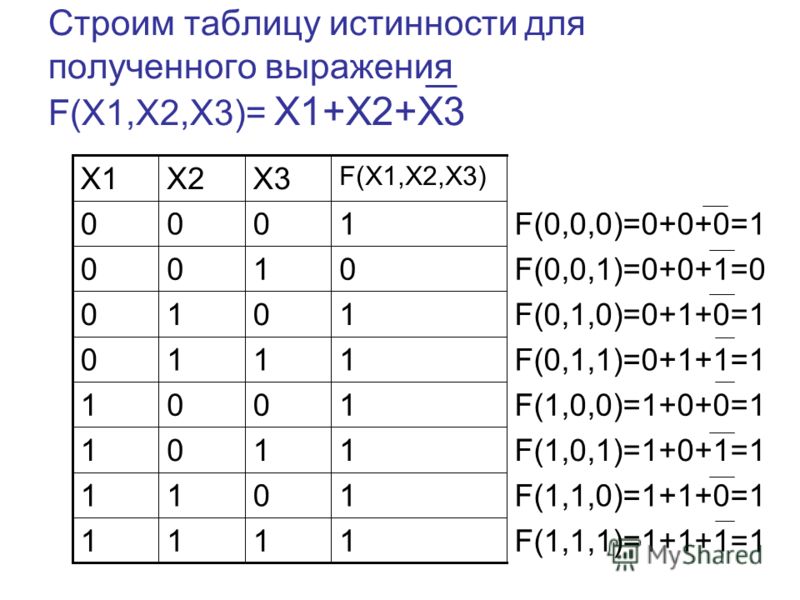 Такое возможно только при z = 1, у = 0, т. е. переменная1 − z, а переменная2 − y.
Такое возможно только при z = 1, у = 0, т. е. переменная1 − z, а переменная2 − y.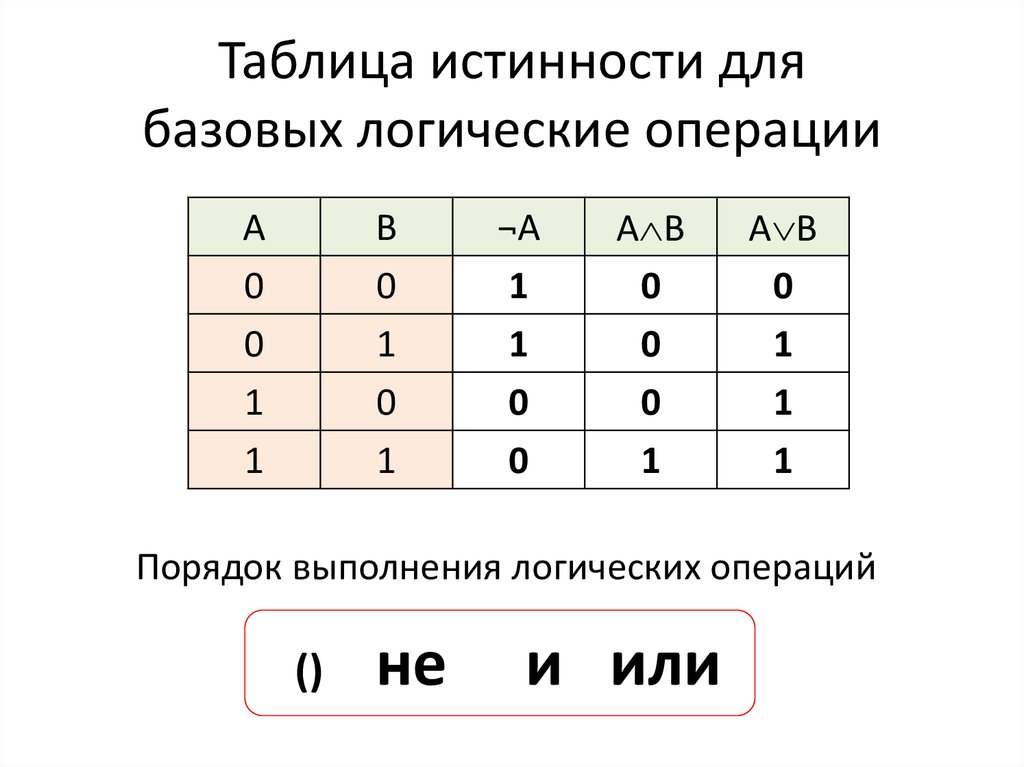
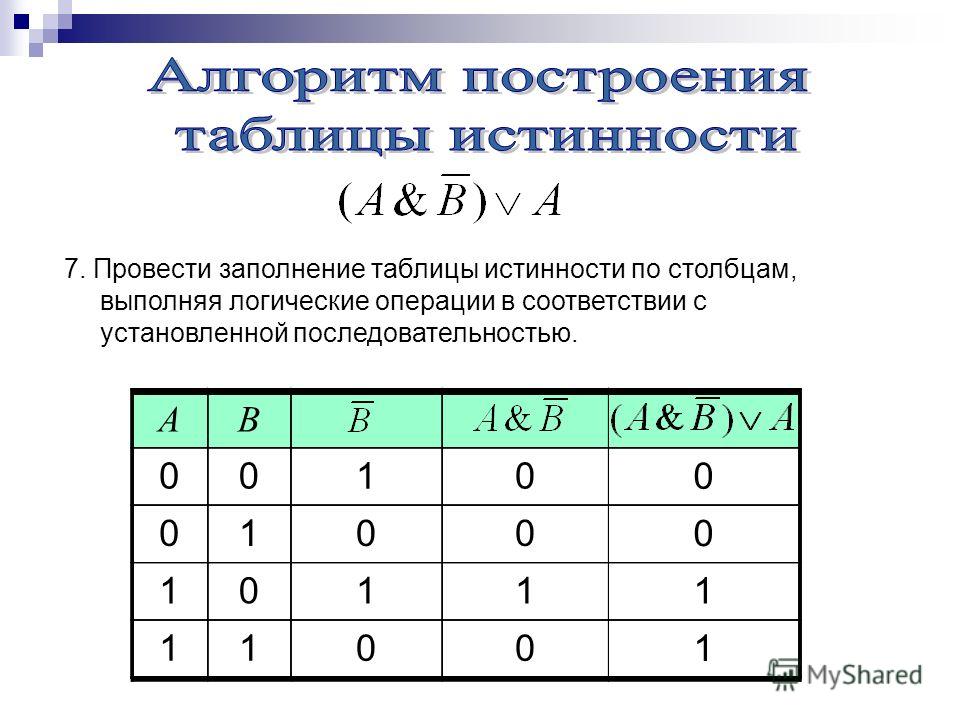
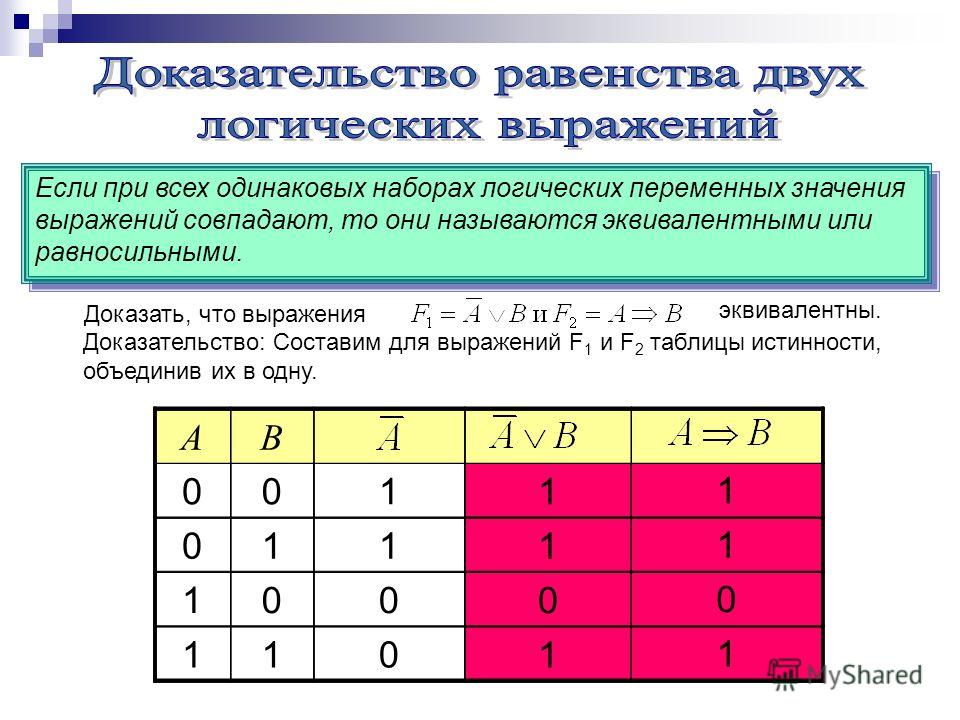

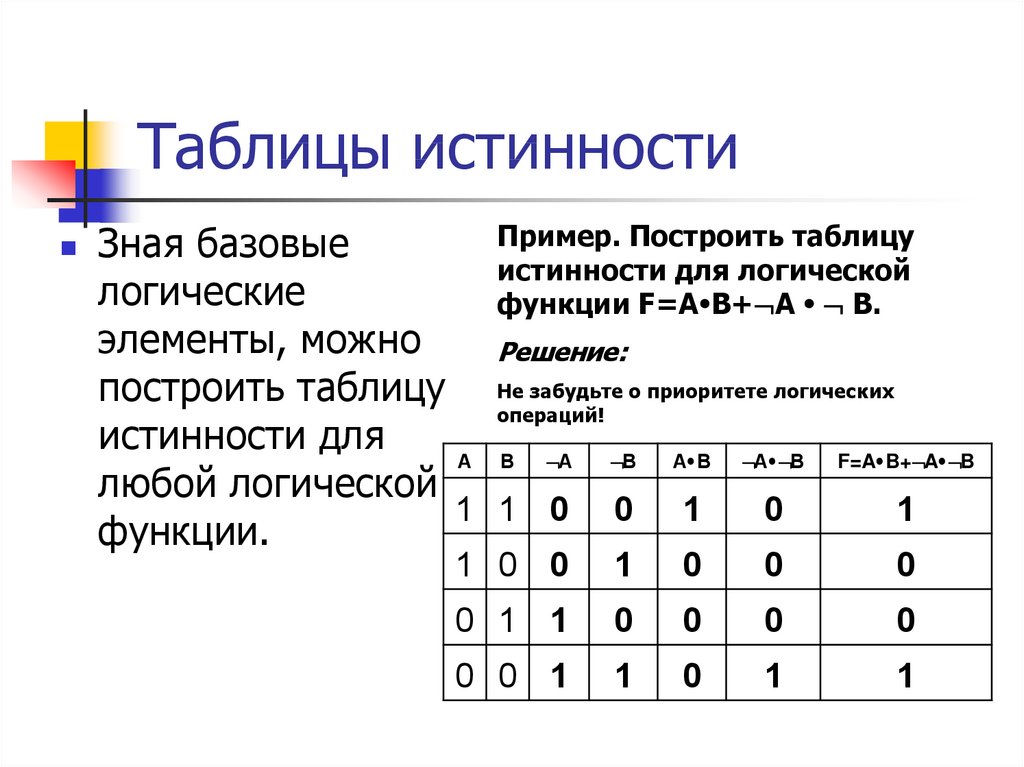
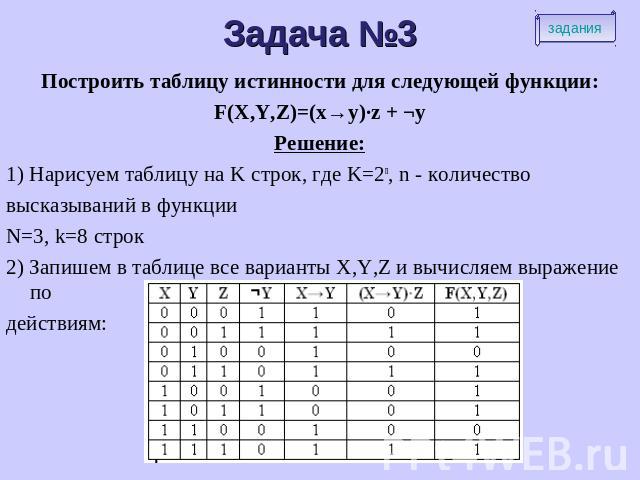
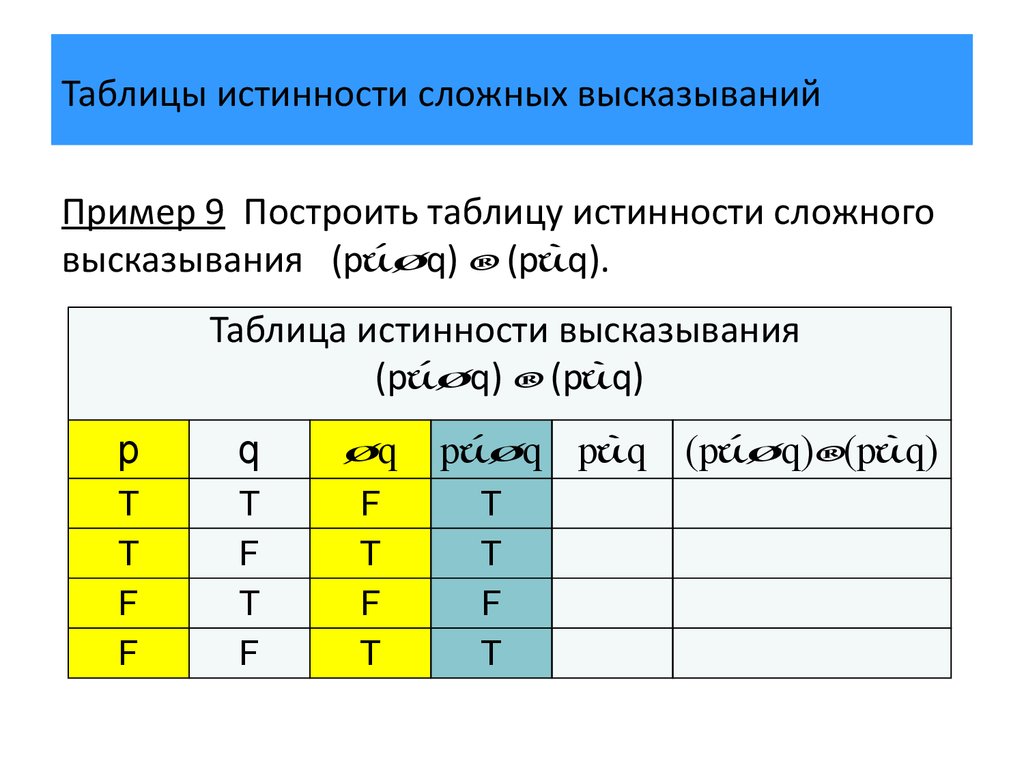 В размера 2 номер , причем входы расположены в возрастающем двоичном порядке.
В размера 2 номер , причем входы расположены в возрастающем двоичном порядке. 




 ..
.. ..
..