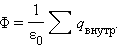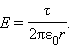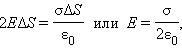Электростатический (кулоновский) потенциал. Потенциал поля точечного заряженного тела (№1) | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Особенности электрического взаимодействия имеют много общего с гравитационными. В частности, работа силы тяжести и работа электрической силы выражаются подобными зависимостями.
Для силы тяготения:
A = mg(h1 — h2) = -(mgh1 — mgh2).
Для электрической силы:
A = qE(l1 — l2) = -(qEl2 — qEl1).
Из этого можно сделать вывод, что работа электрической силы равна изменению потенциальной энергии тела, взятой с противоположным знаком. То есть заряженное тело в однородном электрическом поле имеет потенциальную энергию
Wp = qEl.
Заряженное тело в электростатическом поле имеет потенциальную энергию.
Потенциальная энергия заряженного тела определяется как электрическими характеристиками тела (его заряд), так и характеристиками выбранной точки электрического поля — напряженность и координата. Изменение одной из трех характеристик ведет к изменению
Значение потенциальной энергии заряженного тела зависит от его заряда, напряженности электрического поля и координаты.
Исследуем одну из точек электрического поля с целью определения ее энергетических характеристик. Для этого проведем несколько мысленных экспериментов с точечным заряженным телом.
Пусть точечное тело имеет заряд q1 и находится в поле напряженностью E̅ на расстоянии l от источника поля. Его потенциальная энергия будет равна
Wp1 = q1El.
Увеличим значение заряда в 2 раза. Его потенциальная энергия будет
Wp2 = 2q1El.
Таким образом, потенциальная энергия тела увеличится в 2 раза. Любые изменения заряда тела ведут к соответствующему изменению его потенциальной энергии. Но в каждом случае отношение потенциальной энергии заряженного тела к его электрическому заряду в данной точке поля будет оставаться постоянным
Wp / q = φ.
Величина φ называется
φ = qEl / q = El.
В значении потенциала отсутствуют характеристики тела, в том числе и его заряд. Поэтому можно считать справедливым утверждение, что потенциал является характеристикой электрического поля.
Физическая величина, которая является энергетической характеристикой электрического поля и равна отношению потенциальной энергии заряженного тела в электрическом поле к его заряду, называется потенциалом
φ = Wp / q,
где Wp — потенциальная энергия заряженного тела; q — заряд тела.
При измерении потенциала пользуются единицей, которая называется вольтом (В). Единица названа в честь итальянского ученого Алессандро Вольта.
Алессандро Вольта (1745 — 1825) — итальянский физик и физиолог, один из основателей учения об электрическом токе. Изобрел смоляной электрофор, чувствительный электроскоп с конденсатором, первый химический источник электрического тока, проводил широкие исследования электрических возбуждений мышц и нервов.
В соответствии с определением
1 В = 1 Дж / 1 Кл.
Применяются также кратные и дольные единицы потенциала:
1 милливольт = 1 мВ = 10-3 В;
1 микровольт = 1 мкВ = 10-6 В;
1 киловольт = 1 кВ = 103 В;
1 мегавольт = 1 MB = 106 В.
Все вышеизложенные соображения касаются однородного поля, напряженность которого не зависит от координаты точки наблюдения.
Но их можно распространить и на другие случаи, в частности на электрическое поле точечного заряженного тела. Оно неоднородно, напряженность изменяется от точки к точке вдоль силовых линий по закону
E = (1 / 4πε0) • (q / r2).
Воспользуемся определением потенциала точки электрического поля:
φ = El = (1 / 4πε0) • (q • l / r2)
Учитывая, что l = r, получим
φ = (1 / 4πε0) • (q / r).
Потенциал поля точечного заряженного тела уменьшается обратно пропорционально расстоянию.
Потенциал является скалярной величиной и не имеет направления. Поэтому можно говорить, что вокруг точечного заряженного тела существует бесконечно большое множество точек, в которых потенциалы будут одинаковы. Все они будут лежать на сферической поверхности радиуса r с центром в источнике поля. Такую поверхность называют эквипотенциальной. Материал с сайта http://worldofschool.ru
| Рис. 4.60. Потенциал является аддитивной величиной |
На понятие потенциала распространяется
φA = φ1 + φ2 — φ3.
В общем случае
φ = φ1 + φ2 + φ3 + … + φn.
Для измерения потенциала можно использовать электрометр, который в этом случае называют
Кулоновский потенциальная энергия
Как определяется потенциал точечного заряженного тела
Як визначається потенціал точкового зарядженого тіла?
Урок физики. потенциальная энергия заряженного тела. потенциал
Почему заряженное тело в электрическом поле имеет потенциальную энергию?
От чего зависит потенциальная энергия заряженного тела в электрическом поле?
Какое свойство поля характеризует потенциал?
Как определяется потенциал поля точечного заряженного тела?
Какие единицы измерения потенциала?
Каким прибором можно измерять потенциал?
Как применяется принцип суперпозиции к потенциалу?
1.3. Потенциал электростатического поля
Рассмотрим
электрическое поле одиночного точечного
электрического заряда 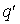 :
:
| (1.17) |
где 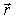 —
вектор, проведенный из точки расположения
заряда
—
вектор, проведенный из точки расположения
заряда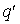 в
точку наблюдения,
в
точку наблюдения,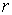 —
модуль вектора
—
модуль вектора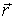 .
Если в точке наблюдения помещен точечный
заряд
.
Если в точке наблюдения помещен точечный
заряд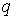 ,
то по определению понятия «напряженность
электрического поля» имеем
,
то по определению понятия «напряженность
электрического поля» имеем
| (1.18) |
где 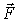 —
сила, действующая на точечный заряд
—
сила, действующая на точечный заряд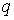 со
стороны электрического поля
со
стороны электрического поля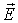 .
Располагая зависимостью(1.18),
легко написать выражение для элементарной
работы
.
Располагая зависимостью(1.18),
легко написать выражение для элементарной
работы 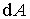
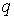 из
точки М1,
описываемой вектором
из
точки М1,
описываемой вектором 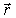 ,
в соседнюю точку М2,
описываемую вектором
,
в соседнюю точку М2,
описываемую вектором 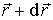 :
:
| (1.19) |
Элементарное
смещение 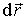 заряда
заряда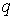 можно
разложить на составляющую
можно
разложить на составляющую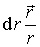 ,
параллельную вектору
,
параллельную вектору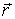 ,
и на составляющую
,
и на составляющую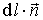 ,
перпендикулярную вектору
,
перпендикулярную вектору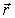 (рис.
1.4):
(рис.
1.4):
| (1.20) | |
| ||
Рис.
1.4.
Схема элементарного перемещения
точечного заряда в электростатическом
поле заряда | ||
где 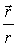 —
орт направления вдоль
—
орт направления вдоль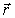 ,
,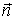 —
орт направления, перпендикулярного
направлению
—
орт направления, перпендикулярного
направлению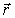 .
По построению имеем
.
По построению имеем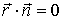 .
В этом случае элементарная работа сил
поля по перемещению заряда
.
В этом случае элементарная работа сил
поля по перемещению заряда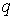 с
учетом соотношения(1.19) описывается выражением:
с
учетом соотношения(1.19) описывается выражением:
| (1.21) |
При
перемещении постоянного точечного
заряда 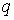 из
положения 1 в положение 2 имеем
из
положения 1 в положение 2 имеем
| (1.22) |
Если
перемещение заряда заканчивается в
исходной точке, то, очевидно, 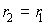 и
мы получаем
и
мы получаем
| (1.23) |
где индексом «0» помечено, что перемещение осуществлялось по замкнутому контуру.
Поскольку электрическое поле образовано системой неподвижных зарядов, для каждого из них соотношение (1.23) справедливо, то можно утверждать, что описанным выше свойством потенциальности обладает произвольное электростатическое поле.
Рассмотрим некоторые следствия из установленного принципа.
Если 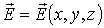 произвольное
векторное электростатическое поле;
произвольное
векторное электростатическое поле;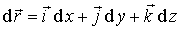 —
направленный отрезок контура
—
направленный отрезок контура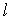 ,
то работу электростатического поля по
перемещению положительного единичного
точечного заряда можно описать с помощью
криволинейного интеграла
,
то работу электростатического поля по
перемещению положительного единичного
точечного заряда можно описать с помощью
криволинейного интеграла
| (1.24) |
Циркуляцией
вектора 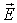 по
замкнутому контуру называют величину
по
замкнутому контуру называют величину
| (1.25) |
В
силу установленного выше принципа
потенциальности электростатического
поля выражение (1.25) должно обращаться в нуль для любого
замкнутого контура 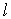 :
:
| (1.26) |
Условие (1.26) играет важную роль в электростатике: электростатическое поле реально существует, если только для него выполнено интегральное условие потенциальности (1.26).
Заметим,
что условие (1.26) будет выполнено, если дифференциальная
форма Пфаффа 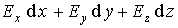 является
полным дифференциалом. Последнее влечет
за собой необходимость выполнения
совокупности условий:
является
полным дифференциалом. Последнее влечет
за собой необходимость выполнения
совокупности условий:
| (1.27) |
Условия (1.27) являются дифференциальными (локальными)
условиями потенциальности поля 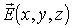 .
Поле
.
Поле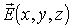 является
потенциальным в области, если условия(1.27) выполнены в каждой точке этой области.
является
потенциальным в области, если условия(1.27) выполнены в каждой точке этой области.
Условия (1.27) можно компактно записать в векторной
форме, если ввести в рассмотрение вектор
«ротор» напряженности электрического
поля 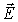 :
:
| (1.28) |
где  —
орты декартовой системы координат,
определитель в(1.28) раскрывается по обычному правилу с тем
условием, что дифференциальные операторы
не должны стоять после функций
—
орты декартовой системы координат,
определитель в(1.28) раскрывается по обычному правилу с тем
условием, что дифференциальные операторы
не должны стоять после функций 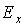 ,
,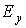 ,
,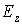 .
.
С использованием определения (1.28) условие потенциальности имеет вид:
| (1.29) |
Внутренняя связь условий (1.26) и (1.29) проявляется при рассмотрении теоремы Стокса:
| (1.30) |
где 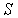 —
произвольная гладкая поверхность,
натянутая на контур
—
произвольная гладкая поверхность,
натянутая на контур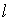 ,
а направление нормали
,
а направление нормали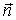 к
элементу площади поверхности
к
элементу площади поверхности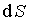 выбрано
так, чтобы с конца вектора
выбрано
так, чтобы с конца вектора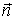 обход
контура
обход
контура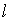 осуществлялся
против часовой стрелки.
осуществлялся
против часовой стрелки.
Если
левая часть соотношения (1.30) равна нулю, то для произвольной поверхности 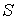 это
эквивалентно требованию условия(1.29).
это
эквивалентно требованию условия(1.29).
Заметим,
что теорема Стокса (1.30) служит основой для формального определения
компонент вектора  безотносительно
к выбору системы координат:
безотносительно
к выбору системы координат:
| (1.31) |
Соотношением (1.31) определяется математический смысл понятия (1.28).
Потенциал электростатического поля вводят соотношением
| (1.32) |
Легко
видеть, что дифференциал потенциала 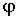 равен
элементарной работе против сил
электростатического поля, совершаемой
над единичным точечным зарядом на
перемещении
равен
элементарной работе против сил
электростатического поля, совершаемой
над единичным точечным зарядом на
перемещении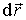 .
.
Если
в определении (1.32) учесть, что 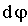 —
полный дифференциал, т.е.:
—
полный дифференциал, т.е.:
| (1.33) |
и сравнить соответствующие члены в формулах (1.32) и (1.33), то легко получить:
| (1.34) |
В компактной форме записи формулы (1.34) имеют вид:
| (1.35) |
где
вектор 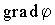 определен
соотношениями:
определен
соотношениями:
| (1.36) |
Градиент скалярного поля выделяет направление наискорейшего возрастания скалярной функции, а его модуль численно равен максимальной интенсивности возрастания этой функции.
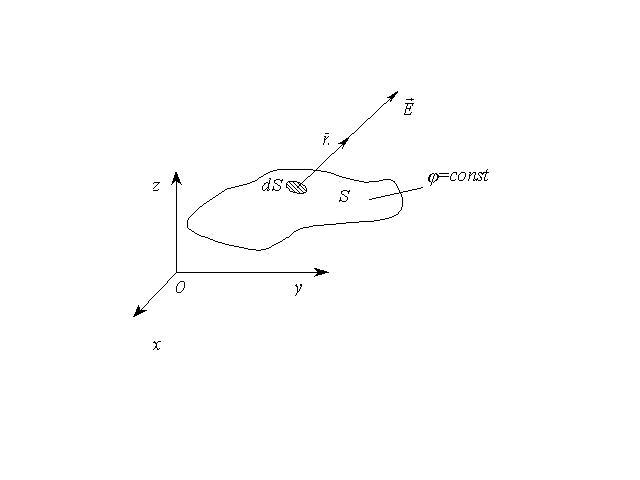
Скалярное поле часто описывают с помощью «поверхностей уровня», эквипотенциальных или изоповерхностей, которые определяются уравнением
| (1.37) |
На эквипотенциальной поверхности
| (1.38) |
что можно переписать в векторном виде:
| (1.39) |
| |
Рис. 1.5. Эквипотенциальная поверхность и вектор напряженности электростатического поля | |
где 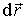 принадлежит
поверхности
принадлежит
поверхности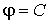 .
Из условия(1.39) следует, что вектор
.
Из условия(1.39) следует, что вектор  перпендикулярен
любому вектору
перпендикулярен
любому вектору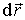 ,
принадлежащему поверхности
,
принадлежащему поверхности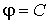 ,
то есть перпендикулярен элементу площади
поверхности
,
то есть перпендикулярен элементу площади
поверхности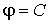 .
.
Если при этом вспомнить, что справедливо соотношение (1.35), то получим утверждение, что силовые линии электростатического поля должны быть перпендикулярны соответствующим элементам площади эквипотенциальной поверхности.
Заметим, что иногда встречается обозначение
| (1.40) |
где 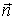 —
вектор единичной нормали (величина
безразмерная!) к поверхности
—
вектор единичной нормали (величина
безразмерная!) к поверхности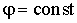 в
точке, в которой вычисляется вектор
в
точке, в которой вычисляется вектор ,
ориентированный в сторону увеличения
,
ориентированный в сторону увеличения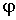 ;
;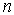 —
обозначение координаты (
—
обозначение координаты (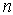 — величина, имеющая размерность длины)
вдоль направления
— величина, имеющая размерность длины)
вдоль направления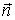 .
Таким образом
.
Таким образом —
вектор, направленный вдоль описанного
выше направления
—
вектор, направленный вдоль описанного
выше направления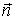 и
численно равный производной от величины
и
численно равный производной от величины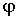 по
координате
по
координате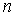 вдоль
этого направления.
вдоль
этого направления.
Соотношением (1.32) потенциал произвольной точки пространства определен с точностью до произвольной постоянной:
| (1.41) |
При
решении большого числа задач (но не
всех!) удобно считать, что точка с
координатами 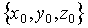 расположена
«на бесконечности», а потенциал ее
равен нулю.
расположена
«на бесконечности», а потенциал ее
равен нулю.
Следует иметь в виду, что «силовое» проявление электростатического поля (формула (1.35)) связано с производными от потенциала, при этом нет нужды учитывать «произвольную постоянную». В задачах, использующих энергетические характеристики отдельных элементов системы, необходимо иметь в виду, что потенциальная энергия системы определяется с точностью до одной произвольной постоянной, поэтому выбор произвольных постоянных для подсистем не может быть произвольным: энергии подсистем должны рассчитываться от одного уровня.
Задача 1.
Проверить условие потенциальности (1.27) для вектора напряженности электростатического поля, образованного точечным электрическим зарядом, расположенным в произвольной точке пространства.
Задача 2. Используя определение ротора векторного поля в символической форме записи (1.31), получить выражения для его физических компонент в декартовой, цилиндрической и сферической системе координат.
Работа электростатического поля. Потенциал. Эквипотенциальные поверхности
Работа электростатического поля. Потенциал. Эквипотенциальные поверхности
Электростатическое поле — это электрическое поле неподвижного заряда.
Сила F эл, действующая на заряд, перемещает его, совершая раборту.
В однородном электрическом поле Fэл = qE — постоянная величина
Работа поля (электрической силы) не зависит от формы траектории и на замкнутой траектории равна нулю.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
Электростатическая энергия — потенциальная энергия системы заряженных тел (т.к. они взаимодействуют и способны совершить работу).
Так как работа поля не зависит от формы траектории, то одновременно
Сравнивая формулы работы, получим потенциальную энергию заряда в однородном электростатическом поле
Если поле совершает положительную работу ( вдоль силовых линий ), то потенциальная энергия заряженного тела уменьшается (но согласно закону сохранения энергии увеличивается кинетическая энергия ) и наоборот.
ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
-энергитическая характеристика электрического поля.
— равен отношению потенциальной энергии заряда в поле к этому заряду.
— скалярная величина, определяющая потенциальную энергию заряда в любой точке электрического поля.
Величина потенциала считается относительно выбранного нулевого уровня.
РАЗНОСТЬ ПОТЕНЦИАЛОВ ( или иначе НАПРЯЖЕНИЕ )
— это разность потенциалов в начальной и конечной точках траектории заряда.
Напряжение между двумя точками ( U ) равно разности потенциалов этих точек и равно работе поля по перемещению единичного заряда.
СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ
Чем меньше меняется потенциал на отрезке пути, тем меньше напряженность поля.
Напряженность электрического поля направлена в сторону уменьшения потенциала.
ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ
— поверхности, все точки которых имеют одинаковый потенциал
для однородного поля — это плоскость
для поля точечного заряда — это концентрические сферы
Эквипотенциальная поверхность имеется у любого проводника в электростатическом поле, т.к. силовые линии перпендикулярны поверхности проводника.
Все точки внутри проводника имеют одинаковый потенциал ( =0).
Напряженность внутри проводника = 0, значит и разность потенциалов внутри = 0.
Электростатика и законы постоянного тока — Класс!ная физика
Электрический заряд. Электризация. Закон сохранения электрического заряда. Закон Кулона. Единица электрического заряда —
Близкодействие и дальнодействие. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей. Силовые линии электрического поля —
Проводники и диэлектрики в электростатическом поле. Поляризация диэлектриков
—
Потенциальная энергия тела в электростатическом поле. Потенциал электростатического поля и разность потенциалов. Связь между напряженностью электростатического поля и разхностью потенциалов —
Электроемкость. Конденсаторы. Энергия заряженного конденсатора —
Электрический ток. Сила тока. Условия, необходимые для существования электрического тока. Закон Ома для участка цепи. Сопротивление —
Работа и мощность тока
Потенциал электростатического поля. Общее выражение, связывающее потенциал с напряженностью.
Потенциал φ в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку. Потенциал поля, создаваемого точечным зарядом Q, равен
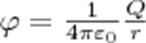
Потенциал — физическая величина, которая определяется работой по перемещению единичного положительного электрического заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, которую совершают внешние силы (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.
Единица потенциала — вольт (В): 1 В равен потенциалу такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В = 1 Дж/Кл). Учитывая размерность вольта, можно показать, что введенная ранее единица напряженности электростатического поля действительно равна 1 В/м: 1 Н/Кл=1 Н•м/(Кл•м)=1 Дж/(Кл•м)=1 В/м.
Из формул (3) и (4) следует, что если поле создается несколькими зарядами, то потенциал данного поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:
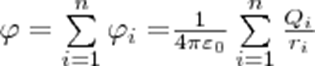
Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала.
E = — grad фи = — N фи.
Для установления связи между силовой характеристикой электрического поля — напряжённостью и его энергетической характеристикой — потенциалом рассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q: dA = q E dl, эта же работа равна убыли потенциальной энергии заряда q: dA = — dWп = — q dфи , где d фи — изменение потенциала электрического поля на длине перемещения dl. Приравнивая правые части выражений, получаем: E dl = -d фи или в декартовой системе координат
Ex dx + Ey dy + Ez dz = -d фи
где Ex, Ey, Ez — проекции вектора напряженности на оси системы координат. Поскольку выражение представляет собой полный дифференциал, то для проекций вектора напряженности имеем
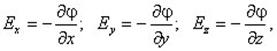
Откуда
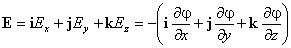
Стоящее в скобках выражение является градиентом потенциала фи.
Принцип суперпозиции как фундаментальное свойство полей. Общие выражения для напряженности и потенциала поля, создаваемого в точке с радиус-вектором системой точечных зарядов, находящихся в точках с координатами.(см п.4)
Если рассмотреть принцип суперпозиции в самом общем смысле, то согласно ему, сумма воздействия внешних сил, действующих на частицу, будет складываться из отдельных значений каждой из них. Данный принцип применяется к различным линейным системам, т.е. таким системам, поведение которых можно описать линейными соотношениями. Примером может послужить простая ситуация, когда линейная волна распространяется в какой-то определённой среде, в этом случае её свойства будут сохраняться даже под действием возмущений, возникающих из-за самой волны. Эти свойства определяются как конкретная сумма эффектов каждой из гармоничных составляющих.
Принцип суперпозиции может принимать и иные формулировки, которые полностью эквивалентны приведённой выше:
· Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя.
· Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.
· Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.
6 Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L
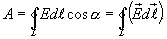
Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.
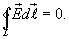
Потенциал поля. Работа любого электростатического поля при перемещении в нем заряженного тела из одной точки в другую также не зависит от формы траектории, как и работа однородного поля. На замкнутой траектории работа электростатического поля всегда равна нулю. Поля, обладающие таким свойством, называют потенциальными. Потенциальный характер, в частности, имеет электростатическое поле точечного заряда.
Работу потенциального поля можно выразить через изменение потенциальной энергии. Формула 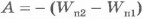 справедлива для любого электростатического поля.
справедлива для любого электростатического поля.
7-11Если силовые линии однородного электрического поля напряженностью 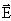 пронизывают некоторую площадку S, то поток вектора напряженности (раньше мы называли число силовых линий через площадку) будет определяться формулой:
пронизывают некоторую площадку S, то поток вектора напряженности (раньше мы называли число силовых линий через площадку) будет определяться формулой:
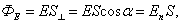 |
где En – произведение вектора 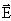 на нормаль
на нормаль 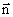 к данной площадке (рис. 2.5).
к данной площадке (рис. 2.5).
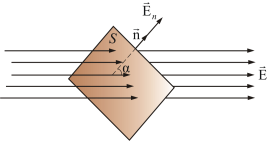
Рис. 2.5
Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности ФЕ через эту поверхность.
В векторной форме можно записать 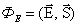 – скалярное произведение двух векторов, где вектор
– скалярное произведение двух векторов, где вектор 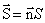 .
.
Таким образом, поток вектора 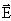 есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным.
есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным.
Рассмотрим примеры, изображенные на рисунках 2.6 и 2.7.
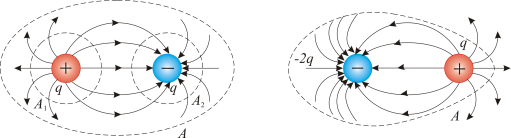 | |||
| Рис. 2.6 | Рис. 2.7 | ||
Для рисунка 2.6 – поверхность А1 окружает положительный заряд и поток здесь направлен наружу, т.е. 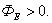 Поверхность А2– окружает отрицательный заряд, здесь
Поверхность А2– окружает отрицательный заряд, здесь 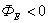 и направлен внутрь. Общий поток через поверхность А равен нулю.
и направлен внутрь. Общий поток через поверхность А равен нулю.
Для рисунка 2.7 – поток будет не равен нулю, если суммарный заряд внутри поверхности не равен нулю. Для этой конфигурации поток через поверхность А отрицательный (подсчитайте число силовых линий).
Таким образом, поток вектора напряженности зависит от заряда. В этом смысл теоремы Остроградского-Гаусса.
Теорема Гаусса
Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.
Введем новую физическую величину, характеризующую электрическое поле – поток Φ вектора напряженности электрического поля. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка ΔS. Произведение модуля вектора 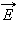 на площадь ΔS и на косинус угла α между вектором
на площадь ΔS и на косинус угла α между вектором 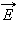 и нормалью
и нормалью 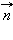 к площадке называется элементарным потоком вектора напряженности через площадку ΔS (рис. 1.3.1):
к площадке называется элементарным потоком вектора напряженности через площадку ΔS (рис. 1.3.1):
| ΔΦ = E ΔS cos α = En ΔS, |
где En – модуль нормальной составляющей поля 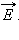
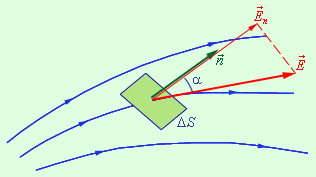 |
| Рисунок 1.3.1. К определению элементарного потока ΔΦ |
Рассмотрим теперь некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки ΔSi, определить элементарные потоки ΔΦi поля 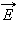 через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора
через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора 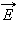 через замкнутую поверхность S (рис. 1.3.2):
через замкнутую поверхность S (рис. 1.3.2):
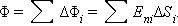 |
В случае замкнутой поверхности всегда выбирается внешняя нормаль.
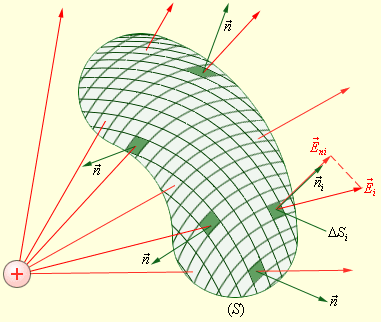 |
| Рисунок 1.3.2. Вычисление потока Ф через произвольную замкнутую поверхность S |
Теорема Гаусса утверждает:
Поток вектора напряженности электростатического поля 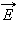 через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
|
Для доказательства рассмотрим сначала сферическую поверхность S, в центре которой находится точечный заряд q. Электрическое поле в любой точке сферы перпендикулярно к ее поверхности и равно по модулю
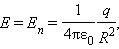 |
где R – радиус сферы. Поток Φ через сферическую поверхность будет равен произведению E на площадь сферы 4πR2. Следовательно, 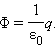
Окружим теперь точечный заряд произвольной замкнутой поверхностью S и рассмотрим вспомогательную сферу радиуса R0 (рис. 1.3.3).
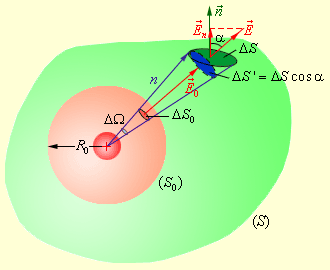 |
| Рисунок 1.3.3. Поток электрического поля точечного заряда через произвольную поверхность S, окружающую заряд |
Рассмотрим конус с малым телесным углом ΔΩ при вершине. Этот конус выделит на сфере малую площадку ΔS0, а на поверхности S – площадку ΔS. Элементарные потоки ΔΦ0 и ΔΦ через эти площадки одинаковы. Действительно,
| ΔΦ0 = E0ΔS0, ΔΦ = EΔS cos α = EΔS ‘. |
Здесь ΔS’ = ΔS cos α – площадка, выделяемая конусом с телесным углом ΔΩ на поверхности сферы радиуса n.
Так как 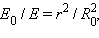 а
а 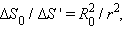 следовательно
следовательно 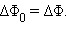 Отсюда следует, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ0 через поверхность вспомогательной сферы:
Отсюда следует, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ0 через поверхность вспомогательной сферы:
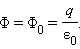 |
Аналогичным образом можно показать, что, если замкнутая поверхность S не охватывает точечного заряда q, то поток Φ = 0. Такой случай изображен на рис. 1.3.2. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, поэтому в этой области силовые линии не обрываются и не зарождаются.
Обобщение теоремы Гаусса на случай произвольного распределения зарядов вытекает из принципа суперпозиции. Поле любого распределения зарядов можно представить как векторную сумму электрических полей 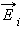 точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S будет складываться из потоков Φi электрических полей отдельных зарядов. Если заряд qi оказался внутри поверхности S, то он дает вклад в поток, равный
точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S будет складываться из потоков Φi электрических полей отдельных зарядов. Если заряд qi оказался внутри поверхности S, то он дает вклад в поток, равный 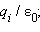 если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю.
если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю.
Таким образом, теорема Гаусса доказана.
Теорема Гаусса является следствием закона Кулона и принципа суперпозиции. Но если принять утверждение, содержащееся в этой теореме, за первоначальную аксиому, то ее следствием окажется закон Кулона. Поэтому теорему Гаусса иногда называют альтернативной формулировкой закона Кулона.
Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать.
Примером может служить задача о вычислении поля тонкостенного полого однородно заряженного длинного цилиндра радиуса R. Эта задача имеет осевую симметрию. Из соображений симметрии электрическое поле должно быть направлено по радиусу. Поэтому для применения теоремы Гаусса целесообразно выбрать замкнутую поверхность S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов (рис. 1.3.4).
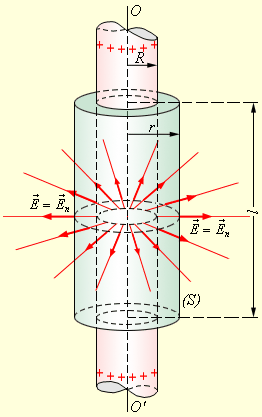 |
| Рисунок 1.3.4. Вычисление поля однородно заряженного цилиндра. OO’ – ось симметрии |
При r ≥ R весь поток вектора напряженности будет проходить через боковую поверхность цилиндра, площадь которой равна 2πrl, так как поток через оба основания равен нулю. Применение теоремы Гаусса дает:
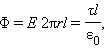 |
где τ – заряд единицы длины цилиндра. Отсюда
|
Этот результат не зависит от радиуса R заряженного цилиндра, поэтому он применим и к полю длинной однородно заряженной нити.
Для определения напряженности поля внутри заряженного цилиндра нужно построить замкнутую поверхность для случая r < R. В силу симметрии задачи поток вектора напряженности через боковую поверхность гауссова цилиндра должен быть и в этом случае равен Φ = E 2πrl. Согласно теореме Гаусса, этот поток пропорционален заряду, оказавшемуся внутри замкнутой поверхности. Этот заряд равен нулю. Отсюда следует, что электрическое поле внутри однородно заряженного длинного полого цилиндра равно нулю.
Аналогичным образом можно применить теорему Гаусса для определения электрического поля в ряде других случаев, когда распределение зарядов обладает какой-либо симметрией, например, симметрией относительно центра, плоскости или оси. В каждом из таких случаев нужно выбирать замкнутую гауссову поверхность целесообразной формы. Например, в случае центральной симметрии гауссову поверхность удобно выбирать в виде сферы с центром в точке симметрии. При осевой симметрии замкнутую поверхность нужно выбирать в виде соосного цилиндра, замкнутого с обоих торцов (как в рассмотренном выше примере). Если распределение зарядов не обладает какой-либо симметрией и общую структуру электрического поля угадать невозможно, применение теоремы Гаусса не может упростить задачу определения напряженности поля.
Рассмотрим еще один пример симметричного распределения зарядов – определение поля равномерно заряженной плоскости (рис. 1.3.5).
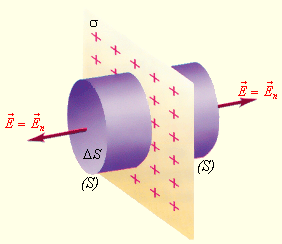 |
| Рисунок 1.3.5. Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность |
В этом случае гауссову поверхность S целесообразно выбрать в виде цилиндра некоторой длины, закрытого с обоих торцов. Ось цилиндра направлена перпендикулярно заряженной плоскости, а его торцы расположены на одинаковом расстоянии от нее. В силу симметрии поле равномерно заряженной плоскости должно быть везде направлено по нормали. Применение теоремы Гаусса дает:
|
где σ – поверхностная плотность заряда, т. е. заряд, приходящийся на единицу площади.
Полученное выражение для электрического поля однородно заряженной плоскости применимо и в случае плоских заряженных площадок конечного размера. В этом случае расстояние от точки, в которой определяется напряженность поля, до заряженной площадки должно быть значительно меньше размеров площадки.
И графики к 7 – 11
1. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью.
Пусть сферическая поверхность радиуса R (рис. 13.7) несет на себе равномерно распределенный заряд q, т.е. поверхностная плотность 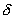 заряда в любой точке сферы будет одинакова.
заряда в любой точке сферы будет одинакова.
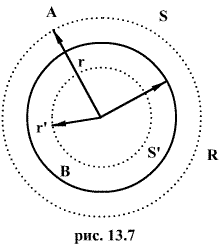
a. Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R. Поток вектора напряженности через поверхность S будет равен
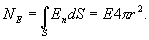
По теореме Гаусса
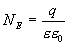
Следовательно
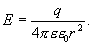 | (13.8) |
Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре.
b. Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать
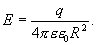 | (13.9) |
c. Проведем через точку В, находящуюся внутри заряженной сферической поверхности, сферу S радиусом г<R. Внутри сферы S зарядов нет, т.к. все они расположены на внешней сферической поверхности, т.е. 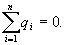 Следовательно, по теореме Гаусса,
Следовательно, по теореме Гаусса, 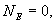 и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю. Зависимость напряженности поля заряженной сферы от расстояния r приведена на рис. 13.8.
и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю. Зависимость напряженности поля заряженной сферы от расстояния r приведена на рис. 13.8.
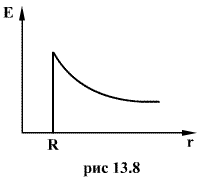
2. Электростатическое поле шара.
Пусть имеем шар радиуса R, равномерно заряженный с объемной плотностью . 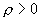
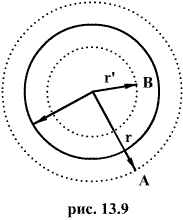
В любой точке А, лежащей вне шара на расстоянии r от его центра (r>R), его поле аналогично полю точечного заряда 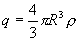 , расположенного в центре шара. Тогда вне шара
, расположенного в центре шара. Тогда вне шара
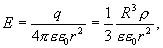 | (13.10) |
а на его поверхности (r=R)
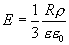 | (13.11) |
В точке В, лежащей внутри шара на расстояний r от его центра (r>R), поле определяется лишь зарядом 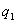 , заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен
, заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен
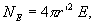
с другой стороны, в соответствии с теоремой Гаусса
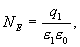
Из сопоставления последних выражений следует
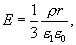 | (13.12) |
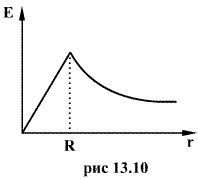
где 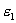 — диэлектрическая проницаемость внутри шара. Зависимость напряженности поля, создаваемого заряженной сферой, от расстояния до центра шара приведена на (рис.13.10)
— диэлектрическая проницаемость внутри шара. Зависимость напряженности поля, создаваемого заряженной сферой, от расстояния до центра шара приведена на (рис.13.10)
3. Напряженность поля равномерно заряженной бесконечной прямолинейной нити (или цилиндра).
Предположим, что полая цилиндрическая поверхность радиуса R заряжена с постоянной линейной плотностью 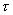 .
.
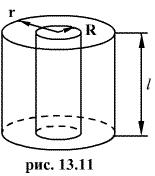
Проведем коаксиальную цилиндрическую поверхность радиуса 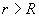 Поток вектора напряженности через эту поверхность
Поток вектора напряженности через эту поверхность
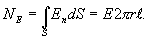
По теореме Гаусса
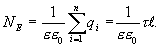
Из последних двух выражений определяем напряженность поля, создаваемого равномерно заряженной нитью:
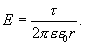 | (13.13) |
4. Напряженность поля, создаваемого, бесконечной равномерно заряженной плоскостью.
Пусть плоскость имеет бесконечную протяженность и заряд на единицу площади равен σ. Из законов симметрии следует, что поле направлено всюду перпендикулярно плоскости, и если не существует никаких других внешних зарядов, то поля по обе стороны плоскости должны быть одинаковы. Ограничим часть заряженной плоскости воображаемым цилиндрическим ящиком, таким образом, чтобы ящик рассекался пополам и его образующие были перпендикулярны, а два основания, имеющие площадь S каждое, параллельны заряженной плоскости (рис 1.10).
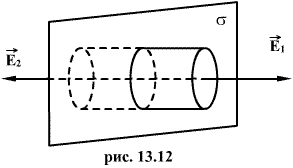
Суммарный поток вектора; напряженности равен вектору 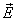 , умноженному на площадь S первого основания, плюс поток вектора
, умноженному на площадь S первого основания, плюс поток вектора 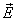 через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают. Таким образом,
через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают. Таким образом, 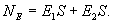 С другой стороны по теореме Гаусса
С другой стороны по теореме Гаусса
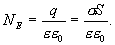
Следовательно
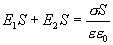
но 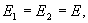 тогда напряженность поля бесконечной равномерно заряженной плоскости будет равна
тогда напряженность поля бесконечной равномерно заряженной плоскости будет равна
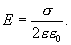 | (13.14) |
В это выражение не входят координаты, следовательно электростатическое поле будет однородным, а напряженность его в любой точке поля одинакова.
5. Напряженность поля, создаваемого двумя бесконечными параллельными плоскостями, заряженными разноименно с одинаковыми плотностями.
Как видно из рисунка 13.13, напряженность поля между двумя бесконечными параллельными плоскостями, имеющими поверхностные плотности зарядов 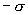 и
и 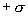 , равны сумме напряженностей полей, создаваемых пластинами, т.е.
, равны сумме напряженностей полей, создаваемых пластинами, т.е.
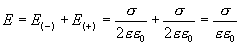
Таким образом,
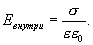 | (13.15) |
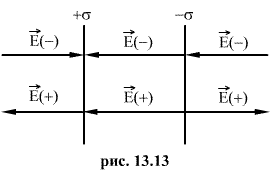 Вне пластины векторы
Вне пластины векторы 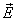 от каждой из них направлены в противоположные стороны и взаимно уничтожаются. Поэтому напряженность поля в пространстве, окружающем пластины, будет равна нулю Е=0.
от каждой из них направлены в противоположные стороны и взаимно уничтожаются. Поэтому напряженность поля в пространстве, окружающем пластины, будет равна нулю Е=0.
12. Поле равномерно заряженной сферы.
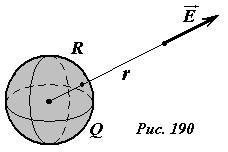
Пусть электрическое поле создается зарядом Q, равномерно распределенным по поверхности сферы радиуса R (Рис. 190). Для вычисления потенциала поля в произвольной точке, находящейся на расстоянии r от центра сферы, необходимо вычислить работу, совершаемую полем при перемещении единичного положительного заряда от данной точки до бесконечности. Ранее мы доказали, что напряженность поля равномерно заряженной сферы вне ее эквивалентно полю точечного заряда, расположенного в центре сферы. Следовательно, вне сферы потенциал поля сферы будет совпадать с потенциалом поля точечного заряда
φ(r)=Q4πε0r . (1)
В частности, на поверхности сферы потенциал равен φ0=Q4πε0R . Внутри сферы электростатическое поле отсутствует, поэтому работа по перемещению заряда из произвольной точки, находящейся внутри сферы, на ее поверхность равна нулю A = 0, поэтому и разность потенциалов между этими точками также равна нулю Δφ = —A = 0. Следовательно, все точки внутри сферы имеют один и тот же потенциал, совпадающий с потенциалом ее поверхности φ0=Q4πε0R .
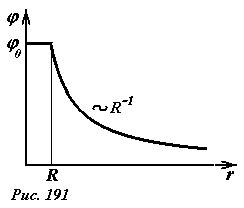
Итак, распределение потенциала поля равномерно заряженной сферы имеет вид (Рис. 191)
φ(r)=⎧⎩⎨Q4πε0R, npu r<RQ4πε0r, npu r>R . (2)
Обратите внимание, поле внутри сферы отсутствует, а потенциал отличен от нуля! Этот пример является яркой иллюстрацией, того, что потенциал определяется значением поля от данной точки до бесконечности.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
Тест по физике Работа сил электростатического поля. Потенциал электростатического поля для 10 класса
Тест по физике Работа сил электростатического поля. Потенциал электростатического поля для 10 класса с ответами. Тест включает в себя 2 варианта. В каждом варианте по 5 заданий.
1 вариант
1. В однородном электростатическом поле перемещается положительный заряд из точки М в точку N по разным траекториям (рис. 43). В каком случае работа сил электростатического поля больше?

А. 1
Б. 2
В. Во всех случаях работа сил электростатического поля одинакова.
2. На рисунке 44 показаны линии напряженности электростатического поля и две эквипотенциальные поверхности. В какой точке (М или N) потенциал больше?

А. В точке М
Б. В точке N
В. Потенциал в точках М и N одинаков
3. Как меняется кинетическая энергия электрона при его приближении к положительному заряду (рис. 45)?

А. Увеличивается
Б. Уменьшается
В. Не изменяется
4. На рисунке 46 представлена картина эквипотенциальных поверхностей некоторого электростатического поля. По какой траектории нужно перемещать электрический заряд из точки 1, чтобы работа сил поля была наибольшей?

А. По траектории 1-2
Б. По траектории 1-3
В. По всем траекториям одинакова
5. Напряженность электростатического поля между двумя точками в однородном электростатическом поле равна 100 В/м, а расстояние между ними 5 см. Чему равна разность потенциалов между этими точками?
А. 5 В
Б. 10 В
В. 20 В
2 вариант
1. В однородном электростатическом поле положительный заряд из точки М в точку N перемещается по разным траекториям (рис. 47). В каком случае работа сил электростатического поля больше?

А. 1
Б. 2
В. Во всех случаях работа сил электростатического поля одинакова
2. На рисунке 48 показаны линии напряженности электростатического поля и две эквипотенциальные поверхности. В какой точке (М или N) меньше потенциал?

А. Потенциал в точках М и N одинаков
Б. В точке N
В. В точке М
3. Как меняется кинетическая энергия электрона при его удалении от положительного заряда (рис. 49)?

А. Увеличивается
Б. Уменьшается
В. Не изменяется
4. На рисунке 50 представлена картина эквипотенциальных поверхностей некоторого электростатического поля. По какой траектории нужно перемещать электрический заряд из точки 1, чтобы работа электрических сил поля была наименьшей?

А. По траектории 1-2
Б. По траектории 1-3
В. По всем траекториям одинакова
5. Напряженность электростатического поля между двумя точками в однородном электростатическом поле равна 200 В/м, а расстояние между ними 4 см. Чему равна разность потенциалов между этими точками?
А. 8 В
Б. 100 В
В. 200 В
Ответы на тест по физике Работа сил электростатического поля. Потенциал электростатического поля для 10 класса
1 вариант
1-В
2-Б
3-А
4-В
5-А
2 вариант
1-В
2-Б
3-Б
4-В
5-А
Тест по теме «Потенциал электростатического поля»
Потенциал электростатического поля. Электроемкость
Вариант 1
Потенциал электростатического поля – это …
А) физическая величина, характеризующая способность тел к электрическим взаимодействиям
Б) энергетическая характеристика поля
В) силовая характеристика поля
Г) кинетическая энергия заряда в данной точке
Д) способность проводников накапливать электрический заряд
2. Электроемкость в системе СИ имеет размерность:
А) В Б) Кл В) Ф Г) В/Кл Д) Ф/Кл
3. Плоский воздушный конденсатор заряжен и отключен от источника тока. Как изменится напряжение между пластинами конденсатора, если расстояние между ними увеличить в 2 раза?
А) уменьшится в 2 раза Б) уменьшится в 4 раза В) увеличится в 4 раза Г) увеличится в 2 раза Д) не изменится
4. Как изменится электроемкость плоского конденсатора при уменьшении расстояния между пластинами в 2 раза и введении между пластинами диэлектрика с ε=4?
А) увеличится в 8 раз Б) увеличится в 2 раза В) не изменится Г) уменьшится в 2 раза Д) ) уменьшится в 8 раз
5. Конденсатор емкостью 20 мкФ заряжен до разности потенциалов 300 В. Энергия электрического поля конденсатора равна:
А) 1,8 Дж Б) 0,9 Дж В) 0,6 Дж Г)1,2 Дж Д) 3,6 Дж
6. Емкость конденсатора 5 мкФ, его энергия 0,1 Дж. Напряжение на обкладках конденсатора равно:
А) 100 В Б) 200 В В) 500 В Г) 2000 В Д) 250 В
7. На пластины конденсатора, расположенные на расстоянии 3 см, подано напряжение 300 В. Электрон, имеющий в некоторой точке скорость 2*106 м/с, пролетает против силовой линии 5 мм. Какую скорость он будет иметь в конце этого пути?
Потенциал электростатического поля. Электроемкость
Вариант 2
Электроемкость — это …
А) энергетическая характеристика поля
Б) способность проводников накапливать электрический заряд
В) силовая характеристика поля
Г) физическая величина, характеризующая работу по перемещению электрического заряда
Д) физическая величина, характеризующая способность тел к электрическим взаимодействиям
2. Электроемкость двух проводников вычисляется по формуле :
А) Uq Б) q/U В)F/q Г)U/q Д)Eq
3. Плоский воздушный конденсатор подключен к источнику постоянного напряжения. Как изменится электрически заряд на одной обкладке конденсатора при уменьшении расстояния между его пластинами в 2 раза?
А) уменьшится в 2 раза Б) уменьшится в 4 раза В) увеличится в 4 раза Г) увеличится в 2 раза Д) не изменится
4. Как изменится электроемкость плоского конденсатора при увеличении расстояния между пластинами в 2 раза и введении между пластинами диэлектрика с ε=4?
А) увеличится в 8 раз Б) увеличится в 2 раза В) не изменится Г) уменьшится в 2 раза Д) ) уменьшится в 8 раз
5. Плоскому конденсатору емкостью 50 пФ сообщен заряд 2*10-5 Кл. Энергия электрического поля конденсатора равна:
А) 0,4 Дж Б) 2 Дж В) 4 Дж Г) 8 Дж Д) 1 Дж
6. Емкость конденсатора 3 мкФ, его энергия 1,5 Дж. Заряд конденсатора равен:
А) 3*10-4 Кл Б)9*10-6 Кл В) 3*10-3 Кл Г) 9*10-4 Кл Д) 2*10-5 Кл
7. Электрон с начальной скоростью 1,8*104 м/с влетает в электрическое поле с напряженностью 3*10-3 В/м и движется против поля на расстояние 7,1 см. Какую скорость электрон будет иметь в конце этого пути?
как доказать,что электростатическое поле потенциально?
Потенциал электростатического поля.  Введенная функция U(x, y, z) (потенциальная энергия взаимодействия точного заряда и электрического поля) , естественно, зависит от свойств поля и от величины пробного заряда. Сила, действующая на заряженное тело, пропорциональна заряду, следовательно, работа и потенциальная энергия взаимодействия также пропорциональны величине пробного заряда. Поэтому если работу, по перемещению заряженного тела, разделить на величину пробного заряда, то получим характеристику поля (не зависящую от пробного заряда) . Аналогично, если разделить потенциальную энергию взаимодействия заряда с полем на величину заряда, то получим характеристику поля, которая называется потенциалом электрического поля. Итак, потенциалом электрического поля φ(x, y, z) называется отношение потенциальной энергии взаимодействия электрического поля и пробного точечного U(x, y, z) заряда к величине заряда: Отклонение пробного заряда в электростатическом поле и есть доказателство!
работа сил электростатического поля при перемещении заряженной частицы из одной точки в другую не зависит от формы траектории, а зависит лишь от начального и конечного положений частицы . Это означает, что электростатическое поле потенциально


 ,
,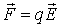 ,
, .
. ,
,
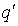 .
.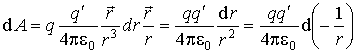 .
.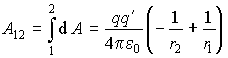 .
.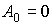 ,
,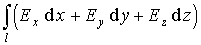 .
.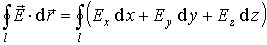 .
.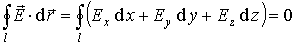 .
.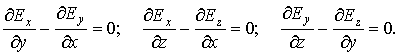
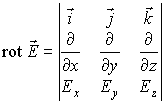 ,
,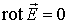 .
.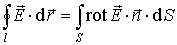 ,
,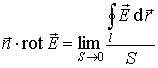 .
.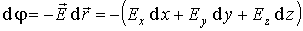 .
.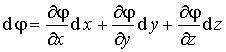 ,
,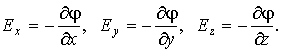
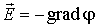 ,
,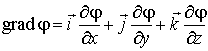 .
.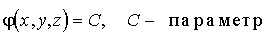 .
.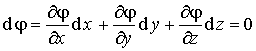 ,
,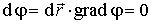 ,
,
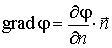 ,
,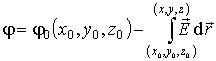 .
.