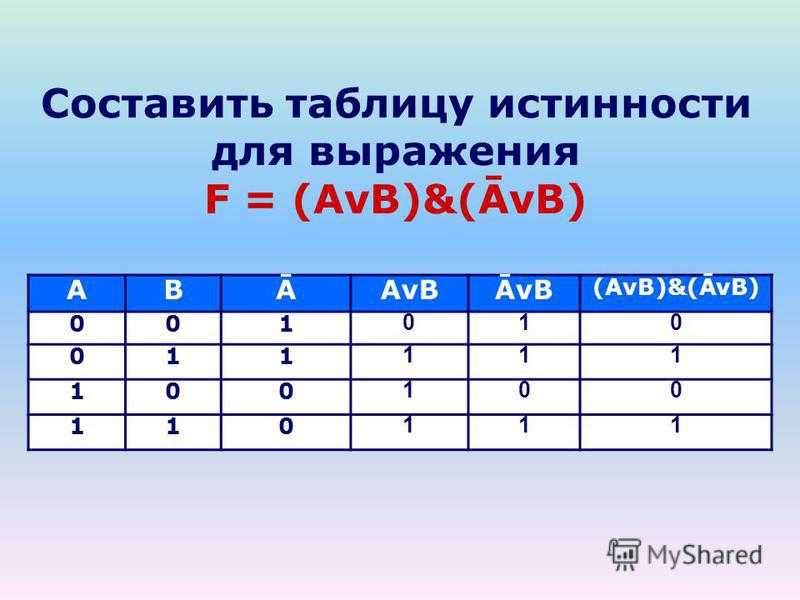
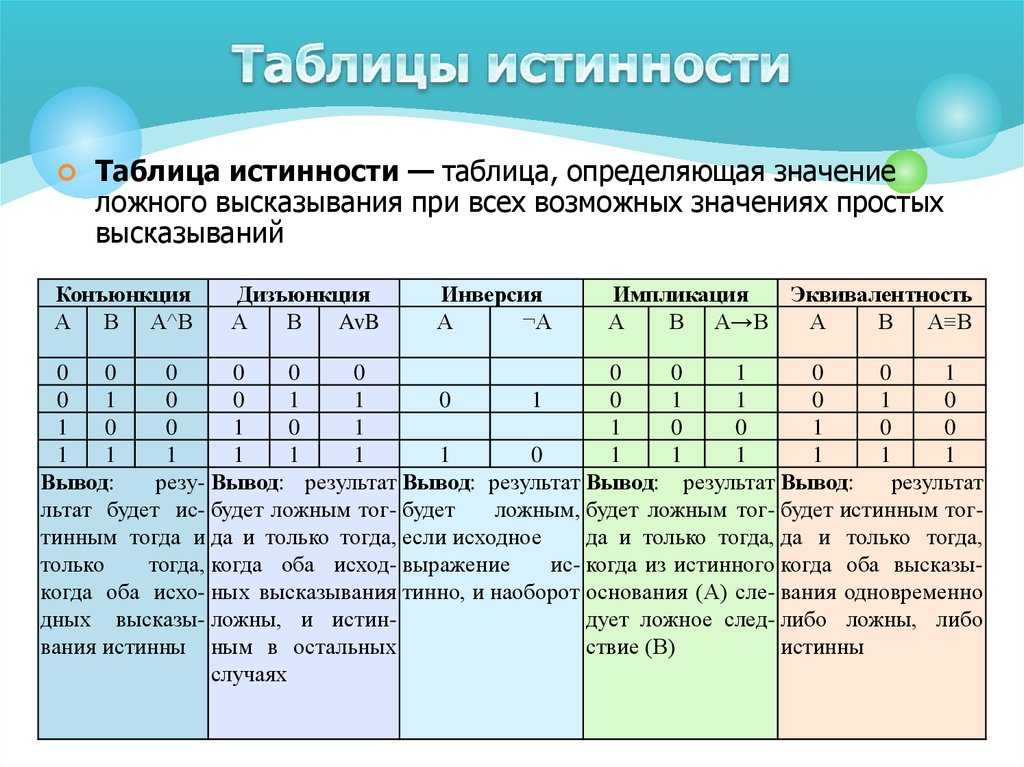
Дискретная математика 04
1. С помощью построения таблиц истинности доказать формулы:
=
Решение:
Построим таблицу истинности для правой и левой части формулы, принимая обозначения 0 – ложь, 1 – истина.
Так как значения правой и левой части на одинаковых наборах переменных совпадают, то формула
=
Является тавтологией, то есть верна для любых значений переменных.
Ответ: формула является тавтологией.
2. С помощью построения таблиц истинности проверить, является ли формула тавтологией:
Решение:
Формула является тавтологией, если на всех наборах переменных принимает значение «истина».
Построим таблицу истинности
Данная формула является противоречием, то есть ложна для любых наборов переменных.
Ответ: формула не является тавтологией.
3. Записать с помощью кванторов следующие утверждения и их отрицания.
Функция достигает наибольшего значения на отрезке в точке
Решение:
— исходное утверждение.
Отрицание утверждения:
Функция не достигает наибольшего значения на отрезке в точке .
.
Ответ: — утверждение, — отрицание утверждения.
4. Установить и изобразить графически область истинности предиката: ,
Решение:
Область определения предиката – числовая плоскость . Аргументы предиката – пары чисел (х, у). Условие задаёт прямую на плоскости у = х – 1.
Область истинности предиката — это прямая у = х – 1, на рисунке изображена линией синего цвета.
5. Пусть – натуральное число. Даны следующие утверждения:
· – “число кратно 5”;
· – “число кратно 2”;
· – “число кратно 4”;
· – “число кратно 10”;
· – “число кратно 20”.
Укажите, какое высказывание истинно, какое ложное
Решение:
— предикат, обозначающий “число не кратно 5”;
— предикат, обозначающий “число не кратно 20”.
— высказывание «если произвольное натуральное число не кратно 5, то оно также не кратно 20».
Так как условие кратности 5 является необходимым для выполнения условия кратности 20, то высказывание является истинным.
Ответ: высказывание истинно.
6. Построить вывод формулы
Решение:
Рассмотрим правила введения и удаления отрицания:
; .
Здесь G – некоторый набор формул (возможно, пустой), Х – одна формула.
Согласно закону исключённого третьего, или . Подставим вместо Х формулу ØА, получим
или . Обозначим во второй формуле , тогда получим . Воспользуемся правилом удаления отрицания
.
Отсюда, возвращаясь к А, получаем
.
И, по теореме дедукции, или .
Формула доказана.
7. Методом резолюций доказать теоремы
├
Решение:
Приведем отрицание доказываемого высказывания к конъюнктивной нормальной форме (КНФ):
Используя тавтологию , получим
Учитывая тавтологию и раскрывая скобки, получим
Далее преобразуем при помощи закона де Моргана:
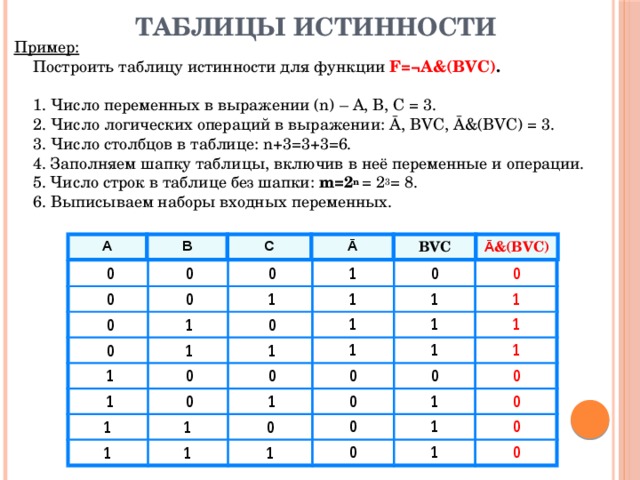
Получили КНФ отрицания исходного высказывания. Используя КНФ как допущение некоторой секвенции, по правилу расщепления получим список допущений:
1) А;
2) ;
3) .
Список содержит явное противоречие – строки 1 и 2. Следовательно, отрицание исходного высказывания является противоречием. Тогда само высказывание – теорема (тавтология), что и требовалось доказать.
8. Определить значение высказывания, полученного из трехместного предиката на множестве .
,
Решение:
Высказывание может быть истинным, если x<z, и ложным в противном случае, потому что x, y,z – натуральные числа и, соответственно, y≥1. Высказывание, которое на одних значениях переменных принимает значение «истинно», а на других – «ложно», называется выполнимым.
В приведенном случае высказывание ложно, потому что не выполняется для произвольных значений x, z. Например, ложно для x=5, z=4.
Ответ: высказывание ложно.
9. Доказать, что первая формула логически влечет вторую формулу.
;
Решение:
Требуется доказать ╞ .
Применим теорему дедукции: если G, S ╞ V, то G╞ S→V. Получим
╞ .
Справа от знака ╞ (выводимо) записана в точности аксиома 8 Гильберта логики высказываний, что есть тавтология. Следовательно, первая формула логически влечет вторую формулу.
Утверждение доказано.
10. Доказать, что формула является тавтологией, без построения таблицы истинности. Во всех формулах выделить всевозможные подформулы.
.
Решение:
Подформулы исходной формулы, всего 5 подформул: .
Проведём преобразования исходной формулы, последовательно используя тавтологию .
.
Далее преобразуем при помощи закона де Моргана:
Учитывая закон снятия двойного отрицания и раскрывая скобки, получим
Используем закон идемпотентности для первой скобки
Учтём закон поглощения и получим запись закона исключённого третьего (аксиома 11 Гильберта):
Формула доказана.
| < Предыдущая | Следующая > |
|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
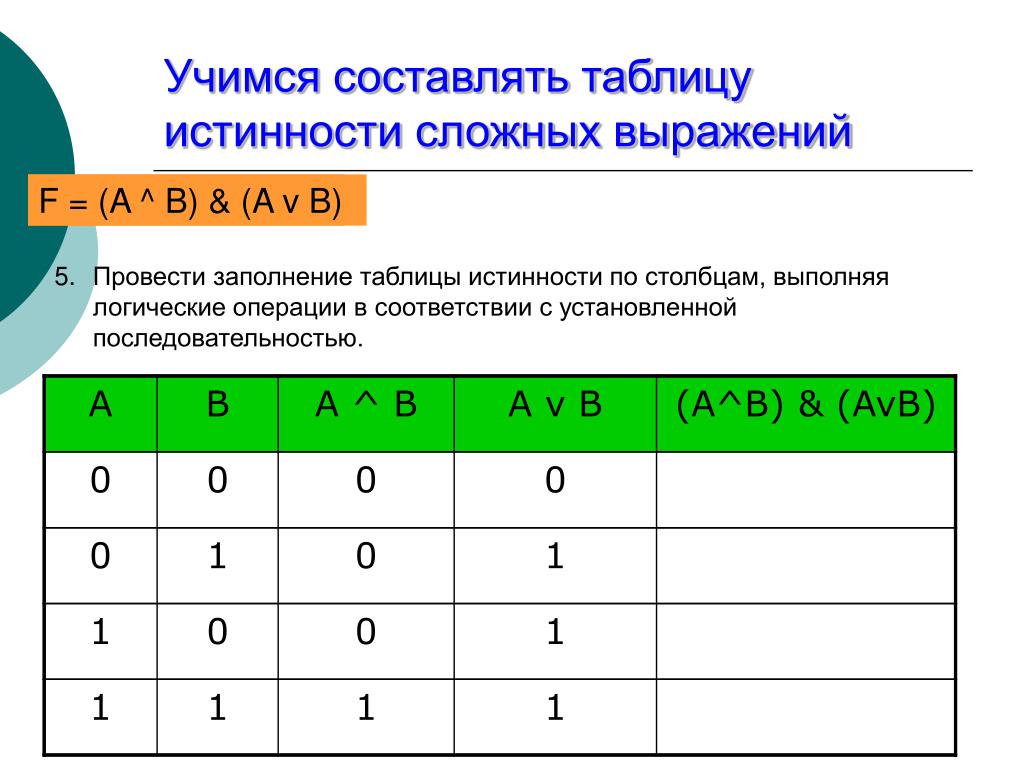
Логические выражения. Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними. Запишем в форме логического выражения составное высказывание «(2 • 2 = 5 или 2 • 2 = 4) и (2 • 2= 5 или 2 • 2=4)». Проанализируем составное высказывание. Оно содержит два простых высказывания: А = «2 • 2 = 5» — ложно (0), В = «2 • 2 = 4» — истинно (1). Тогда составное высказывание можно записать в следующей форме: «(А или В) и (А или В)». Теперь необходимо записать высказывание в форме логического выражения с учетом последовательности выполнения логических операций. При выполнении логических операций определен следующий порядок их выполнения: инверсия, конъюнкция, дизъюнкция. F = (А v В) & (А v В). Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний. Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции: F = (А v В)&(А v В) = (О v 1)&(1 v 0) = 1 & 1 = 1. Таблицы истинности. Для каждого составного высказывания (логического выражения) можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний (логических переменных). При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий. Во-первых, необходимо определить количество строк в таблице истинности. В нашем случае логическая функция F — (АvВ)&(АvВ) имеет 2 переменные и, следовательно, количество строк в таблице истинности должно быть равно 4. Во-вторых, необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций. В нашем случае количество переменных равно двум, а количество логических операций — пяти, то есть количество столбцов таблицы истинности равно семи. В-третьих, необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных. В-четвертых, необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности (табл. Таблица 3.4. Таблица истинности логической функции
Равносильные логические выражения. Докажем, что логические выражения !(А & В) и !(АvВ) равносильны. Построим сначала таблицу истинности логического выражения А & В (табл. 3.5). Таблица 3.5. Таблица истинности логического выражения А & В
Теперь построим таблицу истинности логического выражения АvВ (табл. Таблица 3.6. Таблица истинности логического выражения АvВ
Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны: !(А&В) = !(АvВ). Логическое следование (импликация). Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…». Логическая операция импликации «если А, то В», обозначается А -> В и выражается с помощью логической функции F14, которая задается соответствующей таблицей истинности (табл. Таблица 3.8. Таблица истинности логической функции «импликация»
Составное высказывание, образованное с помощью операции логического следования (импликации), ложно тогда и только тогда, когда из истинной предпосылки(первого высказывания) следует ложный вывод (второе высказывание). Например, высказывание «Если число делится на 10, то оно делится на 5» истинно, так как истинны и первое высказывание (предпосылка), и второе высказывание (вывод). Высказывание «Если число делится на 10, то оно делится на 3» ложно, так как из истинной предпосылки делается ложный вывод. Однако операция логического следования несколько отличается от обычного понимания слова «следует». Если первое высказывание (предпосылка) ложно, то вне зависимости от истинности или ложности второго высказывания (вывода) составное высказывание истинно. Это можно понимать таким образом, что из неверной предпосылки может следовать что угодно. В алгебре высказываний все логические функции могут быть сведены путем логических преобразований к трем базовым: логическому умножению, логическому сложению и логическому отрицанию. Докажем методом сравнения таблиц истинности (табл. 3.8 и 3.9), что операция импликации А -> В равносильна логическому выражению А vВ. Таблица 3.9. Таблица истинности логического выражения АvВ
Таблицы истинности совпадают, что и требовалось доказать. Логическое равенство (эквивалентность). Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «… тогда и только тогда, когда …». Логическая операция эквивалентности «А тогда и только тогда, когда В» обозначается А~В и выражается с помощью логической функции .F10, которая задается соответствующей таблицей истинности (табл. 3.10). Таблица 3.10. Таблица истинности логической функции эквивалентности
Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны. Рассмотрим, например, два высказывания: А = «Компьютер может производить вычисления» и В = «Компьютер включен». Составное высказывание, полученное с помощью операции эквивалентности, истинно, когда оба высказывания либо истинны, либо ложны: «Компьютер может производить вычисления тогда и только тогда, когда компьютер включен». «Компьютер не может производить вычисления тогда и только тогда, когда компьютер не включен». Составное высказывание, полученное с помощью операции эквивалентности, ложно, когда одно высказывание истинно, а другое — ложно: «Компьютер может производить вычисления тогда и только тогда, когда компьютер не включен». «Компьютер не может производить вычисления тогда и только тогда, когда компьютер включен». |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. Схемы и таблицы истинности — Сиреум Логика
В этой главе мы рассмотрим основные понятия о воротах и изучим взаимосвязь
между схемами и компьютерными программами, основанными на назначениях. Это создает основу для анализа современных программ.
Это создает основу для анализа современных программ.
2.1. Гейтс и таблицы правды
Вот четыре основных врата:
П И К | ПОР КВ | НЕ П | П ИМПУЛЬС Q |
На приведенных выше рисунках входные провода обозначены именами P и Q .
Выходной сигнал, который вычисляется, испускается из крайнего правого провода, который выходит из
ворота. Для этих простых вентилей можно исчерпывающе протестировать каждую перестановку.
потенциальных входных данных и суммировать результаты в таблице, называемой таблицей истинности.
Давайте рассмотрим вентиль И. Логический элемент И излучает высокое напряжение ( 1 ) точно
при обнаружении высокого напряжения на входных проводах P и Q ; в противном случае
выдается низкое напряжение ( 0 ). Физическое поведение ворот резюмируется
в следующей таблице.:
Физическое поведение ворот резюмируется
в следующей таблице.:
И: П Q |
------------
1 1 | 1
1 0 | 0
0 1 | 0
0 0 | 0
В оставшейся части этого курса мы будем использовать T (читай «истина») вместо 1 и F (читается как «ложь») вместо 0 .
Это потому, что мы будем исследовать приложения, выходящие далеко за рамки теории схем.
и арифметика с основанием два.
Вот таблицы истинности для логических элементов И, ИЛИ, НЕ и ПРЕДПОЛАГАЕТ:
Примечание
Заглавные буквы P и Q предназначены для заполнения, а не переменные строго именуются P и Q. Их использование позволяет избежать многословия: «Правая рука». Боковой операнд» и «Левый операнд».
ИЛИ иногда называют «включающим ИЛИ», потому что до тех пор, пока один из
его входные данные истинны, то его выходные данные истинны. Это отличается от обычных Соединенных
Указывает использование английского языка. Как правило, в разговорном и письменном английском языке «или» несет в себе
эксклюзивный оттенок. Если предлагается выбор «кофе или чай», это понимается
что вы можете выбрать один, но не оба. Логическое «или» допускает возможность
обоих. На английский язык более точно переводится как «и/или».
Если предлагается выбор «кофе или чай», это понимается
что вы можете выбрать один, но не оба. Логическое «или» допускает возможность
обоих. На английский язык более точно переводится как «и/или».
Значение ворот ПОДРАЗУМЕВАЕТСЯ будет раскрыто позже в этой главе. Это включены сюда, поэтому вся информация о воротах консолидирована.
Стандартно записывать каждый вентиль в линейной записи, то есть вместо
рисунок, пишем P ∧ Q .
(Традиция написания линейных обозначений для представления двумерных
структур восходит к столетиям в физике и математике.)
Обозначения следующие (традиционные математические обозначения предусмотрены для
ваша ссылка.)
Ворота | ASCII | Математика | ЮНИКОД |
И | ∧ | ∧ | |
ИЛИ | v | ∨ | |
НЕ | ~ | ¬ | |
ПОДРАЗУМЕВАЕТСЯ | -> | ⇒ | |
В этих примечаниях обычно используются обозначения UNICODE.
Мы также можем составить элементы для определения новых операций.
Например, эта схема, написанная ¬ (P ∧ Q) , определяет это
вычисление выходов:
П К | ¬ (P ∧ Q) -------------- Т Т | Ф Т Ф | Т Ф Т | Т Ф Ф | Т
, который мы можем вычислить поэтапно, вот так:
Начнем с того, что запишем значение каждого набора входов слева под их
соответствующий символ справа. Далее мы применяем оператор (гейт) с
наивысший приоритет (рассматривается в разделе «Приоритет логических операторов» ниже). В нашем случае
«()» делает символ И ( ∧ ) самым высоким.
Присвоение истинности — это уникальная перестановка возможных входных данных для системы.
Для ∧-гейта это последовательность с двумя переменными. Рассматривая первую строку, мы видим
у нас есть «T ∧ T» — глядя на это в таблице истинности ∧-ворот, мы видим, что результат
также «T», и мы записываем это под символом «∧». Мы делаем то же самое все
другие задания на правду.
После первоначальной расшифровки значений истинности под их соответствующие переменные, мы ищем значения истинности в таблицах вентилей, а не переменные. Также обратите внимание, что в то время как ∧ является симметричным, то есть «TF» == «FT» == «F» ворота IMPLY — нет.
Теперь ищем значение под символом «∧» в таблице ¬gate. Во-первых мы видим, что истинное назначение для первой строки, «T», равно «F», и записываем под символом «¬». Сделайте это для каждой строки, и мы закончили.
2.1.1. Характеристика таблиц истинности
В нашем изучении логики будет удобно характеризовать логическую формулу с помощью
описание их таблиц истинности. Если все назначения истинности для логической формулы
Верны, формула называется тавтологией. Формула p ∨ ¬ p является
тавтология. В следующем примере * отмечает верхний или последний уровень.
оцененный оператор.
1 * 2------------ 3п | р ∨ ¬ р 4------------ 5Т | Т Т Ф Т 6F | Ф Т Т Ф 7------------ 8Тавтология
Формула, для которой каждое присваивание истинности равно False, называется противоречивой. формула
формула p ∧ ¬ p противоречива (или противоречие).
1 * 2------------ 3п | р ∧ ¬ р 4------------ 5Т | Т Ф Ф Т 6F | Ф Ф Т Ф 7------------ 8Противоречивый
Формула, для которой одни присваивания истинности являются ложными, а другие — истинными, называется
контингент. Уравнение p q | ¬ (q ∧ q) , сверху условно.
1 * 2--------------- 3п д | ¬ (р ∧ д) 4--------------- 5Т Т | Ф Т Т Т 6Т Ф | Т Т Ф Ф 7Ф Т | Т Ф Ф Т 8Ф Ф | Т Ф Ф Ф 9--------------- 10Контингент 11- Т : [ТФ] [ФТ] [ФФ] 12- Ф : [Т Т]
В этом разделе мы использовали таблицы истинности Logika. Они объясняются более подробно ниже. В этом классе, если вы создадите таблицу истинности как часть ответа, он должен соответствовать синтаксису Logika. 932 записи. Это займет немного (каламбур) более 1100 лет, чтобы написать вручную, если вы можете усреднить одно назначение истины в секунду.
Учитывая, что вас, вероятно, никогда не попросят написать реальное приложение
так же просто, как сложение целых чисел, легко сделать вывод, что это
невозможно доказать правильность программ с помощью таблиц истинности. Неспособность
протестировать программу на
исчерпывающая проверка каждого входа или состояния известна как комбинаторный взрыв
проблема.
Неспособность
протестировать программу на
исчерпывающая проверка каждого входа или состояния известна как комбинаторный взрыв
проблема.
Ладно… тогда зачем мы заставляем вас учить таблицы истинности? Ну, даже когда более продвинутый методы применяются для доказательства логических утверждений, подтверждая обоснованность методов эти примитивные правила, которые легко выражаются и изучаются с помощью таблиц истинности.
2.2. Таблицы истинности Logika
С этого момента курс предполагает, что вы будете использовать формат Logika.
таблицы истинности. Таблица истинности логики для формулы ¬ (P ∧ Q) :
1 * 2------------ 3п | р ∨ ¬ р 4------------ 5Т | Т Т Ф Т 6F | Ф Т Т Ф 7------------ 8ТавтологияТаблицы истинности
Logika имеют стандартный формат (синтаксис) и семантическое значение. Все элементы таблицы истинности должны быть включены, чтобы считаться правильным.
Первая строка всегда будет содержать одну звездочку ( * ) над последним оцененным оператором
в формуле. Это также может упоминаться как «высший уровень» или «самый низкий прецедент».
оператор. Почему его называют оператором «высшего уровня», будет рассказано
конец этой главы.
Это также может упоминаться как «высший уровень» или «самый низкий прецедент».
оператор. Почему его называют оператором «высшего уровня», будет рассказано
конец этой главы.
Далее идет строка из - (знак минус) символов, длина этих строк должна быть не меньше
в качестве третьей строки, чтобы избежать ошибок.
Третья строка содержит «переменные | формула». Поскольку в Logika используются заглавные буквы, зарезервированные слова, строчные буквы используются в качестве имен переменных. Кроме того, переменные должны быть перечислены в алфавитном порядке.
Четвертая строка — еще одна строка -- .
Далее идут задания на правду. Соглашение состоит в том, чтобы начать со всего True и прогрессировать
линейно ко всем False. Необходимо использовать Capital T и F . В задании правды
каждая переменная отображается либо в true, либо в false.
После заданий Правды идет еще ряд -.
Наконец идет стол. Когда все присваивания истинности делают формулу истинной,
слово
Когда все присваивания истинности делают формулу истинной,
слово Тавтология используется без сопроводительной таблицы. Точно так же, когда
все присваивания истинности ложны, используется Contradictory . Все остальные результаты Контингент , см. пример на рисунке выше.
Порядок приоритета логических операторов от высшего к низшему:
Скобки изменяют порядок операций, как в обычной алгебре. Выражения в скобках оцениваются от наиболее глубоко вложенных к наименее глубоко вложенные (внутри наружу).
2.3. Странный случай имплицитных ворот
Внимательный читатель заметит, что → таблицы истинности работают совсем не так, как ∧ и ∨ . Начнем с того, что ∧ и ∨ истинностные назначения симметричны;
если [T F] == F, то [F T] == F.
Это неверно по смыслу, потому что p → q является составным
утверждение, утверждающее, что p содержит знания, достаточные для вывода q.
Возьмем конкретный пример из K-State. Если я знаю, что вы специализируетесь по информатике (факт p), то я знаю, что вы специализируетесь на инженерии (факт q).
по специальности компьютерные науки → по специальности инженер
п → д
Однако наоборот, по специальности «Инженерное дело» → по специальности «Информатика» не обязательно верно.
Некоторые учащиеся склонны смешивать фразу «р содержит знания, достаточные для вывода q», что означает «p == q», и удивляются и возмущаются тем, что присваивание истины [F T] в ворота ПОДРАЗУМЕВАЕМЫЕ — Истина. p → q не означает p == q или q == p
В таблице истинности для p → q результат отражает существование последовательного
связь между p и q . Сначала p должно быть истинным, затем q тоже должно быть истинным
быть истинным, чтобы импликация была истинной.
Если оба верны, ссылка
верно, и следствие (отношение) между p и q верно.
Если p верно, а q ложно, то очевидно, что p не обладает достаточным знанием
вывести q, поэтому отношение не верно (ложно).
Наконец, если p неверно, нет никакого способа узнать, сохраняется ли связь. В этом случае импликация считается истинной или беспричинно истинной. Конечно нет доказательства, доказывающие, что это ложь.
Импликация в логике была формализована Уильямом Оккамом в его книге Summa Logicae в 14 веке. Эти несколько запутанные правила добавляют огромную выразительную силу логике и вычислениям. Без них в программах не было бы ветвлений (без IF, FOR, WHILE).
2.4. Общая логическая формула (схема) Эквивалентности
2.4.1. Равенство
Говорят, что два (или более) логических утверждения равны IFF (тогда и только тогда, когда ↔ ) они имеют
одно и то же значение истинности для каждого присваивания истинности; то есть их таблицы истинности
оценивают точно так же. Примером равенства являются q ∧ p и p ∧ (q ∧ p)
1 * 2-------------- 3п д | (р ∧ д) 4-------------- 5Т Т | Т Т Т 6Т Ф | Т Ф Ф 7Ф Т | Ф Ф Т 8Ф Ф | Ф Ф Ф 9--------------- 10Контингент 11- Т : [Т Т] 12- Ф : [Ф Ф] [Ф Т] [Т Ф]
1 * 2------------------- 3п д | р ∧ (д ∧ р) 4 -------------------- 5Т Т | Т Т Т Т Т 6Т Ф | Т Ф Ф Ф Т 7Ф Т | Ф Ф Т Ф Ф 8Ф Ф | Ф Ф Ф Ф Ф 9 -------------------- 10Контингент 11- Т : [Т Т] 12- Ф : [Ф Ф] [Ф Т] [Т Ф]
Нахождение эквивалентных логических операторов меньшего количества вентилей (состояний) важно для несколько полей. В компьютере науки, меньшее количество состояний может привести к меньшему объему памяти, меньшему количеству операций и программ меньшего размера. В компьютерная инженерия, меньше вентилей означает меньше цепей, меньше энергии и меньше тепла.
С технической точки зрения, биимпликация — это еще один способ выразить качество. Однако мы еще не ввели оператор «равно».
p = q ↔ (p → q) ∧ (q → p)
2.
 4.2. Двойной негатив
4.2. Двойной негатив В логике и во многих логических приложениях двойное отрицание
эффективно компенсируют друг друга. Это не единственная возможная интерпретация ¬ ¬ p , но именно он реализован в Logika. Мы можем обсудить другие
интерпретации в разделе о логике высказываний.
¬ ¬ р ↔ р
2.4.3. Эксклюзивное ИЛИ (исключающее ИЛИ)
Как обсуждалось ранее, в английском языке «или» используется в исключительном смысле. (p XOR q) можно выразить несколькими способами:
(p ∧ ¬ q) ∨ (¬p ∧ q) (p ∨ q) ∧ ¬ (p ∧ q)
В классе мы не примем использование оператора XOR, вы должны выразить все формулы в терминах И, ИЛИ, НЕ и ПОДРАЗУМЕВАЮТ.
2.4.4. Закон Де Моргана
Закон Де Моргана — это утверждение о взаимосвязи между И
и НЕ-ИЛИ (НИ) ( ¬ ( p ∨ q ) ). Конкретно:
p ∧ q ↔ ¬ (¬ p ∨ ¬ q)
p ∨ q ↔ ¬ (¬ p ∧ ¬ q)
Это имеет важное значение для вычислительной техники, позволяя
все логические конструкции должны быть выражены только двумя типами основных
ворота, И-НЕ и НЕ; значительно экономит интегрированное производство чипов.
Август Де Морган также ввел термин «Математическая индукция» и дал строгую подход к его доказательству. Математическая индукция лежит в основе многих доказательства информатики в области алгоритмов, языков и вычислительная сложность.
2.4.5. Эквивалентности следствий
Наконец, импликация может быть выражена как отрицание и ИЛИ; или как его контрпозитивное утверждение.
(p → q) ↔ ¬ p ∨ q
(p → q) ↔ (¬ q → ¬ p) противоположное утверждение
Обратное следствие может быть истинным, а может и не быть
(р → к) ??? (q → p) обратное (НЕ ОБЯЗАТЕЛЬНО ЭКВИВАЛЕНТНОСТЬ)
Примечание
Хотя большая часть формул, представленных в этом разделе, верна
эквивалентности, ЕСЛИ вас просят доказать, что они равны по таблице истинности,
ожидается, что вы составите таблицу истинности для каждой стороны ↔ и покажите, что их значения совпадают для каждого присваивания истинности.
2.5. Почему его называют оператором «Верхнего уровня»
Вернемся к 2-разрядному сумматору и рассмотрим схему только для Q1. В цепи, можно сказать, что знания текут по проводам, где они трансформируются воротами, и новое знание распространяется на следующую точку.
В аннотированной выше схеме видно, какие знания (факты и выведенные факты) поток в каждом сегменте провода. Обычная математика, следовательно, информатика метод заключается в том, чтобы представить этот тип потока знаний в специализированном виде граф называется деревом. Дерево представлено набором узлов и ребер, один узел выбирается в качестве «корня», и все узлы имеют уникальный путь (набор ребер), ведущих к корневому узлу. По соглашению дерево рисуется перевернутым, с корнем вверху и листьями, свисающими снизу.
В информатике корень выбирается как узел, который обеспечивает
«окончательный ответ» на проблему. Как видите, ребра несут факты и узлы.
являются операторами, выводящими новые факты.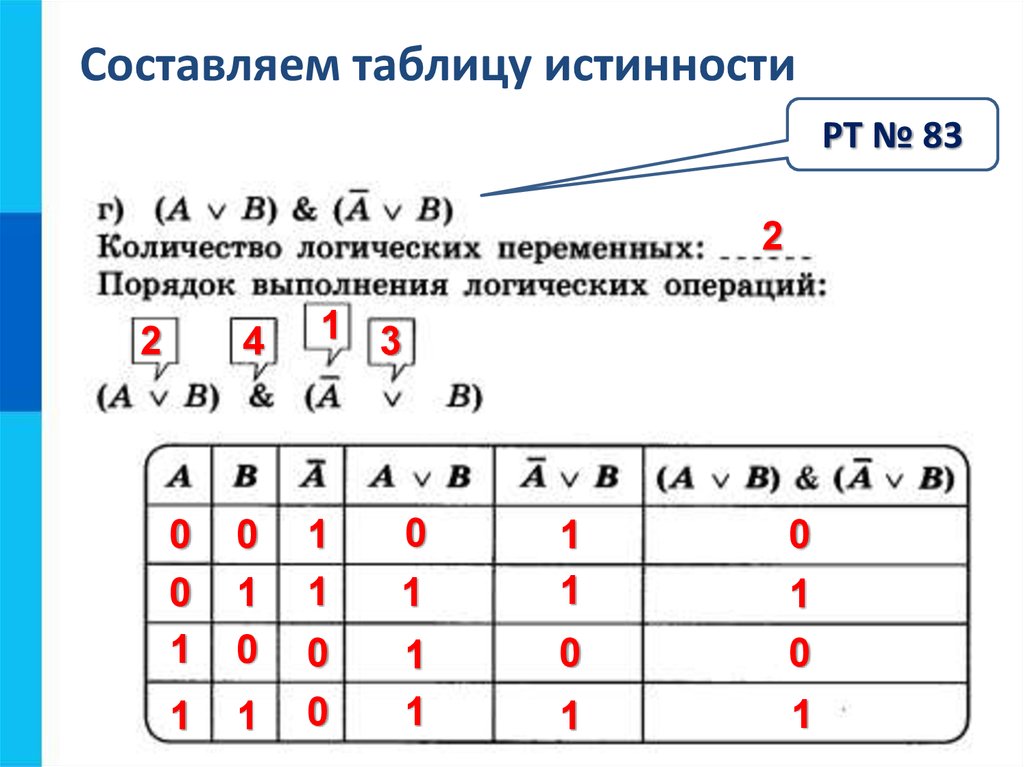
Древовидное представление компьютерной программы является фундаментальной абстракцией для специалист в области информатики. Современные компиляторы и интерпретаторы принимают программу, написанную на языке программирования высокого уровня и преобразовать его в абстрактное синтаксическое дерево (АСТ), что затем преобразованы в машинный код. Для языков функциональной парадигмы (C# и Java находятся в императивной и/или объектной парадигмах), существует сильная корреляция между структурой программы высокого уровня и структурой AST.
Когда мы сравниваем дерево с логическим оператором, мы видим самый низкий приоритет оператор — корень дерева; отсюда и термин «оператор верхнего уровня».
* (¬(A1 ∧ B1)) ∧ (A1 ∧ B1)
2.6. Знания путешествуют по проводам цепи
До сих пор мы делали вид, что уровни низкого и высокого напряжения проходят по проводке. цепи. Но на самом деле это знание путешествует по кругу. Это понятно по некоторым картинкам. Вот схема:
и вот его кодировка в уравнениях:
Р = П ∧ Q S = R ∨ Q Т = ¬ S
Перерисуем схему по вертикали и положим рядом с заданием уравнения:
Каждому проводу в цепи присваивается имя. Это всего лишь имен переменных .
Действительно, 90 205 первых (электронных) компьютерных программ в 1940-х годах были
описания электрических схем вроде этой.
Современный компьютер с хранимой в памяти программой, разработанный Джоном фон Нейманом в 1950-х гг.
использовали регистры хранения для хранения значений имен переменных и использовали
процессор для вычисления значений уравнений.
Таким образом, процессор плюс регистры могут имитировать схему, и все компьютерные программы являются просто описаниями цепей, в которых информация
течет по проводам (переменным) .
Это всего лишь имен переменных .
Действительно, 90 205 первых (электронных) компьютерных программ в 1940-х годах были
описания электрических схем вроде этой.
Современный компьютер с хранимой в памяти программой, разработанный Джоном фон Нейманом в 1950-х гг.
использовали регистры хранения для хранения значений имен переменных и использовали
процессор для вычисления значений уравнений.
Таким образом, процессор плюс регистры могут имитировать схему, и все компьютерные программы являются просто описаниями цепей, в которых информация
течет по проводам (переменным) .
Это источник компьютерного программирования, основанного на переменных и присваиваниях.
Теперь в каждой из программных точек , отмеченных звездочками на приведенной выше диаграмме, что
информация распространяется по проводам?
Мы могли бы использовать схему с некоторыми входами, чтобы увидеть, «что происходит».
Допустим, мы поставляем true для P и false для В :
На схеме показаны значения на проводах с маркировкой P , Q , R и S по мере их прохождения по цепи.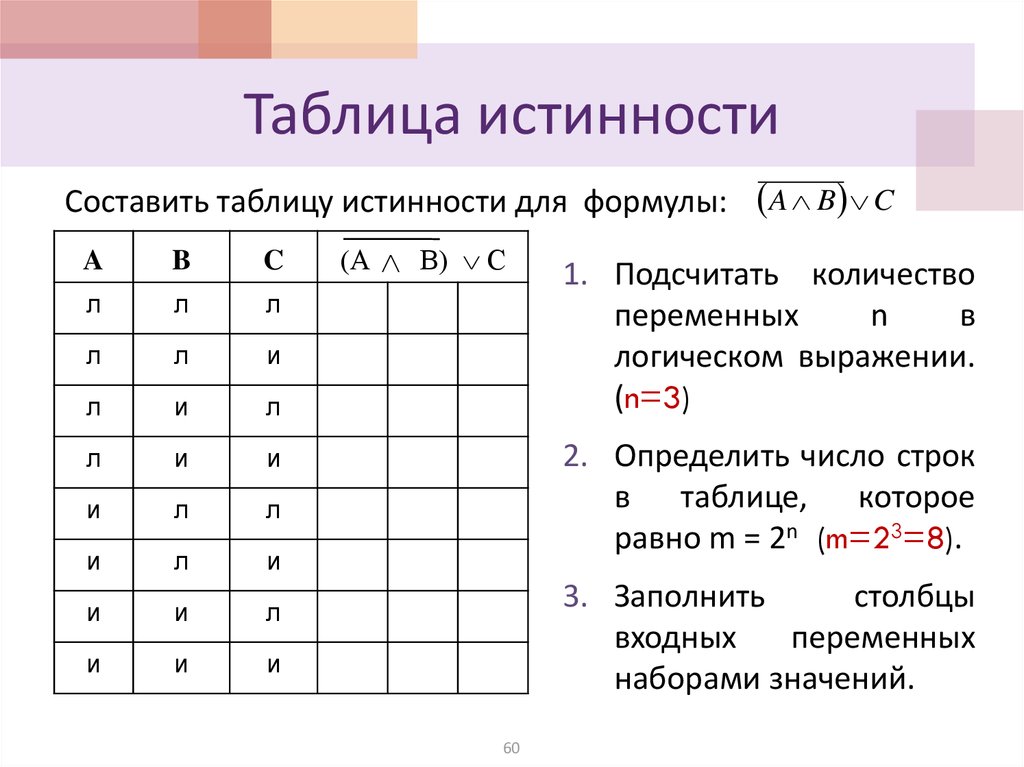 Но это просто отслеживание значений переменных в программе присваивания
мы написали!
«Выходная переменная»/запись, названная
Но это просто отслеживание значений переменных в программе присваивания
мы написали!
«Выходная переменная»/запись, названная T , имеет значение true .
Так же интересно, что мы можем проанализировать программу/схему до .
полностью протестировано.
Например, скажем, что схема будет вставлена в плату, где ее Р wire всегда будет получать t в качестве входных данных, но мы не знаем, что получит Q .
Что мы можем предсказать о поведении схемы после того, как она будет встроена в плату?
Это:
На диаграмме мы видим, что R = Q указано после вентиля И.
Откуда нам это знать?
Во-первых, мы знаем, что R = P ∧ Q . Но P = true .
Мы заменяем true на P и получаем R = true ∧ Q .
Далее мы делаем анализ случаев и рассматриваем случаи Q возможное значение:
Если Q равно true , то true ∧ Q равно true ∧ true , что упрощает до true ,
то есть к значению Q .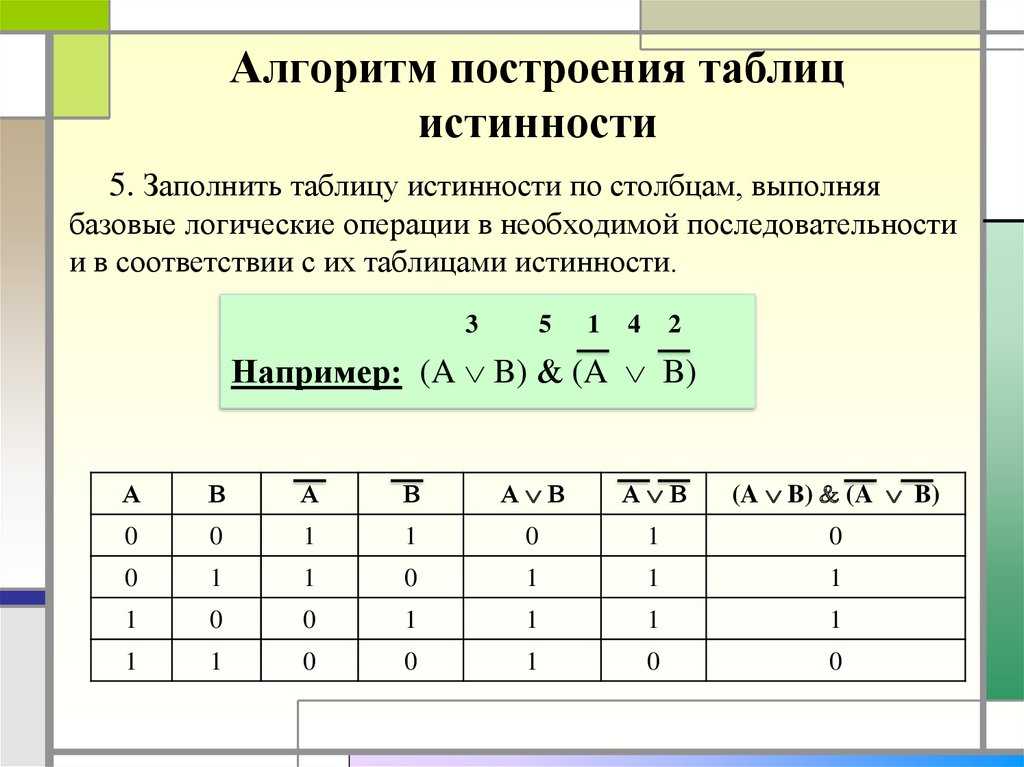 Точно так же, когда
Точно так же, когда Q равно false , тогда t ∧ Q также равно false .
Следовательно, в обоих случаях true ∧ Q равно Q .
Приведенное выше рассуждение является вычетом — мы вывели из фактов P = true и R = P ∧ Q что R = Q .
Весь смысл этого курса в том, чтобы научиться делать такие выводы.
Другие вычеты в примере рассчитываются с аналогичным использованием замена, упрощение и анализ случаев.
Суть предыдущего примера в том, что мы можем вывести (предсказать) свойства схему до ее использования. Эти выводы дополняют тестирование.
Далее скажем, что мы ничего не знаем о P и Q в качестве входов.
Что можно сказать о выходе схемы?
Ну, это:
Т = ¬((P ∧ Q) ∨ Q)
констатируя очевидное!
Но, внимательно изучив таблицы истинности, мы также можем утверждать, что Т = ¬Q .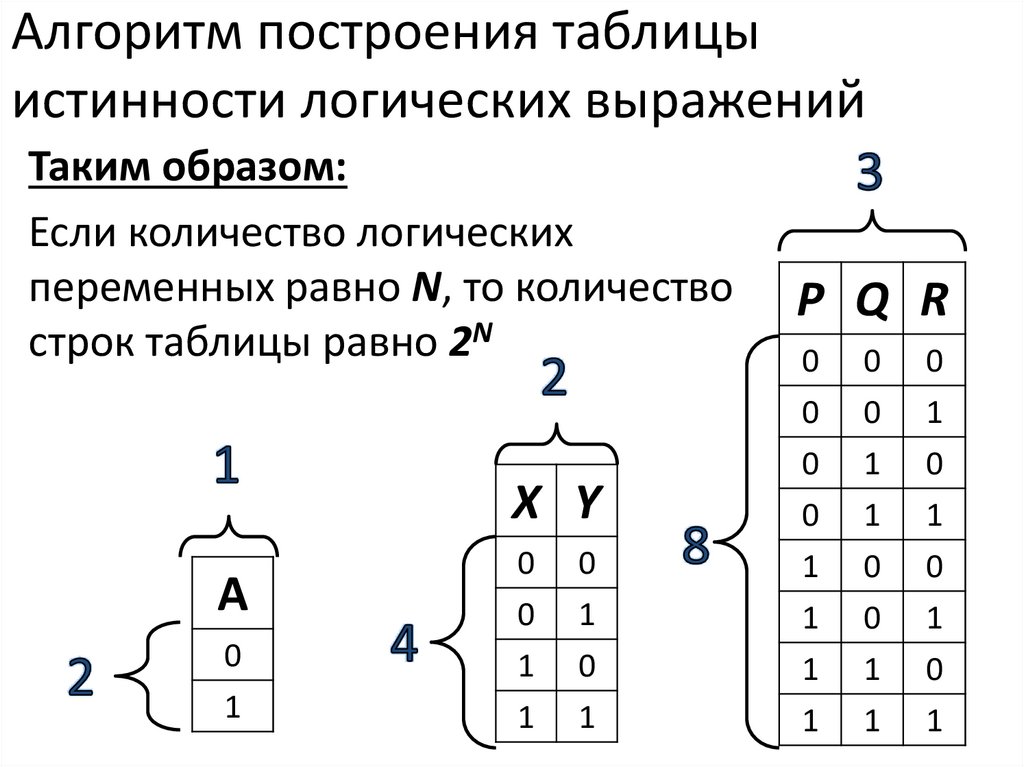 Позже в курсе мы узнаем правила вывода , которые вычисляют этот результат, а не
опираясь на таблицы истинности.
Позже в курсе мы узнаем правила вывода , которые вычисляют этот результат, а не
опираясь на таблицы истинности.
Наконец, мы можем создавать схемы с тремя или более входами, например, (¬(P ∧ Q)) ∨ R вычисляет:
Здесь столбец под оператором ИЛИ определяет вывод.
Мы видим, что эта схема выдает ложь только тогда, когда P и Q оба истинны и R неверно.
Это намек на то, что схема ¬(P ∧ Q ∧ ~R) ведет себя точно так же.
(имеет ту же таблицу истинности), что и выше.
Еще одна эквивалентная схема: (¬P) ∨ (¬Q) ∨ R . (Почему?)
В схемотехнике поиск эквивалентных схем с меньшим количеством вентилей и переменных экономит энергию, время и материал.
Это примечание было адаптировано из CIS 301 Дэвида Шмидта, 2008 г., Глава 0 примечание к курсу.
Он был обновлен в 2018 году доктором Джоном Хэтклиффом и Джорджем Лавецци
, чтобы соответствовать синтаксису Logika и более точно соответствовать курсу
KSU 301, преподаваемому весной 2018 года.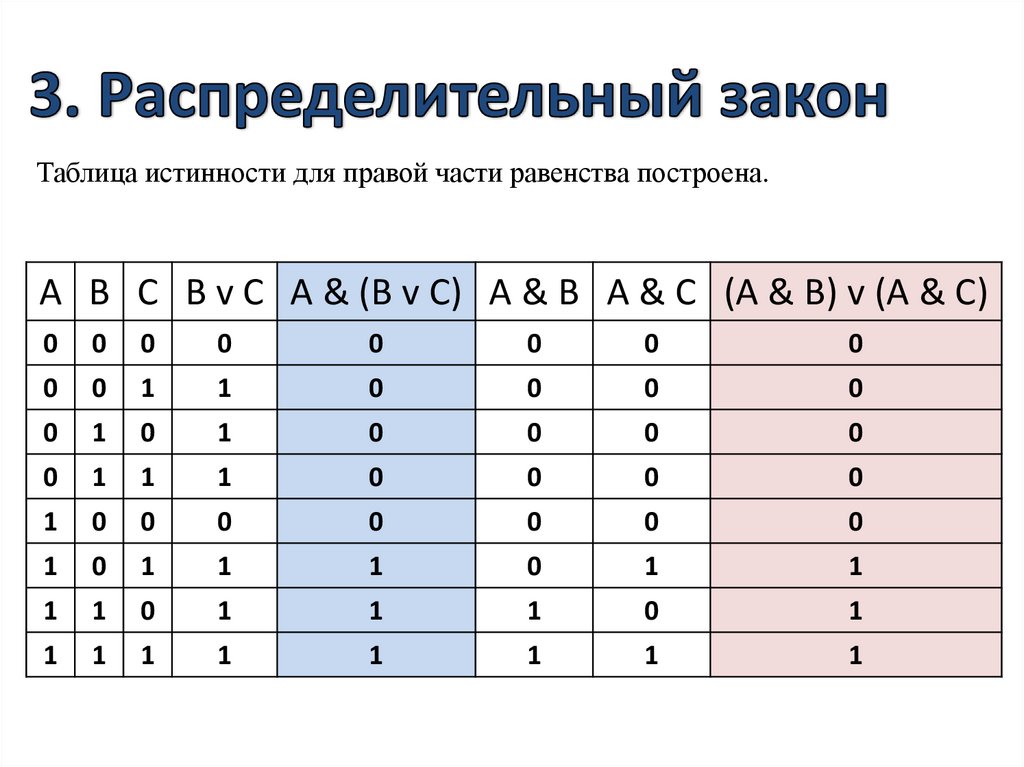
Страница не найдена – Khoury College Development
В мире, где информатика (CS) везде, CS для всех. CS пересекает все дисциплины и отрасли.
Колледж компьютерных наук Хури стремится создавать и развивать разнообразную инклюзивную среду.
Колледж Хури, первый в стране колледж информатики, основанный в 1982 году, вырос в размерах, разнообразии, программах на получение степени и превосходстве исследований.
В наших региональных кампусах, расположенных в промышленных и технологических центрах, Khoury College предлагает сильные академические программы в оживленных городах для жизни, работы и учебы.
Khoury College — это сообщество людей, преданных обучению, наставничеству, консультированию и поддержке студентов по всем программам.
Программы награждения колледжей и университетов проливают свет на выдающихся преподавателей, студентов, выпускников и отраслевых партнеров.
Наши реальные исследования, выдающиеся преподаватели, выдающиеся докладчики, динамичные выпускники и разные студенты рассказывают свои истории и попадают в новости.
В Колледже Хури обучение происходит в классе и за его пределами. Мероприятия в нашей сети кампусов обогащают образовательный опыт.
Информатика повсюду. Студенты Khoury College занимаются соответствующей работой, исследованиями, глобальными исследованиями и опытом обслуживания, которые помогают им расти.
Студенты магистратуры углубляют свои знания посредством проектной работы, профессионального опыта работы и стажировки в научных исследованиях.
Работа над исследованиями с преподавателями занимает центральное место в работе доктора философии. Докторанты колледжа Хури также могут проводить исследования с отраслевыми партнерами.
Преподаватели и студенты Khoury College проводят эффективную работу по различным дисциплинам. Благодаря широкому спектру областей исследований мы каждый день решаем новые проблемы в области технологий.
Благодаря широкому спектру областей исследований мы каждый день решаем новые проблемы в области технологий.
Наши институты и исследовательские центры объединяют ведущих академических, отраслевых и государственных партнеров для использования вычислительной мощности.
Исследовательские проекты, разработанные и проводимые профессорско-преподавательским составом Khoury College мирового уровня, вовлекают студентов и других исследователей в получение новых знаний.
Исследовательские лаборатории и группы сосредотачиваются на ряде проблем в определенном контексте, поощряя исследования и сотрудничество.
Эта новая инициатива направлена на устранение рисков для конфиденциальности и личных данных с помощью коллективных усилий на низовом уровне с упором на прозрачность и подотчетность.
Современное оборудование, бесшовные системы и инновационные лаборатории и помещения позволяют нашим преподавателям и студентам проводить передовые исследования.
9Колледж 0002 Khoury гордится нашим совместным инклюзивным сообществом. Каждый день мы стремимся создавать программы, которые приветствуют самых разных студентов в CS.
Более 20 компьютерных клубов в колледже Хури и Северо-Восточном колледже предлагают что-то для каждого студента. Мы всегда рады новым членам на каждом уровне.
Учащиеся учатся в современных классах, конференц-залах для совместной работы, а также в ультрасовременных лабораториях и исследовательских центрах.
Сети обеспечивают безопасную и бесперебойную работу кода, современное и надежное оборудование, а наша квалифицированная системная команда управляет поддержкой и обновлениями.
Заинтригован Колледжем Хури и северо-восточным университетом? Начните здесь, чтобы увидеть общую картину: академические науки, экспериментальное обучение, студенческая жизнь и многое другое.
Готовы сделать следующий шаг в технической карьере? Наши магистерские программы сочетают в себе академическую строгость, исследовательское превосходство и значимые экспериментальные возможности.
Добро пожаловать в магистерскую программу Align, предназначенную для людей, готовых добавить информатику (CS) в свой набор навыков или переключиться на совершенно новую карьеру в области технологий.
Будучи аспирантом Хури, вы погрузитесь в строгую учебную программу, будете сотрудничать с известными преподавателями и окажете влияние в выбранной вами области исследований.
Где бы вы ни находились на пути бакалавриата в Хури, у нас есть консультанты, ресурсы и возможности, которые помогут вам добиться успеха и сделать информатику доступной для всех.
Где бы вы ни находились на пути к аспирантуре Хури, наши консультанты, информационные ресурсы и возможности помогут вам выбрать индивидуальный путь.
В любой момент пути Align — и в любом из наших кампусов — консультанты Khoury, ресурсы и возможности поддержат вас на пути к карьере в сфере технологий.
Консультанты и преподаватели помогут вам пройти путь докторантуры в Khoury College — от исследовательских пространств и междисциплинарных проектов до студенческой жизни и ресурсов.


 Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
 Для изменения указанного порядка могут использоваться скобки:
Для изменения указанного порядка могут использоваться скобки:
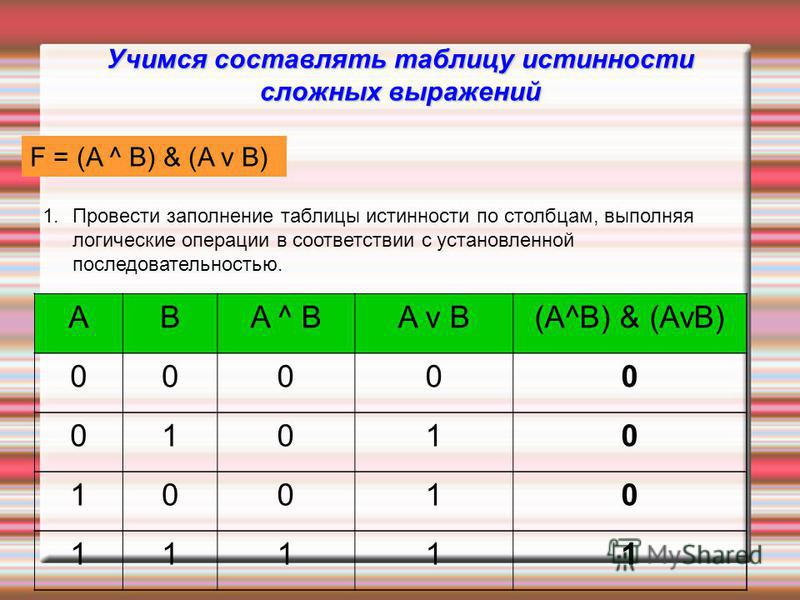 Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:
количество строк = 2n.
Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:
количество строк = 2n.
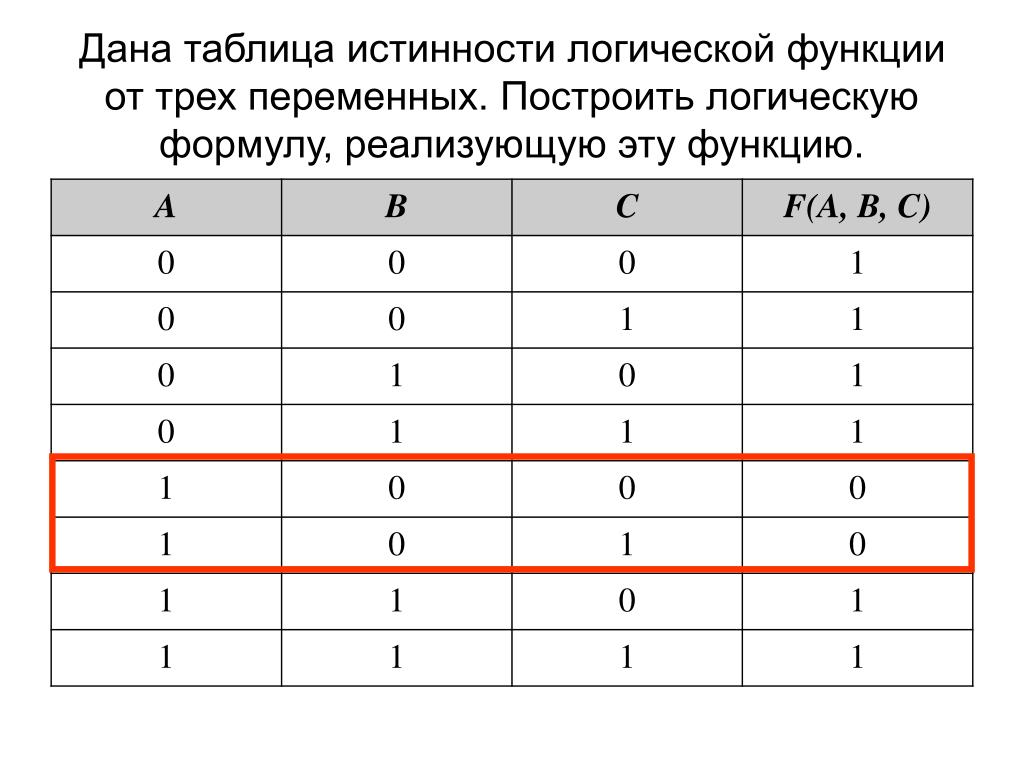 3.4). Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
3.4). Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
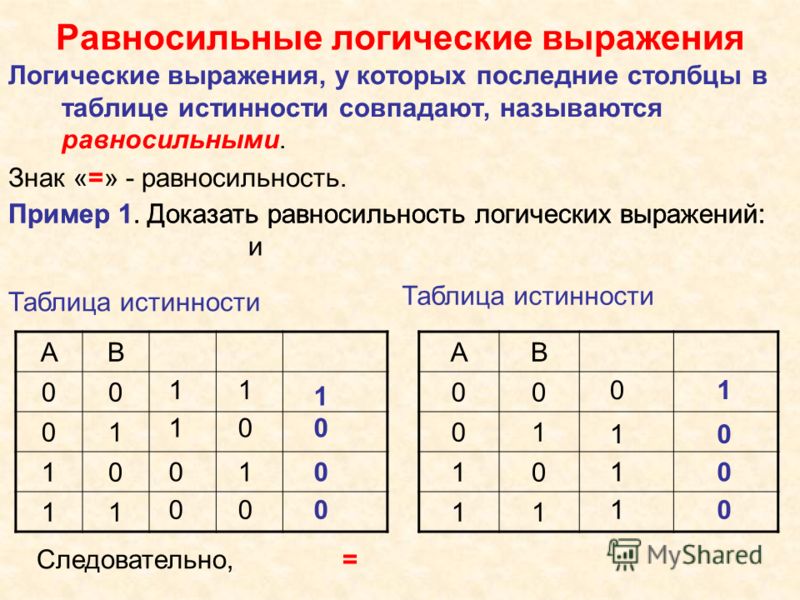
 Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».
Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».
 3.6).
3.6).
 3.8).
3.8).