Что такое двоичная система счисления? Как перевести десятичное число в двоичное? :: SYL.ru
С двоичной системой счисления мы сталкиваемся при изучении компьютерных дисциплин. Ведь именно на базе этой системы построена работа процессора и некоторые виды шифрования. Существуют специальные алгоритмы для записи десятичного числа в двоичной системе и наоборот. Если знать принцип построения системы, оперировать в ней будет несложно.

Принцип построения системы из нулей и единиц
Двоичная система счисления построена с использованием двух цифр: ноль и один. Почему именно эти цифры? Это связано с принципом построения сигналов, которые используются в работе процессора. На самом низком уровне сигнал принимает только два значения: «ложь» и «истина». Поэтому было принято отсутствие сигнала, «ложь», обозначать нулем, а наличие его, «истину», единицей. Такое сочетание легко реализовать технически. Числа в двоичной системе формируются так же, как и в десятичной. Когда разряд достигает своей верхней границы, он обнуляется, и добавляется новый разряд. По такому принципу осуществляется переход через десяток в десятичной системе. Таким образом, числа состоят из сочетаний нулей и единиц, и это сочетание называется «двоичная система счисления».
Запись числа в системе | |||
В десятичной | В двоичной | В десятичной | В двоичной |
0 | 0 | 5 | 101 |
1 | 1 | 6 | 110 |
2 | 10 | 7 | 111 |
3 | 11 | 8 | 1000 |
4 | 100 | 9 | 1001 |
Как двоичное число записать в виде десятичного?
Существуют онлайн-сервисы, которые осуществляют перевод числа в двоичную систему и наоборот, но лучше уметь делать это самостоятельно. Двоичная система при переводе обозначается нижним индексом 2, например, 1012. Каждое число в любой системе можно представить в виде суммы чисел, например: 1428 = 1000 + 400 + 20 + 8 – в десятичной системе. Так же представляется число в двоичной. Возьмем произвольное число 101 и рассмотрим его. В нем 3 разряда, поэтому раскладываем число по порядку таким способом: 1012=1×22+0×21+1×20=4+1=510, где индекс 10 обозначает десятичную систему.

Как записать простое число в двоичной системе?
Очень легко осуществить перевод в двоичную систему счисления с помощью деления числа на два. Делить необходимо до тех пор, пока это будет возможно выполнить нацело. Например, возьмем число 871. Начинаем делить, обязательно записывая остаток:
871:2=435 (остаток 1)
435:2=217 (остаток 1)
217:2=108 (остаток 1)
108:2=54 (остаток 0) и так далее до конца.
Ответ записывается по полученным остаткам по направлению от конца к началу: 87110=1011001112. Проверить правильность вычислений можно с помощью обратного перевода, описанного ранее.

Для чего нужно знать правила перевода?
Двоичная система счисления применяется в большинстве дисциплин, связанных с микропроцессорной электроникой, кодированием, передачей и шифрованием данных, в различных направлениях программирования. Знания основ перевода из любой системы в двоичную помогут программисту разрабатывать различные микросхемы и осуществлять управление работой процессора и других подобных систем программным способом. Двоичная система счисления также необходима для реализации способов передачи пакетов данных по зашифрованным каналам и создания на их основе программных проектов типа «Клиент-сервер». В школьном курсе информатики основы перевода в двоичную систему и наоборот являются базовым материалом для изучения программирования в будущем и создания простейших программ.
Системы счисления и их практическое применение
Память человечества не сохранила, не донесла до нас имя изобретателя колеса или гончарного круга. Это и неудивительно: более 10 тысяч лет прошло с тех пор, как люди всерьез занялись земледелием, скотоводством и производством простейших товаров. Назвать же имя гения, впервые задавшего вопрос «Сколько?», тем более невозможно.
В каменном веке, когда люди собирали плоды, ловили рыбу и охотились на животных, потребность в счете возникла так же естественно, как и потребность в добывании огня. Об этом свидетельствуют находки археологов на стоянках первобытных людей. Например, в 1937 году в Вестонице (Моравия) на месте одной из таких стоянок найдена волчья кость с 55 глубокими зарубками. Позже в других местах ученые находили столь же древние каменные предметы с точками и черточками, сгруппированными по три или по пять.
Развитие чисел тесно связано с потребностями общества в измерениях, контроле, особенно в областях аграрной, промышленной и налогообложения. Первые области применения чисел были связаны с созерцанием звезд и земледелием. Изучение звездного неба позволило проложить торговые морские пути, караванные дороги в новые районы и резко увеличить эффект торговли между государствами. Обмен товарами приводил к обмену культурными ценностями, к развитию толерантности как явления, лежащего в основе мирного сосуществования различных рас и народов. Понятие числа всегда сопровождалось и нечисловыми понятиями. Например, один, два, много. Эти нечисловые понятия всегда ограждали числа. Числа придавали законченный вид всем наукам, где они применялись.
Язык чисел, как и обычный язык, имеет свой алфавит. В том языке чисел, которым сейчас пользуются практически на всём земном шаре, алфавитом служат десять цифр от 0 до 9. Этот язык называется десятичной системой счисления. Однако не во все времена и не везде люди пользовались десятичной системой счисления. С точки зрения чисто математической она не имеет специальных преимуществ перед другими возможными системами счисления, и своим повсеместным распространением эта система обязана вовсе не общим законам математики, а причинам совсем иного характера. О свойствах, истории возникновения и применения различных систем счисления будет рассказано в нашей работе.
Потребность в записи числа появилась в очень древние времена, как только люди начали считать.
Представим себе то далекое время, когда люди только начали изобретать числа. В те времена для счета человеку хватало четырех слов: один, два три и много. Именно так считают и сейчас некоторые племена, живущие в джунглях Южной Америки. С развитием человечества этих слов стало не хватать. Земледельцу надо было подсчитать урожай, скотоводу животных, строителю количество бревен Умение считать и производить операции с числами высоко ценилось. Числа вызывали удивление, потому что они могли обозначать количество любых предметов, например, два пальца, две руки, два человека или два камня.
Способов счета было придумано немало: люди рисовали палочки на стенах и делали зарубки на костях животных или ветках деревьев. Такая система записи чисел называется единичной. Любое число в ней образуется повторением одного знака — единицы. Для записи больших чисел используются группировки и вспомогательные значки.
Поштучно считать предметы удобно тогда, когда их не очень много, т. к. чем большее число надо записать, тем длиннее будет строка из палочек.
Поэтому появился счет группами, так появились первые нумерации — системы счисления.
Со времени их происхождение сформировалось большое количество отличных систем счисления: пятеричная, десятичная, мультипликативная
Машинная группа систем счисления
Перед математиками и конструкторами 50-х годов встала проблема отыскания таких систем счисления, которые отвечали бы требованиям, как разработчиков ЭВМ, так и создателей программного обеспечении. Одним из итогов этих исследований стало значительное изменение представлений о системах счисления и о методах вычислений. Оказалось, что арифметический счет, которым человечество пользуется с древнейших времен, может совершенствоваться, подчас весьма неожиданно и на удивление эффективно.
Специалисты выделили так называемую «машинную» группу систем счисления и разработали способы преобразования чисел этой группы. К «машинной» группе систем счисления относятся: двоичная, восьмеричная, шестнадцатеричная. Однако на начальном этапе развития информационных технологий использовалась троичная система счисления.
Двоичная система проста, так как для представления информации в ней используются всего два состояния или две цифры. Такое представление информации принято называть двоичным кодированием. Представление информации в двоичной системе использовалось человеком с давних времен. Так, жители островов Полинезии передавали необходимую информацию при помощи барабанов: чередование звонких и глухих ударов. Звук над поверхностью воды распространялся на достаточно большое расстояние, таким образом «работал» полинезийский телеграф. В телеграфе в Х1Х-ХХ веках информация передавалась с помощью азбуки Морзе — в виде последовательности из точек и тире.
В конце XX века, века компьютеризации, Человечество пользуется двоичной системой ежедневно, так как вся информация, обрабатываемая современными ЭВМ, хранится в них в двоичном виде. Каким же образом осуществляется это хранение? Каждый регистр арифметического устройства ЭВМ, каждая ячейка памяти представляет собой физическую систему, состоящую из некоторого числа однородных элементов. Каждый такой элемент способен находиться в нескольких состояниях и служит для изображения одного из разрядов числа. Именно поэтому каждый элемент ячейки называют разрядом. Нумерацию разрядов в ячейке принято вести справа налево, самый левый разряд имеет порядковый номер 0. Если при записи чисел в ЭВМ мы хотим использовать обычную десятичную систему счисления, то мы должны получать 10 устойчивых состояний для каждого разряда, как на счетах при помощи костяшек. Такие машины существуют. Однако конструкция элементов такой машины чрезвычайно сложна. Наиболее надежным и дешевым является устройство, каждый разряд которого может принимать два состояния: намагничено — не намагничено, высокое напряжение — низкое напряжение и т. д. В современной электронике развитие аппаратной базы ЭВМ идет именно в этом направлении. Следовательно, использование двоичной системы счисления в качестве внутренней системы представления информации вызвано конструктивными особенностями элементов вычислительных машин.
Преимущества двоичной системы счисления:
1. Простота совершаемых операций
2. Возможность осуществлять автоматическую обработку информации, реализуя только два состояния элементов компьютера.
Недостаток двоичной системы счисления:
1. Быстрый рост числа разрядов в записи, представляющей двоичное число
Для представления двоичных чисел вне компьютера используют более компактные по длине чисел восьмеричную (для записи кодов чисел и машинных команд) и шестнадцатеричную (для записи адреса команд) системы счисления.
3. Предоставление информации в компьютере.
В данный момент для кодировки информации в компьютере используется двоичная система счисления. Каждый символ в компьютере представляется в виде последовательности единиц и нулей, любая такая последовательность состоит из восьми знаков. Знакоместа в таких последовательностях называется битом, а восемь битов это байт.
Для перевода значений отдельных байтов в понятные человеку знаки (буквы и цифры) компьютер использует специальные «кодовые таблицы», в которых каждому знаку сопоставлен байт с определенным значением.
Впрочем, измерять компьютерную информацию байтами весьма неудобно из-за объема. Вот почему на практике в компьютерном мире оперируют такими величинами:
• килобайт (кб) — 2 в степени 10 байт — 1024 байт;
• мегабайт (Мб) — 2 в степени 20 байт — 1 048 576 байт —
1024 кб;
• гигабайт (Гб) — 2 в степени 30 байт — 1 073 741 824 байт —
1 048 576 кб-1024 Мб;
• терабайт (Тб) — 2 в степени 40 байт — 1 099 511 627 776 байт —
1 073 741 824 кб — 1 048 576 Мб — 1024 Гб;
• петабайт (Пб) — 2 в степени 50 байт — 1125 899 906 842 624 байт —
1 099 511 627 776 кб — 1073 741 824 Мб — 1 048 576 Гб — 1024 Тб
Биты используются в компьютерной терминологии значительно реже, — например, в показателях скорости передачи данных:
• килобит (кбит) — 2 в степени 10 бит —’1024 бит — 128 байт;
• мегабит (Мбит) — 2 в степени 20 бит — 1 048 576 бит —
1024 кбит-128 кб;
• гигабит (Гбит) — 2 в степени 30 бит — 1 073 741 824 бит —
1 048 576 кбит — 1024 Мбит — 128 Мб.
3. 1Представление чисел.
Как было уже сказано, все числовые данные хранятся в машине в двоичном виде, то есть в виде последовательности нулей и единиц, однако формы хранения целых и вещественных чисел различны.
Целые числа хранятся в форме с фиксированной запятой, вещественные числа хранятся в форме с плавающей запятой. В темах 8 и 9 можно прочитать подробное описание способов представления чисел в компьютерах. Заметим, что термин «действительные числа» в компьютерной терминологии заменяется на вещественные числа.
Необходимость различного представления целых и вещественных чисел вызвана тем, что скорость выполнения арифметических операций над числами с плавающей запятой существенно ниже скорости выполнения этих же операций над числами с фиксированной запятой. Существует большой класс задач, в которых не используются вещественные числа. Например, задачи экономического характера, при решении которых данными служат количество деталей, акций, сотрудников и так далее, работают только с целыми числами. Текстовая, графическая и звуковая информация, как это будет показано ниже, также кодируются в компьютере с помощью целых чисел. Для повышения скорости выполнения таких задач и используется представление целых чисел в форме с фиксированной запятой.
Для решения математических и физических задач, в которых трудно обойтись только целыми числами, используется представление чисел в форме с плавающей запятой.
Более того, в современных персональных компьютерах процессоры выполняют операции только над целыми числами в форме с фиксированной запятой.
3. 2Представление текстовых данных
Любой текст состоит из последовательности символов. Символами могут быть буквы, цифры, знаки препинания, знаки математических действий, круглые и квадратные скобки и т. д. Особо обратим внимание на символ «пробел», который используется для разделения слов и предложений между собой. Хотя на бумаге или экране дисплея «пробел» — это пустое, свободное место, этот символ ничем не хуже» любого другого символа. На клавиатуре компьютера или пишущей машинки символу «пробел» соответствует специальная клавиша.
Текстовая информация, как и любая другая, хранится в памяти компьютера в двоичном виде. Для этого каждому символу ставится в соответствие некоторое неотрицательное число, называемое кодом символа, и это число записывается в компьютерную память в двоичном виде. Конкретное соответствие между символами и их кодами называется системой кодировки.
В современных компьютерах, в зависимости от типа операционной системы и конкретных прикладных программ, используются 8-разрядные и 16-разрядные (Windows 95, 98, ХР) коды символов. Использование 8-разрядных кодов позволяет закодировать 256 различных знаков, этого вполне достаточно для представления многих символов, используемых на практике. При такой кодировке для кода символа достаточно выделить в памяти один байт. Так и делают: каждый символ представляют своим кодом, который записывают в один байт памяти. В персональных компьютерах обычно используется система кодировки ASCII (American standard Соде for Information Interchange) — американский стандартный код для обмена информации. В этой системе не предусмотрены коды для русского алфавита, поэтому в нашей стране используются варианты этой системы кодировки, в которые включают буквы русского алфавита. Чаще всего используется вариант, известный под названием «Альтернативная кодировка».
Компьютерные технологии постоянно совершенствуются, и в настоящее время все большее число программ начинает поддерживать шестнадцатибитовый стандарт Unicode, который позволяет кодировать практически все языки и диалекты жителей Земли в силу того, что кодировка включает в себя 65 536 различных двоичных кодов.
3. 3. Представление графической информации
Мониторы современных компьютеров могут работать в двух режимах: текстовом и графическом.
В текстовом режиме экран обычно разбивается на 25 строк по 80 символов в строке. В каждую позицию экрана (знакоместо) может быть помещен один символ. В текстовом режиме на экран монитора можно выводить тексты и простые рисунки, составленные из символов псевдографики. Всего на экране 25 • 80 = 2000 знакомест. В каждом знакоместе находится ровно один символ (пробел — равноправный символ), этот символ может быть высвечен одним из 16 цветов. При этом можно изменять цвет фона (8 цветов), на котором рисуется символ и, кроме того, символ может мерцать, для представления цвета символа нам требуется 4 бита (2 = 16), для представления цвета фона требуется 3 бита (23 = 8), один бит — для реализации мерцания (0 — не мерцает, 1 — мерцает). Следовательно, для описания каждого знакоместо нам требуется 2 байта: первый байт — символ, второй байт — его цветовые характеристики. Таким образом, любой текст или рисунок в текстовом режиме монитора в памяти компьютера (в видеопамяти) занимает 2000 • 2 байта = 4000 байт 4 Кбайта.
В графическом режиме экран разделяется на отдельные светящиеся точки (пиксели), количество которых определяет разрешающую способность монитора и зависит от его типа и режима. Любое графическое изображение хранится в памяти в виде информации о каждом пикселе на экране. Если пиксель не участвует в изображении картинки, то он не светится, если участвует, то светится и имеет определенный цвет. Поэтому состояние каждого пикселя описывается последовательностью нулей и единиц. Такую форму представления графических изображений называют растровой. В зависимости от того, сколькими цветами (размер палитры) мы можем высветить каждый пиксель, рассчитывается размер информации, отводимый под каждый пиксель. Если монитор может работать с 16 цветами, то цвет каждого пикселя описывается 4 битами (24 = 16). Для работы с 256 цветами под каждый пиксель надо будет отвести 8 бит, или 1 байт (28 = 256).
Посчитаем, сколько байт занимает при хранении в памяти картинка, если на экран можно вывести 640 * 480 пикселей, и монитор поддерживает 256 цветов:
640. 480 • 1 байт = 307200 байт 300 Кбайт.
Компьютерное кодирование видеоинформации, также как кино и телевидение, основаны на том, что человеческое зрение позволяет создавать иллюзию движения при частой смене кадров (более 15 раз в секунду), на которых изображены последовательные фазы движения. Для записи 1 секунды цветного изображения без звука (25 кадров размером 1024 * 768 пикселей) потребуется примерно 60 Мбайт (25 4024. 768 • 3 = 58 982 400 байт). При этом на запись двухчасового фильма потребуется более 400 Гбайт.
Из-за больших размеров графических и видео файлов они очень редко хранятся в компьютере в неупакованном виде.
Простейший методов упаковки графических изображений RLE-кодирование ( англ. Run-Length Encoding) — кодирование путем учета числа повторений), позволяющее компактно кодировать длинные последовательности одинаковых байтов. Упакованная последовательность состоит из управляющих байтов, за каждым из которых следуют один или несколько байтов данных. Если старший (самый левый) бит управляющего байта ранен 1, то следующий байт надо при распаковке повторить несколько раз (сколько именно — записано в оставшихся семи битах управляющего байта). Например, управляющий байт 10000101 говорит, что следующий за ним байт нужно повторить 5 раз (так как двоичное число 101 равно 5). Если же старший бит управляющего байта равен 0, то надо взять несколько следующих байтов данных без всяких изменений. Сколько именно — тоже записано в оставшихся 7 битах. Например, управляющий байт 00000011 говорит, что следующие за ним 3 байта нужно взять без изменений.
Другие алгоритмы сжатия графической и видео информации основываются на том, что человеческий глаз более восприимчив к яркости отдельной точкУ1, чем к её цветности.
Поэтому можно при упаковке выбросить данные о цвете каждой второй точки изображения (сохранив только ее яркость), a при распаковке — брать вместо выброшенного цвет соседней точки. Формально распакованное изображение будет отличаться от исходного, однако это отличие будет практически незаметно на глаз. При таком методе упаковки экономия составляет менее 50%. Голее сложные методы упаковки изображений позволяют добиться значительно лучших результатов. Например, алгоритм JPEG (от названия разработавшей его группы — Joint Photographic Experts Group) способен упаковывать графические изображения в несколько десятков раз без заметной потери качества.
Чтобы решить проблему большого объёма информации при записи фильмов, например, сохраняют не кадры, а изменения кадров. К тому же, при упаковке видеоинформации допустимы большие искажения, чем при сжатии статических изображений: кадры меняются быстро, и зритель не успевает рассматривать их детально.
Вводи хранение в компьютере технических чертежей и им подобных графических изображений осуществляется по-другому. Любой чертеж содержит отрезки, окружности, дуги. Например, положение каждого отрезка на чертеже можно задать координатами двух точек, определяющих его начало и конец. Окружность — координатами центра и длиной радиуса. Дугу — координатами конца и начала, центра и длиной радиуса. Кроме того, для каждой линии указывается ее тип: тонкая, штрихпунктирная и Т. д. Такая информация о чертеже вводится в компьютер как обычная буквенно-цифровая и обрабатывается в дальнейшем специальными программами. Эта форма представления изображения называется векторной.
Примером современной компьютерной системы автоматизации черчения, ориентированной на векторную форму представления графической информации, является система AutoCAD. Появившиеся в последние годы высококачественные программы векторизации (преобразования графического изображения из растровой формы в векторную) позволили в значительной мере автоматизировать работу по вводу чертежа в память компьютера с помощью сканеров. Хранение чертежа в компьютере в векторной форме на несколько порядков сокращает необходимый объем памяти и значительно облегчает внесение изменений (редактирование).
3. 4 Представление звуковой информации
Развитие аппаратной базы современных компьютеров параллельно с развитием программного обеспечения позволяет сегодня записывать и воспроизводить на компьютерах музыку и человеческую речь. Существуют два способа звукозаписи:
• цифровая запись, при которой реальные звуковые волны преобразуются в цифровую информацию путем измерения звука тысячи раз в секунду;
• MIDI-запись, при которой, вообще говоря, записывается не реальный звук, а определенные команды-указания (какие клавиши надо нажимать, например, на синтезаторе).
MIDI-запись является электронным эквивалентом записи игры на фортепиано.
Для того чтобы можно было воспользоваться первым указанным способом, в компьютере должна быть звуковая карта (плата).
Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой (сила, интенсивность звука) и частотой (высота тона звука). Частота волны (количество «волн» в секунду) измеряется в герцах (Гц). Чем больше амплитуда сигнала, тем громче звук, чем больше частота сигнала, тем выше тон. Человек воспринимает звуковые волны с частотой из диапазона от 20 Гц до 20 000 Гц.
Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть превращен в цифровую последовательность, состоящую из нулей и единиц. Данную функцию выполняет специальный блок, входящий в состав звуковой карты и называемый аналого-цифровым преобразователем (АЦII).
Реальные звуковые волны имеют весьма сложную форму, и для получения их высококачественного цифрового представления требуется высокая частота дискретизации
АЦП производит дискретизацию звукового сигнала по времени путем измерения уровня интенсивности звука несколько тысяч раз в секунду (через равные пpомежyтки). Частота, с которой производят измерения звукового сигнала, называется частотой дискретизации. Например, при записи музыкальных компакт-дисков используют частоту дискретизации 44 кГц, а при записи речи вполне достаточно частоты дискретизации 8 кГц.
В результате дискретизации амплитуды звукового сигнала непрерывная зависимость амплитуды от времени А(t) заменяется на дискретную последовательность стандартных (заранее определенных) уровней громкости. Графически это выглядит как замена гладкой кривой на последовательность «ступенек». Число разрядов, используемых для записи уровней громкости звука, определяет качество звучания
Таким образом, в ходе оцифровки звука мы получаем поток целых чисел, представляющих собой номера стандартных амплитуд сигналов. Получившиеся значения записываются в виде 0 и 1 в память компьютера (в файлы с расширением. WAV).
Аналоговый электрический сигнал (запись на грампластинке, магнитной ленте) теоретически представляет собой точную копию исходной звуковой волны, а цифровой код — лишь более или менее точное приближение. Тем не менее, цифровая звукозапись имеет множество преимуществ. Так, например, цифровые копии всегда идентичны цифровым оригиналам, а это значит, что записи можно копировать много раз без ухудшения качества.
При воспроизведении записанного в компьютерный файл звука имеет место обратное преобразование: из дискретной цифровой формы — в непрерывную аналоговую. Это преобразование осуществляет устройство, находящееся на звуковой плате и называемое цифро-аналоговый преобразователь (ЦАП).
Хранение звука в виде цифровой записи занимает достаточно много места в памяти компьютера. В качестве примера оценим объем файла, в котором хранится стереоаудио звучание длительностью 1 секунда. При этом при оцифровке звука использовалось 65 536 стандартных уровней звука (для хранения номера уровня требуется 16 бит), а частота дискретизации равна 48 кГц. Следовательно, для хранения в компьютере 1 секунды звучания в оцифрованном виде при заданных характеристиках оцифровки нам требуется
16 бит. 48 000 • 2 = 1 536 000 бит = 192 000 байт = 187,5 Кб.
Умножение на коэффициент 2 связано с тем, что хранится стереозвук.
MIDI-запись была разработана в начале 80-х годов ХХ века (MIDI — Musical Instrument Digital Interfase — интерфейс цифровых музыкальных инструментов). MIDI-иxформация представляет собой команды, а не звуковую волну. Эти команды — инструкции синтезатору. В качестве команды музыкальному синтезатору может передаваться указание нажать или отпустить определенную клавишу, изменить высоту или тембр звучания, изменить силу давления на клавиатуру, включить или выключить полифонический режим и Т. П. MIDI–команды делают запись музыкальной информации более компактной, чем цифровая запись. Однако для записи MIDI-команд вам потребуется устройство, имитирующее клавишный синтезатор, которое воспринимает MIDI-команды и при их получении может генерировать соответствующие звуки.
Из всех видов информации, представимых и обрабатываемых в компьютерах, звуковая информация хуже всего поддается упаковке. Это связано с тем, что звуковые сигналы обладают малой избыточностью (в частности, в закодированных звуковых фрагментах редко появляются повторяющиеся последовательности байтов).
4. Классификация
Система счисления — способ записи чисел с помощью заданного набора специальных знаков (цифр).
Базис – это последовательность чисел, каждое из которых задает значение цифры «по месту» или «вес» каждого разряда.
Основание системы счисления — отношение весов соседних разрядов основной позиционной системы счисления.
Позиционная система счисления — система счисления, в которой вес цифры меняется с изменением положения цифры в числе, но при этом полностью определяется написанием цифры и местом, которое она занимает. В частности, это означает, что вес цифры не зависит от значений окружающих ее цифр.
Непозиционная система счисления — система счисления, в которой вес цифры не зависит от ее положения.
Универсальная система счисления — система счисления, которая позволяет записать любое вещественное число (конечной или бесконечной последовательностью цифр).
Неуниверсальная система счисления — система счисления, которая позволяет записать лишь относительно небольшие числа, иногда только целые (либо наоборот, только меньшие единицы).
Основная система счисления — позиционная система счисления, в которой вес каждой цифры изменяется в одно и то же число раз при ее переносе из любого разряда в соседний с ним.
Неосновная система счисления — позиционная система счисления, в которой соотношение весов соседних разрядов может меняться.
Традиционная система счисления — система счисления, в которой запись числа состоит из двух частей — целой и дробной. Количество цифр перед разделяющей эти части запятой (точкой) заранее не известно и может быть сколь угодно большим. Фактически запись числа образует две последовательности цифр, разбегающиеся влево и вправо от запятой.
Информационная система счисления — система счисления, в которой запись числа (в отличие от традиционной) состоит из единственной последовательности цифр. При этом каждая очередная цифра (бит) уточняет значение числа (его положение на оси).
5. Переход к другому основанию
Любая позиционная система счисления характеризуется тем, что базисом этой системы являются последовательные степени основания, иначе говоря, число единиц соответствующие основанию образуют единицу следующего разряда.
Так неотрицательное число, а в любой системе счисления можно записать как
Таким образом, позиционная система счисления позволяет с помощью заранее ограниченного набора цифр записать в виде суммы степеней основания системы.
На этом и основывается перевод из любой позиционной системы счисления в десятичную систему.
5. 1 Перевод из произвольной позиционной системы счисления в десятичную систему.
Для перевода из любой позиционной системы счисления в десятичную систему используется следующий алгоритм:
Пронумеруем цифры в изначальной записи числа справа налево, начиная с нуля (номера соответствуют степени основания в многочлене )
Умножим каждое число на соответствующую степень основания.
Складываем получившиеся произведения.
Приведем пример:
11012 =1*23 + 1*22 + 0*21+ 1*20= 8+4+0+1=1310
3 2 1 0
1204205= 1*55+2*54+0*53+4*52+2*51+0*50= 3125+1250+0+100+10+0=448510
5. 2 Перевод из десятичной системы в произвольную позиционную систему счисления
Для перевода из десятичной системы счисления в любую позиционную необходимо придерживаться следующего алгоритма:
1. Делим исходное число на основание нацело в десятичной системы счисления и записываем в качестве нового значения десятичного целую часть результата от деления.
2. Остаток от деления (он должен быть не больше основания данной системы) записываем начиная с последнего.
Приведем пример:
4410 переведём в двоичную систему
44 делим на 2. частное 22, остаток 0
22 делим на 2. частное 11, остаток 0
11 делим на 2. частное 5, остаток 1
5 делим на 2. частное 2, остаток 1
2 делим на 2. частное 1, остаток 0
1 делим на 2. частное 0, остаток 1
Частное равно нулю, деление закончено. Теперь записав все остатки, справа налево получим число 1011002
5. 3 Перевод в машинной группе.
Для этого типа операций существует упрощенный алгоритм.
Для восьмеричной — разбиваем число на триады, для шестнадцатеричной — разбиваем на тетрарды, преобразуем триады по таблице
Пример: преобразуем 1011002 восьмеричная — 101 100 → 548 шестнадцатеричная — 0010 1100 → 2C16
Обратный перевод из восьмеричной и шестнадцатеричной в двоичную осуществляется за счет замены цифр соответствующими триадами и тетрардами.
548 → 101 1002
2C16 → 0010 11002
5. 4 Дробное счисление в других системах счисления
До этого в рассмотренных примерах показателем степени основания системы счисления являлось натуральное число, но ничто не мешает перевести показатель степени в диапазон целых чисел, т. е. расширить его в отрицательную полуплоскость. При этом формула, данная в определении будет, также верна.
Рассмотрим пример: число 103,625 можно представить как
Таким образом, из примера видно, что не только целое, но и дробное число можно представить как комбинацию из цифр системы счисления.
5. 4. 1 Перевод из произвольной системы счисления в десятичную систему.
Рассмотрим пример перевода двоичного числа 1100,0112 в десятичное систему. Целая часть этого числа равна 12 (см. выше), а вот перевод дробной части рассмотрим подробнее:
Итак, число 1100,0112 = 12,37510.
Точно также осуществляется перевод из любой системы счисления, только вместо «2» ставится основание системы.
Для удобства перевода, целую и дробную части числа почти всегда переводят по отдельности, а результат потом суммируют.
5. 4. 2 Перевод из двоичной системы в 8- и 16-ричную
Перевод дробной части из двоичной системы счисления в системы счисления с основаниями 8 и 16 осуществляется точно так же, как и для целых частей числа, за тем лишь исключением, что разбивка на триады и тетрады идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа. Например, рассмотренное выше число 1100,0112 будет выглядеть как 14,38 или C,616.
5. 4. 3 Перевод из десятичной системы в произвольную систему
Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в нуль и начать умножение получившегося числа на основании той системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в нуль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль. Ниже приводится пример перевода числа 103,62510 в двоичную систему счисления.
Переводим целую часть по правилам, описанным выше, получаем 10310 = 11001112.
0,625 умножаем на 2. Дробная часть 0,250. Целая часть 1.
0,250 умножаем на 2. Дробная часть 0,500. Целая часть 0.
0,500 умножаем на 2. Дробная часть 0,000. Целая часть 1.
Итак, сверху вниз получаем число 1012
103,62510 = 1100111,1012
Точно также осуществляется перевод в системы счисления с любым основанием.
Сразу нужно отметить, что этот пример специально подобран, в общем случае очень редко удаётся завершить перевод дробной части числа из десятичной системы в другие системы счисления, а потому, в подавляющем большинстве случаев, перевод можно осуществить с какой либо долей погрешности. Чем больше знаков после запятой — тем точнее приближение результата перевода к истине. В этих словах легко убедиться, если попытаться, например, перевести в двоичный код число 0,626.
6. Арифметические действия в позиционных системах счисления.
Все позиционные системы счисления одинаковы, а именно, во всех них арифметические действия выполняются по одним и тем же правилам:
• Справедливы все законы: сочетательный, переместительный, распределительный;
• Справедливы все правила арифметических действий, которые действуют в десятичной системе счисления;
• Правила выполнения арифметических действий опираются на таблицу сложения и умножения Р-ичных цифр.
Для того чтобы производить арифметические действия в позиционных системах счисления необходимо знать соответствующие таблицы умножения и сложения.
5. 1 Сложение.
10012 1111
+10102 + 1
100112 10000
Из приведенных примеров видно, что при сложении столбиком чисел, в данном случае двоичной системы, как и в любой позиционной системе счисления, в следующий разряд переносится только единица.
Нужно сказать, что само действие выполняется аналогично десятичному: цифры по разрядно складываются и при образовании переполнения, оно переносится в следующий разряд в виде степени образовавшегося переполнения. Так же для выполнения сложения используются соответствующие таблицы
6. 2 Вычитание
Чтобы найти разность чисел a и b необходимо найти такое число c, a+c=b.
На этом принципе и основано вычитание во всех позиционных системах счисления.
Например:
-12346 -1101012
1356 110102
10556 110112
6. 3 Умножение
Как известно умножение можно заменить сложением. Например:
6*b=b+b+b+b+b+b
Из этого следует, что умножение в других позиционных системах счисления так же можно заменить сложением то есть:
101*11=101+101+101(так 11 в десятичной системе счисления )
Из этого можно сделать вывод, что умножение во всех позиционных система счисления происходит по одному принципу. В основном для умножения различных чисел недесятичных систем счисления используются соответствующие таблицы умножения
Например:
*1100112 *745628
1112 4458
+ 110011 +457472
+110011 +362710
110011 362710
1011001012 425775728
6. 4 Деление
Деление-это процесс последовательного вычитания одного числа из другого. При делении в десятичной системе счисления мы отнимаем определенное количество делителей из делимого, то есть, уменьшаем число на определенное количество и получаем необходимое число.
Например:
-5568 3
Вывод очевиден, деление во всех позиционных системах счисления происходит по одному и тому же принципу, для сравнения поделим двоичное число 1101102 на 112 и восьмеричное число 554768 на 58:
-110110 11 55476 5
11 10010 — 5 11077
— 0011 -05
00 — 047
Так же для работы используются соответствующие таблицы умножения.
Почему компьютеры используют двоичную систему счисления
Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.
А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
представление информации посредством только двух состояний надежно и помехоустойчиво;
возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
двоичная арифметика намного проще десятичной.
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.
Применение восьмеричной и шестнадцатеричной систем счисления
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре(шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Например:
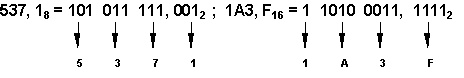
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой натриады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
Например,
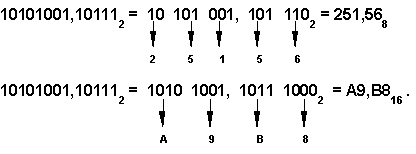
Перевод чисел из десятичной системы счисления в другие позиционные системы счисления
При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q-1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.
Пример: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
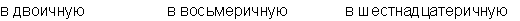
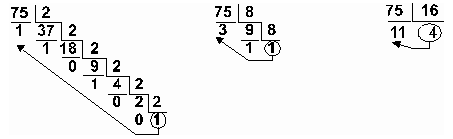
Ответ: 7510 = 1 001 0112 = 1138 = 4B16.
Перевод простой десятичной дроби в другие позиционные системы счисления
Пpи переводе правильной десятичной дpоби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть пpоизведения. Число в новой системе счисления записывается как последовательность полученных целых частей пpоизведения.
Умножение пpоизводится до тех поp, пока дpобная часть пpоизведения не станет pавной нулю. Это значит, что сделан точный пеpевод. В пpотивном случае пеpевод осуществляется до заданной точности. Достаточно того количества цифp в pезультате, котоpое поместится в ячейку.
Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Ответ: 0,3510 = 0,010112 = 0,2638 = 0,5916 .
Двоичная система счисления

Однажды в Риме
Древних римлян часто поминают дурным словом за их громоздкую систему записи чисел. Люди не любят римские числа, так как они обременяют вычисления. Никто не обрадуется перспективе перемножать XLVII и DCDXXIV. А вот задача умножить 47 на 924 не выглядит настолько угрожающей (хотя большинство из нас все равно побежит за калькулятором). Впрочем, прежде чем сбрасывать римские числа со счетов как причудливый анахронизм, нам необходимо признать, что их основополагающий принцип – буквы вместо цифр – используется до сих пор. Этот ключевой аспект римских чисел обрел новое воплощение. Что легче прочесть?
• Реновация школ в нашем округе обойдется в 23000000 долларов
• Реновация школ в нашем округе обойдется в 23 млн долларов
Разумеется, я не стал разделять разряды в первом случае, чтобы число было сложнее прочесть (и я попал в точку, не правда ли?). Но, даже если проставить пробелы, фраза «Пентагон требует дополнительные 19 000 000 000 долларов» сложнее для восприятия, чем «Пентагон требует дополнительные 19 млрд долларов». Иногда удобнее использовать слова вместо чисел.
Мнимое преимущество позиционной системы счисления (это такая система счисления, в которой значение каждого символа в записи числа зависит от его позиции/разряда) – это то, что в ней проще производить вычисления. Но давайте задумаемся о том, сколько сил уходит на перемножение двух чисел. Во-первых, нам необходимо запоминать дополнительные математические данные. К тому же мы обязаны помнить таблицу умножения. Во-вторых, мы проделываем многоуровневую процедуру: сортируем числа по разрядам, умножаем по соответствующему правилу, получаем промежуточные данные, складываем.
Да, десятичные числа легче перемножать, чем их римские аналоги, однако это по-прежнему утомительно. Возникает вопрос, есть ли способ записывать числа, который бы облегчал вычисления. Мы выяснили, что да, есть, но для этого придется пожертвовать наглядностью.
Простейший способ записи чисел – единичная система счисления: мы просто записываем столько же символов (будем использовать цифру 1), сколько единиц в интересующем нас числе. Например, число 3 окажется трехзначным: 111. Сложение и умножение становятся исключительно простыми. Чтобы сложить 3 и 5, мы просто запишем два числа, 111 и 11111, друг за другом (без пробела) – и вот он, ответ: 11111111. Умножать тоже просто. Мы запишем одно число вертикально, а другое горизонтально и получим следующую таблицу:

Затем мы заполним таблицу, поставив единичку в каждом столбце и в каждой колонке:
 Наконец, мы выпишем все единички в ряд и получим ответ: 111111111111111. Складывать и перемножать числа в единичной системе счисления существенно проще, чем десятичные или римские числа. Разумеется, такая простота вычислений дается ценой титанических затрат внимания и времени. Никому не захочется прибегать к этому методу, чтобы перемножить 47 и 924.
Наконец, мы выпишем все единички в ряд и получим ответ: 111111111111111. Складывать и перемножать числа в единичной системе счисления существенно проще, чем десятичные или римские числа. Разумеется, такая простота вычислений дается ценой титанических затрат внимания и времени. Никому не захочется прибегать к этому методу, чтобы перемножить 47 и 924.Компромисс
Числа, записанные в двоичной системе счисления (система счисления с основанием 2), не так привычны нам, как десятичные или римские, но с ними проще делать вычисления. Вот почему в компьютерах используется именно двоичная система. Чтобы разобраться, как она устроена, нам нужно припомнить особенности десятичной системы.
Для записи чисел в десятичной системе счисления используют десять символов, располагаемых в разных комбинациях в ряд по горизонтали. Значение символа зависит от его места в ряду. 29 и 92 означают разные числа, потому что 2 и 9 занимают разные позиции. 29 означает «два десятка и девять единиц». 5804 означает «пять тысяч, восемь сотен, ни одного десятка и четыре единицы». Позиция цифры в десятичном числе означает, на какую степень десяти мы ее умножаем. Напомним, что показатель степени означает, сколько раз мы перемножаем основание: например, 10³ = 10 × 10 × 10. Естественно, 101 = 10. По договоренности, 100 = 1. Это логично, так как каждая следующая степень десяти в десять раз больше предыдущей. Разряды растут справа налево: единицы, десятки, сотни, тысячи, десятки тысяч и т. д. Иными словами, запись 5804 означает:
5 × 10³ + 8 × 10² + 0 × 101 + 4 × 100
1 × 2⁴ + 0 × 2³ + 1 × 2² + 1 × 21 + 0 × 20 = 16 + 4 + 2 = 22
Двоичные числа труднее для чтения, чем десятичные. Двоичная запись 1011001 кажется менее привычной, чем десятичная запись того же числа: 89. Преимущество двоичных чисел в том, что их использование облегчает вычисления. Вместо огромного количества математических данных нам необходимы всего две таблицы:

Заметьте, что в таблице умножения 10 означает число два. Сложение двоичных чисел устроено так же, как в десятичной системе. Например, нам нужно найти сумму 101002 и 11102. Расположим эти числа друг над другом:

Дальше нужно двигаться справа налево, складывая цифры в каждом столбце и при необходимости перемещая единицу на столбец влево. В нашем случае мы сложим два нуля и получим ноль:

Дальше идет столбец двоек. Мы складываем 1 и 0 (переносить ничего не требуется):

Дальше – столбец четверок. Мы складываем 1 и 1, получаем 10, пишем 0, держим 1 в уме и переносим на столбец влево:
 Следующий столбец – восьмерки. Складываем 1 и 0 и 1, получаем 10, пишем 0 и держим 1 в уме:
Следующий столбец – восьмерки. Складываем 1 и 0 и 1, получаем 10, пишем 0 и держим 1 в уме:
Заканчиваем на столбце, означающем, сколько раз в числе встречается 16. Сложение дает 10, мы пишем 0 в текущем столбце и 1 в столбце с разрядом 32:

Мы обнаружили, что 10100 + 1110 = 100010.
Переведем это на язык десятичных чисел:
101002 = 20, 11102 = 14, 1000102 = 34.
Разумеется, 20 + 14 = 34.
Умножение в двоичной системе проще, чем в десятичной. Достаточно усвоить два принципа: сложение двоичных чисел (мы в нем только что разобрались) и умножение на степени двойки.
Умножение числа на 10 в десятичной системе не представляет сложности: мы просто добавляем цифру 0 справа: 23 × 10 = 230. Точно так же выглядит умножение на 2 в двоичной системе: 1101 × 10 = 11010. В случае десятичных чисел это очевидно, в случае двоичных 1101 означает:
1 × 8 + 1 × 4 + 0 × 2 + 1 × 1.
Умножение на 2:
1 × 16 + 1 × 8 + 0 × 4 + 1 × 2 + 0 × 1
Лишний ноль на конце дает 11010.
Умножение на 4, 8 и другие степени двойки тоже просто: например, умножение на 810 (10002) равнозначно приращению трех нулей с правой стороны числа. Итак, умножение превращается в игру «перемести-и-добавь-цифры». Проиллюстрируем это на примере умножения 11010 на 1011. Для начала запишем второе число так:
1011 = 1000 + 10 + 1.
Умножение на 11010 можно представить так:
11010 × 1011 = 11010 × (1000 + 10 + 1) = 11010 × 1000 + 11010 × 10 + 11010 × 1 = 11010000 + 110100 + 11010.
Удобнее умножать в столбик:

А вот и ответ:

Давайте переведем числа в десятичные, чтобы удостовериться, что все правильно:
110102 = 16 + 8 + 2 = 26;
10112 = 8 + 2 + 1 = 11;
1000111102 = 256 + 16 + 8 + 4 + 2 = 286.
Мы не ошиблись: 26 × 11 = 286.
В десятичной системе мы можем записывать не только целые числа. Если поставить в конце запятую, мы получим новые места для цифр: по мере движения вправо степени десяти будут все меньше. Например, 34,27 – это компактный способ записи такого выражения:

Двоичная система тоже позволяет записывать дробные значения. Каждую следующую цифру после запятой (в случае с двоичной системой неправильно говорить «десятичная запятая», лучше называть ее двоичной запятой, или запятой в позиционном представлении числа) мы умножаем на предыдущую степень двойки. Например, 101,0112 означает:

Непривычный способ записать одну вторую: 0,12! Есть и другие системы счисления, помимо десятичной, единичной и двоичной. Программисты нередко пользуются шестнадцатеричной системой счисления. В десятичной системе 10 цифр (от 0 до 9), в шестнадцатеричной нам нужно 16 разных символов, поэтому числа от 10 до 15 обозначают с помощью букв от A до F. В третичной системе мы пользуемся цифрами 0, 1 и 2, здесь все строится на степенях тройки. Скажем, 11023 означает:
1 × 27 + 1 × 9 + 0 × 3 + 2 × 1 = 38
В дробях первая позиция справа от запятой означает умножение на одну третью, вторая позиция – на одну девятую и т. д.:

Ответ на задачу
Если представить 42 в виде суммы степеней двойки, мы увидим, что это 1010102. А число 110112 можно представить как 16 + 8 + 2 + 1 = 27.
Двоичная система счисления — Знаешь как
Содержание статьи
 При вычислениях мы обычно пользуемся десятичной позиционной системой. В этой системе знаки 0, 1,2, 3, 4, 5, 6, 7, 8, 9, называемые цифрами, представляют нуль и первые девять целых чисел. Десять обозначается двумя цифрами 1 и 0 и является основанием системы. Каждая цифра представленного ряда имеет различную значимость в зависимости от ее позиции или места в числе. Например, в числе 345,2: справа от запятой, две десятых — 2•10-1; слева от запятой — пять единиц — 5-10°; четыре десятка — 4 • 101 и три сотни — 3 • 102. Следовательно, все число представляется так:
При вычислениях мы обычно пользуемся десятичной позиционной системой. В этой системе знаки 0, 1,2, 3, 4, 5, 6, 7, 8, 9, называемые цифрами, представляют нуль и первые девять целых чисел. Десять обозначается двумя цифрами 1 и 0 и является основанием системы. Каждая цифра представленного ряда имеет различную значимость в зависимости от ее позиции или места в числе. Например, в числе 345,2: справа от запятой, две десятых — 2•10-1; слева от запятой — пять единиц — 5-10°; четыре десятка — 4 • 101 и три сотни — 3 • 102. Следовательно, все число представляется так:345,2 = 3 • 102 + 4 • 101 + 5 • 100 + 2 • 10-1 единиц.
Рис. 16-10. Двоичное счисление при работе на конторских счетах
Если представить себе счетчик любой системы, то он в каждом разряде должен быть способным принимать девять различных устойчивых положений. Для ЦВУ оказалась удобной система с основанием 2, называемая двоичной, при которой имеются только две цифры 0 и 1. Когда в первом (правом) разряде вместо единицы должно появиться два (2), то двойка переносится в виде единицы (1) в старший разряд, а в младшем ставится
Такой счет получается, если пользоваться счетами, имеющими на каждой спице только по две костяшки (рис. 16-10).
Ниже приведены несколько чисел, написанных в двоичной системе:
| 1 | — один | 1011 | — одиннадцать |
| 10 | — два | 1100 | — двенадцать |
| 11 | — три | 1101 | — тринадцать |
| 100 | — четыре | 1110 | — четырнадцать |
| 101 | — пять | 1111 | — пятнадцать |
| 110 | — шесть | 10000 | — шестнадцать |
| 111 | — семь | 0,1 | — половина |
| 1000 | — восемь | 0,01 | — четверть |
| 1001 | — девять | 0,001 | — восьмая |
| 1010 | — десять | 0,11 | — три четверти |
Таким образом, число двоичной системы 1011,1 представляет: справа от запятой, одна половина— 1•2-1 и слева от запятой одна единица — 1-20, одна двойка — 1•21, нуль четверок — 0•22 и одна восьмерка—1•23, т. е. (1011,1)2 = 1•23+0•22+1•21+1•20+1•2-1= (8 + 0 + 2 + 1 + 0,5= 11,5)10. Индексы 2 и 10 обозначают основание системы.
 Как можно видеть, в этом случае наличие цифры в каждом разряде (1) или отсутствие ее (0) может характеризоваться счетчиками релейного типа, управляемыми импульсами: включено — выключено,есть сигнал напряжения — нет сигнала, намагничен участок магнитной ленты — не намагничен и т. д.
Как можно видеть, в этом случае наличие цифры в каждом разряде (1) или отсутствие ее (0) может характеризоваться счетчиками релейного типа, управляемыми импульсами: включено — выключено,есть сигнал напряжения — нет сигнала, намагничен участок магнитной ленты — не намагничен и т. д.
Например, двоичное число 10111 может быть передано сигналами (импульсами) напряжения, показанными на рис. 16-11. Этот принцип и применяется в ЦВУ. Недостаток двоичной системы; в большом количестве разрядов счетчика по сравнению с системой десятичной, но он искупается большей простотой всего ЦВУ в целом. Перевод чисел из десятичной системы в двоичную и обратно производит само
ЦВУ.
Рис. 16-11. Передача двоичного числа серией импульсов.
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ В ДВОИЧНОЙ СИСТЕМЕ
Большое достоинство двоичной системы в простоте арифметических действий с числами, которые производятся так же, как и в десятичной системе. Сложим два числа, изображенные слева в десятичной системе, а справа — в двоичной..
В десятичной системе при сложении 5 + 9 единица (т. е. один десяток) переносится в старший разряд (десятков) и прибавляется к числам десятков 2 + 1. Точно так же и в двоичной системе: две единицы первого (правого) разряда дают двойку, которая, как единица, переходит в разряд двоек, а в сумме первого разряда получается нуль. Две единицы (двоек) второго разряда дают в сумме четверку, которая, как единица, переносится в разряд четверок. Сумма в разряде двоек равна нулю, а в разряде четверок — единице и т. д.
При вычитании в десятичной системе из разряда десятков пришлось занимать единицу и разность равна шести. При двоичной системе, в случае необходимости, из старшего разряда приходится занимать двойку, четверку и т. д. В первом разряде разность равна нулю. Во втором разряде из занятой двойки вычитается единица и в разности остается единица. В третьем разряде остается единица, а в четвертом и пятом нули.
В ЦВУ вычитание обычно заменяется сложением с числом, записанным обратным кодом, т. е. когда единицы числа заменены нулями,-а нули — единицами. При десятичной системе это делается так: уменьшаемое 25 складывается с числом, дополняющим вычитаемое до числа, выраженного единицей с нулями (100—19 = 81), и в сумме отбрасывают единицу высшего разряда. Ответ получается шесть, как и при вычитании.
В двоичной системе к числу 11001. прибавляется число 10011, записанное обратным кодом, т. е. число 01100. Далее, единица старшего разряда суммы переносится в младший разряд и прибавляется к нему. Ответ получается тот же, что и при вычитании. Все это выполняет самостоятельно арифметическое устройство ЦВУ. Таблица умножения в двоичной системе необычайно проста:
0.0 = 0; 1.0 = 0.1 = 0; 1.1 = l.
Таким образом, при умножении на единицу множимое число переписывается в соответствующий разряд, а при умножении на нуль производится сдвиг влево на один разряд. Все умножение сводится к сдвигу умножаемого числа на один разряд и сложению, что и выполняет арифметическое устройство.
Деление сводится к многократному вычитанию делителя из делимого и дополнению получаемого остатка справа
т. е. 56 : 8 = 7.
Так как умножение заменяется многократным сложением, деление — многократным вычитанием, а вычитание может быть заменено сложением, то все арифметические действия сводятся к сложению.
ПРИНЦИП РАБОТЫ НЕКОТОРЫХ ЭЛЕМЕНТОВ ЦВУ
Все ЦВУ состоит из устройств: запоминающего, управления, арифметического и др., а каждое из них из отдельных типовых элементов, называемых ячейками. Каждая ячейка выполняет определенные действия и, будучи включена определенным образом в общую схему, пропускает или задерживает посланный импульс усиливает его или сдвигает на разряд и т, д.
Данное состояние ячейки определяется высоким или низким уровнем напряжения, подаваемого на нее, наличием или отсутствием импульса напряжения или использованием импульсов двух полярностей. В ЦВУ используются приборы с односторонней проводимостью, электронные и полупроводниковые диоды и триоды.
Эти приборы в дальнейшем изображаются так, как показано на рис. 16-12. Прибор пропускает ток, когда потенциал анода выше потенциала катода (сопротивление прибора мало) и запирается при обратной полярности напряжения (сопротивление прибора очень большое).
а) Клапан или вентиль
 Рис. 16-12. Условное изображение вентиля.
Рис. 16-12. Условное изображение вентиля.
Клапан (вентиль) показан на рис. 16-13. Само название показывает, что он предназначен для задержки или пропуска импульса напряжения. Действительно, если на верхнюю точку входа подан прямоугольный импульс положительной полярности, то через вентиль пойдет ток от анода к катоду и через электрические цепи управляющего входа, не показанные на рисунке, к заземлению. Сопротивление rвелико, а сопротивление вентиля ничтожно и можно считать, что все напряжение падает на сопротивлении r. Следовательно, потенциал анода, а значит, и выход схемы почти не отличается от потенциала земли. Поэтому считают, что на выход импульс не передался (на выходе нуль). Если одновременно с импульсом на входе подать на управляющий вход положительный импульс такой же величины или большей, чем на входе, то вентиль запрется. Ток в сопротивлении r будет равен нулю,
а потенциал выхода равен потенциалу входа, т. е. положительный импульс передан на выход (единица). Этот механизм работы осуществляется во всех схемах с вентилями, приведенных ниже.
Рис. 16-13. Схема работы клапана.
б) Схема совпадения
Схема совпадения (условное обозначение И) показана на рис. 16-14. При появлении положительного импульса на анодах вентилей через них проходит ток. На сопротивлении r падает почти все напряжение и импульс на выход не передается (нуль). Если подать положительный импульс на один из входов A, Б и В, дело не меняется, так как ток будет проходить через два других вентиля. Положительный импульс (единица) передается на выход только в том случае, когда одновременно все три вентиля заперты положительными импульсами на управляющих входах A, Б и В почему и схема называется схемой совпадения.
 в) Собирательная схема
в) Собирательная схема
Рис. 16-14. Логическая схема совпадения.
Собирательная схема (условное обозначение ИЛИ) показана на рис. 16-15. При подаче положительного импульса, хотя бы на один из входов А, Б, В, через сопротивление r будет протекать ток. Так как внутреннее сопротивление вентилей ничтожно, то все падение напряжения сосредоточено на сопротивлении r, а верхняя точка его и, значит, верхняя точка выхода будут точкой высокого потенциала (единица). Схема потому и называется собирательной, что собирает
импульсы (единицы), поступающие с разных направлений. Одновременно она при подаче положительного импульса на один из входов, например А, запирает высоким потенциалом два других входа Б и В.
г) Схема инвертора
 Рис. 16-14. Логическая схема совпадения.
Рис. 16-14. Логическая схема совпадения.
Схема инвертора (условное обозначение НЕ) показана на рис. 16-16. При отсутствии сигнала (нуль) на входе триод заперт отрицательным напряжением смещения Ес. Потенциал верхней точки выхода равен потенциалу положительного зажима источника анодного напряжения Еа, т. е. на выходе единица. При появлении положительного импульса на входе (сетке) триод проводит ток и напряжение нижней точки сопротивлений r, т. е, навходе резко падает (нуль). Таким образом, входной сигнал — единица преобразуется в сигнал — нуль.
Из схем основных схем формируются все более сложные схемы ЦВУ. В дальнейших схемах заземляющая их часть для простоты не показывается.
д) Цепочка клапанов
Цепочка клапанов с одним управляющим входом показана на рис. 16- 17. Импульсы с входов на выходы могут быть переданы только в том случае, когда на управляющий вход подан импульс, Запирающий вентили. Если этого импульса нет, то при положительных импульсах на входах через вентили проходит ток и благодаря большому падению напряжения на сопротивлениях r потенциал анодов и выходов близок к нулю.

Рис. 16-15. Логическая схема собирательная.
е) Схема сдвигателя
Схема сдвигателя на один разряд дана на рис. 16-18. Как было показано выше, при умножении на единицу в двоичной системе само множимое число записывалось в соответствующий разряд, а при умножении на нуль это же число записывалось со сдвигом на один разряд. Операцию сдвига и выполняет сдвигатель.
Если высокий потенциал существует только на входах цифр, а на шинах I и II такого потенциала нет, то токи проходят через диоды 1,2,8,4и потенциалы на выходах очень малы (сигналов нет). При подаче положительного импульса на шину I запираются диоды 1 и 2; импульсы проходят через диоды 6 и 8 на средний и правый выходы. Диод 7 заперт высоким потенциалом левого входа. Если подать импульс на шину II, то запираются диоды 3 и 4. Через диоды 5 и 7 импульсы передаются на левый и средний выходы (сдвигаются влево), а диод 6 блокирован высоким потенциалом.
ж) Электронный триггер
Рис. 16-16. Логическая схема инвертора.

Электронный триггер или электронное реле является наиболее важным элементом ЦВУ. Он собирается из двух триодов или одного двойного триода, как показано на рис. 16-19. Особенность этого реле в том, что устойчивое состояние его будет только тогда, когда через одну половину лампы, например правую, ток проходит, а через другую — левую, нет, и наоборот.
Предположим невозможное, что через лампы Л1 и Л2 проходят равные токи. Пусть под влиянием ничтожнейшего, случайного изменения сопротивления в цепи лампы Л1 ток ее возрос. Тогда потенциал точки 1 уменьшится, ток делителя r5r6 уменьшится, потенциал точки 2, а значит, напряжение на сетке лампы Л2 упадет и ток в ее анодной цепи уменьшится. При этом увеличится потенциал точки 3, а следовательно, и напряжение на сетке лампы Лг. В результате этого ток в анодной цепи лампы Л1 лавинообразно нарастает, а лампы Л2 — падает. Таким образом, триггер за микросекунды приходит в такое состояние, когда лампа Л1 проводит ток (триод открыт), а лампа Л2 — заперта. Если подать положительный импульс на вход 2 или отрицательный на вход 1, то мгновенно лампа Л1запирается, а лампа Л2 — открывается.
Рис. 16-17. Цепочка клапанов с одним управляющим входом.
Схема триггера применяется в запоминающих устройствах и служит для запоминания только одного разряда числа.
 Она может быть выполнена и на полупроводниковых триодах. Емкости, включенные параллельно сопротивлениям r3, r5 служат для ускорения переброса триггера, так как, представляя в этот момент очень малые сопротивления, они шунтируют большие сопротивления r3 и r5.
Она может быть выполнена и на полупроводниковых триодах. Емкости, включенные параллельно сопротивлениям r3, r5 служат для ускорения переброса триггера, так как, представляя в этот момент очень малые сопротивления, они шунтируют большие сопротивления r3 и r5.
ПРИНЦИП РАБОТЫ ДВОИЧНОГО СЧЕТЧИКА
Как было сказано выше, триггер служит для запоминания одного разряда числа двоичной системы и фиксирует наличие цифры в разряде (единица) или отсутствие ее (нуль). Таким образом, количество триггеров равно количеству разрядов числа. Цепочка триггеров для запоминания одного числа называется регистром.
На рис. 16-20 показана схема работы двоичного счетчика на три разряда — три последовательно соединенные триггера. Пусть триггеры № 7, №2, №3, показанные в верхнем ряду, находятся в таком состоянии, когда проводит ток их левая часть (заштриховано) и не проводит — правая. Это состояние принято за нуль и число, записанное триггерами, 000. На вход триггера № 1 приходит серия равномерно следующих импульсов.
Рис. 16-18. Схема сдвигателя на один разряд.
 Первый из них произведет переброс триггера в обратное состояние (1), что показано стрелкой → слева направо, на второй строке на рис. 16-20. На счетчике записано число 001. Второй импульс производит обратный переброс триггера № 1, справа налево, при котором проводит левая половина (0), но при этом перебросе триггер выдает свой импульс триггеру 2, в котором произойдет переброс слева направо. Таким образом, записано число 010.
Первый из них произведет переброс триггера в обратное состояние (1), что показано стрелкой → слева направо, на второй строке на рис. 16-20. На счетчике записано число 001. Второй импульс производит обратный переброс триггера № 1, справа налево, при котором проводит левая половина (0), но при этом перебросе триггер выдает свой импульс триггеру 2, в котором произойдет переброс слева направо. Таким образом, записано число 010.
При третьем импульсе на входе триггера № 1 происходит запись еще единицы —001; при четвертом прибавляется еще единица, а так как переброс был справа налево, то происходит передача импульса на триггер № 2. Переброс последнего был справа налево, следовательно, триггеру № 3 передается импульс уже с триггерами. Число, записанное на счетчике, равно 100, и т. д. Восьмой импульс произведет сброс всего числа. Таким образом, трехразрядный счетчик записывает числа от 0 до 7 десятичной системы.
ПРИНЦИП РАБОТЫ СУММАТОРА АРИФМЕТИЧЕСКОГО УСТРОЙСТВА
Предположим, что следует сложить два двоичных числа А = 1110 и Б = 1101. Сложение производится последовательно, разряд за разрядом, как при обычном счете.
 Рис. 16-19. Схема триггера.
Рис. 16-19. Схема триггера.
При сложении чисел первого разряда 0+1 в сумме получается 1; так же и при сложении чисел второго разряда 1 + 0 получается 1. При сложении чисел третьего разряда 1 +1 получается 2 . Следовательно, двойка, как единица, переносится в четвертый разряд или, как мы говорим, (единица вуме). Эта единица поставлена в строке переноса П, над числом А, Складывая четвертый разряд, получаем 3; половина двойки, т, в/1, идет и сумму С, а единица переноса переходит в сумму пятого разряда, где
С = П + А + Б = 1 + 0 + 0 = 1
Очевидно, устройство для суммирования — сумматор пpи последовательном суммировании, как это делалось, должен иметь два входа для чисел А и Б, вход для переноса П, выход для суммы С и выход для числа П, переносимого в следующий разряд. Блок-схема такого устройства, состоящего из запоминающего блока, однозарядного сумматора и устройства задержки (для переноса) на один разряд, показана на рис. 16-21.
Рис. 16-20. Работа двоичного счетчика.
 Схема работы сумматора (рис. 16-22), осуществляется при помощи логических схем И, ИЛИ, НЕ. Для простоты все устройства заземления, формирования импульсов, усиления их на рис. 16-22 не показаны. При разборе схемы необходимо вспомнить следующее.
Схема работы сумматора (рис. 16-22), осуществляется при помощи логических схем И, ИЛИ, НЕ. Для простоты все устройства заземления, формирования импульсов, усиления их на рис. 16-22 не показаны. При разборе схемы необходимо вспомнить следующее.
Так как все схемы И, кроме И1, присоединены к положительному зажиму источника энергии Еа, то через сопротивления r этих схем и внутреннее сопротивление источников сигналов проходит ток. Отрицательный зажим источников заземлен. Потенциал анодов этих схем невысок, так как значительная часть напряжения падает на сопротивлениях r. Импульсы высокого потенциала на анодах появляются только в те моменты, когда на все катоды приходят положительные импульсы напряжения, способные запереть вентили. Только тогда положительные импульсы схем И передаются дальше.
Через схемы ИЛИ положительный импульс проходит, если он подается хотя бы к одному аноду вентиля.
Схема НЕ заперта отрицательным потенциалом на сетке лампы. При этом потенциал ее анода высок, так как в ее анодном сопротивлении r ток не протекает. Этим потенциалом нормально заперт вентиль И1, и только в этом состоянии через его сопротивление г может пройти положительный импульс на выход С.
При появлении положительного импульса напряжения на сетке лампы она пропускает ток, потенциал на ее аноде падает и схема И1 открывается. В этом случае потенциал анода вентиля И1 при поступлении импульса от схемы ИЛИ1 будет низким, так как ток проходит через лампу схемы НЕ. Потенциал выхода С тоже, будет низким.
 Рис. 16-21. Блок-схема работы сумматора.
Рис. 16-21. Блок-схема работы сумматора.
Теперь можно рассмотреть процесс сложения двух предложенных выше чисел. Триггеры регистра суммы С запоминающего устройства (рис. 16-21) перед началом операции сложения ставятся на нуль. Устройство управления посылает периодически импульсы, которыми и управляется схема. За каждый период складываются цифры одного разряда.
В течение первого импульса из запоминающего устройства (рис. 16-21) выбираются цифры младшего разряда А = 0 и Б = 1. Другими словами, на вход Б сумматора (рис. 16-22) поступает импульс положительного потенциала, а на входе А его нет. Тогда импульс проходит схему ИЛИ 1, сопротивление r схемы И 1, ИЛИ 2, на выход Сив младшем разряде регистра запоминающего устройства суммы С триггер перебрасывается в положения 1. Вторым импульсом из запоминающего устройства выбираются цифры А = 1 и 5 = 0. Импульс через вход (рис. 16-22) проходит схему ИЛИ 1, И1, ИЛИ2 и попадает на выход С. Триггер второго разряда запоминающего устройства перебрасывается в положение 1 (рис. 16-21).
 Ряс. 16-22. Схема работы сумматора.
Ряс. 16-22. Схема работы сумматора.
Третий импульс выбирает из запоминающего устройства цифры А = 1 и Б = 1 и на входе сумматора А, Б получаются положительные импульсы. Тогда запирается схема И2 и выдает положительный импульс на схему ИЛИ3. Импульс проходит на схему задержки Я и на сетку лампы схемы НЕ. Лампа отпирается и начинает проводить ток. Диод схемы И 1 отпирается, импульсы А и Б через схему ИЛИ 1 и схему И 1 проходят через лампу схемы НЕ. Потенциал анода схемы И1 низкий и на выход С через схему ИЛИ 2сигнал не поступает. Триггер третьего разряда С запоминающего устройства остается в положении 0.
Импульс напряжения на линии задержки задерживается до момента суммирования цифр четвертого разряда. Это равносильно тому, как человек держит единицу «в уме». Об устройстве линии задержки (З)будет сказано ниже.
В четвертый такт сложения, два импульса А, Б и импульс Я, выходящий из линии задержки, запирают схемы И2, И3, И4, которые через схему ИЛИ3 выдают второй импульс на схему задержки и схему НЕ. В этом случае, как уже указывалось, схемы ИЛИ 1 и И1 не выдают импульса на выход С. Однако поскольку схема И 5 заперта высоким потенциалом входа А, Б и первым импульсом схемы задержки П, то потенциал ее анодов становится высоким и через схему ИЛИ 2 на выход, в запоминающее устройство поступает импульс высокого напряжения. Происходит переброс триггера четвертого разряда в положение 1.
При пятом такте импульсы А, Б отсутствуют, но возникший импульс переноса при суммировании предыдущего разряда через линию задержки схемы ИЛИ 1, И 1, ИЛИ 2 выдается на выход С в пятый разряд сумматора. Триггер этого разряда записывает 1. Таким образом, просуммированы числа 1110 + 1101 = 11011 или в десятичной системе 14 + 13 = 27.
 На рис. 16-23 показан один из способов устройства линии задержки, Он основан на акустическом принципе. В стальную трубку 1, заполненную ртутью 2, вставлены две пластины из кварца 3, при помощи резиновых колец 4. Кварц имеет способность изменять свой объем при помещении его в изменяющееся электрическое поле. Если на вход одной пластинки подать импульс напряжения, то он вызовет механические колебания самого кварца и ртути в трубке, которые, с определенной скоростью, будут переданы другой кварцевой пластинке на выходе. Эти механические колебания кварц способен переобразовывать в электрические колебания на выходе. Скорость прохождения механических колебаний в ртути неизмеримо меньше скорости распространения электрических импульсов и поэтому электрический импульс передается с задержкой. Время задержки обычно составляет микросекунды. Меняя длину трубки, можно изменять время задержки.
На рис. 16-23 показан один из способов устройства линии задержки, Он основан на акустическом принципе. В стальную трубку 1, заполненную ртутью 2, вставлены две пластины из кварца 3, при помощи резиновых колец 4. Кварц имеет способность изменять свой объем при помещении его в изменяющееся электрическое поле. Если на вход одной пластинки подать импульс напряжения, то он вызовет механические колебания самого кварца и ртути в трубке, которые, с определенной скоростью, будут переданы другой кварцевой пластинке на выходе. Эти механические колебания кварц способен переобразовывать в электрические колебания на выходе. Скорость прохождения механических колебаний в ртути неизмеримо меньше скорости распространения электрических импульсов и поэтому электрический импульс передается с задержкой. Время задержки обычно составляет микросекунды. Меняя длину трубки, можно изменять время задержки.
Рис. 16-23. Устройство акустической линии задержки.
Статья на тему Двоичная система счисления
Двоичная система — это… Что такое Двоичная система?
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:
- Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток — нет тока, индукция магнитного поля больше пороговой величины или нет и т. д.
- Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину индукции магнитного поля, потребуется ввести два пороговых значения, что не будет способствовать помехоустойчивости и надёжности хранения информации.
- Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.
- Возможно применение аппарата алгебры логики для выполнения побитовых операций над числами.
В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).
1 + 0 = 1 1 + 1 = 10 10 + 10 = 100
Таблица умножения двоичных чисел
0 • 0 = 0 0 • 1 = 0 1 • 0 = 0 1 • 1 = 1
Использование двоичной системы при измерении дюймами
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 715/16″, 311/32″ и т. д.
Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1 называется двоичной точкой.
Преобразование двоичных чисел в десятичные
Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | ||||
| 32 | +16 | +2 | +1 |
Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Либо 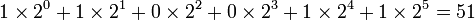 .
.
Преобразование методом Горнера
Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.
Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа
Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.
unsigned int to_deg_2(unsigned int num){
int i;
if ( num == 1 ) return 2;
for( num-=1,i=1; i < sizeof(unsigned int)*8; i*=2 ) num = num|(num>>i);
return num+1;
}
Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
19 /2 = 9 с остатком 1 9 /2 = 4 c остатком 1 4 /2 = 2 с остатком 0 2 /2 = 1 с остатком 0 1 /2 = 0 с остатком 1
Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.
Другие системы счисления
В статье «Системы счисления (продолжение)»[1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.
См. также
Ссылки
- ↑ http://potan.livejournal.com/91399.html Системы счисления (продолжение)
Wikimedia Foundation. 2010.
Обсуждение:Двоичная система счисления — Википедия
Уважаемые «викиавторы» (не знаю как к вам обратиться :)) В статье не раскрыт маленький, но очень спорный вопрос — как правильно читать числа в двоичной записи. к примеру: 112 — следует считать как «три» или как «одиннадцать»? для меня это казалось очевидным, до тех пор, пока я не встретил противоположную точку зрения. Изученная литература также не дала ответа, в математической литературе не встречаются числа прописью. 188.92.110.27 09:07, 17 сентября 2012 (UTC)CTPAHHuK
- Вопрос интересный. Я не встречал таких правил, но я бы произносил по символам «один-один». Так например число записанное с шеснадцатиричным основание 1B3F по другому прочитать просто нельзя. —Pintg 08:33, 18 сентября 2012 (UTC)
Отрицательные числа вообще нераскрыты 217.151.131.30 07:13, 30 июня 2010 (UTC)
В двоичной системе же нельзя чтобы первая была 0!Но так получается если переводить чётное по примеру в вики:
18|0
9 |1
4 |0
2 |0
Замечание не верно даже на половину ;-).Произведенные вычисления не верны. По примеру следует так:
18/2=9 | 0 9/2=4 | 1 4/2=2 | 0 2/2=1 | 0 1/2=0 | 1 Полученное таким образом двоичное число 10010 легко переводится в десятичное 18. Утверждать что:"В двоичной системе же нельзя чтобы первая была 0!" - вообще кощунство!!! :-D То есть: начинаем счет с "0" - записывается в двоичном формате как "0" или "000000", причем нолей ставте сколько необходимо, в переводе на десятичный формат все равно будет "0". Так же запись в двоичном формате единицы выглядит как "01" или "000000001". Даже число "18" можно в двоичной системе записать как "10010" и как "0010010" Все верно! 95.28.19.149 06:27, 24 октября 2009 (UTC)Oll
Вопросы и пожелания пишите сюда.
«Двоичная система счисления (или система счисления с основанием 2) — это положительная целочисленная позиционная (поместная) система счисления, позволяющая представить различные численные значения с помощью двух символов. Чаще всего это 0 и 1.» ограничения «положительная», «целочисленная» — лишние. Никто не запрещает поставить ни запятую, ни знак «-» перед числом. 79.98.53.214 20:17, 12 января 2009 (UTC)
«Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину индукции магнитного поля, потребуется ввести два пороговых значения, что не будет способствовать помехоустойчивости и надёжности хранения информации.» ещё раз «что не будет способствовать помехоустойчивости и надёжности хранения информации.»
- -)))
«и тем быстрее он может работать»
очень спорно
79.98.53.214 20:50, 12 января 2009 (UTC)
Спорно — для тех, кто не понял, для тех, кто понял — бесспорно.92.243.182.100 21:51, 4 января 2011 (UTC)
Как двоичные в десятичные переводить с помошью таблицы понятно а вот «наоборот» табличным способом, что то я не разобрался!
94.253.45.207 13:56, 5 апреля 2009 (UTC)
Предлагается дату 10.10.10 (в полном формате — «10.10.10 10:10:10») сделать датой (днём) двоичной системы счисления Fractaler 14:17, 10 сентября 2009 (UTC)
Сравнение с другими системами счисления[править код]
Сравнение с другими системами счисления имеет смысл только в контексте применения двоичной системы счисления в цифровых устройствах. Именно поэтому информация перенесена в раздел Применения -> В цифровых устройствах. Maxal 19:08, 3 ноября 2009 (UTC)
А как называется система: 1-цифра, отвечает есть ли там 1 2-есть ли там 2 3-есть ли там 4 и т.д.
к примеру: 0001 — 8 1010 — 5 1000 — 1 00001-16 — Эта неподписанная реплика была добавлена участником 14:01, 6 марта 2010 (обс. · вклад) в 95.190.58.127 (UTC). Подписывайте свои сообщения с помощью ~~~~.
- Та же двоичная, но задом наперёд? Разве это где-нибудь употребляется? infovarius 19:51, 6 марта 2010 (UTC)
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″
Это что за бред? Какое отношение имеет обыкновенная дробь к двоиным числам? 91.151.37.213 11:53, 27 февраля 2011 (UTC)
- Это двоичная дробь — т.е. дробь, знаменатель которой является степенью двойки. Даже если она записана как обычная, она всё равно остаётся двоичной. — Monedula 18:57, 27 февраля 2011 (UTC)
Парадокс? или Я где-то ошибся?[править код]
Расчитывая «простейшие» расчеты в двоичной системе «нашел» парадокс.
Перевожу 510 в двоичною.
[5\2=2] 1
[2\2=1] 0
[1\2=0] 1
510=1012
Так-же перевел 2 и 3 из десятичной в двоичною.
210=102
310=112
Добавим 112 и 102.
1
10
+11
101
Пока что всё правильно:2+3=5.
Дальше 1012-112.
1 101
-11
000
СТОП. 5-3=0? Ну ладно пусть 1012-102.
1 101
-10
001
Да ладно, вы серьзно думаете что 5-3=0 и 5-2=1? Найдите в расчетах ошибку, а то кажеться полный бред здесь. 93.75.45.28 13:33, 12 апреля 2014 (UTC)
- Вычитание в столбик как делается забыли?
1 101
-11
010
- ASDFS 15:35, 12 апреля 2014 (UTC)
Хорошо, может быть человек где-то ошибся, но програмы расчёта!!! Например здесь: http://math.semestr.ru/inf/operation.php
Подставим 101-11 и 101-10(поставить вычитание и двоичную систему, изначально цифры подаються в 10-чной) и получим по нулю и единице! То есть и компьютеры и люди ошиблись? 93.75.45.28 21:51, 12 апреля 2014 (UTC)
- Это все последствия краха школьного образования. Если программист необразован то компьютер не виноват. Заканчивайте этот балаган, а то мне кажется что вы это затеяли чтобы ссылку прилепить. ASDFS 22:26, 12 апреля 2014 (UTC)

