Длительность — сигнал — Большая Энциклопедия Нефти и Газа, статья, страница 1
Длительность — сигнал
Cтраница 1
Длительность сигнала практически всегда конечна, а ширина частотного спектра ограничивается диапазоном частот гармоник, сумма которых описывает сигнал с приемлемой для практики допустимой погрешностью. [1]
Длительность сигнала определяет время его существования, ширина спектра — диапазон частот, в котором сосредоточена основная энергия. Эти характеристики полезны при определении требований, предъявляемых к каналам связи. Например, для неискаженной передачи сигналов емкость канала ( см. § 1.3) должна быть не меньше объема сигнала. [2]
Длительность сигнала Pi1 0 задается изменением сдвига пневмоповторителя, а длительность сигнала Pi1 1 уже сдвигом другого пневмоповторителя. [3]
Длительность сигнала и ширина его спектра подчиняются соотношению неопределенности, гласящему, что произведение этих параметров ( база сигнала) не может быть меньше единицы. Ограничений максимального значения базы сигнала не существует. А вот короткий сигнал с узким спектром, согласно соотношению неопределенности, существовать не может. [5]
Длительность сигнала и ширина набора частот волн, из которых сигнал состоит, связаны обратно пропорциональной зависимостью. Качественно это соотношение понятно: если имеется длинный обрывок синусоиды, соответствующий сигналу большой длительности ( Д велико), то это почти монохроматическая волна ( Дш мало), А чтобы составить короткий сигнал, нужно сложить много волн с разными частотами. Все, наверное, замечали, что удар молнии вызывает помехи в радиоприемнике во всех диапазонах частот. [7]
Длительность сигнала ( импульса электромагнитных волн) составляет миллионные доли секунды. На экране электронно-лучевой трубки радиолокатора луч развертывается с постоянной скоростью, причем частота развертки равна числу сигналов, посылаемых в секунду станцией. В момент отправления очередного импульса подается и импульс напряжения на пластины конденсатора, управляющего вертикальным смещением луча. После этого антенна радиолокатора переключается на прием. Радиосигнал, достигая цели, рассеивается на ней и частично отражается обратно. Отраженный сигнал принимается, усиливается и дает вторую вертикальную отметку на экране осциллографа. Положение первой отметки, получаемой при отправлении сигнала, строго неподвижно. [8]
Длительность сигнала на выходах определяется интервалом времени между приходом сигнала на переключение триггера и сигналом, который должен вернуть его в исходное состояние. [10]
Длительность сигнала ( импульса электромагнитных волн) составляет миллионные доли секунды. На экране электронно-лучевой трубки радиолокатора луч развертывается с постоянной скоростью, причем частота развертки равна числу сигналов, посылаемых в секунду станцией. В момент отправления очередного импульса подается и импульс напряжения на пластины конденсатора, управляющего вертикальным смещением луча. После этого антенна радиолокатора переключается на прием. Радиосигнал, достигая цели, рассеивается на ней и частично отражается обратно. Отраженный сигнал принимается, усиливается и дает вторую вертикальную отметку на экране осциллографа. Положение первой отметки, получаемой при отправлении сигнала, строго неподвижно. [11]
Длительность сигналов
Длительность сигнала У1 должна превышать время переключения триггера. При занесении кода на регистр триггеры 77 — 75 сохраняют свое состояние. [13]
Длительность сигнала на выходах схемы определяется интерзалом времени между приходом сигнала на переключение триггера и сигналом, который должен вернуть его в исходное состояние. Это время, очевидно, будет определяться работой того блока, который управляет триггером. [15]
Страницы: 1 2 3 4 5
речевые (телефонные), вещательные, телевизионные, телеграфные сигналы, сигналы передачи данных.
Параметры сигнала: длительность сигнала Тс, его динамический диапазон Нс и ширина спектра
Всякий сигнал, рассматриваемый как временной процесс, имеет начало и конец. Длительность сигналаТс определяет интервал времени, в пределах которого сигнал существует.
Динамический диапазон определяется как отношение небольшой мгновенной мощности сигнала к той наименьшей мощности, которую необходимо отличать от нуля при заданном качестве передачи. Динамический диапазон речи диктора, например равен 25–30 дБ, симфонического оркестра 65-75 дБ.
Третьим параметром является ширина спектра сигнала Fc. Эта величина дает представление о скорости изменения внутри интервала его существования. Спектр сигнала, в принципе, может быть неограниченным. Однако, для любого сигнала можно указать диапазон частот, в пределах которого сосредоточена его основная энергия. Этим диапазоном и определяется ширина спектра сигнала.
В технике связи спектр сигнала часто сознательно ограничивается. Это обусловлено тем, что аппаратура и линия связи имеют ограниченную полосу пропускаемых частот. При телефонной связи требуется, чтобы речь была разборчива, и чтобы корреспонденты могли узнать друг друга по голосу. Для выполнения этих условий спектр речевого сигнала можно ограничить полосой от 300 до 3400 Гц.
Объем сигнала Vcдает общее представление о возможностях данного ансамбля сигналов как переносчиков сообщений. Чем больше объем сигнала, тем больше информации можно «вложить» в этот объем.
Билет 3
3.Пояснить принцип амплитудно-импульсной модуляции.
В основе построения ЦСП с ВРК лежит теорема Найквиста-Котельникова, которая гласит: непрерывный во времени сигнал
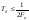
Процесс преобразования непрерывного во времени и ограниченного по спектру сигнала c(t) в сигнал с(пТд), определенный в точках отсчета Тд, 2Тд … nТд — называется дискретизацией.
Процесс дискретизации можно представить как процесс амплитудно-импульсной модуляции (АИМ) сигналом
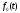 с
амплитудой Ат, длительностью
с
амплитудой Ат, длительностью 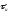 и периодомТд или частотой
и периодомТд или частотой 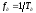 .
. Различают
амплитудно-импульсную модуляцию первого
рода (АИМ-1) и
второго рода (АИМ-2). При АИМ-1 мгновенное
значение импульсов отсчетов
на их длительности 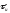
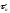 .
Таким образом, импульсы отсчетов при
АИМ-2 имеют плоскую вершину. При достаточно
большой скважности импульсовПППИ q > 10
сигналы АИМ-1 и АИМ-2 идентичны по
спектрам.
.
Таким образом, импульсы отсчетов при
АИМ-2 имеют плоскую вершину. При достаточно
большой скважности импульсовПППИ q > 10
сигналы АИМ-1 и АИМ-2 идентичны по
спектрам.Определение активной длительности сигнала и активной ширины его спектра
При
практических расчетах длительности
сигнала 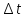 и ширины его спектра
и ширины его спектра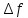 в ряде случаев удобно пользоваться
энергетическим критерием . Активную
длительность импульса
в ряде случаев удобно пользоваться
энергетическим критерием . Активную
длительность импульса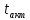 и
активную ширину спектра
и
активную ширину спектра 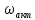 (или
(или 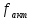 )
определяют
как интервал времени и диапазон частот
соответственно, внутри которых
сосредоточена подавляющая часть
полной энергии Э импульса (например, 95%). Если сигнал s(t) задан
на интервале времени
)
определяют
как интервал времени и диапазон частот
соответственно, внутри которых
сосредоточена подавляющая часть
полной энергии Э импульса (например, 95%). Если сигнал s(t) задан
на интервале времени 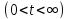 ,
то его активная длительность рассчитывается
из условия
,
то его активная длительность рассчитывается
из условия

В
левой части равенства записана энергия
сигнала, сосредоточенная в интервале
времени 0 – 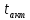 (рис. 4.33,а). В правой части равенства –
доля (определяемая заданным коэффициентом
(рис. 4.33,а). В правой части равенства –
доля (определяемая заданным коэффициентом 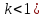 полной
энергии сигнала.
полной
энергии сигнала.
Исходя из равенства Парсеваля, аналогично рассчитывается активная ширина спектра сигнала
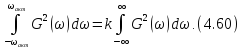
Таким
образом, активная ширина спектра сигнала
соответствует полосе частот, в пределах
которой заключена 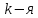 доля
полной энергии сигнала (рис. 4.33, б).
доля
полной энергии сигнала (рис. 4.33, б).
В случае простых видеоимпульсов (например, прямоугольного, треугольного, косинусоидального), спектр которых сосредоточен в области низких частот, можно считать с достаточной для практики точностью, что
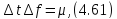
где ,
— постоянная величина, зависящая от
формы импульса и критерия оценки величин
,
— постоянная величина, зависящая от
формы импульса и критерия оценки величин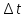 и
и 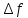 .
.
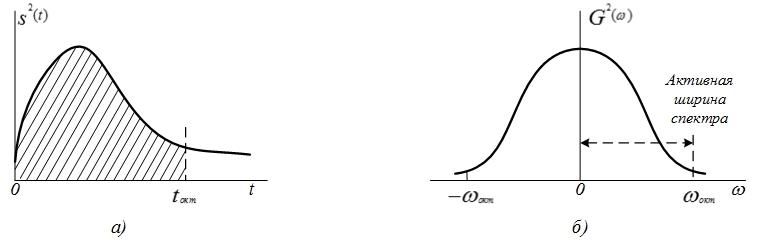
Рис.4.33. Сигнал (а) и его спектр (б)
Как
видно из (4.61), уменьшение длительности
импульса неизбежно приводит к
увеличению ширины его спектра, и наоборот.
Пользуясь соотношением (4.61), можно
рассчитать полосу частот, занимаемую
спектром сигнала в зависимости от его
длительности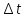 .
.
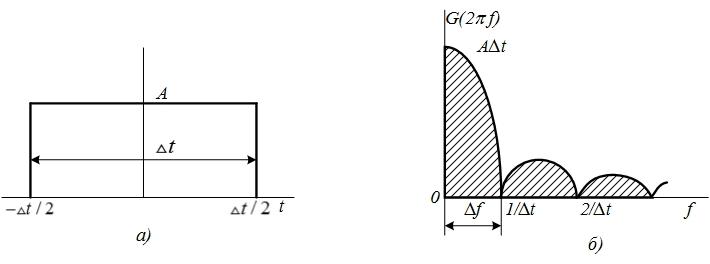
Рис 4.34. Прямоугольный импульс (а) и его спектр (б)
Для перечисленных
выше типов видеоимпульсов значение 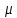 близко к единице. В частности, если
оценивать активную ширину спектра
прямоугольного импульса длительностью
близко к единице. В частности, если
оценивать активную ширину спектра
прямоугольного импульса длительностью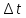 (рис. 4.34, а) как полосу частот
(рис. 4.34, а) как полосу частот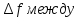 f= 0 и тем значением частоты, когда
спектральная плотность первый раз
обращается в нуль (рис. 4.34, б), т. е. когда
аргумент спектральной плотности (4.42)
принимает
значение
f= 0 и тем значением частоты, когда
спектральная плотность первый раз
обращается в нуль (рис. 4.34, б), т. е. когда
аргумент спектральной плотности (4.42)
принимает
значение 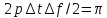 ,то
,то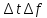 = 1.
Следовательно, для прямоугольного
импульса
= 1.
Следовательно, для прямоугольного
импульса 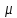 =
1.
=
1.
Пользуясь
соотношением (4.60),
можно
показать, что в полосе (0, 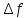 )
(в
первом лепестке) сосредоточено свыше
90% полной энергии сигнала.
)
(в
первом лепестке) сосредоточено свыше
90% полной энергии сигнала.
Вопросы и задания для самопроверки:
Из каких тригонометрических функций можно сформировать периодический сигнал?
Что такое постоянная и основная составляющие, гармоники сигнала?
Какие формулы ряда Фурье используют для описания периодических сигналов?
Записать ряд Фурье (4.4) в тригонометрической и комплексных формах, ограничившись третьей гармоникой.
Что такое спектр амплитуд?
Периодический сигнал задан рядом Фурье в форме
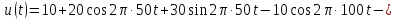
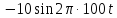
Представить этот ряд в тригонометрической форме (4.10).
Каким образом длительность периодических импульсов, период их следования и скважность влияют на спектр сигнала?
Как определить реакцию цепи на периодическое воздействие?
Как рассчитывается комплексная передаточная функция цепи, на вход которой поступает периодический сигнал?
Каков физический смысл коэффициента передачи и фазового сдвига цепи на частотах гармоник?
Сформулировать задачу спектрального анализа цепи при периодическом воздействии.
Как рассчитывается спектр реакции цепи на периодическое воздействие?
Что понимается под тригонометрическим рядом Фурье? Какие формы этого ряда Вы знаете?
Что понимается под комплексным рядом Фурье? Запишите формулу определения коэффициентов комплексного ряда Фурье.
Как рассчитывается комплексная спектральная плотность непериодического сигнала?
Как восстановить непериодический сигнал по его комплексной спектральной плотности?
Что такое спектральная плотность амплитуд и спектральная плотность фаз?
Как изменится график спектральной плотности амплитуд прямоугольного импульса, если его длительность уменьшить в три раза?
Как связаны между собой спектры непериодического и периодического сигналов?
В чем заключается интегральное преобразование Фурье? Приведите формулы прямого и обратного преобразования Фурье. При каких условиях можно пользоваться формулой прямого преобразования Фурье?
Как определяется частотный спектр непериодического сигнала? Какой физический смысл имеет модуль спектральной плотности сигнала? Чем определяются амплитудный и фазовый спектры непериодического сигнала?
Как выражается связь между спектральной плотностью одиночного импульса
 и комплексной амплитудой
и комплексной амплитудой ряда Фурье, описывающего периодическую
последовательность, составленную из
таких импульсов?
ряда Фурье, описывающего периодическую
последовательность, составленную из
таких импульсов?Как измениться спектральная функция
 при умножении сигналаs(t)
на
при умножении сигналаs(t)
на  ?
?Как измениться функция
 при умножении сигналаs(t) на
при умножении сигналаs(t) на  ?
?Что происходит со спектром при сжатии (растяжении) сигнала?
Как изменяются амплитудный и фазовый спектры сигнала при его запаздывании?
Как выражается спектральная плотность произведения двух функций, если известны спектральные плотности сомножителей?
Какой физический смысл имеет квадрат спектральной плотности сигнала
 ?
?Как формулируется равенство Парсеваля для непериодического сигнала?
Энергетический метод определения эффективной длительности сигнала
Эффективная длительность сигнала определяется как интервал времени, внутри которого сосредоточена заданная часть (например 90 %) полной энергии сигнала.
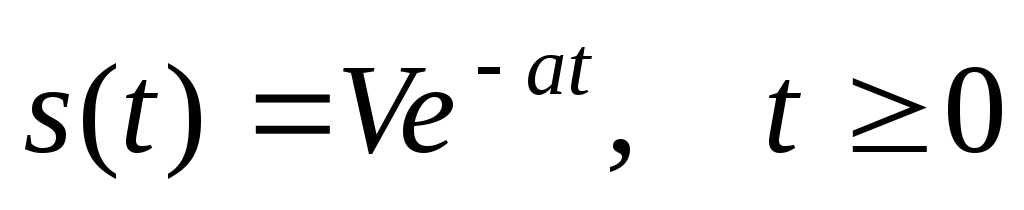
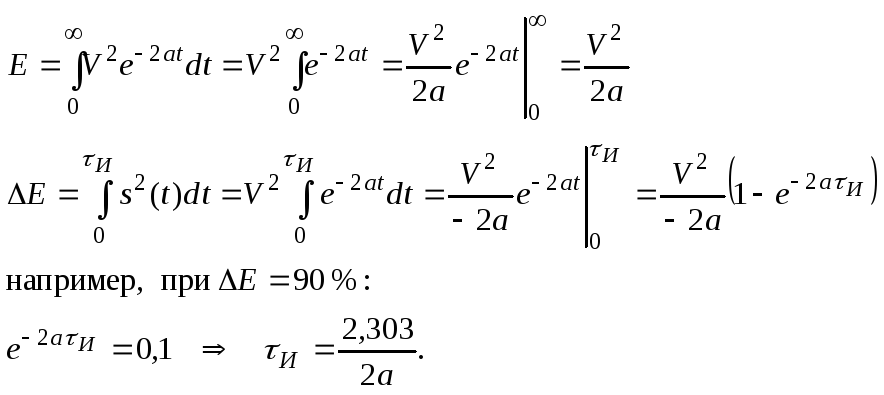
1.3. Спектральные характеристики сигналов
Для описания одного и того же сигнала в зависимости от решаемых задач могут быть использованы различные математические представления:
временное представление,
спектральное (частотное) представление.
Временное представление – это описание сигнала с помощью функций времени. Оно определяет свойство и параметры сигнала во временной области (форму, длительность сигнала, энергию, мощность).
Однако при практическом применении сигналов важно знать их свойства не только во временной, но и в частотной области. В этом случае при анализе и расчетах сигналы представляются своими частотными характеристиками, что облегчает решение многих практических задач обработки сигнала. Обычно частотные характеристики называют частотными спектрами, или спектрами, сигнала. Принято и другое название – спектральные характеристики. Спектральные характеристики сигналов изучают на специальных приборах – анализаторах спектра, например на С4-27.
Определение спектра сигнала составляет задачу спектрального анализа. В основе спектрального анализа лежит разложение сигнала на спектральные составляющие. Математические методы спектрального анализа различаются для периодических и непериодических сигналов.
Спектральный анализ периодических сигналов
Периодическим называется сигнал, значение которого повторяется через определенные интервалы времени, которые называют периодом сигнала и обычно обозначают буквой Т.
Простейшие периодические сигналы основаны на функциях косинуса или синуса.
 ,
,
где ω – круговая частота,
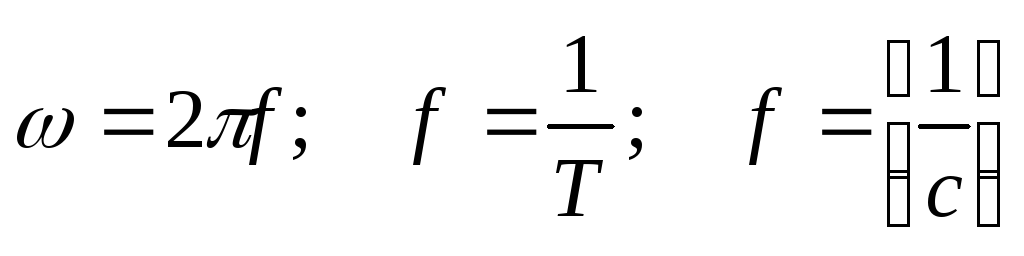 ,
,
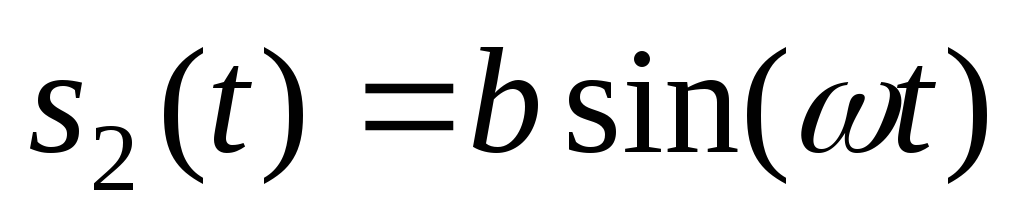

Одно из простейших гармонических колебаний – это сумма колебаний синуса и косинуса. В данном случае частота одинакова для обоих слагаемых.
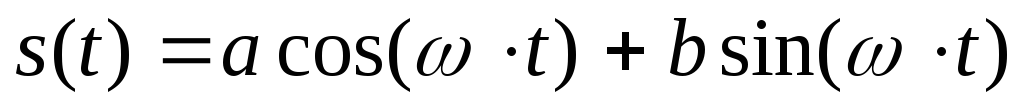

Начало координат в данном случае может располагаться произвольно.
Сложим колебания:
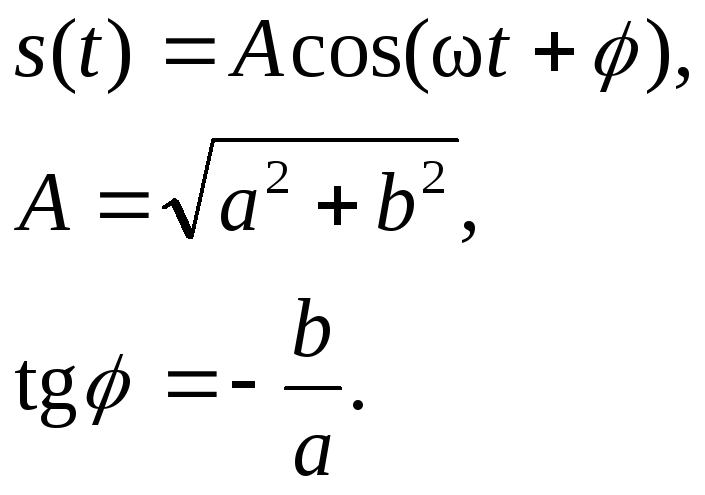
На рисунке показан результат сложения двух сигналов: f1 = 600 Гц, f2 = 1000 Гц.
Сдвиг между фазами φ = 45°, одно деление (клеточка) = 1мс.

Фурье в 20 гг. XIX века доказал, что любой периодический сигнал можно представить в виде разложения на гармонические (составляющие) колебания
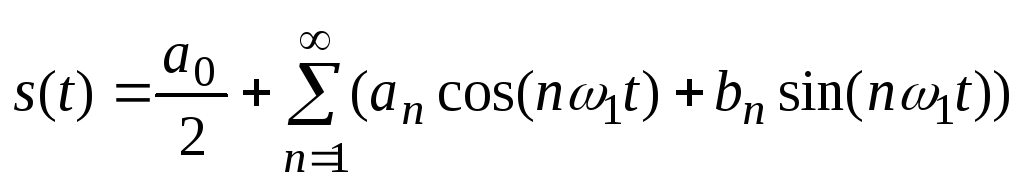 ,
,
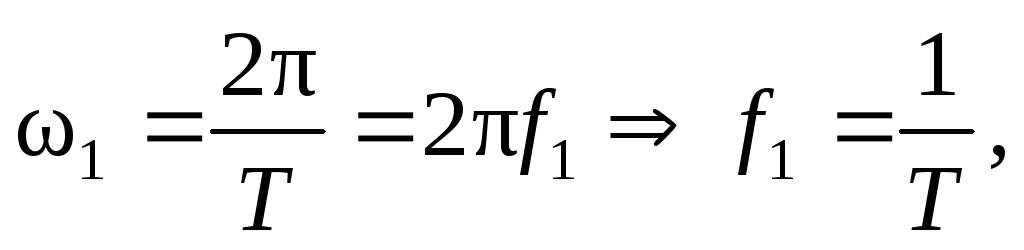
где Т – период,
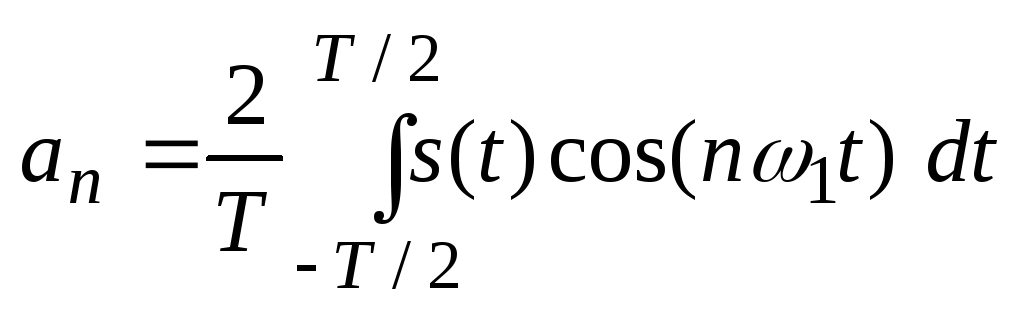 ,
,
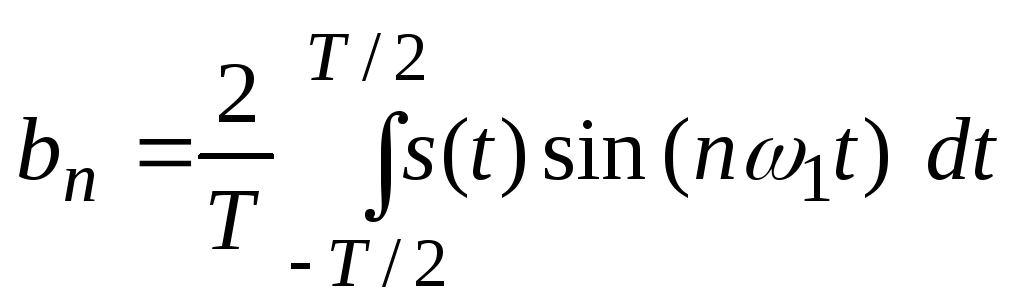 .
.
Если сигнал описывается четной функцией времени (s(-t) = s(t)), то тогда все коэффициенты bn равны нулю и можно записать, что
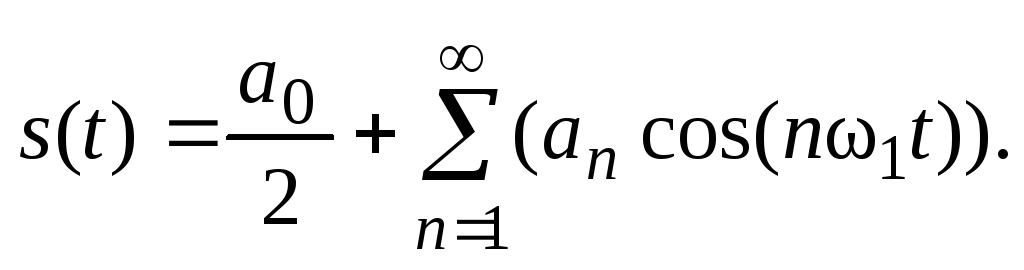
Если сигнал s(t) описывается нечетной функцией времени (s(-t) = — s(t)), то тогда все коэффициенты an равны нулю и можно записать, что
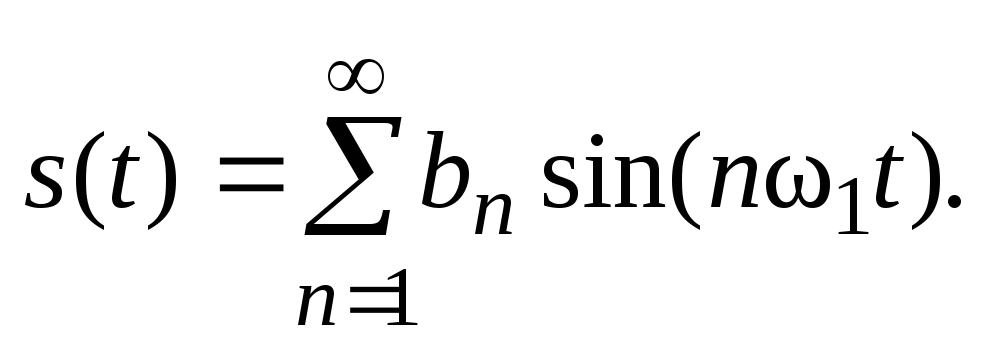
В общем случае, когда сигнал произвольный, используют другую, более удобную форму записи ряда Фурье:
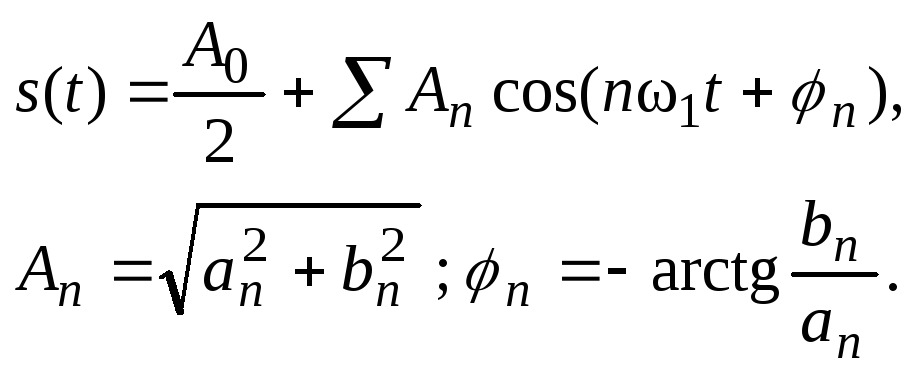
Формулы для нахождения an и bn остаются такие же:
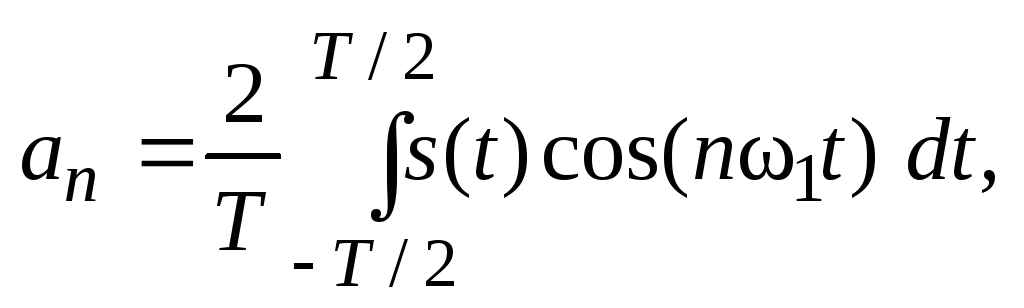
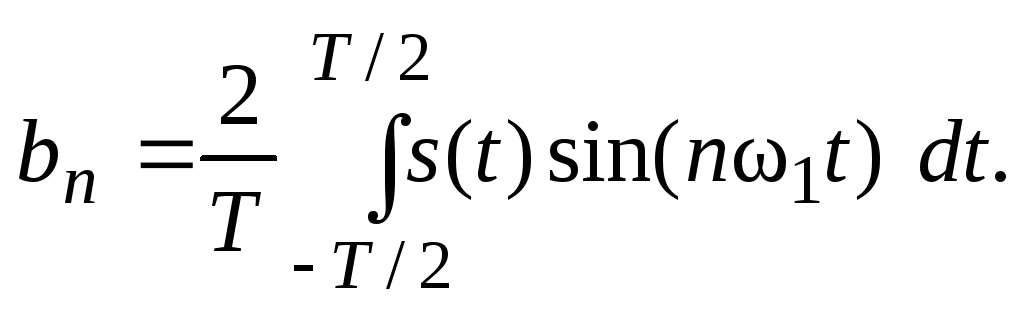
Это представление называют спектральным, или частотным, представлением сигнала. Спектральное представление сигнала — это постоянная составляющая (А0/2) и бесконечное число гармонических составляющих (гармонических сигналов). Число n определяет порядковый номер гармоники. Каждая гармоника характеризуется амплитудой An, частотой nω1 и начальной фазой φn∙ Гармоника, соответствующая n = 1 – это первая (основная) гармоника. Она имеет частоту, равную частоте сигнала.
Совокупность всех амплитуд гармоник An определяет амплитудный спектр сигнала, а совокупность всех начальных фаз называется фазовым спектром сигнала.
Графическое изображение спектра называется спектральной диаграммой. Пример амплитудной спектральной диаграммы.

Пример фазовой спектральной диаграммы.

Графический спектр состоит из отдельных линий, и поэтому он называется линейчатым. Расстояния между гармониками равны основной частоте (чаще бывает так, что какая-либо гармоника равна нулю, и кажется, что расстояние между гармониками разное). На самом деле, это не так и гармонику, равную нулю, тоже необходимо считать (см. пример ниже). Спектр периодического сигнала называют также дискретным, поскольку гармоники определены на дискретных частотах ω1, 2ω1, 3ω1…
Длительность сигналов — Справочник химика 21
Увеличение параметров шероховатости стохастически неровной поверхности приводит к монотонному уменьшению амплитуды и существенному возрастанию длительности принимаемых сигналов. Так, например, при Яг 80 мкм длительность сигнала возрастает на 10 %, а при Кг 320 мкм на 100. .. 200 %. Мертвая зона увеличивается в последнем случае на 200. .. 300 % в контактном варианте и на 20. .. 30 % в иммерсионном. [c.243]
Тем не менее, часто при проектировании информационно-измерительных систем используют частоту дискретизации, определяемую указанной теоремой, считая незначительным вклад составляющих сигнала, частота которых превышает некоторое пороговое значение, выбранное из физических соображений. Если верхняя частота спектра равна / , а частота дискретизации — 2/ а интервал времени между отсчетами — 1/2. Если длительность сигнала равна, то необходимое для описания сигнала число отсчетов составляет [c.134]
Сколько же нужно отсчетов для полного описания сигналов Ведь приведенная формула для определения их числа предусматривает конечность сигнала во времени, а сигнал (6.20) не имеет конца, и для его описания нужно бесконечно большое количество отсчетов. В качестве разумного компромисса длительность сигнала ограничивают тем временем, при истечении которого величина сигнала становится столь малой, что он «теряется» на фоне электри -ческих шумов электронного устройства, чаще всего входного каскада усилителя сигналов. [c.135]
Диапазон измерения длительности сигнала не менее 65 мс, разрешение не более 1 мкс. [c.325]
Толщину задержки выбирают равной целому числу полуволн — только в этом случае она будет прозрачной для УЗК. Вместе с тем толщина задержки должна быть такой, чтобы время прохождения в ней УЗК было больше времени прохождения их в контролируемом изделии. В этом случае на экране ЭЛТ будут раздельно фиксироваться отраженные сигналы от верхней и нижней поверхностей изделия (см. рис. 90). Амплитуда и длительность сигнала, отраженного от верхней поверхности изделия, в этом случае будут меньше амплитуды начального сигнала и сигнала, отраженного от нижней поверхности, что увеличивает разрешающую способность дефектоскопа и уменьшает мертвую зону. [c.180]
Эффективность метода периодического сканирования зависит от закона модуляции сигнала и способа регистрации [748]. Если форма периодического сигнала известна, то оптимальным будет корреляционный прием (см. стр. 43). Наиболее выгодным энергетически является прямоугольный закон модуляции с равной длительностью сигнала и паузы. Но и в этом наиболее благоприятном случае отношение сигнал/шум будет в 2 раза меньше, чем теоретическое отно- [c.64]
К тому же, поскольку вибрирующий электрод смещался в горизонтальной плоскости в большей степени, чем менялся зазор, возбуждающая частота составляла четвертую часть основной резонансной частоты конденсатора. Следовательно, детектироваться могли только шумы от третьей гармоники возбуждающей частоты. Ими вполне можно пренебречь. Прн наибольшей чувствительности эти шумы позволяли измерять +0,5 мВ при длительности сигнала 0,1 В/с. При увеличении длительности сигнала чувствительность можно повысить. [c.137]
Устройство работает в диапазоне температур окружающей среды от -30 до 50 С и относительной влажности 80%. «Сигнал—39» обеспечивает круглосуточную работу в течение не менее 250 ч. Длительность сигнала тревоги 1-4 мин. [c.20]
В рассматриваемом случае длительность сигнала, как правило, значительно превышает длительность шумовых выбросов, поэтому последние могут лишь увеличить амплитуду импульсов сигнала. [c.82]
При выборе соотношения между длительностью сигнала и постоянной времени гальванометра следует, разумеется, считаться лишь с полезными сигналами, а из
Согласование физических характеристик сигнала и канала
Для рассмотрения данного вопроса вводят понятие объема сигнала.
Vc=TcFcDc, гдеDc=10lg(Pmax/Pmin)
Tc— средняя длительность сигнала
Fc— ширина спектра
Dc— динамический диапазон сигнала
Pmax,Pmin— максимальное (пиковое) и минимальное значение мощности сигнала.
Величина Vcчаще всего характеризует весь ансамбль используемых в данной системе связи сигналов. Эта характеристика описывает сигнал как случайный процесс.PmaxиPmin— уровни мощности, которые превышаются или не превышаются с какой-то заданной вероятностью. Физический объем канала — характеристика, позволяющая оценить трудности, связанные с его передачей. При наличии шумов в канале допустимы минимальныйPмин , обычно определяется средней мощностью шумов в канале.
Поэтому можно
записать: 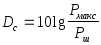
Максимальная мощность Pмаксиногда выражается через усредненную за достаточно большой интервал времени.
В этом случае: 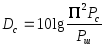 ,
где
,
где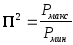 — пикфактор сигнала по мощности
— пикфактор сигнала по мощности
2— определяется статистическими характеристиками сигнала.
Dcизмеряется либо в децибелах, либо в
битах —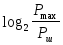 .
.
Понятие объема канала вводят аналогично
Vк=TкFкDк, гдеTк— время использования канала
Fк— полоса пропускания канала
Dк — динамический диапазон уровней пропускаемых каналом с допустимыми искажениями.
Для согласования канала и сигнала необходимо:
а) 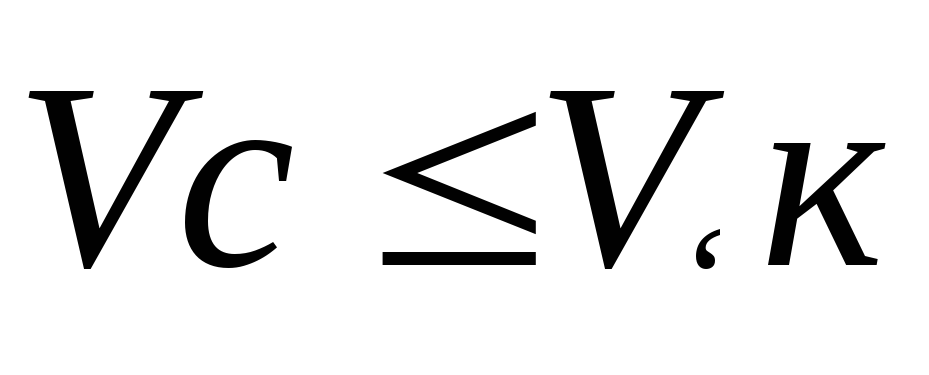
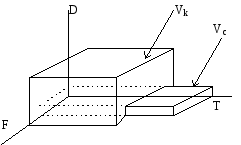
При этом достаточным условием будет одновременное выполнение условий:
б) 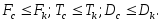
Выполнение условия а) говорит о возможности выполнения условий б) при выполнении необходимых преобразований характеристик сигнала. Например, когда канал имеет меньшую полосу пропускания, чем ширина спектра сигнала, подлежащего передаче, последнюю можно уменьшить за счет увеличения длительности сигнала. (Объем сигнала сохраняется неизменным). Практически такое преобразование можно осуществить посредством записи сигнала на магнитный носитель с высокой скоростью и последующего воспроизведения со скоростью, при которой ширина его спектра равна полосе пропускания канала.
При низком допустимом динамическом диапазоне канала преобразование заключается в уменьшении динамического диапазона сигнала с одновременным увеличением его длительности путем многократного повторения передачи.
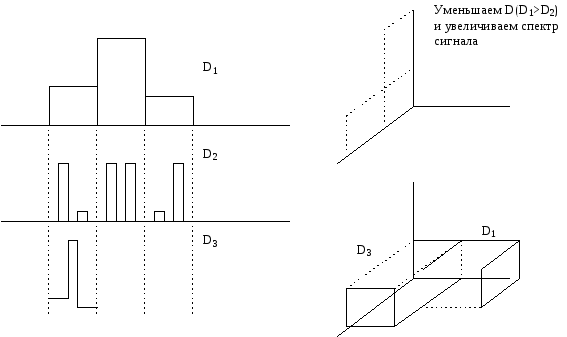 Уменьшаем
длительность, но расширяем спектр при
том же динамическом диапазоне.
Уменьшаем
длительность, но расширяем спектр при
том же динамическом диапазоне.
Тема 3 Преобразование информационных характеристик сигналов.
Цель: Рассмотрение вопросов преобразования информационных параметров сигналов, возникающих при согласовании характеристик сигналов и каналов.
Преобразование непрерывных (аналоговых) сигналов в цифровую форму.
Преобразование информационных параметров сигнала, связанных с согласованием их с характеристиками канала связи, часто требует преобразования сигнала из одной формы в другую. Наиболее часто возникает задача преобразования непрерывных сигналов в цифровую форму.
Под непрерывными (аналоговыми) сигналами мы понимаем такие, у которых два нетождественных значения могут отличаться друг от друга сколь угодно мало.





































































































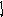
S





D
S(t)
t





















 Этапы преобразования:
Этапы преобразования:1.Дискретизация по времени(АИМ). Результат: непрерывные сигналы дискретного времени.
Если поменять порядок этапов дискретизации и квантования, то после первого этапа квантования получим дискретный сигнал непрерывного времени.
2.Квантование по уровню. Произвольные амплитуды заменяются на континиум разрешенных. В строгом смысле получаем дискретный сигнал, говорят получаем дискретный сигнал дискретного времени. Если диапазон задания амплитуд конечен, то уровни можно пронумеровать.
Кодирование дискретного сигнала (импульсно-кодовая модуляция). Дискретные уровни сигнала заменяются на цифровые эквивaленты.
Дискретизация и
квантование могут быть равномерными,
когда шаг дискретизации 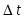 и шаг квантования
и шаг квантования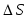 постоянны, и неравномерными в противном
случае.
постоянны, и неравномерными в противном
случае.
Дискретизация непрерывного сигнала по времени.
В технике связи очень часто возникает необходимость представления непрерывного сигнала совокупностью его значений в дискретных точках(сечениях). Такое представление называется дискретизацией функции сигнала по времени.
Очень часто
дискретизацию осуществляют на основе
теоремы В. А. Котельникова, согласно
которой функция S(t), спектральная
плотность которой отлична от нуля только
в полосе частот(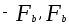 )
полностью определяется своими значениями,
отсчитанными в дискретных точках через
интервал
)
полностью определяется своими значениями,
отсчитанными в дискретных точках через
интервал
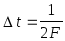
Значение функции S(t) в любой точке t выражаются формулой
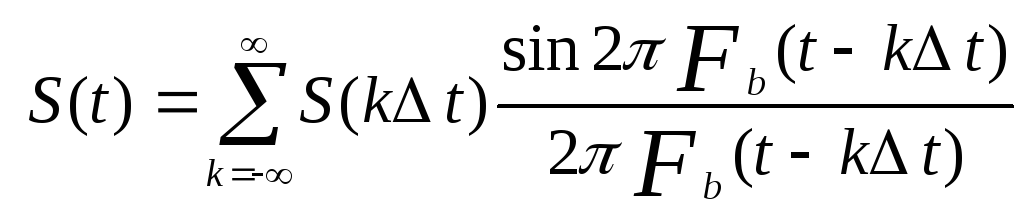
где S(k t)-отсчеты
непрерывной функцииS(t)
в дискретные моменты времени
t)-отсчеты
непрерывной функцииS(t)
в дискретные моменты времени 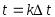 .Доказательство
теоремы Котельникова приведено на
стр.74-79[7] В.И.Дмитриев «Прикладная теория
информации».
.Доказательство
теоремы Котельникова приведено на
стр.74-79[7] В.И.Дмитриев «Прикладная теория
информации».
Г еометрическая
интерпретация ряда Котельникова.
еометрическая
интерпретация ряда Котельникова.
О ртогональная
функция Котельникова
ртогональная
функция Котельникова

Теорема Котельникова справедлива для сигнала с ограниченным спектром и неограниченным во времени(нефинитная функция). На практике это не выполняется и для реальных сигналов это приводит к увеличению погрешности.
Средний квадрат усечения спектра можно оценить
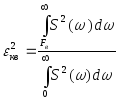


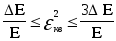

 ,
где Е -энергия сигнала,
,
где Е -энергия сигнала, 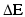 -неучтенная
энергия.
-неучтенная
энергия.

Пример. Определить по теореме Котельникова шаг дискретизации для детерминированной функции
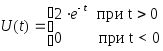
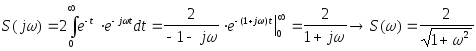
Практическая ширина спектра

Таким образом,
восстановление ограниченного во времени
сигнала по отсчетам, полученным по
теореме Котельникова при условии
принудительного ограничения спектра
сигнала, возможно только приближенно.
Ошибка возникает не только за счет
принудительного ограничения спектра,
но и за счет конечного числа отсчетов
в интервале времени T, которых в
соответствии с теоремой Котельникова
будет 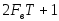

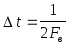
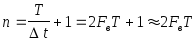
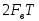 -база
сигнала
-база
сигнала
Эта составляющая
является следствием пренебрежения
вкладом бесконечного числа функций
отсчетов, соответствующих выборкам за
пределами интервала T. Меньше выборок,
чем определено 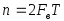 при сигнале со спектром
при сигнале со спектром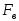 и на отрезке
и на отрезке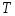 брать нельзя, иначе теряется информационное
содержание. Увеличение n позволяет
повысить точность восстановления
сигнала.
брать нельзя, иначе теряется информационное
содержание. Увеличение n позволяет
повысить точность восстановления
сигнала.
Квантование сигнала по уровню.
D-
динамический диапазон,max—
максимальный. уровень помехи искажающего.
сигнала. Весь диапазонDразбивается на участки с шагом квантованияS.Dприн=Dпередав+2max.
Рассмотрим 3 уровня квантования.
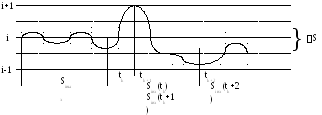
Для того, чтобы не было искажений сигнала помехой необходимо:


Число уровней квантования

Такое кодовое преобразование предполагает выбор системы счисления, то есть такое основание кода, которое лучшим образом подходит к задаче.
Коды, использующие основание системы счисления 2, носят название «бинарные» или «двоичные». Все остальные- «многоосновные».
Максимальное число возможных сообщений кода с основанием n N=nm
Число всевозможных элементов, применяемых для отображения сообщений из этой совокупности чисел M=m n
Отсюда
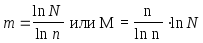
При заданном max числе сообщений определяем код с таким основанием n, который бы использовал наименьшее количество элементов M для передачи сообщений.
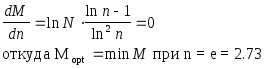
n | 2 | e | 3 | 4 | 8 | 10 |
M/Mopt | 1.06 | 1 | 1.006 | 1.06 | 1.42 | 1.58 |
Наиболее оптимальным с точки зрения количества элементов для передачи данного объема информации является код с основанием 3, использующий трехпозиционную логику.
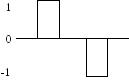
Коды бывают равномерные, неравномерные.
Равномерные коды- последовательности одинаковой длительности.
Число сообщений, которое необходимо отображать, лежит для кода с основанием m и разрядностью n.
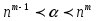
В этом случае код первичен. В основном для передачи информации используют первичные коды.
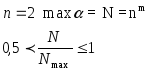
Это означает, что число сообщений, которое передается бинарным первичным кодом всегда больше половины max возможного.
В заключении к теме рассмотрим пример преобразования динамического диапазона сигнала при использовании ИКМ..
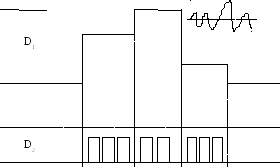
Выбираем амплитуду
импульсов ИKM значительно меньше
амплитуды(диапазона) дискретного
сигнала. При переходе от D к D
к D ,
происходит трансформация объема сигнала
в сторону увеличения его спектра.
,
происходит трансформация объема сигнала
в сторону увеличения его спектра.

Сравнение информационных емкостей дискретного и непрерывного сигналов.
Под информационной емкостью понимают максимально возможную скорость передачи данного сигнала.
а) двоичный сигнал
Пусть информация передается с помощью импульсов , таким образом что длительность элементарной информационной посылки равна длительности импульса. Амплитуда дискретного сигнала — А и выбрана таким образом , что помехи не могут привести к сбою.




А






Количество информации, передаваемой за nэлементарных информационных посылок:
Jn=n*log2 L,
где L- число уровней квантования.
L=2 , тоJn=n, ноn=T/и.
Вспомним соотношение и*f=1 , запишемn=T*f, тогда
Jn=Т*fС=Jn/T=f(бит/сек).
б)многопозиционные импульсные сигналы



Jn= Т*f*log2 L
С=f*log2 L(бит/сек)







Скорость передачи такой информации выше, чем в первом случае ( при условии, что интервал квантования выбран так , что шумы также не могут привести к сбою.
в)непрерывный сигнал
Сигнал ограничен во времени, его длительность Т. Можно уменьшить интервал дискретизации до 0, тем самым будет увеличена точность представления сигнала.









Т


J=n*log2 L приt
приt 0,
т.к.n
0,
т.к.n
Приходим к абсурду — сигнал ограничен во времени , но имеет бесконечную информационную емкость. Из теоремы Котельникова знаем , что число выборок, больше которого с точки зрения информационного содержания передавать нет смысла, равно: n=2*Fв*Т
Откуда количество передаваемой информации:
J=n*log2 L=2*Fв*Т*log2 L
Необходимо задаться числом уровней квантования. При передаче непрерывного сигнала на него действует шум мощностью 2. Эффективное напряжение сигнал+помеха выражается следующим радикалом:
U
 эфф=U2эфф.сигн.+2 , где
эфф=U2эфф.сигн.+2 , где
U2эфф.сигн.+2





L=
=
Pc+Pш
Pш

о
Pc Pш
тсюдаJ
Pc+Pш
Pш

 =2*Fв*Т*log2 ( )1/2=Fв*Т*log2(1+
) ,
=2*Fв*Т*log2 ( )1/2=Fв*Т*log2(1+
) ,откуда
Pc Pш
J
T
Формула Шеннона для скорости передачи информации
С

 =
=Fв*log2(1+
) —
=
=Fв*log2(1+
) —
Полученные отношения справедливы и по отношению к каналам (пропускная способность каналов).
Н
Pc Pш
С1Fk
ормированная пропускная способность гауссова непрерывного канала определяется: =
 log2(1+ ) [бит]
log2(1+ ) [бит]
Нормированная пропускная способность двоичного симметричного канала без памяти определяется:
=
С2Fk
2 [1+Polog2Po+(1-Po)log2(1-Po) ] ,где Po– вероятность ошибочной передачи элементарной посылки.
C/Fk ,бит
2.4. Эффективная длительность и эффективная ширина спектра сигнала. 2. Детерминированные сигналы. Радиотехнические цепи и сигналы. Учебное пособие
Для решения практических задач радиотехники крайне важно знать значения длительности и ширины спектра сигнала, а также соотношение между ними. Знание длительности сигнала позволяет решать задачи эффективного использования времени, предоставляемого для передачи сообщений, а знание ширины спектра – эффективного использования диапазона радиочастот.
Решение указанных задач требует строгого определения понятий «эффективная длительность» и «эффективная ширина спектра». На практике существует большое число подходов к определению длительности. В том случае, когда сигнал ограничен во времени (финишный сигнал), как это имеет место, например, для прямоугольного импульса, определение длительности не встречает затруднений. Иначе обстоит дело, когда теоретически сигнал имеет бесконечную длительность, например, экспоненциальный импульс
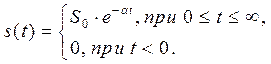
В этом случае в качестве эффективной длительности 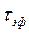 может быть принят интервал времени
может быть принят интервал времени 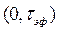 , в течение которого значение сигнала
, в течение которого значение сигнала 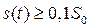 . При другом способе в качестве
. При другом способе в качестве 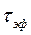 выбирают интервал времени, в течение которого
выбирают интервал времени, в течение которого 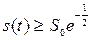 . То же самое можно сказать и в отношении определения эффективной ширины спектра
. То же самое можно сказать и в отношении определения эффективной ширины спектра 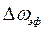 .
.
Хотя в дальнейшем, некоторые из этих способов будут использоваться при анализе радиотехнических сигналов и цепей, следует отметить, что выбор способа существенно зависит от формы сигнала и структуры спектра. Так для экспоненциального импульса более предпочтителен первый из указанных способов, а для сигнала колоколообразной формы – второй способ.
Более универсальным является подход, использующий энергетические критерии. При таком подходе в качестве эффективной длительности и эффективной ширины спектра рассматриваются соответственно интервал времени и диапазон частот, в пределах которых сосредоточена подавляющая часть энергии сигнала
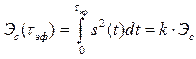 , (2.52)
, (2.52)
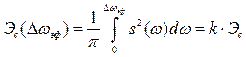 , (2.53)
, (2.53)
где 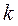 – коэффициент, показывающий, какая часть энергии сосредоточена в интервалах
– коэффициент, показывающий, какая часть энергии сосредоточена в интервалах 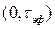 или
или 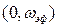 . Обычно величину
. Обычно величину 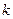 выбирают в пределах
выбирают в пределах 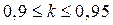 .
.
Применим критерии (2.52) и (2.53) для определения длительности и ширины спектра прямоугольного и экспоненциального импульсов. Для прямоугольного импульса вся энергия сосредоточена в интервале времени 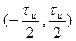 или
или 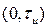 , поэтому его длительность
, поэтому его длительность 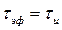 . Что касается эффективной ширины спектра, то установлено, что более 90% энергии импульса сосредоточено в пределах первого лепестка спектра. Если рассматривать односторонний (физический) спектр импульса, то ширина первого лепестка спектра составляет
. Что касается эффективной ширины спектра, то установлено, что более 90% энергии импульса сосредоточено в пределах первого лепестка спектра. Если рассматривать односторонний (физический) спектр импульса, то ширина первого лепестка спектра составляет 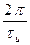 в круговых частотах или
в круговых частотах или 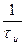 в циклических частотах. Отсюда следует, что эффективная ширина спектра прямоугольного импульса равна
в циклических частотах. Отсюда следует, что эффективная ширина спектра прямоугольного импульса равна
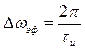 или
или 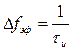 .
.
Перейдем к определению 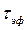 и
и 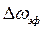 экспоненциального импульса. Полная энергия импульса составляет
экспоненциального импульса. Полная энергия импульса составляет
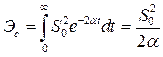 .
.
Воспользовавшись (2.52), получим
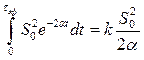 .
.
Вычислив интеграл в левой части уравнения и решив его, можно прийти к следующему результату
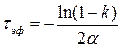 .
.
Спектр экспоненциального импульса найдем, воспользовавшись преобразованием Фурье
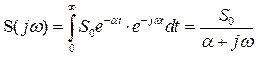 ,
,
откуда следует
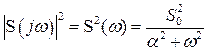 .
.
Подставляя это выражение в (2.53) и решая уравнение, получим
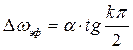 .
.
Найдем произведение эффективной длительности на эффективную ширину спектра. Для прямоугольного импульса это произведение составляет
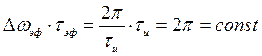 ,
,
или для циклических частот
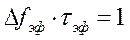 .
.
Для экспоненциального импульса
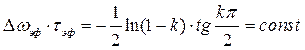 .
.
Таким образом, произведение эффективной длительности на эффективную ширину спектра одиночного сигнала есть постоянная величина, зависящая только от формы сигнала и величины коэффициента 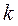 . Это означает, что при уменьшении длительности сигнала его спектр расширяется и наоборот. Этот факт уже отмечался пи рассмотрении свойства (2.46) преобразования Фурье. На практике это означает, что невозможно сформировать короткий сигнал, обладающий узким спектром, что является проявлением физического принципа неопределенности.
. Это означает, что при уменьшении длительности сигнала его спектр расширяется и наоборот. Этот факт уже отмечался пи рассмотрении свойства (2.46) преобразования Фурье. На практике это означает, что невозможно сформировать короткий сигнал, обладающий узким спектром, что является проявлением физического принципа неопределенности.


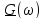 и комплексной амплитудой
и комплексной амплитудой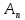 ряда Фурье, описывающего периодическую
последовательность, составленную из
таких импульсов?
ряда Фурье, описывающего периодическую
последовательность, составленную из
таких импульсов?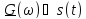 при умножении сигналаs(t)
на
при умножении сигналаs(t)
на 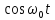 ?
?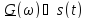 при умножении сигналаs(t) на
при умножении сигналаs(t) на 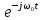 ?
?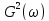 ?
?