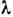Длинные волны: Длинные волны — Википедия – Длинные волны — это… Что такое Длинные волны? — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

ДЛИННЫЕ ВОЛНЫ — это… Что такое ДЛИННЫЕ ВОЛНЫ?

ДЛИННЫЕ ВОЛНЫ

— радиоволны с длиной волны от 10⁴ до 10³ м (диапазон частот 30-300 кГц). Загоризонтное распространение радиоволн ДВ-диапазона осуществляется в виде земной волны (на расстояние до 2000 км) или благодаря их многократному отражению от стенок сферич. волновода (нижняя — поверхность Земли, верхняя — ионосферный слой D в дневные и слой E в ночные часы). На больших расстояниях существенно волноводное распространение Д. в., к-рое зависит от анизотропии ионосферной плазмы, её неоднородности и т. п.

Д. в. используют в радиовещании (1000<

<2000 м), дальней связи, системах радионавигации, они являются одним из средств изучения параметров ниж. ионосферы.

Л. M. Ерухимов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.

ДЛИНА РАССЕЯНИЯ
ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ

Смотреть что такое «ДЛИННЫЕ ВОЛНЫ» в других словарях:

Длинные волны

— (также километровые волны) диапазон радиоволн с частотой от 30 кГц (длина волны 10 км) до 300 кГц (длина волны 1 км). Длинные волны распространяются на расстояния до 1 2 тысяч км за счёт дифракции на сферической поверхности Земли. Затем их… … Википедия
ДЛИННЫЕ ВОЛНЫ — радиоволны с длиной волны от 1 до 10 км. Огибают земную поверхность за счет дифракции радиоволн и отражения от ионосферы. Обеспечивают устойчивую радиосвязь; применяются для дальней (2000 км) радиосвязи и в радионавигации … Большой Энциклопедический словарь
Длинные волны — «Длинные волны» – см. Кондратьева циклы … Экономико-математический словарь

длинные волны — ДВ Участки диапазонов километровых и гектометровых волн, предназначенные для радиовещания и определенных служб радиосвязи. Примечание Указанный терминыдопустимык применению для тех служб радиосвязи, которым распределены определенные полосы… … Справочник технического переводчика
длинные волны — радиоволны с длиной волны от 1 до 10 км. Огибают земную поверхность за счёт дифракции радиоволн и отражения от ионосферы. Обеспечивают устойчивую радиосвязь; применяются для дальней (2000 км) радиосвязи и в радионавигации. * * * ДЛИННЫЕ ВОЛНЫ… … Энциклопедический словарь
длинные волны — ilgosios bangos statusas T sritis automatika atitikmenys: angl. long waves vok. lange Wellen, f rus. длинные волны, f pranc. ondes longues, f … Automatikos terminų žodynas
длинные волны — ilgosios bangos statusas T sritis fizika atitikmenys: angl. long waves vok. Langwellen, f rus. длинные волны, f pranc. ondes longues, f … Fizikos terminų žodynas
Длинные волны — 20. Длинные волны ДВ Участки диапазонов километровых и гектометровых волн, предназначенные для радиовещания и определенных служб радиосвязи Источник: ГОСТ 24375 80: Радиосвязь. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
Длинные волны — радиоволны с длиной волны от 1 км до 10 20 км. Могут распространяться за счёт дифракции радиоволн (См. Дифракция радиоволн) на сферической поверхности Земли на расстояния до 1 2 тыс. км. На более далёкие расстояния Д. в. распространяются… … Большая советская энциклопедия
ДЛИННЫЕ ВОЛНЫ — радиоволны с длиной волны от 1 до 10 км. Огибают земную поверхность за счёт дифракции и отражения от ионосферы. Обеспечивают устойчивую радиосвязь; применяются для дальней (2000 км) радиосвязи и в радионавигации … Естествознание. Энциклопедический словарь

Длинные волны — это… Что такое Длинные волны?

Длинные волны: радиоволны с длиной волны от 1 км до 10—20 км. Могут распространяться за счёт дифракции радиоволн (См. Дифракция радиоволн) на сферической поверхности Земли на расстояния до 1—2 тыс. км. На более далёкие расстояния Д. в. распространяются за счёт направляющего действия сферического атмосферного волновода, образованного поверхностью Земли и нижней границей ионосферы (см. Распространение радиоволн).

Длиннохвостые мухоловки
Длинные курганы

Смотреть что такое «Длинные волны» в других словарях:

Длинные волны — (также километровые волны) диапазон радиоволн с частотой от 30 кГц (длина волны 10 км) до 300 кГц (длина волны 1 км). Длинные волны распространяются на расстояния до 1 2 тысяч км за счёт дифракции на сферической поверхности Земли. Затем их… … Википедия
ДЛИННЫЕ ВОЛНЫ — радиоволны с длиной волны от 104 до 103 м (диапазон частот 30 300 кГц). Загоризонтное распространение радиоволн ДВ диапазона осуществляется в виде земной волны (на расстояние до 2000 км) или благодаря их многократному отражению от стенок сферич.… … Физическая энциклопедия
ДЛИННЫЕ ВОЛНЫ
— радиоволны с длиной волны от 1 до 10 км. Огибают земную поверхность за счет дифракции радиоволн и отражения от ионосферы. Обеспечивают устойчивую радиосвязь; применяются для дальней (2000 км) радиосвязи и в радионавигации … Большой Энциклопедический словарь
Длинные волны — «Длинные волны» – см. Кондратьева циклы … Экономико-математический словарь
длинные волны — ДВ Участки диапазонов километровых и гектометровых волн, предназначенные для радиовещания и определенных служб радиосвязи. Примечание Указанный терминыдопустимык применению для тех служб радиосвязи, которым распределены определенные полосы… … Справочник технического переводчика
длинные волны — радиоволны с длиной волны от 1 до 10 км. Огибают земную поверхность за счёт дифракции радиоволн и отражения от ионосферы. Обеспечивают устойчивую радиосвязь; применяются для дальней (2000 км) радиосвязи и в радионавигации. * * * ДЛИННЫЕ ВОЛНЫ… … Энциклопедический словарь
длинные волны — ilgosios bangos statusas T sritis automatika atitikmenys: angl. long waves vok. lange Wellen, f rus. длинные волны, f pranc. ondes longues, f … Automatikos terminų žodynas
длинные волны — ilgosios bangos statusas T sritis fizika atitikmenys: angl. long waves vok. Langwellen, f rus. длинные волны, f pranc. ondes longues, f … Fizikos terminų žodynas
Длинные волны — 20. Длинные волны ДВ Участки диапазонов километровых и гектометровых волн, предназначенные для радиовещания и определенных служб радиосвязи Источник: ГОСТ 24375 80: Радиосвязь. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
ДЛИННЫЕ ВОЛНЫ — радиоволны с длиной волны от 1 до 10 км. Огибают земную поверхность за счёт дифракции и отражения от ионосферы. Обеспечивают устойчивую радиосвязь; применяются для дальней (2000 км) радиосвязи и в радионавигации … Естествознание. Энциклопедический словарь

Длинные волны — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Длинные волны (также километровые волны, англ. Longwave (LW), Low frequency («Низкие частоты», LF), фр. ondes longues, Basse fréquence («Низкие частоты»), grandes ondes («большие волны», GO)) — диапазон радиоволн с частотой от 30 кГц (длина волны 10 км) до 300 кГц (длина волны 1 км).

Длинные волны распространяются на расстояния до 1—2 тысяч км за счёт дифракции на сферической поверхности Земли. Затем их распространение происходит за счёт направляющего действия сферического волновода, не отражаясь.

Диапазон используется для радиовещания (148,5—283,5 кГц; ранее вещательный ДВ-диапазон был 148,5—408 кГц), для радиотелеграфной связи, радионавигационных служб и для связи с подводными лодками (9—148,5 кГц). В бытовых радиоприёмниках иностранного производства называется LW (Long Waves).

Участок 135,7—137,8 кГц используется для любительской радиосвязи. В этом диапазоне используется сверхузкополосная (полоса до единиц Гц) телеграфная связь с медленной амплитудной манипуляцией (длина точек и тире может составлять, в зависимости от ширины полосы, десятки секунд и даже минуты). В месте приёма это эквивалентно многократному увеличению мощности передатчика и позволяет при помощи маломощного передатчика установить сеанс связи со всем Земным шаром. Скорость передачи информации при этом очень мала (в лучшем случае единицы бит в минуту), потому в эфир передаются только позывные, а приём ведётся с записью для последующей расшифровки (слуховой приём невозможен).

Длинные волны способны обогнуть Земной шар.

Радио в диапазоне ДВ

До недавнего времени в России на длинных волнах вещал только радиоканал «Радио России» (с 1991 года — главный государственный радиоканал) Всероссийской государственной телерадиокомпании. В 2014 г. было прекращено вещание радиостанции «Голос России» на частоте 171 кГц. В настоящий момент на длинных волнах вещают государственные (теле-)радиокомпании:

Кроме того в направлении Франции на французском языке на длинных волнах вещают частные радиоканалы:

Вещание на длинных волнах прекратили государственные (теле-)радиокомпании:

Напишите отзыв о статье «Длинные волны»

Отрывок, характеризующий Длинные волны

– Я бы не исполнил своей обязанности, граф, – сказал он робким голосом, – и не оправдал бы того доверия и чести, которые вы мне сделали, выбрав меня своим секундантом, ежели бы я в эту важную минуту, очень важную минуту, не сказал вам всю правду. Я полагаю, что дело это не имеет достаточно причин, и что не стоит того, чтобы за него проливать кровь… Вы были неправы, не совсем правы, вы погорячились…
– Ах да, ужасно глупо… – сказал Пьер.
– Так позвольте мне передать ваше сожаление, и я уверен, что наши противники согласятся принять ваше извинение, – сказал Несвицкий (так же как и другие участники дела и как и все в подобных делах, не веря еще, чтобы дело дошло до действительной дуэли). – Вы знаете, граф, гораздо благороднее сознать свою ошибку, чем довести дело до непоправимого. Обиды ни с одной стороны не было. Позвольте мне переговорить…
– Нет, об чем же говорить! – сказал Пьер, – всё равно… Так готово? – прибавил он. – Вы мне скажите только, как куда ходить, и стрелять куда? – сказал он, неестественно кротко улыбаясь. – Он взял в руки пистолет, стал расспрашивать о способе спуска, так как он до сих пор не держал в руках пистолета, в чем он не хотел сознаваться. – Ах да, вот так, я знаю, я забыл только, – говорил он.
– Никаких извинений, ничего решительно, – говорил Долохов Денисову, который с своей стороны тоже сделал попытку примирения, и тоже подошел к назначенному месту.
Место для поединка было выбрано шагах в 80 ти от дороги, на которой остались сани, на небольшой полянке соснового леса, покрытой истаявшим от стоявших последние дни оттепелей снегом. Противники стояли шагах в 40 ка друг от друга, у краев поляны. Секунданты, размеряя шаги, проложили, отпечатавшиеся по мокрому, глубокому снегу, следы от того места, где они стояли, до сабель Несвицкого и Денисова, означавших барьер и воткнутых в 10 ти шагах друг от друга. Оттепель и туман продолжались; за 40 шагов ничего не было видно. Минуты три всё было уже готово, и всё таки медлили начинать, все молчали.

– Ну, начинать! – сказал Долохов.
– Что же, – сказал Пьер, всё так же улыбаясь. – Становилось страшно. Очевидно было, что дело, начавшееся так легко, уже ничем не могло быть предотвращено, что оно шло само собою, уже независимо от воли людей, и должно было совершиться. Денисов первый вышел вперед до барьера и провозгласил:
– Так как п’отивники отказались от п’ими’ения, то не угодно ли начинать: взять пистолеты и по слову т’и начинать сходиться.
– Г…’аз! Два! Т’и!… – сердито прокричал Денисов и отошел в сторону. Оба пошли по протоптанным дорожкам всё ближе и ближе, в тумане узнавая друг друга. Противники имели право, сходясь до барьера, стрелять, когда кто захочет. Долохов шел медленно, не поднимая пистолета, вглядываясь своими светлыми, блестящими, голубыми глазами в лицо своего противника. Рот его, как и всегда, имел на себе подобие улыбки.
– Так когда хочу – могу стрелять! – сказал Пьер, при слове три быстрыми шагами пошел вперед, сбиваясь с протоптанной дорожки и шагая по цельному снегу. Пьер держал пистолет, вытянув вперед правую руку, видимо боясь как бы из этого пистолета не убить самого себя. Левую руку он старательно отставлял назад, потому что ему хотелось поддержать ею правую руку, а он знал, что этого нельзя было. Пройдя шагов шесть и сбившись с дорожки в снег, Пьер оглянулся под ноги, опять быстро взглянул на Долохова, и потянув пальцем, как его учили, выстрелил. Никак не ожидая такого сильного звука, Пьер вздрогнул от своего выстрела, потом улыбнулся сам своему впечатлению и остановился. Дым, особенно густой от тумана, помешал ему видеть в первое мгновение; но другого выстрела, которого он ждал, не последовало. Только слышны были торопливые шаги Долохова, и из за дыма показалась его фигура. Одной рукой он держался за левый бок, другой сжимал опущенный пистолет. Лицо его было бледно. Ростов подбежал и что то сказал ему.
– Не…е…т, – проговорил сквозь зубы Долохов, – нет, не кончено, – и сделав еще несколько падающих, ковыляющих шагов до самой сабли, упал на снег подле нее. Левая рука его была в крови, он обтер ее о сюртук и оперся ею. Лицо его было бледно, нахмуренно и дрожало.
– Пожалу… – начал Долохов, но не мог сразу выговорить… – пожалуйте, договорил он с усилием. Пьер, едва удерживая рыдания, побежал к Долохову, и хотел уже перейти пространство, отделяющее барьеры, как Долохов крикнул: – к барьеру! – и Пьер, поняв в чем дело, остановился у своей сабли. Только 10 шагов разделяло их. Долохов опустился головой к снегу, жадно укусил снег, опять поднял голову, поправился, подобрал ноги и сел, отыскивая прочный центр тяжести. Он глотал холодный снег и сосал его; губы его дрожали, но всё улыбаясь; глаза блестели усилием и злобой последних собранных сил. Он поднял пистолет и стал целиться.

Гравитационные волны (гидродинамика) — Википедия

Гравитацио́нные во́лны на воде́ — разновидность волн на поверхности жидкости, при которых сила, возвращающая деформированную поверхность жидкости к состоянию равновесия, есть просто сила тяжести, связанная с перепадом высот гребня и впадины в гравитационном поле.

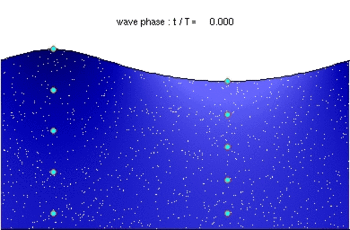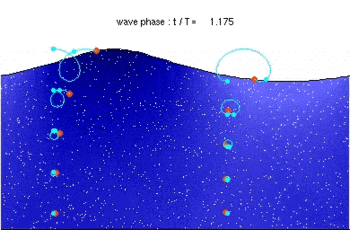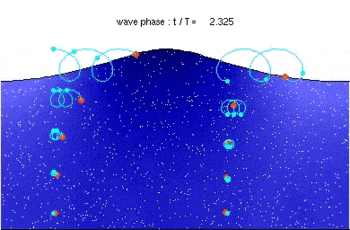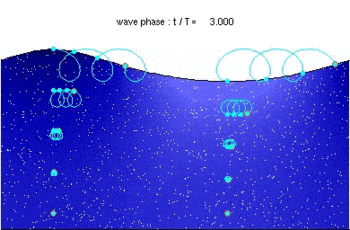
Траектории условных частиц воды при не очень большой (сравнимой с длиной волны) глубине представляют собой эллипс, что иллюстрируется качанием бутылки

Гравитационные волны на воде — это нелинейные волны. Точный математический анализ возможен лишь в линеаризованном приближении и в отсутствие турбулентности. Кроме того, обычно речь идёт про волны на поверхности идеальной жидкости. Результаты точного решения в этом случае описаны ниже.

Гравитационные волны на воде не поперечны и не продольны. При колебании частицы жидкости описывают некоторые кривые, то есть перемещаются как в направлении движения, так и поперёк него. В линеаризованном приближении эти траектории имеют вид окружностей. Это приводит к тому, что профиль волн не синусоидальный, а имеет характерные заострённые гребни и более пологие провалы.

Нелинейные эффекты сказываются, когда амплитуда волны становится сравнимой с её длиной. Одним из характерных эффектов в этом режиме является появление изломов на вершинах волн. Кроме того, появляется возможность опрокидывания волны. Эти эффекты пока не поддаются точному аналитическому расчёту.

Поведение волн малой амплитуды можно с хорошей точностью описать линеаризованными уравнениями движения жидкости. Для справедливости этого приближения необходимо, чтобы амплитуда волны была существенно меньше как длины волны, так и глубины водоёма.

Имеется две предельные ситуации, для которых решение задачи имеет наиболее простой вид — это гравитационные волны на мелкой воде и на глубокой воде.

Гравитационные волны на мелкой воде[править | править код]

Приближение волн на мелкой воде справедливо в тех случаях, когда длина волны существенно превышает глубину водоёма. Классический пример таких волн — это цунами в океане: до тех пор, пока цунами не вышла на берег, она представляет собой волну амплитудой порядка нескольких метров и длиной в десятки и сотни километров, что, конечно же, существенно больше глубины океана.

Закон дисперсии и скорости волны в этом случае имеет вид:

ω=gH⋅k;vph=vgr=gH,{\displaystyle \omega ={\sqrt {gH}}\cdot k\,;\quad v_{ph}=v_{gr}={\sqrt {gH}},}

где H{\displaystyle H} — глубина водоёма (расcтояние до дна от поверхности),

g{\displaystyle g} — напряженность гравитационного поля (ускорение свободного падения).

ω{\displaystyle \omega } — угловая частота колебания в волне,

k{\displaystyle k} — волновое число (величина, обратная длине волны),

vph,vgr{\displaystyle v_{ph},v_{gr}} — фазовая и групповая скорости соответственно.

Такой закон дисперсии приводит к некоторым явлениям, которые можно легко заметить на морском берегу.

Даже если волна в открытом море шла под углом к берегу, то при выходе на берег гребни волны имеют тенденцию разворачиваться параллельно берегу. Это связано с тем, что вблизи берега, когда глубина начинает постепенно уменьшаться, скорость волны падает. Поэтому косая волна притормаживает на подходе к берегу, разворачиваясь при этом.
За счёт аналогичного механизма при подходе к берегу уменьшается продольный размер цунами, при этом высота волны возрастает.

Гравитационные волны на глубокой воде[править | править код]

Приближение волны на глубокой воде справедливо, когда глубина водоёма значительно превышает длину волны. В этом случае для простоты рассматривают бесконечно глубокий водоём. Это обоснованно, поскольку при колебаниях поверхности реально движется не вся толща воды, а лишь приповерхностный слой глубиной порядка длины волны.

Закон дисперсии и скорости волны в этом случае имеет вид:

ω=gk;vph=2vgr=gk.{\displaystyle \omega ={\sqrt {gk}}\,;\quad v_{ph}=2v_{gr}={\sqrt {g \over k}}.}

Из выписанного закона следует, что и фазовая, и групповая скорость гравитационных волн в этом случае оказывается пропорциональной длине волны. Другими словами, длинноволновые колебания будут распространяться по воде быстрее коротковолновых, что приводит к ряду интересных явлений:

Бросив камень в воду и глядя на круги, образуемые им, можно заметить, что граница волн расширяется не равномерно, а примерно равноускоренно. При этом чем больше граница, тем более длинноволновыми колебаниями она формируется.
Красивым следствием выписанного закона дисперсии являются корабельные волны.

Гравитационные волны в общем случае[править | править код]

Если длина волны сравнима с глубиной бассейна H, то закон дисперсии в этом случае имеет вид:

ω=gk⋅th(kH).{\displaystyle \omega ={\sqrt {gk\cdot th(kH)}}\,.}

Некоторые проблемы теории гравитационных волн на воде[править | править код]

До сих пор не понят механизм формирования и устойчивости так называемых волн-убийц — внезапных волн экстремальной амплитуды.

Грац Ю. В. Лекции по гидродинамике.-М., Ленанд, 2014

Волновод — Википедия

Полые металлические волноводы прямоугольного сечения с соединительными фланцами Изогнутый отрезок металлического волновода прямоугольного сечения с соединительными фланцами.

Волново́д — искусственный или естественный направляющий канал, в котором может распространяться волна. При этом поток мощности, переносимый волной, сосредоточен внутри этого канала или в области пространства, непосредственно примыкающей к каналу.

По природе распространяющихся волн различают электромагнитные и акустические волноводы. Частным случаем первых являются оптоволоконные линии передачи. Наиболее часто под термином «волновод» подразумеваются металлические трубки, предназначенные для передачи энергии электромагнитных волн диапазонов СВЧ и КВЧ. Такой волново́д — линия передачи, имеющая одну или несколько проводящих поверхностей, с поперечным сечением в виде замкнутого проводящего контура, охватывающего область распространения электромагнитной энергии^[1].

Впервые конструкция для передачи волн была предложена английским физиком Джозефом Джоном Томсоном в 1893 году, а первым её принцип экспериментально проверил английский физик и изобретатель Оливер Лодж в 1894 году. Первым математический анализ хода электромагнитных волн в металлическом цилиндре выполнил британский физик и механик Лорд Рэлей в 1897 году^[2]. В процессе тщательного изучения звуковых волн (поверхностных акустических волн), Лорд Рэлей опубликовал полный математический анализ принципа их распространения в своём фундаментальном исследовании «Теория звука»^[3].

В дальнейшем, в 20-е годы двадцатого века началось изучение диэлектрических волноводов (в том числе и оптических волокон). Несколько учёных, среди которых наиболее известными являлись британский физик и механик Рэлей, немецкий физик-теоретик и математик Зоммерфельд, а также нидерландский физик Дебай^[4]. Фундаментальные исследования привели к тому, что в 1960-е годы стекловолокна стали привлекать к себе особое внимание в связи с открывающимися возможностями их использования для передачи данных и обеспечения связи.

Экранированные[править | править код]

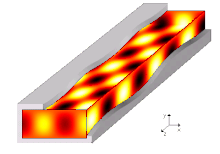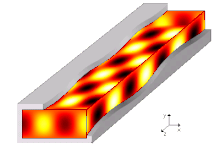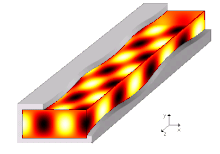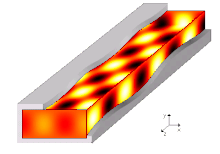Графическое представление напряжённости магнитного поля распространяющейся электромагнитной волны внутри прямоугольного металлического волновода.

Экранированные волноводы имеют хорошо отражающие стенки для распространяющейся в нём волны, благодаря чему поток мощности волны сосредоточен внутри волновода. Как правило, такие волноводы выполнены в виде полых или заполненных средой со специально подобранными параметрами трубок. Поперечное сечение этих трубок имеет форму окружности, эллипса, прямоугольника, что связано с большей конструктивной простотой, хотя для специальных целей используются волноводы и с другими формами поперечного сечения. Чтобы волна по мере распространения в волноводе не отражалась в обратном направлении, волновод выполняют регулярным: форма и размеры поперечного сечения, а также физические свойства материалов должны быть постоянны вдоль длины волновода. Поскольку волна отражается от стенок экранированного волновода, то в поперечном направлении возникает стоячая волна с определённым составом мод.

Для передачи электромагнитных волн используются металлические трубки, полые или заполненные диэлектриком. Также используются коаксиальные и многожильные экранированные кабели, которые относят к проводным линиям передачи. Термин «радиочастотный волновод» (англ. radiofrequency guide, обозначение RG) подчёркивает назначение и отличие от проводных линий передачи постоянного тока и тока промышленной частоты, а также от низкочастотных коммуникационных кабелей. Металлические волноводы и коаксиальные кабели со сквозными отверстиями-щелями в экране служат для построения волноводно-щелевых антенн и излучающих кабелей.

К экранированным волноводам относят также акустические волноводы, это трубы с достаточно жёсткими стенками, например, металлические или пластмассовые. В таких волноводах акустические колебания распространяются в газе, наполняющем волновод, как правило, в воздухе. Ранее широко применялись на судах и кораблях под названием «переговорные трубы».

Практически все типы волноводов можно рассматривать как разновидности длинных линий передачи, то есть таких, длина которых существенно превышает длину распространяющейся в них волны.

Неэкранированные[править | править код]

В открытых (неэкранированных) волноводах локализация поля обычно обусловлена явлением полного внутреннего отражения от границ раздела двух сред (в волноводах диэлектрических и оптоволоконных световодах), либо от областей с плавно изменяющимися параметрами среды (например, ионосферный волновод, атмосферный волновод, подводный звуковой канал, градиентное оптоволокно). Поле локализуется преимущественно внутри специально предназначенной для этого области поперечного сечения волновода и быстро убывает за пределами этой области. Благодаря этому волна канализируется в волноводе. Открытые планарные волноводы оптического диапазона используются для построения различных интегральных оптоэлектронных устройств.

Акустические открытые волноводы служат основой устройств на поверхностных акустических волнах, в таких волноводах ультразвуковая волна распространяется вдоль границы раздела сред с различными акустическими свойствами.

В волноводах, как в системах с распределёнными параметрами, возможно существование дискретного (при не очень сильном поглощении) набора (ансамбля) типов колебаний (мод), каждый тип колебаний распространяется со своими фазовыми и групповыми скоростями. Все моды обладают дисперсией, то есть их фазовые скорости зависят от частоты и отличаются от групповых скоростей.

В экранированном волноводе фазовые скорости обычно превышают скорость распространения плоской однородной волны в заполняющей среде (скорость света, скорость звука), эти волны называются быстрыми. При неполном экранировании они могут просачиваться сквозь стенки волновода, переизлучаясь в окружающее пространство. Это так называемые утекающие волны. В открытых волноводах, как правило, распространяются медленные волны, амплитуды которых быстро убывают при удалении от направляющего канала.

Каждая мода характеризуется предельной частотой ωk{\displaystyle \omega _{k}} , называемой критической; мода может распространяться и переносить вдоль волновода поток энергии только на частотах ω{\displaystyle \omega }, превышающих ωkr{\displaystyle \omega _{kr}}. Однако в некоторых случаях (многопроводные линии передачи, полые акустические волноводы) существуют моды, для которых ωkr=0{\displaystyle \omega _{kr}=0}, их называют главными или квазистатическими.

При больших ω{\displaystyle \omega } волновод становится сверхразмерным (поперечные размеры волновода значительно превышают длину волны): тогда в нём одновременно распространяется множество мод, которые при определённых соотношениях между амплитудами и фазами могут группироваться в бегущие вдоль волновода сгустки. В предельном случае, в волноводе образуется стоячая волна с узлами и пучностями, например, для акустических волноводов — узлы акустического давления. В узлах стенки можно убрать, заменив сплошную трубу последовательно расставленными отражателями. Такие, а также аналогичные им линзовые системы классифицируют как квазиоптические волноводы или квазиоптические линии передачи.

$\omega$ $\omega$ Система радиочастотных волноводов ускорителя Арагонской Национальной лаборатории. $\omega$

Радиочастотные электрические волноводы всегда применяются в современных радиолокационных станциях, технике для ускорения элементарных частиц.

Акустические волноводы (переговорные трубы) применяются на современных судах, дублируя электронные переговорные устройства при их отказе.

Волноводы на поверхностных акустических волнах применяются в обработке сигналов для построения электромеханических фильтров.

Калинин В. А., Лобов Г. Д., Штыков В. В. Радиофизика для инженеров / Под ред. С.И.Баскакова. — М.: Изд-во МЭИ, 1994. — 130 с. — 500 экз.
Шаров Г.А. Волноводные устройства сантиметровых и миллиметровых волн. — М.: Горячая линия — Телеком, 2015. — 640 с. — 500 экз. — ISBN 978-5-9912-0473-6.

Длинная линия — Википедия

Длинная линия — модель линии передачи, продольный размер (длина) которой превышает длину волны, распространяющейся в ней (либо сравнима с длиной волны), а поперечные размеры (например, расстояние между проводниками, образующими линию) значительно меньше длины волны.

С точки зрения теории электрических цепей длинная линия относится к четырёхполюсникам. Характерной особенностью длинной линии является проявление интерференции двух волн, распространяющихся навстречу друг другу. Одна из этих волн создается подключенным ко входу линии генератором электромагнитных колебаний и называется падающей. Другая волна называется отражённой и возникает из-за частичного отражения падающей волны от нагрузки, подключенной к выходу (противоположному генератору концу) линии. Всё разнообразие колебательных и волновых процессов, происходящих в длинной линии, определяется соотношениями амплитуд и фаз падающей и отраженной волн. Анализ процессов упрощается, если длинная линия является регулярной, то есть такой, у которой в продольном направлении неизменны поперечное сечение и электромагнитные свойства (ε_r, μ_r, σ) заполняющих сред ^[1].

Дифференциальные уравнения длинной линии[править | править код]

Двухпроводная длинная линия
Z_Н = R_Н + iX_Н — комплексное сопротивление нагрузки;
z — продольная координата линии, отсчитываемая от места подключения нагрузки.

Первичные параметры[править | править код]

Из электродинамики известно, что линия передачи может быть охарактеризована её погонными параметрами:

R₁ — погонное сопротивление металла проводов, Ом/м;
G₁ — паразитная, параллельная(источник термина ) погонная(продольная, аддитивная) проводимость диэллектрика линии,1/Ом·м или См/м; ,- погонная вдоль линии, ортогонально токам утечки через диэллектрик, в противовес g[Cм·м] — проводимости погонной,приведённой к единице длины паразитного тока, текущего через диэллектрик линии(поперечно-погонной проводимости изолятора линии)!
L₁ — погонная индуктивность Гн/м;
C₁ — погонная ёмкость Ф/м;
Z1=R1+iωL1{\displaystyle Z_{1}=R_{1}+i\omega L_{1}}
Y1=G1+iωC1{\displaystyle Y_{1}=G_{1}+i\omega C_{1}}

Погонные сопротивление и проводимость G₁ зависят от проводимости материала проводов и качества диэлектрика, окружающего эти провода, соответственно. Согласно закону Джоуля — Ленца, чем меньше тепловые потери в металле проводов и в диэлектрике, тем меньше погонное сопротивление металла R₁ и меньше погонная проводимость диэлектрика G₁. (Уменьшение активных потерь в диэлектрике означает увеличение его сопротивления, так как активные потери в диэлектрике — это токи утечки. Для модели используется обратная величина — погонная проводимость G₁.)

Погонные индуктивность L₁ и ёмкость C₁ определяются формой и размерами поперечного сечения проводов, а также расстоянием между ними.

А Z1{\displaystyle Z_{1}} и Y1{\displaystyle Y_{1}} — погонные комплексные сопротивление и проводимость линии, зависящие от частоты ω{\displaystyle \omega }.

Выделим из линии элементарный участок бесконечно малой длины dz и рассмотрим его эквивалентную схему.

Эквивалентная схема участка длинной линии[править | править код]

Эквивалентная схема участка длинной линии. Стрелками обозначены направления отсчета напряжения U и тока I в линии; dU и dI — приращения напряжения и тока в линии на элементе длины dz

Значения параметров схемы определяются соотношениями:

{dR=R1dz;dG=G1dz;dL=L1dz;dC=C1dz;{\displaystyle {\begin{cases}dR=R_{1}dz;\\dG=G_{1}dz;\\dL=L_{1}dz;\\dC=C_{1}dz;\\\end{cases}}}

(1)

Используя эквивалентную схему, запишем выражения для приращений напряжения и тока:

{dU=−I(dR+iωdL)dI=−U(dG+iωdC){\displaystyle {\begin{cases}dU=-I(dR+i\omega dL)\\dI=-U(dG+i\omega dC)\\\end{cases}}}

Подставляя сюда значения параметров схемы из (1), получаем:

{dU=−IZ1dzdI=−UY1dz{\displaystyle {\begin{cases}dU=-IZ_{1}dz\\dI=-UY_{1}dz\\\end{cases}}}

Из последних соотношений находим дифференциальные уравнения линии. Эти уравнения определяют связь между током и напряжением в любом сечении линии и называются телеграфными уравнениями длинной линии:

Телеграфные уравнения[править | править код]

{dUdz=−IZ1dIdz=−UY1{\displaystyle {\begin{cases}{\frac {dU}{dz}}=-IZ_{1}\\{\frac {dI}{dz}}=-UY_{1}\\\end{cases}}}

(2)

Следствия[править | править код]

Решим телеграфные уравнения относительно напряжения и тока. Для этого продифференцируем их по z:

{d2Udz2=−dIdzZ1d2Idz2=−dUdzY1{\displaystyle {\begin{cases}{\frac {d^{2}U}{dz^{2}}}=-{\frac {dI}{dz}}Z_{1}\\{\frac {d^{2}I}{dz^{2}}}=-{\frac {dU}{dz}}Y_{1}\\\end{cases}}}

(3)

При этом учтем условие регулярности линии:

Условие регулярности линии[править | править код]

{dZ1dz=0dY1dz=0{\displaystyle {\begin{cases}{\frac {dZ_{1}}{dz}}=0\\{\frac {dY_{1}}{dz}}=0\\\end{cases}}}

(4)

Данные соотношения являются математическим определением регулярности длинной линии. Смысл соотношения (4) состоит в неизменности вдоль линии её погонных параметров.

Подставляя в (3) значения производных напряжения и тока из (2), после преобразований получаем:

Однородные волновые уравнения длинной линии[править | править код]

{d2Udz2−γ2U=0d2Idz2−γ2I=0{\displaystyle {\begin{cases}{\frac {d^{2}U}{dz^{2}}}-\gamma ^{2}U=0\\{\frac {d^{2}I}{dz^{2}}}-\gamma ^{2}I=0\\\end{cases}}},

(5)

где γ=Z1Y1{\displaystyle \gamma ={\sqrt {Z_{1}Y_{1}}}} — коэффициент распространения волны в линии.

Соотношения (5) называются однородными волновыми уравнениями длинной линии. Их решения известны и могут быть записаны в виде:

{U=BUeγz+AUe−γzI=BIeγz+AIe−γz{\displaystyle {\begin{cases}U=B_{U}e^{\gamma z}+A_{U}e^{-\gamma z}\\I=B_{I}e^{\gamma z}+A_{I}e^{-\gamma z}\\\end{cases}}},

(6)

где A_U, B_U и A_I, B_I — коэффициенты, имеющие единицы измерения напряжения и тока соответственно, смысл которых будет ясен ниже.

Решения волновых уравнений в виде (6) имеют весьма характерный вид: первое слагаемое в этих решениях представляет собой отраженную волну напряжения или тока, распространяющуюся от нагрузки к генератору, второе слагаемое — падающую волну, распространяющуюся от генератора к нагрузке. Таким образом, коэффициенты A_U, A_I представляют собой комплексные амплитуды падающих волн напряжения и тока соответственно, а коэффициенты B_U, B_I — комплексные амплитуды отраженных волн напряжения и тока соответственно. Так как часть мощности, передаваемой по линии, может поглощаться в нагрузке, то амплитуды отраженных волн не должны превышать амплитуды падающих:

|BU|⩽|AU|{\displaystyle |B_{U}|\leqslant |A_{U}|}

|BI|⩽|AI|{\displaystyle |B_{I}|\leqslant |A_{I}|}

Направление распространения волн в (6) определяется знаком в показателях степени экспонент: плюс — волна распространяется в отрицательном направлении оси z; минус — в положительном направлении оси z (см. рис. 1). Так, например, для падающих волн напряжения и тока можно записать:

{UΠ=AUe−γzIΠ=AIe−γz{\displaystyle {\begin{cases}U_{\Pi }=A_{U}e^{-\gamma z}\\I_{\Pi }=A_{I}e^{-\gamma z}\\\end{cases}}},

(7)

Коэффициент распространения волны в линии γ в общем случае является комплексной величиной и может быть представлен в виде:

γ=Z1Y1=(R1+iωL1)(G1+iωC1)=α+iβ{\displaystyle \gamma ={\sqrt {Z_{1}Y_{1}}}={\sqrt {(R_{1}+i\omega L_{1})(G_{1}+i\omega C_{1})}}=\alpha +i\beta },

(8)

где α — коэффициент затухания волны^[2] в линии; β — коэффициент фазы^[3]. Тогда соотношение (7) можно переписать в виде:

{UΠ=AUe−αze−iβzIΠ=AIe−αze−iβz{\displaystyle {\begin{cases}U_{\Pi }=A_{U}e^{-\alpha z}e^{-i\beta z}\\I_{\Pi }=A_{I}e^{-\alpha z}e^{-i\beta z}\\\end{cases}}}.

(9)

Так как при распространении падающей волны на длину волны в линии λ_Л фаза волны изменяется на 2π, то коэффициент фазы можно связать с длиной волны λ_Л соотношением

β=2πλΛ{\displaystyle \beta ={\frac {2\pi }{\lambda _{\Lambda }}}}.

(10)

При этом фазовая скорость волны в линии V_Ф определяется через коэффициент фазы:

VΦ=ωβ{\displaystyle V_{\Phi }={\frac {\omega }{\beta }}}.

(11)

Определим коэффициенты A и B, входящие в решения (6) волновых уравнений, через значения напряжения U_Н и тока I_Н на нагрузке. Это является оправданным, так как напряжение и ток на нагрузке практически всегда можно измерить с помощью измерительных приборов. Воспользуемся первым из телеграфных уравнений (2) и подставим в него напряжение и ток из (6). Тогда получим:

AUγe−γz−BUγeγz=Z1(AIe−γz+BIeγz){\displaystyle A_{U}\gamma e^{-\gamma z}-B_{U}\gamma e^{\gamma z}=Z_{1}(A_{I}e^{-\gamma z}+B_{I}e^{\gamma z})}

Сравнив коэффициенты при экспонентах с одинаковыми показателями степеней, получим:

{AI=AUWBI=−BUW{\displaystyle {\begin{cases}A_{I}={\frac {A_{U}}{W}}\\B_{I}=-{\frac {B_{U}}{W}}\\\end{cases}}},

(12)

где W=Z1Y1{\displaystyle W={\sqrt {\frac {Z_{1}}{Y_{1}}}}} — волновое сопротивление линии^[4].

Перепишем (6) с учётом (12):

{U=AUe−γz+BUeγzI=−AUe−γz+BUeγzW{\displaystyle {\begin{cases}U=A_{U}e^{-\gamma z}+B_{U}e^{\gamma z}\\I={\frac {-A_{U}e^{-\gamma z}+B_{U}e^{\gamma z}}{W}}\\\end{cases}}}.

(13)

Для определения коэффициентов A и B в этих уравнениях воспользуемся условиями в начале линии z = 0:

{U(z=0)=UHI(z=0)=IH{\displaystyle {\begin{cases}U(z=0)=U_{H}\\I(z=0)=I_{H}\\\end{cases}}}.

Тогда из (13) при z = 0 найдем

{AU=12(UH+IHW)BU=12(UH−IHW){\displaystyle {\begin{cases}A_{U}={\tfrac {1}{2}}(U_{H}+I_{H}W)\\B_{U}={\tfrac {1}{2}}(U_{H}-I_{H}W)\\\end{cases}}},

(14)

Подставив полученные значения коэффициентов из (14) в (13), после преобразований получим:

{U=UHch⁡(γz)+IHWsh⁡(γz)I=IHch⁡(γz)+UHWsh⁡(γz){\displaystyle {\begin{cases}U=U_{H}\operatorname {ch} (\gamma z)+I_{H}W\operatorname {sh} (\gamma z)\\I=I_{H}\operatorname {ch} (\gamma z)+{\frac {U_{H}}{W}}\operatorname {sh} (\gamma z)\\\end{cases}}}.

(15)

При выводе (15) учтены определения гиперболических синуса и косинуса^[5].

Соотношения для напряжения и тока (15) так же, как и (6), являются решениями однородных волновых уравнений. Их отличие состоит в том, что напряжение и ток в линии в соотношении (6) определены через амплитуды падающей и отраженной волн, а в (15) — через напряжение и ток на нагрузке.

Рассмотрим простейший случай, когда напряжение и ток в линии определяются только падающей волной, а отраженная волна отсутствует^[6]. Тогда в (6) следует положить B_U = 0, B_I = 0:

{U=AUe−αze−iβzI=AIe−αze−iβz{\displaystyle {\begin{cases}U=A_{U}e^{-\alpha z}e^{-i\beta z}\\I=A_{I}e^{-\alpha z}e^{-i\beta z}\\\end{cases}}}.

Распределение поля падающей волны[править | править код]

Рис.3. Эпюры напряжений падающей волны в длинной линии. а) амплитуда; б) фаза

На рис.3. представлены эпюры изменения амплитуды |U| и фазы φ_U напряжения вдоль линии. Эпюры изменения амплитуды и фазы тока имеют такой же вид. Из рассмотрения эпюр следует, что при отсутствии в линии потерь (α^[2] = 0) амплитуда напряжения в любом сечении линии остается одной и той же. При наличии потерь в линии (α^[2] > 0) часть переносимой мощности преобразуется в тепло (нагревание проводов линии и окружающего их диэлектрика). По этой причине амплитуда напряжения падающей волны экспоненциально убывает в направлении распространения.

Фаза напряжения падающей волны φ_U = β z изменяется по линейному закону и уменьшается по мере удаления от генератора.

Рассмотрим изменение амплитуды и фазы, например, напряжения при наличии падающей и отраженной волн. Для упрощения положим, что потери в линии отсутствуют, то есть α^[2] = 0. Тогда напряжение в линии можно представить в виде:

U=AUe−iβz+BUeiβz=AU(e−iβz+Γeiβz){\displaystyle U=A_{U}e^{-i\beta z}+B_{U}e^{i\beta z}=A_{U}(e^{-i\beta z}+\Gamma e^{i\beta z})},

(16)

где Γ=BU/AU{\displaystyle \Gamma =B_{U}/A_{U}} — комплексный коэффициент отражения по напряжению.

Комплексный коэффициент отражения по напряжению[править | править код]

Характеризует степень согласования линии передачи с нагрузкой. Модуль коэффициента отражения изменяется в пределах: 0⩽|Γ|⩽1{\displaystyle 0\leqslant |\Gamma |\leqslant 1}

| Г | = 0, если отражения от нагрузки отсутствуют и B_U = 0^[6];
| Г | = 1, если волна полностью отражается от нагрузки, то есть |AU|=|BU|{\displaystyle |A_{U}|=|B_{U}|};

Соотношение (16) представляет собой сумму падающей и отраженной волн.

Рис.4. Векторная диаграмма напряжений в линии с отраженной волной

Отобразим напряжение на комплексной плоскости в виде векторной диаграммы, каждый из векторов которой определяет падающую, отраженную волны и результирующее напряжение (рис. 4). Из диаграммы видно, что существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в фазе. Напряжение в этих сечениях достигает максимума, величина которого равна сумме амплитуд падающей и отраженной волн:

Umax=|AU|+|BU|{\displaystyle U_{max}=|A_{U}|+|B_{U}|}.

Кроме того, существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в противофазе. При этом напряжение достигает минимума:

Umin=|AU|−|BU|{\displaystyle U_{min}=|A_{U}|-|B_{U}|}.

Если линия нагружена на сопротивление, для которого |Г| = 1, то есть амплитуда падающей и отраженной волн равны |B_U| = |A_U|, то в этом случае U_max = 2|A_U|, а U_min = 0.

Рис.5. Эпюры распределения напряжения вдоль линии с отражённой волной. а) Модуль напряжения; б) фаза напряжения.

Напряжение в такой линии изменяется от нуля до удвоенной амплитуды падающей волны. На рис. 5 представлены эпюры изменения амплитуды и фазы напряжения вдоль линии при наличии отраженной волны.

Коэффициенты бегущей и стоячей волны[править | править код]

По эпюре напряжения судят о степени согласования линии с нагрузкой. Для этого вводятся понятия коэффициента бегущей волны — k_БВ и коэффициента стоячей волны k_СВ:

kbv=UminUmax=\|AU\|−\|BU\|\|AU\|+\|BU\|=1−\|Γ\|1+\|Γ\|{\displaystyle k_{bv}={\frac {U_{min}}{U_{max}}}={\frac {\|A_{U}\|-\|B_{U}\|}{\|A_{U}\|+\|B_{U}\|}}={\frac {1-\|\Gamma \|}{1+\|\Gamma \|}}}	(17)
ksv=1kbv{\displaystyle k_{sv}={\frac {1}{k_{bv}}}}	(18)

Эти коэффициенты, судя по определению, изменяются в пределах:

0⩽kbv⩽1{\displaystyle 0\leqslant k_{bv}\leqslant 1},

1⩽ksv⩽∞{\displaystyle 1\leqslant k_{sv}\leqslant \infty }.

На практике наиболее часто используется понятие коэффициента стоячей волны, так как современные измерительные приборы (панорамные измерители k_СВ) на индикаторных устройствах отображают изменение именно этой величины в определенной полосе частот.

Входное сопротивление длинной линии[править | править код]

Входное сопротивление линии является важной характеристикой, которое определяется в каждом сечении линии как отношение напряжения к току в этом сечении:

ZBX=RBX+iXBX{\displaystyle Z_{BX}=R_{BX}+iX_{BX}}
ZBX(z)=U(z)I(z){\displaystyle Z_{BX}(z)={\frac {U(z)}{I(z)}}}	(19)

Так как напряжение и ток в л

Ветровые волны — Википедия

Штормовые волны в Северной части Тихого Океана

Океанские волны

Ветровые волны создаются вследствие воздействия ветра (передвижение воздушных масс) на поверхность воды, то есть нагнетания. Причина колебательных движений волн становится легко понятна, если заметить воздействие того же ветра на поверхность пшеничного поля. Хорошо заметна непостоянность ветровых потоков, которые и создают волны.

В силу того что вода является веществом более плотным, чем воздух (примерно в 800 раз) — реакция воды на воздействие ветра несколько «запаздывает», и рябь переходит в волны лишь через некоторое расстояние и время при условии постоянного воздействия ветра. Если учесть такие параметры, как постоянность потока ветра, его направление, скорость, площадь воздействия, а также предыдущее состояние колебания поверхности водной глади, то мы получаем направление волны, высоту волны, частоту волны, наложение нескольких колебаний-направлений на один и тот же участок поверхности воды. Следует отметить, что направление волны не всегда совпадает с направлением ветра. Это особо заметно при изменении направления ветра, смешивании разных воздушных потоков, изменении условий среды воздействия (открытое море, гавань, суша, залив или любое другое достаточно большое тело, способное внести изменение в тенденцию воздействия и образования волн)- это означает, что иногда ветер гасит волны. В глубоком море размеры волн и характер волнения определяются скоростью ветра, продолжительностью его действия, структурой ветрового поля и конфигурацией береговой черты, а также расстоянием от подветренного берега в направлении ветра до точки наблюдения^[1].

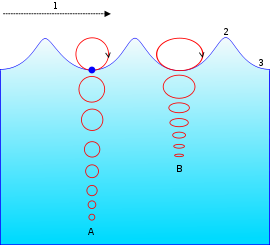Движение частиц в ветровой волне.
A = на большой глубине
B = на мелководье
1 = направлении распространения.
2 = гребень волны
3 = подошва волны

В отличие от постоянных потоков в реках, что идут в практически одном и том же направлении, энергия волн содержится в их вертикальном колебании и частично горизонтальном при малой глубине. Высота волны, а точнее, её распределение, расценивается как 2/3 над среднестатистической поверхностью воды и всего лишь на 1/3 в глубь. Примерно такое же соотношение отмечается и в скорости движения волны вверх и вниз. Вероятно, эта разница вызвана разной природой сил воздействия на движение волны: при подъёме водной массы действует в основном давление (волну буквально выдавливает из моря повышенное давление воды на данном участке и сравнительно низкое сопротивление-давление воздуха). При движении волны вниз в основном действуют сила гравитации, вязкость жидкости, давление ветра на поверхность. Противодействуют этому процессу: инерция предыдущего движения воды, внутреннее давление моря (вода медленно уступает место опускающейся волне — перемещая давление в близлежащие районы воды), плотность воды, вероятные восходящие потоки воздуха (пузыри), возникающие при опрокидывании гребня волны, и т. д.

Волны как возобновляемый источник энергии[править | править код]

Морская волна и движение частиц в воде, когда длина волны намного больше глубины. Формирование ребристого песчаного дна.

Особенно важно отметить тот факт, что ветровые волны являются сконцентрированной энергией ветра. Волны передаются на большие расстояния и сохраняют в себе потенциал энергии на долгое время. Так, часто можно наблюдать волнение моря после бури или шторма, когда ветер давно стих, или волнение моря при штиле. Это даёт волнам большое преимущество как возобновляемому источнику энергии в ввиду его сравнительного постоянства и возможности прогнозирования, поскольку волны возникают практически с небольшой задержкой после возникновения ветра и продолжают существовать долго после него, перемещаясь на далёкие расстояния, что делает получение электроэнергии от волн более рентабельным по сравнению с ветрогенераторами. Сюда следует добавить постоянство морского волнения вне зависимости от времени суток или облачности, что делает волновые генераторы более рентабельными по сравнению с солнечными батареями, так как солнечные батареи вырабатывают электричество только днём и желательно при ясной летней погоде — зимой же процент производительности ниспадает до 5 % от предполагаемой мощности батареи.

Колебания водной поверхности являются результатом воздействия солнечной активности. Солнце нагревает поверхность планеты (причём неравномерно — суша нагревается быстрее, чем море), повышение температуры поверхности приводит к повышению температуры воздуха — а это, в свою очередь, приводит к расширению воздуха, что означает повышение давления. Разность давления воздуха в различных областях атмосферы вместе с силой Кориолиса являются основными факторами формирования ветра. А ветер нагнетает волны. Надо отметить, что этот феномен также хорошо действует и в обратном направлении, когда поверхность планеты неравномерно остывает.

Если учесть возможность повышения концентрации энергии на квадратный метр поверхности путём уменьшения глубины дна и (или) создания волновых «загонов» — вертикальных барьеров, то получение электричества от волновых колебаний водной поверхности становится очень выгодным предложением. Подсчитано, что при использовании лишь 2-5 % энергии волн мирового океана человечество в силах перекрыть все свои нынешние потребности в электроэнергии на глобальном уровне в 5 раз^{[источник не указан 3089 дней]}.

Сложность воплощения волновых генераторов в реальность заключается в самой водной среде и её непостоянстве. Известны случаи высоты волн в 30 и более метров. Сильны волнения или высокая энергоконцентрация волн в районах ближе к полюсам (в среднем 60-70 кВт/кв.м.). Этот факт ставит перед изобретателями, работающими в северных широтах, задачу обеспечить должную надежность устройства, чем уровень КПД. И наоборот — в Средиземном море и Чёрном море, где энергоёмкость волн составляет в среднем около 10 кВч/квадратный метр, конструкторы, кроме живучести установки в неблагоприятных условиях, вынуждены искать способы повышения эффективности установки (КПД), что неизменно приведёт последних к созданию более рентабельных установок. Примером может послужить Австралийский проект Oceanlinx.

В Российской Федерации эта ниша производства электроэнергии пока не заполнена, несмотря на практически неограниченные водные просторы разной энергоёмкости, начиная с Байкала, Каспийского, Чёрного морей и кончая Тихим Океаном и другими северными водными просторами (на период незамерзания), но Российские компании уже работают над собственными волновыми генераторами способными извлекать электрическую энергию из волн. Примером может послужить OceanRusEnergy из г. Екатеринбурга.

Кроме того, в местах преобразования волн в электроэнергию морская жизнь становится более богатой ввиду того, что дно не подвергается деструктивным воздействиям во время шторма.

Волны морские // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
Carr, Michael «Understanding Waves» Sail Oct 1998: 38-45.
Rousmaniere, John. The Annapolis Book of Seamanship, New York: Simon & Schuster 1989
G.G. Stokes. On the theory of oscillatory waves (неопр.) // Transactions of the Cambridge Philosophical Society. — 1847. — Т. 8. — С. 441—455.
Reprinted in: G.G. Stokes. Mathematical and Physical Papers, Volume I (англ.). — Cambridge University Press, 1880. — P. 197—229.
Phillips, O.M. (1977), The dynamics of the upper ocean (2^nd ed.), Cambridge University Press, ISBN 0 521 29801 6
Holthuijsen, L.H. (2007), Waves in oceanic and coastal waters, Cambridge University Press, ISBN 0521860288
Falkovich, Gregory (2011), Fluid Mechanics (A short course for physicists), Cambridge University Press, ISBN 978-1-107-00575-4, <http://www.weizmann.ac.il/complex/falkovich/fluid-mechanics>