Свойства волн: длина, частота и скорость
Физика > Длина волны, частота в соотношении со скоростью
Характеристика волны – длина, скорость и частота. Узнайте, что такое частота на графике волны, фазовая и групповая скорость, распространение волны и амплитуда.
Волны характеризуются по частоте, длине и амплитуде. Есть также два типа скорости: фазовая и групповая.
Задача обучения
- Рассмотреть главные характерные свойства волн.
Основные пункты
- Длина волны – пространственный период.
- Частота – число циклов за временной промежуток. Нельзя смешивать с угловой частотой.
- Фазовую скорость можно определить в качестве произведения длины и частоты.
Термины
- Скорость волны – абсолютный показатель скорости, при которой проходит фаза любого частотного компонента волны.
- Частота – соотношение числа периодического явления к временному промежутку: f = n/t.
Пример
Если мы рассмотрим видимый свет, то можем отобразить его как электромагнитную волну. Она будет представлена электрическими и магнитными полями, смещающимися в среде. Частоту определяют как цвет: 4 × 10
Свойства волн
Волны характеризуются по их свойствам. Амплитуда представляет половину дистанции от гребня к впадине. Также можно заметить длину волны – пространственный период (от гребня к гребню), обозначающийся буквой λ.
Частота – количество пройденных циклов за определенный временной промежуток. В виде формулы:

Красная волна наделена низкочастотным синусом, поэтому наблюдается мало повторений циклов. А вот у фиолетовой высокая частота. Заметьте, что время растет по горизонтали
f = 1/T (T – период колебаний).
Частота и длина волны также могут быть связаны друг с другом по отношению к «скорости» волны. Получаем:
v = fλ (v – скорость волны или фазовая скорость, с которой фаза волны распространяется в пространстве).
Есть также групповая скорость волны – показатель, с которым общая форма волновых амплитуд (модуляция или огибающая волны) распространяется в пространстве.

Перед вами волна с групповой (положительная) и фазовой (отрицательная) скоростями, движущихся в разных направлениях
3. Длина волны. Связь длины волны со скоростью её распространения и периодом (частотой)
Каждая волна распространяется с какой-то скоростью.
Под скоростью волны понимают скорость распространения возмущения.
Пример:
удар по торцу стального стержня вызывает в нём местное сжатие, которое затем распространяется вдоль стержня со скоростью около \(5\) км/с.
Обрати внимание!
Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую её скорость изменяется.
Помимо скорости, важной характеристикой волны является длина волны.
Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Рассмотрим процесс передачи колебаний от точки к точке при распространении поперечной волны.
Для этого используем: частицы среды, в которой будет распространяться волна, примем за цепочку пронумерованных шариков (рис. \(1\)).
Будем считать, что между шариками, как и между частицами среды, существуют силы взаимодействия, в частности при небольшом удалении шариков друг от друга возникает сила притяжения.

Рис. \(1\)
Если привести первый шарик в колебательное движение, то есть заставить его двигаться вверх и вниз от положения равновесия, то благодаря силам взаимодействия каждый шарик в цепочке будет повторять движение первого, но с некоторым запаздыванием (сдвигом фаз). Это запаздывание будет тем больше, чем дальше от первого шарика находится данный шарик.
Четвёртый шарик отстаёт от первого на \(1/4\) колебания (рис. \(2\)). Когда первый шарик прошёл \(1/4\) часть пути полного колебания, максимально отклонившись вверх, четвёртый шарик только начал движение из положения равновесия.

Рис. \(2\)
Движение седьмого шарика отстаёт от движения первого на \(1/2\) колебания (рис. \(3\)), десятого — на \(3/4\) колебания (рис. \(4\)).

Рис. \(3\)

Рис. \(4\)
Тринадцатый шарик отстаёт от первого на одно полное колебание (рис. \(5\)), то есть находится с ним в одинаковых фазах.

Рис. \(5\)
Движения этих двух шариков совершенно одинаковы (рис. \(6\)).

Рис. \(6\)
Расстояние между ближайшими друг к другу точками, колеблющимися в одинаковых фазах, называется длиной волны.
Обрати внимание!
Длина волны обозначается греческой буквой \(λ\) («ламбда»).
Расстояние между первым и тринадцатым шариками (см. рис. \(6\)), вторым и четырнадцатым, третьим и пятнадцатым и так далее, то есть между всеми ближайшими друг к другу шариками, колеблющимися в одинаковых фазах, будет равно длине волны \(λ\).
Из рисунков выше видно, что колебательный процесс распространился от первого шарика до тринадцатого, то есть на расстояние, равное длине волны \(λ\), за то же время, за которое первый шарик совершил одно полное колебание, то есть за период колебаний \(T\).
Значит,
λ=VT,
где \(V\) — скорость волны.
Поскольку период колебаний связан с их частотой ν зависимостью
T=1ν,
то длина волны может быть выражена через скорость волны и частоту:
λ=Vν.
Обрати внимание!
Длина волны зависит от частоты ν (или периода \(T\)) колебаний источника, порождающего эту волну, и от скорости \(V\) распространения волны.
Из формул для определения длины волны можно выразить скорость волны:
V=λT
и
V=λν.
Обрати внимание!
Формулы для нахождения скорости волны справедливы как для поперечных, так и для продольных волн.
Длину волны при распространении продольных волн можно представить с помощью рисунка \(7\).

Рис. \(7\)
Обрати внимание!
Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна.
При переходе волны из одной среды в другую её частота не изменяется, меняются лишь скорость и длина волны.
Длина волны. Скорость распространения волны (Ерюткин Е.С.)
В ходе урока вы сможете самостоятельно изучить тему «Длина волны. Скорость распространения волны». На этом уроке вы сможете познакомиться с особенными характеристиками волн. В первую очередь вы узнаете, что такое длина волны. Мы рассмотрим ее определение, способ ее обозначения и измерения. Затем мы также подробно рассмотрим скорость распространения волны.
Для начала вспомним, что механическая волна – это колебание, которое распространяется с течением времени в упругой среде. Раз это колебание, волне будут присущи все характеристики, которые соответствуют колебанию: амплитуда, период колебания и частота.
Кроме этого, у волны появляются свои особые характеристики. Одной из таких характеристик является длина волны. Обозначается длина волны греческой буквой 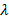 (лямбда, или говорят «ламбда») и измеряется в метрах. Перечислим характеристики волны:
(лямбда, или говорят «ламбда») и измеряется в метрах. Перечислим характеристики волны:
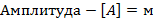
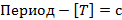
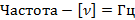
Что такое длина волны?
Длина волны – это наименьшее расстояние между частицами, совершающими колебание с одинаковой фазой.
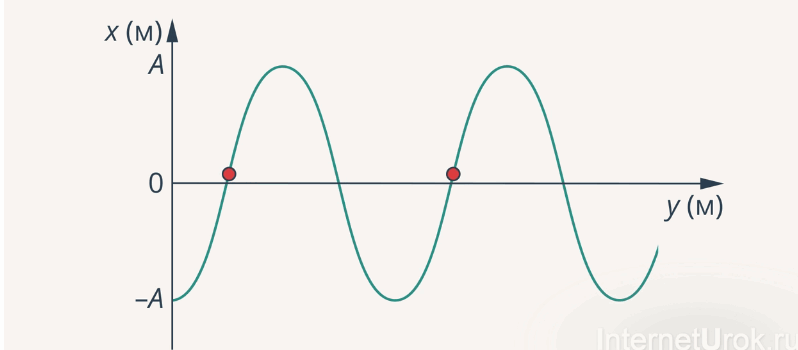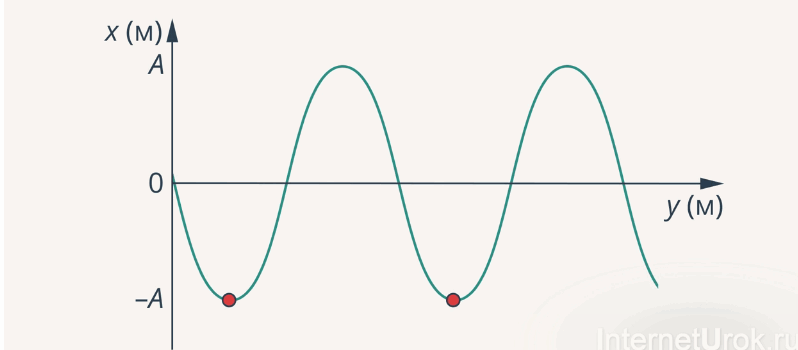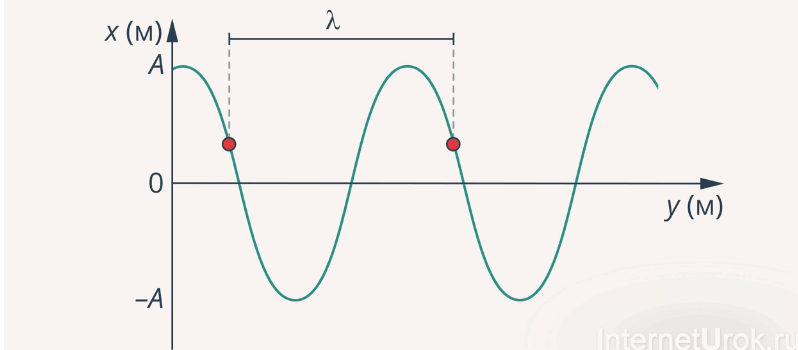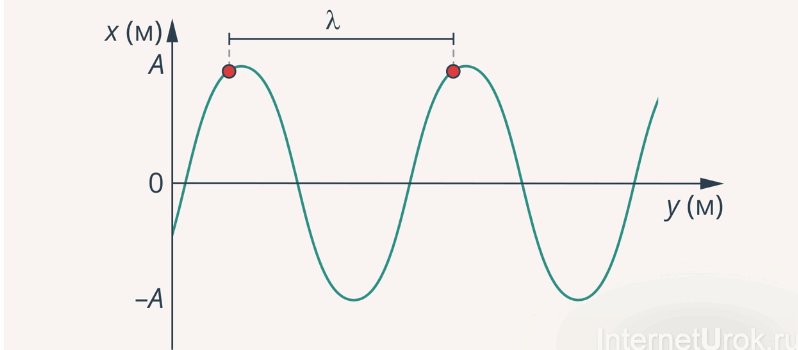
Рис. 1. Длина волны, амплитуда волны
Говорить о длине волны в продольной волне сложнее, потому что там пронаблюдать частицы, которые совершают одинаковые колебания, гораздо труднее. Но и там есть характеристика –
Также длиной волны можно назвать расстояние, пройденное волной, за один период колебания частицы (рис. 2).
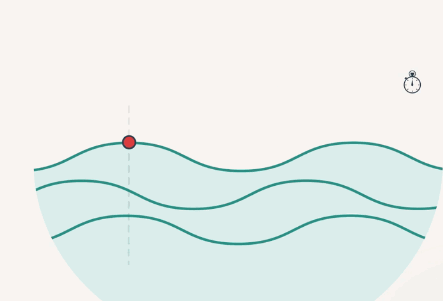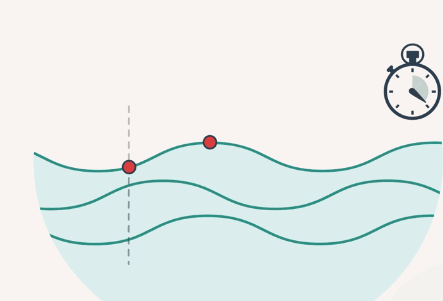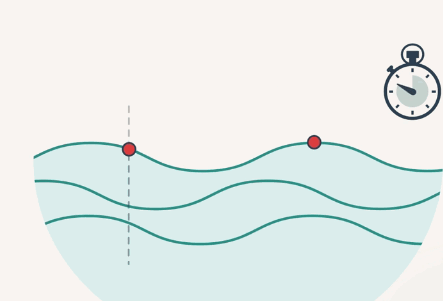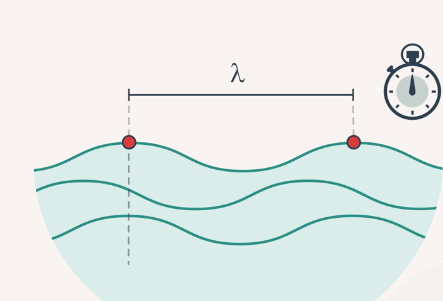
Рис. 2. Длина волны
Следующая характеристика – это скорость распространения волны (или просто скорость волны). Скорость волны обозначается так же, как и любая другая скорость, буквой 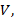
 . Как наглядно объяснить, что такое скорость волны? Проще всего это сделать на примере поперечной волны.
. Как наглядно объяснить, что такое скорость волны? Проще всего это сделать на примере поперечной волны.Поперечная волна – это волна, в которой возмущения ориентированы перпендикулярно направлению ее распространения (рис. 3).
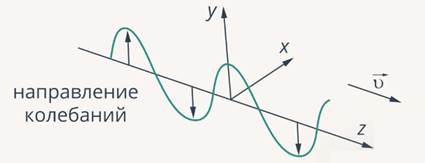
Рис. 3. Поперечная волна
Представьте себе летящую над гребнем волны чайку. Ее скорость полета над гребнем и будет скоростью самой волны (рис.4).
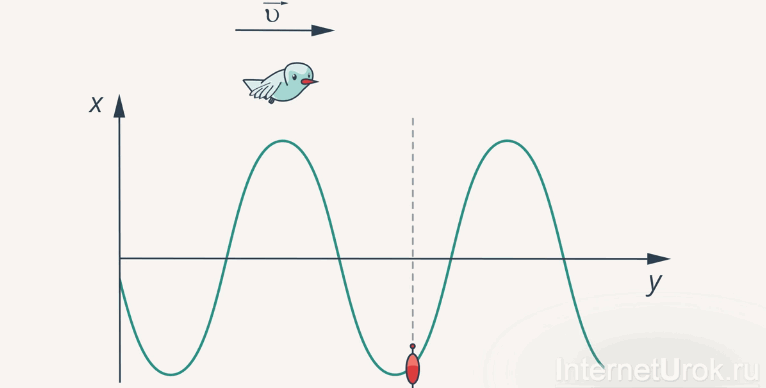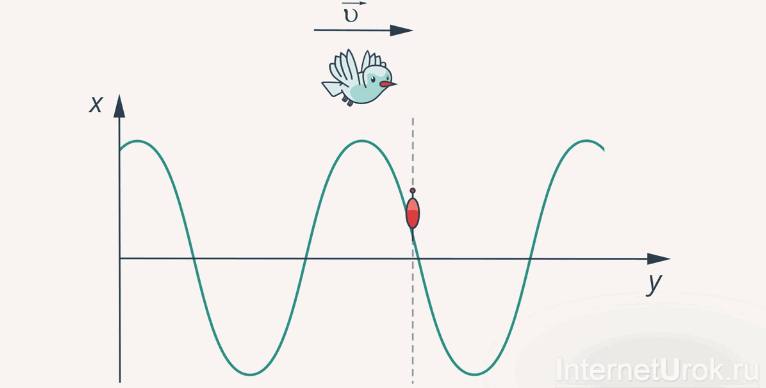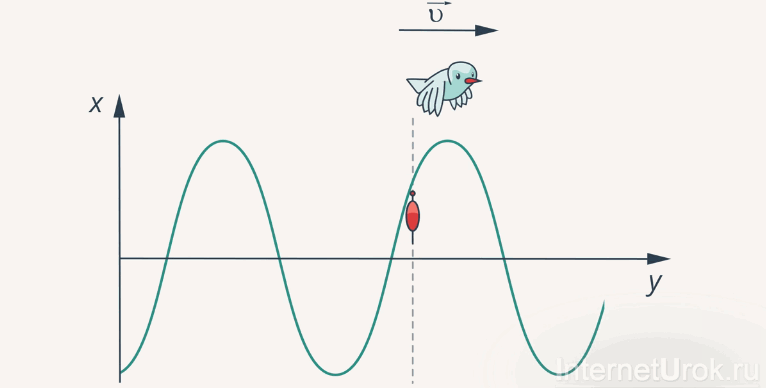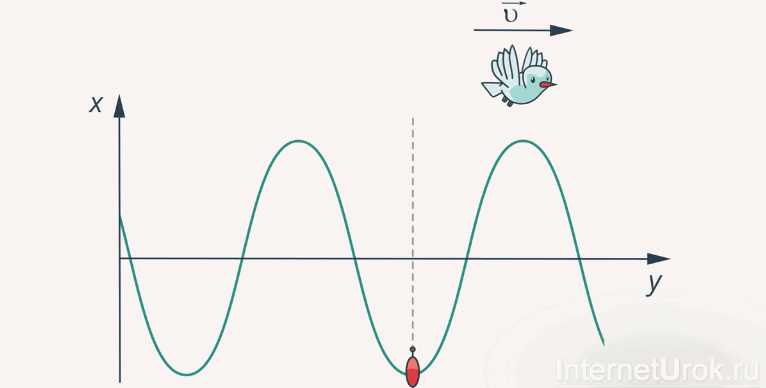
Рис. 4. К определению скорости волны
Скорость волны зависит от того, какова плотность среды, каковы силы взаимодействия между частицами этой среды. Запишем связь между скоростью волны, длиной волны и периодом волны:  .
.
Скорость можно определить, как отношение длины волны, расстояние, пройденное волной за один период, к периоду колебания частиц среды, в которой распространяется волна. Кроме этого, вспомним, что период связан с частотой следующим соотношением:
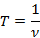
Тогда получим соотношение, которое связывает скорость, длину волны и частоту колебаний: 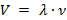 .
.
Мы знаем, что волна возникает в результате действия внешних сил. Важно заметить, что при переходе волны из одной среды в другую изменяются ее характеристики: скорость движения волн, длина волны. А вот частота колебания остается прежней.
Список литературы
- Соколович Ю.А., Богданова Г.С. Физика: справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: издательство «Ранок», 2005. – 464 с.
- Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений / А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «eduspb» (Источник)
- Интернет-портал «eduspb» (Источник)
- Интернет-портал «class-fizika.narod.ru» (Источник)
Домашнее задание
- Поплавок совершает колебания на волнах. За 10 с он совершил 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?
- Тело совершает гармонические колебания по закону
 м. Определите амплитуду, период, частоту, смещение и скорость в момент времени 0,1 с.
м. Определите амплитуду, период, частоту, смещение и скорость в момент времени 0,1 с. - Определите длину звуковой волны ноты, если ее частота колебаний 430 Гц, а скорость звука в воздухе 340 м/с?
Длина волны — это… Что такое Длина волны?
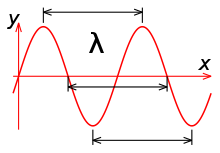 Длина волны λ может быть измерена между любыми двумя точками волны с одинаковой фазой, максимумами, минимумами или узлами волны.
Длина волны λ может быть измерена между любыми двумя точками волны с одинаковой фазой, максимумами, минимумами или узлами волны.Получить соотношение, связывающее длину волны с фазовой скоростью () и частотой () можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой проходит за время, равное периоду колебаний , поэтому
Волнам де Бройля также соответствует определенная длина волны. Частице с энергией Е и импульсом p, соответствуют:
- частота:
- длина волны:
где h — постоянная Планка.
Примеры
Приближённо, с ошибкой около 0,07%, рассчитать длину радиоволны можно так: 300 делим на частоту в мегагерцах, получаем длину волны в метрах, например для 80 Гц, длина волны 3750 километра, для 89 МГц — 3,37 метра, для 2,4 ГГц — 12,5 см.
Точная формула для расчёта длины волны электромагнитного излучения в вакууме выглядит так:
где — скорость света, равная в Международной системе единиц (СИ) 299 792 458 м/с точно.
Для определения длины волны электромагнитного излучения в какой-либо среде следует использовать формулу:
где — показатель преломления среды для излучения с данной частотой.
Примечания
- ↑ Мякишев Г. Я., Буховцев Б. Б. Колебания и волны // Физика. Учебник для 11 класса общеобразовательных учреждений. — 12-е изд. — М.: Просвещение, 2004. — С. 121. — 336 с. — 50 000 экз. — ISBN 5-09-013165-1
Литература
Волновое число — Википедия
Волново́е число́ (также[1] называемое пространственной частотой [2]) — это отношение 2π радиан к длине волны:
- k≡2πλ,{\displaystyle k\equiv {\frac {2\pi }{\lambda }},}
пространственный аналог угловой частоты[3].
Обычное обозначение[4]: k{\displaystyle k}.
Определение: волновым числом k называется быстрота роста фазы волны φ по пространственной координате[5]:
- k≡dφdx.{\displaystyle k\equiv {\frac {d\varphi }{dx}}.}
В одномерном случае волновому числу обычно приписывают знак минус, если волна распространяется в отрицательном направлении (против оси). В многомерном — это обычно синоним абсолютной величины волнового вектора или его компонент (несколько волновых чисел по количеству осей координат), также может быть проекцией волнового вектора на некоторое определенное выбранное направление.
Поскольку в большинстве случаев волновое число имеет смысл только применительно к монохроматической волне (строго монохроматической или по крайней мере почти монохроматической), производную в определении можно (для этих самых распространенных случаев) заменить на выражение с конечными разностями:
- k≡ΔφΔx.{\displaystyle k\equiv {\frac {\Delta \varphi }{\Delta x}}.}
Исходя из этого, можно получить разные более-менее удобные формулировки[6]:
- Волновое число есть разность фазы волны (в радианах) в один и тот же момент времени в пространственных точках на расстоянии единицы длины (одного метра).
- Волновое число есть количество пространственных периодов (горбов) волны, приходящееся на 2π метров.
- Волновое число равно числу радиан волны на отрезке в 1 метр.
В спектроскопии волновым числом часто называют просто величину, обратную длине волны (1/λ), измеряемую обычно в обратных сантиметрах (см−1). Такое определение отличается от обычного отсутствием множителя 2π.
Единица измерения — рад·м−1, физическая размерность м−1 (в системе СГС: см−1).
Используется в физике, математике[7] (преобразование Фурье) и таких приложениях, как обработка изображений.
- k≡2πλ=2πνvφ=ωvφ,{\displaystyle k\equiv {\frac {2\pi }{\lambda }}={\frac {2\pi \nu }{v_{\varphi }}}={\frac {\omega }{v_{\varphi }}},}
где:
- λ — длина волны,
- ν{\displaystyle \nu } (греческая буква «ню») — частота,
- v{\displaystyle v}φ — фазовая скорость волны,
- ω — угловая частота.
Для монохроматической бегущей волны можно записать:
- φ=kx−ωt{\displaystyle \varphi =kx-\omega t} — для фазы;
- u(x,t)=const⋅cos(kx−ωt+φ0){\displaystyle u(x,t)=const\cdot \mathrm {cos} (kx-\omega t+\varphi _{0})} — для самой волны;
или
- u(x,t)=const⋅ei(kx−ωt){\displaystyle u(x,t)=const\cdot e^{i(kx-\omega t)}}
- — для комплексной волны; здесь φ0{\displaystyle \varphi _{0}} может быть спрятано в const{\displaystyle const},
для монохроматической стоячей волны:
- u(x,t)=const⋅cos(k⋅(x−x0))cos(ω⋅(t−t0)).{\displaystyle u(x,t)=const\cdot \mathrm {cos} (k\cdot (x-x_{0}))\mathrm {cos} (\omega \cdot (t-t_{0})).}
Волновое число точно определено для монохроматической волны. К волнам другого вида волновое число относится через понятие спектра (то есть через преобразования Фурье), то есть немонохроматическая волна вообще говоря содержит в разных пропорциях монохроматические компоненты с разными волновыми числами; впрочем, почти монохроматические волны могут приближенно быть описаны как волны с определенным волновым числом (их спектр в основном сосредоточен вблизи одного значения волнового числа).
Иногда, например, в квазигеометрическом (квазиклассическом) приближении, можно рассматривать волновое число (волновой вектор) как медленно меняющийся в пространстве, то есть волну не как монохроматическую, а как квазимонохроматическую. В этом случае, естественно, лучше использовать определение волнового числа (волнового вектора) с производной, а не с конечными разностями.
В сущности, единственный физически осмысленный случай, когда волновое число (волновой вектор) может меняться с x, даже относительно быстро, это случай формализма интеграла по траекториям. В этом случае в теории для описания волны присутствуют волны весьма специального вида:
- u(x,t)=ei∫(kdx−ωdt),{\displaystyle u(x,t)=e^{i\int (kdx-\omega dt)},}
для которых упомянутое вполне корректно и осмысленно.
В квантовой физике связывается с компонентой импульса по данному направлению:
- px=ℏkx,{\displaystyle p_{x}=\hbar k_{x},}
где
- px — компонента импульса по направлению x (для одномерной системы — полный импульс),
- kx — волновое число (компонента волнового вектора) по направлению x (для одномерной системы — просто волновое число),
- ħ — редуцированная постоянная Планка (постоянная Дирака).
Поскольку константа Планка — универсальная константа, можно выбором системы единиц просто сделать ħ = 1. Тогда
- px=kx,{\displaystyle p_{x}=k_{x},}
то есть в квантовой физике понятия компоненты импульса и волнового числа по сути совпадают. Это можно считать одним из фундаментальных принципов квантовой механики.
То же можно сказать для полного импульса и волнового числа без указания направления абсолютной величины волнового вектора):
- p=ℏk,{\displaystyle p=\hbar k,}
а в единицах ħ = 1:
- p=k{\displaystyle p=k}
В частном случае, для света в вакууме (и, в принципе, любых других безмассовых полей; приближенно — для ультрарелятивистских частиц) можно также написать:
- k=Eℏc,{\displaystyle k={\frac {E}{\hbar c}},}
где
- E — энергия,
- ħ — редуцированная постоянная Планка (постоянная Дирака),
- c — скорость света в вакууме.
- ↑ Это практически полные синонимы, различающиеся несколько лишь традиционными предпочтениями употребления в разных областях, так, термин волновое число в основном употребляется в физике (впрочем, наряду с термином пространственная частота), в математике же и различных приложениях (таких, как обработка изображений) обычно употребляется для сходного понятия термин пространственная частота и даже просто частота. Дополнительно заметим, что для термина пространственная частота (частота) нередко допускается многомерное понимание, то есть он употребляется и в качестве практического синонима термина волновой вектор, тогда как для термина волновое число такое употребление по понятным причинам практически исключено. Впрочем, компоненты волнового вектора могут называться волновыми числами по осям координат.
- ↑ Физическая энциклопедия. В 5 томах/ Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин.- М.: Советская энциклопедия + Большая российская энциклопедия. — 1998.
- ↑ Круговая частота измеряется в радианах в секунду, волновое число — в радианах на метр
- ↑ Зачастую используются и другие, как правило, оговоренные явно.
- ↑ В одномерном случае выбор пространственной координаты однозначен (с точностью до зеркального отражения), в многомерном же случае по умолчанию координата x выбирается так, чтобы совпадать с направлением максимальной скорости роста фазы, то есть перпендикулярно фазовому фронту; в этом случае волновое число есть абсолютная величина волнового вектора. Наконец иногда направление x задается явно и может не совпадать с упомянутым только что; тогда обычно говорят о волновом числе по направлению x и явно указывают это в обозначении: kx{\displaystyle k_{x}}.
- ↑ Включая и формулировку в начале статьи
- ↑ В математике (и многих приложениях) — в основном в терминологической форме пространственная частота или даже просто частота.
Скорость и длина волны в физике
Скорость волны
Скорость распространения волны зависит от типа волны (продольная или поперечная) и от свойств среды (плотности и температуры), в которой распространяется волна.
Длина волны
Так как частота волны
можно получить формулу связи длины волны и частоты:
Очевидно, что поскольку скорость распространения волны зависит от свойств среды, длина волны при одинаковой частоте будет меняться при переходе волны из одной среды в другую.
На рис.1 представлена геометрическая интерпретация длины волны. Исходя из геометрической интерпретации, можно утверждать, что длина волны равна наименьшему расстоянию между точками, которые колеблются в одинаковой фазе.
Рис.1. Геометрическая интерпретация длины волны (здесь x-смещение колеблющихся точек; — расстояние, на которое распространяется волновой фронт; — длина волны; — амплитуда колебаний)
Таким образом, бегущая синусоидальная волна периодична как во времени, так и пространстве. Временной период равен периоду колебаний частиц среды, пространственный период равен длине волны . Волновое число является пространственным аналогом циклической частоты .
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Микроволновое излучение — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 марта 2017; проверки требуют 15 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 марта 2017; проверки требуют 15 правок.Микрово́лновое излучение, сверхвысокочасто́тное излуче́ние (СВЧ-излучение) — электромагнитное излучение, включающее в себя дециметровый, сантиметровый и миллиметровый диапазоны радиоволн, частоты микроволнового излучения изменяются от 300 МГц до 300 ГГц (длина волны от 1 м до 1 мм). Данное определение относит к микроволнам как УВЧ диапазон (дециметровые волны), так и КВЧ диапазон (миллиметровые волны), тогда как в радиолокации микроволновым диапазоном принято обозначать волны с частотами от 1 до 100 ГГц (с длинами волн от 300 до 3 мм). В обоих определениях микроволновое излучение включает в себя СВЧ диапазон.
Микроволновое излучение большой интенсивности используется для бесконтактного нагрева тел (в бытовых микроволновых печах — для разогрева продуктов, в промышленных — для термообработки металлов, в хирургии — при радиочастотной абляции вен[1]; основным элементом здесь служит магнетрон), а также для радиолокации.
Микроволновое излучение малой интенсивности используется в средствах связи, преимущественно портативных — рациях, сотовых телефонах (кроме первых поколений), устройствах Bluetooth, Wi-Fi и WiMAX.
Поддиапазоны СВЧ в различных системах обозначений различаются; используемые в спутниковой связи приведены в таблице.
| Диапазоны частот | ||
| Название | Частотный диапазон, ГГц | |
|---|---|---|
| Название диапазона | Диапазон частот РЛС | Диапазон частот в спутниковой связи |
| L | 1,0—2,0 | |
| S | 2,0—4,0 | |
| C | 4,0—8,0 | 3,4—8,0 |
| X | 8,0—12,0 | 7,0—10,7 |
| Ku | 12,0—18,0 | 10,7—18,0 |
| K | 18,0—26,5 | 18,3—20,2; 27,5—31,5 |
| Ka | 26,5—40,0 | |


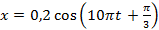 м. Определите амплитуду, период, частоту, смещение и скорость в момент времени 0,1 с.
м. Определите амплитуду, период, частоту, смещение и скорость в момент времени 0,1 с.