Вторая характеристика света — его частота. О чем рассказывает свет

Вторая характеристика света — его частота

Длина волны — не единственная характеристика света. Другой его характеристикой является частота света. От длины волны света нетрудно перейти к его частоте. Для этого надо знать его скорость в пустоте, т. е. в пространстве, в котором отсутствует вещественная среда.

Распространяется свет очень быстро. Когда-то даже думали, что он проходит любое расстояние мгновенно. Итальянский ученый Галилей (1564—1642) сомневался в этом и пытался измерить скорость света на опыте. Однако техника опыта в то время была примитивной, при этой технике невозможно было измерить такую огромную скорость, какой оказалась впоследствии скорость света, и опыт Галилея не дал результатов.

Но уже в XVII веке был получен первый положительный результат на основе астрономических наблюдений. Датский астроном Олаф Ремер обнаружил, что систематическое затмение спутника Юпитера запаздывает во времени, если Земля по отношению к Юпитеру находится не в ближайшей точке земной орбиты, а на другом конце диаметра орбиты.

Запоздание можно объяснить тем, что свету от Юпитера надо пройти дополнительное расстояние, равное диаметру земной орбиты. Зная диаметр орбиты и время запаздывания, Ремер определил (1675) скорость света в 215 тыс. км в секунду. Теперь мы сказали бы, что ошибка Ремера достигает примерно 28%; но важно было другое: после Ремера уже нельзя было говорить о мгновенном распространении света, и кроме того, Ремеру все же удалось определить порядок величины столь большой скорости, какой является скорость света.

Примерно в то же время, когда шли исследования спектров различных веществ, французский физик Леон Фуко (1819—1868) нашел способ измерить скорость света в земных условиях, в опытах с вращающимися зеркалами. Мы не будем рассказывать об этих опытах. В результате их Фуко нашел, что скорость света равна 298 тысячам километров в секунду. Эта величина отличается от той, какую мы знаем теперь, только на 0,6%! В 1927 году американский физик Майкельсон измерил скорость света и нашел, что она равна 299 796 км в сек.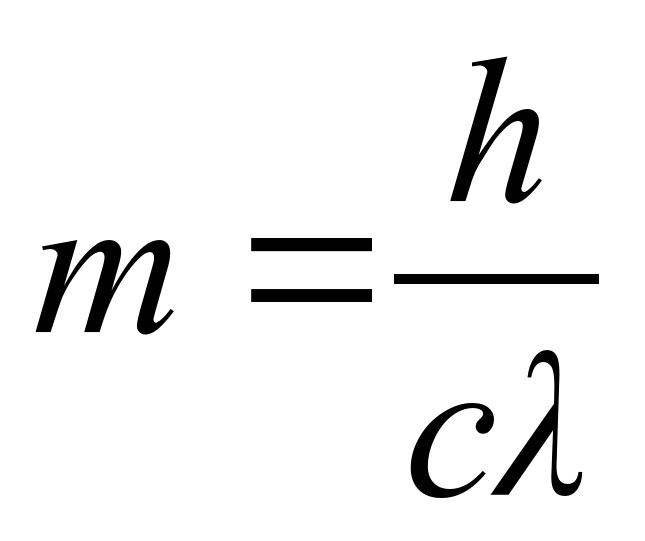

Округляя, говорят, что скорость света равна 300 тыс. км в секунду.

Как ни велика скорость света, но есть такие расстояния, которые свет проходит длительное время. Свет от Солнца до Земли идет около 8 1/2 минут, от ближайшей к нам звезды он идет 4 года, а есть такие удаленные от нас галактики, от которых свет идет миллионы лет.

Очень важно, что скорость света в безвоздушном пространстве не зависит от длины волны: она одинакова для световых излучений любого цвета.

Частота света и длина световой волны связаны со скоростью света так же, как и в случае незатухающих волн на воде. Чтобы узнать частоту красного излучения с длиной волны 7500?, надо скорость света, выраженную в ангстремах в секунду, разделить на 7500? ; таким образом находим, что она равна 400 тысячам миллиардов в секунду. Это число — 400 000 000 000 000 — для краткости записывается так: 4·10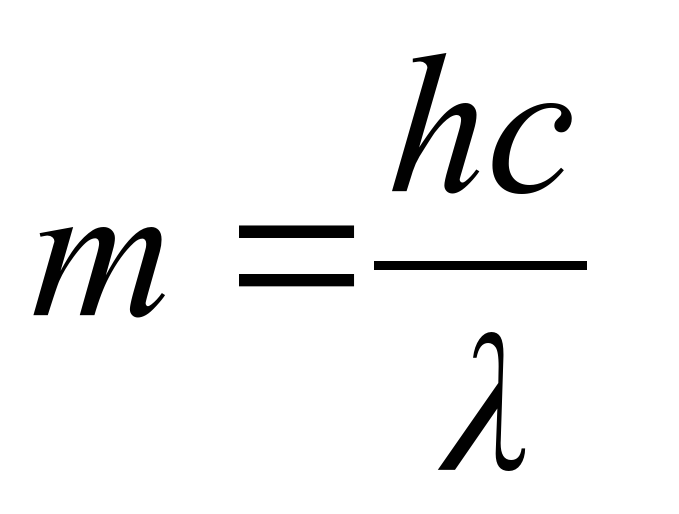

14, т. е. четыре, умноженное на число, у которого первая цифра единица, а за ней стоит 14 нулей, или 4, умноженное на десять в четырнадцатой степени. Частота в одно колебание в секунду носит название цикла, или герца (мегагерц равен миллиону герц). Таким образом, частота красного света равна 4·10¹⁴ циклам.

Частота фиолетового излучения равна 750 тысячам миллиардов, или 7,5·10¹⁴ циклам. Она, как видим, больше, чем у красного излучения, почти в два раза.

Итак, физики получили две характеристики одного и того же цветного луча: длину волны и частоту.

В этой книжке мы будем применять иногда одну характеристику, а иногда другую. Переход же от одной характеристики к другой очень прост.

1. Общая характеристика растворов

1. Общая характеристика растворов Растворы – термодинамически устойчивые системы переменного состава, состоят не менее чем из двух компонентов и продуктов их взаимодействия. Это дисперсные системы, состоящие из дисперсной фазы и дисперсионной среды. Различают девять

Модуляция света. Преобразование света

Модуляция света. Преобразование света Об активном отношении человека к природе Могущество разума человека состоит в его активном отношении к природе. Человек не только созерцает, но и преобразует природу. Если бы он только пассивно созерцал свет, как нечто найденное в

Глава вторая Опыты со звуком

Глава вторая Опыты со звуком Некоторые сведения о звуке. Наше ухо — удивительно тонкий инструмент, воспринимающий звуковые явления. Каждое вызванное хотя бы легким толчком воздуха колебание тонкой кожицы, так называемой барабанной перепонки, туго натянутой в ухе,

Глава вторая. Атомы

Глава вторая. Атомы Физические явления, происходящие в окружающем нас мире, представляют бесконечную цепь загадок. Вода, охлаждаясь, превращается в твердый, бесцветный лед, нагреваясь же, становится невидимым водяным паром. Если ее слегка подкислить серной кислотой и

Вторая фотовкладка

Вторая фотовкладка Один из цехов Хэнфордского механического завода вблизи Паско (штат Вашингтон) Одна из производственных установок Клинтонского механического завода в Ок-Ридже (штат

Глава 9 Частота столкновений малых тел с Землей и оценки рисков

Глава 9 Частота столкновений малых тел с Землей и оценки рисков Можно считать курьезом, что научное сообщество ревностно изучает далекие галактики и в то же время игнорирует любую возможность серьезного столкновения Земли с космическими объектами. Для меня это типичный

10.9. Сравнительная характеристика способов противодействия

10. 9. Сравнительная характеристика способов противодействия В этом разделе рассмотрены различные способы противодействия угрожающему телу. Перечислим основные способы воздействия на космические объекты, угрожающие столкновением с Землей, которые предлагались в

Глава вторая На воде и под водой

Глава вторая На воде и под водой Почему киты живут в море? Задолго до того, как появился человеческий род, жили на суше животные таких больших размеров, каких нынешние сухопутные животные не достигают. Особенно крупны били ящеры, один из них – диплодок – имел 22 м в длину,

ГЛАВА ВТОРАЯ,

ГЛАВА ВТОРАЯ, в которой рассказывается об истории открытия атомов и) элементарных частиц и делается попытка объяснить, каким образом в протоне оказывается мезон, а в мезоне — протон Еще со школьной скамьи нам известно, что вещество — твердые тела, жидкости, газы — все

3.

2. Фазовая скорость и длина волны в волноводе

Знание критической длины волны позволяет определить фазовую скорость для заданной длины волны возбуждения при любом индексе моды колебания:

(3.6)

Эта формула весьма показательна. Если длина волны возбуждения больше критической, под корнем в знаменателе получится отрицательное число, а корень из отрицательного числа мнимый. Значит, мнимой станет фазовая скорость и распространяющейся волны не будет. При длине волны возбуждения меньше критической под корнем будет действительное число меньше единицы. Фазовая скорость также станет действительным числом, большим, чем скорость света в вакууме и волна будет распространяться.

Фазовая скорость продольных волн, распространяющихся в волноводе, больше скорости света

Это происходит из-за того, что продольная волна в волноводе распространяются за счет многократного отражения от стенок. Значит, от начала до конца волновода ее фронт пройдет путь, превышающий физическую длину волновода.

Если длина волны возбуждения будет равна критической, под корнем получается нуль и фазовая скорость станет бесконечно большой. В этом случае волна существует в волноводе, но не распространяется.

Отличительной особенностью этой формулы является ее универсальность: фазовая скорость зависит только от отношения длин волн возбуждения и критической. Значит, формула (3.6) применима для вычисления фазовой скорости волн в любом полом металлическом волноводе.

Для определения длины волны в волноводе фазовую скорость надо разделить на частоту. Получим:

(3.7)

Формулы (3.6) и (3.7) получены в предположении о том, что пространство между плоскостями заполнено вакуумом. Если заполнение будет иным, иными будут исходная фазовая скорость и длина волны.

Мы изучили распространение электромагнитных волн в плоском волноводе и установили, что при определенных условиях в нем могут распространяться продольные Е- и Н-волны, а так же поперечная Т-волна. Однако плоский волновод не имеет практического значения так как его поперечные размеры не ограничены и плотность энергии остается бесконечно малой. Значит, надо уменьшить область существования поля.

Для этого можно перпендикулярно имеющимся плоскостям вдоль направления распространения волны установить две перегородки из идеального проводника. В результате получится полый металлический волновод прямоугольного сечения. При этом характеристики исходной системы, плоского волновода, изменились. Плоский волновод состоял из двух изолированных проводников, а в прямоугольном волноводе остался только один. По этому признаку, количеству изолированных проводников, направляющие системы делятся на односвязные и многосвязные.

Односвязной называется направляющая система, состоящая из одного проводника

Односвязная направляющая система, полый металлический волновод, может иметь любую форму поперечного сечения.

Полым металлическим волноводом называется труба произвольного сечения, изготовленная из материала с высокой электропроводностью

В нашем случае волновод получился прямоугольным. Это одна из наиболее часто встречающихся форм поперечного сечения. Кроме прямоугольного, для передачи электромагнитной энергии используются волноводы круглого, эллиптического, Г-образного, П-образного и Н-образного. Однако поперечное сечение трубы может быть любым. Нет физических причин для того, чтобы в металлической трубе любого сечения не могли распространяться электромагнитные волны, отвечающие определенным требованиям.

В полых металлических волноводах волны распространяются за счет многократного отражения от стенок, то есть имеет место быть полная аналогия с распространением Е- и Н-волн в плоском волноводе. Следовательно, в полом металлическом волноводе могут распространяться только продольные волны, а длина волны возбуждения должна быть меньше критической. От формы поперечного сечения зависит только способ вычисления критической частоты.

Плоский металлический волновод с Т-волной является прототипом многосвязной направляющей системы, в структуре которой изолированных проводников должно быть не менее двух.

Многосвязной называется направляющая система, имеющая в своем составе более одного изолированного проводника

Наиболее распространены двухсвязные системы, то есть системы с двумя проводниками. Это двухпроводная, коаксиальная и полосковая линии, однако в полосковой линии количество изолированных проводников может быть и больше двух.

Таким образом, в направляющих системах, теория работы которых опирается на плоский волновод, могут распространяться продольные Е- и Н-волны и поперечные Т-волны.

Фазовая скорость Е- и Н-волн в полых металлических волноводах больше фазовой скорости волн в свободном пространстве со свойствами среды заполнения волновода. Такие направляющие системы называются волноводами быстрых волн.

Волноводом быстрых волн называется направляющая система, в которой фазовая скорость волн больше скорости в свободном пространстве

Т-волна в многосвязной направляющей системе имеет такие же характеристики, как и поперечная волна в свободном пространстве. Такие волноводы называются волноводами Т-волн.

Волноводом Т-волн называется направляющая система, в которой фазовая скорость волн равна скорости в свободном пространстве

В них волна распространяется без отражения от направляющих проводников.

Однако есть еще один способ создания волноводов. Известно, что вдоль границы с оптически менее плотной средой может распространяться направляемая волна. Граница с оптически менее плотной средой – это, например, граница между диэлектриком и воздухом, если волна падает из диэлектрика. Этот эффект позволяет создавать диэлектрические волноводы. В них фазовая скорость волн меньше, чем в окружающем пространстве, поэтому они называются волноводами медленных волн.

Волноводом медленных волн называется направляющая система, в которой фазовая скорость волн меньше, чем в окружающем пространстве

Волноводы медленных волн будут описаны далее, а в настоящем разделе коротко рассмотрены основные характеристики направляющих систем на основе плоского волновода. При этом упор сделан не на описания деталей, а на основных принципах и особенностях их работы.

Объяснение урока: Импульс фотона | Nagwa

В этом эксплейнере мы научимся вычислять импульс фотона, заданного его частота или длина волны.

Вспомним, что есть некоторые физические явления, связанные со светом, которые лучше всего описывается волновой моделью.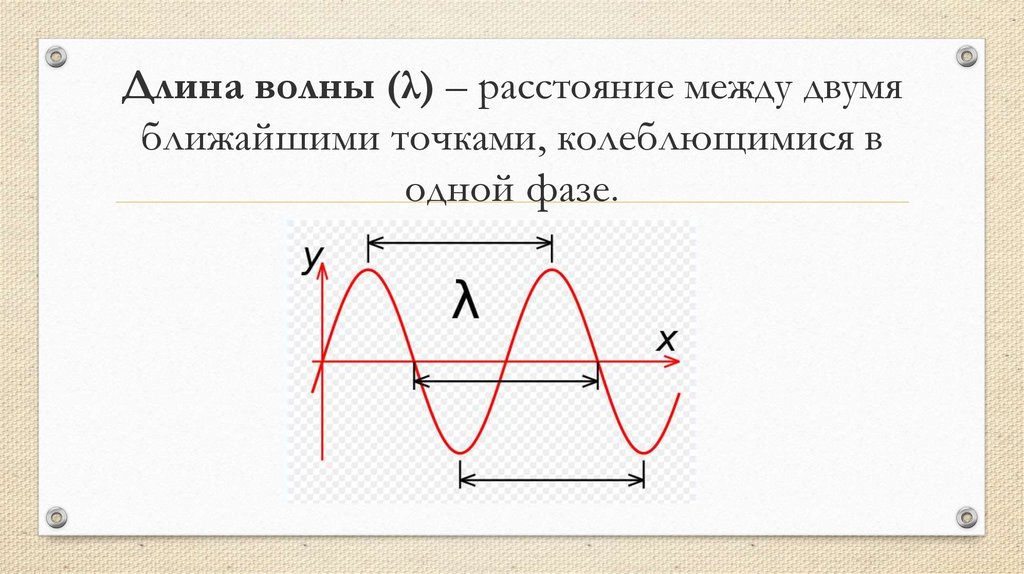 К таким явлениям относятся преломление и дифракция. Другие явления лучше всего описываются с помощью модели частиц. свет. К таким явлениям относится фотоэффект.

В волновой модели света свет имеет длину волны и частоту. Длина волны – это расстояние между любыми двумя соответствующими точками на волна, как показано на диаграмме ниже. Частота волны – это число циклов волны, которые проходят через точку каждый второй.

Напомним, что если длина волны равна 𝜆 и частота волна равна 𝑓, тогда скорость волны 𝑣, дан кем-то 𝑣=𝑓𝜆.

Напомним также, что в свободном пространстве свет распространяется со скоростью примерно 3,00×10 м/с. Этой константе присвоена метка 𝑐, так для световой волны, 𝑐=𝑓𝜆.

В корпускулярной модели света энергия света делится на «пакеты» энергии, называемые фотонами . Фотоны могут поглощаться или испускаемые атомами. Фотоэффект – это когда электрон в атоме поглощает фотон, выбрасывается из атома и оставляет материал, который атом является частью всего.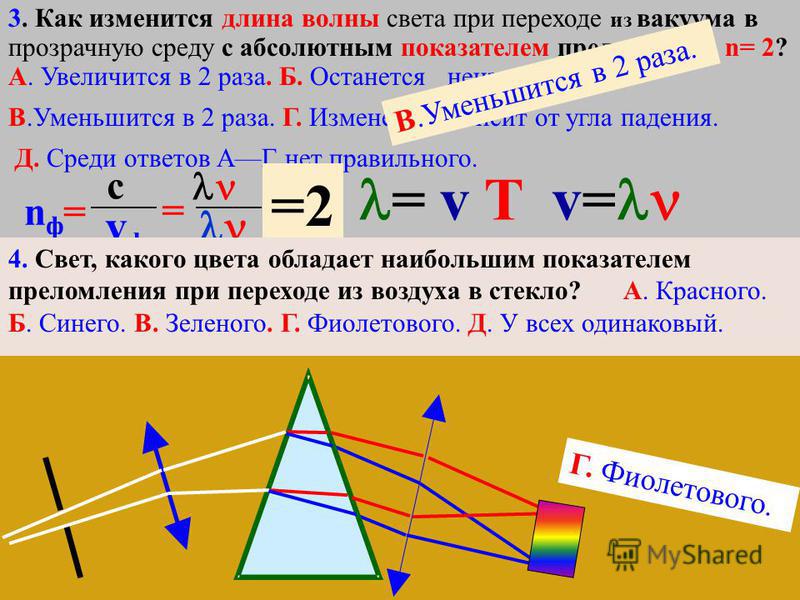

Напомним, что энергия отдельного фотона связана с частотой волна, описывающая свет. Энергия 𝐸 фотона определяется выражением 𝐸=ℎ𝑓, где ℎ — постоянная Планка, имеет значение 6,63×10 Дж⋅с.

Поскольку частота и длина волны световой волны связаны соотношением 𝑐=𝑓𝜆, мы также можем выразить энергию фотона через длина волны: 𝐸=ℎ𝑐𝜆.

Помимо того, что фотоны являются дискретными «пакетами» энергии, они также есть импульс и как таковой может оказывать силу . Это может показаться поначалу противоречащим здравому смыслу, так как в наших повседневных взаимодействиях со светом мы делаем не чувствовать это оказывает силу. Если поднести руку к лампочке, вы не чувствуете силы на руке из-за света.

Это может показаться неинтуитивным, поскольку импульс обычно рассчитывается по формуле 𝑝=𝑚𝑣. Для объекта с массой 𝑚 двигаться на скорости 𝑣, его импульс, 𝑝, является произведением его масса и его скорость. Но у фотонов нулевая масса . Если 𝑚=0, тогда 𝑝=𝑚𝑣=0𝑣=0. Следуя этой формуле, если что-то нулевую массу, то он также должен иметь нулевой импульс, независимо от его скорость.

Однако существуют ограничения на использование 𝑝=𝑚𝑣. Формула 𝑝=𝑚𝑣 нельзя использовать для объектов, которые движутся очень быстро — объекты движутся со скоростью, близкой к скорости света. Одно это означает, что формула не может быть использована для фотонов, которые, конечно, движутся со скоростью света. Формула 𝑝=𝑚𝑣 также не может быть использована для безмассовых частиц, в том числе фотоны.

Вместо этого импульс фотона связан с его длиной волны и может быть рассчитывается по формуле 𝑝=ℎ𝜆, где 𝑝 — импульс фотона и ℎ — постоянная Планка, как и прежде.

Обратите внимание, что импульс фотона обратно пропорционален его длина волны. Это означает, что по мере увеличения длины волны фотона , или по мере того, как свет становится краснее , его импульс уменьшается .

Мы можем использовать эту формулу, чтобы понять, почему мы не испытываем моментум фотонов в нашем повседневном взаимодействии со светом. Рассмотрим фотон красного цвета свет, имеющий длину волны около 700 нм или 7,00×10 м. Импульс фотона равен 𝑝=ℎ𝜆𝑝=6,63×10⋅7,00×10𝑝=9,47×10⋅/.JsmJsm

Единицы джоулей-секунд на метр (Дж⋅с/м) эквивалентны единицам килограмм-метров в секунду (кг⋅м / с), поэтому импульс фотона 90,47×10 кг⋅м/с.

Это очень маленькое значение. Один фотон не имеет много импульс. Даже если мы рассмотрим суммарный импульс всех испущенных фотонов на лампочку каждую секунду, это все еще очень маленькое значение. А Лампа мощностью 100 Вт излучает примерно 3×10 фотонов каждую секунду. Суммарный импульс всех эти фотоны 3×10×9,47×10⋅/=2,84×10⋅/.kgmskgms

Это очень малое значение импульса, поэтому мы не воспринимаем импульс света в наших повседневных взаимодействиях с ним.

Импульс фотонов становится очень важным, однако, когда мы имеем дело с взаимодействия между фотонами и другими частицами, такими как электроны. Фотоны — особенно фотоны высокой энергии, такие как рентгеновские фотоны — может сообщают значительный импульс другим частицам.

Формула: импульс фотона в терминах его длины волны

Импульс фотона 𝑝 равен постоянной Планка, ℎ, деленная на длину волны, 𝜆, фотона: 𝑝=ℎ𝜆.

Поскольку для света длина волны и частота связаны соотношением 𝑐=𝑓𝜆, мы также можем выразить импульс фотона через его частота. Если сначала мы переставим 𝑐=𝑓𝜆 так, чтобы 𝜆 предмет, получаем 𝜆=𝑐𝑓.

Подставляя это в формулу импульса фотона, получаем 𝑝=ℎ𝑝=ℎ𝑓𝑐.

Формула: Импульс фотона через его частоту

Импульс фотона 𝑝 равен постоянной Планка, ℎ, умноженное на частоту, 𝑓, фотона, деленное на скорость света, 𝑐: 𝑝=ℎ𝑓𝑐.

Пример 1.

Расчет импульса фотона с учетом его Длина волны

Чему равен импульс фотона с длиной волны 500 нм? Используйте значение 6,63 × 10 Дж⋅с для постоянной Планка. Дайте ответ в экспоненциальном представлении с точностью до двух знаков после запятой.

Ответ

Мы можем использовать формулу 𝑝=ℎ𝜆 вычислить импульс 𝑝 фотона, где ℎ — постоянная Планка, а 𝜆 — длина волны фотона.

Во-первых, давайте преобразуем значение, которое мы получили для длина волны в метрах. Напомним, что 1=10 нм, поэтому 500 = 5 × 10 нм.

Теперь мы можем подставить это значение, а также значение для постоянной Планка, указанной в вопросе, в формула выше. Делая это, мы получаем 𝑝=6,63×10⋅5×10𝑝=1,326×10⋅/.JsmJsm

Единицы джоулей-секунд на метр (Дж⋅с/м) эквивалентны единицам килограмм-метр в секунду (кг⋅м/с). Вопрос говорит нам давать ответ с точностью до 2 знаков после запятой, так что наш окончательный ответ 𝑝=1,33×10⋅/. кгс

Пример 2. Расчет импульса Фотон с заданной частотой

Низкочастотная радиоволна имеет частоту 200 кГц. Чему равен импульс радиоволнового фотона? с этой частотой? Используйте значение 6,63 × 10 Дж⋅с для постоянной Планка. Дайте ответ в экспоненциальном представлении с точностью до двух знаков после запятой.

Ответ

Мы можем использовать формулу 𝑝=ℎ𝑓𝑐 найти импульс 𝑝 фотона, где ℎ — постоянная Планка, 𝑓 — частота фотона, а 𝑐 — скорость света.

Во-первых, давайте преобразуем значение, которое мы получили для частоту в герцах. Напомним, что 1=1000 кГц, поэтому 200=200000 кГц.

Теперь мы можем подставить это значение, а также значение для постоянной Планка, указанной в вопросе, в формула выше. Мы можем использовать значение 3,00×10 м/с для скорости света. Делая это, мы получаем 𝑝=6,63×10⋅×2000003,00×10/𝑝=4,42×10⋅⋅/⋅.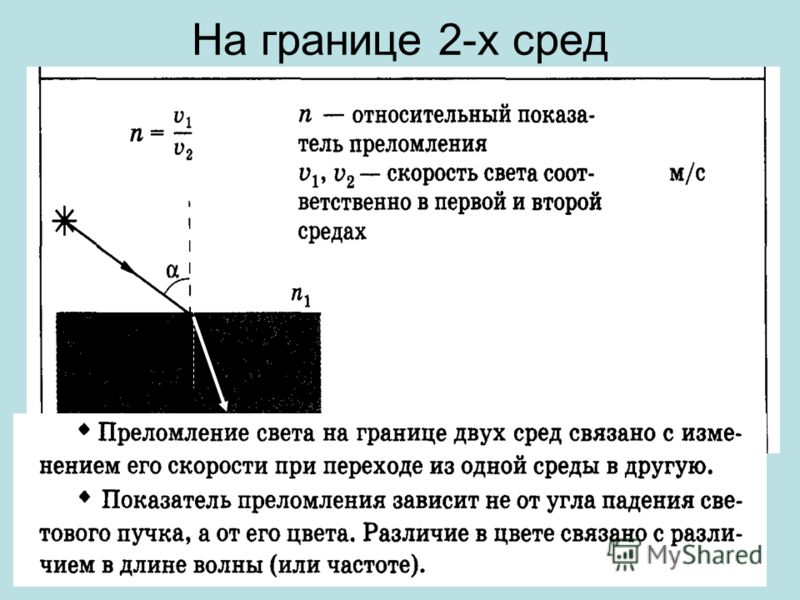 JsHzmsJsHzms

Напомним, что единицы герц равны единицам 1/с, поэтому JsHzmsJssmsJmsJsm⋅⋅/=⋅⋅1//=/=⋅.

Единицы джоуль-секунда на метр (Дж⋅с/м) равны единицам килограмм-метр в секунду (кг⋅м/с), поэтому импульс фотона 4,42×10 кг⋅м/с.

В сценарии, где у нас есть 𝑛 одинаковых фотонов, если мы зная длину волны фотона, мы можем найти суммарный импульс фотонов по формуле 𝑝=𝑛ℎ𝜆.

Альтернативно, если мы знаем частоту фотонов, мы можем найти полный импульс фотонов, используя формула 𝑝=𝑛ℎ𝑓𝑐.

Пример 3: расчет общего импульса множества одинаковых фотонов

Лазер испускает 4,00×10 фотонов, каждый с частота 4,25×10 Гц. Какую величину импульса создают эти фотоны? на лазере? Используйте значение 6,63×10 Дж⋅с для постоянной Планка. Дайте ответ до трех знаков после запятой места.

Ответ

Нас попросили найти величину импульса переданные лазеру фотонами, поскольку они излучаемый. В силу закона сохранения импульса изменение импульса лазера будет одинаковым величине, но в противоположном направлении к изменению импульс фотонов. Так как фотоны будучи произведенным лазером, изменение импульс фотонов — это всего лишь суммарный импульс фотоны.

Все фотоны имеют одинаковую частоту, поэтому они идентичный. Поэтому мы можем использовать формулу 𝑝=𝑛ℎ𝑓𝑐 чтобы найти полный импульс, 𝑝, фотонов, где 𝑛 — количество фотонов, ℎ — постоянная Планка, 𝑓 — частота фотонов, а 𝑐 — скорость света.

Замена значений, указанных в вопросе, и используя значение 3,00×10 м/с для скорости света, получаем 𝑝=4,00×10×6,63×10⋅×4,25×103,00×10/𝑝=3,757⋅⋅/⋅.JsHzmsJsHzms

Напомним, что единицы герц равны единицы 1/с, поэтому JsHzmsJssmsJmsJsm⋅⋅/=⋅⋅1//=/=⋅.

Единицы джоулей-секунд на метр (Дж⋅с/м) равны единицам килограмм-метр в секунду (кг⋅м/с), поэтому полный импульс фотонов равен 3,757 кг⋅м/с.

Импульс такой величины будет воспринимаемым. Однако полная энергия этих фотонов превышает 1 ГДж. Даже самые мощные лазеры в миру потребовалось бы много времени, чтобы выпустить столько энергии, поэтому изменение скорости лазера будет очень медленно.

Ключевые моменты

• Фотоны обладают импульсом, хотя у них нет массы.
• Импульс фотона прямо пропорционален его частоты и обратно пропорциональна его длине волны.
• Если длина волны фотона известна, его импульс можно вычислить по формуле 𝑝=ℎ𝜆.
• Если частота фотона известна, его импульс можно вычислить по формуле 𝑝=ℎ𝑓𝑐.
• Суммарный импульс 𝑛 одинаковые фотоны можно вычислить с помощью 𝑝=𝑛ℎ𝜆 или 𝑝=𝑛ℎ𝑓𝑐.

Свет

Цели обучения

1. Описать свет, его частоту и длину волны.
2. Опишите свет как частицу энергии.

То, что мы знаем как свет, правильнее называть электромагнитным излучением . Мы знаем из экспериментов, что свет действует как волна. Таким образом, его можно описать как имеющий частоту и длину волны. Длина волны Расстояние между соответствующими точками в двух соседних световых циклах. света — это расстояние между соответствующими точками в двух соседних световых циклах, а частота — число световых циклов, которые проходят данную точку за одну секунду. света — это количество световых циклов, проходящих через данную точку за одну секунду. Длина волны обычно обозначается буквой λ, строчной греческой буквой 9.0159 lambda , а частота представлена ​​буквой ν, строчной греческой буквой nu (хотя она выглядит как римская «vee», на самом деле это греческий эквивалент буквы «en»). Длина волны имеет единицы длины (метры, сантиметры и т. д.), а частота имеет единицы измерения 90 159 в секунду 90 160, записывается как s 90 167 −1 90 168 и иногда называется 90 159 герц 90 160 (Гц). На рис. 8.1 «Характеристики световых волн» показано, как определяются эти две характеристики.

Рисунок 8.1 Характеристики световых волн

Свет действует как волна и может быть описан длиной волны λ и частотой ν.

Одним из свойств волн является то, что их скорость равна произведению длины волны на частоту. Это означает, что мы имеем

скорость=λν

Однако для света скорость на самом деле является универсальной константой, когда свет движется через вакуум (или, в очень хорошем приближении, через воздух). Измеренная скорость света ( c ) в вакууме составляет 2,9979 × 10 ⁸ м/с, или примерно 3,00 × 10 ⁸ м/с. Таким образом, мы имеем

c=λν

Поскольку скорость света постоянна, длина волны и частота света связаны друг с другом: одно увеличивается, а другое уменьшается, и наоборот. Мы можем использовать это уравнение, чтобы вычислить, каким должно быть одно свойство света, если задано другое свойство.

Пример 1

Какова частота света, если его длина волны равна 5,55 × 10 ⁻⁷ м?

Решение

Мы используем уравнение, связывающее длину волны и частоту света с его скоростью. У нас есть

3,00×108м/с=(5,55×10−7м)ν

Разделим обе части уравнения на 5,55×10 ⁻⁷ м и получим

ν=5,41×1014 с−1

Обратите внимание, как m единиц сокращаются, оставляя s в знаменателе. Единица в знаменателе обозначается степенью −1 — s ⁻¹ — и читается как «в секунду».

Проверь себя

Какова длина волны света, если его частота равна 1,55 × 10 ¹⁰ с ⁻¹ ?

Ответ

0,0194 м или 19,4 мм

Свет также ведет себя как сгусток энергии. Получается, что для света энергия «пакета» энергии пропорциональна его частоте.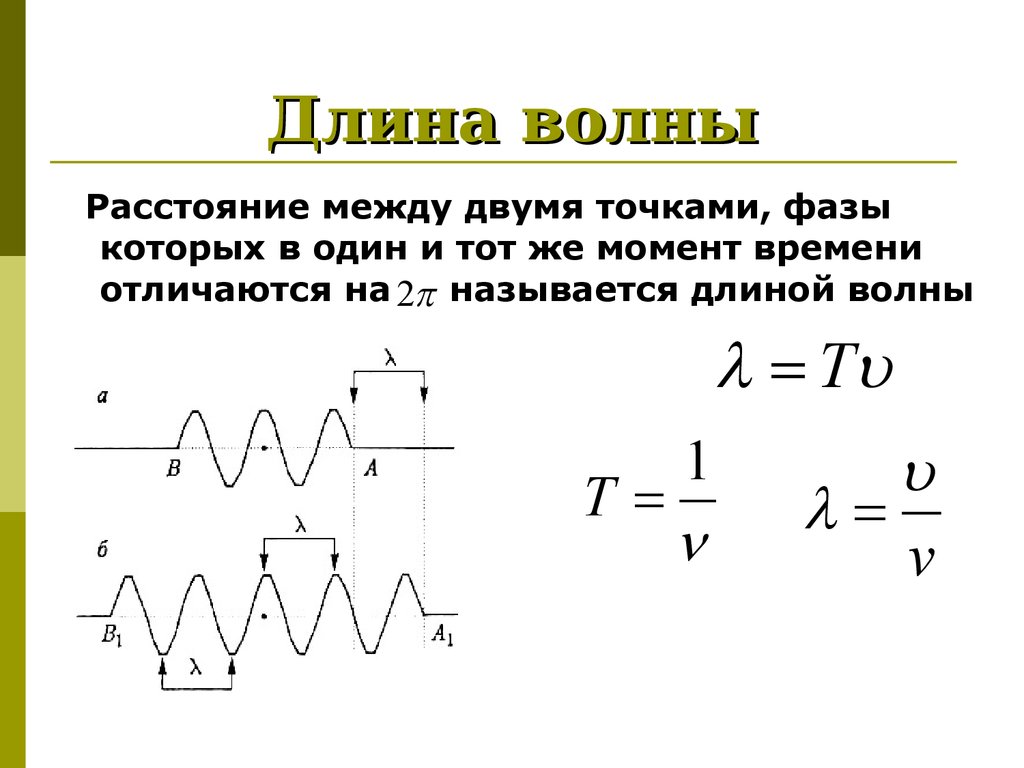 (Для большинства волн энергия пропорциональна амплитуде волны или высоте волны.) Математическое уравнение, которое связывает энергию ( E ) света с его частотой, имеет вид

E=hν

, где ν — частота света, а ч — постоянная, называемая постоянной Планка. Константа пропорциональности между частотой и энергией света. Ее значение равно 6,626 × 10 ⁻³⁴ Дж·с — очень маленькое число, которое является еще одной фундаментальной константой нашей Вселенной, подобно скорости света. Единицы постоянной Планка могут показаться необычными, но эти единицы необходимы для того, чтобы алгебра работала.

Пример 2

Чему равна энергия света, если его частота равна 1,55 × 10 ¹⁰ с ⁻¹ ?

Решение

Используя формулу для энергии света, имеем

E = (6,626 × 10 ⁻³⁴ Дж·с)(1,55 × 10 ¹⁰ с ⁻¹ )

Секунды находятся в числителе и знаменателе, поэтому они сокращаются, оставляя нам джоули, единицу энергии. Итак,

E = 1,03 × 10 ⁻²³ Дж.

Это крайне малое количество энергии, но только для одной световой волны.

Проверь себя

Какова частота световой волны, если ее энергия равна 4,156 × 10 ⁻²⁰ Дж?

Ответить

6,27 × 10 ¹³ с ⁻¹

Поскольку световая волна ведет себя как маленькая частица энергии, световые волны имеют имя типа частицы: фотонНазвание волны света, действующей как частица.. Нередко свет называют фотонами.

Длина волны, частота и энергия света охватывают широкий диапазон; весь диапазон возможных значений света называется электромагнитным спектром. Полный диапазон возможных длин волн, частот и энергий света. Мы в основном знакомы с видимым светом, который представляет собой свет с длиной волны в диапазоне от 400 до 700 нм. . Свет может иметь гораздо более длинные и более короткие длины волн, чем это, с соответствующими изменениями частоты и энергии. На рис. 8.2 «Электромагнитный спектр» показан весь электромагнитный спектр и то, как обозначены определенные области спектра. Возможно, вы уже знакомы с некоторыми из этих регионов; все они световые — с разными частотами, длинами волн и энергиями.

Рисунок 8.2 Электромагнитный спектр

Электромагнитный спектр с помеченными его различными областями. Границы каждой области приблизительны.

Ключевые выводы

• Свет действует как волна, с частотой и длиной волны.
• Частота и длина волны света связаны скоростью света, константой.
• Свет действует как частица энергии, значение которой связано с частотой света.

Упражнения

1. Опишите характеристики световой волны.

2. Что является характеристикой частицы света?

3. Какова частота света, если его длина волны равна 7,33 × 10 ⁻⁵ м?

4. Какова частота света, если его длина волны равна 1,226 м?

5. Какова частота света, если его длина волны равна 733 нм?

6. Какова частота света, если его длина волны равна 8,528 см?

7. Чему равна длина волны света, если его частота равна 8,19 × 10 ¹⁴ с ⁻¹ ?

8. Какова длина волны света, если его частота равна 3,66 × 10 ⁶ с ⁻¹ ?

9. Чему равна длина волны света, если его частота равна 1,009 × 10 ⁶ Гц?

10. Чему равна длина волны света, если его частота равна 3,79 × 10 ⁻³ Гц?

11. Чему равна энергия фотона, если его частота равна 5,55 × 10 ¹³ с ⁻¹ ?

12. Чему равна энергия фотона, если его частота равна 2,06 × 10 ¹⁸ с ⁻¹ ?

13. Чему равна энергия фотона, если его длина волны равна 5,88 × 10 ⁻⁴ м?

14. Чему равна энергия фотона, если его длина волны равна 1,888 × 10 ² м?

Ответы

1. Свет имеет длину волны и частоту.