в чем измеряется, обозначение, формула нахождения через частоту
Содержание:
- Что такое длина волны
- Физические характеристики волны
-
Виды волн, какие бывают
- Продольные волны
- Поперечные волны
- Стоячие волны
- Бегущие волны
-
Формулы длины волны
- Длина стоячей и бегущей волны
- Длина электромагнитной волны
- Длина звуковой волны
- Расчет длины волны через энергию фотона
- Примеры решения задач
Содержание
- Что такое длина волны
- Физические характеристики волны
-
Виды волн, какие бывают
- Продольные волны
- Поперечные волны
- Стоячие волны
- Бегущие волны
- Длина стоячей и бегущей волны
- Длина электромагнитной волны
- Длина звуковой волны
- Расчет длины волны через энергию фотона
- Примеры решения задач
Что такое длина волны
Волна — изменение характеристик физического поля или среды, способное удаляться от места возникновения или колебаться внутри ограниченной области пространства.
Длина волны — расстояние между точками, которое волна проходит за одно колебание.
Если точки отстоят на расстояние \(\lambda\) друг от друга, их смещения из положений равновесия будут одинаковы, и колебания в них будут происходить в одинаковой фазе.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В системе СИ длина волны измеряется в метрах.
Чем меньше длина волны, тем легче сконцентрировать ее энергию в заданном направлении. Поэтому, например, в эхолокации используют ультразвук. Поскольку ультразвуковые волны в воде затухают гораздо слабее, чем в воздухе, эхолокацию особенно широко используют в гидроакустике.
Физические характеристики волны
Два главных параметра волны — частота колебаний f (число полных циклов колебаний в секунду) и длина волны \(\lambda\) — зависят друг от друга.
Зная эти параметры, можно произвести вычисления, чтобы выяснить период повторения колебаний Т и скорость распространения волны v.
Интенсивность волны описывается такими параметрами, как:
- амплитуда;
- плотность энергии;
- плотность потока мощности.
Геометрически волна состоит из гребней и ложбин.
Для продольных волн чаще используют понятия точек максимального сжатия и максимального растяжения.
Для стоячих волн — понятия пучности и узла, характеризующие участки с максимальной и минимальной амплитудой колебаний.
Виды волн, какие бывают
Продольные волны
Продольные волны — волны, при которых частицы вещества колеблются перпендикулярно направлению распространения.
Они возникают при сопротивлении среды изменению ее объема, их причина — деформация сжатия/растяжения (в твердой среде) или уплотнения/разрежения (в газах и жидкостях).
Продольная волна заставляет частицы среды колебаться у своих положений равновесия, и этот процесс перемещается параллельно направлению распространения волны. Частицы сдвигаются строго по одной линии.
Частицы сдвигаются строго по одной линии.
Чтобы узнать длину волны, нужно измерить расстояние между ближайшими точками сжатия или растяжения. Продольные волны могут распространяться в любой среде: твердой, жидкой, газообразной. Во время этого процесса непрерывно изменяется давление в каждой точке среды.
Примечание
В твердых телах продольные волны распространяются быстрее, чем поперечные. Для сравнения: продольная волна движется в стали со скоростью около 5900 м/с, поперечная — примерно 3250 м/с.
Поперечные волны
Поперечные волны — волны, при которых частицы вещества колеблются перпендикулярно направлению распространения.
Они возникают при сдвиге слоев среды относительно друг друга. В поперечной волне колебания элементов происходят в направлениях, перпендикулярных направлению распространения волны. Среда стремится вернуть деформированные частицы на место, при этом на несмещенные частицы рядом со смещенными воздействуют силы упругости и отклоняют их от положения равновесия.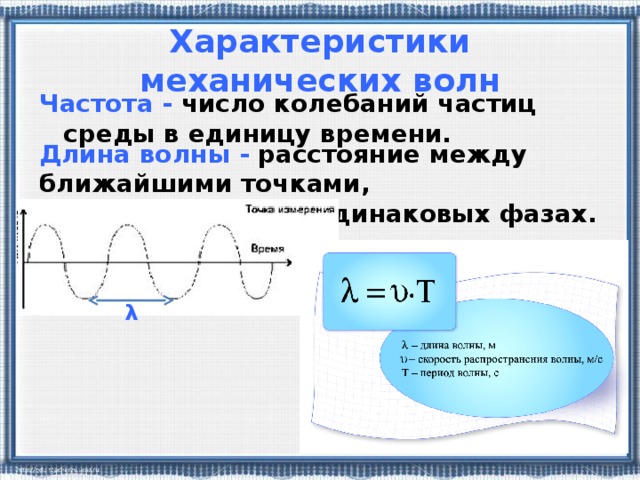
Длина поперечной волны — расстояние между двумя ближайшими ее впадинами или горбами.
Примечание
И продольные, и поперечные волны относятся к упругим — возникающим только в упругой среде, обладающей свойством после деформации возвращаться к прежней форме.
Стоячие волны
Стоячие волны — волновые процессы в распределенных колебательных системах с устойчивым в пространстве расположением участков с максимальной и минимальной амплитудой.
Самую простую одномерную стоячую волну можно возбудить, запустив колебательный процесс с одного конца стержня или гибкой струны. Добравшись до конца стержня или струны, волна отразится, что вызовет наложение.
Бегущие волны
Бегущие волны — процессы последовательного изменения (с определенным запаздыванием) состояния взаимодействующих тел, когда они друг за другом приходят в движение.
Ее можно запустить, например, в системе из косточек домино, выстроенных строго друг за другом на ровной поверхности. Если осторожно толкнуть первую, она, падая, уронит вторую, та — следующую, и в результате такого последовательного падения по ряду побежит волна.
Формулы длины волны
Длина стоячей и бегущей волны
\(\lambda_{}\;=\;v\;\times\;T\;=\;\frac vf\;=\;\frac{2\mathrm{πv}}\omega\)
v здесь — фазовая скорость волны, Т — период колебаний, f — частота, \(\omega\) — круговая частота.
Длина стоячей волны — это расстояние между двумя пучностями или двумя узлами, которое можно рассчитать с помощью формулы:
\(\lambda_{ст}\;=\;\frac\lambda2.\)
Длина стоячей волны равна половине длины соответствующей бегущей волны, так как возникает при наложении двух волн, падающей и отраженной, и сумма их амплитуд равна нулю.
Длина электромагнитной волны
Электромагнитная волна — это электрическое и магнитное поля, взаимно превращающиеся друг в друга. 8\;\frac мс.\)
8\;\frac мс.\)
Длина звуковой волны
Колебания частотой от 16 до 20 000 Гц воспринимаются ухом человека. Колебания источников звуковых волн, например, струн или голосовых связок, создают в среде последовательно сменяющие друг друга сжатия и разрежения.
Когда периодические изменения давления достигают барабанной перепонки, она совершает вынужденные колебания. Эти колебания анализирует по амплитуде и частоте внутреннее ухо, имеющее форму улитки, рецепторы которого настроены на различные звуковые частоты. Затем колебания передаются в мозг по слуховому нерву и воспринимаются как слышимые звуки.
Длину звуковой волны вычисляют по общей формуле:
\(\lambda\;=\;v\;\times\;T\;.\)
Расчет длины волны через энергию фотона
Электромагнитное излучение испускается не непрерывно, а отдельными порциями, которые называют квантами или фотонами. Их энергия пропорциональна частоте и высчитывается по формуле:
\(E\;=\;h\times\nu\)
Где h — постоянная Планка, равная \(6,6\;\times\;10^{-34}\;Дж\times с. {-19}\;Дж.\)
{-19}\;Дж.\)
Кванты видимого излучения обладают энергиями 2–3 эВ и занимают лишь небольшую область исследуемого в астрофизике электромагнитного спектра, который простирается от значений энергии порядка миллионных долей электронвольта для метровых радиоволн до миллионов электронвольт для гамма-излучения.
Так как частота равна скорости распространения излучения, деленной на длину волны, длину волны можно вычислить, зная энергию фотона и частоту.
\(\lambda\;=\frac{\;h\times\;c\;}E\)
Примеры решения задач
Задача № 1
Найдите длину волны при звучании ноты «ля», если известно, что частота ее колебаний равна 440 Гц, а скорость распространения звука в воздухе — 340 м/с.
Решение:
\(\lambda\;=\;v\;\times\;T\;\)
Для нахождения периода Т воспользуемся формулой \(Т\;=\frac{\;1\;}f. \)
\)
Следовательно, \(\lambda\;=\;\frac{v\;}f.\)
Подставив известные данные, получим \(\lambda\;=\;\frac{340\;}{440}\;=\;0,78\;м.\)
Ответ: 78 см.
Задача № 2
Найдите длину волны, если известно, что ее скорость 8 м/с, а период — 1 час.
Решение:
\(\lambda\;=\;v\;\times\;T\;\)
1 час = 3600 секунд
Подставив известные данные, получим \(\lambda\;=\;8\;\times\;3600\;=\;28800\;м.\)
Ответ: 28800 м.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Поиск по содержимому
формула, задачи, примеры и факты
Как найти частоту волны? Процесс прост; количество оборотов, которое требуется для завершения конкретной вещи, называется частотой.
Когда объект движется, мы обычно определяем движение, силу и многие другие факторы. Но нам также нужно знать, с какой частотой он будет двигаться в данный момент времени. Таким образом, обратное время дается как частота в стандартных терминах.
В подробном случае мы также могли бы определить частоту данной волны, частицы в краткосрочной перспективе, а также более широкий контекст. частота является широко используемым фактором с точки зрения волны. Скажем, например, волна распространяется с определенной скоростью, и мы должны найти частоту волны.
Обычно мы погружаемся в математическую часть решения, но, говоря простым языком, мы также можем быстро определить волны. То частота сколько циклов он делает за одну секунду. Таким образом, если волна завершает один цикл, частота составляет половину от него.
Частота — это то, что появляется постоянно или в определенный момент времени. Подобно соленоиду, он имеет несколько витков при намотке на проводник и производит электричество. Точно так же частота — это количество циклов, которые волна совершает за одну секунду, и она обычно равна 2 герцам.
Точно так же частота — это количество циклов, которые волна совершает за одну секунду, и она обычно равна 2 герцам.
Игровой автомат количество циклов световой волны сделанное за одну секунду, также оценивается с точки зрения длины волны и скорость световой волны. Звуковая волна является наиболее распространенной областью, где часто рассматривается частотный термин.
Существует также научная вещь: собаки и птицы слышат звук за пределами определенного уровня, который даже люди не способны слышать. Мы созданы таким образом, что только определенное количество частота звука мы могли вынести услышать.
«Файл:Amfm3-en-de.gif» by Берсеркерус под лицензиейЧастота волновой формулыЧастота имеет общую формулу, которую можно применять во всех контекстах. Период времени является основной причиной, которая помогает в формуле частоты.
Количество циклов, которые волна делает за один, рассматривается как частота этой конкретной волны. Следовательно, формула частоты в повседневном исчислении такова: f=1/T. Здесь Т — период времени, за который волны совершают число циклов.
Следовательно, формула частоты в повседневном исчислении такова: f=1/T. Здесь Т — период времени, за который волны совершают число циклов.
Чтобы рассчитать частоту, нам нужно знать характеристики волны. Волна — это совокупность вибраций, называемых энергиями. Они достигли пика на обоих концах. Верхний узел называется впадина, а нижний узел называется гребень.
Высота волны обычно считается амплитудой волны. Высота волны будет определять, будет ли амплитуда больше или меньше. Поэтому, когда они изменяются, циклы, сделанные в секунду, также будут изменены.
Таким образом, когда волна завершает один цикл, то есть если волна имеет и гребень, и впадину в одной и той же фазе, тогда получаемая частота равна половине.
Волна совершает определенное количество циклов за одну секунду, что в основном известно как частота волны. И это дается формулой f=1/Т. Тип волны может зависеть от среды, через которую она проходит.
Теперь давайте посмотрим, как найти частоту волны на графике. Во-первых, частота — это количество циклов, которые волна пытается совершить, чтобы совершить один полный круг в данный конкретный момент времени.
Когда волна сделает один цикл, на это потребуется некоторое время. На графике мы называем это единицами. По сути, на графике есть несколько единиц, по которым мы можем быстро определить, как найти частоту волны в данном конкретном случае.
Скажем, например, волна движется с определенной скоростью, и мы также должны знать, сколько секунд это занимает. Скажи, что есть 12 секунд отмечены на графике, поэтому этой волне требуется 4 секунды, чтобы завершить один полный цикл. Итак, по формуле f=1/Т, частота волны 0.25Гц.
«синусоидальная форма волны» by Творчество103 под лицензией CC BY-SA 2.0Давайте рассмотрим несколько задач по расчету частоты.
Типичная волна совершает два цикла за 30 секунд, и какова будет частота волны, если она будет распространяться в той же среде?
Решение:f=1/Т
f=2/30
f=0.0667 Гц
Всегда возникает путаница между частота волны и скорость волны. Есть амплитуда волны, которая в основном является высотой волны. Таким образом, скорость рассчитывается, чтобы найти скалярную часть скорости, которая является скоростью.
Когда мы обнаруживаем, что волна является световой, звуковой или электромагнитной волной, нам нужно найти частоту волна, завершающая циклы. Период времени между циклами, совершаемыми волной, обычно определяется формулой как обратную частоту.
Как найти частоту волны по длине и амплитуде?Как найти частоту волны по длине и амплитуде? Когда мы рассматриваем волну как свет, мы должны знать все факторы, влияющие на частоту волны.
Во-первых, необходимо учитывать длину волны. Как найти частоту волны с длиной волны? Формула очень проста, и нам нужно найти формулу скорости света.
Будет формула, называемая скоростью света, с = fλ. Здесь c — скорость света, f — определяемая частота, λ — длина волны света. Из этой формулы мы можем найти частоту волны через длину волны, переставив члены, данные в формуле.
Если говорят, что волна движется с определенной скоростью и временем, нам также нужно найти частота с которым распространяется световая волна. Таким образом, формула, упомянутая выше, будет использоваться для расчета частоты в заданный период времени.
Найдем частоту волны и посмотрим, как частота определяется по формуле.
Проблема:Световая волна распространяется со скоростью 3×108 РС. Данную длину волны световой волны называют равной 2000 Å. Какова частота?
Решение:с = fλ
f = с / λ
ф = 3×108 / 2000 Å
f= 1. 5 х 1018 герц
5 х 1018 герц
Итак, из вышеприведенной задачи видно, что частоту можно найти, используя длину волны.
Теперь нам нужно знать, как найти частоту волны через амплитуду. Для этого рассмотрим теперь общую формулу частоты, т. е. f=1/Т. Здесь f также можно записать как f = ω / 2 π.
Здесь формула для T дается как 2 π/ω. Отсюда легко найти значение амплитуды, если упомянут период времени. А частоту можно найти по приведенной выше формуле, если в конкретной задаче задана амплитуда.
Как найти частоту волны, зная только длину волны?Нам нужно знать, как длина волны влияет на волну, когда она распространяется с определенной скоростью и в заданном направлении. Это то, как далеко волна сможет пройти в среде.
Мы все знаем, что скорость света является стандартом для большинства формул, и мы также знаем, как переставить детали данной формулы, чтобы найти частоту данной волны. Как правило, когда световая волна распространяется в определенном направлении со скоростью 3×108, он также будет собирать информацию о частоте волны.
Формула скорости света является основой для определения длины волны или частоты распространяющейся световой волны. Скорость формулы света определяется выражением с = fλ. Отсюда мы получаем частоту волны через длину волны, соответствующим образом изменяя формулу.
Окончательная формула f = с / λ. Давайте посмотрим на проблему, как работает формула для электромагнитной волны.
Проблема:Вычислите частоту электромагнитной волны, которая распространяется со скоростью 2×106м/с с длиной волны 1000 Å. С заданными деталями используйте формулу частота по длине волны.
Решение:с = fλ
f = с / λ
f = 0.002 х 106 герц
f = 2 х 106/ 1000 Å
Таким образом, мы можем быстро определить частоту волны, используя значение скорости и, главным образом, значение длины волны.
Длина волны волны — это в основном пространство между гребнями или впадинами волны, которые следуют друг за другом. В основном концы одной и той же волны, которая была передана с точки зрения звука или электромагнитная волна.
В основном концы одной и той же волны, которая была передана с точки зрения звука или электромагнитная волна.
Когда гребни и впадины волны, находящиеся в одной и той же фазе, встречаются в одном и том же месте, обычно считается, что это длина волны.
Как найти частоту волны по заданному периоду?Как найти частоту волны через период времени? Ответ на этот вопрос прост, так как это общая формула для определения частоты волны.
Мы должны знать, что период времени в волне — это расстояние между гребнем и впадиной в одной и той же фазе. Поэтому, когда волна в основном распространяется с определенной частотой в заданный промежуток времени, нам нужна формула для расчета частоты.
Вот формула для частота с точки зрения периода времени, f=1/Т. Период времени обычно является еще одним термином для амплитуды волны. Т можно также записать как 2 π/ω, Где ω является мерой амплитуды.
Игровой автомат амплитуда — это в основном высота волны в зависимости от чего нам нужно сделать вывод, что амплитуда большая или малая. Если высота волны велика, то амплитуда называется значительной, а если высота волны мала, то говорят, что амплитуда волны мала.
Амплитуда имеет два конца, называемые гребень и впадина. Впадина — это верхний узел амплитуды, а гребень — нижний узел амплитуды.
Когда расстояние между двумя волнами называется длиной волны, а количество циклов, которое совершает одна волна, называется частота, когда период времени равен единице единица на графике, что в стандартном выражении составляет одну секунду.
Как найти частоту волны без скорости?Из формулы скорости света мы могли бы заметить, что длина волны обратно пропорциональна частоте волны, то есть циклам, совершаемым волной за период времени.
Мы также знаем, что частота не прямо пропорциональна периоду времени; следовательно, длина волны и период времени пропорциональны друг другу. Длина волны связана с энергией, поэтому, когда длина волны увеличивается, энергия уменьшается. Формула основана на энергии фотона.
Длина волны связана с энергией, поэтому, когда длина волны увеличивается, энергия уменьшается. Формула основана на энергии фотона.
Мы предполагаем, что длина волны и период времени пропорциональны, а частота и энергия быть пропорциональным. Частота волны без скорости была бы формулой энергии, где E=hf, где E — энергия, h — постоянная Планка, f — частота.
Итак, зная конкретную базовую формулу света и энергии, мы можем соответствующим образом переставить термины и узнать, как найти частоту волны во всех возможных терминах. Кроме того, все эти факторы влияют на волну и ее количество, способствуя ее собственному распространению.
Руководство по изучению длины волны и частоты
Частота и длина волны обратно пропорциональны друг другу. Следовательно, важно знать, как рассчитать частоту по длине волны.
ВВЕДЕНИЕ
Изучение длины волны и частоты волновых форм является важнейшей концепцией физики и техники. Соответствующие исследования помогают выяснить взаимосвязь между ними и в конечном итоге решить требуемые численные задачи.
ЧАСТОТА
Количество раз, когда весь сигнал проходит определенную точку за определенный период, называется частотой сигнала. Единицей измерения частоты является Гц, то есть количество сигналов, повторяющихся за одну секунду. Буквы f и греческие буквы nu (ν) являются наиболее часто используемыми символами, обозначающими частоту.
ДЛИНА ВОЛНЫ
Расстояние между двумя последовательными гребнями или впадинами последовательных колебаний волны называется длиной волны этой конкретной волны. Этим свойством обладают как бегущие, так и стоячие волны. Он измеряется в единицах расстояния, таких как миллиметры, сантиметры, метры и т. д., и обозначается лямбдой (λ).
Источник
РАСЧЕТ ЧАСТОТЫ И ДЛИНЫ ВОЛНЫ
Длина волны – это отношение скорости волны, с которой она распространяется, и частоты волны. Формула длины волны частоты задается как
λ = 𝜈/f
Где 𝜈 — скорость волны, если указано только значение частоты, а скорость неизвестна, при расчете длины волны обычно берется значение скорости света в вакууме.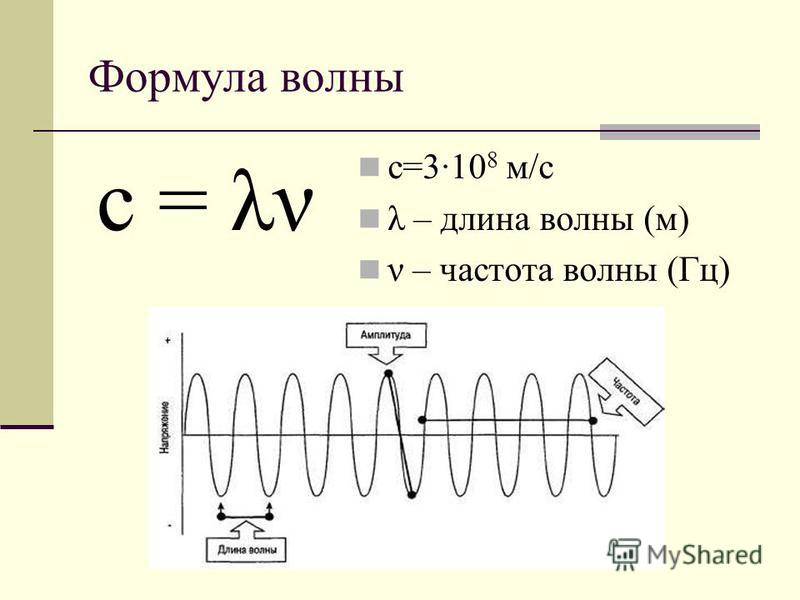 Давайте ответим на некоторые часто задаваемые вопросы.
Давайте ответим на некоторые часто задаваемые вопросы.
Источник
Часто задаваемые вопросы
1. Как рассчитать длину волны при заданной частоте?
Длина волны – это отношение скорости волны, с которой она распространяется, к частоте волны. Формула частоты длины волны определяется следующим образом: λ = 𝜈/f
где 𝜈 — скорость волны, если указано только значение частоты, а скорость неизвестна, при расчете длины волны обычно берется значение скорости света в вакууме.
2. Что происходит при изменении длины волны и частоты?
Формула частоты волны может быть записана как
f = 𝜈/ λ
, где f — частота волны, 𝜈 — скорость волны в конкретной среде, а λ — соответствующая длина волны волны в этой среде. При сохранении постоянной скорости волны длина волны изменяется с изменением частоты.
3. Какая связь между длиной волны и частотой?
В случае бегущих волн длина волны связана с ее частотой и скоростью, с которой она распространяется. Волна, которая совершает большее количество волновых циклов за фиксированное время — скажем, на 1 секунду быстрее, чем ее более медленный аналог. Следовательно, скорость волны имеет решающее значение при расчете частоты волны. Две разные волны с двумя разными длинами волн могут иметь одинаковую частоту. Две волны, волна A и волна B с длинами волн 1 и 3, могут иметь одинаковую частоту только в том случае, если волна A может двигаться со скоростью, в 3 раза превышающей скорость волны B. Представлено частотное уравнение.
Волна, которая совершает большее количество волновых циклов за фиксированное время — скажем, на 1 секунду быстрее, чем ее более медленный аналог. Следовательно, скорость волны имеет решающее значение при расчете частоты волны. Две разные волны с двумя разными длинами волн могут иметь одинаковую частоту. Две волны, волна A и волна B с длинами волн 1 и 3, могут иметь одинаковую частоту только в том случае, если волна A может двигаться со скоростью, в 3 раза превышающей скорость волны B. Представлено частотное уравнение.
Частота(f) = скорость(𝜈)/длина волны(λ)
4. Частота и длина волны обратно пропорциональны?
Да, частота и длина волны обратно пропорциональны друг другу. При сохранении постоянной скорости частота сигнала увеличивается с уменьшением длины волны и уменьшается с увеличением длины волны.
Мы надеемся, что вам понравился этот урок, и вы узнали что-то интересное о Длина волны и частота ! Присоединяйтесь к нашему сообществу Discord, чтобы получить ответы на любые вопросы и пообщаться с другими студентами, такими же, как и вы! Не забудьте загрузить наше приложение, чтобы испытать наши веселые классы виртуальной реальности — мы обещаем, что это сделает учебу намного веселее! 😎
ИСТОЧНИКИ
- Отношение частоты к длине волны: https://www.
 everythingrf.com/rf-calculators/frequency-to-wavelength. По состоянию на 28 февраля 2022 г.
everythingrf.com/rf-calculators/frequency-to-wavelength. По состоянию на 28 февраля 2022 г. - Расчеты длины волны и частоты: https://chem.libretexts.org/Bookshelves/Introductory_Chemistry/Introductory_Chemistry_(CK-12)/05%3A_Electrons_in_Atoms/5.02%3A_Wavelength_and_Frequency_Calculations. По состоянию на 28 февраля 2022 г.
Длина волны — Энциклопедия Нового Света
Материал из Энциклопедии Нового Света
Перейти к:навигация, поиск
Предыдущая (Волна)
Следующая (Ваянг)
Длина волны синусоидальной волны.
В физике длина волны — это расстояние между повторяющимися единицами распространяющейся волны на заданной частоте. Обычно его обозначают греческой буквой лямбда (λ). Примерами волнообразных явлений являются свет, волны на воде и звуковые волны.
Свойства волны зависят от ее типа. Например, в звуковой волне давление воздуха колеблется, а в случае света и других форм электромагнитного излучения различается напряженность электрического и магнитного полей.
Содержание
- 1 Связь с частотой
- 1.1 В невакуумных средах
- 2 Длина волны де Бройля частиц
- 3 См. также
- 4 Примечания
- 5 Каталожные номера
- 6 Внешние ссылки
- 7 кредитов
Длина волны (и частота) видимого света зависит от цвета света. Например, длина волны темно-красного цвета составляет примерно 700 нанометров (нм), а фиолетового — примерно 400 нм. [1] Длины волн звуковых частот, слышимых человеческим ухом (20 Гц–20 кГц), составляют примерно от 17 метров (м) до 17 миллиметров (мм). Таким образом, длины волн слышимых звуковых волн намного больше, чем у видимого света.
Связь с частотой
Длина волны (или волнообразного явления) связана с частотой по формуле:
длина волны = скорость волны / частота. Таким образом, длина волны обратно пропорциональна частоте волны. Волны с более высокими частотами имеют более короткие длины волн; те, у кого более низкие частоты, имеют более длинные волны, при условии, что скорость волны одинакова.
В символах уравнение для длины волны может быть записано как:
- λ=vf{\displaystyle \lambda ={\frac {v}{f}}}
, где λ представляет длину волны, v – скорость распространения волны, а f – ее частота.
В случае электромагнитного излучения, такого как свет, в вакууме скорость волны равна скорости света, 299 792 458 метров в секунду (м/с) или примерно 3×10 8 м/с. Для звуковых волн в воздухе это скорость звука 345 м/с (1238 км/ч) в воздухе при комнатной температуре и атмосферном давлении. Обычно используются единицы СИ, где длина волны выражается в метрах, частота – в герцах (Гц), а скорость распространения – в м/с.
Например, длина волны электромагнитной (радио) волны частотой 100 МГц составляет примерно: λ = 3×10 8 м/с разделить на 100×10 6 Гц = 3 метра. Инженеры-электронщики часто используют сокращенную формулу: длина волны λ в метрах = 300 мегаметров (Мм)/с, деленная на частоту в МГц, чтобы избежать подсчета (многих) нулевых цифр в десятичных или экспоненциальных представлениях.
Следует отметить, что для многих волновых явлений длина волны — это не расстояние, которое частицы проходят за период. Например, в акустике и волнах на воде смещения частиц в течение периода составляют лишь небольшую часть длины волны, за исключением экстремальных условий, таких как прибойные волны и ударные волны.
Следует также отметить, что частота и длина волны могут меняться независимо друг от друга, но только при изменении скорости волны. Например, когда свет входит в другую среду, его скорость и длина волны изменяются, а частота остается неизменной.
В невакуумных средах
Скорость света в большинстве сред ниже, чем в вакууме, а значит, одной и той же частоте будет соответствовать более короткая длина волны в среде, чем в вакууме. Длина волны в среде равна
- λ′=λ0n{\displaystyle \lambda ‘={\frac {\lambda _{0}}{n}}}
, где n — показатель преломления среды. Длины волн электромагнитного излучения обычно указываются в терминах длины волны в вакууме, если специально не указано как «длина волны в среде». В акустике, где для существования волн необходима среда, термин «длина волны» всегда означает длину волны в среде. Тогда показатель преломления зависит от средних свойств среды, например среднего давления или изменений в составе материала.
В акустике, где для существования волн необходима среда, термин «длина волны» всегда означает длину волны в среде. Тогда показатель преломления зависит от средних свойств среды, например среднего давления или изменений в составе материала.
Длина волны де Бройля частиц
Луи де Бройль постулировал, что все частицы с импульсом имеют длину волны
- λ = hp {\ displaystyle \ lambda = {\ frac {h} {p}}}
, где h — постоянная Планка, а p — импульс частицы. Эта гипотеза легла в основу квантовой механики. В настоящее время эту длину волны называют длиной волны де Бройля. Например, электроны в ЭЛТ-дисплее имеют длину волны де Бройля около 10 -13 м.
См. также
- Амплитуда
- Электромагнитный спектр
- Частота
- Свет
- Звук
- Wave
Примечания
- ↑ По частоте диапазон составляет 430–750 терагерц (ТГц).
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
- French, AP 1971.
 Vibrations and Waves . Массачусетский технологический институт Вводный курс по физике. Нью-Йорк: Нортон. ISBN 0393099245
Vibrations and Waves . Массачусетский технологический институт Вводный курс по физике. Нью-Йорк: Нортон. ISBN 0393099245 - Pain, HJ 2005. Физика вибраций и волн. Чичестер: Джон Уайли. ISBN 978-0470012963
- Рейц, Джон Р., Фредерик Дж. Милфорд и Роберт В. Кристи. 1992. Основы электромагнитной теории. Рединг, Массачусетс: паб Addison-Wesley. Компания ISBN 0201526247
- Серуэй, Рэймонд А. и Джон В. Джуэтт. 2004. Физика для ученых и инженеров , 6-е изд. Бельмонт, Калифорния: Брукс/Коул. ISBN 0534408427
- Типлер, Пол Аллен и Джин Моска. 2004. Физика для ученых и инженеров , 5-е изд. Нью-Йорк: WH Фримен. ISBN 0716743892
- Уилсон, Джерри Д. и Энтони Дж. Буффа. 2003. Колледж физики. Река Аппер-Сэдл, Нью-Джерси: Прентис-Холл. ISBN 0130676446
Внешние ссылки
Все ссылки получены 11 июня 2020 г.
- Акустические волны или звуковые волны в воздухе (преобразование длины волны в частоту)
- Добро пожаловать в Sounds Amazing (Учебный ресурс.



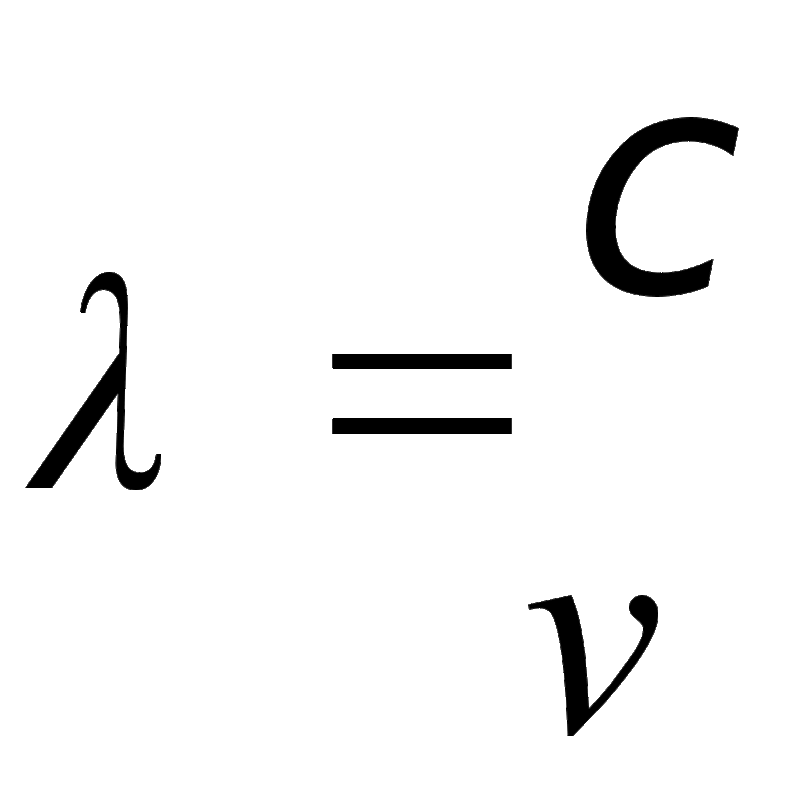 everythingrf.com/rf-calculators/frequency-to-wavelength. По состоянию на 28 февраля 2022 г.
everythingrf.com/rf-calculators/frequency-to-wavelength. По состоянию на 28 февраля 2022 г. Vibrations and Waves . Массачусетский технологический институт Вводный курс по физике. Нью-Йорк: Нортон. ISBN 0393099245
Vibrations and Waves . Массачусетский технологический институт Вводный курс по физике. Нью-Йорк: Нортон. ISBN 0393099245