определения, свойства, формулы, примеры и решения

Определение векторного произведения

Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a→, b→, c→ в трехмерном пространстве.

Отложим для начала векторы a→, b→, c→ от одной точки. Ориентация тройки a→, b→, c→ бывает правой или левой, в зависимости от направления самого вектора c→. От того, в какую сторону осуществляется кратчайший поворот от вектора a→ к b→ с конца вектора c→, будет определен вид тройкиa→, b→, c→.

Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a→, b→, c→ называется правой, если по часовой стрелке – левой.

Далее возьмем два не коллинеарных вектора a→ и b→. Отложим затем от точки A векторы AB→=a→ и AC→=b→. Построим вектор AD→=c→, который одновременно перпендикулярный одновременно и AB→ и AC→. Таким образом, при построении самого вектора AD→=c→ мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).

Упорядоченная тройка векторов a→, b→, c→ может быть, как мы выяснили правой или левой в зависимости от направления вектора.

Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.

Определение 1

Векторным произведением двух векторов a→ и b→ будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:

• если векторы a→ и b→ коллинеарны, он будет нулевым;
• он будет перпендикулярен и вектору a→​​​​ и вектору b→ т.е. ∠a→c→=∠b→c→=π2 ;
• его длина определяется по формуле: c→=a→·b→·sin∠a→,b→;
• тройка векторов a→, b→, c→ имеет такую же ориентацию, что и заданная система координат.

Векторное произведение векторов a→ и b→ имеет следущее обозначение: a→×b→.

Координаты векторного произведения

Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.

Определение 2

В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a→=(ax; ay; az) и b→=(bx; by; bz)

 называют вектор c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, где i→, j→, k→ являются координатными векторами.

Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i→, j→, k→, вторая строка содержит координаты вектора a→, а третья – координаты вектора b→ в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c→=a→×b→=i→j→k→axayazbxbybz

Разложив данный определитель по элементам первой строки, получим равенство: c→=a→×b→=i→j→k→axayazbxbybz=ayazbybz·i→-axazbxbz·j→+axaybxby·k→==a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→

Свойства векторного произведения

Известно, что векторное произведение в координатах представляется как определитель матрицы c→=a→×b→=i→j→k→axayazbxbybz, то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:

1. антикоммутативность a→×b→=-b→×a→;
2. дистрибутивность a(1)→+a(2)→×b=a(1)→×b→+a(2)→×b→ или a→×b(1)→+b(2)→=a→×b(1)→+a→×b(2)→;
3. ассоциативность λ·a→×b→=λ·a→×b→ или a→×(λ·b→)=λ·a→×b→, где λ — произвольное действительное число.

Данные свойства имеют не сложные доказательства.

Для примера можем доказать свойство антикоммутативности векторного произведения.

Доказательство антикоммутативности

По определению a→×b→=i→j→k→axayazbxbybz и b→×a→=i→j→k→bxbybzaxayaz. А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно,a→×b→=i→j→k→axayazbxbybz =-i→j→k→bxbybzaxayaz=-b→×a→, что и доказывает антикоммутативность векторного произведения.

Векторное произведение – примеры и решения

В большинстве случаев встречаются три типа задач.

В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулойc→=a→·b→·sin∠a→,b→ .

Пример 1

Найдите длину векторного произведения векторов a→ и b→, если известноa→=3, b→=5, ∠a→,b→=π4.

Решение

С помощью определения длины векторного произведения векторов a→ и b→ решим данную задач: a→×b→=a→·b→·sin∠a→,b→=3·5·sinπ4=1522.

Ответ: 1522.

Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a→=(ax; ay; az) и b→=(bx; by; bz).

Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов  a→ и b→, а их разложения по координатным векторам вида

b→=bx·i→ +by·j→+bz·k→ и c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, или векторы a→ и b→ могут быть заданы координатами точек их начала и конца.

Рассмотрим следующие примеры.

Пример 2

В прямоугольной системе координат заданы два вектора a→=(2; 1; -3), b→=(0; -1; 1). Найдите их векторное произведение.

Решение

По второму определению найдем векторное произведение двух векторов в заданных координатах:a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→==(1·1-(-3)·(-1))·i→+((-3)·0-2·1)·j→+(2·(-1)-1·0)·k→==-2i→-2j→-2k→.

Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a→×b→=i→j→k→axayazbxbybz=i→j→k→21-30-11=-2i→-2j→-2k→.

Ответ: a→×b→=-2i→-2j→-2k→.

Пример 3

Найдите длину векторного произведения векторов i→-j→ и i→+j→+k→, где i→, j→, k→ — орты прямоугольной декартовой системы координат.

Решение

Для начала найдем координаты заданного векторного произведения i→-j→×i→+j→+k→ в данной прямоугольной системе координат.

Известно, что векторы i→-j→ и i→+j→+k→ имеют координаты (1; -1; 0)  и (1; 1; 1) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i→-j→×i→+j→+k→=i→j→k→1-10111=-i→-j→+2k→.

Следовательно, векторное произведение i→-j→×i→+j→+k→ имеет координаты (-1; -1; 2) в заданной системе координат.

Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i→-j→×i→+j→+k→=-12+-12+22=6.

Ответ: i→-j→×i→+j→+k→=6. .

Пример 4

В прямоугольной декартовой системе координат заданы координаты трех точек A(1,0,1), B(0,2,3), C(1,4,2) . Найдите какой-нибудь вектор, перпендикулярный AB→ и AC→ одновременно.

Решение

Векторы  AB→ и AC→ имеют следующие координаты (-1; 2; 2) и (0; 4; 1) соответственно. Найдя векторное произведение векторов AB→ и AC→, очевидно, что оно является перпендикулярным вектором по определению и к  AB→​​​​​ и к AC→, то есть, является решением нашей задачи. Найдем его AB→×AC→=i→j→k→-122041=-6i→+j→-4k→.

Ответ: -6i→+j→-4k→. — один из перпендикулярных векторов.

Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.

Пример 5

Векторы  a→ и b→ перпендикулярны и их длины равны соответственно 3 и 4. Найдите длину векторного произведения 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→.

Решение

По свойству дистрибутивности векторного произведения мы можем записать 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→

По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→==3·a→×a→+3·(-2)·a→×b→+(-1)·b→×a→+(-1)·(-2)·b→×b→==3·a→×a→-6·a→×b→-b→×a→+2·b→×b→

Векторные произведения a→×a→ и b→×b→ равны 0, так как a→×a→=a→·a→·sin0=0 и b→×b→=b→·b→·sin0=0, тогда 3·a→×a→-6·a→×b→-b→×a→+2·b→×b→=-6·a→×b→-b→×a→.

.

Из антикоммутативности векторного произведения следует -6·a→×b→-b→×a→=-6·a→×b→-(-1)·a→×b→=-5·a→×b→..

Воспользовавшись свойствами векторного произведения, получаем равенство 3·a→-b→×a→-2·b→==-5·a→×b→.

По условию векторы  a→ и b→ перпендикулярны, то есть угол между ними равен π2. Теперь остается лишь подставить найденные значения в соответствующие формулы: 3·a→-b→×a→-2·b→=-5·a→×b→==5·a→×b→=5·a→·b→·sin(a→,b→)=5·3·4·sinπ2=60.

Ответ: 3·a→-b→×a→-2·b→=60.

Геометрический смысл векторного произведения

Длина векторного произведения векторов по орпеделению равна a→×b→=a→·b→·sin∠a→,b→. Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма — удвоенного треугольника, а именно произведению сторон в виде векторов  a→ и b→, отложенные от одной точки, на синус угла между ними sin∠a→,b→.

Это и есть геометрический смысл векторного произведения.

Физический смысл векторного произведения

В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.

Определение 3

Под моментом силы F→, приложенной к точке B, относительно точки A будем понимать следующее векторное произведение AB→×F→.

Векторное и смешанное произведение векторов

Download 39.05 Kb. bet 1/4 Sana 18.03.2023 Hajmi 39.05 Kb. #1282359 Turi Литература

  1   2   3   4

Bog’liq
Векторное и смешанное произведение векторов
Hujjat (10), Hujjat (10), Test savollari, 49c4d4b1-d167-44ee-9d72-ec2bf1152cef, s tilining kutubxonalari va ularning programma tuzishdagi ahamiyati (3), ucell 998938376779 04. 02.2022-06.02.2022, 4-ma’ruza (bahorgi), устав купайтири баён орг, 1667966596, 1-mustaqil, 91, CamScanner 07-29-2022 14.48, kurs ishi, PUL OQIMLARI HISOBOTI — Copy, Boboqulov Otabek Xorijiy til 2 smestr 2

Bu sahifa navigatsiya:

• Введение

Тема: Векторное и смешанное произведение векторов. План: Введение 1 Определение 2 Правые и левые тройки векторов в трёхмерном пространстве 3 Свойства 3.1 Геометрические свойства векторного произведения 3.2 Алгебраические свойства векторного произведения 4 Выражение для векторного произведения в декартовых координатах 5 Обобщения 6 Алгебра Ли векторов Примечания Литература Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны. Векторное произведение определено только в трёхмерном и семимерном пространстве. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства. В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности». Векторное произведение в трёхмерном пространстве. Векторным произведением вектора на вектор в пространстве называется вектор , удовлетворяющий следующим требованиям: длина вектора равна произведению длин векторов и на синус угла ; между ними вектор ортогонален каждому из векторов и вектор направлен так, что тройка векторов является правой. в случае пространства требуется ассоциативность тройки векторов . Обозначение: В литературе [1] определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов. Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводиться остальное. Download 39.05 Kb. Do’stlaringiz bilan baham:

  1   2   3   4

---

Ma’lumotlar bazasi mualliflik huquqi bilan himoyalangan ©fayllar.org 2023
ma’muriyatiga murojaat qiling

Перекрестное произведение векторов в R-программировании

В математике перекрестное произведение или также известное как векторное произведение представляет собой бинарную операцию над двумя векторами в трехмерном пространстве и обозначается символом ‘ х ‘. Для двух линейно независимых векторов a и b перекрестное произведение a × b представляет собой вектор, который перпендикулярен обоим векторам a и b и, следовательно, нормален к плоскости, содержащей их.

Пусть мы дали два вектора,

и,

где,

i: единичный вектор вдоль направления x

j: единичный вектор вдоль направления y

k: единичный вектор вдоль направлений z

Тогда векторное произведение рассчитывается как:

где

— коэффициент единичного вектора вдоль направлений i, j и k.

Пример:

Даны два вектора A и B as,

A = 3i + 5j + 4k,

и

B = 2i + 7j + 5k

Перекрестное произведение = (5 ? 5 – 4 ? 7)i + (4 ? 2 – 3 ? 5)j + (3 ? 7 – 5 ? 2)k    

                      = (?3)i + (?7)j + (11)k

Перекрестное произведение в языке R

R предоставляет очень эффективный метод вычисления перекрестного произведения двух векторов. Используя метод cross() , доступный в версии 9.Библиотека 0003 pracma . Эта функция вычисляет перекрестное или векторное произведение векторов в трех измерениях. В случае матриц он берет первое измерение длины 3 и вычисляет перекрестное произведение между соответствующими столбцами или строками.

Синтаксис: cross(x, y)

Параметры:

x: числовой вектор или матрица

y: числовой вектор или матрица

# Принятие входных данных в виде векторов

Пример 1:

R

библиотека 9011 5 (пракма)     а = с (3, 5, 4) b = c (2, 7, 5)     печать ( 9 0116 крест (а, б))

Выход:

 [1] -3 -7 11
 

Пример 2:

R

библиотека 901 15 (пракма)     а = с (23, 15, 49) b = c (28, 17, 25)     печать ( крест (а, б))

Вывод:

 [1] -458 797 -29
 

 

# Использование входных данных в виде матрицы

Пример 1:

R

901 59

библиотека (пракма)     а = матрица (     c (1, 2, 3, 4, 5, 6, 7, 8, 9),      nrow = 3,                 ncol = 3,                  byrow = TRUE             )  b = матрица (    c (5, 2, 1, 4, 6, 6, 3, 2, 9),      n строка = 3,                 ncol = 3,                  byrow = TRUE             901 15 )      печать ( крест (а, б))

Вывод:

 [ 1] [ 2] [ 3]
[1, ] -4 14 -8
[2, ] -6 0 4
[3, ] 54 -36 -10
 

Пример 2:

R

библиотека (практическая) 9 0116   а = матрица (     с (11, 2, 31 , 4, 52, 64, 7, 8, 9),      nrow = 3,                  9011 5 ncol = 3,                  byrow = ИСТИНА             )  b = матрица (     901 16 c (85, 21, 1, 4, 61, 6, 32, 2, 9),   nrow = 3,                  ncol = 3,                  9 0116 byrow = TRUE             )      print ( крест (а, б))

Вывод:

 [ 1] [ 2] [ 3]
[1, ] -649 2624 61
[2, ] -3592 232 36
[3, ] 54 225 -242
 

Умножение векторов: векторное произведение

Мы видели в предыдущем разделе о точке продукты, которые точка продукт принимает два вектора и производит скаляр, что делает его примером скалярного произведения. В этом разделе мы введем вектор произведение, правило умножения, которое берет два вектора и производит новый вектор. Мы обнаружим, что эта новая операция, векторное произведение, является действительны только для наших 3-мерных векторов и не могут быть определены в 2-мерных векторах. габаритный случай. Причины этого станут ясны, когда мы обсудим виды свойств, которые мы хотим, чтобы перекрестный продукт имел.

Вращательная инвариантность

Одна важная особенность скалярного произведения, о которой мы не упоминали в предыдущем сечением является его -инвариантность относительно вращений. Другими словами, если мы возьмем пару векторов на плоскости и повернуть их на один и тот же угол (представьте, например, что векторы сидят на записи и вращают запись), их скалярный продукт останется прежним. Рассмотрим длину одного вектора (которое дается скалярным произведением): если вектор вращается вокруг начала координат под некоторым углом его длина не изменится, даже если его направление может измениться весьма драматично! Точно так же из геометрической формулы скалярного произведения мы видим, что результат зависит только от длин двух векторов и угол между ними. Ни одна из этих величин не меняется, когда мы поворачиваем два векторы вместе, так что их скалярное произведение тоже не может. Вот что мы имеем в виду, когда мы говорим, что скалярное произведение равно инвариант при вращении.

Вращательная инвариантность оказывается очень важным свойством в физике. Представьте себе, что вы записываете векторные уравнения для описания некоторой физической ситуации, принимая поставить на стол. Теперь поверните стол (или оставьте стол неподвижным и поверните себя под некоторым углом вокруг стола). Вы действительно ничего не изменили о физике на столе, просто повернув все на какой-то фиксированный угол. Из-за этого вы должны ожидать, что ваши уравнения сохранят свою форму. Этот означает, что если эти уравнения включают произведения векторов, эти произведения лучше быть вращательно инвариантным. Скалярный продукт уже прошел этот тест, так как мы отмечено выше. Теперь мы хотим потребовать того же от перекрестного произведения.

Ужесточение требования вращательной инвариантности для кросса произведение, нам нужно перекрестное произведение двух векторов, чтобы получить другое вектор. Рассмотрим, например, два трехмерных вектора u и v в плоскость (два непараллельных вектора всегда определяют плоскость точно так же, как две строки делают. Если мы повернем эту плоскость, векторы изменят направление, но нам не нужно перекрестное произведение w = u × v менять вообще. Однако, если w имеет любые ненулевые компоненты в плоскости u и v , эти компоненты будут обязательно меняются при вращении (вращаются, как и все остальное). Единственные векторы, которые совсем не изменятся при вращении плоскости u - v это те векторы, которые перпендикулярны плоскости. Следовательно, векторное произведение двух векторов u и v должен дать новый вектор, который перпендикулярно обоим u и v .

Это простое наблюдение на самом деле в значительной степени ограничивает наши возможности. варианты того, как мы можем определить перекрестный продукт. Например, мы можем видеть сразу, что нельзя определить перекрестное произведение для двух- размерных векторов, , так как нет направления, перпендикулярного плоскости двумерных векторов! (Для этого нам понадобится третье измерение).

Теперь, когда мы знаем направление , в котором векторное произведение двух векторов точек, звездная величина результирующего вектора еще не определена. Если я возьму векторное произведение двух векторов в плоскости x - y , я теперь знаю, что результирующий вектор должен указывать строго в направлении z . Но если это направлена ​​вверх (т. е. лежит вдоль положительной оси z ) или должна указывать вниз? Как долго должно быть?

Давайте начнем с определения векторного произведения для единичных векторов i , j и k . Так как все векторы могут быть разложены по единичным векторам (см. Единичные векторы), как только мы определили векторные произведения для этого особого случая, и будет легко расширить определение, включив в него все векторы. Как мы отмечено выше, перекрестное произведение между i и j (поскольку они оба лежат в плоскости x - y ) должно указывать чисто в з -направление. Следовательно:

i × j = c k

для некоторой константы c . Потому что позже нам понадобится величина чтобы результирующий вектор имел геометрическую значимость, нам нужно c k , чтобы иметь единичную длину. Другими словами, c может быть либо +1, либо -1. Теперь мы делаем совершенно произвольный выбор в соответствии с соглашением: мы выбираем c = + 1. Факт то, что мы выбрали c как положительное, известно как правило правой руки (мы могли бы так же легко выбрать c = -1, и все математические расчеты будут одинаковыми, если мы будем последовательны — но мы должны выбрать одно или другое, и нет смысла идти против того, что делают все остальные. ) Оказывается, чтобы быть последовательным с правой рукой Правило, все перекрестные произведения между единичными векторами определены однозначно:

906 39 906 39

i × j	=	k = - j × i 9056 7
j × k	=	i = - k × j
к × i	=	j = - i × k

В частности, обратите внимание, что порядок векторов в векторных произведениях имеет значение. В общем, u × u = - u х u . Отсюда мы видим, что перекрестное произведение вектора с самим собой всегда равно нулю, так как по приведенному выше правилу u × u = - u × u , а это означает, что обе стороны должны исчезнуть, чтобы сохранялось равенство. Теперь мы можем завершить наш список перекрестных продуктов между единичные векторы, заметив, что:

i × i = j × j = k × k = 0

Чтобы взять векторное произведение двух общих векторов, мы сначала разложим векторы используя единичные векторы i , j и k , а затем продолжить распределить перекрестное произведение по суммам, используя приведенные выше правила для выполнения перекрестного произведения произведения между единичными векторами. Мы можем сделать это для произвольных векторов u = ( u ₁ , u ₂ , u ₃ ) и v = ( v ₁ , v ₂ , v ₃ ), чтобы получить общую формулу:

u	=	u 1 i + u 90 499 2 к + и 3 к
v	=	v 1 i + v 2 9073 8 j + v 3 k
u × v	=	( u 1 i + u 2 j + u 3 k )×( v 1 я + v 2 j + v 3 k )
	=	u 1 v 1 ( i × i ) + u 1 v 2 ( i × j ) + u 1 v 3 ( i × k ) + . ..(всего 9 членов!)
	=	( u 1 v 2 - u 2 v 1 ) k + ( u 3 v 1 - u 1 v 3 ) j + ( u 2 v 3 - u 3 v 2 ) i

К сожалению, это настолько просто, насколько это возможно, когда дело доходит до написания креста. произведение явно через компоненты вектора. Наверное, это хорошо, чтобы сохранить эта формула удобна до тех пор, пока вы не привыкнете к вычислению векторных перекрестных произведений.

Геометрическая формула векторного произведения

К счастью, как и в случае со скалярным произведением, существует простая геометрическая формула для вычисления перекрестного произведения двух векторов, если их соответствующие длины и угол между ними известен.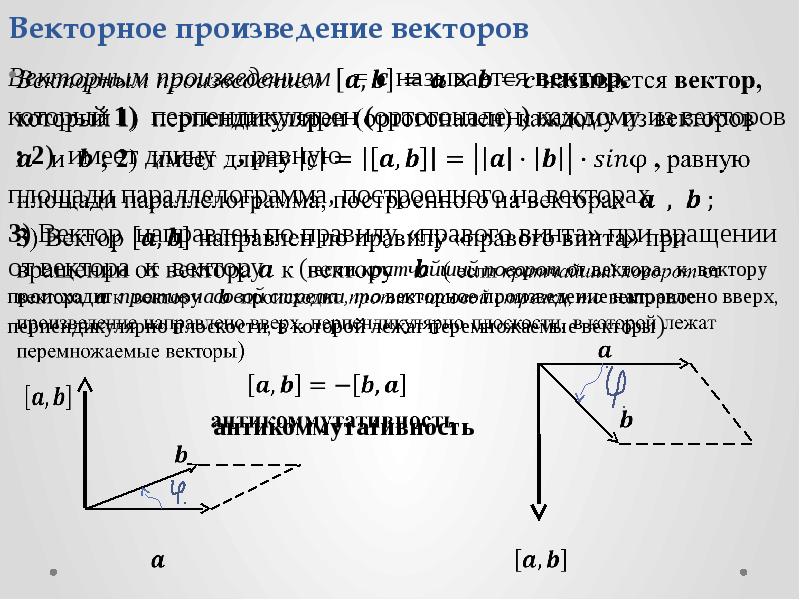 Рассмотрим перекрестное произведение двух (не обязательно единичной длины) векторов, лежащих строго вдоль x и y осей (как i и j делать). Таким образом, мы можем записать векторы как u = a i и v = b j , для некоторых констант a и b . Таким образом, векторное произведение u × v равно равно

u × v = ab ( i × j ) = ab 905 66 к

Обратите внимание, что величина результирующего вектора равна площади прямоугольник со сторонами х и х ! Как и было обещано выше, величина креста произведение между двумя векторами, | u × v |, имеет геометрическую интерпретацию. В в общем случае она равна площади параллелограмма, состоящего из двух данных векторы как его стороны (см. ).

Из базовой геометрии мы знаем, что эта площадь определяется выражением площадь = | и || против | sin θ , где | и | и | против | это длины сторон параллелограмм, а θ — угол между двумя векторами. Уведомление что когда два вектора перпендикулярны друг другу, θ = 90 градусов, поэтому sin θ =1 и мы восстанавливаем знакомую формулу площади квадрата. С другой стороны, когда два вектора параллельны, θ = 0 градусов, и грех θ = 0, что означает, что площадь исчезает (как мы и ожидали). В общем, тогда мы найти, что величина векторного произведения между двумя векторами u и v которые разделены углом θ (идя по часовой стрелке от u до v , как определяется правилом правой руки) определяется как:

| и × против | = | и || против | грех θ

В частности, это означает, что для двух параллельных векторов векторное произведение равно 0.