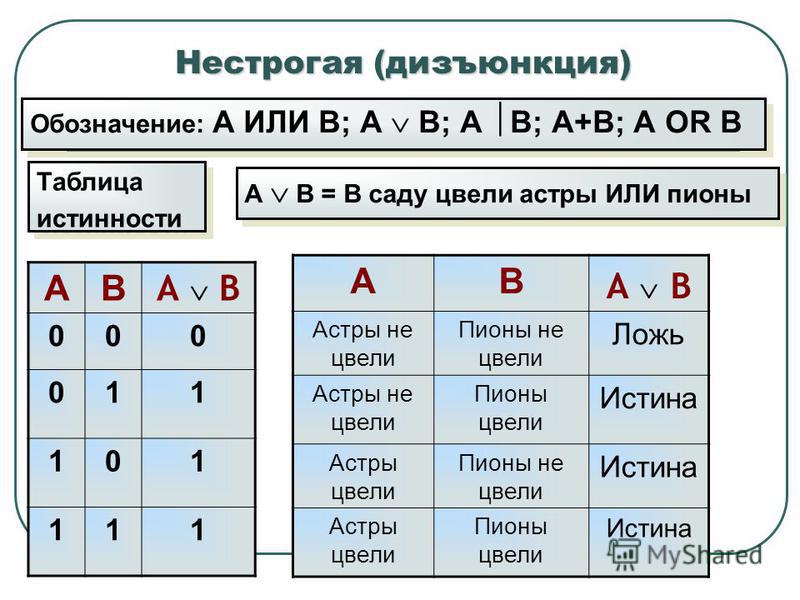
2.3. Операция логического сложения (дизъюнкция)

Эта операция также бинарная. Соответствует союзу «или». Обозначается АВ. Она определяется следующей таблицей истинности:

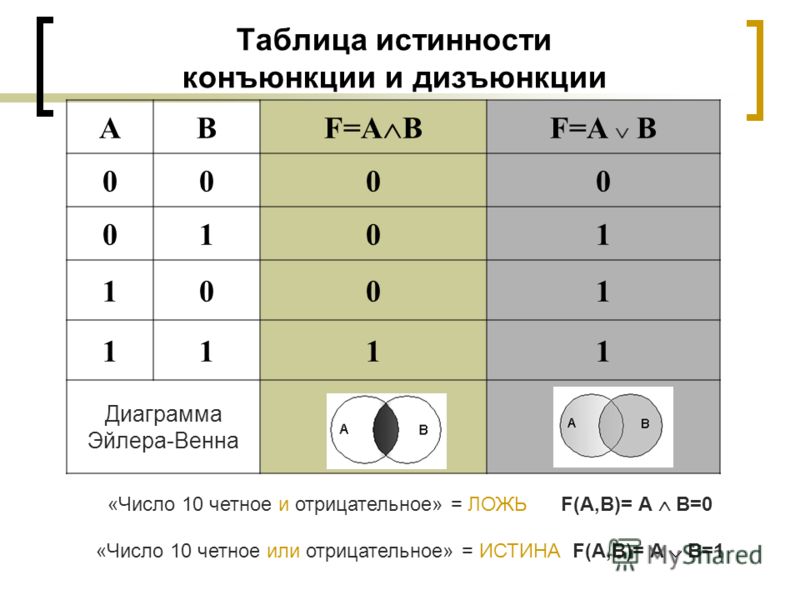
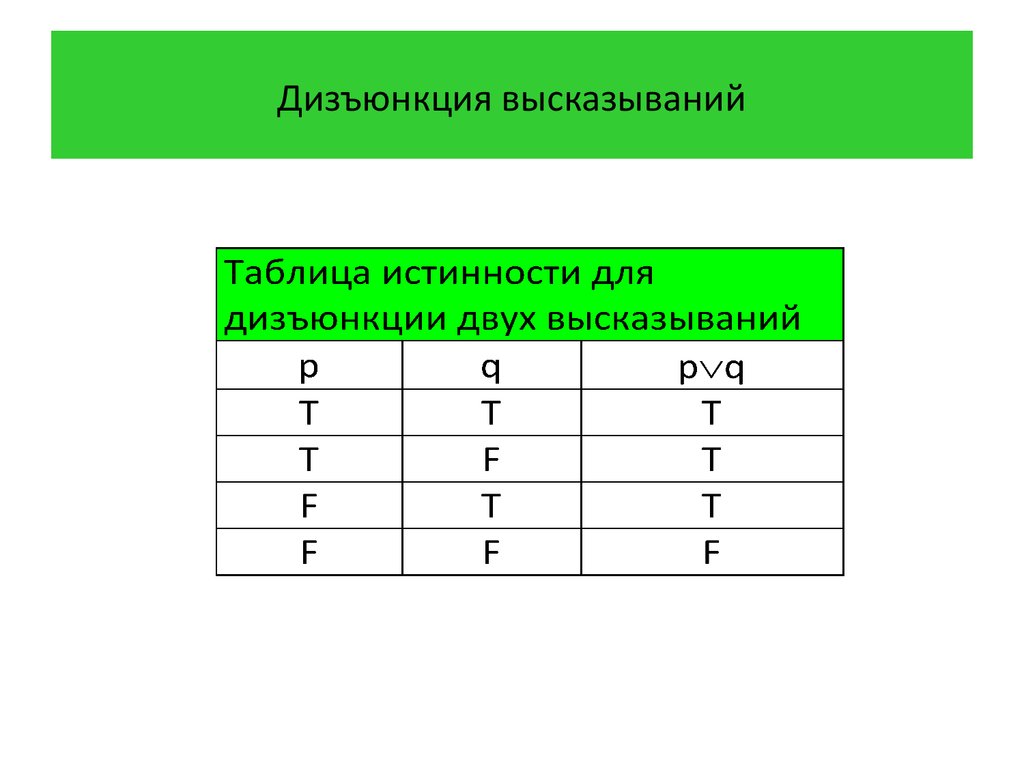
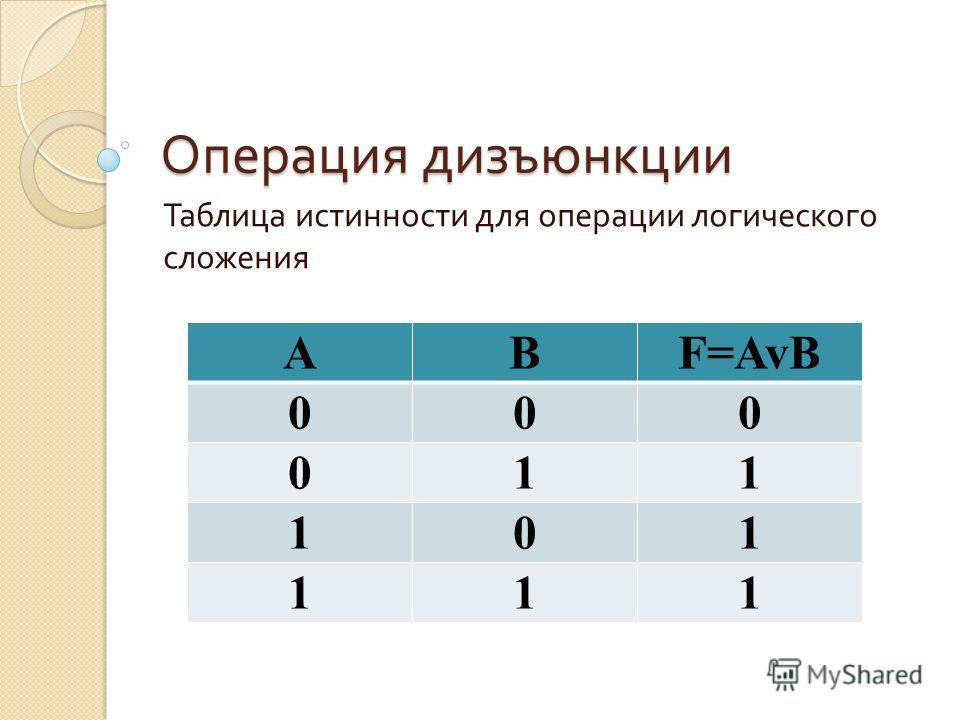
Дизъюнкция (логическая сумма) АВложна тогда и только тогда, когда ложны оба высказыванияАиВ. А	В	АВ
0	0	0
0	1	1
1	0	1
1	1	1

Пример дизъюнкции: «В отпуске мы будем посещать театры, или выставки, или музеи».

2.4. Операция «исключающее или» (строгая дизъюнкция)

Бинарная. Соответствует словосочетанию «или…, или …» («либо …, либо …»). Обозначается АВ. Таблица истинности для этой операции:

А	В	АВ
0	0	0
0	1	1
1	0	1
1	1	0

Пример строгой дизъюнкции: «Саша либо дома, либо вышел погулять с собакой».

2.5. Операция «импликация»

Бинарная. Определяется словосочетанием «если …, то …». Обозначается

АВ. Это одна из самых важных операций логики высказываний. Таблица истинности:

Импликация АВ истинна всегда, за исключением слу-чая, когда А  истина, а В  ложь. А	В	АВ
0	0	1
0	1	1
1	0	0
1	1	1

Пример импликации: «Если завтра будет тепло, то мы пойдем гулять».

2.6. Операция «эквиваленция»

Бинарная. Обозначается АВ или АВ (читается А эквивалентно В). Определяется словосочетанием: «Тогда и только тогда, когда …». Таблица истинности выглядит следующим образом:

Высказывание АВ истинно в том и только в том случае, когда А  истинно и В – истинно или А – ложно и В  ложно. А	В	АВ
0	0	1
0	1	0
1	0	0
1	1	1

Пример эквиваленции: «Я заведу себе щенка тогда и только тогда, когда хорошо изучу, как с ним надо обращаться».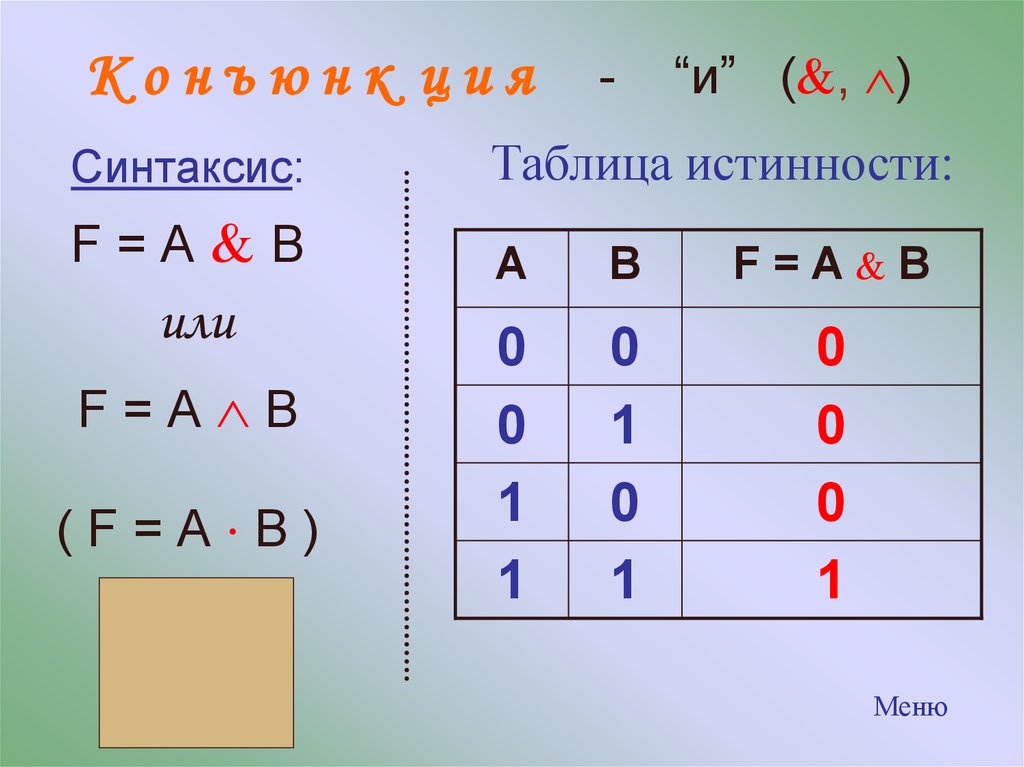

3. Логические выражения. Построение таблиц истинности

Используя основные логические операции, можно построить более сложные высказывания (логические выражения), например:

Скобки в логических выражениях указывают последовательность выполнения операций. Если нет скобок, то приоритеты выполнения логических операций следующие:

1. операция отрицания (инверсия)

2. логическое умножение (конъюнкция)

3. логическое сложение (дизъюнкция)

4. исключающее «или»

5. импликация

6. эквиваленция

Например, в следующем логическом выражении порядок выполнения действий указан цифрами над знаками логических операций:

7 8 5 4 6 1 3 2

Для каждого логического выражения может быть построена таблица истинности. Порядок её построения рассмотрим на конкретном примере:

Пусть задано логическое выражение

1. Сначала составим таблицу всевозможных значений переменных А и В, входящих в данную формулу.

2. Затем проведем анализ строения этой формулы, то есть, определим порядок выполнения логических операций и запишем каждую операцию в отдельный столбец таблицы.

В результате получится следующая таблица:

0 0 0 1 0

0 1 0 0 1 0

1 0 1 1 0 1

1 1 0 0 1 1

Замечание.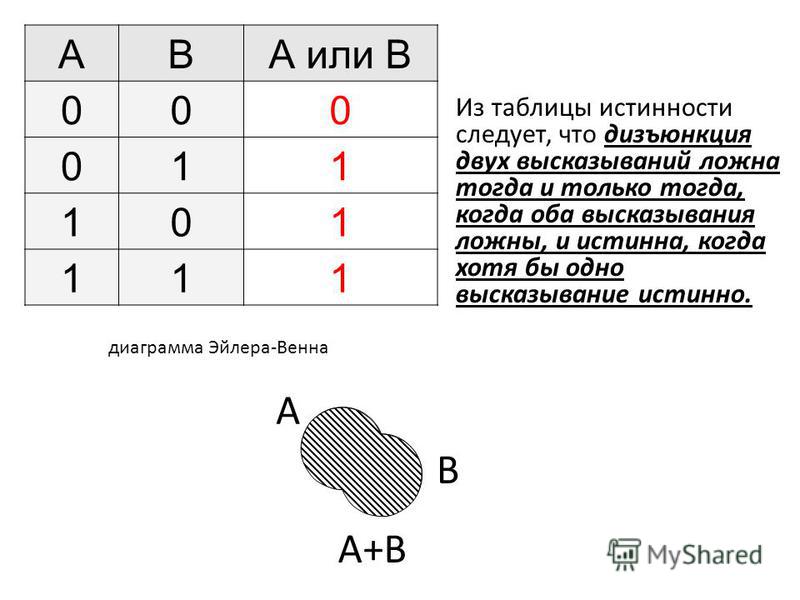 Значения, стоящие в первом столбце, совпадают со значениями, стоящими в последнем. Такие логические выражения называют

равносильными. Для обозначения равносильности пользуются обычно знаком равенства, то есть

Рассмотрим пример, в котором проверяется равносильность высказываний с помощью таблиц истинности.

Проверим равносильность

Построим таблицу истинности:

0 0 1 1 1

0 1 1 1 1

1 0 0 0 0

1 1 1 0 1

Для наглядности значения равносильных логических выражений заключены в овал.

Равносильные выражения взаимозаменяемы.

Кроме понятия равносильности, рассмотрим такие понятия как совместимость, несовместимость, противоположность, логическое следование.

Определение. Два логических выражения называют совместимыми, если хотя бы при одной оценке переменных

они одновременно являются истинными. В противном случае они несовместимые.

Определение. Два логических выражения называют противоположными, если при любой оценке переменных они принимают противоположные значения, и в этом случае каждая из формул является отрицанием другой.

Определение. Логическое выражение В называется логическим следствием логического выражения А, если при любых оценках переменных импликация АВ принимает только истинные значения.

Все формулы (логические выражения) логики высказываний можно разделить на три класса:

 нейтральные, или выполнимые – принимающие как истинные, так и ложные значения;

 тождественно-истинные формулы (или тавтологии) – принимающие истинные значения при любых оценках переменных;

 тождественно-ложные формулы – принимающие ложные значения при любых оценках переменных.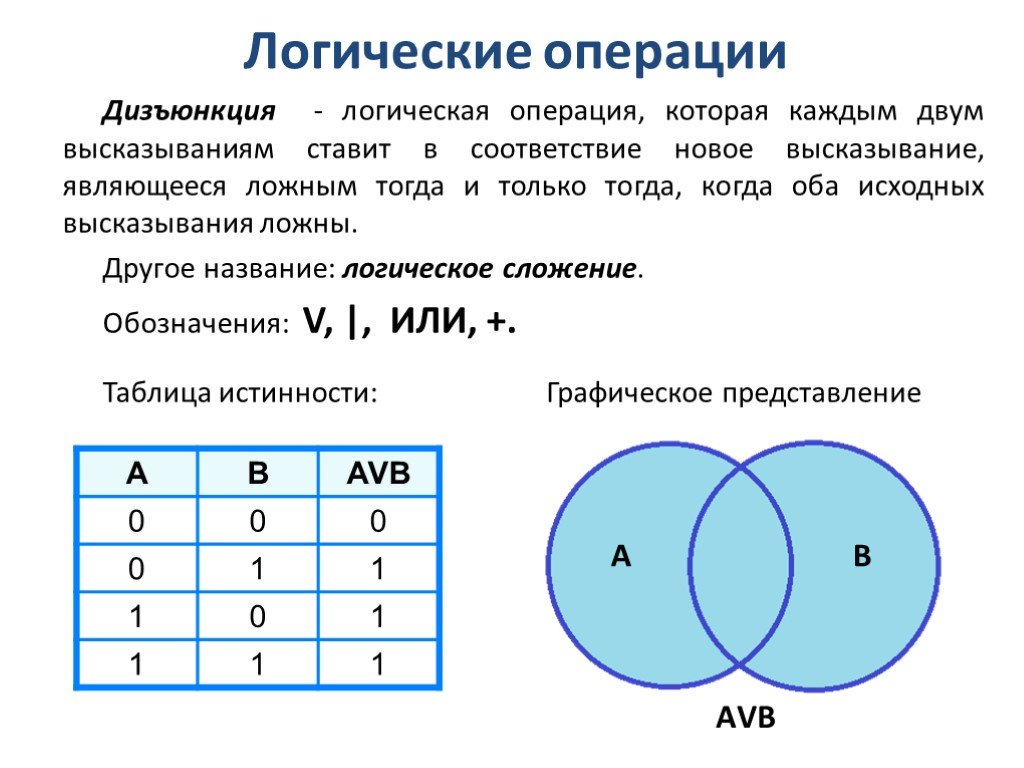

Существуют два способа определения истинного значения формулы. Первый  с помощью таблиц истинности, второй – путем приведения формул к нормальной форме.

Формула имеетнормальную форму, если в ней отсутствуют знаки эквиваленции, импликации, исключающего «или», двойного отрицания, при этом знаки отрицания находятся только при переменных. Например,

Замечание. Табличный способ определения истинного значения формул имеет ограниченное применение, поскольку при увеличении количества переменных приходится рассматривать слишком много вариантов.

Тем не менее, начнем с первого способа, то есть будем определять истинность значения формулы с помощью таблицы истинности. Причем, строить таблицу истинности тоже можно несколькими способами. Рассмотрим три способа. Решим один и тот же пример двумя способами. Решения будут отличаться способами построения таблиц. Итак, требуется определить значение следующей формулы:

§19.

Таблицы истинности | Анализ таблиц истинности (продолжение) (курс фгос 34 ч.)

Планирование уроков на учебный год (ФГОС)

Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 10 классы | Планирование уроков на учебный год (ФГОС) | Таблицы истинности

Содержание урока:

19.1. Построение таблиц истинности

19.1. Построение таблиц истинности (продолжение)

19.2. Анализ таблиц истинности

19.2. Анализ таблиц истинности (продолжение)

САМОЕ ГЛАВНОЕ. Вопросы и задания

Материалы к уроку

		19.2. Анализ таблиц истинности (продолжение)
	19. 2. Анализ таблиц истинности		САМОЕ ГЛАВНОЕ Вопросы и задания

19.2. Анализ таблиц истинности (продолжение)

Пример 3. Логическая функция F задаётся выражением:

Ниже приведён фрагмент таблицы истинности, содержащий все наборы переменных, на которых F истинна.

Определим, какому столбцу таблицы истинности функции F соответствует каждая из переменных х, y > z.

В исходном логическом выражении задействовано три логические переменные. Полная таблица истинности для этого выражения должна состоять из 8 (2³) строк.

Наборам переменных, на которых логическое выражение истинно, соответствуют десятичные числа 0, 2, 3, 4 и 7.

Следовательно, наборам переменных, на которых логическое выражение ложно, должны соответствовать десятичные числа 1, 5 и 6 (их двоичные коды 001, 101 и 110).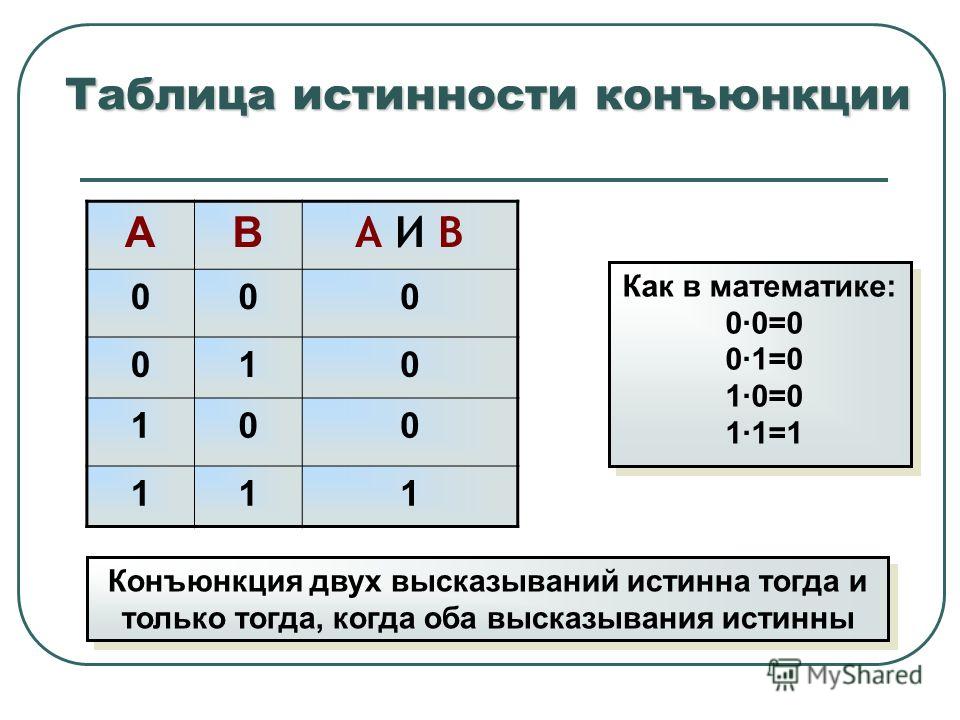 Построим по этим данным вторую часть таблицы истинности:

Теперь выясним, при каких значениях х, у, z логическое выражение ложно: Логическое произведение ложно, если хотя бы один из операндов равен нулю. Таким образом, мы имеем две дизъюнкции, каждая из которых должна быть ложной. Это возможно только в случае равенства нулю каждого из операндов, входящих в дизъюнкцию. Подберём подходящие значения х, у и z, заполняя следующую таблицу:

Первая дизъюнкция равна нулю на наборе 011. Для равенства нулю второй дизъюнкции требуется, чтобы х = 1, у = 0, а z может быть и 0, и 1.

Сравним эту таблицу с восстановленным нами фрагментом исходной таблицы истинности, предварительно подсчитав, сколько раз каждая переменная принимает единичное значение.

Переменная у принимает единичное значение только один раз. Следовательно, ей соответствует второй столбец исходной таблицы. Из таблицы со значениями х, у и z следует, что при у = 1: х = 0, а z = 1.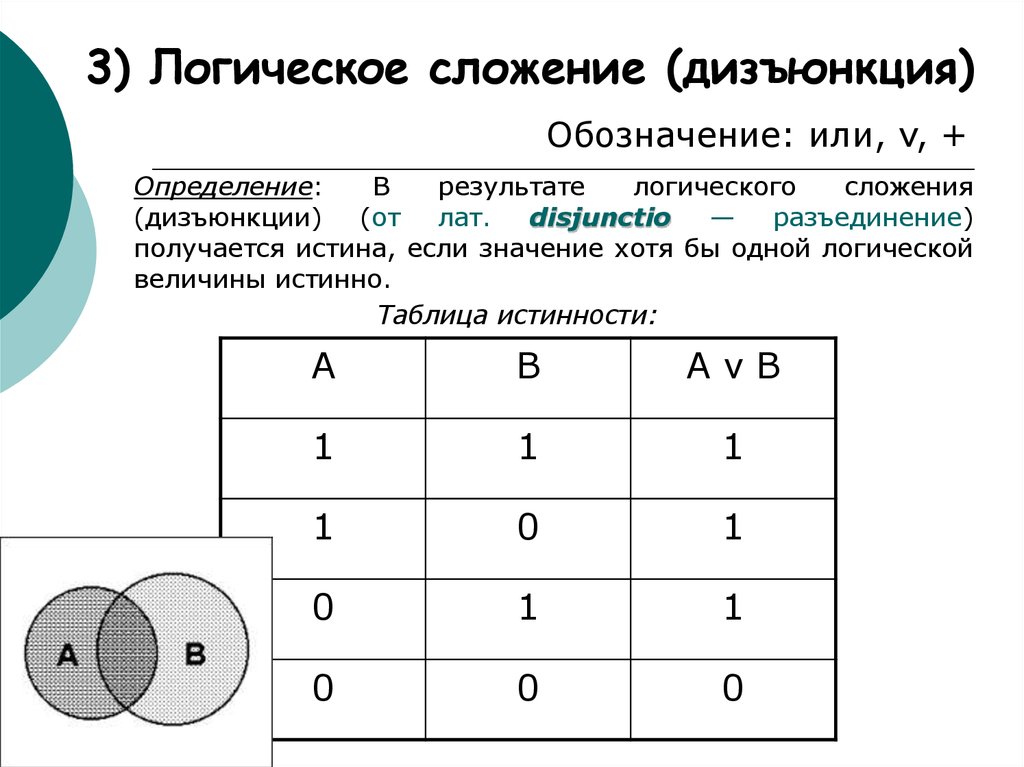 Следовательно, переменной z соответствует первый столбец, а переменной х — третий столбец исходной таблицы.

Убедиться в правильности полученного ответа можно, полностью заполнив следующую таблицу:

Cкачать материалы урока

Эксклюзивная дизъюнкция в логике высказываний

В других моих заметках под названием «Включающая дизъюнкция в логике высказываний» я обсуждал природу и характеристики инклюзивной дизъюнкции, включая ее правила и способы определения ее истинностного значения. В этих заметках я сосредоточусь на исключительной дизъюнкции.

Исключающая дизъюнкция — это тип дизъюнкции, связанный словами « Либо…или, но не оба ». Как мы уже знаем, символ связки дизъюнктивного высказывания равен 9.0005 v (клин). Однако исключительная дизъюнкция символизируется иначе, чем включающая дизъюнкция. Рассмотрим следующие примеры ниже:

1. Либо Джон поет , либо он танцует, , но не оба .
2. Либо Джон спит либо он учится.

Пример №1 явно является исключающей дизъюнкцией из-за слов «но не обоих». Обратите внимание, что Джон может петь и танцевать одновременно (следовательно, включительно), но из-за уточнения «но не и того, и другого», которое четко подчеркивает тот факт, что Джон не поет и не танцует одновременно. , то утверждение явно является исключительным.

Теперь, если мы допустим, что p означает «Джон поет», а q — «Он танцует», тогда утверждение «Либо Джон поет, либо он танцует, но не то и другое» возможно, символизируется как p v q . Однако это ошибочно, потому что в нем четко не указано, что говорится в утверждении «Либо Джон поет, либо танцует, но не то и другое». Итак, как нам символизировать пример № 1 выше?

Как уже упоминалось, если мы допустим, что p означает «Джон поет», а q означает «Он танцует», то мы можем получить p

85 д

. Но это еще не все. Нам нужно принять во внимание фразу «но не то и другое». Если мы вспомним обсуждение союзных утверждений, мы знаем, что символом «но» является • (точка), а при обсуждении отрицательных утверждений мы узнали, что символом отрицания является 9.0005 ~ (тильда). Теперь слово «оба» в заявлении относится к «Джон поет ( p )» и «Он танцует ( q )».

Таким образом, фраза «но не оба» символизируется следующим образом: • ~ ( p • q ).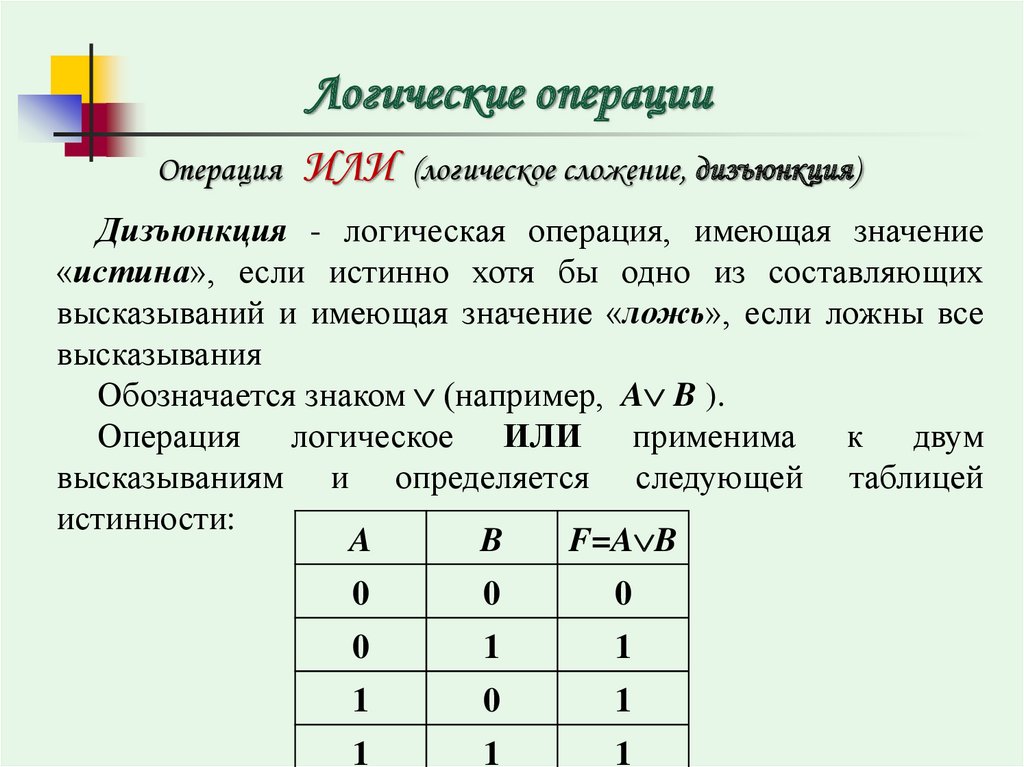 Если мы добавим этот символ к предыдущему утверждению p v q , то мы получим

( P V Q ) • ~ ( P. • Q ) 9007

Таким is singing or he is dancing, but not both” is:

( p v q ) • ~ ( p • q )

Однако логики использовали более упрощенный символ для фразы «но не то и другое». Они использовали подчеркнутый клин v , чтобы символизировать «но не то и другое одновременно». Таким образом, исключительная дизъюнкция «Либо Джон поет, либо он танцует, но не то и другое» символизируется следующим образом:

p v q

93004

8 Обратите внимание, что символ

8 v q читается так: « p или q, но не p и q ».

В некоторых случаях исключающая дизъюнкция не содержит словосочетания «но не оба», но если проанализировать высказывание, то она обозначает исключительность. Давайте рассмотрим пример #2 , который гласит:

Либо Джон спит либо он учится.

Хотя в утверждении нет фразы «но не то и другое», совершенно очевидно, что Джон не может спать и учиться одновременно. Следовательно, пример № 2 выше является исключающей дизъюнкцией.

Если мы допустим, что p означает «Джон спит», а q — «Он учится», то утверждение «Либо Джон спит, либо он учится» символизируется следующим образом:

( p v q ) • ~ ( p • q )

or, simply,

p v q

Правила исключающей дизъюнкции

• Исключительная дизъюнкция ложна, если обе дизъюнкции имеют одинаковое истинностное значение.
• Таким образом, чтобы исключительная дизъюнкция была истинной, одна дизъюнкция должна быть истинной, а другая ложной, и наоборот.

Приведенная ниже таблица истинности иллюстрирует этот момент.

Таблица истинности выше говорит:

1. Если p верно и q равно true , затем p v q равно false .
2. Если P IS True и Q — FALSE , затем P V Q IS TRUE .
3. Если p равно false и q равно true , то p v q это правда .
4. IF P IS FALSE и Q IS FALSE , затем P V Q IS FALSE .

Теперь, учитывая правило исключающей дизъюнкции, как мы, например, определяем истинное значение исключающей дизъюнкции ~ p v q ?

Предположим, что истинностное значение p равно true и q равно true .

SO, если P — верно и Q True, затем заявление ~ P V Q — True .

Для иллюстрации:

На иллюстрации указано, что p верно и q верно. Теперь, прежде чем мы применим правило исключающей дизъюнкции в операторе ~p v q , нам нужно сначала упростить ~p , потому что истинностное значение « истинно» присвоен p , а не ~p . Если мы вспомним наше обсуждение правила в отрицании , мы узнали, что отрицание правда это ложь . Итак, если p равно true , то ~p равно false . Таким образом, в конце концов, ~p v q будет истинным , если p истинным и 9009 9003 q 9009 истинным

Таблица истинности дизъюнкции | Gate Vidyalay

Propositions-

 

Прежде чем читать эту статью, убедитесь, что вы прочитали предыдущую статью на Предложения .

 

Мы обсудили-

• Предложение — это декларативное утверждение, которое либо истинно, либо ложно, но не то и другое одновременно.
• Связки используются для объединения предложений.

 

 

В этой статье мы обсудим связки в логике высказываний.

 

Логические связки-

 

Связки — это операторы, которые используются для объединения одного или нескольких предложений.

 

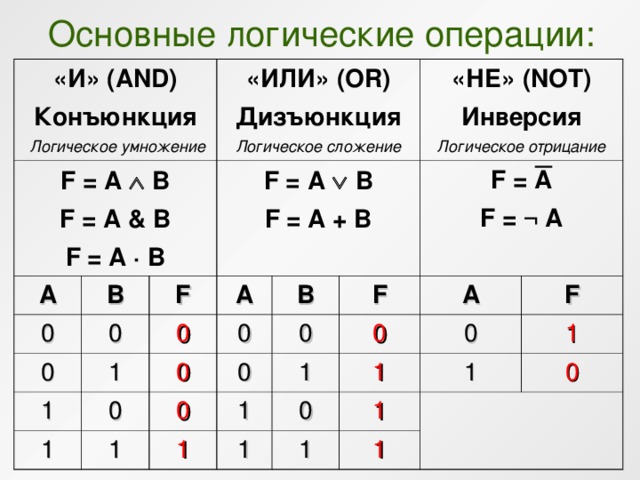
In propositional logic, there are 5 basic connectives-

 

40006

Name of Connective	Connective Word	Symbol
Negation	Not	⌉ или ∼ или ‘ или –
Соединение	И
Disjunction	Or	∨
Conditional	If-then	→
Biconditional	If and only if	↔

1. Отрицание-

 

Если р есть высказывание, то отрицание р есть высказывание, которое-

• Истинно, когда р ложно
• Ложь, если p равно true.

 

Truth Table-

 

p	∼p
F	T
T	F

 

Пример:

 

Если p : На улице идет дождь.

Тогда, Отрицание p is-

∼p : На улице нет дождя.

 

2. Конъюнкция-

 

Если p и q — два суждения, то конъюнкция p и q — суждение, которое является

• Истинно, когда оба p и q истинны and q are false

 

Truth Table-

 

p	q	p ∧ q
F	F	F
F	T	F
T	F	F
T	T	T

 

Example-

 

Если p и q два предложения, где-

• p : 2 + 4 = 6
• q : На улице идет дождь.

 

Тогда соединение p и q равно-

p ∧ q : 2 + 4 = 6 и на улице идет дождь

 

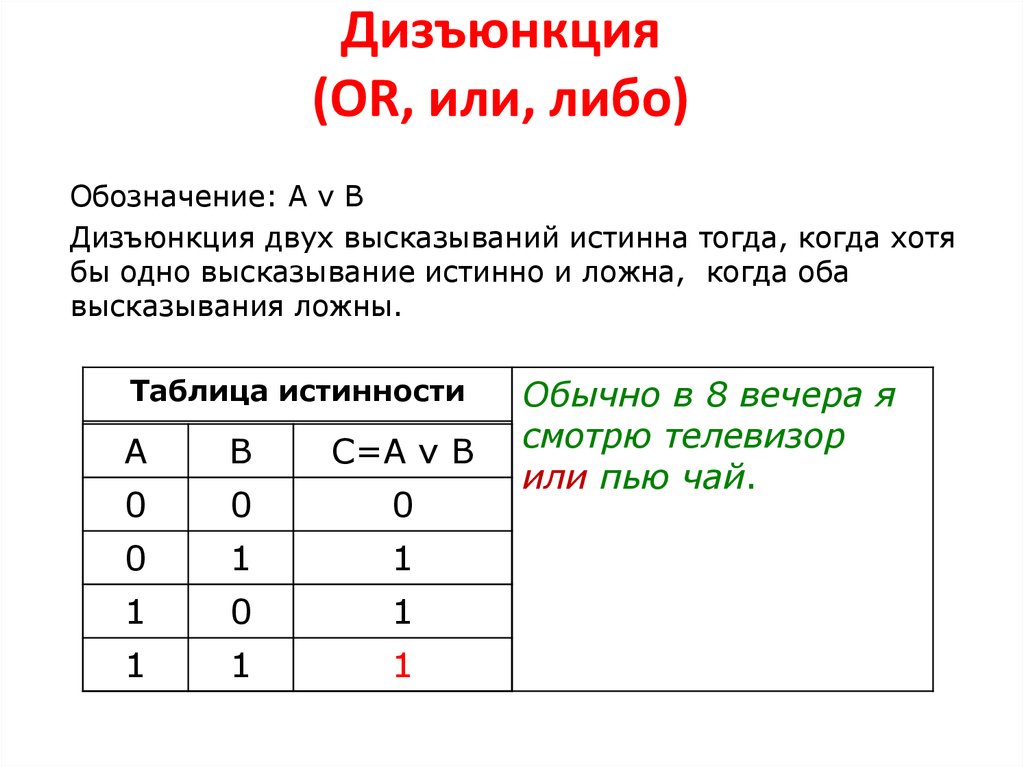
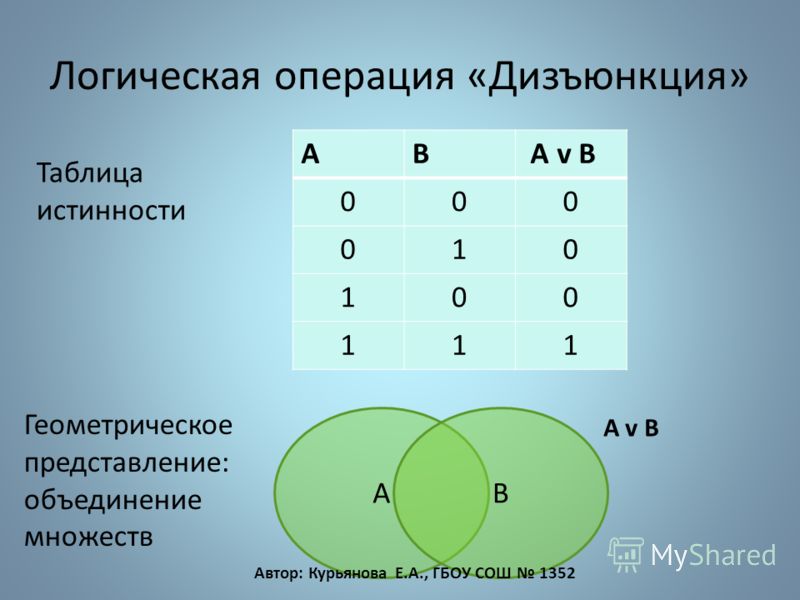
3. Дизъюнкция-

 

Если р и q — два суждения, то дизъюнкция р и q — это суждения, которое истинно, когда истинно одно из р или 9024 или оба

False when both p and q are false

 

Truth Table-

 

p	q	p ∨ q
F	F	F
F	T	T
T	F	T
T	T	T

 

Example —

 

Если p и q два предложения, где-

• p : 2 + 4 = 6
• q : На улице идет дождь0007

  p ∨ q : 2 + 4 = 6 или на улице дождь

   

  4. Условно-

   

  то q» называется условным или импликационным предложением.

• Истинно, когда и p, и q истинны, или когда p ложно.
• Ложь, когда p истинно, а q ложно.

 

Таблица истинности-

 

p	q	p → q
F	F	T
F	T	T
T	F	F
T	T	T

If Aerding- 9052

.

Если я поеду в Австралию, то заработаю больше денег.

 

5. Биусловное-

 

Если p и q два суждения, то-

• Предложение типа «p тогда и только тогда, когда q» называется двуобусловленным.
• Истинно, когда оба p и q истинны или оба p и q ложны.
• Ложь во всех остальных случаях.

 

Таблица истинности-

 

p	q	p ↔ q
F	F	T
F	T	F
T	F	F
T	T	T

 

Examples-

 

• Он идет на матч тогда и только тогда, когда не идет дождь.
• Птицы летают тогда и только тогда, когда небо чистое.

 

Важные примечания-

 

Примечание-01:

 

• Отрицание электронных.
• Соединение ≡ И Ворота цифровой электроники.