19.2. Интегрирующие и дифференцирующие цепи

В импульсных устройствах задающий генератор часто вырабатывает импульсы прямоугольной формы определенной длительности и амплитуды, которые предназначаются для представления чисел и управления элементами вычислительных устройств, устройств обработки информации и др. Однако для правильного функционирования различных элементов в общем случае требуются импульсы вполне определенной формы, отличной от прямоугольной, имеющие заданные длительность и амплитуду. Вследствие этого возникает необходимость предварительно преобразовывать импульсы задающего генератора. Характер преобразования может быть разным. Так, может потребоваться изменить амплитуду или полярность, длительность задающих импульсов, осуществить их задержку во времени.

Преобразования в основном осуществляются с помощью линейных цепей — четырехполюсников, которые могут быть пассивными и актив­ными. В рассматриваемых цепях пассивные четырехполюсники не содер­жат в своем составе источников питания, активные используют энергию внутренних или внешних источников питания. С помощью линейных цепей осуществляются такие преобразования, как дифференцирование, интегрирование, укорочение импульсов, изменение амплитуды и поляр­ности, задержка импульсов во времени. Операции дифференцирования, интегрирования и укорочения импульсов выполняются соответственно дифференцирующими, интегрирующими и укорачивающими цепями. Изменение амплитуды и полярности импульса может производиться с помощью импульсного трансформатора, а задержка его во времени — линией задержки.

Интегрирующая цепь

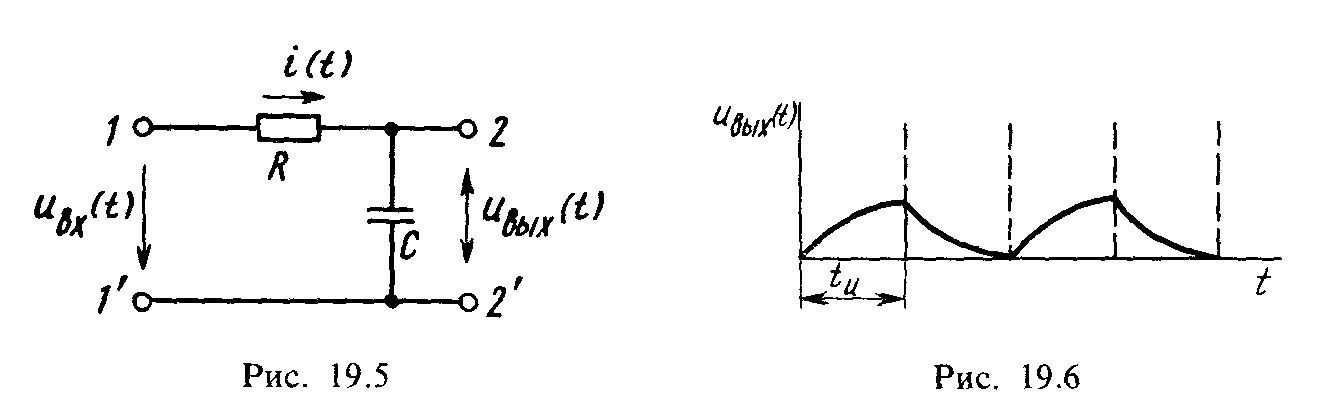. На рис. 19.5 приведена схема простейшей цепи (пассивного четырехполюсника), с помощью которой можно выполнить операцию интегрирования входного электрического сигнала, подан­ного на зажимы 1-1^|, если выходной сигнал снимать с зажимов 2-2′.

Составим уравнение цепи для мгновенных значений токов и напря­жений по второму закону Кирхгофа:

Отсюда следует, что ток цепи будет изменяться по закону

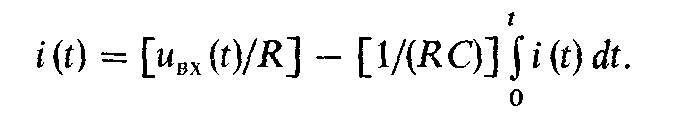
Если выбрать постоянную временидостаточно большой, то вторым слагаемым в последнем уравнении можно пренебречь, тогдаi(t) = u_вх(t)/R.

Напряжение на конденсаторе (на зажимах 2-2′) будет равно

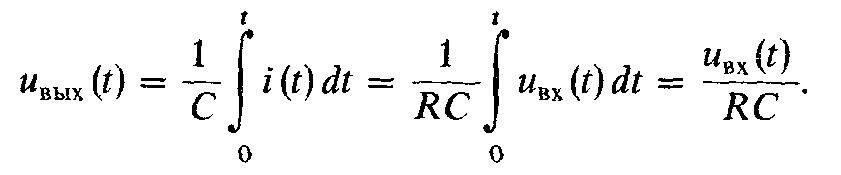(19.1)

Из (19.1) видно, что цепь, приведенная на рис. 19.5, выполняет опе­рацию интегрирования входного напряжения и умножения его на коэф­фициент пропорциональности, равный обратному значению постоянной времени цепи: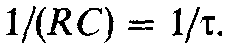

Временная диаграмма выходного напряжения интегрирующей цепи при подаче на вход последовательности прямоугольных импульсов показана на рис. 19.6.

Дифференцирующая цепь. С помощью цепи, схема которой приведена на рис. 19.7 (пассивного четырехполюсника), можно выполнять операцию дифференцирования входного электрического сигнала, поданного на зажимы 1-1′, если выходной сигнал снимать с зажимов 2-2′. Составим уравнение цепи для мгновенных значений тока и напряжений по второму закону Кирхгофа:

Если сопротивление R мало и членом i(t)R можно пренебречь, то ток в цепи 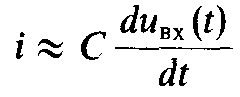и выходное напряжение цепи, снимаемое с R,

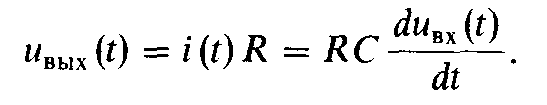(19.2)

Анализируя (19.2), можно видеть, что с помощью рассматриваемой цепи выполняют операции дифференцирования входного напряжения и умножения его на коэффициент пропорциональности, равный постоян­ной времени τ = RC. Форма выходного напряжения дифференцирующей цепи при подаче на вход серии прямоугольных импульсов приведена на рис. 19.8. В этом случае теоретически выходное напряжение должно представлять собой знакопеременные импульсы бесконечно большой амплитуды и малой (близкой к нулю) длительности.

Однако вследствие различия свойств реальной и идеальной диф­ференцирующих цепей, а также конечной крутизны фронта импульса на выходе получают импульсы, амплитуда которых меньше амплитуды входного сигнала, а длительность их определяется как t_и = (3 ÷ 4) τ = (3 ÷ 4)RС.

В общем случае форма выходного напряжения зависит от соотно­шения длительности импульса входного сигнала t_и и постоянной вре­мени дифференцирующей цепи τ. В момент t₁

входное напряжение при­ложено к резистору R, так как напряжение на конденсаторе скачком изменяться не может. Затем напряжение на конденсаторе возрастает по экспоненциальному закону, а напряжение на резисторе R, т. е. выходное напряжение, снижается по экспоненциальному закону и становится рав­ным нулю в момент t₂, когда зарядка конденсатора закончится. При малых значениях τ длительность выходного напряжения мала. Когда напряжение u_BX(t) становится равным нулю, конденсатор начинает разряжаться через резистор R. Таким образом формируется импульс обратной полярности.

П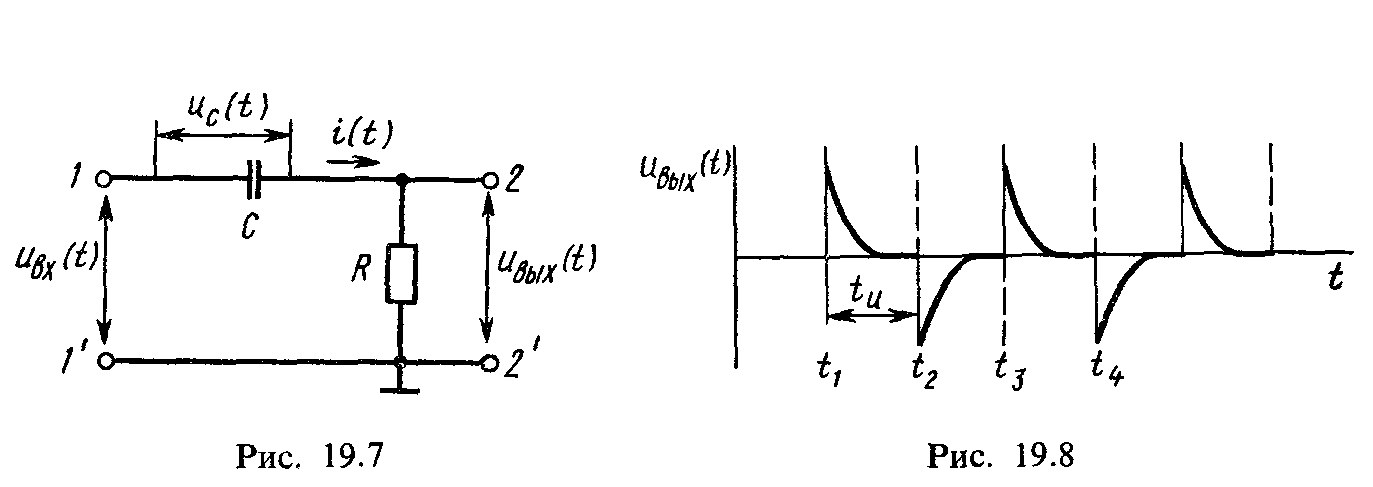ассивные интегрирующие и дифференцирующие цепи имеют сле­дующие недостатки: обе математические операции реализуются прибли­женно, с известными погрешностями. Приходится вводить корректи­рующие звенья, которые, в свою очередь, сильно снижают амплитуду выходного импульса, т. е. без промежуточного усиления сигналов практически невозможныn-кратные дифференцирование и интегриро­вание.

Эти недостатки не свойственны активным дифференцирующему и интегрирующему устройствам. Одним из возможных способов реали­зации этих устройств является применение операционных усилителей (см. гл. 18).

Активное дифференцирующее устройство. Схема такого устройства на операционном усилителе приведена на рис. 19.9. Ко входу 1 подключен конденсатор С, а в цепь обратной связи включен резистор R

oc. Так как входное сопротивление чрезвычайно велико (R_вх -> ∞), то входной ток обтекает схему по пути, указанному пунктиром. С другой сторо­ны, напряжение и_вхОУ в этом включении очень мало, так как К_u -> ∞, поэтому потенциал точки В схемы практически равен нулю. Следовательно, ток на входе

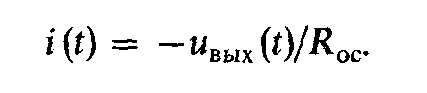(19.3)

Ток на выходе i(t) одновременно является зарядным током кон­денсатора С: dq= Сdu _BX

(t), откуда

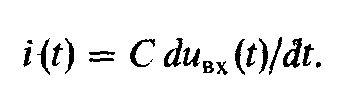(19.4)

Приравнивая левые части уравнений (19.3) и (19.4), можно написать -и_вых(t)/R_oc = С du_вх (t)/dt, откуда

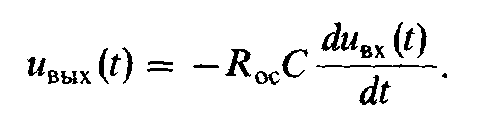(19.5)

Таким образом, выходное напряжение операционного усилителя является произведением производной входного напряжения по времени, умноженной на постоянную времени τ = R_ОСС.

А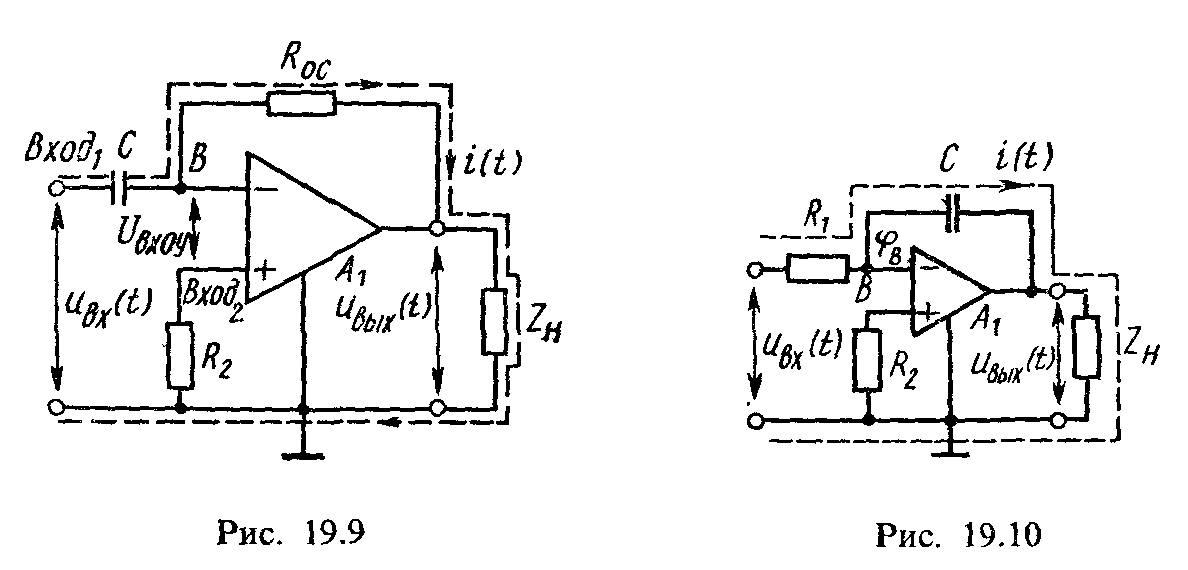ктивное интегрирующее устройство

. Схема интегрирующего устройст­ва на операционном усилителе, приведенная на рис. 19.10, отличается от дифференцирующего устройства рис. 19.9 только тем, что конденсатор С и резистор R_oc (на рис. 19.10 —R₁) поменялись местами. По-прежнему R_вх -> ∞ и коэффициент усиления по напряжению К_u -> ∞. Следовательно, в устройстве конденсатор С заряжается током i(t) =u_BX(t)/R₁. Так как напряжение на конденсаторе практически равно выходному напряжению (φ_B = 0), а операционный усилитель изменяет фазу входного сигнала на выходе на угол π, имеем

(19.6)

Таким образом, выходное напряжение активного интегрирующего устройства есть произведение определенного интеграла от входного напряжения по времени на коэффициент 1/τ.

Дифференцирующая и интегрирующая электрические цепи

Интегрирующая цепь.

Рассмотрим электрическую цепь из резистора сопротивлением R и конденсатора ёмкостью C.

Элементы R и C соединены последовательно, значит, ток в их цепи можно выразить, исходя из производной напряжения заряда конденсатора dQ/dt = C(dU/dt) и закона Ома U/R. Напряжение на выводах резистора обозначим U_R. Тогда будет иметь место равенство:

Проинтегрируем последнее выражение

Интеграл левой части уравнения будет равен U_out + Const.

Перенесем постоянную составляющую Const в правую часть с тем же знаком. В правой части постоянную времени RC вынесем за знак интеграла

В итоге получилось, что выходное напряжение U_out прямопропорционально интегралу напряжения на выходах резистора, следовательно, и входному току I_in.

Постоянная составляющая Const не зависит от номиналов элементов цепи. Чтобы обеспечить прямую пропорциональную зависимость выходного напряжения U_out от интеграла входного U_in, необходима пропорциональность входного напряжения от входного тока. Нелинейное соотношение U_in/I_in во входной цепи вызвано тем, что заряд и разряд конденсатора происходит по экспоненте e^—t/τ, которая наиболее нелинейна при t/τ ≥ 1, то есть, когда значение t соизмеримо или больше τ.

Здесь t – время заряда или разряда конденсатора в пределах периода.

τ = RC – постоянная времени – произведение величин R и C.

Если взять номиналы RC цепи, когда τ будет значительно больше t, тогда начальный участок экспоненты для короткого периода (относительно τ) может быть достаточно линейным, что обеспечит необходимую пропорциональность между входным напряжением и током. Для простой цепи RC постоянную времени обычно берут на 1-2 порядка больше периода переменного входного сигнала, тогда основная и значительная часть входного напряжения будет падать на выходах резистора, обеспечивая в достаточной степени линейную зависимость U_in/I_in ≈ R.

В таком случае выходное напряжение U_out будет с допустимой погрешностью пропорционально интегралу входного U_in. Чем больше величины номиналов RC, тем меньше переменная составляющая на выходе, тем более точней будет кривая функции. В большинстве случаев, переменная состовляющая интеграла не требуется при использовании таких цепей, нужна только постоянная Const, тогда номиналы RC можно выбирать по возможности большими, но с учетом входного сопротивления следующего каскада.

В качестве примера, сигнал с генератора – положительный меандр 1V периодом 2 mS подадим на вход простой интегрирующей цепи RC с номиналами:

R = 10 kOhm, C = 1uF. Тогда τ = RC = 10 mS.

В данном случае постоянная времени лишь в пять раз больше времени периода, но визуально интегрирование прослеживается в достаточной степени точно. График показывает, что выходное напряжение на уровне постоянной состовляющей 0.5 будет треугольной формы, потому как участки, не меняющиеся во времени, для интеграла будут константой (обозначим её α), а интеграл константы будет линейной функцией. ʃαdx = αx + Const. Величина константы α определит тангенса угла наклона линейной функции.

Проинтегрируем синусоиду, получим косинус с обратным знаком ʃsinxdx = -cosx + Const. В данном случае постоянная составляющая Const = 0.

Если подать на вход сигнал треугольной формы, на выходе будет синусоидальное напряжение. Интеграл линейного участка функции – парабола. В простейшем варианте ʃxdx = x²/2 + Const. Знак множителя определит направление параболы.

Недостаток простейшей цепочки в том, что переменная составляющая на выходе получается очень маленькой относительно входного напряжения.

Дифференцирующая цепь RC.

Для простейшей дифференцирующей цепочки RC из двух элементов используем пропорциональную зависимость выходного напряжения от производной напряжения на выводах конденсатора.

U_out = RI_R = RI_C = RC(dU_C / dt)

Если взять номиналы элементов RC, чтобы постоянная времени была на 1-2 порядка меньше длины периода, тогда отношение приращения входного напряжения к приращению времени в пределах периода может определять скорость изменения входного напряжения в определенной степени точно. В идеале это приращение должно стремится к нулю. В таком случае основная часть входного напряжения будет падать на выводах конденсатора, а выходное будет составлять незначительную часть от входного, поэтому для вычислений производной такие схемы практически не используются.

Наиболее часто дифференцирующие и интегрирующие цепи RC применяют для изменения длины импульса в логических и цифровых устройствах. В таких случаях номиналы RC расчитывают по экспоненте e^-t/RC исходя из длины импульса в периоде и требуемых изменений. Например, ниже на рисунке показано, что длина импульса T_i на выходе интегрирующей цепи увеличится на время 3τ. Это время разряда конденсатора до 5% амплитудного значения.

На выходе дифференцирующей цепи амплитудное напряжение после подачи импульса появляется мгновенно, так как на выводах разряженного конденсатора оно равно нулю. Далее следует процесс заряда и напряжение на выводах резистора убывает. За время 3τ оно уменьшится до 5% амплитудного значения.

5% – величина показательная. В практических расчетах этот порог определится входными параметрами применяемых логических элементов.

19.2. Интегрирующие и дифференцирующие цепи

В импульсных устройствах задающий генератор часто вырабатывает импульсы прямоугольной формы определенной длительности и амплитуды, которые предназначаются для представления чисел и управления элементами вычислительных устройств, устройств обработки информации и др. Однако для правильного функционирования различных элементов в общем случае требуются импульсы вполне определенной формы, отличной от прямоугольной, имеющие заданные длительность и амплитуду. Вследствие этого возникает необходимость предварительно преобразовывать импульсы задающего генератора. Характер преобразования может быть разным. Так, может потребоваться изменить амплитуду или полярность, длительность задающих импульсов, осуществить их задержку во времени.

Преобразования в основном осуществляются с помощью линейных цепей — четырехполюсников, которые могут быть пассивными и актив­ными. В рассматриваемых цепях пассивные четырехполюсники не содер­жат в своем составе источников питания, активные используют энергию внутренних или внешних источников питания. С помощью линейных цепей осуществляются такие преобразования, как дифференцирование, интегрирование, укорочение импульсов, изменение амплитуды и поляр­ности, задержка импульсов во времени. Операции дифференцирования, интегрирования и укорочения импульсов выполняются соответственно дифференцирующими, интегрирующими и укорачивающими цепями. Изменение амплитуды и полярности импульса может производиться с помощью импульсного трансформатора, а задержка его во времени — линией задержки.

Интегрирующая цепь. На рис. 19.5 приведена схема простейшей цепи (пассивного четырехполюсника), с помощью которой можно выполн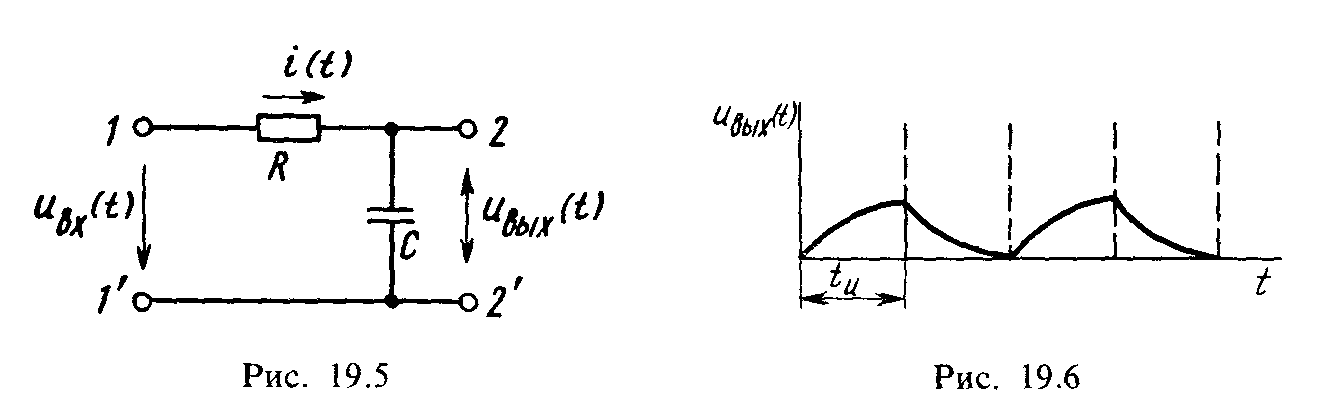ить операцию интегрирования входного электрического сигнала, подан­ного на зажимы 1-1^|, если выходной сигнал снимать с зажимов 2-2′.

Составим уравнение цепи для мгновенных значений токов и напря­жений по второму закону Кирхгофа:

Отсюда следует, что ток цепи будет изменяться по закону

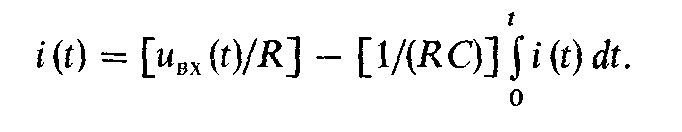
Если выбрать постоянную времени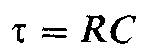достаточно большой, то вторым слагаемым в последнем уравнении можно пренебречь, тогдаi(t) = u_вх(t)/R.

Напряжение на конденсаторе (на зажимах 2-2′) будет равно

(19.1)

Из (19.1) видно, что цепь, приведенная на рис. 19.5, выполняет опе­рацию интегрирования входного напряжения и умножения его на коэф­фициент пропорциональности, равный обратному значению постоянной времени цепи: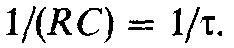

Временная диаграмма выходного напряжения интегрирующей цепи при подаче на вход последовательности прямоугольных импульсов показана на рис. 19.6.

Дифференцирующая цепь. С помощью цепи, схема которой приведена на рис. 19.7 (пассивного четырехполюсника), можно выполнять операцию дифференцирования входного электрического сигнала, поданного на зажимы 1-1′, если выходной сигнал снимать с зажимов 2-2′. Составим уравнение цепи для мгновенных значений тока и напряжений по второму закону Кирхгофа:

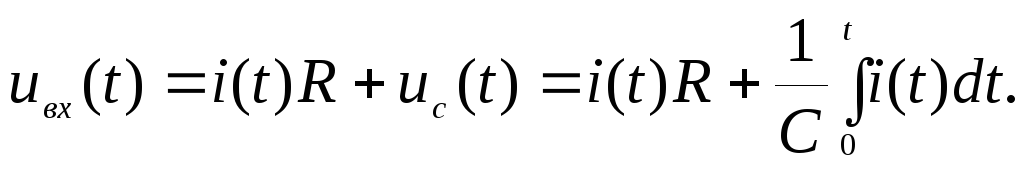
Если сопротивление R мало и членом i(t)R можно пренебречь, то ток в цепи 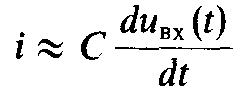и выходное напряжение цепи, снимаемое с R,

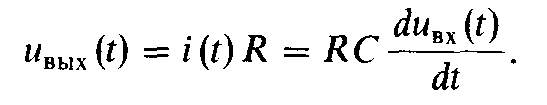(19.2)

Анализируя (19.2), можно видеть, что с помощью рассматриваемой цепи выполняют операции дифференцирования входного напряжения и умножения его на коэффициент пропорциональности, равный постоян­ной времени τ = RC. Форма выходного напряжения дифференцирующей цепи при подаче на вход серии прямоугольных импульсов приведена на рис. 19.8. В этом случае теоретически выходное напряжение должно представлять собой знакопеременные импульсы бесконечно большой амплитуды и малой (близкой к нулю) длительности.

Однако вследствие различия свойств реальной и идеальной диф­ференцирующих цепей, а также конечной крутизны фронта импульса на выходе получают импульсы, амплитуда которых меньше амплитуды входного сигнала, а длительность их определяется как t_и = (3 ÷ 4) τ = (3 ÷ 4)RС.

В общем случае форма выходного напряжения зависит от соотно­шения длительности импульса входного сигнала t_и и постоянной вре­мени дифференцирующей цепи τ. В момент t₁ входное напряжение при­ложено к резистору R, так как напряжение на конденсаторе скачком изменяться не может. Затем напряжение на конденсаторе возрастает по экспоненциальному закону, а напряжение на резисторе R, т. е. выходное напряжение, снижается по экспоненциальному закону и становится рав­ным нулю в момент t₂, когда зарядка конденсатора закончится. При малых значениях τ длительность выходного напряжения мала. Когда напряжение u_BX(t) становится равным нулю, конденсатор начинает разряжаться через резистор R. Таким образом формируется импульс обратной полярности.

П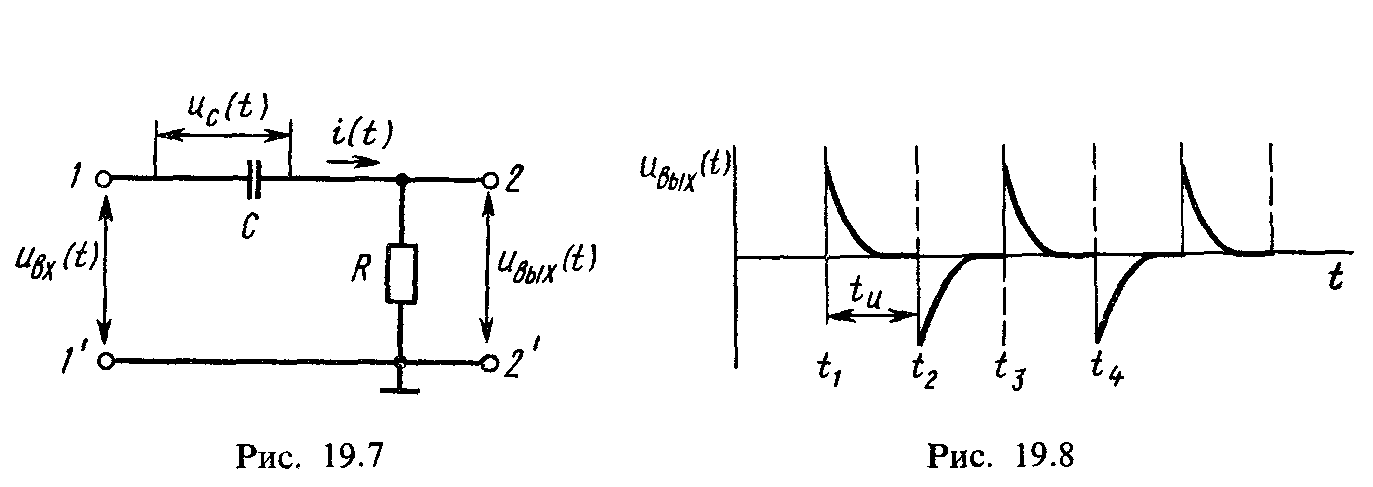ассивные интегрирующие и дифференцирующие цепи имеют сле­дующие недостатки: обе математические операции реализуются прибли­женно, с известными погрешностями. Приходится вводить корректи­рующие звенья, которые, в свою очередь, сильно снижают амплитуду выходного импульса, т. е. без промежуточного усиления сигналов практически невозможныn-кратные дифференцирование и интегриро­вание.

Эти недостатки не свойственны активным дифференцирующему и интегрирующему устройствам. Одним из возможных способов реали­зации этих устройств является применение операционных усилителей (см. гл. 18).

Активное дифференцирующее устройство. Схема такого устройства на операционном усилителе приведена на рис. 19.9. Ко входу 1 подключен конденсатор С, а в цепь обратной связи включен резистор R_oc. Так как входное сопротивление чрезвычайно велико (R_вх -> ∞), то входной ток обтекает схему по пути, указанному пунктиром. С другой сторо­ны, напряжение и_вхОУ в этом включении очень мало, так как К_u -> ∞, поэтому потенциал точки В схемы практически равен нулю. Следовательно, ток на входе

(19.3)

Ток на выходе i(t) одновременно является зарядным током кон­денсатора С: dq= Сdu _BX (t), откуда

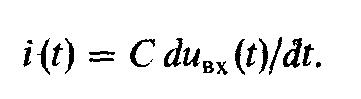(19.4)

Приравнивая левые части уравнений (19.3) и (19.4), можно написать -и_вых(t)/R_oc = С du_вх (t)/dt, откуда

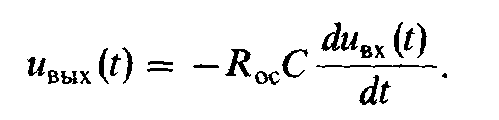(19.5)

Таким образом, выходное напряжение операционного усилителя является произведением производной входного напряжения по времени, умноженной на постоянную времени τ = R_ОСС.

Активное интегрирующее устройство. Схема интегрирующего устройст­ва на операционном усилителе, приведенная на рис. 19.10, отличается от дифференцирующего устройства рис. 19.9 только тем, что конденсатор С и резистор R_oc (на рис. 19.10 —R₁) поменялись местами. По-прежнему R_вх -> ∞ и коэффициент усиления по напряжению К_u -> ∞. Следовательно, в устройстве конденсатор С заряжается током i(t) =u_BX(t)/R₁. Так как напряжение на конденсаторе практически равно выходному напряжению (φ_B = 0), а операционный усилитель изменяет фазу входного сигнала на выходе на угол π, имеем

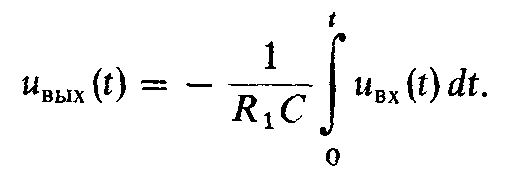(19.6)

Таким образом, выходное напряжение активного интегрирующего устройства есть произведение определенного интеграла от входного напряжения по времени на коэффициент 1/τ.

Интегрирующие и дифференцирующие цепи

Важной практической задачей является возможность создания четырехполюсников, напряжение на выходе которых представляет собой производную или интеграл входного напряжения. Обладающие указанными свойствами четырехполюсники получили название дифференцирующих и интегрирующих цепей. Рассмотрим простейшие дифференцирующие и интегрирующие цепи.

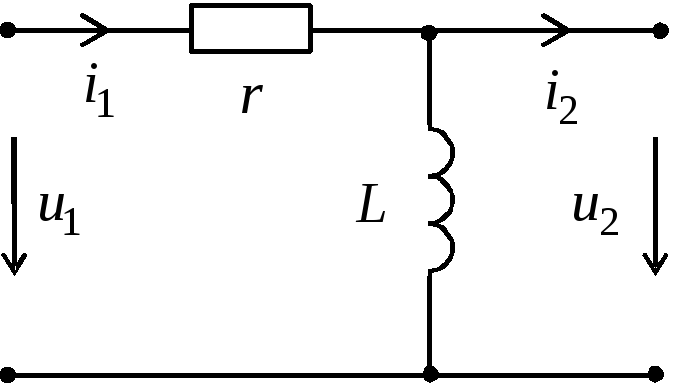Примером дифференцирующего звена является представленная на рисунке цепь. Предположим, что для данного четырехполюсника сопротивление нагрузки столь велико, что ток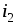весьма мал по сравнению с током, поэтому будем полагать.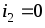

Определим для этой цепи передаточную функцию по напряжению в комплексной форме

где 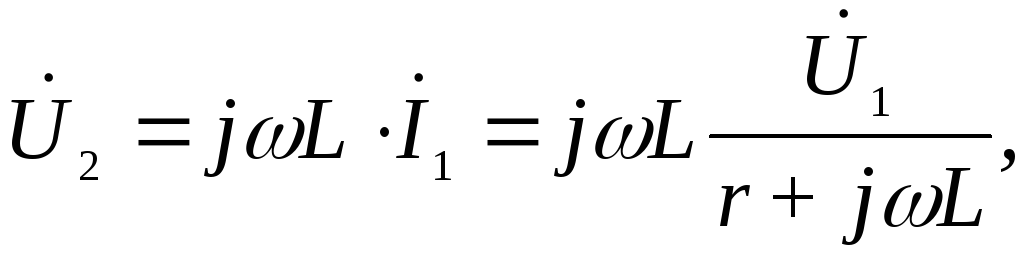откуда получим:

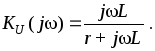
Предположим, что для заданной частоты 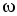соотношение параметров таково, что выполняются следующие соотношения

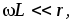т.е. Передаточная функция четырехполюсника при указанных допущениях примет вид

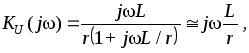
и, соответственно,

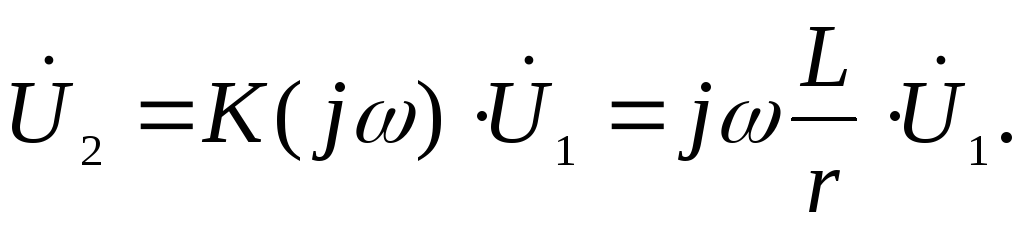
Как известно, умножению на 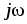комплексного изображения соответствует операция взятия производной по времени от действительной функции

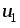
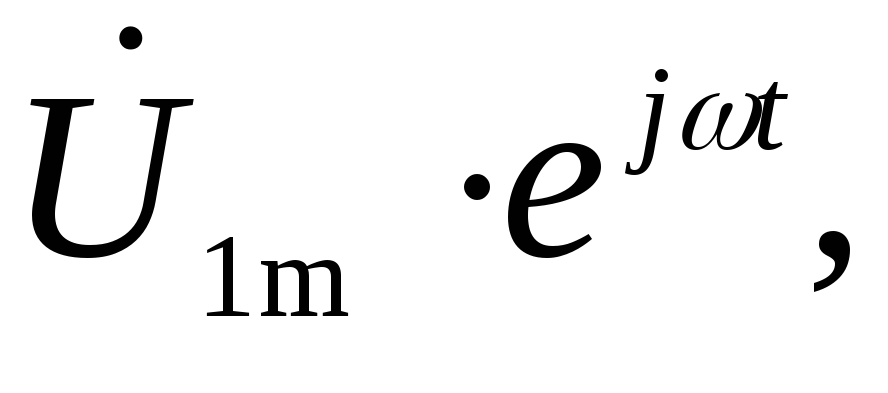
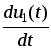
поэтому окончательно для величины 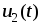получим:

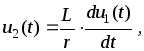
то есть выходное напряжение 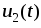будет пропорционально производной от входного напряжения.

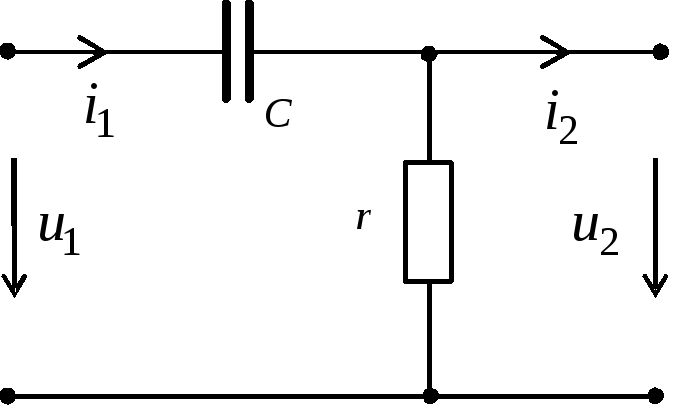
Дифференцирующими свойствами обладает также цепь, представленная на рисунке. Пусть, как и ранее, справедливо допущение 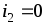. Тогда для данной схемы справедливо соотношение

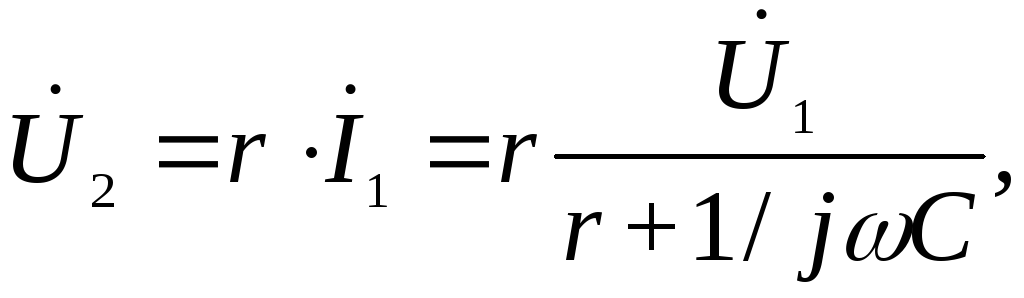
и передаточная функция примет вид:

Введем при заданной частоте 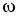дополнительное допущение о соотношении сопротивлений элементов цепи

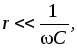или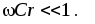

Для передаточной функции по напряжению теперь можно записать:

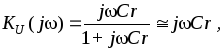
что соответствует выражению для выходного напряжения

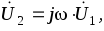или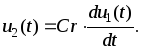

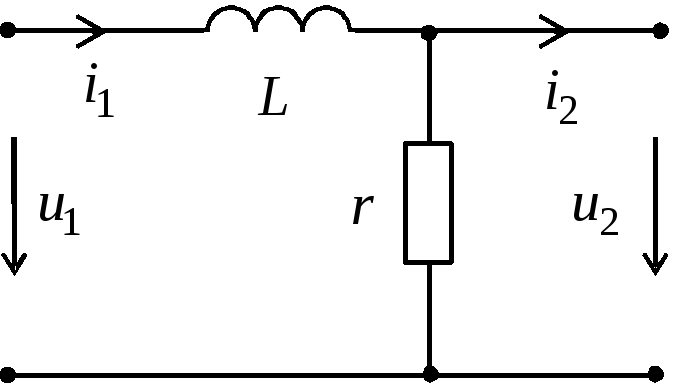Простейшей интегрирующей цепью является представленный на рисунке четырехполюсник. Пусть для данной цепи, так же как в предыдущих случаях, справедливо условие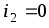. Тогда передаточная функция цепи в комплексной форме определиться следующим образом

Предположим, что имеют место следующие допущения:

т.е.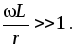

Тогда передаточная функция цепи примет вид

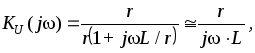
то есть выходное и входное напряжения связаны соотношением:

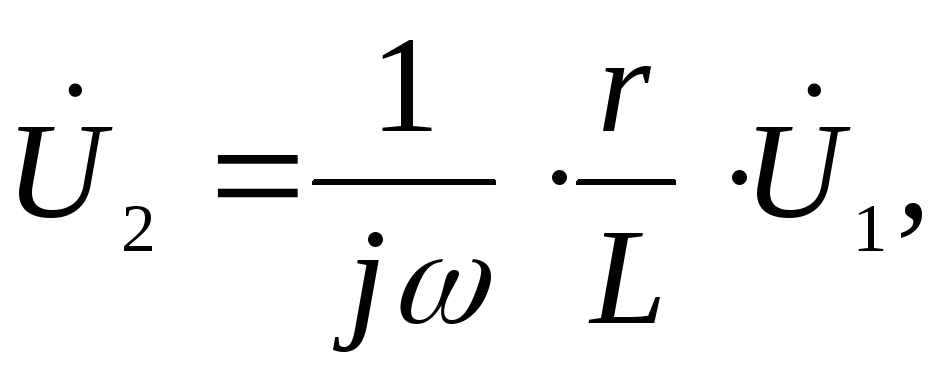
причем

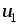
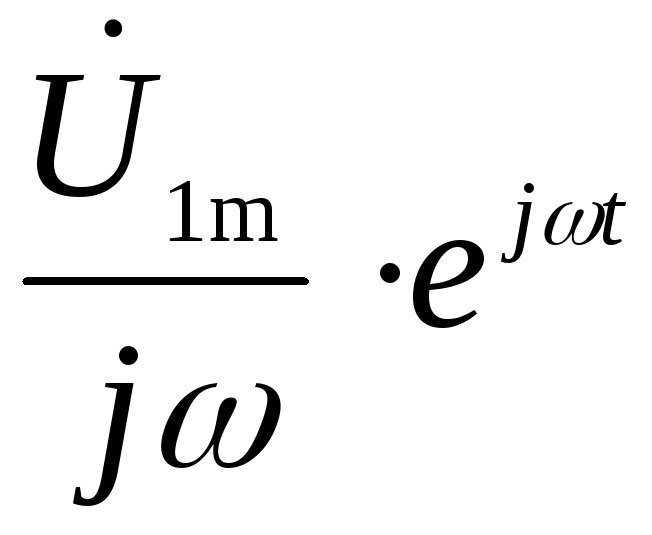
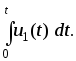
Таким образом, использование данной электрической цепи позволяет получить на выходе четырехполюсника функцию 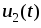, пропорциональную интегралу входного напряжения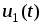

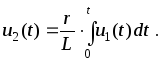
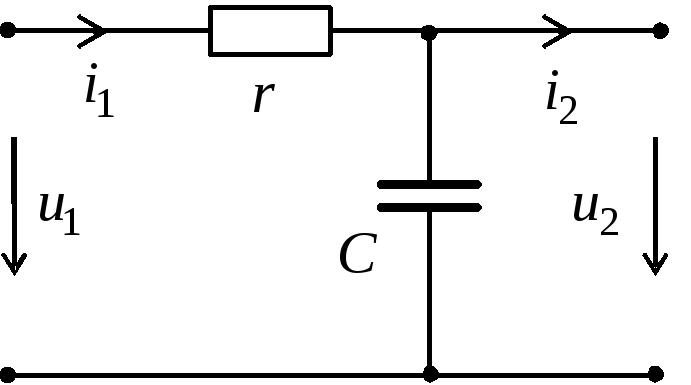
Другим примером интегрирующей цепи может служить схема, представленная на рисунке. При условии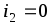справедливо равенство:

то есть для передаточной функции получим

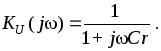
Предположив, что

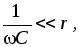имеем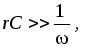

и окончательно получим

что соответствует интегральному соотношению

.

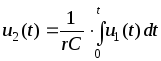Существенным недостатком рассмотренных простых электрических цепей является то, что их дифференцирующие и интегрирующие свойства проявляются лишь при определенном соотношении параметров:

Рассмотрим примеры определения параметров простейших дифференцирующих и интегрирующих цепей.

Пример 1.Входной сигнал является синусоидальной функцией времени, изменяющейся с частотойГц. Индуктивность катушкиГн. Определить сопротивление резистора, при котором происходит дифференцирование входного сигнала.

Запишем условие дифференцирования 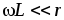для данной цепи в виде

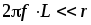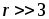, откуда получим Oм .

Таким образом, для решения поставленной задачи сопротивление резистора должно иметь величину значительно превышающую 3 Ом.

Пример 2. На вход изображенной на рисунке цепи подается синусоидальный сигнал частоты 50 герц. Определить величину емкости 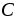, при которой цепь является интегрирующей. Сопротивление резистора 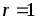кОм.

Условие интегрирования сигнала такой электрической цепью приводит к неравенству

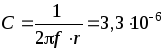Ф.

Следовательно, в данных условиях интегрирующая цепочка должна включать в себя конденсатор емкостью, значительно превышающей 3 мкФ.

В заключение отметим, что для всех рассмотренных цепей сопротивления элементов, с которых снимается выходной сигнал, много меньше сопротивления элемента, включенного «последовательно», что приводит к неравенству 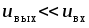. Этот недостаток рассмотренных электрических цепей приводит к необходимости использования усилителя сигнала, что существенно усложняет электрическую цепь. В качестве еще одного недостатка следует отметить необходимость подбора параметров этих цепей в зависимости от частотных свойств входного сигнала.

216

Дифференцирующие и интегрирующие цепи

⁄ ,

где α2 — постоянный коэффициент.

Полагая, что сопротивление нагрузки обобщенной цепи столь велико, что то ком можно пренебречь по сравнению с , находим выражения для коэффи циента передачи обобщенной цепи по напряжению:

Очевидно, что операторный коэффициент передачи обобщенной цепи может быть пропорционален р или р―1 только при

	|		⁄	| 1.		6.93
В этом случае для дифференцирующей цепи приближенно выполняется соот
ношение		для интегрирующей цепи —				/ .

Для дифференцирующей цепи соблюдение условия (6.93) равносильно тому, что постоянная времени цепи / (см. рис. 6,14, а) или (см. рис. 6.14, б) намного меньше длительности дифференцируемого сигнала.

Для интегрирующей цепи условие (6.93) означает, что постоянная времени це пи должна быть значительно больше интервала интегрирования. Из (6.93) также вытекает, что напряжение на выходе u2 простейших дифференцирующих и интегри рующих цепей оказывается намного меньшим, чем напряжение на входе их этих це пей. Увеличение напряжения u2 может быть достигнуто путем усложнения схем дифференцирующих и интегрирующих цепей, в частности путем применения цепей, содержащих не только пассивные, но и активные элементы (см. модуль 7.4).

Вопросы для самопроверки

1.Укажите последовательность и содержание этапов решения задачи о реак ции цепи на экспоненциальное воздействие.

2.Что такое обобщённая комплексная амплитуда? обобщённая (комплексная частота)?

3.Дайте определение операторной характеристике (ОХ) цепи.

4.Может ли цепь, для которой определяют (вычисляют) ОХ, содержать источ ник энергии? Если да, то какой именно источник?

5.Почему ОХ цепи имеет второе название обобщённая частотная характери стика (ОЧХ)?

6.Докажите, что КЧХ цепи можно рассматривать как частный случай ОХ. Име ет ли этот факт практическую ценность?

7.Покажите на плоскости комплексной частоты р области определения КЧХ и ОХ.

8.Перечислите и дайте определения всем входным и передаточным ОХ (ОЧХ).

дифф. цепи

Тема занятия 25: Дифференцирующие и интегрирующие цепи.

25.1 Дифференцирующие цепи.

Дифференцирующая цепь – это четырехполюсник, в котором мгновенное значение напряжения на выходе пропорционально производной от напряжения на входе.

RC- цепь.

В качестве пассивных дифференциальных уравнений чаще всего используются RC-цепи.

Докажем, что эта цепь является дифференциальной.

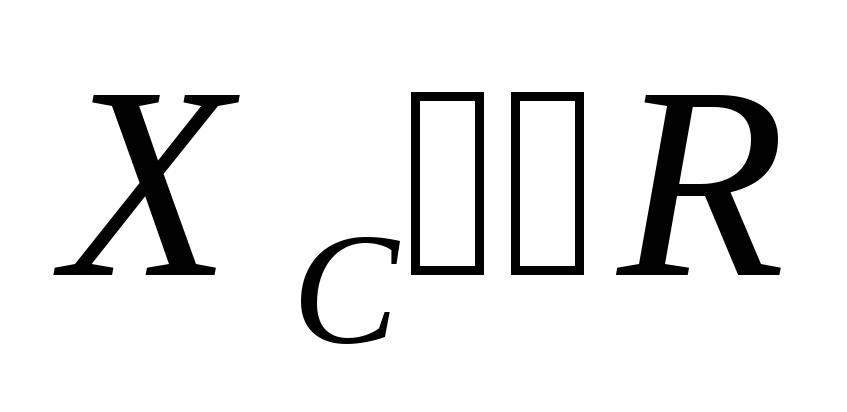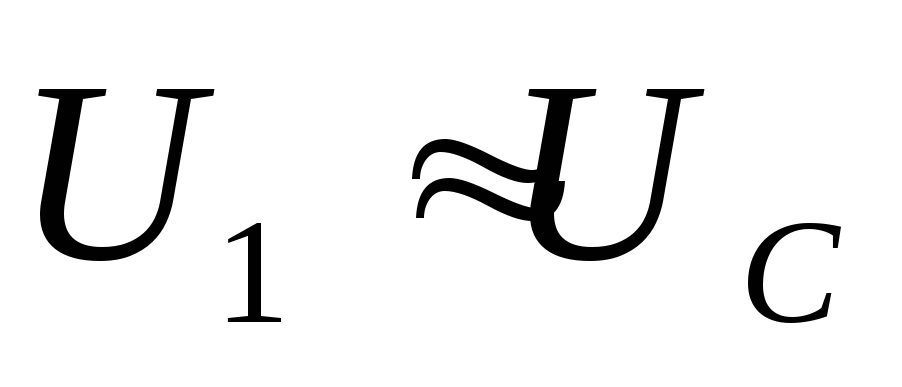
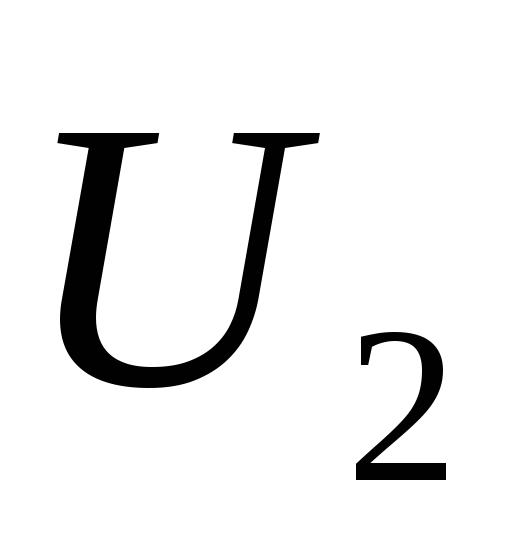Если , то , тогда напряжением на резисторе можно пренебречь, следовательно — мало, следовательно

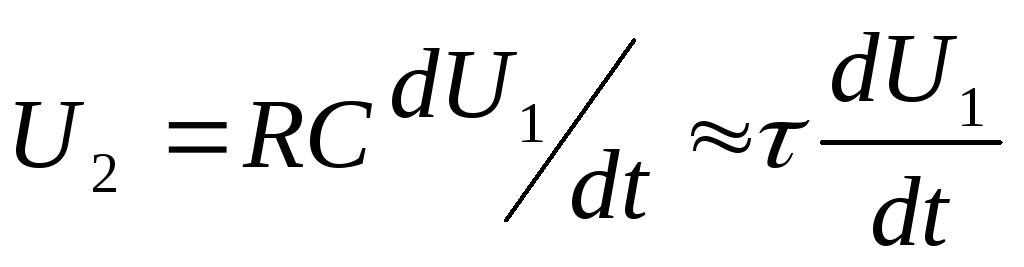, где — постоянная дифференциальной цепи.

Вывод: цепь RC является дифференциальной при условии, что активное сопротивление много меньше сопротивления конденсатора.

На практике — условие, при котором цепь RC является дифференцирующей.

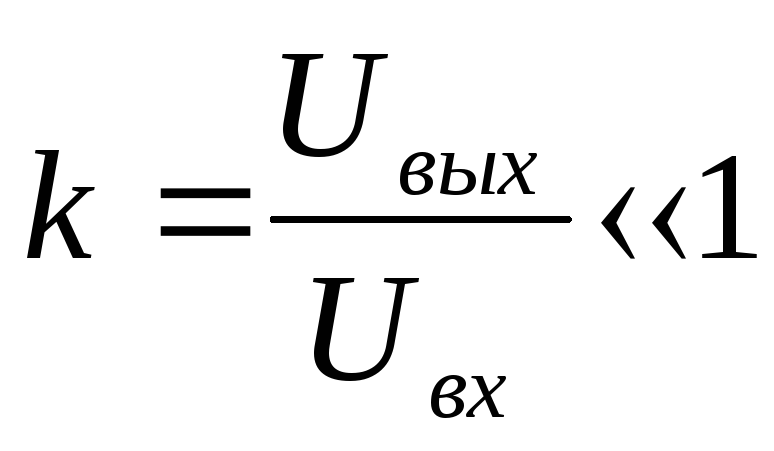
RL-цепь.

Д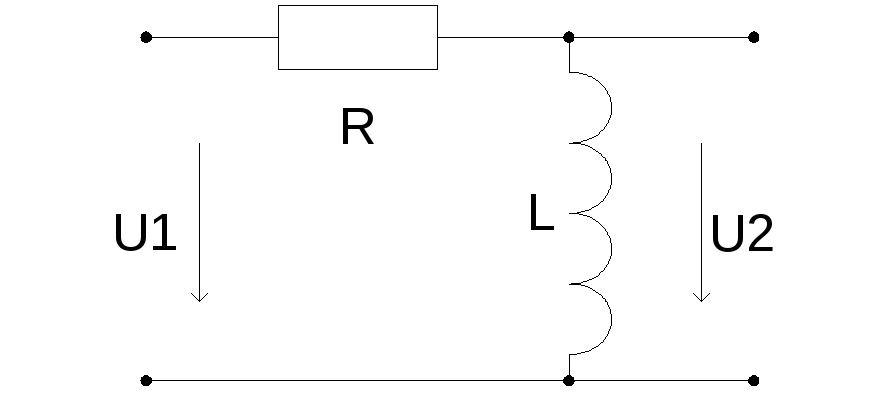окажем, что данная цепь дифференциальная.

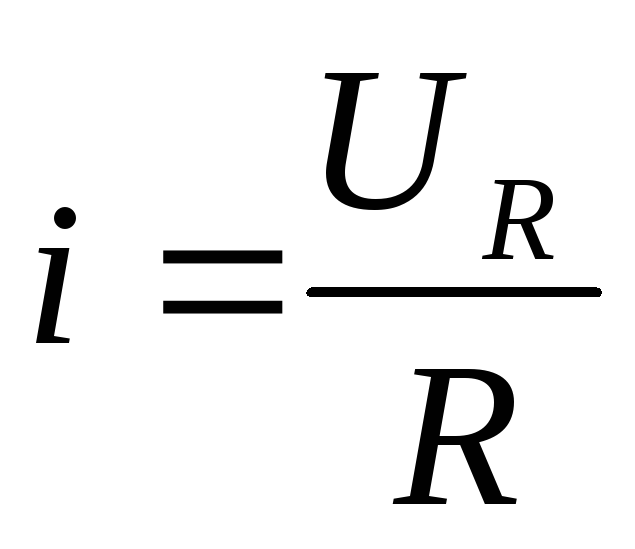
По второму закону Кирхгоффа

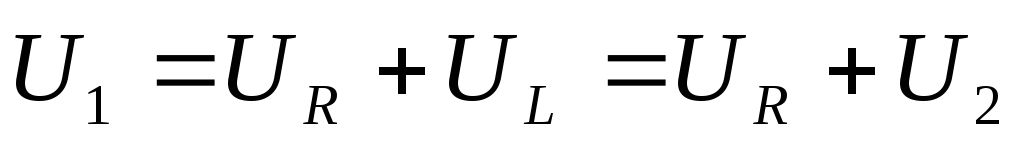
Если сопротивление катушки индуктивности много меньше активного сопротвления, то значением напряжения на катушке можно пренебречь,так как оно мало, следовательно

U₁~U_R подставим данное выражение в 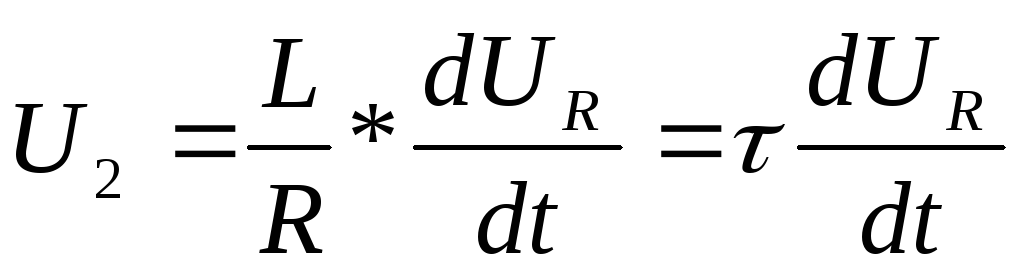и получим, что .

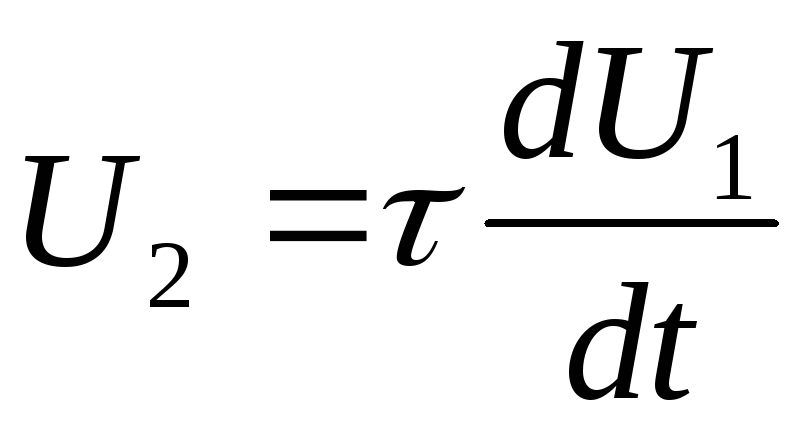Вывод: цепь RL является дифференциальной при условии, что .

На практике 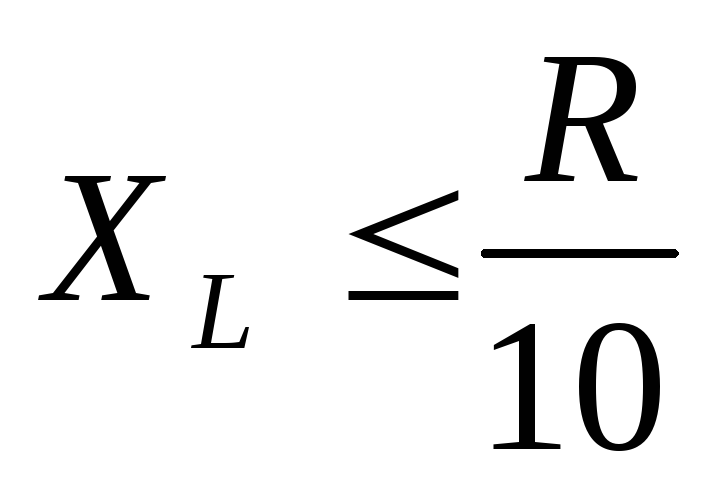— условие при котором цепь RL – дифференциальная.

.

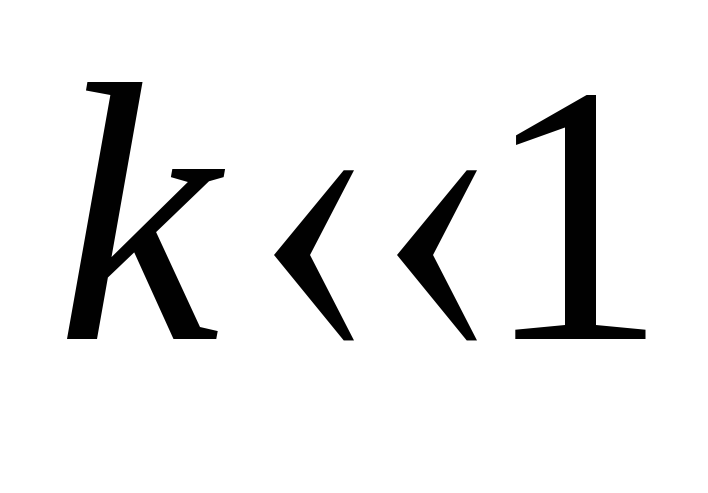25.2 Форма некоторых сигналов после дифференцирования.

После дифференцирования синусоидального сигнала получается косинусоидальный. На рисунке входной сигнал обозначен сплошной линией, а выходной пунктиром.

После дифференцирования треугольного сигнала получается сигнал прямоугольной формы.

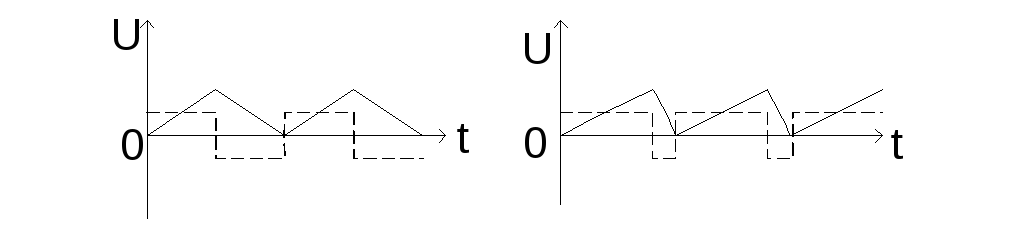
После дифференцирования прямоугольных импульсов получаются узкие (короткие по времени) импульсы, поэтому дифференциальные цепи называют еще укорачивающими.

Д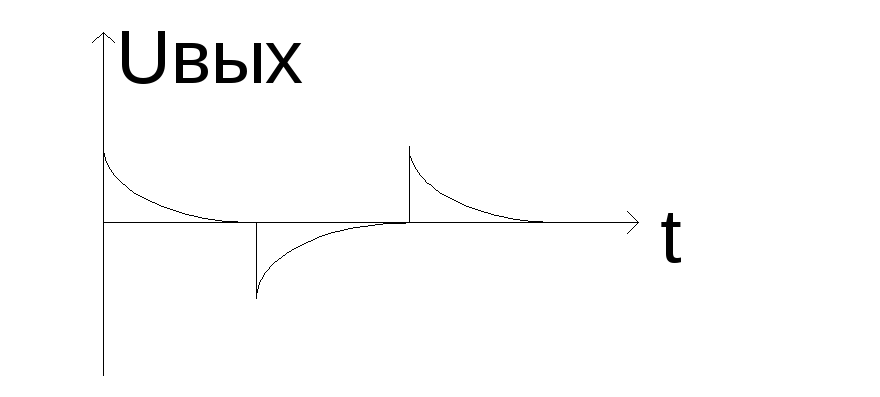лительность импульсов зависит от , чем выше тем медленнее заряжается конденсатор и на выходе может получиться:

Дифференциальные цепи используют для получения коротких импульсов с крутым фронтом.

25.3 Коэффициент передачи

.

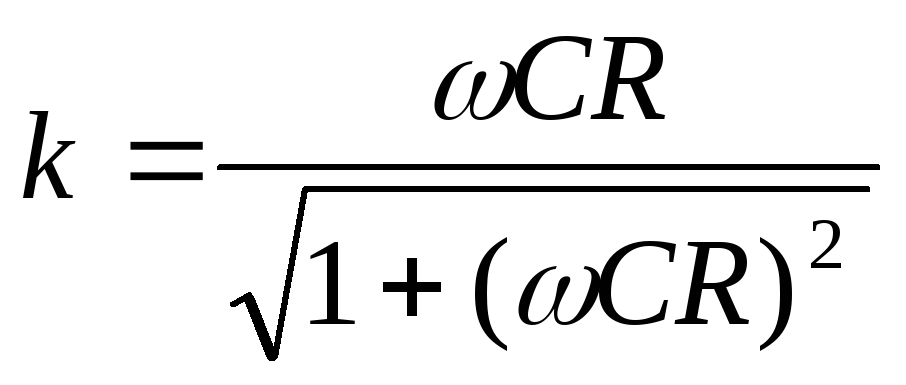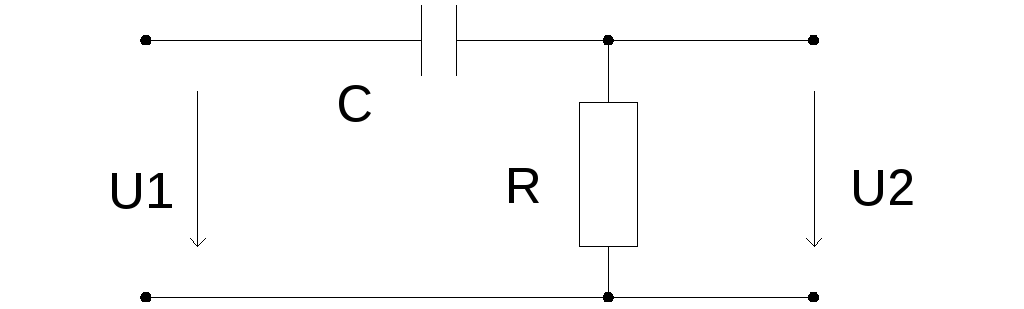
На практике и в знаменателе этой величиной можно пренебречь.

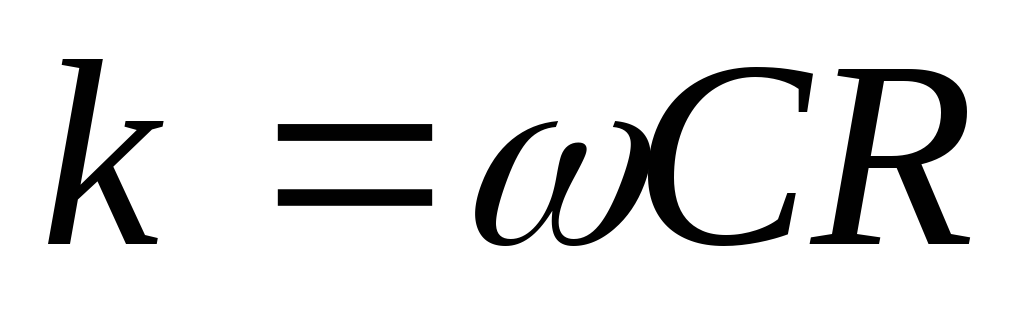— условие дифференцирования, то есть цепь является дифференцирующей, если ее коэффициент передачи пропорционален частоте.

25.4 Активные дифференцирующие цепи.

Недостатком пассивных дифференцирующих цепей является очень маленький коэффициент передачи. Поэтому используются активные дифференцирующие цепи на основе операционных усилителей, у которых .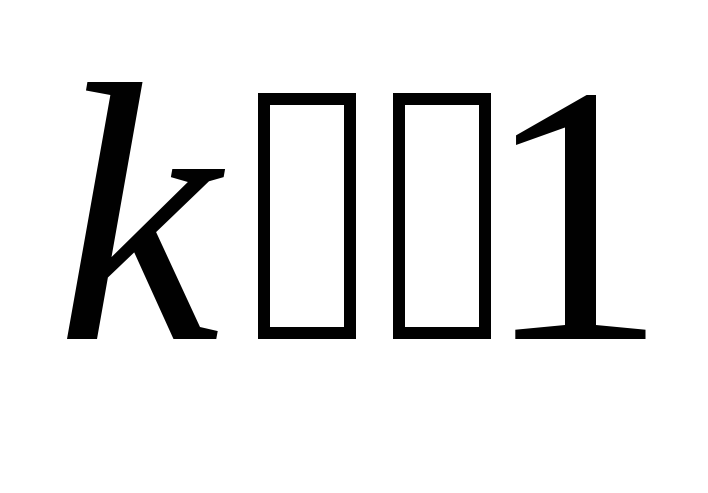

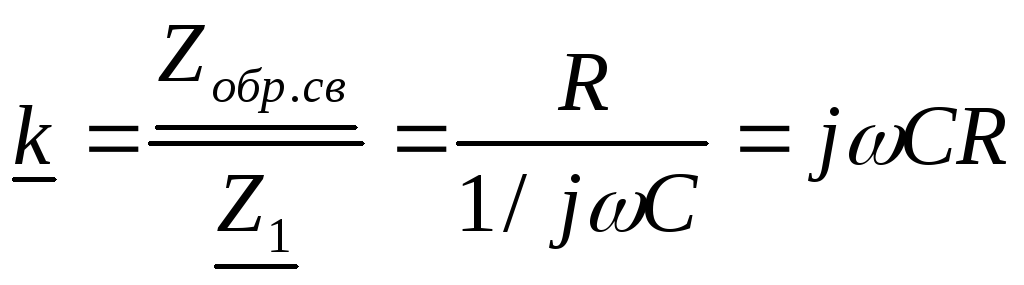, следовательно так как 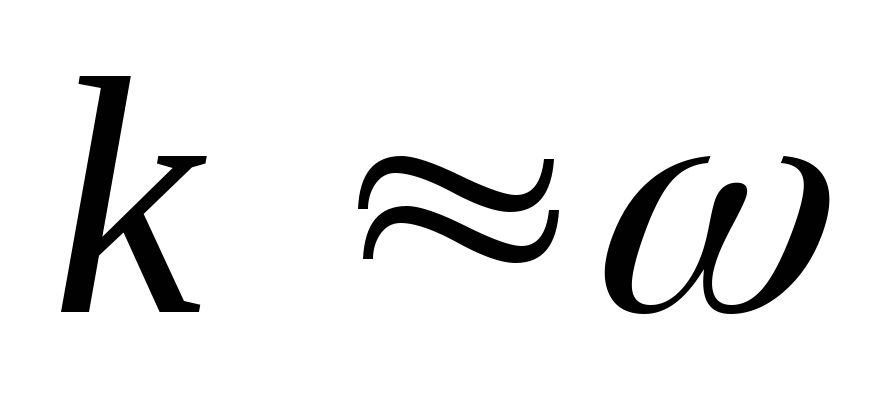, то цепь дифференцирующая, а .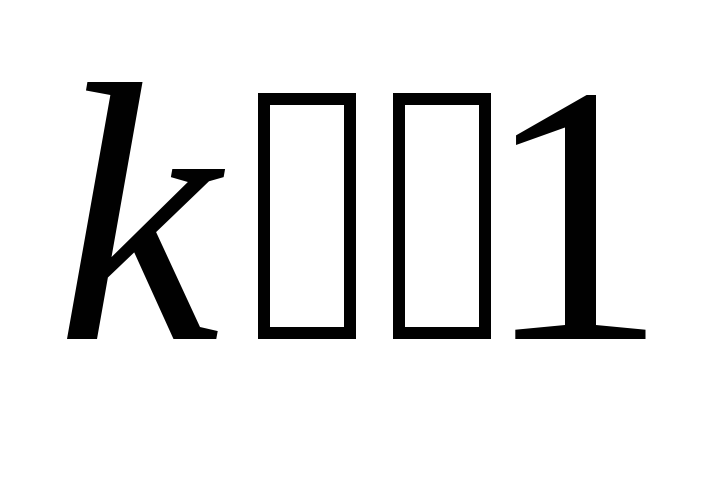

Активные дифференцирующие цепи являются основными для получения узких коротких импульсов.

Тема занятия 26: Интегрирующие цепи.

Четырехполюсник называется интегрирующим если напряжение на его выходе пропорционально интегралу от напряжения на входе.

RC-цепь.

Д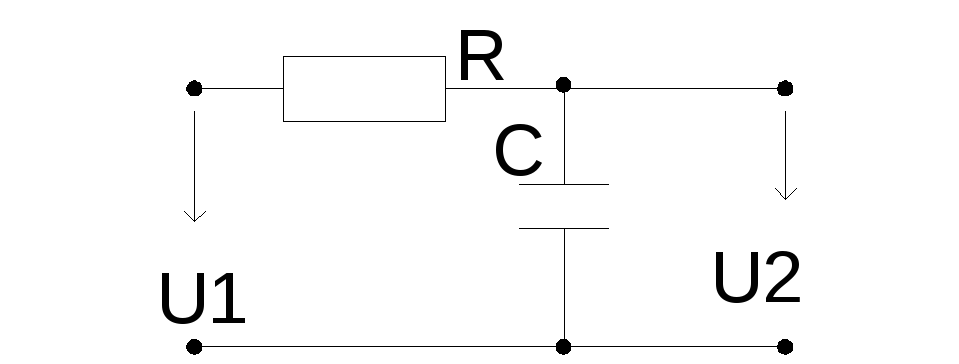окажем, что данная цепь является интегрирующей.

U_L=U_C

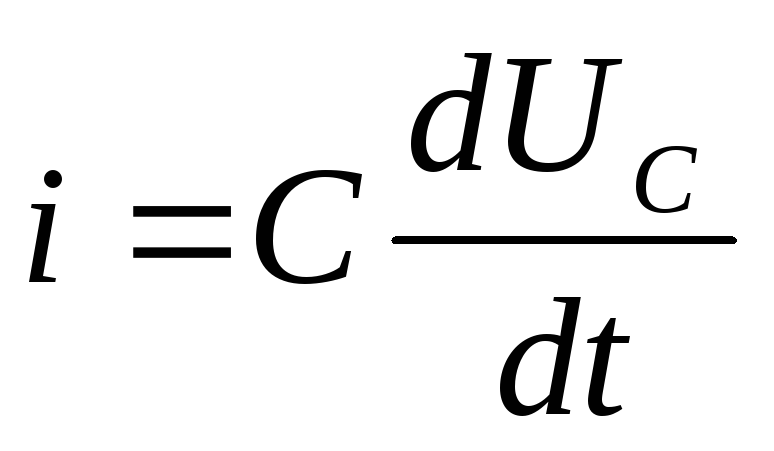, следовательно , то есть

.

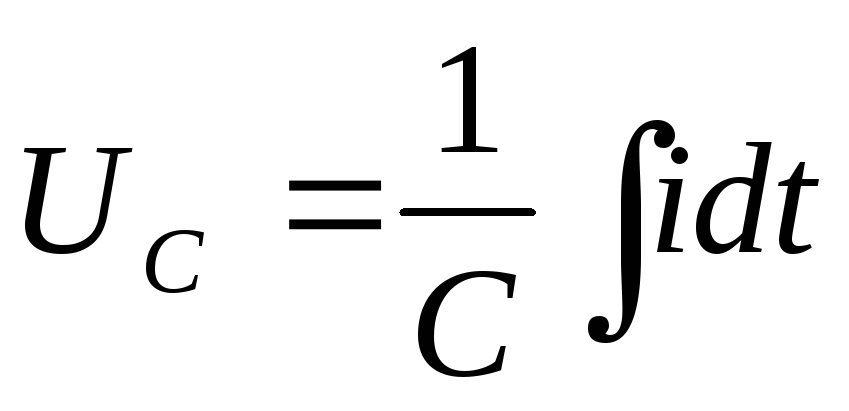Запишем уравнения по второму закону Кирхгоффа:

U₁=U_R+U_C=U_R+U₂

Если активное сопротивление много больше реактивного емкостного сопротивления, то U_C можно пренебречь, так как U₁~U_R=iR, следовательно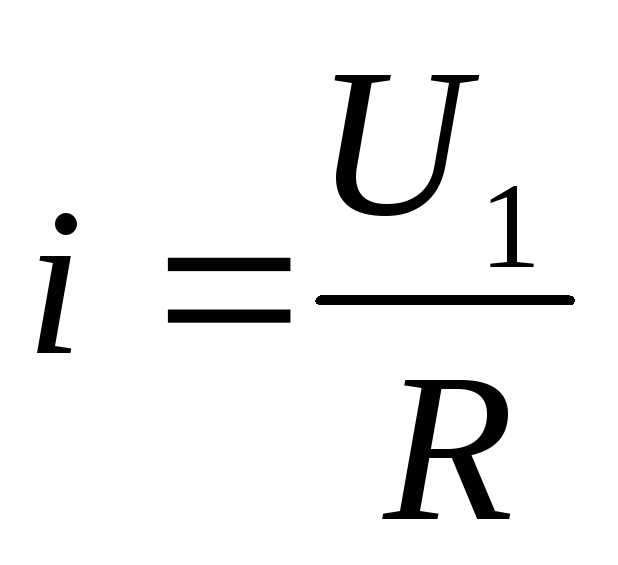

.

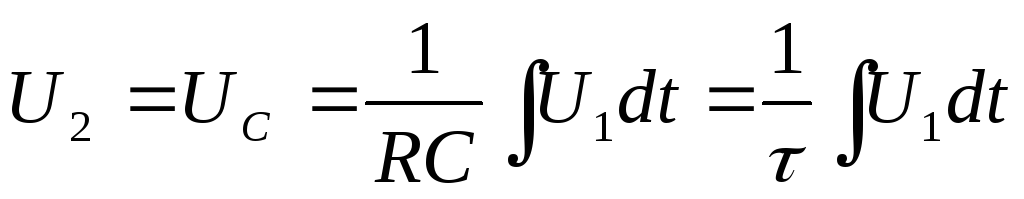Вывод: эта цепь является интегрирующей, при условии, что активное сопротивлении намного больше емкостного.

На практике 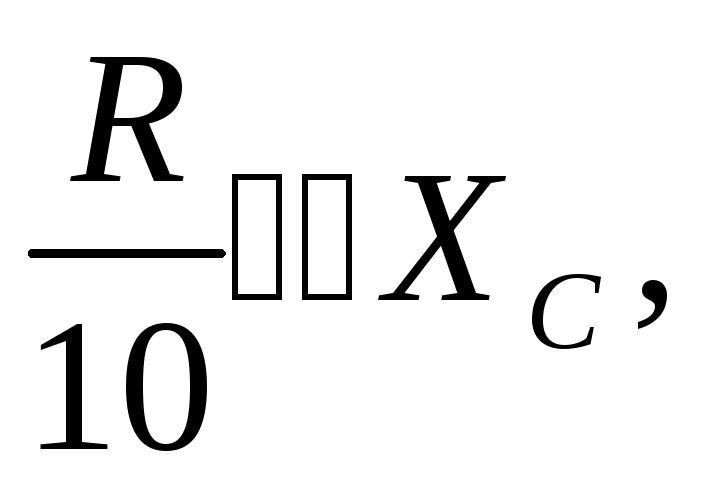k<1, так как U₂ – мало.

R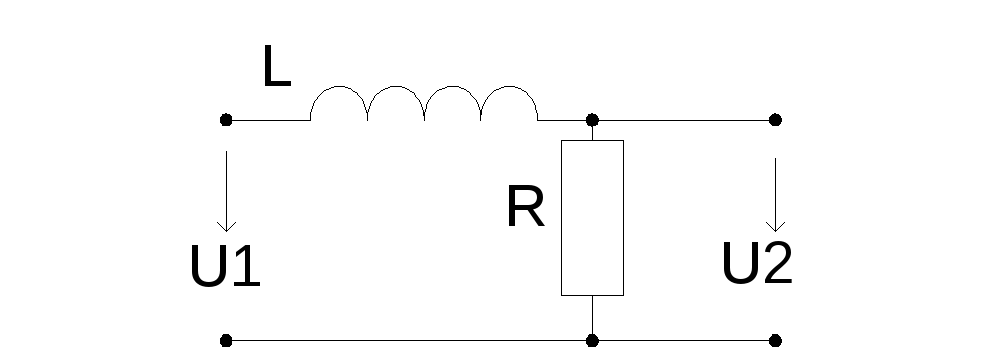L-цепь.

Докажем, что этаdt цепь интегрирующая

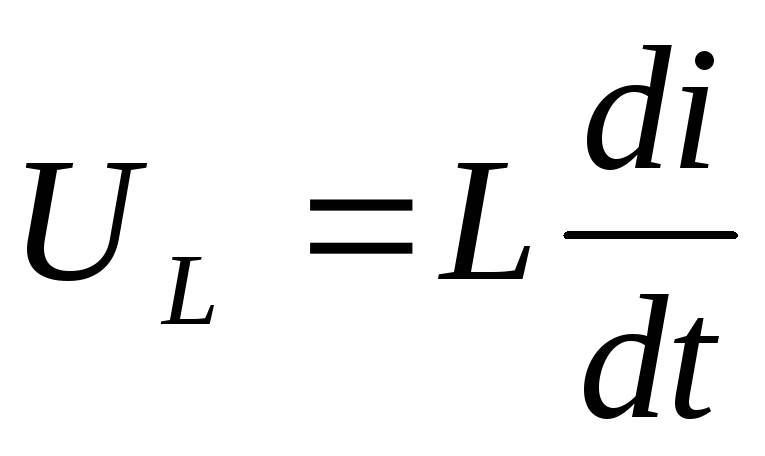, тогда .

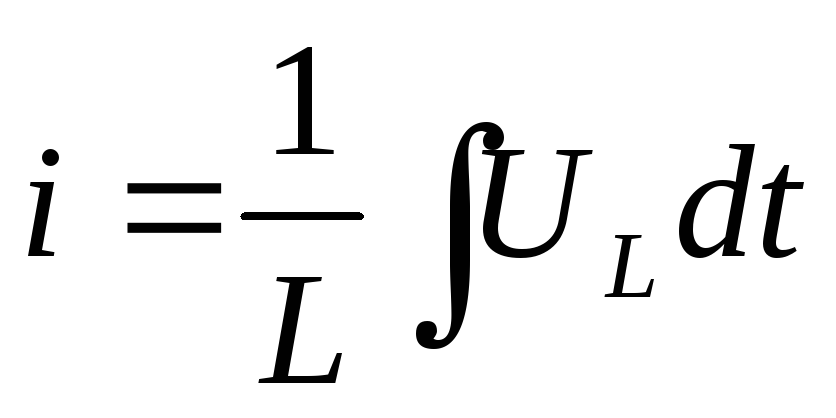Запишем уравнения по второму закону Кирхгоффа:

U₁=U_L+U_R=U_L+U₂

Если R<<X_L, то выходным напряжением можно пренебречь Тогда входное напряжение практически равно индуктивному, следовательно

с другой стороны

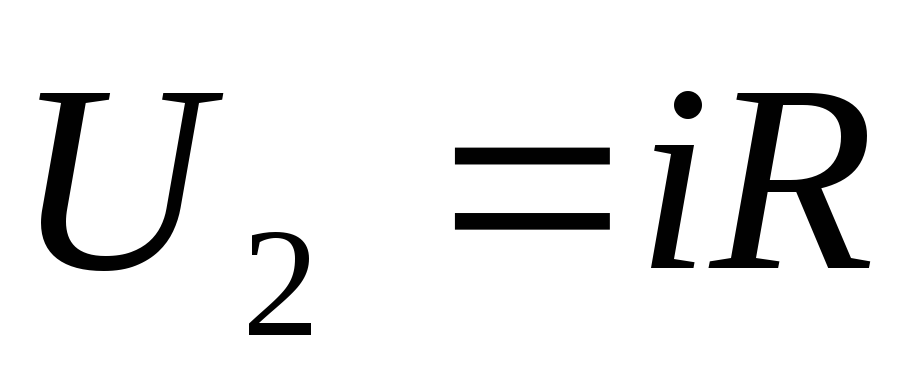, то есть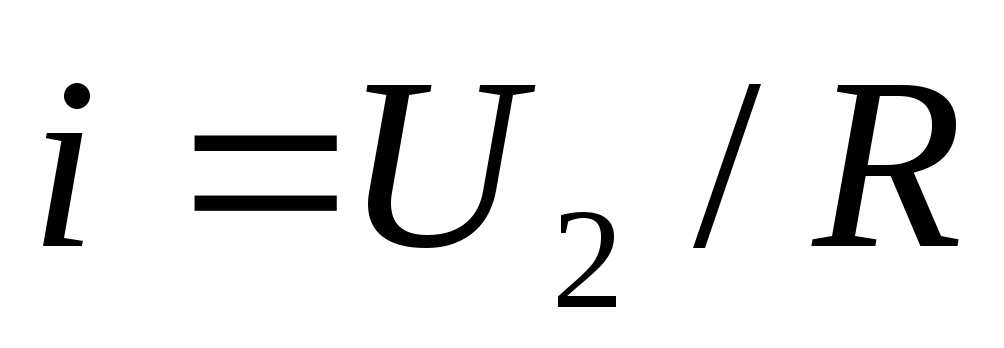

Приравняем значения для тока

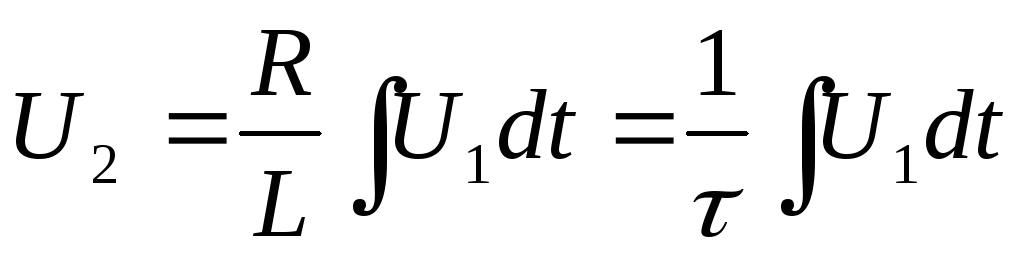
Вывод: данная цепь является интегрирующей при условии, что активное сопрлтивление намного меньше индуктивного.

На практике 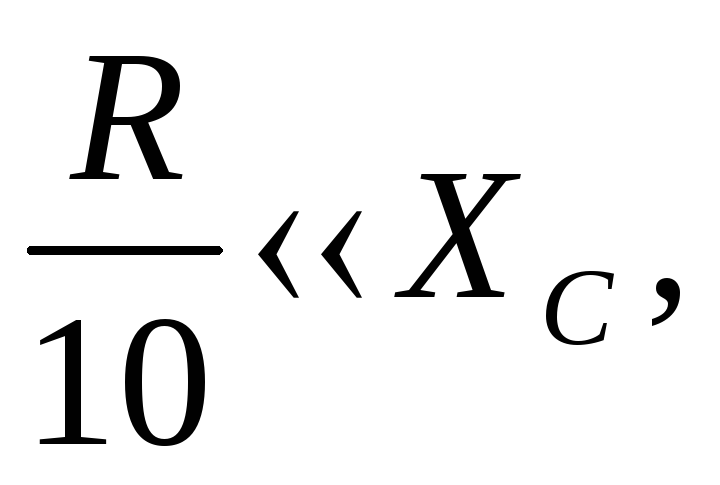k>1.

26. 2 Коэффициент передачи интегрирующей цепи.

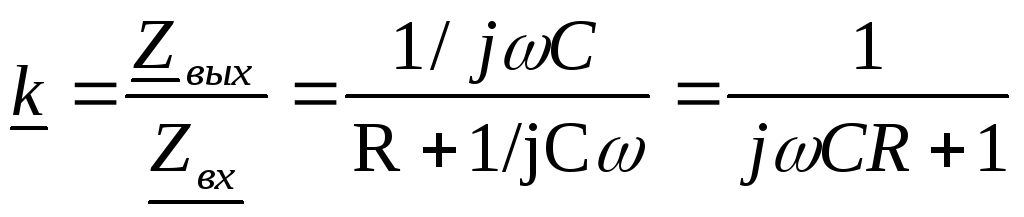
Цепь является интегрирующей, если ее k обратнопропорционально .

26.3 Активные интегрирующие цепи

Недостатком интегрирующих пассивных цепей является маленькое . Активные цепи обеспечивают хорошее качество интегрирования .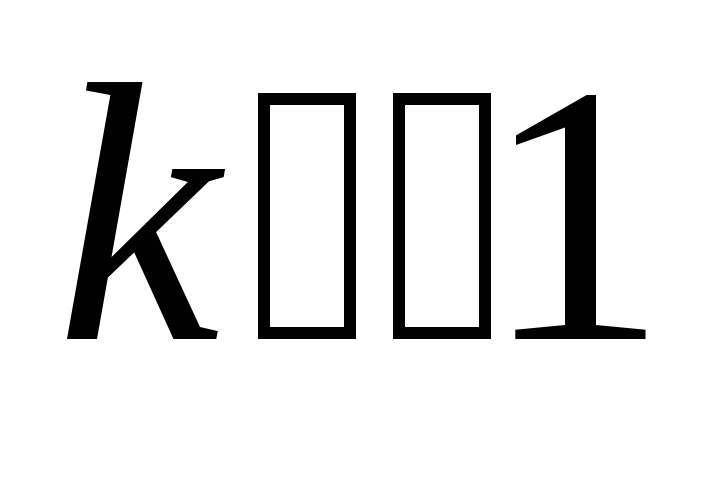

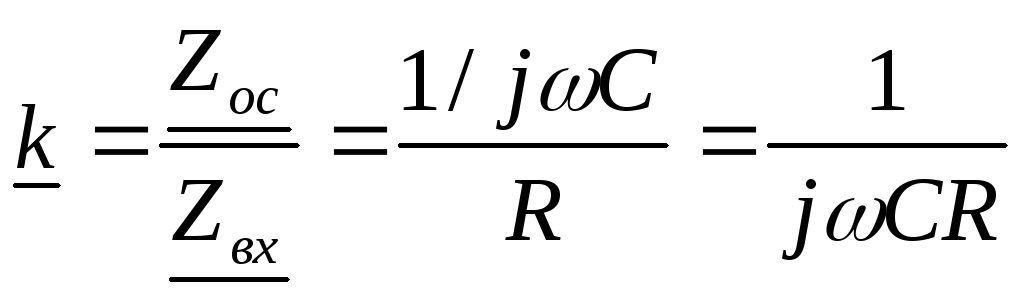, цепь является интегрирующей, так как 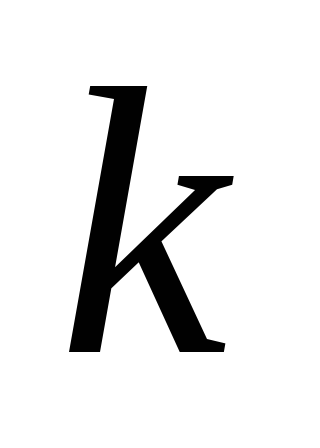обратно пропорционально частоте.

26.4 Форма сигнала на выходе

Интегрирующие цепи применяются как удлиняющие цепи, так как напяжение на выходе больше по длительности напряжения на входе.

— Если напряжение на входе имеет прямоугольную форму, то напряжение на выходе будет треугольником.

— При узких коротких импульсах на входе получается пилообразный сигнал на выходе.

— При косинусодальном сигнале на входе получается синусоидальный сигнал на выходе.

Интегрирующие цепипреобразут сигналы, отличающиеся по длительности в сигналы, отличающися по амплитуде.

При воздействии короткого импульса конденсатор не успевает зарядится, а при воздействии длительного – успевает. За счет этого возникает разница в амплитуде.

На рисунке входной сигнал изображен сплошной линией, а выходной – пунктиром.

5.3. Дифференцирующая и интегрирующая цепи

5.2.2. Временные характеристики

Основными характеристиками линейных цепей во временной области являются импульсная и переходная характеристики. Эти характеристики позволяют определить выходной сигнал для любого входного воздействия, не обращаясь к спектральному представлению сигналов.

Импульсная характеристика цепи h(t)– это реакция цепи на сигнал, опи-

сываемый дельта-функцией (t). Другими словами, выходной сигнал, формируемый линейной цепью при поступлении на ее вход сигнала в виде дельтафункции, является импульсной характеристикой. На практике сигнал в виде дельта-функции – это импульс прямоугольной формы, имеющий большую амплитуду (в пределах линейного участка характеристики цепи) и длительность, которая намного меньше постоянной времени цепи.

Переходная характеристика цепи g(t)– это реакция цепи на сигнал, пред-

ставляющий собой единичный скачок (t). Таким образом, выходной сигнал, формируемый линейной цепью при поступлении на ее вход сигнала в виде резкого перепада, является переходной характеристикой.

Функциональная связь между временными характеристиками h(t) и g(t) обусловлена взаимной зависимостью дельта-функции и единичного скачка (производная и интеграл):

		dg(t)	t
	h(t)		и g(t) h(t)dt.
		dt
			0

Взаимная зависимость частотной и временных характеристик будет рассмотрена ниже.

Анализ линейных цепей с использованием частотных характеристик и анализ с использованием временных характеристик равносильны по результатам. Выбор одного из этих подходов диктуется простотой вычислений, исходными данными в части, касающейся сигналов и цепей, и характером необходимых результатов.

Рассмотрим некоторые линейные цепи и их характеристики.

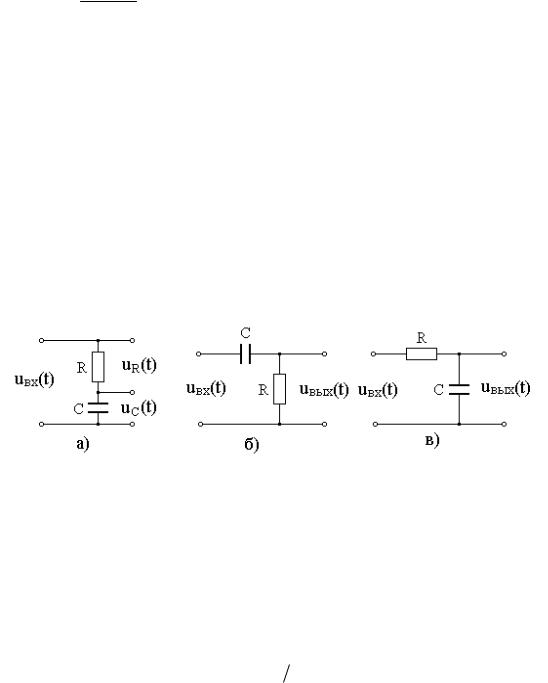
На рис. 5.1,а представлена схема линейного четырехполюсника в виде последовательной RC-цепи с постоянной времени RC. На входе цепи действует напряжение uвх(t), а выходное напряжение uвых(t) может сниматься либо с сопротивления R, либо с конденсатора C. Определим зависимость выходного напряжения от входного для каждого из этих случаев. В соответствии со вторым законом Кирхгофа можно составить уравнение

	uвх(t) Ri(t)	1	i(t)dt, или	Cuвх(t) i(t) i(t)dt.
		C

Выполним анализ данного уравнения при большом и малом значениях .

1. Постоянная времени	– малая величина.
Тогда Cuвх(t) i(t)dt	или i(t) C	duвх	(t)
				.
		dt

В этом случае выходное напряжение, снимаемое с сопротивления R, будет

равно uR(t) duвх(t). Следовательно, если выходное напряжение снимать с dt

сопротивления, то при малых значениях постоянной времени последовательная RC-цепь может дифференцировать входной сигнал.

2. Постоянная времени – большая величина.

Тогда Cu

(t) i(t)

или i(t)

Cuвх(t)

1

u

вх

(t).

вх

R

В этом случае выходное напряжение, снимаемое с конденсатора C, будет

равно uc(t)

1

i(t)dt

1

uвх(t)dt. Следовательно, если выходное напряже-

C

ние снимать с конденсатора, то при больших значениях постоянной времени последовательная RC-цепь может интегрировать входной сигнал.

Схема дифференцирующей цепи представлена на рис. 5.1,б, интегрирующей цепи – на рис. 5.1,в.

Рис. 5.1. Последовательная RC-цепь (а), дифференцирующая (б) и интегрирующая (в) цепи

5.3.1. Дифференцирующая цепь

Определим частотный коэффициент передачи K( j ) дифференцирующей цепи. Комплексная амплитуда тока в цепи определяется законом Ома

Следовательно, комплексная амплитуда выходного напряжения равна

Uвых IR Uвх	j	.
	1 j

Отсюда:

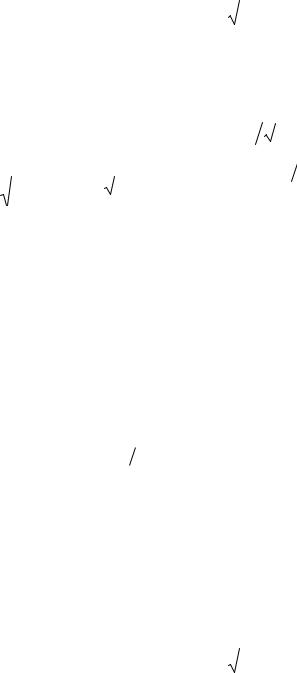
частотный коэффициент передачи K( j )

Uвых

j

;

(5.2)

Uвх

1 j

K( )

амплитудно-частотная характеристика

;

1 2 2

фазочастотная характеристика

( )

arctg .

2

Графики АЧХ и ФЧХ приведены на рис. 5.2,а.

Как следует из графика АЧХ, дифференцирующая цепь является фильтром

верхних частот. Определим частоту среза с

на уровне 1

0,707:

2

K( с)

с

1

;

с2 2 1;

с 1 .

2

2

2

1 с

Для приближения к точному дифференцированию необходимо, чтобы на всех частотах спектра входного сигнала соблюдалось неравенство 1. Тогда K( j ) j – частотная характеристика идеальной дифференцирующей цепи.

5.3.2. Интегрирующая цепь

Определим частотный коэффициент передачи K( j ) интегрирующей цепи. Если комплексная амплитуда тока в цепи равна

I

Uвх

,

R 1

j C

то комплексная амплитуда выходного напряжения равна

1

1

Uвых I

U

вх

1 j

.

j C

Отсюда:

Uвых

K(j )

1

частотный коэффициент передачи

; (5.3)

Uвх

1 j

амплитудно-частотная характеристика

K( )

1

;

1 2 2

фазочастотная характеристика

( ) arctg .

Графики АЧХ и ФЧХ приведены на рис. 5.2,б.

Как следует из графика АЧХ, интегрирующая цепь является фильтром нижних частот. Частота среза также равна 1 .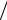

Для приближения к точному интегрированию необходимо, чтобы на всех частотах спектра входного сигнала соблюдалось неравенство 1. Тогда K( j ) 1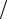 – частотная характеристика идеальной интегрирующей цепи.