Системы счисления

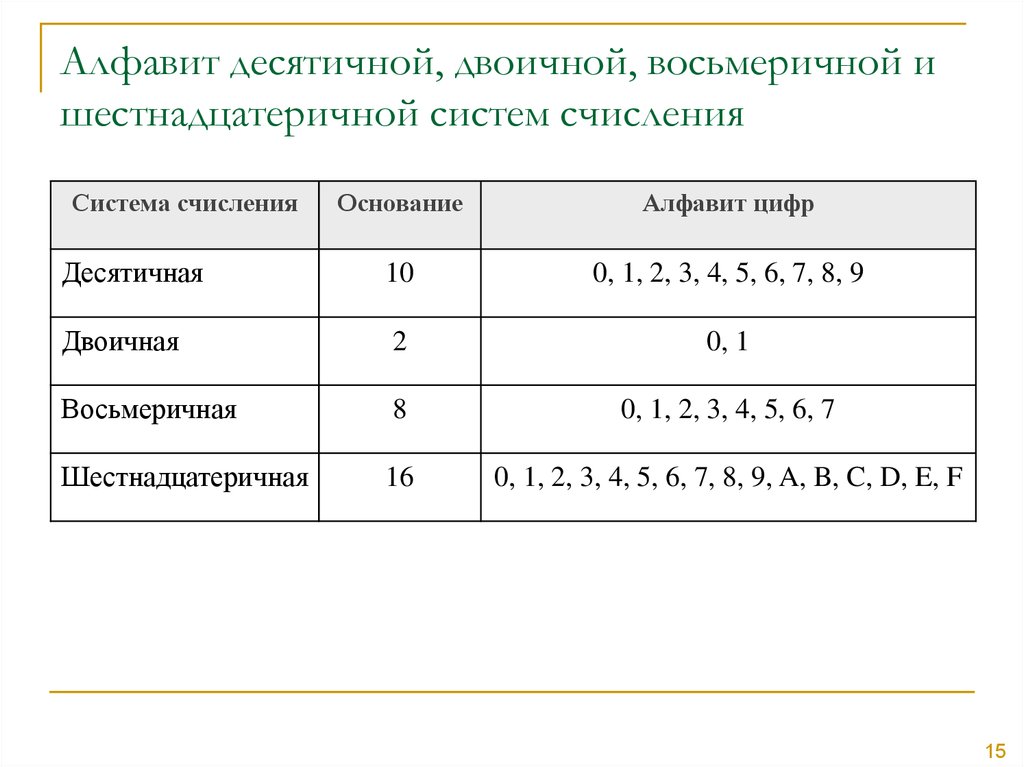
Под системой счисления понимается совокупность приемов и правил представления чисел в виде конечного числа символов. Система счисления имеет свой алфавит – упорядоченный набор символов (цифр) и совокупность операций образования чисел из этих символов. Различают непозиционные и позиционные системы счисления. В позиционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных – не зависит.

Римская непозиционная система счисления. Алфавит включает символы I (1), V (5), X (10), L (50), C (100), D(500), M (1000). Значение числа, представленного в римской системе, определяется как сумма или разность цифр в числе, при этом, если меньшая цифра стоит перед большей цифрой, то она вычитается из последней, если после – прибавляется. Например, десятичное число 1998 в римской системе имеет вид MCMXCVIII. Непозиционные системы сложны и громоздки при записи чисел и мало удобны при выполнении арифметических операций.

Среди позиционных систем наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы. До сих пор используются отголоски 60 –ричной и 12 – ричной систем (в 1 минуте 60 секунд, в 1 часе 60 минут, часто применяется дюжина -12, в круге содержится 30 дюжин градусов, в сутках две дюжины часов, 1 фут равен 12 дюймам и т.д.).

В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Каждая позиционная система характеризуется своим алфавитом цифр и основанием (2, 8, 10, 16). Основание системы равно количеству цифр используемого алфавита. В качестве алфавита берутся последовательные целые числа 0, 1, 2….(p-1). Если система счисления требует использования цифр больших 9, то применяются буквы латинского алфавита (например, в 16- ричной системе это буквы A, B, C, D, E, F). Арифметические действия над числами в системе с любым основанием выполняются по тем же правилам, что и в наиболее привычной для нас десятичной системе, с той только разницей, что надо применять те таблицы сложения и умножения, которые справедливы для данной системы счисления.

Само число в произвольной p — ичной системе счисления (основание системы равно p) представляется в следующем виде

, (1)

при этом число изображается как последовательность цифр , т.е.

.

Целесообразно рассмотреть следующие задачи:

1. Перевод чисел в десятичную систему из других систем (двоичной, восьмеричной, шестнадцатеричной).

Эта задача решается наиболее просто: процедура сводится к вычислению многочлена в правой части (1) в десятичной системе.

Например, .

2. Перевод чисел из десятичной системы в двоичную, восьмеричную, шестнадцатеричную системы.

Перевод целой части числа осуществляется делением этой части числа а основание системы, в которую выполняется перевод, а дробной части – ее умножением на основание системы.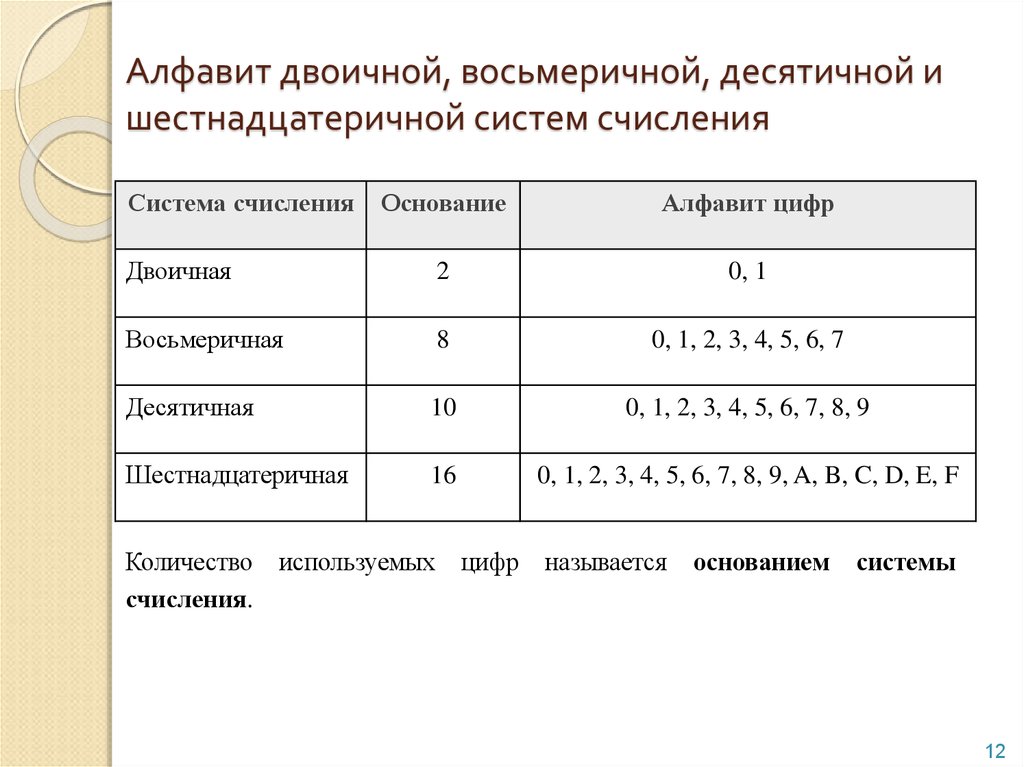 При этом обе операции выполняются в десятичной системе.

Пример 1. Перевести число 23 из десятичной системы в двоичную систему:

23 —22	2
	11 —10	2
1		5 — 4	2
	1		2 — 2	2
		1		1
			0

=10111₂ (собираются остатки от деления на 2 в порядке, обратном их получению).

Пример 2. Перевести число 0.24 из десятичной системы в пятеричную систему:

0.24₁₀ = =0.11₅ (умножается дробная часть числа на основание системы, равное в нашем примере 5, дробная часть полученного произведения снова умножается на 5 и т.д., а затем собираются целые части полученных произведений в порядке их получения).

Пример 3. Перевести число 0.24 из десятичной системы в шестнадцатеричную систему:

0.24₁₀= 0.3D7₁₆

3. Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную системы и обратный перевод.

Эту операцию проводят с использованием триад и тетрад (три и четыре разряда в двоичном представлении числа). Для перевода числа из двоичной системы в восьмеричную число разбивают на триады влево о вправо от запятой, и в случае, когда последняя триада оказывается неполной, она дополняется нулями: для целой части – слева до трех разрядов, а для дробной части – справа.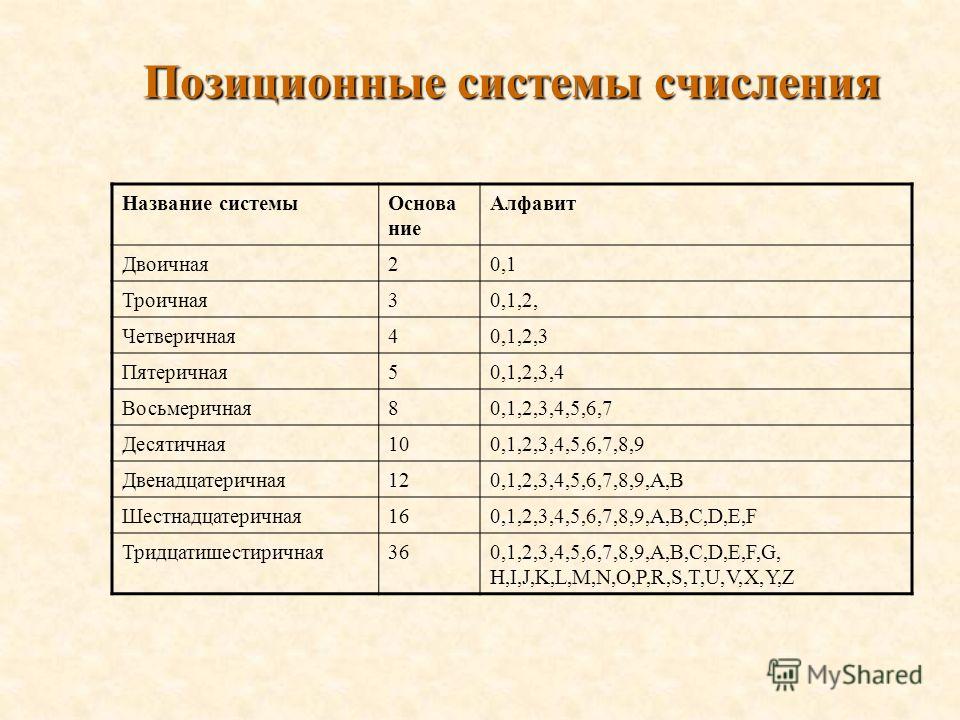

Затем каждая триада заменяется восьмеричной цифрой. Аналогично для перевода числа из двоичной системы в шестнадцатеричную число разбивают на тетрады, и каждая тетрада заменяется шестнадцатеричной цифрой.

Пример 1. Перевести число из двоичной системы в восьмеричную.

10011100,1001₂=010’011’100,100’100₂=234,44₈

Обратный перевод осуществляется заменой каждой цифры триадой или тетрадой.

В задачах индикации данных в десятичном представлении оказывается удобной двоично-десятичная система счисления. В этой системе десятичные цифры от 0 до 9 представляются двоичными комбинациями от 0000 до 1001.

При работе с отрицательными числами удобна двоичная дополнительная или обратная арифметика.

В современной вычислительной технике используется в основном двоичная система счисления. Ее главное преимущество состоит в том, что практическая реализация устройств, построенных на базе этой системе, возможно при использовании технических устройств лишь с двумя устойчивыми состояниями (материал намагничен или размагничен, заряд есть или нет, отверстие есть или нет и т.

д.). В результате обеспечивается высокая надежность, помехоустойчивость систем, появляется возможность применять хорошо разработанный аппарат булевой алгебры и существенно упрощается выполнение арифметических операций. Главный недостаток двоичной системы — большое число разрядов при записи больших чисел.

Следует отметить, что с точки зрения построения кодов для устройств передачи, хранения и преобразования данных наиболее экономичной является система счисления с основанием 3. При этом произведение количества различных символов в алфавите системы и количества разрядов оказывается минимальным.

Системы счисления

     

Лабораторная  работа №7

     

Тема: «Системы счисления»

 

      Цель  работы: Рассмотреть позиционные системы счисления, а также получить навыки по представлению числовых данных в различных системах счисления.  

   Порядок выполнения работы

1. Изучить общие понятия, лежащие в основе систем счисления: алфавит, основание.
2. Освоить правила перевода чисел из одной системы счисления в другую, а также правила выполнения арифметических операций с двоичными числами.
3. Получить навыки представления чисел в машинных двоичных кодах.

     

Теоретическая часть

     Под системой счисления понимается определенный способ записи числа с помощью некоторого алфавита символов a₁, a₂,…, a_n. При этом каждой цифре a_i в записи числа ставится в соответствие определенное количественное значение.

Системы счисления
Непозиционная	Каждый символ сохраняет свое количественное значение при изменении его положения в числе.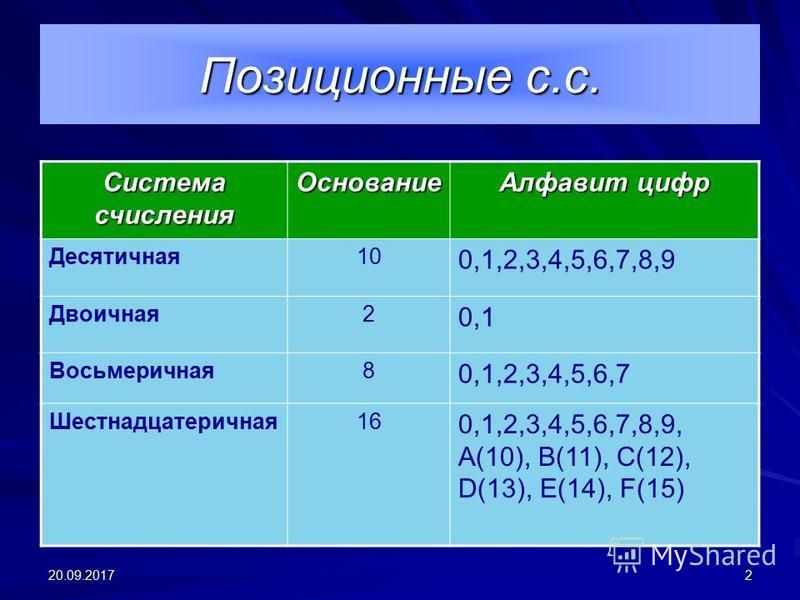 Примером такой системы является римская система счисления.
Позиционная	Количественное  значение каждой цифры (символа) зависит  от ее местоположения в числе.

     Количество  цифр, используемых для изображения  числа в позиционной системе  счисления, называется основанием системы счисления (S).

     Любое число A в позиционной системе счисления может быть представлено в виде суммы коэффициентов a_i из алфавита данной системы умноженных на степени основания S системы счисления:

     A_S=a_na_n-1a_n-2…a₂a₁a₀,a_-1a_-2…a_—m=

    =a_n*Sⁿ + a_n-1*S^n-1 + a_n-2*S^n-2 + …a₂*S² + a₁*S¹ + a₀*S⁰ +a_-1*S^-1 + a_-2*S^-2 + … + a_-m*S^-m.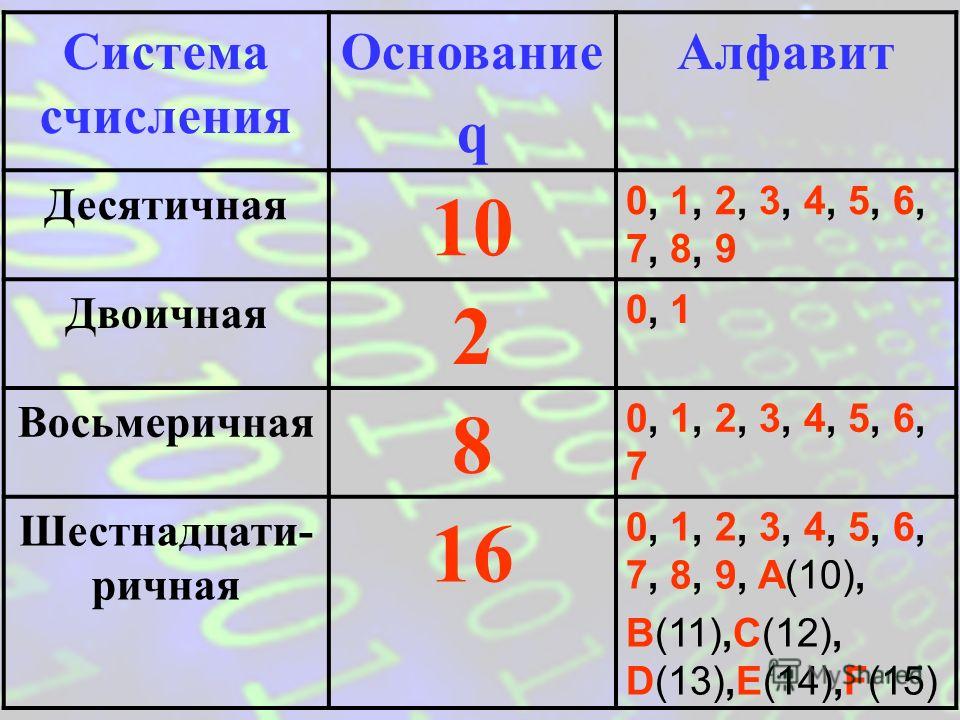

Таблица 1

Алфавит основных систем счисления

Система счисления	Основание (S)	Цифры
Двоичная	2	0,1
Троичная	3	0, 1, 2
Четверичная	4	0, 1, 2, 3
Пятеричная	5	0, 1, 2, 3, 4
Восьмеричная	8	0, 1, 2, 3, 4, 5, 6, 7
Десятичная	10	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Шестнадцатеричная	16	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

 

     В математике для записи числа используется десятичная система счисления (S=10), ее алфавит состоит из десяти арабских цифр 0, 1, 2,…, 9. Любое число в этой системе счисления можно представить следующим образом:

     A₁₀=a_n*10ⁿ + a₁*10¹ + a₀*10⁰+a_-1*10^-1 … + a_-m*10^-m_.

     Например, 32,19₁₀=3·10¹+2·10⁰+1·10^-1+9·10^-2.

     В аппаратной основе вычислительной техники  для физического представления  чисел, предназначенных для обработки, используются двухпозиционные элементы, которые могут находиться только в одном из устойчивых состояний. Одно из этих состояний обозначает цифру 0, а другое – цифру 1. Поэтому наибольшее распространение в ЭВМ получила двоичная система счисления, основание которой S=2. Ее алфавит состоит из двух цифр 0 и 1.

Например, двоичное число

10011,01=1·2⁴+0·2³+0·2²+1·2¹+1·2⁰+0·2^-1+1·2^-2=16+2+1+0,25=19,25₁₀

соответствует десятичному числу 19,25₁₀.

Таблица 2

Правила двоичного сложения, вычитания и умножения

сложение	вычитание	умножение
0+0=0	0-0=0	0·0=0
0+1=1	1-0=1	0·1=0
1+0=1	1-1=0	1·0=0
1+1=10	10-1=1	1·1=1

 

     Для более компактной записи чисел обычно используются восьмеричная и шестнадцатеричная системы счисления. Поэтому большое практическое значение имеют процедуры перевода из одной системы счисления в другую. 

Правила перевода из одной  позиционной системы в другую
1. Перевод целого числа из десятичной системы счисления в систему счисления с основанием Q	осуществляется  последовательным делением данного  числа на основание Q, до тех пор, пока частное не станет равным нулю. Число в новой системе (S=Q) будет представлено в виде остатков от деления, записанных начиная с последнего.      Например, десятичное число 2210 запишется в двоичной системе следующим образом          Остаток      22:2 = 11        (0)      11:2 = 5        (1)      5:2 = 2         (1)      2:2 = 1         (0)      1:2 = 0         (1)             2210=101102.
2. Перевод правильной дроби из десятичной системы счисления в другую систему с основанием Q	осуществляется  последовательным умножением ее на основание новой системы счисления. Целая часть полученного числа будет первой цифрой после запятой. Дробную же часть необходимо вновь умножить на Q. Целая часть полученного числа будет следующей цифрой и т. д.
3. Для  перевода неправильных дробей в новую систему счисления	необходимо, с  помощью рассмотренных выше правил 1 и 2, отдельно выполнить перевод целой и дробной части.
4. Перевод чисел в десятичную систему счисления	осуществляется  путем составления степенного ряда с основанием той системы счисления, из которой это число переводится.

 

     В восьмеричной системе счисления (S=8) используется восемь цифр 0,1,…,7. Например, переведем число из восьмеричной системы счисления 237,4₈ в десятеричную систему счисления

     237,4₈=2·8² + 3·8¹ + 7·8⁰ + 4·8^-1 = 128+24+7+0,5=159,5₁₀.

     Переведем число из десятичной системы счисления  75,59₁₀ в восьмеричную систему счисления

                       Остаток

      75:8 = 9        (3)

     9:8 = 1         (1)

     1:8 = 0         (1) 

     0,59·8 = 4,72;

     0,72·8 = 5,76;

     0,76·8 = 6,08, …

     Таким образом, 75,59₁₀ = 113,456₈ 

     В шестнадцатеричной системе счисления алфавит состоит из 16 цифр, где первые десять символов обозначаются цифрами от 0 до 9, а далее используются буквенные обозначения: 10 – A, 11 – B, 12 – C, 13 – D, 14 – E, 15 – F. Предложенный алфавит позволяет записать все десятичные цифры от 0 до 15, остальные цифры представляются следующим образом: 

                  Остаток    Остаток            Остаток

           16:16 = 1      (0)            17:16 = 1      (1)       18:16 = 1        (2)

            1:16 = 0      (1)             1:16 = 1      (1)        1:16 = 0          (1) 

16₁₀=10₁₆ = 1·16¹+0·16⁰; 17₁₀=11₁₆ = 1·16¹+1·16⁰; 18₁₀=12₁₆ = 1·16¹+2·16⁰.  

     Существует  также способ взаимного перевода чисел из восьмеричной и шестнадцатеричной системы счисления в двоичную систему счисления, благодаря использованию таблицы соответствия чисел в двоичной, восьмеричной и шестнадцатеричной системах счисления (Табл.3).

Таблица 3

Соответствие чисел в двоичной, восьмеричной и

  шестнадцатеричной  системах счисления

Двоичная  (S=2)	Восьмеричная  (S=8)		Шестнадцатеричная  (S=16)
		триады		тетрады
0  1	0  1  2  3  4  5  6  7	000  001  010  011  100  101  110  111	0  1  2  3  4  5  6  7  8  9  A  B  C  D  E  F	0000  0001  0010  0011  0100  0101  0110  0111  1000  1001  1010  1011  1100  1101  1110  1111

 

     Например, переведем число 162,37₈ из восьмеричной системы счисления в двоичную и шестнадцатеричную системы счисления

     162,37₈ = 001 110 010, 011 111 ₂,

                    1    6     2      3     7

     0111 0010, 0111 1100 ₂ = 72,7C₁₆

        7       2        7       C

     Получаем, 162,37₈ = 1110010,011111₂ = 72,7C₁₆ 

     Для выполнения арифметических операций над  числами в ЭВМ используют специальные машинные коды: прямой, обратный и дополнительный.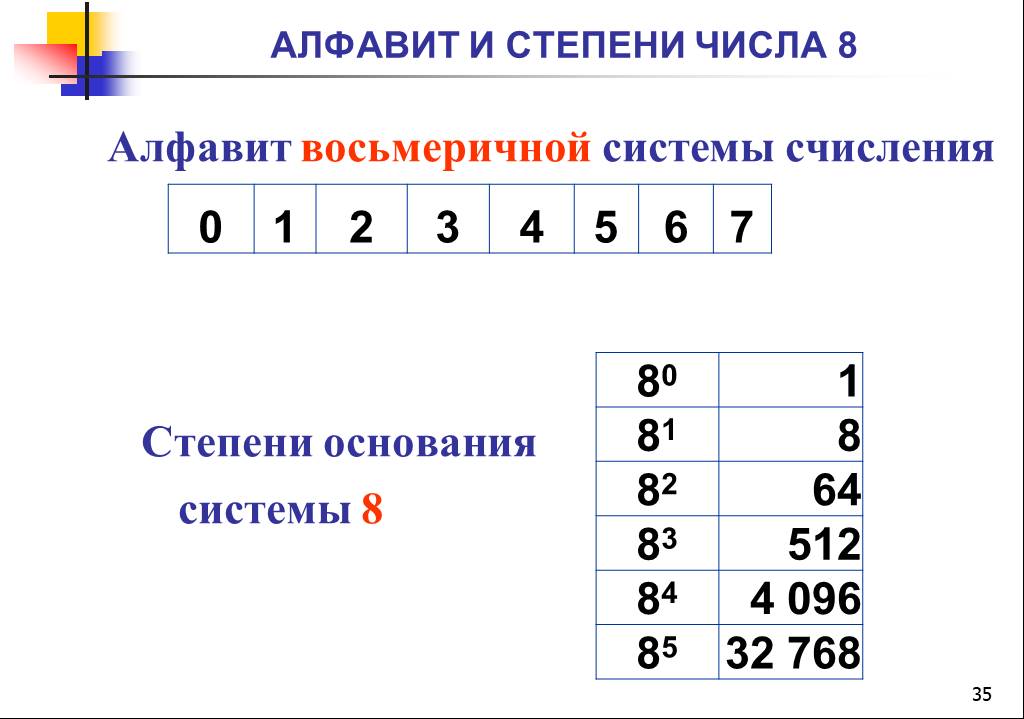 Применение машинных кодов сводит операцию вычитания к алгебраическому суммированию кодов этих чисел, упрощается определение знака результата операции.

     В данных машинных кодах перед старшим  цифровым разрядом располагается знаковый разряд, в котором записывается нуль для положительного числа и единица для отрицательного числа. В дальнейшем при написании машинных кодов будем отделять знаковый разряд от цифровых разрядов точкой.

     Прямой  код двоичного числа содержит цифровые разряды, перед которыми записан знаковый разряд. Прямой код используется для представления отрицательных чисел в запоминающем устройстве ЭВМ.

     Например, для двоичных чисел x = +1010₂ и y = -1101₂ их прямые коды будут иметь следующий вид:

     x_пр = 0.1010₂ и y_пр = 1.1101₂.

     Обратный  код положительного числа полностью совпадает с его прямым кодом. Для отрицательного числа он содержит единицу в знаковом разряде, а значащие цифровые разряды числа заменяются на инверсные, то есть единицы заменяются нулями, а нули – единицами.

     Таким образом, для приведенного выше примера  имеем:

     x_обр = x_пр = 0.1010₂ и y_обр = 1.0010₂.

     Дополнительный  код положительного числа полностью совпадает с прямым кодом, а следовательно и с обратным. Для отрицательного числа он образуется из обратного путем прибавления к нему единицы к младшему цифровому разряду.

     Следовательно, получаем:

     x_доп = x_обр = x_пр = 0.1010₂ и y_доп = 1.0011₂. 

 

     

Практическая работа

     Задание 1. Переведите число из указанной системы счисления (см. вариант) в десятичную систему счисления.

Варианты	Задание	Варианты	Задание
1.	242,38	2.	A2F,C16
3.	161,28	4.	12B,816
5.	146,28	6.	22C,816
7.	103,248	8.	172,28
9.	11D,416	10.	12F,816
11.	214,48	12.	22D,316

 

     Задание 2. Переведите число (см. вариант) из десятичной системы счисления в двоичную систему счисления с точностью 3 знака после запятой.

Варианты	Задание	Варианты	Задание
1.	51,7610	2.	57,4910
3.	39,5410	4.	64,510
5.	56,4210	6.	61,2910
7.	47,2910	8.	54,6110
9.	45,3110	10.	65,5210
11.	36,7410	12.	66,3610

Греческий алфавит

Греческий алфавит происходит от финикийского алфавита и использовался для письма на греческом языке с 8 века до н.э.

Приведенную ниже таблицу можно использовать для поиска правильных символов или кодов для представления греческого алфавита в HTML-документах или подобных документах.

Добавление выражений Entity, Decimal или Hex непосредственно в html-код отобразит письмо в веб-браузере, как показано в ¹⁾ .

Форматирование обычного символа как «Symbol font» отобразит символ, как показано на ²⁾ .

Внимание! Не все браузеры могут правильно отображать коды и шрифты.

229888. 0059 rho 9¹⁹

The Greek Alphabet
Character	Entity	Decimal	Hex	Rendering in Your Browser 1)			Rendering with the Symbol Font 2)
				Entity	Десятичный	Шестнадцатеричный	Обычный шрифт	Символьный шрифт
Greek capital letter alpha	Α	Α	Α	Α	Α	Α	A	A
Greek capital letter beta	β	β	β	β	β	β	B	B
GREEK GEAT gamma	Γ	Γ	Γ	Γ	Γ	Γ	G	G
Greek capital letter delta	Δ	Δ	Δ	Δ	Δ	Δ	D	D
Greek capital letter epsilon	Ε	Ε	Ε	Ε	Ε	Ε	E	E
Greek capital letter zeta	Ζ	Ζ	Ζ	Ζ	Ζ	Ζ	Z	Z
Greek capital letter eta	Η	Η	Η	Η	Η	Η	H	H
Greek capital letter theta	Θ	Θ	Θ	Θ	Θ	Θ	Q	Q
Greek capital letter iota	Ι	Ι	Ι	Ι	Ι	Ι	I	I
Greek capital letter kappa	Κ	Κ	Κ	Κ	Κ	Κ	K	K
Greek capital letter lambda	Λ	Λ	Λ	Λ	Λ	Λ	L	L
Greek capital letter mu	Μ	Μ	Μ	Μ	Μ	Μ	M	M
Greek capital letter nu	Ν	Ν	Ν	Ν	Ν	Ν	N	N
Greek capital letter xi	Ξ	Ξ	Ξ	Ξ	Ξ	Ξ	X	X
Greek capital letter omicron	Ο	Ο	Ο	Ο	Ο	Ο	O	O
Greek capital letter PI	π	π	π	π	π	π	P	P
P	P
P	P
Ρ	Ρ	Ρ	Ρ	Ρ	Ρ	R	R
Greek capital letter sigma	Σ	Σ	Σ	Σ	Σ	Σ	S	S
Greek capital letter tau	Τ	Τ	Τ	Τ	Τ	Τ	T	T
Greek capital letter upsilon	Υ	Υ	Υ	Υ	Υ	Υ	U	U
Greek capital letter phi	Φ	Φ	Φ	Φ	Φ	Φ	F	F
Greek capital letter chi	Χ	Χ	Χ	Χ	Χ	Χ	C	C
Greek capital letter psi	Ψ	Ψ	Ψ	Ψ	Ψ	Ψ	Y	Y
Greek capital letter omega	Ω	Ω	Ω	Ω	Ω	Ω	W	W
Greek small letter alpha	α	α	α	α	α	α	a	a
Greek small letter beta	β	β	β	β	β	β	b	b
Greek small letter gamma	γ	γ	γ	γ	γ	γ	g	g
Greek small letter delta	δ	δ	δ	δ	δ	δ	d	d
Greek small letter epsilon	ε	ε	ε	ε	ε	ε	e	e
Greek small letter zeta	ζ	ζ	ζ	ζ	ζ	ζ	z	z
Greek small letter eta	η	η	η	η	η	η	h	h
Greek small letter theta	θ	θ	θ	θ	θ	θ	q	q
Greek small letter iota	ι	ι	ι	ι	ι	ι	i	i
Greek small letter kappa	κ	κ	κ	κ	κ	κ	k	k
Greek small letter lambda	λ	λ	λ	λ	λ	λ	l	l
Greek small letter mu	μ	μ	μ	μ	μ	μ	m	m
Greek small letter Nu	ν	ν	ν	ν	ν	ν	NA	N
NA	N
	N
				. xi	ξ	ξ	ξ	ξ	ξ	ξ	x	x
Greek small letter omicron	ο	ο	ο	ο	ο	ο	o	o
Greek small letter pi	π	π	π	π	π	π	p	p
Greek small letter rho	ρ	ρ	ρ	ρ	ρ	ρ	r	r
Greek small letter final sigma	ς	ς	ς	ς	ς	ς	z	z
Greek small letter sigma	σ	σ	σ	σ	σ	σ	s	s
Greek small letter tau	τ	τ	τ	τ	τ	τ	T	T
T	T
T	T
0015 upsilon	υ	υ	υ	υ	υ	υ	u	u
Greek small letter phi	φ	φ	φ	φ	φ	φ	j	j
Greek small letter chi	χ	χ	χ	χ	χ	χ	c	c
Greek small letter psi	ψ	ψ	ψ	ψ	ψ	ψ	y	y
Greek small letter omega	ω	ω	ω	ω	ω	ω	w	w

Scientific and Engineering use of the Greek Alphabet

Character	Symbol	Typically Used For
			Greek small letter alpha	α	Углы, угловое ускорение
Строчная греческая буква бета	β	Углы, коэффициенты
Greek small letter gamma	γ	Shear strain, kinematic viscosity
Greek small letter delta	δ	Differences, damping coefficient
Greek small letter epsilon	ε	Линейная деформация
Строчная греческая буква дзета	ζ
Строчная греческая буква eta	η	Dynamic viscosity, efficiency
Greek small letter theta	θ	Angles, temperature
Greek small letter iota	ι
Строчная греческая буква каппа	κ	Сжимаемость жидкостей
Строчная греческая буква лямбда	λ	Wavelength, thermal conductivity
Greek small letter mu	μ	Coefficient of friction, dynamic viscosity, Poisson’s ratio
Greek small letter nu	ν	Кинематическая вязкость
Строчная греческая буква xi	ξ
Строчная греческая буква omicron	ο
Greek small letter pi	π	Mathematical constant
Greek small letter rho	ρ	Density
Greek small letter final сигма	ς
Строчная греческая буква сигма	σ	Нормальное напряжение, стандартное отклонение
Greek small letter tau	τ	Shear stress
Greek small letter upsilon	υ
Greek small letter phi	φ	Angles , расход, потенциальная энергия
Строчная греческая буква хи	χ
Строчная греческая буква psi	ψ	Gears helix angle
Greek small letter omega	ω	Angular velocity, solid angle

HTML 4.

0 Entities for Symbols and Greek Letters.

Латинская маленькая f с крючком = функция = флорин	ƒ	ƒ	ƒ	ƒ	№	ƒ
Греческая заглавная буква альфа	&Альфа;	Α	Α	А	А	А
Заглавная греческая буква бета	&Бета;	Β	Β	Б	Б	Б
Греческая заглавная буква гамма	&Гамма;	Γ	Γ	Г	Г	Г
Заглавная греческая буква дельта	&Дельта;	Δ	Δ	Δ	Δ	Δ
Греческая заглавная буква эпсилон	&Эпсилон;	Ε	Ε	Ε	Ε	Ε
Заглавная греческая буква дзета	&Зета;	Ζ	Ζ	Ζ	Ζ	Ζ
Греческая заглавная буква эта	&Эта;	Η	Η	Х	Х	Х
Греческая заглавная буква тета	&Тета;	Θ	Θ	Θ	Θ	Θ
Заглавная греческая буква йота	&Йота;	Ι	Ι	Ι	Ι	Ι
Греческая заглавная буква каппа	&Каппа;	Κ	Κ	К	К	К
Заглавная греческая буква лямбда	&лямбда;	Λ	Λ	Λ	Λ	Λ
Заглавная греческая буква мю	&Мю;	Μ	Μ	М	М	М
Греческая заглавная буква ню	Ν	Ν	Ν	Ν	Ν	Ν
Заглавная греческая буква xi	Ξ	Ξ	Ξ	Ξ	Ξ	Ξ
Греческая заглавная буква омикрон	&Омикрон;	Ο	Ο	О	О	О
Греческая заглавная буква пи	&Пи;	Π	Π	Π	Π	Π
Греческая заглавная буква ро	&Ро;	Ρ	Ρ
Греческая заглавная буква сигма	&Сигма;	Σ	Σ	Σ	Σ	Σ
Греческая заглавная буква тау	&Тау;	Τ	Τ	Т	Т	Т
Греческая заглавная буква ипсилон	&Ипсилон;	Υ	Υ	Υ	Υ	Υ
Греческая заглавная буква фи	Φ	Φ	Φ	Ф	Ф	Ф
Греческая заглавная буква хи	&Чи;	Χ	Χ	х	х	х
Заглавная греческая буква psi	Ψ	Ψ	Ψ	Ψ	Ψ	Ψ
Греческая заглавная буква омега	&Омега;	Ω	Ω	Ом	Ом	Ом
Строчная греческая буква альфа	&альфа;	α	α	α	α	α
Строчная греческая буква бета	&бета;	β	β	β	β	β
Строчная греческая буква гамма	γ	γ	γ	γ	γ	γ
Строчная греческая буква дельта	&дельта;	δ	δ	δ	δ	дельта
Строчная греческая буква эпсилон	&эпсилон;	ε	ε	ε	ε	ε
Строчная греческая буква дзета	&дзета;	ζ	ζ	ζ	ζ	ζ
Строчная греческая буква эта	&эта;	η	η	η	η	η
Строчная греческая буква тета	&тета;	θ	θ	θ	θ	θ
Строчная греческая буква йота	ι	ι	ι	и	и	и
Строчная греческая буква каппа	&каппа;	κ	κ	κ	κ	κ
Строчная греческая буква лямбда	&лямбда;	λ	λ	λ	λ	λ
Строчная греческая буква мю	мкм;	μ	μ	мк	мк	мк
Строчная греческая буква ню	ν	ν	ν	ν	ν	ν
Строчная греческая буква xi	ξ	ξ	ξ	ξ	ξ	ξ
Строчная греческая буква омикрон	&омикрон;	ο	ο	или	или	или
Строчная греческая буква пи	π	π	π	номер	№	№
Строчная греческая буква ро	ρ	ρ	ρ	р	р	р
Строчная греческая последняя сигма	&сигмаф;	ς	ς	ς	ς	ς
Строчная греческая сигма	&сигма;	σ	σ	σ	σ	σ
Строчная греческая буква тау	&тау;	τ	τ	т	т	т
Строчная греческая буква ипсилон	υ	υ	υ	х	х	х
Строчная греческая буква фи	φ	φ	φ	φ	φ	φ
Строчная греческая буква хи	&чи;	χ	χ	х	х	х
Строчная греческая буква psi	фунтов на квадратный дюйм;	ψ	ψ	ψ	ψ	ψ
Строчная греческая буква омега	&омега;	ω	ω	ω	ω	ω
Строчная греческая буква тета	&тетасимвол;	ϑ	ϑ	ϑ	ϑ	ϑ
Греческий ипсилон с символом крючка	ϒ	ϒ	ϒ	ϒ	ϒ	ϒ
Греческий символ пи	ϖ	ϖ	ϖ	ϖ	ϖ	ϖ
пуля = черный маленький кружок	&бык;	•	•	•	•	•
горизонтальное многоточие = выноска из трех точек	…	…	…	…	…	…
штрих = минуты = футы	′	′	′	′	′	′
двойной штрих = секунды = дюймы	&Прайм;	″	″	″	″	″
надчеркивание = отступ над чертой	&олайн;	‾	‾	‾	‾	‾
косая черта дроби	⁄	⁄	⁄	⁄	⁄	⁄
заглавная буква P = набор мощности = Weierstrass p	℘	℘	℘	℘	℘	℘
заглавная буква I = мнимая часть	&изображение;	ℑ	ℑ	ℑ	ℑ	ℑ
заглавная буква R = символ реальной части	&реальный;	ℜ	ℜ	ℜ	ℜ	ℜ
товарный знак	&торговля;	™	™	™	™	™
символ алеф = первый трансфинитный кардинал	ℵ	ℵ	ℵ	ℵ	ℵ	ℵ
стрелка влево	←	←	←	←	←	←
стрелка вверх	↑	↑	↑	↑	↑	↑
стрелка вправо	→	→	→	→	→	→
стрелка вниз	↓	↓	↓	↓	↓	↓
стрелка влево вправо	↔	↔	↔	↔	↔	↔
стрелка вниз с углом влево = возврат каретки	↵	↵	↵	↵	↵	↵
двойная стрелка влево	⇐	⇐	⇐	⇐	⇐	⇐
двойная стрелка вверх	⇑	⇑	⇑	⇑	⇑	⇑
двойная стрелка вправо	⇒	⇒	⇒	⇒