Делитель напряжения на резисторах ⋆ diodov.net
Рассмотрим, как рассчитать практически любой делитель напряжения на резисторах. Преимущественное большинство радиоэлектронных элементов и микросхем питаются относительно низким напряжением – 3…5 В. А многие блоки питания выдают U = 9 В, 12 В или 24 В. Поэтому для надежной и стабильной работы различных электронных элементов необходимо снижать величину напряжения до приемлемого уровня. В противном случае может наступить пробой радиоэлектронных элементов. Особенно следует уделять внимание микросхемам – наиболее чувствительным элементам к повышенному напряжению.
Существуют много способов, как снизить напряжение. Выбор того или другого способа зависит от конкретной задачи, что в целом определяет эффективность всего устройства. Мы рассмотрим самый простой способ – делитель напряжения на резисторах, который, тем не менее, довольно часто применяется на практике, но исключительно в маломощных цепях, что поясняется далее.
Расчет делителя напряжения на резисторах
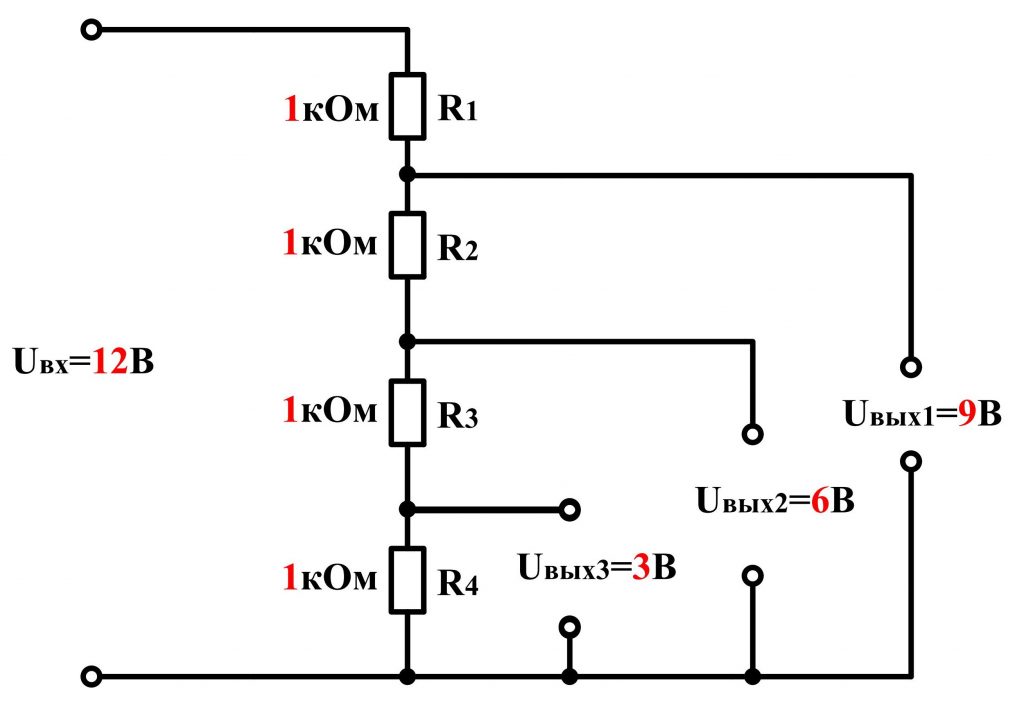
Чтобы сделать и рассчитать простейший делитель напряжения достаточно соединить последовательно два резистора и подключить их источнику питания. Такая схема очень распространенная и применяется более чем в 90 % случаев.
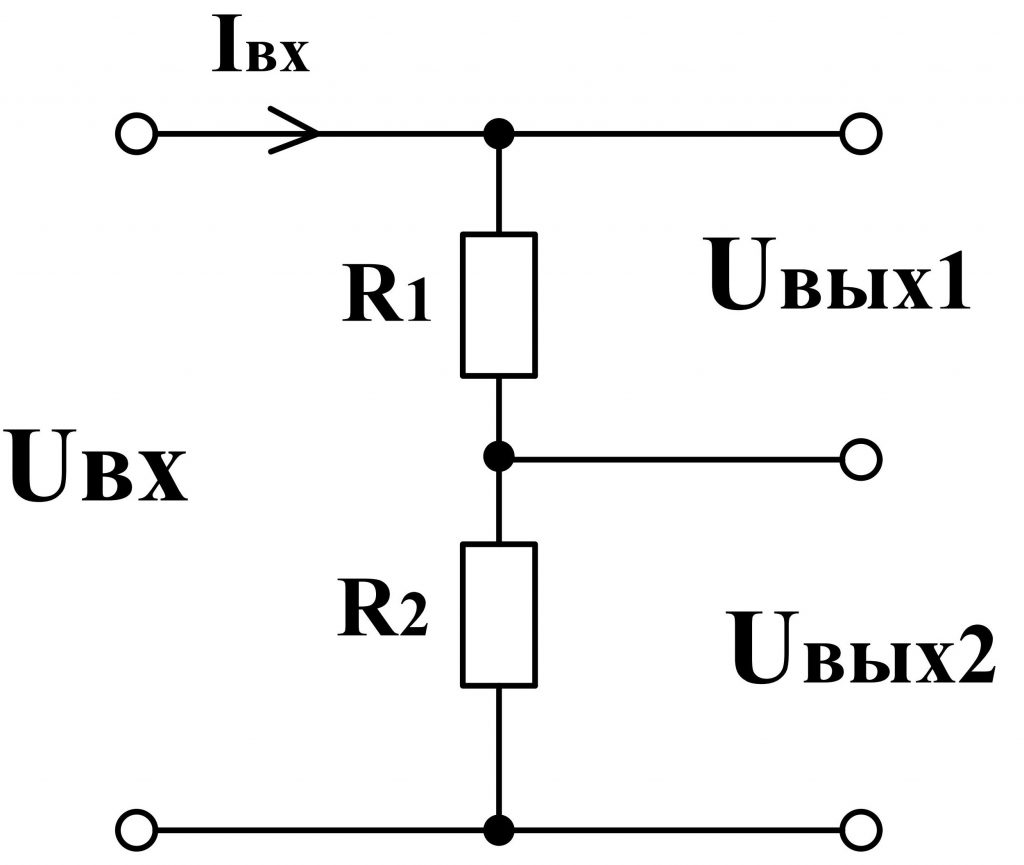
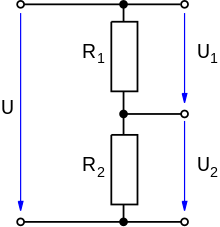
Вход схемы имеет два вывода, а выход – три. При одинаковых значения сопротивлений
Точное соотношение Uвых1 к Uвых2 рассчитаем, обратившись к закону Ома. Резисторы вместе с источником питания образуют последовательную цепь, поэтому величина электрического тока, протекающего через
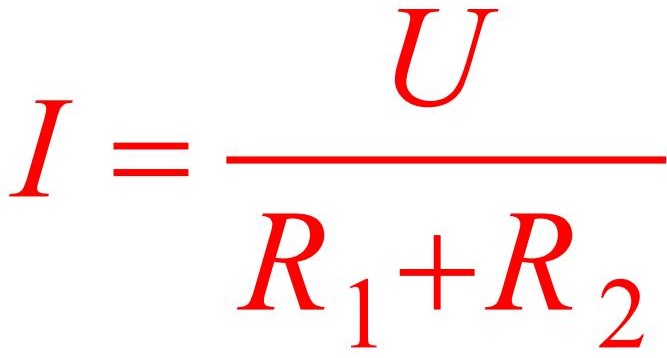
Следует обратить внимание, чем больше сумма сопротивлений, тем меньший ток I при том же значении Uвх.
Далее, согласно закону Ома, подставив значение тока, находим Uвых1
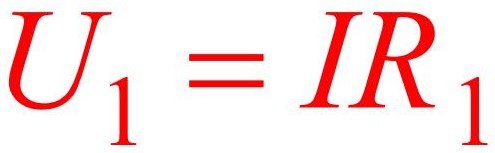
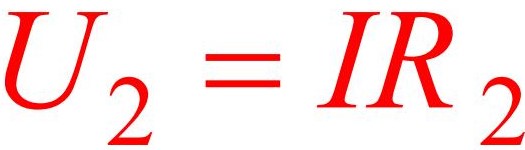
Путем подстановки в две последние формулы значение из самой первой формулы, находим значение выходного U в зависимости от входного и сопротивлений двух резисторов:
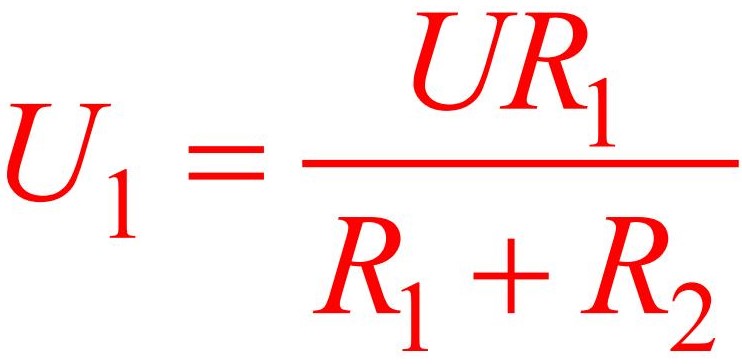
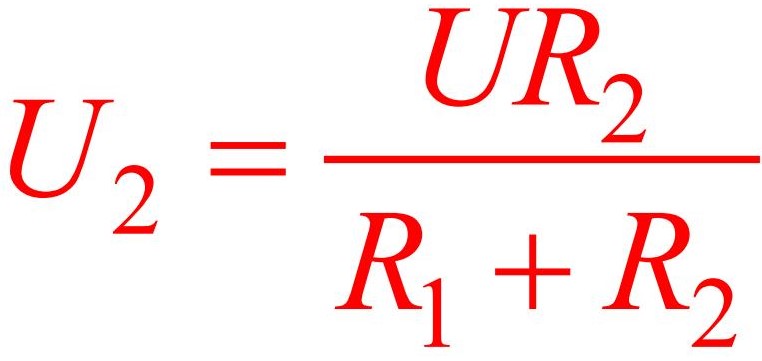
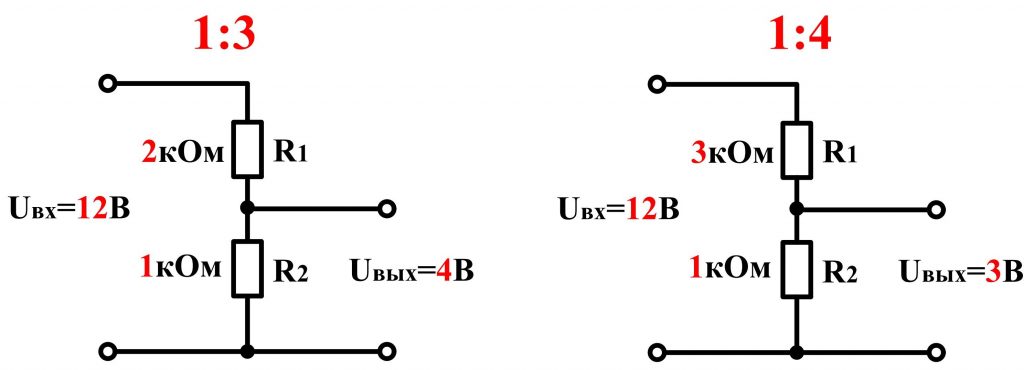
Применяя делитель напряжения на резисторах, необходимо понимать и помнить следующее:
- Коэффициент полезного действия такой схемы довольно низкий, поскольку только часть мощности источника питания поступает к нагрузке, а остальная мощность преобразуется в тепло, выделяемое на резисторах. Чем больше понижается напряжение, тем меньше мощности от источника питания поступит к нагрузке.
- Так как нагрузка подключается параллельно к одному из резисторов делителя, то есть шунтирует его, то общее сопротивление цепи снижается и происходит перераспределение падений напряжений. Поэтому сопротивление нагрузки должно быть гораздо больше сопротивления резистора делителя. В противном случае схема будет работать нестабильно с отклонением от заданных параметров.
- Распределение U между R1 и R2 определяется исключительно их относительными значениями, а не абсолютными величинами. В данном случае неважно, будут ли R1 и R2 иметь значение 2 кОм и 1 кОм или 200 кОм и 100 кОм. Однако при более низких значениях сопротивлений можно получить большую мощность на нагрузке, но следует помнить, что и больше мощности преобразуется в тепло, то есть израсходуется невозвратно впустую.
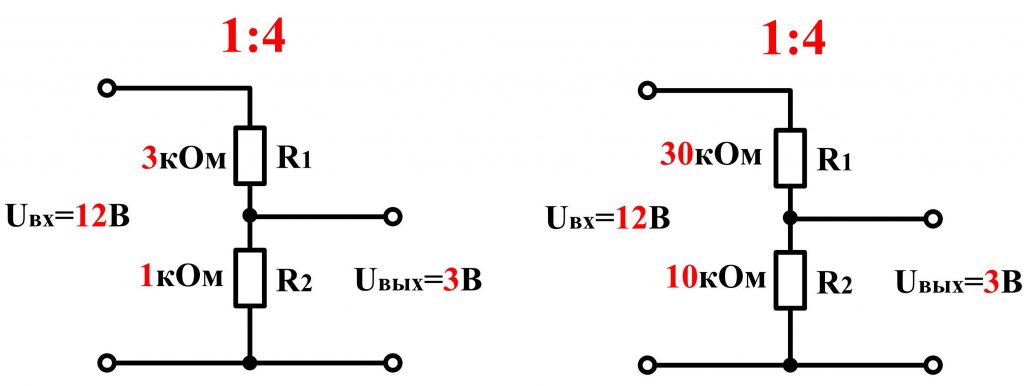
Также иногда находят применение и более сложные делители напряжений, состоящие из нескольких последовательно соединенных резисторов.
Делитель напряжения на переменном резисторе
Схему делителя напряжения на переменном резисторе называют схемой потенциометра. Вращая рукоятку громкости музыкального центра или автомагнитолы, вы таким действием плавно изменяете напряжение, подаваемое на усилитель модности звуковой частоты. Принцип работы и сборка простейшего усилителя мощности уже были ранее рассмотрены здесь.
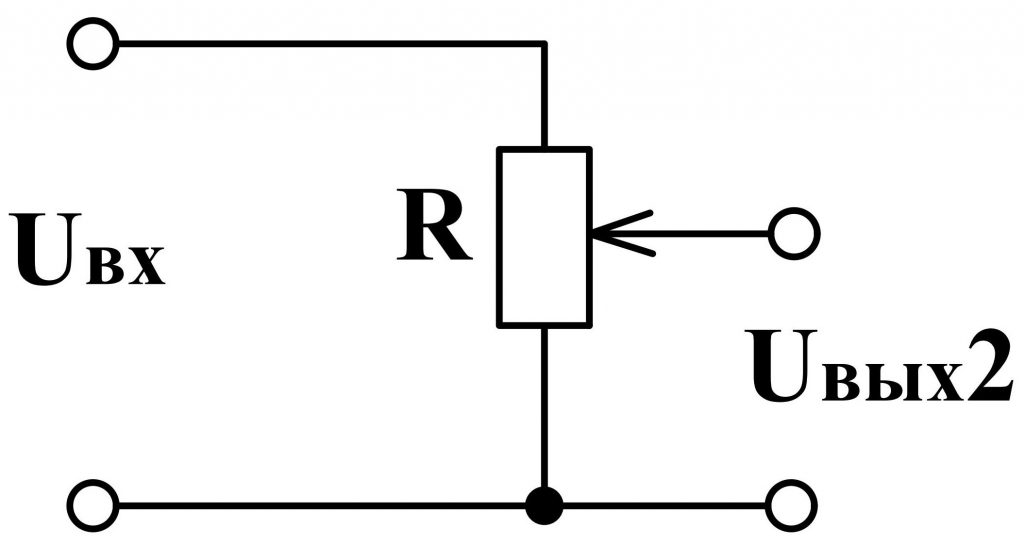
При перемещении (вращении) ручки переменного резистора сверху вниз по чертежу происходит плавное изменение U от значения источника питания до нуля.
В звуковой технике главным образом применяются переменные резисторы с логарифмической зависимостью, поскольку слуховой аппарат человек воспринимает звуки с данной зависимостью. Для регулирования уровня звука одновременно по двум каналам используют сдвоенные переменные резисторы.
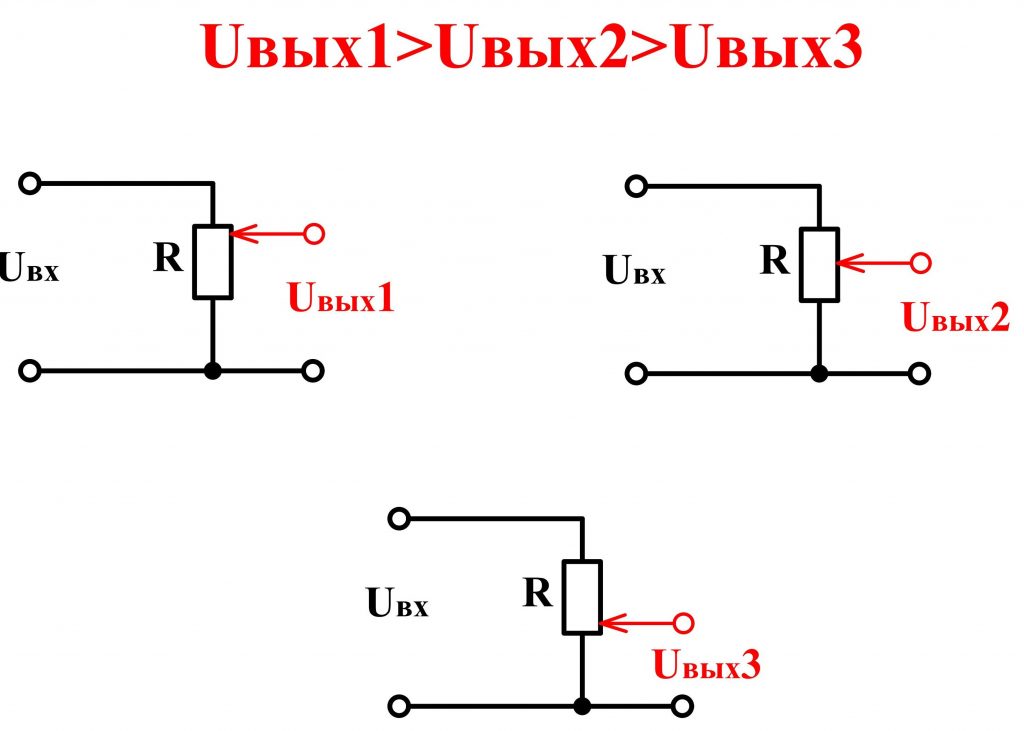
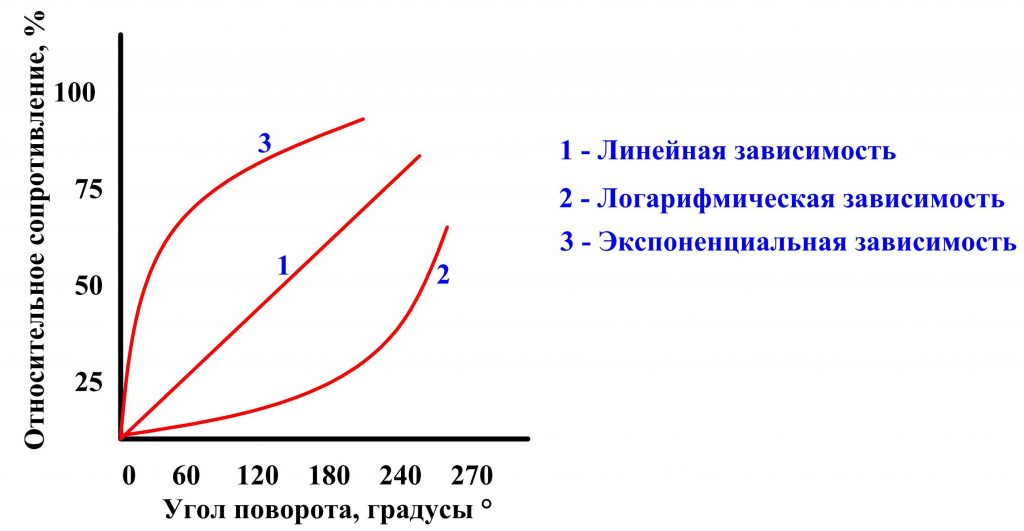
В качестве делителя напряжения находят применение переменные резисторы, имеющие следующие зависимости сопротивления от угла поворота ручки: логарифмическую, линейную и экспоненциальную. Конкретный тип зависимости применяется для решения отдельной задачи.
Еще статьи по данной теме
Делитель напряжения — Википедия
Дели́тель напряже́ния — устройство , в котором входное и выходное напряжение связаны коэффициентом передачи 0 ⩽ a ⩽ 1 {\displaystyle 0\leqslant a\leqslant 1} .[1]
Делитель напряжения можно представить как два последовательных участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним (с него обычно снимается выходное напряжение делителя), а другое —
Резистивный делитель напряжения
Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения U {\displaystyle U} . Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа. Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
U = I R {\displaystyle \ U=IR} .
Для каждого резистора имеем:
{
U
1
=
I
R
1
U
2
=
I
R
2
.
{\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}\\U_{2}=IR_{2}.\end{array}}\right.}
Сложив выражения, получаем:
U 1 + U 2 = I ( R 1 + R 2 ) . {\displaystyle U_{1}+U_{2}=I(R_{1}+R_{2}).}
Далее:
I = U 1 + U 2 R 1 + R 2 = U R 1 + R 2 . {\displaystyle I={\frac {U_{1}+U_{2}}{R_{1}+R_{2}}}={\frac {U}{R_{1}+R_{2}}}.}
Из этого следует:
{ U 1 = I R 1 = U R 1 R 1 + R 2 U 2 = I R 2 = U R 2 R 1 + R 2 . {\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}=U{\frac {R_{1}}{R_{1}+R_{2}}}\\U_{2}=IR_{2}=U{\frac {R_{2}}{R_{1}+R_{2}}}.\end{array}}\right.}
Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно R 2 {\displaystyle R_{2}} , можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму. Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения U {\displaystyle U} . Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R = R 1 + R 2 {\displaystyle R=R_{1}+R_{2}} . Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность.
Применение
Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр, а в качестве нелинейного — параметрический стабилизатор напряжения.
Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ. В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.[1]
Цепи обратной связи в усилителях
С помощью резистивного делителя напряжения в цепи обратной связи задаётся коэффициент усиления каскада на ОУ.
Простейшие электрические фильтры
RC, LC, RL-цепи, представляющие собой примеры простейших электрических фильтров, могут рассматриваться как частотно-зависимые делители напряжения, в которых в соответствующих плечах используются реактивные элементы.
Усилитель напряжения
Делитель напряжения может использоваться для усиления входного напряжения — это возможно, если | R 2 | ⩾ | R 1 | {\displaystyle |R_{2}|\geqslant |R_{1}|} , а R 1 {\displaystyle R_{1}} — отрицательно, например как на участке вольт-амперной характеристики туннельного диода.
Параметрический стабилизатор напряжения
Делитель напряжения может использоваться для стабилизации входного напряжения — это возможно, если в качестве нижнего плеча делителя использовать стабилитрон.
Ограничения в применении резистивных делителей напряжения
Для обеспечения приемлемой точности работы делителя требуется проектировать его таким образом, чтобы величина тока, протекающего через цепи делителя, была не менее чем в 10 раз больше, нежели ток, протекающий через нагрузку. Увеличение этого соотношения до ×100, ×1000 и более при прочих равных условиях пропорционально повышает точность работы делителя. Таким же образом, вообще говоря, должны соотноситься и величины сопротивлений делителя и нагрузки. Нетрудно видеть, что идеальным (с точки зрения КПД) режимом работы делителя, является режим т.н. холостого хода, т.е. режим работы при отключенной нагрузке, когда её свойствами можно пренебречь. Увеличение тока нагрузки приводит к существенному падению КПД делителя, из-за того, что существенная часть мощности тратится на нагрев резисторов делителя. Вот почему резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы. Для решения этой задачи используют другие схемотехнические решения, в частности применяют стабилизаторы напряжения. Если же не требуется большой мощности, но требуется исключительно высокая точность поддержания величины выходного напряжения, то используют разнообразные источники опорного напряжения.
Нормативно-техническая документация
- ГОСТ 11282-93 (МЭК 524-75) — Резистивные делители напряжения постоянного тока
См. также
Примечания
- ↑ 1 2 3 Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е. — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5.
- ↑ В некоторых случаях возможно построение делителя напряжения по упрощённой схеме, когда в явном виде присутствует только верхнее плечо делителя, а в качестве нижнего плеча используется сопротивление самой нагрузки.
Ссылки
Делитель напряжения — Википедия
Дели́тель напряже́ния — устройство , в котором входное и выходное напряжение связаны коэффициентом передачи 0 ⩽ a ⩽ 1 {\displaystyle 0\leqslant a\leqslant 1} .[1]
Делитель напряжения можно представить как два последовательных участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним (с него обычно снимается выходное напряжение делителя), а другое — верхним[2]. Различают линейные и нелинейные делители напряжения. В линейных выходное напряжение изменяется по линейному закону в зависимости от входного. Такие делители используются для задания потенциалов и рабочих напряжений в различных точках электронных схем. В нелинейных делителях выходное напряжение зависит от коэффициента a {\displaystyle a} нелинейно. Нелинейные делители напряжения применяются в функциональных потенциометрах.[1] Сопротивление может быть как активным, так и реактивным, а также и вовсе нелинейным, как, например, в параметрическом стабилизаторе напряжения.
Резистивный делитель напряжения
Схема простейшего резистивного делителя напряженияПростейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения U {\displaystyle U} . Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа. Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
U = I R {\displaystyle \ U=IR} .
Для каждого резистора имеем:
{
U
1
=
I
R
1
U
2
=
I
R
2
.
{\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}\\U_{2}=IR_{2}.\end{array}}\right.}
Сложив выражения, получаем:
U 1 + U 2 = I ( R 1 + R 2 ) . {\displaystyle U_{1}+U_{2}=I(R_{1}+R_{2}).}
Далее:
I = U 1 + U 2 R 1 + R 2 = U R 1 + R 2 . {\displaystyle I={\frac {U_{1}+U_{2}}{R_{1}+R_{2}}}={\frac {U}{R_{1}+R_{2}}}.}
Из этого следует:
{ U 1 = I R 1 = U R 1 R 1 + R 2 U 2 = I R 2 = U R 2 R 1 + R 2 . {\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}=U{\frac {R_{1}}{R_{1}+R_{2}}}\\U_{2}=IR_{2}=U{\frac {R_{2}}{R_{1}+R_{2}}}.\end{array}}\right.}
Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно R 2 {\displaystyle R_{2}} , можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму. Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения U {\displaystyle U} . Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R = R 1 + R 2 {\displaystyle R=R_{1}+R_{2}} . Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность.
Применение
Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр, а в качестве нелинейного — параметрический стабилизатор напряжения.
Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ. В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.[1]
Цепи обратной связи в усилителях
С помощью резистивного делителя напряжения в цепи обратной связи задаётся коэффициент усиления каскада на ОУ.
Простейшие электрические фильтры
RC, LC, RL-цепи, представляющие собой примеры простейших электрических фильтров, могут рассматриваться как частотно-зависимые делители напряжения, в которых в соответствующих плечах используются реактивные элементы.
Усилитель напряжения
Делитель напряжения может использоваться для усиления входного напряжения — это возможно, если | R 2 | ⩾ | R 1 | {\displaystyle |R_{2}|\geqslant |R_{1}|} , а R 1 {\displaystyle R_{1}} — отрицательно, например как на участке вольт-амперной характеристики туннельного диода.
Параметрический стабилизатор напряжения
Делитель напряжения может использоваться для стабилизации входного напряжения — это возможно, если в качестве нижнего плеча делителя использовать стабилитрон.
Ограничения в применении резистивных делителей напряжения
Для обеспечения приемлемой точности работы делителя требуется проектировать его таким образом, чтобы величина тока, протекающего через цепи делителя, была не менее чем в 10 раз больше, нежели ток, протекающий через нагрузку. Увеличение этого соотношения до ×100, ×1000 и более при прочих равных условиях пропорционально повышает точность работы делителя. Таким же образом, вообще говоря, должны соотноситься и величины сопротивлений делителя и нагрузки. Нетрудно видеть, что идеальным (с точки зрения КПД) режимом работы делителя, является режим т.н. холостого хода, т.е. режим работы при отключенной нагрузке, когда её свойствами можно пренебречь. Увеличение тока нагрузки приводит к существенному падению КПД делителя, из-за того, что существенная часть мощности тратится на нагрев резисторов делителя. Вот почему резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы. Для решения этой задачи используют другие схемотехнические решения, в частности применяют стабилизаторы напряжения. Если же не требуется большой мощности, но требуется исключительно высокая точность поддержания величины выходного напряжения, то используют разнообразные источники опорного напряжения.
Нормативно-техническая документация
- ГОСТ 11282-93 (МЭК 524-75) — Резистивные делители напряжения постоянного тока
См. также
Примечания
- ↑ 1 2 3 Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е. — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5.
- ↑ В некоторых случаях возможно построение делителя напряжения по упрощённой схеме, когда в явном виде присутствует только верхнее плечо делителя, а в качестве нижнего плеча используется сопротивление самой нагрузки.
Ссылки
Дели́тель напряже́ния — устройство , в котором входное и выходное напряжение связаны коэффициентом передачи 0 ⩽ a ⩽ 1 {\displaystyle 0\leqslant a\leqslant 1} .[1]
Делитель напряжения можно представить как два последовательных участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним (с него обычно снимается выходное напряжение делителя), а другое — верхним[2]. Различают линейные и нелинейные делители напряжения. В линейных выходное напряжение изменяется по линейному закону в зависимости от входного. Такие делители используются для задания потенциалов и рабочих напряжений в различных точках электронных схем. В нелинейных делителях выходное напряжение зависит от коэффициента a {\displaystyle a} нелинейно. Нелинейные делители напряжения применяются в функциональных потенциометрах.[1] Сопротивление может быть как активным, так и реактивным, а также и вовсе нелинейным, как, например, в параметрическом стабилизаторе напряжения.
Резистивный делитель напряжения
Схема простейшего резистивного делителя напряженияПростейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения U {\displaystyle U} . Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа. Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
U = I R {\displaystyle \ U=IR} .
Для каждого резистора имеем:
{
U
1
=
I
R
1
U
2
=
I
R
2
.
{\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}\\U_{2}=IR_{2}.\end{array}}\right.}
Сложив выражения, получаем:
U 1 + U 2 = I ( R 1 + R 2 ) . {\displaystyle U_{1}+U_{2}=I(R_{1}+R_{2}).}
Далее:
I = U 1 + U 2 R 1 + R 2 = U R 1 + R 2 . {\displaystyle I={\frac {U_{1}+U_{2}}{R_{1}+R_{2}}}={\frac {U}{R_{1}+R_{2}}}.}
Из этого следует:
{ U 1 = I R 1 = U R 1 R 1 + R 2 U 2 = I R 2 = U R 2 R 1 + R 2 . {\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}=U{\frac {R_{1}}{R_{1}+R_{2}}}\\U_{2}=IR_{2}=U{\frac {R_{2}}{R_{1}+R_{2}}}.\end{array}}\right.}
Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно R 2 {\displaystyle R_{2}} , можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму. Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения U {\displaystyle U} . Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R = R 1 + R 2 {\displaystyle R=R_{1}+R_{2}} . Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность.
Применение
Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр, а в качестве нелинейного — параметрический стабилизатор напряжения.
Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ. В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.[1]
Цепи обратной связи в усилителях
С помощью резистивного делителя напряжения в цепи обратной связи задаётся коэффициент усиления каскада на ОУ.
Простейшие электрические фильтры
RC, LC, RL-цепи, представляющие собой примеры простейших электрических фильтров, могут рассматриваться как частотно-зависимые делители напряжения, в которых в соответствующих плечах используются реактивные элементы.
Усилитель напряжения
Делитель напряжения может использоваться для усиления входного напряжения — это возможно, если | R 2 | ⩾ | R 1 | {\displaystyle |R_{2}|\geqslant |R_{1}|} , а R 1 {\displaystyle R_{1}} — отрицательно, например как на участке вольт-амперной характеристики туннельного диода.
Параметрический стабилизатор напряжения
Делитель напряжения может использоваться для стабилизации входного напряжения — это возможно, если в качестве нижнего плеча делителя использовать стабилитрон.
Ограничения в применении резистивных делителей напряжения
Для обеспечения приемлемой точности работы делителя требуется проектировать его таким образом, чтобы величина тока, протекающего через цепи делителя, была не менее чем в 10 раз больше, нежели ток, протекающий через нагрузку. Увеличение этого соотношения до ×100, ×1000 и более при прочих равных условиях пропорционально повышает точность работы делителя. Таким же образом, вообще говоря, должны соотноситься и величины сопротивлений делителя и нагрузки. Нетрудно видеть, что идеальным (с точки зрения КПД) режимом работы делителя, является режим т.н. холостого хода, т.е. режим работы при отключенной нагрузке, когда её свойствами можно пренебречь. Увеличение тока нагрузки приводит к существенному падению КПД делителя, из-за того, что существенная часть мощности тратится на нагрев резисторов делителя. Вот почему резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы. Для решения этой задачи используют другие схемотехнические решения, в частности применяют стабилизаторы напряжения. Если же не требуется большой мощности, но требуется исключительно высокая точность поддержания величины выходного напряжения, то используют разнообразные источники опорного напряжения.
Нормативно-техническая документация
- ГОСТ 11282-93 (МЭК 524-75) — Резистивные делители напряжения постоянного тока
См. также
Примечания
- ↑ 1 2 3 Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е. — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5.
- ↑ В некоторых случаях возможно построение делителя напряжения по упрощённой схеме, когда в явном виде присутствует только верхнее плечо делителя, а в качестве нижнего плеча используется сопротивление самой нагрузки.
Ссылки
Дели́тель напряже́ния — устройство , в котором входное и выходное напряжение связаны коэффициентом передачи 0 ⩽ a ⩽ 1 {\displaystyle 0\leqslant a\leqslant 1} .[1]
Делитель напряжения можно представить как два последовательных участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним (с него обычно снимается выходное напряжение делителя), а другое — верхним[2]. Различают линейные и нелинейные делители напряжения. В линейных выходное напряжение изменяется по линейному закону в зависимости от входного. Такие делители используются для задания потенциалов и рабочих напряжений в различных точках электронных схем. В нелинейных делителях выходное напряжение зависит от коэффициента a {\displaystyle a} нелинейно. Нелинейные делители напряжения применяются в функциональных потенциометрах.[1] Сопротивление может быть как активным, так и реактивным, а также и вовсе нелинейным, как, например, в параметрическом стабилизаторе напряжения.
Резистивный делитель напряжения
Схема простейшего резистивного делителя напряженияПростейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения U {\displaystyle U} . Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа. Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
U = I R {\displaystyle \ U=IR} .
Для каждого резистора имеем:
{
U
1
=
I
R
1
U
2
=
I
R
2
.
{\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}\\U_{2}=IR_{2}.\end{array}}\right.}
Сложив выражения, получаем:
U 1 + U 2 = I ( R 1 + R 2 ) . {\displaystyle U_{1}+U_{2}=I(R_{1}+R_{2}).}
Далее:
I = U 1 + U 2 R 1 + R 2 = U R 1 + R 2 . {\displaystyle I={\frac {U_{1}+U_{2}}{R_{1}+R_{2}}}={\frac {U}{R_{1}+R_{2}}}.}
Из этого следует:
{ U 1 = I R 1 = U R 1 R 1 + R 2 U 2 = I R 2 = U R 2 R 1 + R 2 . {\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}=U{\frac {R_{1}}{R_{1}+R_{2}}}\\U_{2}=IR_{2}=U{\frac {R_{2}}{R_{1}+R_{2}}}.\end{array}}\right.}
Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно R 2 {\displaystyle R_{2}} , можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму. Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения U {\displaystyle U} . Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R = R 1 + R 2 {\displaystyle R=R_{1}+R_{2}} . Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность.
Применение
Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр, а в качестве нелинейного — параметрический стабилизатор напряжения.
Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ. В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.[1]
Цепи обратной связи в усилителях
С помощью резистивного делителя напряжения в цепи обратной связи задаётся коэффициент усиления каскада на ОУ.
Простейшие электрические фильтры
RC, LC, RL-цепи, представляющие собой примеры простейших электрических фильтров, могут рассматриваться как частотно-зависимые делители напряжения, в которых в соответствующих плечах используются реактивные элементы.
Усилитель напряжения
Делитель напряжения может использоваться для усиления входного напряжения — это возможно, если | R 2 | ⩾ | R 1 | {\displaystyle |R_{2}|\geqslant |R_{1}|} , а R 1 {\displaystyle R_{1}} — отрицательно, например как на участке вольт-амперной характеристики туннельного диода.
Параметрический стабилизатор напряжения
Делитель напряжения может использоваться для стабилизации входного напряжения — это возможно, если в качестве нижнего плеча делителя использовать стабилитрон.
Ограничения в применении резистивных делителей напряжения
Для обеспечения приемлемой точности работы делителя требуется проектировать его таким образом, чтобы величина тока, протекающего через цепи делителя, была не менее чем в 10 раз больше, нежели ток, протекающий через нагрузку. Увеличение этого соотношения до ×100, ×1000 и более при прочих равных условиях пропорционально повышает точность работы делителя. Таким же образом, вообще говоря, должны соотноситься и величины сопротивлений делителя и нагрузки. Нетрудно видеть, что идеальным (с точки зрения КПД) режимом работы делителя, является режим т.н. холостого хода, т.е. режим работы при отключенной нагрузке, когда её свойствами можно пренебречь. Увеличение тока нагрузки приводит к существенному падению КПД делителя, из-за того, что существенная часть мощности тратится на нагрев резисторов делителя. Вот почему резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы. Для решения этой задачи используют другие схемотехнические решения, в частности применяют стабилизаторы напряжения. Если же не требуется большой мощности, но требуется исключительно высокая точность поддержания величины выходного напряжения, то используют разнообразные источники опорного напряжения.
Нормативно-техническая документация
- ГОСТ 11282-93 (МЭК 524-75) — Резистивные делители напряжения постоянного тока
См. также
Примечания
- ↑ 1 2 3 Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е. — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5.
- ↑ В некоторых случаях возможно построение делителя напряжения по упрощённой схеме, когда в явном виде присутствует только верхнее плечо делителя, а в качестве нижнего плеча используется сопротивление самой нагрузки.
Ссылки
Делитель напряжения — Википедия с видео // WIKI 2
Дели́тель напряже́ния — устройство, в котором входное U i n {\displaystyle U_{in}} и выходное U o u t {\displaystyle U_{out}} напряжение связаны коэффициентом передачи 0 ⩽ a ⩽ 1 {\displaystyle 0\leqslant a\leqslant 1} : U o u t = a ∗ U i n {\displaystyle U_{out}=a*U_{in}} .[1]
Делитель напряжения можно представить как два последовательных участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним (с него обычно снимается выходное напряжение делителя), а другое — верхним[2]. Различают линейные и нелинейные делители напряжения. В линейных выходное напряжение изменяется по линейному закону в зависимости от входного. Такие делители используются для задания потенциалов и рабочих напряжений в различных точках электронных схем. В нелинейных делителях выходное напряжение зависит от коэффициента a {\displaystyle a} нелинейно. Нелинейные делители напряжения применяются в функциональных потенциометрах.[1] Сопротивление может быть как активным, так и реактивным, а также и вовсе нелинейным, как, например, в параметрическом стабилизаторе напряжения.
Энциклопедичный YouTube
1/5
Просмотров:37 041
15 566
1 928
3 758
1 369
✪ Как понизить напряжение? Делитель напряжения на практике
✪ Как понизить напряжение? Делитель напряжения | RadioProsto
✪ Делитель тока
✪ Простейшие делители сигналов
✪ #057 ARDUINO 02 Аналоговые порты ввода-вывода (АЦП, делители напряжения, ШИМ)
Содержание
Резистивный делитель напряжения
Схема простейшего резистивного делителя напряжения
Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения U {\displaystyle U} . Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа. Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
U = I R {\displaystyle \ U=IR} .
Для каждого резистора имеем:
{ U 1 =
I R 1 U 2 =
I R 2 . {\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}\\U_{2}=IR_{2}.\end{array}}\right.}
Сложив выражения, получаем:
U 1 + U 2 = I ( R 1 + R 2 ) . {\displaystyle U_{1}+U_{2}=I(R_{1}+R_{2}).}
Далее:
I = U 1 + U 2 R 1 + R 2 = U R 1 + R 2 . {\displaystyle I={\frac {U_{1}+U_{2}}{R_{1}+R_{2}}}={\frac {U}{R_{1}+R_{2}}}.}
Из этого следует:
{ U 1 = I R 1 = U R 1 R 1 + R 2 U 2 = I R 2 = U R 2 R 1 + R 2 . {\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}=U{\frac {R_{1}}{R_{1}+R_{2}}}\\U_{2}=IR_{2}=U{\frac {R_{2}}{R_{1}+R_{2}}}.\end{array}}\right.}
Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно R 2 {\displaystyle R_{2}} , можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму:
1. Определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока, потребляемого нагрузкой (обычно принимают превышение от 10 раз по величине), но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения U {\displaystyle U} .
2. Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R = R 1 + R 2 {\displaystyle R=R_{1}+R_{2}} .
3. Выбрать конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетному сопротивлению R {\displaystyle R} .
При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность.
Применение
Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр, а в качестве нелинейного — параметрический стабилизатор напряжения.
Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ. В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.[1]
Цепи обратной связи в усилителях
С помощью резистивного делителя напряжения в цепи обратной связи задаётся коэффициент усиления каскада на ОУ.
Простейшие электрические фильтры
RC, LC, RL-цепи, представляющие собой примеры простейших электрических фильтров, могут рассматриваться как частотно-зависимые делители напряжения, в которых в соответствующих плечах используются реактивные элементы.
Усилитель напряжения
Делитель напряжения может использоваться для усиления входного напряжения — это возможно, если | R 2 | ⩾ | R 1 | {\displaystyle |R_{2}|\geqslant |R_{1}|} , а R 1 {\displaystyle R_{1}} — отрицательно, например как на участке вольт-амперной характеристики туннельного диода.
Параметрический стабилизатор напряжения
Делитель напряжения может использоваться для стабилизации входного напряжения — это возможно, если в качестве нижнего плеча делителя использовать стабилитрон.
Ограничения в применении резистивных делителей напряжения
Для обеспечения приемлемой точности работы делителя требуется проектировать его таким образом, чтобы величина тока, протекающего через цепи делителя, была не менее чем в 10 раз больше, нежели ток, протекающий через нагрузку. Увеличение этого соотношения до ×100, ×1000 и более при прочих равных условиях пропорционально повышает точность работы делителя. Таким же образом, вообще говоря, должны соотноситься и величины сопротивлений делителя и нагрузки. Нетрудно видеть, что идеальным (с точки зрения КПД) режимом работы делителя, является режим т.н. холостого хода, т.е. режим работы при отключенной нагрузке, когда её свойствами можно пренебречь. Увеличение тока нагрузки приводит к существенному падению КПД делителя, из-за того, что существенная часть мощности тратится на нагрев резисторов делителя. Вот почему резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы. Для решения этой задачи используют другие схемотехнические решения, в частности применяют стабилизаторы напряжения. Если же не требуется большой мощности, но требуется исключительно высокая точность поддержания величины выходного напряжения, то используют разнообразные источники опорного напряжения.
Нормативно-техническая документация
- ГОСТ 11282-93 (МЭК 524-75) — Резистивные делители напряжения постоянного тока
См. также
Примечания
- ↑ 1 2 3 Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е. — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5.
- ↑ В некоторых случаях возможно построение делителя напряжения по упрощённой схеме, когда в явном виде присутствует только верхнее плечо делителя, а в качестве нижнего плеча используется сопротивление самой нагрузки.
Ссылки
Эта страница в последний раз была отредактирована 24 января 2019 в 15:00.Емкостной делитель напряжения ⋆ diodov.net
Простейший емкостной делитель напряжения состоит из двух последовательно соединенных конденсаторов и используется для снижения величины U на отдельных элементах электрической цепи.
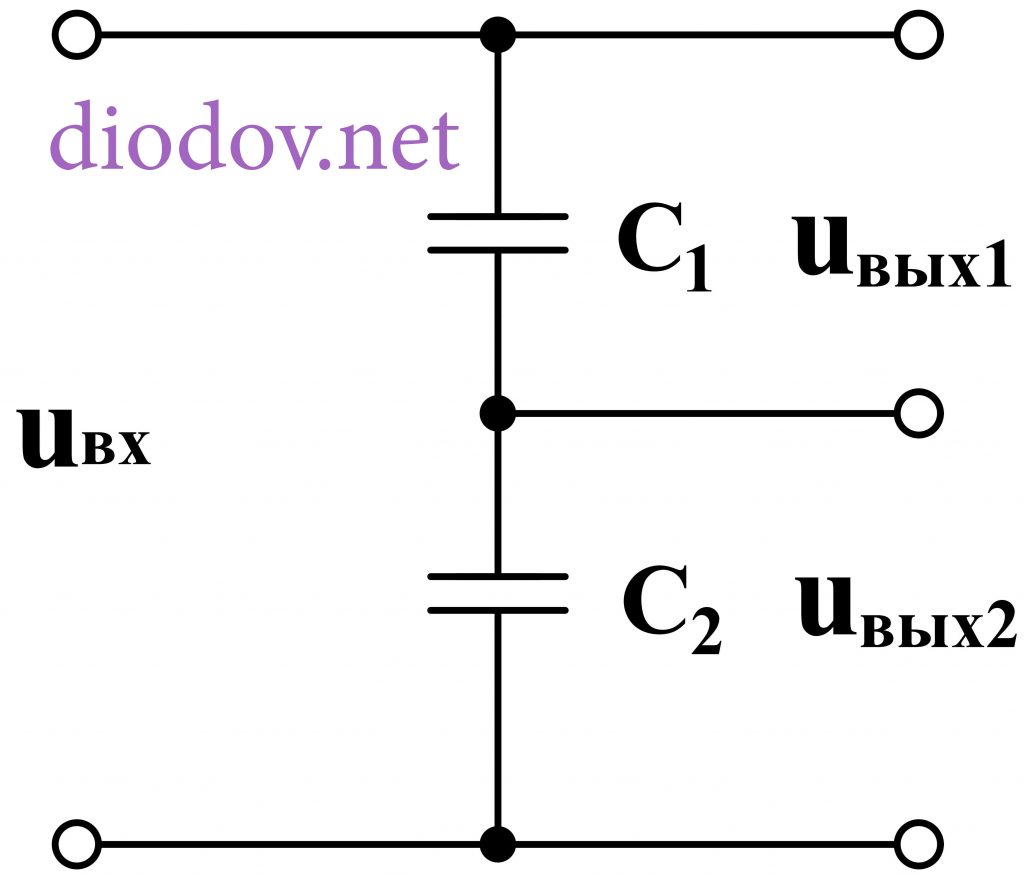
Делитель постоянного напряжения на конденсаторах чаще всего применяют многоуровневых инверторов напряжения, широко используемых как на электроподвижном составе, так и в других направлениях силовой электроники.
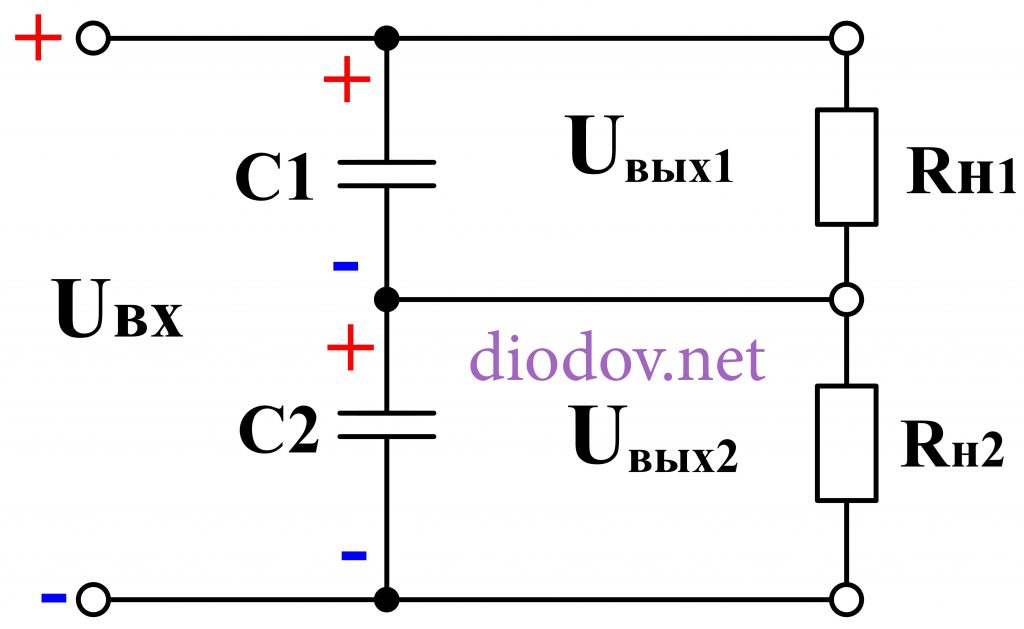
Главная сложность практического применения такой схемы (и всех подобных схем) заключается в невозможности обеспечения равномерного разряда конденсаторов, вследствие чего напряжения на них будет распределяться не поровну. Чем сильнее разряжен один конденсатор по сравнению с другим (иди с другими), тем большая разница в U будет на них, что наглядно отображает формула:
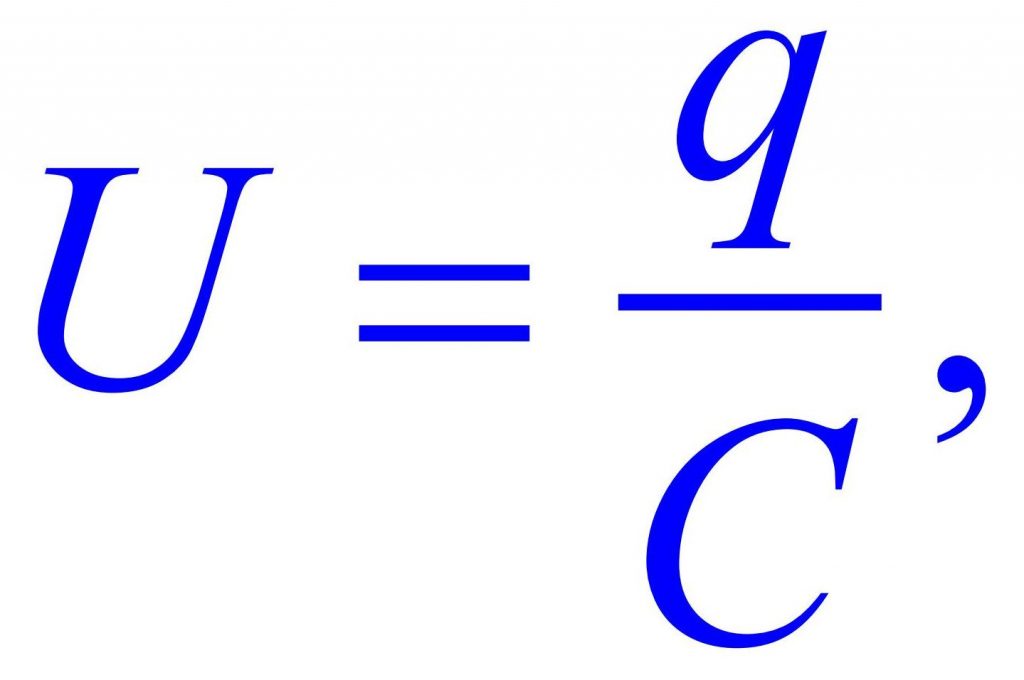
По этой причине подобные схемы крайне нестабильно работают и обязательно предусматривают узлов подзарядки конденсаторов с целью выравнивания напряжения на последних.
Емкостной делитель напряжения в цепи переменного тока
В радиоэлектронике в большей степени находят применение емкостные делители переменного напряжения.
Конденсатор, как и катушка индуктивности, относится к реактивному элементу, то есть потребляет реактивную мощность от источника переменного тока, в отличие от резистора, который является активным элементов и потребляет исключительно активную мощность.
Реактивный элемент
Здесь следует кратко пояснить разницу между активной и реактивной мощностями. Активная мощность выполняет полезную работу и реализуется только в том случае, когда ток и напряжение направлены в одном направлении и не отстают друг от друга, то есть находятся в одной фазе, что имеет место только на резисторе. На конденсаторе ток отстает от напряжения на угол φ = 90°. В результате чего ток напряжение находятся в противофазе, поэтому когда ток имеет максимальное значение напряжение равно нулю, а произведение этих двух величин дают мощность, которая в таком случае равна нулю, так как один из множителей равен нулю. Следовательно, мощность не потребляется.
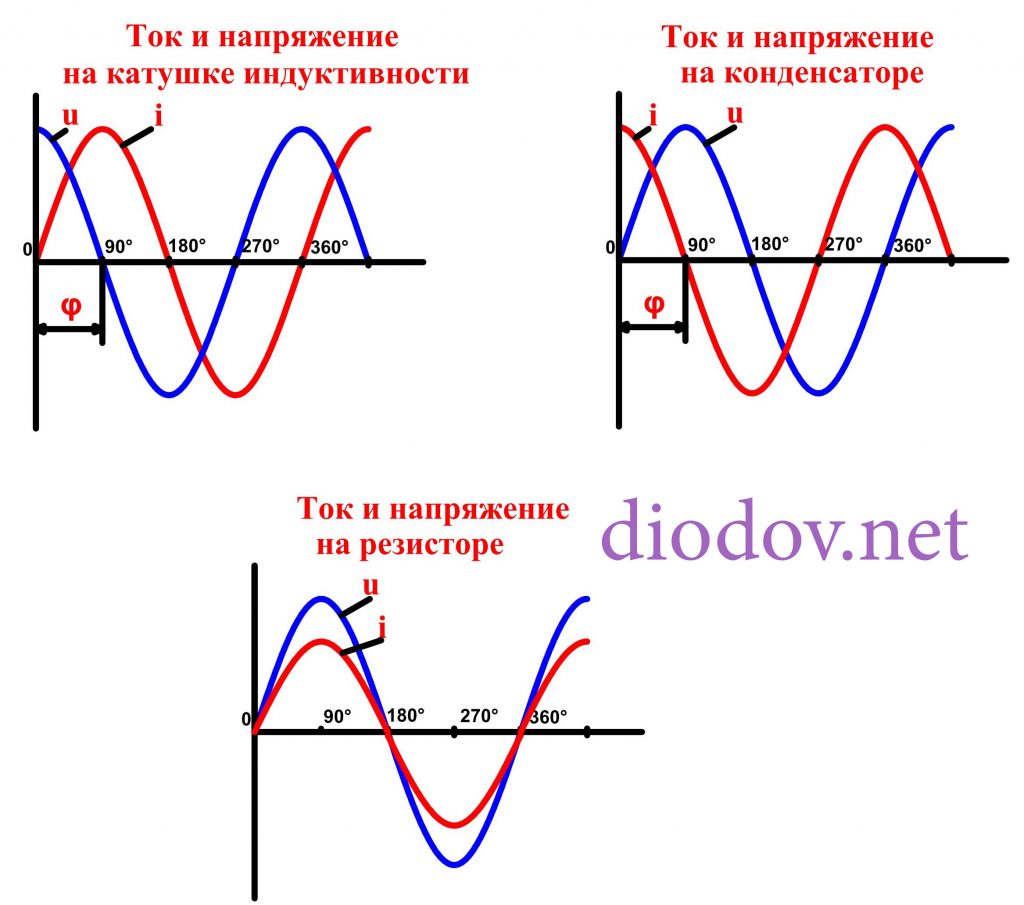
Аналогичные процессы протекают и в цепи с катушкой индуктивности. Разница лишь в том, что на индуктивности i отстает от u на угол φ = 90°.
Реактивная мощность проявляется только в цепях переменного тока. Она составляет часть полной мощности и определяется по формуле:
Реактивная мощность в отличие от активной, не потребляется нагрузкой, а циркулирует между источником питания и нагрузкой. Поэтому конденсатора и катушка индуктивности являются реактивными элементами, не потребляющими активную мощность и по этой причине они практически не нагреваются.
Расчет сопротивления делителя напряжения на конденсаторах заключается в определении необходимых значений сопротивлений.
Сопротивление конденсатора XC является величиной не постоянной и зависит от частоты переменного тока f и емкости C:
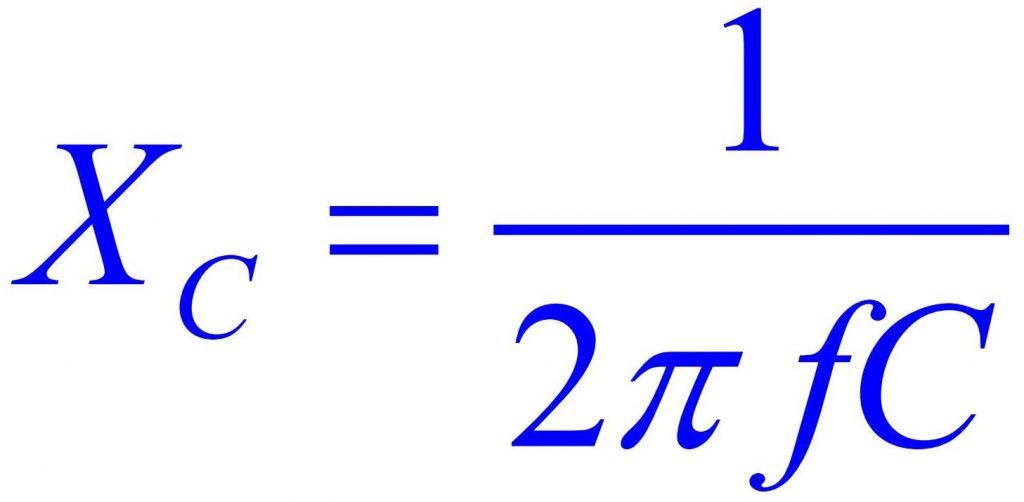
Как видно из формулы, сопротивление снижается с увеличением частоты и емкости. Для постоянного тока, частота которого равна нулю, сопротивление стремится к бесконечности, поэтому, рассматриваемая далее схема емкостного делителя напряжения не применяется постоянном токе.
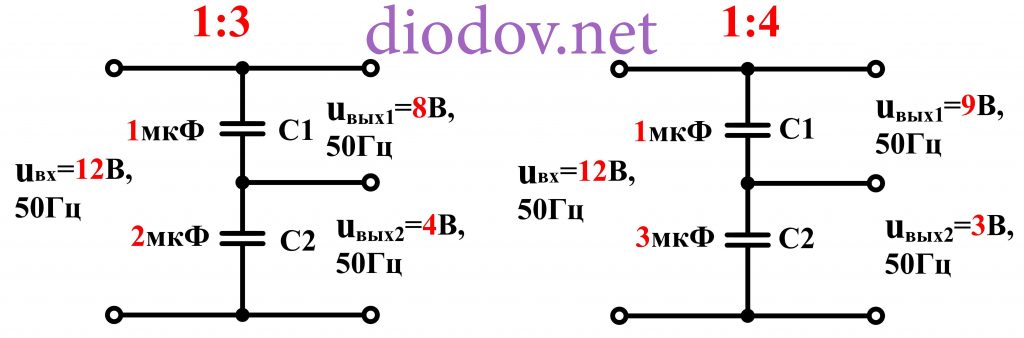
Для снижения величины uвых, например в два раза, емкости C1 и C2 должны быть равны. Универсальные формулами для определения выходных uвых1 и uвых2 в зависимости от входного и емкостей C1 и C2 имеют вид, аналогичный для резисторных делителей:
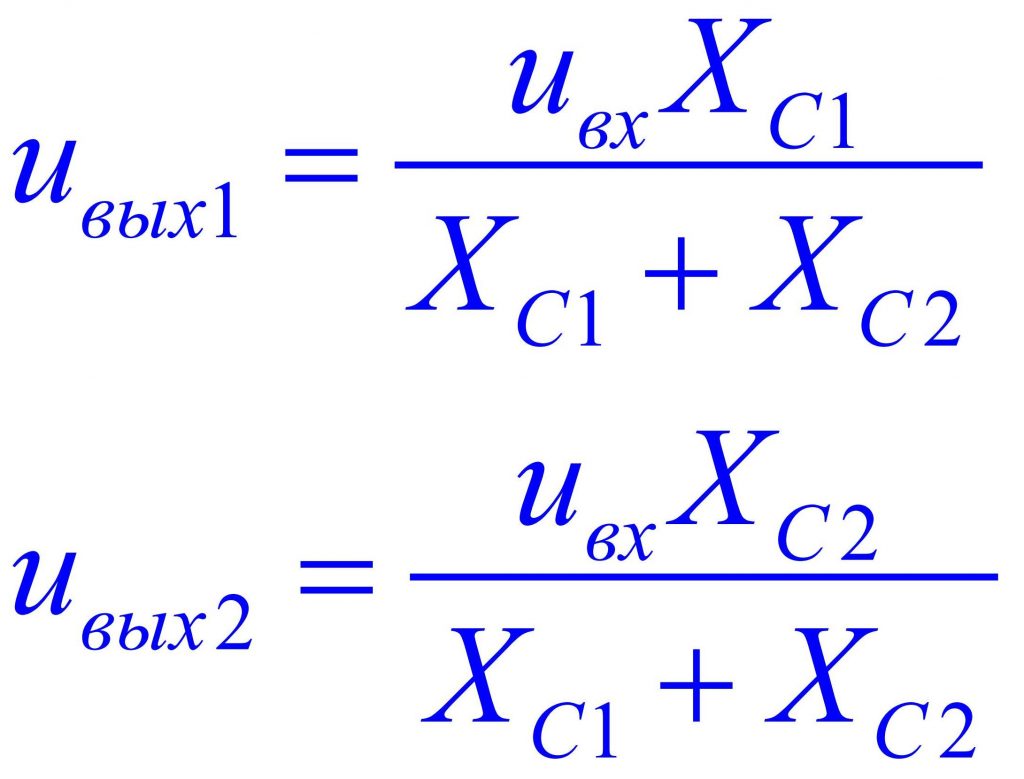
Поскольку частота переменного тока для всех конденсаторов одинакова, то формулу можно упростить:
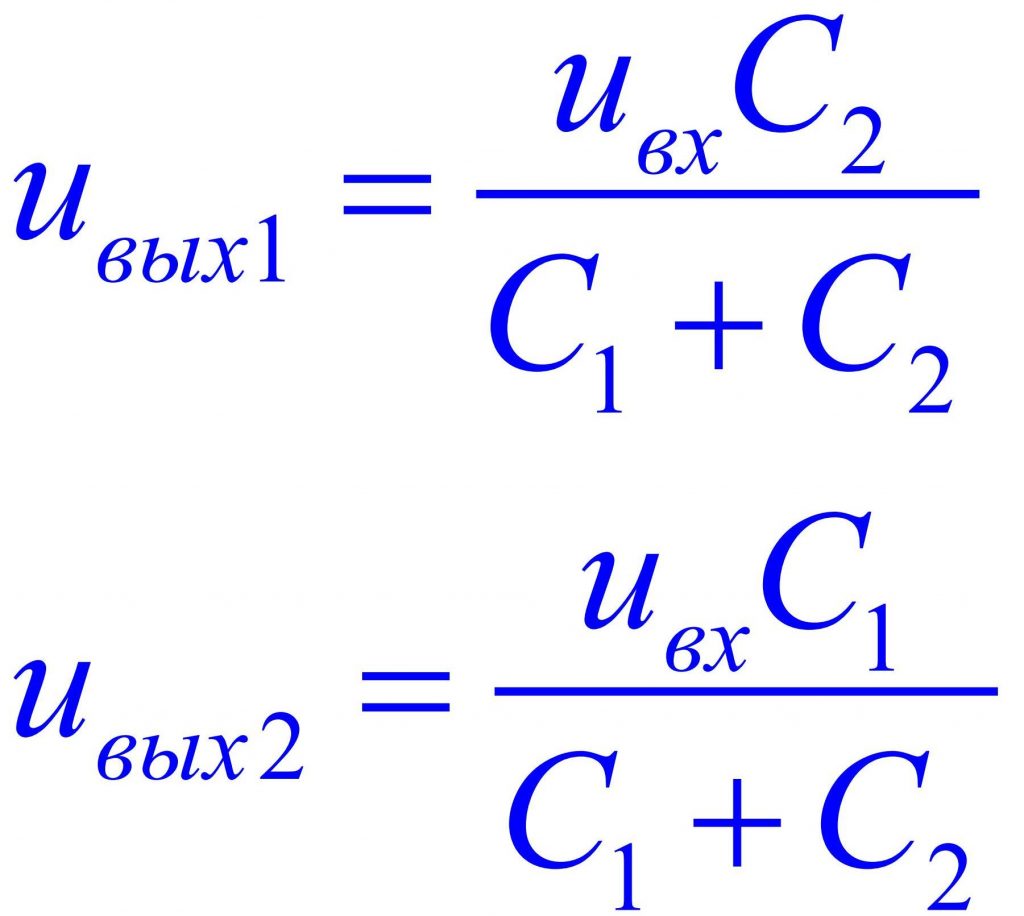
Индуктивный делитель напряжения
В качестве делителей переменного напряжения также, но гораздо реже, применяют катушки индуктивности, которые относятся к реактивным элементам. Однако, в отличие от конденсаторов, которые являются накопителями электрического поля, катушки индуктивности накапливают магнитное поле.
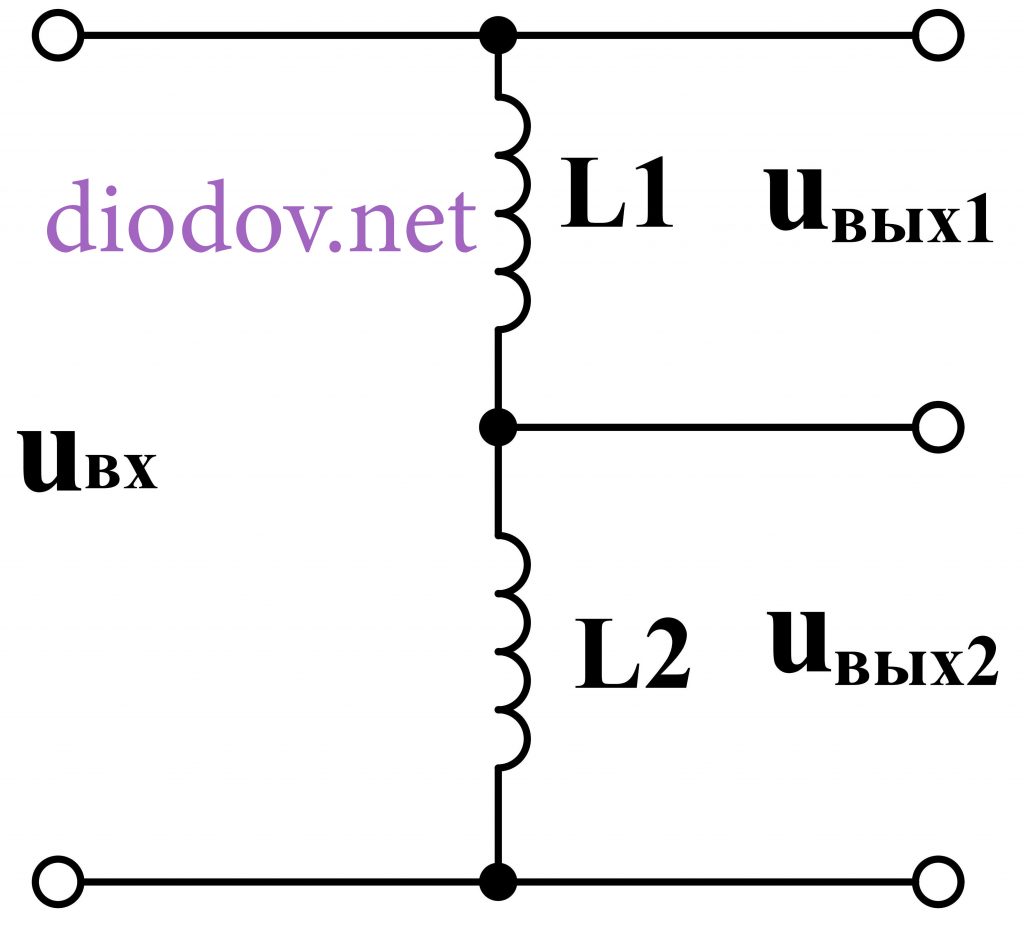
Индуктивное сопротивление зависит от индуктивности L и частоты переменного тока f. С ростом этих параметров сопротивление катушки переменному току возрастает.
XL = 2πfL.
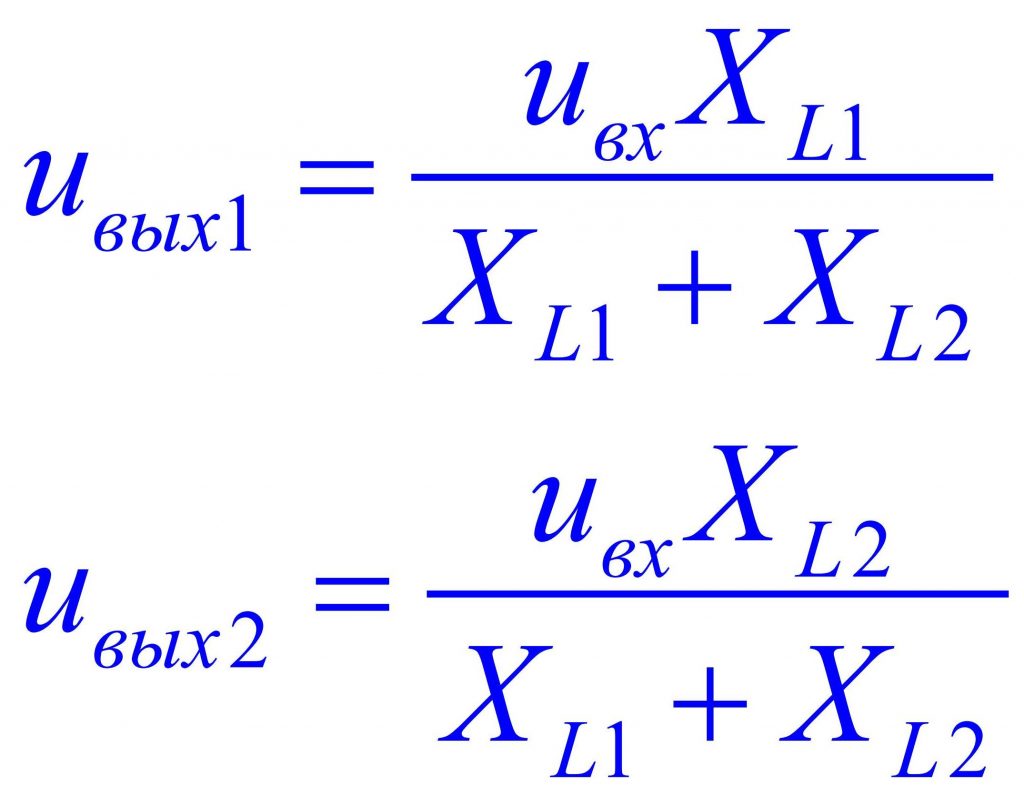
Упрощенный вариант формулы:
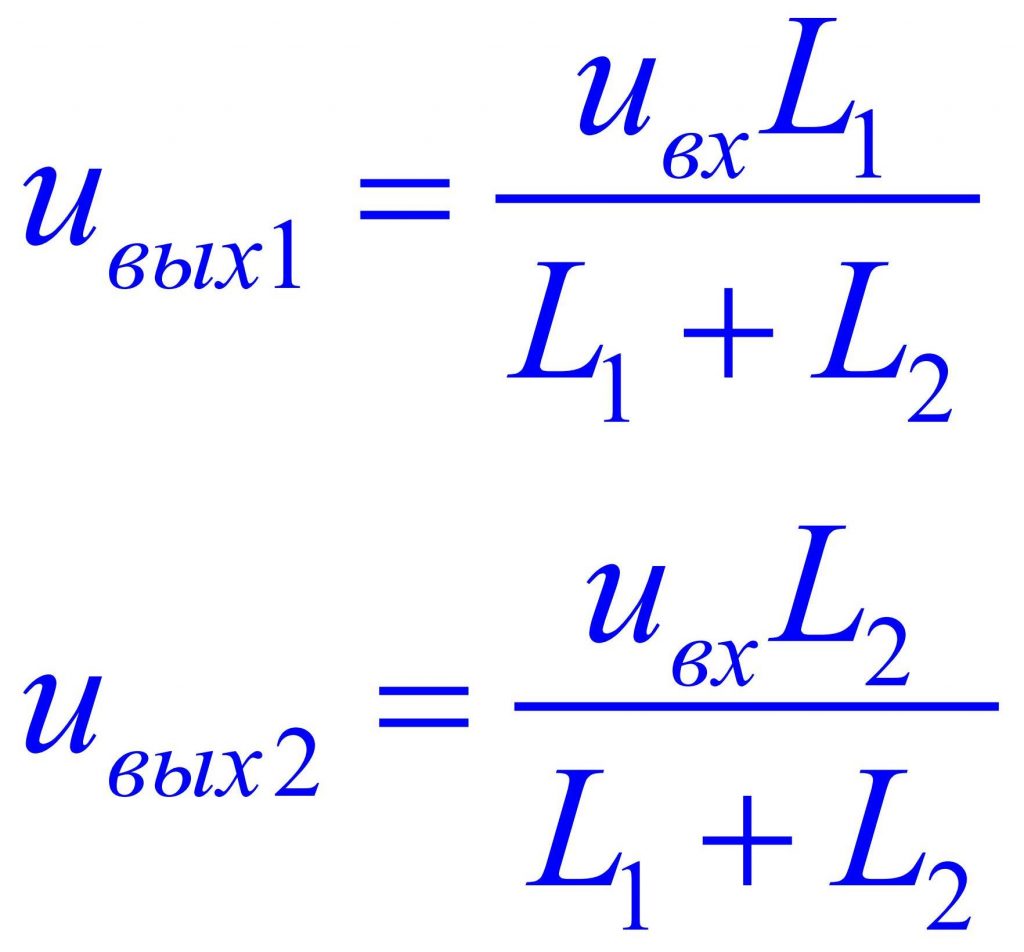
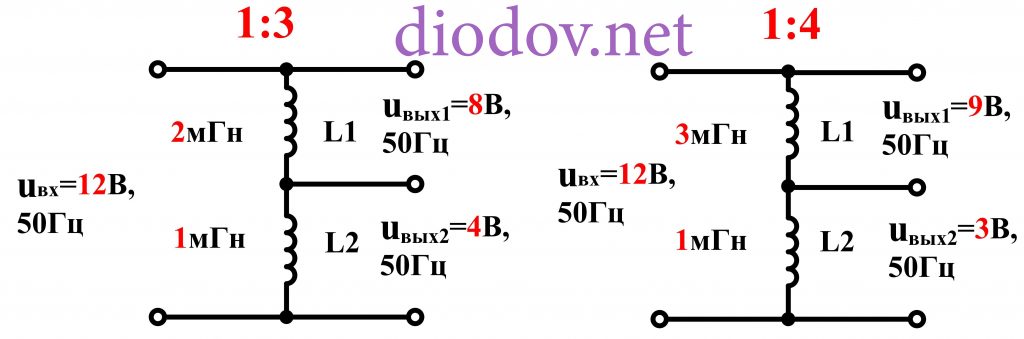
Как вы наверняка уже заметили, чтобы рассчитать емкостной делитель напряжения достаточно знать емкости конденсаторов, а индуктивный делитель – индуктивности.
Еще статьи по данной теме
В электронике правило делителя напряжения — это простая и наиболее важная электронная схема, которая используется для преобразования большого напряжения в небольшое напряжение. Используя только напряжение I / P и два последовательных резистора, мы можем получить напряжение O / P. Здесь выходное напряжение является частью напряжения I / P. Лучший пример для делителя напряжения — два резистора, соединенных последовательно. Когда напряжение i / p подается на пару резисторов, и напряжение o / p появляется из соединения между ними.Как правило, эти разделители используются для уменьшения величины напряжения или для создания опорного напряжения, а также используются на низких частотах в качестве сигнала аттенюатора. Для постоянного тока и относительно низких частот делитель напряжения может быть подходящим образом, если он изготовлен только из резисторов; где частотная характеристика требуется в широком диапазоне.
Правило делителя напряженияПравило делителя напряжения
Правило делителя напряжения используется для решения цепей, чтобы упростить решение. Применение этого правила также может основательно решить простые цепи. Основная концепция этого правила делителя напряжения: «Напряжение делится между два резистора, которые соединены последовательно, прямо пропорционально их сопротивлению.Делитель напряжения состоит из двух важных частей: схемы и уравнения.
Различные схемы делителя напряжения
Делитель напряжения включает в себя источник напряжения через серию из двух резисторов. Вы можете увидеть различные цепи напряжения, изображенные по-разному, как показано ниже. Но эти разные цепи всегда должны быть одинаковыми.
Различные схемы делителя напряженияВ вышеупомянутых различных цепях делителя напряжения резистор R1 находится ближе всего к входному напряжению Vin, а резистор R2 — ближе всего к клемме заземления.Падение напряжения на резисторе R2 называется Vout, которое представляет собой разделенное напряжение цепи.
Расчет делителя напряжения
. Рассмотрим следующую схему, соединенную с использованием двух резисторов R1 и R2. Где переменный резистор подключен между источником напряжения. В приведенной ниже схеме R1 — это сопротивление между скользящим контактом переменной и отрицательной клеммы. R2 — сопротивление между положительной клеммой и скользящим контактом. Это означает, что два резистора R1 и R2 соединены последовательно.
Правило делителя напряжения в двух последовательных резисторах Закон Ома гласит, что V = IR
Из вышеприведенного уравнения мы можем получить следующие уравнения
V1 (t) = R1i (t) …………… (I)
V2 (t) = R2i (t) …………… (II)
Применение закона напряжения Кирхгофа
KVL утверждает, что, когда алгебраическая сумма напряжений вокруг замкнутого пути в цепи равна нулю.
-V (t) + v1 (t) + v2 (t) = 0
V (t) = V1 (t) + v2 (t)
Следовательно,
V (t) = R1i (t) + R2i ( t) = i (t) (R1 + R2)
Следовательно,
i (t) = v (t) / R1 + R2 …………….(III)
Подставляя III в уравнения I и II
V1 (t) = R1 (v (t) / R1 + R2)
В (т) (R1 / R1 + R2)
V2 (t) = R2 ( v (t) / R1 + R2)
В (т) (R2 / R1 + R2)
Приведенная выше схема показывает напряжение, разделенное между двумя резисторами, которое прямо пропорционально их сопротивлению. Это правило делителя напряжения может быть распространено на цепи, которые имеют более двух резисторов.
Правило делителя напряжения в более чем двух последовательных резисторах Правило деления напряжения для вышеупомянутой цепи двух резисторов
V1 (t) = V (t) R1 / R1 + R2 + R3 + R4
V2 (t) = V (t) R2 / R1 + R2 + R3 + R4
V3 (т) = V (т) R3 / R1 + R2 + R3 + R4
V4 (т) = V (т) R4 / R1 + R2 + R3 + R4
Напряжение Уравнение делителя
Уравнение правила делителя напряжения принимает, когда вы знаете три значения в вышеприведенной схеме, это входное напряжение и два значения резистора.Используя следующее уравнение, мы можем найти выходное напряжение.
Vout = Vin. R2 / R1 + R2
Приведенное выше уравнение гласит, что Vout (напряжение o / p) прямо пропорционально Vin (входному напряжению) и отношению двух резисторов R1 и R2.
Пример правила делителя напряжения
Предположим, что полное сопротивление переменного резистора составляет 12 Ом. Скользящий контакт расположен в точке, где сопротивление делится на 4 и 8 Ом. Переменный резистор подключен через 2.Батарея 5 В. Давайте рассмотрим, как появляется напряжение на вольтметре, подключенном к 4-омной секции переменного резистора.
В соответствии с правилом делителя напряжения падение напряжения составит
В = 2,5 В x 4 Ом / 12 Ом = 0,83 В
Применение делителя напряжения
Делитель напряжения используется только там, где напряжение регулируется падением определенного напряжения в схема Он в основном используется в таких системах, где энергоэффективность не стоит рассматривать всерьез.
Правило делителя напряжения в потенциометреВ нашей повседневной жизни чаще всего делитель напряжения используется в потенциометрах. Наилучшими примерами для потенциометров являются ручки регулировки громкости, прикрепленные к нашим музыкальным системам и радиотранзисторам, и т. Д. Базовая конструкция потенциометра включает в себя три контакта, которые показаны выше. При этом два контакта соединены с резистором, который находится внутри потенциометра, а оставшийся контакт соединен с контактом протирания, который скользит по резистору.Когда кто-то меняет ручку на потенциометре, то напряжение будет появляться на устойчивых контактах и чистящих контактах в соответствии с правилом делителя напряжения.
Делители напряжения используются для регулировки уровня сигнала, измерения напряжения и смещения активных устройств в усилителях. Мультиметр и мост Уитстона включают делители напряжения.
Делители напряжения могут использоваться для измерения сопротивления датчика. Для формирования делителя напряжения датчик соединен последовательно с известным сопротивлением, и на делитель подается известное напряжение.Аналого-цифровой преобразователь микроконтроллера подключается к центральному отводу делителя, чтобы можно было измерять напряжение отводов. Используя известное сопротивление, можно рассчитать измеренное сопротивление датчика напряжения.
Это все о правиле деления напряжения со схемами, это правило применимо как к источникам переменного, так и постоянного тока. Кроме того, любые сомнения относительно этой концепции или электроники и электрических проектов, пожалуйста, оставьте свой отзыв, комментируя в разделе комментариев ниже.Вот вопрос или вам, какова основная функция правила делителя напряжения?
Делитель напряжения, также известный как делитель потенциала, представляет собой очень простую простую схему, которая используется для преобразования большого напряжения в маленькое. Из этой статьи вы узнаете о:
- Что такое делитель напряжения?
- Схемы делителя напряжения
- Уравнение / формула делителя напряжения
- Применение делителей напряжения
Что такое делитель напряжения?
- Пассивная линейная цепь, которая производит выходное напряжение, которое является частью его входного напряжения.
- Уменьшает входное напряжение до меньшего напряжения на основе соотношения двух резисторов, распределяя входное напряжение между компонентами делителя.
- Часто используется для подачи напряжения, отличного от имеющейся батареи или источника питания.
- Выходное напряжение делителя напряжения зависит от сопротивления входящей нагрузки.
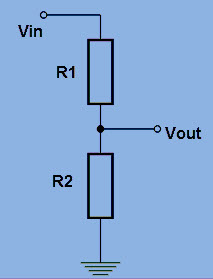
Схема делителя напряжения
Схема делителя напряжения обычно будет выглядеть так в схеме с последовательностью из 2 резисторов.
- R1 = Резистор, ближайший к входному напряжению (Vin)
- R2 = Резистор, ближайший к земле
- В в = Входное напряжение
- В на = Выходное напряжение на R2, которое является деленным напряжением (1/4 от входное напряжение)
Формула делителя напряжения / уравнение
Уравнение для определения выходного напряжения делительной цепи:
R2 / R1 + R2 = Коэффициент определяет масштабный коэффициент пониженного напряжения.
Например,
В в = 100, R 1 = 20, R 2 = 10
С помощью калькулятора вы должны получить:
Правило делителя напряжения
- Правило деления напряжения гласит: Напряжение, разделенное между двумя последовательными резисторами, прямо пропорционально их сопротивлению
- Это означает, что ваша схема может иметь более 2 резисторов!
- Формула делителя напряжения Формула:
Пример уравнения правила делителя напряжения:
ЗаконОма
Теперь мы можем использовать закон Ома для расчета напряжения, протекающего через каждый резистор:
- Уравнение для закона Ома = E = IR
- E = Ток на каждом резисторе
- I = Ток цепи
- R = Сопротивление
| R1 | R2 | R3 | Итого | |
| E (вольт) | 5 | 10 | 901 901 3001 901 3001 901 3001 901 3001 | 2.5м | 2,5 | 2,5м | 2,5м |
| R (Ом) | 2K | 4K | 6K | 12K |
Таким образом, ток на каждом резисторе составляет 5 В, 10 В и 15 В соответственно!
Упрощенные уравнения
- Если вы решаете за R1,
- Если вы решаете для R2,
Применение делителей напряжения
Цепи делителей напряжения очень распространены и используются во многих приложениях.Вот несколько примеров, где находится схема делителя напряжения:
Потенциометр
- Потенциометр — это пассивный электронный компонент с функцией скольжения или вращения, который действует как регулируемый делитель напряжения.
- Входное напряжение подается на всю длину потенциометра, а выходное напряжение (падение напряжения) контролируется неподвижным и скользящим контактом потенциометра.
- Существует два типа потенциометров
- Поворотные потенциометры (вращающаяся ручка)
- Линейный потенциометр (ползунок)
- Здесь, на Seeed, мы предлагаем оба типа!
Grove — Слайд-потенциометр
- Как это работает?
- Ручной стеклоочиститель, который является подвижным, касается резистивной полоски материала.Когда он перемещается ближе к клемме 1 и от клеммы 2, сопротивление снижается до клеммы 1, тогда как сопротивление повышается на клемме 2 и наоборот.
- Потенциометр полезен для получения переменного напряжения от источника постоянного напряжения. Он может подключать внешние клеммы потенциометра к источнику напряжения и контролировать необходимое вам напряжение между вашим потенциометром и одной из внешних клемм для вашей цепи.
- Потенциометр скольжения Grove включает в себя линейный переменный резистор с максимальным сопротивлением 10 кОм.По мере перемещения ползунка выходное напряжение будет варьироваться от 0 В до применяемой Vcc.
- Он подключается к другим модулям Grove через стандартный 4-контактный кабель Grove.
- Ниже приведено изображение принципиальной схемы потенциометра:
- Он имеет много целей, например, является регулируемым резистором, автономным делителем напряжения с Arduino или даже как устройство интерфейса человека (HID), что означает, что его можно использовать для управления автомобилем!
- Некоторые проекты, которые вы можете выполнить с помощью Grove — Slide Potentiometer, похожи на создание собственного Beatbox или Boombox с Arduino!
Grove — Датчик угла поворота (P)
- Датчик угла поворота Grove (P) способен генерировать аналоговый выход между 0 и Vcc (5 В пост. Тока с Seeeduino) на своем разъеме D1.
- Благодаря значению сопротивления 10 кОм оно идеально подходит для использования в Arduino.
- Поддерживается на всех платформах MCU, таких как Arduino, Raspberry Pi, BeagleBone, Wio, а также LinkIt ONE.
- Один из проектов, которые вы можете сделать с этим потенциометром, — использовать его для управления яркостью светодиодов.
Использование Arduino для управления яркостью светодиода через датчик угла поворота Grove (P)Grove — Делитель напряжения
- Grove — Voltage Divider предоставляет интерфейс для измерения внешнего напряжения, который устраняет необходимость подключения сопротивления к входному интерфейсу.
- С помощью переключателя можно легко выбрать коэффициент усиления по напряжению, что делает его простым в использовании.
Чтение резистивных датчиков
- Большинство датчиков — это простые резистивные устройства, такие как Grove — инфракрасный отражающий датчик. Однако большинство из них способны считывать только напряжение, но не сопротивление.
- Добавив еще один резистор в цепь, мы можем создать делитель напряжения вместе с датчиком.
- Поскольку мы можем проверить выходной сигнал делителя напряжения, теперь мы можем рассчитать величину сопротивления датчика.
- Пример схемы показан ниже, где R2 — резистивный датчик:
- Например, резистивный датчик представляет собой датчик Grove — температуры, который представляет собой термистор с сопротивлением комнатной температуры 350 Ом, где сопротивление R1 установлено равным 350 Ом
- Использование уравнения делителя напряжения:
| Температура | Vin (фиксированная) | R2 | R1 | R2 / (R1 + R2) | Vout |
|---|---|---|---|---|---|
| Холодная | 5V | 300 001 | 3000 ,46 | 2,3 В | |
| Комнатная температура | 5 В | 350 Ом | 350 Ом | 0,5 | 2,5 В |
| Горячий | 5В | 901 901 901 901 900001 | 001 901 905 09 2,65 В |
Уровень Shifters
- Что происходит, когда датчик и микроконтроллер с двумя разными напряжениями встречаются? Например, без выравнивания напряжения, непосредственно подключая микроконтроллер с логическим выходом 5 В к 3.Входной датчик 3 В может привести к повреждению цепи 3,3 В.
- Вот где герой: Делитель напряжения входит и сохраняет день, выступая в качестве переключателя уровня, который соединяет две цепи, которые используют разные рабочие напряжения.
- Делитель напряжения может помочь снизить напряжение с микроконтроллера (например, от 5 В до 3,3 В), чтобы избежать повреждения датчика, что делает его безопасным для работы с датчиком.
- Обратите внимание, что делитель напряжения может работать только в одном направлении: понижать напряжение, но не выравнивать.
- Вот таблица комбинаций резисторов для выравнивания часто встречающихся напряжений:
| Комбинация резисторов | Напряжения, подлежащие нивелированию | |
|---|---|---|
| 4,7 кОм и 3,9 кОм | 9В до 5В | |
| 3,6 кОм и 9,1 кОм | 1201 до 3,312 901 кОм 901,30,302 9010,002 и 901Ом 0,010 0010,302 901Ом 10,001,301 9010 005 кОм | 9 В до 3,3 В |
- Обратите внимание, что не рекомендуется использовать делитель напряжения для выравнивания большой нагрузки, например от 12 В до 5 В, поскольку они не предназначены для подачи такой мощности на нагрузку, поскольку при такой нагрузке резистор может расплавиться.(Вместо этого вы можете использовать регуляторы напряжения, такие как наш регулируемый преобразователь постоянного и постоянного тока (1,25 В — 35 В и 3 А)
Резюме
Имея все знания делителя напряжения в своих руках, вы можете превратить любое напряжение в меньшее, как маг! Хотите проверить свои навыки, создав собственный проект делителя напряжения? Вот некоторые идеи проекта, которые помогут вам начать использовать потенциометр и Arduino для создания бит-бокса или бум-бокса на нашей вики-странице: Grove — Slide Potentiometer Wiki
Пожалуйста, следуйте и нам нравится:
Продолжить чтение
,делителей напряжения | Ultimate Electronics Book
Ultimate Electronics: Практическое проектирование и анализ схем
Чрезвычайно распространенная конфигурация резисторов 2+. Аппроксимации, рекомендации по дизайну. Пример светодиодного регулятора тока. 22 минуты чтения
Делители напряжения — это только отдельные комбинации последовательно включенных резисторов при подключении к идеальным источникам напряжения и тока.
Хотя математика решения этих цепей была рассмотрена в предыдущих разделах, делители напряжения заслужили свое имя, потому что они появляются достаточно часто, чтобы быть полезным способом быстрого анализа при анализе многих более крупных цепей.(Поскольку более сложные подсхемы могут быть аппроксимированы как один резистор, термин и методы здесь могут также применяться более широко, чем просто резисторы.) Мы начнем с идеального случая, посмотрим на неидеальный случай, а затем покажем, когда приближения полезны в дизайне и анализе.
Когда вы видите, как опытный инженер-электрик бросает быстрый взгляд на аналоговую схему и быстро определяет, что происходит, он, скорее всего, делает приблизительные делители напряжения в своей голове — иногда даже не осознавая этого!
Идеальный делитель напряжения — это два последовательных резистора.Физически это иногда реализуется как потенциометр, который разделяет один физический резистор на две части с физически подвижным проводящим центральным контактом. Но чаще всего это два дискретных фиксированных резистора.
Когда на пару подается напряжение, выходное напряжение составляет некоторую часть входного напряжения:
Делитель напряжения с DC Sweep
circuitlab.com/c56c4dkqd8xyq
Упражнение Нажмите, чтобы открыть и смоделировать схему выше.Измените сопротивление и посмотрите, как изменяется выходное напряжение в ответ.
Это можно увидеть, используя закон напряжения Кирхгофа плюс закон Ома, чтобы записать сумму разностей напряжений вокруг контура:
Делитель напряжения с маркированной разницей тока и напряжения
circuitlab.com/c268avj7yazre
vin-iR1-iR2 = 0vin = i (R1 + R2) vinR1 + R2 = i
Теперь мы можем написать закон Ома для R2, vout = iR2 (так как другой конец R2 заземлен), и заменить в нашем выражении ток петли я выше:
vout = vin (R2R1 + R2)
Для удобства вытащим дробь , коэффициент делителя напряжения :
f = R2R1 + R2
, где vout = vin⋅f ,Поскольку сопротивления не могут быть отрицательными, 0≤f≤1 ,
Есть несколько особых случаев, о которых нужно подумать:
- В сравнительно частном частном случае двух равных сопротивлений R1 = R2 , соотношение f = 12 ,
- Если R1≫R2 соотношение f → 0 ,
- Если R1≪R2 соотношение f → 1 ,
Эти приближения невероятно полезны, и более подробные версии разрабатываются в алгебраических приближениях.
Делитель напряжения всегда выводит уменьшенную версию входного напряжения.Вот пример с делителем напряжения, управляемым синусоидой от генератора функций:
Делитель напряжения с функциональным генератором
circuitlab.com/c9cuv5ebs6j3q
УпражнениеНажмите, чтобы открыть и смоделировать схему выше, и посмотреть на соотношение между входными и выходными сигналами.
Поскольку делитель напряжения выводит мультипликативно масштабированную версию входного сигнала, если мы возьмем логарифм обеих сторон (в любой базе), мы обнаружим, что коэффициент делителя напряжения превращается в аддитивную постоянную:
vout = vin⋅flog (vout) = log (vin) + log (f)
как f≤1 , всегда будет так, что log (f) ≤0 ,
Вот пример с функциональным генератором, который управляет делителем напряжения, где мы строим графики напряжения в логарифмическом масштабе:
Делитель напряжения с генератором функций — логарифмическая шкала
circuitlab.com/c47n23g79tueb
Упражнение Нажмите, чтобы открыть и смоделировать схему выше. Обратите внимание, что в логарифмическом масштабе эти две трассы выглядят просто вертикально смещенными на постоянное смещение.В разделе «Расширенные графики» измените его на линейный масштаб, чтобы увидеть исходный сигнал.
В этом примере мы позаботились о том, чтобы наш входной сигнал был строго положительным, но вы также можете применить ту же логику к амплитуде сигнала, которая со временем становится как положительной, так и отрицательной. В этом случае делитель напряжения производит сдвиг на графике амплитуды в частотной области:
Делитель напряжения — участок Боде
circuitlab.ком / cdu75x9ht5s2v
Упражнение Нажмите, чтобы открыть и смоделировать схему выше.
При выполнении этой симуляции график входного и выходного напряжения составляет −6 дБ. сдвиг между входной и выходной амплитудой. Это −6 дБ потому что амплитуда напряжения обрезается пополам. См. Разделы «Порядок величин», «Логарифмические шкалы» и «Децибелы».
Делители напряжения могут быть сделаны с N последовательные резисторы имеют N − 1 узлы между ними. До тех пор, пока ток не входит или не выходит из цепи делителя напряжения, с точки зрения любого конкретного отвода, резисторы «выше» могут быть объединены в один, а резисторы «внизу» могут быть объединены в другой.
Это позволяет легко создавать большое количество коэффициентов напряжения для одного входа. Например:
Делитель напряжения с несколькими нажатиями
circuitlab.com/cvjq2abc924k5
Упражнение Нажмите, чтобы открыть и смоделировать схему выше.
На схеме выше пять последовательных резисторов. Он превращает 12-вольтный вход в четыре разных выхода, которые могут быть полезны для питания компьютера.
Поскольку это последовательная цепь, есть только один ток, и его легко определить, если рассмотреть последовательно включенные резисторы:
itotal = vin∑R
Падение напряжения на любом из резисторов тогда равно:
Δvn = Rn⋅itotal
и доля полного падения напряжения на любом резисторе Rn это:
фн = Δvnvinfn
.Делители напряжения с частотной компенсацией[Analog Devices Wiki]
Цель:
Целью этой лабораторной работы является изучение вопросов емкостной нагрузки резистивных делителей напряжения и их влияния на частотную характеристику.
Примечания:
Как и во всех лабораториях ALM, мы используем следующую терминологию при обращении к соединениям с разъемом M1000 и настройке оборудования.Прямоугольники, заштрихованные зеленым цветом, обозначают соединения с разъемом аналогового ввода / вывода M1000. Выводы аналоговых каналов ввода / вывода называются CA и CB. Когда сконфигурировано для принудительного измерения напряжения / измеряемого тока, добавляется –V, как в CA- V , или когда настроено для принудительного измерения тока / измеряемого напряжения, -I добавляется, как в CA-I. Если канал настроен в режиме высокого импеданса только для измерения напряжения, то значение H добавляется как CA-H. Трассировки области аналогично называются каналом и напряжением / током. Например, CA- V , CB- V для сигналов напряжения и CA-I, CB-I для сигналов тока.
Фон:
Делитель или аттенюатор напряжения с частотной компенсацией — это простая двухпортовая RC-сеть, обеспечивающая фиксированный коэффициент деления напряжения или затухание в широком диапазоне частот, а не только при постоянном токе. Такие сети используются там, где часть схемы, нагружающая выход делителя напряжения, является емкостной. Это особенно важно, когда сигнал имеет широкую полосу пропускания, то есть он не является синусоидальным. Простейшим аттенюатором напряжения является чисто резистивный делитель напряжения с передаточной функцией: H (jω) = В 2 / В S = R 2 / (R 1 + R 2 ), где вход В S = В 1 + В 2 , а выход В 2 , как на рисунке 1.Передаточная функция резистивного делителя напряжения не зависит от частоты, только если резисторы идеальны и любые паразитные емкости, связанные с цепью, пренебрежимо малы.
Рисунок 1, простой резисторный делитель напряжения
Проблема, наблюдаемая на высоких частотах, заключается в том, что паразитная (паразитная) емкость влияет на общий отклик резистивного делителя напряжения. Самый простой способ исправить эту проблему — это ввести конденсаторы параллельно резисторам.Рассмотрим схему делителя на рисунке 2. Конденсатор C 2 , который находится на выходе, В 2 , можно рассматривать как любую паразитную паразитную емкость на выходе делителя, которая может быть частью системы. Мы можем видеть, что эта схема, известная как делитель с частотной компенсацией, работает как резистивный делитель напряжения на постоянном или низком частотах и как емкостный делитель напряжения на высоких частотах. Делители напряжения могут быть изготовлены из реактивных компонентов так же, как они могут быть изготовлены из резисторов.Также как и в случае резисторных делителей, коэффициент деления емкостного делителя напряжения не зависит от изменения частоты сигнала, даже если реактивное сопротивление конденсатора зависит от частоты.
Коэффициент деления В 2 / В S = X C2 / (X C1 + X C2 ). Емкостное реактивное сопротивление X C пропорционально 1 / C, поэтому В 2 / В S = C 1 / (C 1 + C 2 ) аналогично формуле для резистор делитель.Для простого случая, когда R 1 = R 2 , мы имеем коэффициент деления 1/2 для резисторов. Иметь такое же соотношение делителей 1/2 для конденсаторов C 1 = C 2 .
Рисунок 2, Делитель с частотной компенсацией
Компенсированный делитель использует подавление полюс-ноль для подавления нежелательной частотной зависимости, вызванной любой паразитной емкостью на выходной стороне сети. Если значения резистора и конденсатора настроены таким образом, что полюс и ноль H (s) накладываются, | H (jω) | становится независимым от частоты.
Поучительный способ узнать об условиях аннулирования полюса — записать предельные, низкочастотные и высокочастотные выражения для | H (jω) | а затем установить их равными друг другу. Результатом является простое соотношение между R 1 , R 2 , C 1 и C 2 .
Рисунок 3, показывающий (a) правильную настройку, (b) под компенсацией, © над компенсацией на краях прямоугольной волны.
Эксперимент по компенсации входной емкости ALM1000
Материалы:
Аппаратный модуль ADALM1000
Резистор 1 — 1 МОм
1 — Конденсатор, значение определяется
Направления:
Возвращаясь к рисунку 2, мы можем рассмотреть R 2 , чтобы представить входное сопротивление 1 МОм каналов ALM1000 в режиме Hi-Z.Аналогично, C 2 может рассматриваться как представляющий паразитную паразитную емкость входов. Резистор и конденсатор внутри зеленого прямоугольника показаны на рисунке 4. Используйте еще 1 МОм как R 1 , чтобы сделать соотношение делителей 1/2. Начните без учета C 1 , чтобы измерить влияние на частотную характеристику из-за C 2 .
Рисунок 4. Настройка делителя напряжения.
Процедура:
Установите AWG A в режим SVMI с минимальным значением, установленным на 1.0 и максимальное значение до 4,0. Установите Shape в Square и частоту в 500 Гц. Установите AWG B в режим Hi-Z. Под Кривыми выберите CA- V и CB- V для отображения. Нажмите Run и настройте горизонтальную шкалу времени так, чтобы было видно около 3 циклов. Вы должны увидеть резкую прямоугольную волну на канале A, а форма волны на каналах B должна выглядеть как красная кривая (b) на рисунке 3. Это потому, что C 1 еще не был включен. Оцените постоянную времени RC и значение C 2 по форме сигнала канала B.
Откройте окно Bode Plotting. Вы можете отключить график времени, если хотите при создании кривых АЧХ. Установите значение AWG A Min на 1,082, а максимальное значение на 3,92 (1 VRMS или 0 дБВ). Убедитесь, что форма была изменена на синус. Установите начальную частоту 100 и конечную частоту 20000. Выберите CH-A в качестве источника развертки. Под кривыми выберите кривые CA-dBV, CB-dBV и CA- дБ — CB- дБ для отображения. Под окном FFT использование окна с плоским верхом работает лучше всего.Установите количество точек развертки равным 300 и единичную развертку. Нажмите кнопку «Выполнить».
Теперь у вас должен быть коэффициент усиления (затухания) и частотная характеристика для некомпенсированного делителя. Из точки -3 дБ на графике усиления оцените постоянную времени RC и значение C 2 . Как эти значения сравниваются с тем, что вы рассчитали, используя ответ во временной области? Основываясь на ваших лучших оценках значения C 2 , рассчитайте значение для C 1 , которое точно компенсирует C 2 .Значение, которое вы получите, вероятно, не будет близко к стандартному значению конденсатора. Найдите параллельную комбинацию (или последовательную комбинацию) из двух или более конденсаторов, которая близко соответствует требуемому значению для C 1 .
Добавьте свою новую комбинацию C 1 по R 1 на макете.
Повторите тесты временной области и частотной области на этой новой схеме. Является ли реакция во временной области на выходе делителя более похожей на синюю форму волны (a) на рисунке 3? Если нет, то почему нет? Сравните частотную характеристику цепи до и после добавления C 1 .Какова частота -3 дБ сейчас?
Реакция пути делителя конденсатора:
Давайте теперь рассмотрим только путь делителя конденсатора. Отсоедините R 1 от конца C 1 и подключите его к фиксированному источнику питания 2,5 В , как показано на рисунке 5. Путь через C 1 блокирует путь постоянного тока от канала A. Подключение R 1 до фиксированного 2,5 В источник питания восстанавливает уровень постоянного напряжения на входе канала B.
Рисунок 5, Путь разделения конденсатора
Повторите тесты временной области и частотной области для этой версии схемы. Сравните отклик схемы во временной и частотной областях с тем, что вы получили только с R 1 и с R 1 и C 1 , соединенными параллельно (рисунок 4). Какова частота -3 дБ сейчас? Является ли частотная характеристика плоской, низкой или высокой частоты? Объяснить, почему.
Использование делителя для измерения 9 В батареи:
Теперь мы будем использовать делитель напряжения для измерения напряжений, превышающих 0… +5 В , разрешенных аппаратным обеспечением ALM1000.Но сначала нам нужно откалибровать смещение делителя и усиление.
Отсоедините конец R 1 , C 1 от канала A, рис. 4, и подключите их к заземлению. Установите для усиления канала B значение 2.0, приблизительное отношение делителя, на данный момент. Контролируя среднее значение постоянного тока канала B, отрегулируйте значение, введенное в окне ввода смещения канала B.
Теперь снова подключите R 1 / C 1 к выходу канала А. Каналы A и B теперь должны более точно совмещаться друг с другом.При необходимости отрегулируйте значение усиления вверх или вниз, чтобы плоские участки верхней и нижней части прямоугольных волн находились прямо друг над другом. Возможно, вам также потребуется немного изменить смещение, чтобы получить идеальное выравнивание. Программное обеспечение теперь откалибровано для делителя напряжения.
Отсоедините R 1 / C 1 от канала A. Подключите отрицательную (-) клемму батареи 9 V к земле и подключите положительную (+) клемму к R 1 / C 1 .Среднее значение постоянного тока, считываемое каналом B, теперь должно быть напряжением постоянного тока батареи 9 9000 9 В . Вам нужно изменить вертикальный диапазон канала B на 1 В / Div и положение на 5,0, чтобы увидеть 9 вольт на сетке прицела.
Осциллограф Зонды:
Пассивный осциллографический датчик 10X использует последовательный резистор (9 МОм), чтобы обеспечить ослабление 10: 1, когда он используется с входным сопротивлением 1 МОм самого прицела. Импеданс 1 МОм является стандартным для большинства входов осциллографа. Это позволяет взаимозаменять зондовые датчики между осциллографами разных производителей.Рисунок представляет собой схему для типичного 10X зонда. Пробники осциллографа 10X также допускают некоторую компенсацию частоты, чтобы учесть изменения входной емкости канала прицела. Конденсаторная сеть делится на зонд, как показано на рисунке. Регулируемый конденсатор, подключенный к земле, затем можно использовать для выравнивания частотного отклика датчика.
Вы можете найти более подробную информацию о том, как подключить разъем BNC датчика зонда к вашей схеме макета или входам ALM1000: Подключение кабелей BNC к модулям активного обучения
Рисунок 6, Типичная схема осциллографа
Входные каналы ALM1000 имеют входное сопротивление 1 МОм, но входная емкость намного больше, чем диапазон регулировки примерно 10 пФ от до 50 пФ для большинства 10-кратных пробников.Конденсатор параллельно резистору 9 МОм обычно составляет 10 пФ , а параллельная комбинация входной емкости оптического прицела и регулируемого компенсационного конденсатора в зонде должна быть близка к 90 пФ . Это означает, что, если стандартный зонд был подключен непосредственно к входу ALM1000, невозможно компенсировать частотную характеристику.
Буферный усилитель с единичным усилением (AD8541 или AD8542) может быть вставлен между цепью зонда и входом ALM1000, как показано на рисунке 7.R 1 и C 1 замыкают цепь делителя резистор / конденсатор датчика 10 X.
Рисунок 7. Вставьте буфер усиления блока, чтобы снизить входную емкость.
С резистором R 1 , подключенным к земле, можно измерять только положительные напряжения. Если R 1 подключен к 2,5 В , в середине диапазона входного сигнала 0-5 В усилителя, вводится смещение, и можно измерять как положительные, так и отрицательные напряжения.
для дальнейшего чтения:
Емкостный делитель напряжения
Осциллографические пробники
Создание собственных осциллографических пробников
Новая функция в ALICE добавляет входной делитель частотной компенсации
Возврат в Лабораторную работу Оглавление
университет / курсы / alm1k / circuit1 / alm-cir-Voltage-divr.txt · Последнее изменение: 02 декабря 2019 19:23 по dmercer
.