2)

E =

1.6829 -1.5136 0.8242 -0.5758 -0.2647 -1.9836

Таким образом, над матрицами возможны поэлементные операции и матричные, соответствующими правилам матричного исчисления. При поэлементном умножении и делении, матрицы должны быть одинаковых размеров. При матричных операциях их размеры должны быть согласованы. Результат операций – матрица.

Поскольку вектор в Матлабе рассматривается как матрица из одной строки

или одного		столбца, то над векторами возможны те же операции,							что и над
матрицами,		и для их	выполнения также			необходимо	согласование		размеров
векторов.
	Векторное исчисление			предусматривает следующие				операции над
векторами:		сложение	и вычитание			векторов	одинакового		размера,

транспонирование векторов, умножение и деление вектора на число, вектора на

вектор (одинакового размера, если один из них вектор–столбец, другой – вектор–

строка или наоборот), скалярное и векторное произведение векторов. (векторное

произведение выполняется для векторов длиной 3)

Операция + и — определена только для сложения/ вычитания одинаковых векторов (можно суммировать или вычитать вектор — строки или вектор –

столбцы одинаковой длины).

29

Зададим 2 вектора:

>>X=[1 2 3]; %Исходные данные

>>Y=[4 5 6];

>>X+Y

ans =

5 7 9

Транспонирование

>>X’

ans = 1 2 3

Умножение вектора на число осуществляется обычной операцией *

>>b=5;

>>X*b

ans =

5 10 15

>> b*X

ans =

5 10 15

Деление вектора на число производится операцией обычного деления (/).

Деление числа на вектор невозможно.

>> X/b

ans =

0.2000 0.4000 0.6000

При делении числа на векторошибка

>> b/X

??? Error using ==> mldivide Matrix dimensions must agree.

Произведение 2-х векторов в математике можно вычислить только если

они имеют одинаковую длину. Если один вектор-строка, а другой вектор-

столбец, то результат – число;

Скалярное произведение

30

>> X*Y’ % Скалярное произведение векторов — сумма произведений

элементов с одинаковыми номерами (X1*Y1+X2*Y2+…)

ans = 32

Для вычисления скалярного произведение векторов X и Y можно

воспользоваться функцией sum.

>> sum(X.*Y)

ans = 32

При умножении вектора-столбца на вектор-строку результат – матрица

>> X’*Y

ans =
4	5	6
8	10	12
12	15	18

Умножение вектора-строки на вектор-строку приводит к ошибке

>> X*Y

??? Error using ==> *

Inner matrix dimensions must agree.

Для векторов из 3-х элементов можно вычислить векторное произведение. 2

 

 

 

A =

 

 

 

 

-1.0000

-0.5000

0

0.5000

1.0000

B =

 

 

 

 

0.2919

0.7702

1.0000

0.7702

0.2919

Остается организовать вывод в виде 2 столбцов.

Для красивого вывода в виде таблицы: disp(‘ A B’)

for

i=1:length(A)

disp(sprintf(‘%5.2f %.4f’,A(i),B(i)))

end

Получим
A	B
-1.00	0.2919
-0.50	0.7702

0.001. 0000

0.500.7702

1.000.2919

Далее будет рассмотрен вариант построения таблицы с использованием

операций с векторами и матрицами (без циклов).

33

Лекция Способы задания векторов. Деление отрезка в заданном отношении. Скалярное произведение двух векторов и его основные свойства.

    Скачать с Depositfiles 

Лекция № 5.

1.4. Способы задания векторов

Вектор может быть задан следующими способами:

1. Координатами вектора 

2. Координатами начальной  z

и конечной  точек.

3. Модулем вектора  и углами , M

которые он образует с координатными осями. 

При этом значения   

называются направляющими косинусами.  Oy

Между этими способами задания  a_z

векторов существует определённая связь. a_x

Например, переход от (2) к (1) xa_y

осуществляется следующим образом:

так как , то z A

. 

Переход от (3) к (1) и наоборот

осуществляется по формулам: B

 x O y

 

1.5. Деление отрезка в заданном отношении

Рассмотрим следующую задачу: даны две точки  и . Требуется найти точку  такую, что отно-шение zА

Построим векторы: М

Из условия коллинеарности векторов

 и  имеем В

Полученное равенство представим в

координатной форме х Оу

или окончательно

 (1)

Замечание 1.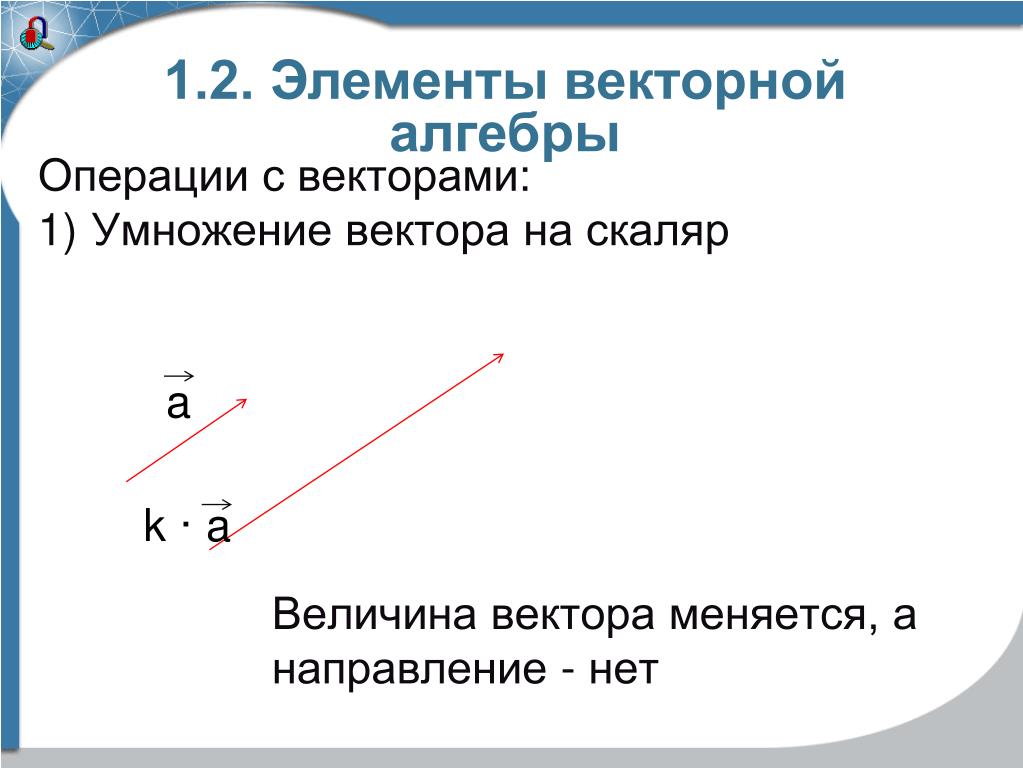  Из формул (1) следует частный случай деления отрезка пополам  

Пример 1. Треугольник задан координатами своих вершин   Найти его центр тяжести. z В

Известно, что центр тяжести треугольника

лежит на пересечении его медиан и, если

точка К  середина стороны ВС, то по А М К

свойству медиан  у

Определим вначале координаты х С

точки К: 

далее по формулам (1) получим координаты точки М:

Тема 2: Скалярное произведение

2.1. Скалярное произведение двух векторов и его основные свойства

Определение. Скалярным произведением двух векторов  и  называется число, равное произведению модулей этих векторов на косинус угла между ними и обозначается

 (2)

Замечание 2.  Формулу (2) можно представить в другой форме

 (3)

откуда получим

 

Рассмотрим механический смысл скалярного произведения. Если   постоянная сила, а   вектор перемещения, то   работа силы на перемещении 

Из определения скалярного произведения следуют его свойства:

1.   скалярное произведение коммутативно.

2. , если векторы  и  перпендикулярны (ортогональны), или хотя бы один из них является нулевым вектором.

3. 

Если воспользоваться замечанием 1 из лекции 4 и формулами (3), то легко доказать следующее свойство:

4. 

Таким образом, операции со скалярным произведением аналогичны операциям с многочленами.

2. 2. Скалярное произведение векторов, заданных координатами

Из определения и свойства (1) скалярного произведения следуют формулы: .

Аналогично получаем: 

Тогда, если

то

 (4)

2.3. Длина вектора. Угол между двумя векторами.

Направляющие косинусы

По формулам (2) и (4) получаем

откуда

 (5)

Из определения скалярного произведения и формул (4), (5) следует

 (6)

Аналогично получим

 (7)

Если в формуле (7) положить , то найдем

.

Аналогично можно получить выражения для оставшихся двух направ-ляющих косинусов

; . (8)

Замечание 3. Формулу (5) для модуля вектора можно было получить, исходя из геометрического смысла координат вектора, используя теоре-му Пифагора.

Замечание 4. Из выражений (8) для направляющих косинусов следует их основное свойство

Пример 2. Даны два вектора  Найти их скалярное произведение и угол между ними.

По формулам (5) и (7) получаем

Пример 3*. Найти координаты единичного вектора, который перпенди-кулярен вектору  и образует угол  с вектором 

Из свойства направляющих косинусов следует, что координаты еди-ничного вектора  равны значениям соответствующих направляющих косинусов и поэтому из условия задачи получаем следующую систему уравнений

Из второго уравнения системы получаем   Тогда из первого уравнения имеем . Если полученные выражения подставить в третье уравнение системы, то приходим к квадратному уравнению 

Из этого уравнения  и . Тогда окончательно нахо-дим два единичных вектора , удовлетворяющих условию задачи.

    Скачать с Depositfiles 

матриц — «Деление» обеих частей неравенства на вектор

спросил 4 года 11 месяцев назад

Изменено 4 года, 11 месяцев назад

Просмотрено 801 раз

$\begingroup$

Как ни смешно звучит вопрос, я просто имею в виду очень конкретный случай. Предположим, что мне даны два $n \times 1$ вектора $x$ и $c$, $m \times n$ матрица $A$ и $m \times 1$ вектор $y$, и следующее неравенство : 9Т А$.

Во втором случае мы можем использовать геометрическое определение, что $vx = |v|\cdot|x|\cdot cos(\theta) > 0$ всякий раз, когда $-\pi/2 <\theta < \pi/2 $.

Для наглядности, если $x$ — вектор, можно представить себе некоторую $n-1$-мерную «плоскость», к которой $x$ перпендикулярен. Тогда $vx$ положительно, когда $v$ указывает на ту же сторону «плоскости», что и $x$. Если каждая компонента $x$ неотрицательна, но не все $0$, то $x$ лежит в первом ортанте (обобщенном квадранте). Итак, если $v$ также находится в первом ортанте и $v\neq0$, то $vx$ будет положительным. Однако ясно, что есть другие $v$, которые не лежат в первом ортанте, но все еще находятся на той же стороне «плоскости», что и $x$.

Чтобы увидеть это, начертите плоскость $xy$ и проведите стрелку из начала координат в первый квадрант, называемый $x$. Тогда «плоскость» — это линия, проходящая через начало координат и перпендикулярная $x$. Наконец, любой вектор $v$, который начинается в начале координат и остается на той же стороне этой линии, что и $x$, будет иметь $vx >

0$.

Простите за грубость рисунка:

$\endgroup$

$\begingroup$

Несколько более количественный ответ: 9{T}e_{j}$ увеличивается для всех $j\neq i$.

$\endgroup$

Утверждение-1 верно, утверждение-2 неверно.

ALLEN-ЕДИНИЦЫ И РАЗМЕРЫ, БАЗОВАЯ МАТЕМАТИКА И ВЕКТОР — Упражнение (O-2) Одиночные вопросы правильного типа.

17 видео.

Войдите, если вы уже приобрели

Обновлено: 27-06-2022

Текст Решение

A

Утверждение -1 верно, утверждение-2 верно и утверждение -2 является правильным объяснением утверждения -1.

B

Утверждение-1 верно, утверждение-2 верно, а утверждение-2 НЕ является правильным объяснением утверждения-1.

C

Утверждение-1 верно, утверждение-2 ложно.

D

Утверждение-1 неверно, утверждение-2 верно.

Ответ

Правильный ответ D

Ответ

Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.

---

Похожие видео

Утверждение: — Единичный вектор используется для описания направления в пространстве. Причина: — Единичный вектор имеет единицу, поскольку его величина равна единице.

15219645

168270715

Если сумма двух единичных векторов также является вектором единичной величины, величина разности двух единичных векторов равна

571105380

Если разность двух единичных векторов также является вектором единичной величины, величина суммы двух единичных векторов равна

571105622

Если сумма двух единичных векторов также является вектором единичной величины , величина разности двух единичных векторов равна

576404403

Если разность двух единичных векторов также является вектором единичной величины, величина суммы двух единичных векторов равна

642675157

Если сумма двух единичных векторов также является вектором единичной величины, величина разности двух единичных векторов равна

642715323

Текстовое решение

величина, величина суммы двух единичных векторов равна

642715455

Если сумма двух единичных векторов также является вектором единичной величины, величина разности двух единичных векторов равна

643395049

Текст Решение

Что такое единичный вектор? Докажите, что модуль единичного вектора равен единице.