Шестнадцатиричная система счисления – умножение, вычитание в таблице
4.1
Средняя оценка: 4.1
Всего получено оценок: 198.
4.1
Средняя оценка: 4.1
Всего получено оценок: 198.
Для записи адресов и содержимого ячеек памяти компьютера используется шестнадцатеричная система счисления. Запись числовых значений в шестнадцатеричной системе счисления, а также выполнение арифметических операций над ними имеет ряд особенностей, о чем можно прочитать в данной статье.
Что такое шестнадцатеричная система счисления
Шестнадцатеричная система счисления использует для записи числовых значений шестнадцать символов: арабские цифры от 0 до 9 и буквы латинского алфавита A, B, C, D, E, F. Соответственно, основанием такой системы счисления будет число 16.
При использовании шестнадцатеричных чисел следует помнить, что в числовом ряду шестнадцатеричных чисел после числа 9 идет А, а после F следует двузначное число 10.
Перевод 16 –10
Для прямого перевода шестнадцатеричного числа в десятичную систему удобно пользоваться развернутой формой записи, когда число представляют в виде суммы, в которой слагаемые получаются путем умножения символа разряда (числа или числового эквивалента буквы) на 16 в степени соответствующего разряда.
Обратный перевод выполняется последовательным делением десятичного числа на 16 и взятия остатков от деления. Причем полученные остатки в диапазоне от 10 до 15 надо заменить соответствующей буквой.
Выполняя обратный перевод, следует помнить, что результирующее значение получают путем записи полученных от деления остатков в обратном порядке, начиная с последнего частного. Каждый остаток от деления должен получаться всегда меньше шестнадцати.
Например: 500 / 16 = 31 (остаток 4)
31 / 16 = 1 (остаток 15 заменяем на букву F)
Таким образом, получено шестнадцатеричное число 1F4.
Перевод 16 – 2
Для перевода шестнадцатеричного числа в десятичную систему каждую его цифру заменяют группой из четырех нулей и единиц, которую принято называть «тетрадой». Для перевода обычно пользуются таблицей соответствия шестнадцатеричных символов и двоичных тетрад.
Рис. 1. Таблица соответствия шестнадцатеричных чисел и их двоичных и десятичных эквивалентовНапример, 1F4 = (0001)(1111)(0100).
Арифметические действия в шестнадцатеричной системе счисления
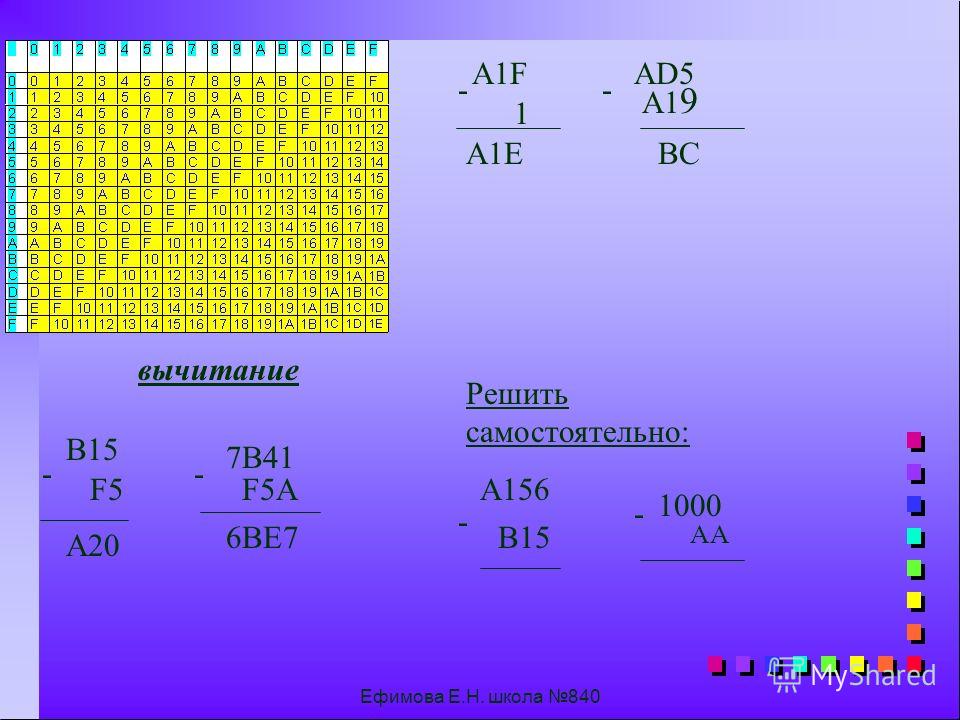
Сложение и вычитание
Операции сложения и вычитания удобно выполнять с использованием таблицы сложения шестнадцатеричных чисел. И сложение или вычитание выполняются поразрядно, начиная с младшего разряда.
Если при сложении двух чисел одинакового разряда получается двузначное число, то значение его старшего разряда (единицу) добавляют в старший разряд.
Например, 1F + 2D = 4C.
Сначала складываются значения младших разрядов F + D. По таблице получается двузначное число1С, единицу старшего разряда которого переносим и добавляем к сумме следующих по величине разрядов суммируемых шестнадцатеричных чисел.
Сумма цифр старших разрядов 1 + 2 равна 3 и еще прибавляется переносимая единица, то есть получается в сумме 4.
Таким образом, получается число 4C.
При выполнении вычитания часто возникает ситуация, когда необходимо выполнять заем из старшего разряда, если уменьшаемое конкретного разряда меньше вычитаемого. Тогда занимается единица из старшего разряда. Значение разности смотрится по таблице.
Тогда занимается единица из старшего разряда. Значение разности смотрится по таблице.
Например, 2D – 1F = E.
Сначала находят разность цифр младших разрядов, то есть D – F (в десятичном представлении 13-15). Уменьшаемое меньше вычитаемого, поэтому происходит заем единицы из старшего разряда исходного числа. То есть вычисляют разность 1D – F = E.
После выполненных манипуляций с младшими разрядами переходят к следующим по величине. В текущем примере следует вычислить 2 – 1. Но ранее произошел заем единицы и в старшем разряде уменьшаемого остается не 2, а 1. Поэтому вычисляется разность 1 – 1 = 0.
Умножение и деление
Умножать и делить числа в шестнадцатеричной системе следует также поразрядно. При вычислениях удобно пользоваться таблицей умножения шестнадцатеричной системы счисления.
Рис. 3. Таблица умножения шестнадцатеричных чиселНапример, 1С * 2 = 38. Используя распределительный закон умножения: (10 + С) * 2 = 10 * 2 + С * 2 = 20 + 18 = 38
Операция деления также выполняется столбиком с использованием таблицы умножения: 1С / 2 = Е.
Что мы узнали?
В шестнадцатеричной системе счисления для записи числовых значений используются цифры от 0 до 9 и латинские буквы от A до F. Прямой перевод шестнадцатеричного числа в десятичную систему выполняется с использованием развернутой формы записи числа. Обратный перевод выполняется путем деления и записи остатков. Каждую шестнадцатеричную цифру в числе можно заменить тетрадой двоичных чисел. Арифметические операции в шестнадцатеричной системе удобнее всего выполнять поразрядно с использованием таблиц сложения и умножения шестнадцатеричных чисел
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Роман Журавлев
10/10
Татьяна Лазарева
10/10
Коля Приходько
8/10
Андрей Букин
10/10
Игорь Карабута
1/10
Александра Цалко
8/10
Оценка статьи
4. 1
1
Средняя оценка: 4.1
Всего получено оценок: 198.
А какая ваша оценка?
Арифметические действия в различных системах счисления.
Примечание: Сложение:
Пример: Сложить 1001001110 и 100111101 в двоичной системе счисления
Ответ: 1110001011 Сложить F3B и 5A в шестнадцатеричной системе счисления
Ответ: FE0 Самое главное, не забывайте про то, что у вас в распоряжении только цифры данной системы счисления, так же не забывайте про переходы между разрядными слагаемыми.
Вычесть из 1001001110 число 100111101 в двоичной системе счисления
Ответ: 100010001 Вычесть из F3B число 5A в шестнадцатеричной системе счисления
Ответ: D96 Самое главное, не забывайте про то, что у вас в распоряжении только цифры данной системы счисления, так же не забывайте про переходы между разрядными слагаемыми. Умножение в других системах счисления происходит точно так же, как и мы привыкли умножать.
Пример: Умножить 10111 на число 1101 в двоичной системе счисления
Ответ: 100101011 Умножить F3B на число A в шестнадцатеричной системе счисления
Ответ: 984E Ответ: 984E Самое главное, не забывайте про то, что у вас в распоряжении только цифры данной системы счисления, так же не забывайте про переходы между разрядными слагаемыми. Деление в других системах счисления происходит точно так же, как и мы привыкли делить.
Пример:Разделить 1011011 на число 1101 в двоичной системе счисления
Ответ: 111 Разделить F3B на число 8 в шестнадцатеричной системе счисления
Ответ: DEF Самое главное, не забывайте про то, что у вас в распоряжении только цифры данной системы счисления, так же не забывайте про переходы между разрядными слагаемыми. НЕПОЗИЦИОННЫЕ Непозиционные системы счисленияНепозиционные системы счисления появились исторически первыми. В этих системах значение каждого цифрового символа постоянно и не зависит от его положения. Простейшим случаем непозиционной системы является единичная, для которой для обозначения чисел используется единственный символ, как правило это черта, иногда точка, которых всегда ставится количество, соответствующее обозначаемому числу:
Таким образом, этот единственный символ имеет значение единицы
Модификацией единичной системы является система с основанием, в которой есть символы не только для обозначения единицы, но и для степеней основания. Например, если за основание взято число 5, то будут дополнительные символы для обозначения 5, 25, 125 и так далее. Примером такой системы с основанием 10 является древнеегипетская, возникшая во второй половине третьего тысячеления до новой эры. В этой системе имелись следующие иероглифы:
Числа получались простым сложением, порядок следования мог быть
любым. Так, для обозначения, например, числа 3815, рисовали три цветка
лотоса, восемь пальмовых листов, одну дугу и пять шестов. Более сложные
системы с дополнительными знаками — старая греческая, римская. Новогреческая и древнерусская системы использовали в качестве цифр 27 букв алфавита, где ими обозначалось каждое число от 1 до 9, а также десятки и сотни. Такой подход обеспечил возможность записывать числа от 1 до 999 без повторений цифр. В старорусской системе для обозначения больших чисел использовались специальные обрамления вокруг цифр. В качестве словесной системы номерации до сих пор практически
везде используется непозиционная. Словесные системы нумерации сильно
привязаны в языку, и общие их элементы в основном относятся к общим
принципам и названиям больших чисел (триллион и выше). Общие принципы,
положенные в основу современных словесных нумераций вредполагают
формирование обозначения посредством сложения и умножения значений
уникальных названий. В качестве словообразующих корней в основном используются названия для чисел первого десятка и степеней десяти:
Второй десяток нередко образуется модификацией названий первого — в русском это добавление в конце суффиксоила Среди больших чисел как правило названия имеют степени тысячи:
Другие степени десяти практически вышли из употребления — 104 — тьма, мириада и т. д. Прочие числа образуются комбинированием набора слов с использованием сложения и перемножения их значений. При этом выполняемая операция зависит от типа языкового согласования слов: семнадцать тысяч — это 17·1000 = 17 000, а тысяча семнадцать — это 1000+17 = 1017. |
Электроника и схемотехника: Примеры шестнадцатеричных делений
Примеры шестнадцатеричных делений
Примеры шестнадцатеричных деленийЭто моя четвертая и последняя статья о шестнадцатеричной арифметике. В этом посте я решу несколько примеров по делению шестнадцатеричных чисел. Прежде чем приступить к этой теме, вы должны знать, как умножать шестнадцатеричные числа. Вот моя статья об умножении шестнадцатеричных чисел.
Ключевые вопросы:
Как выполнить шестнадцатеричное деление?
Как выполнить деление дробных шестнадцатеричных чисел?
Примеры шестнадцатеричного деления:
Деление шестнадцатеричных чисел такое же, как и в других системах счисления. Все правила и принципы одинаковы. Вы можете проверить свои результаты с помощью этого онлайн-калькулятора.
Все правила и принципы одинаковы. Вы можете проверить свои результаты с помощью этого онлайн-калькулятора.
5÷6 в этом 5 делимое и 6 делитель
Я рассмотрю три случая с помощью трех примеров. В первом случае делимое и делитель являются целыми числами. Во втором случае делимое имеет дробную часть, а делитель — целое число. В третьем случае и делимое, и делитель имеют дробные части.
Example#01:AE887)16÷3A)16
Сначала составьте таблицу умножения для числа 3A и его кратных чисел
003A*1 | 3А |
3А*2 | 74 |
3А*3 | АЕ |
3А*4 | Е8 |
3А*5 | 122 |
3А*6 | 15С |
3А*7 | 196 |
3А*8 | 1D0 |
3А*9 | 20А |
3А*А | 244 |
3А*В | 27Е |
3025.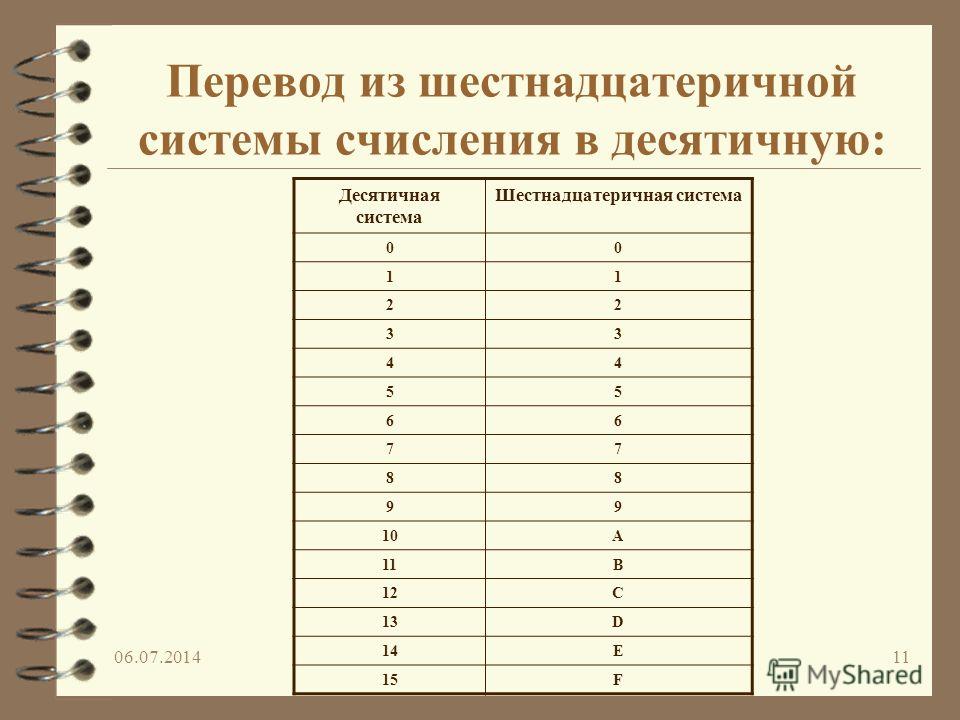 A3
A3
3A⟌AE887
AE
X88
74
147
122
250
244
B0
AE
2
Ответ: 3025.A3) 16
Пример № 02: ECE.46) 16 ÷ 12) 16
Первая таблица умножения для 12
12*1 | |
12*1 | |
12*1 | 12 |
12*2 | 24 |
12*3 | 36 |
12*4 | 48 |
12*5 | 5А |
12*6 | 6С |
12*7 | 7Е |
12*8 | 90 |
12*9 | А2 |
12*А | В4 |
12*В | С6 |
12*С | Д8 |
12*D | ЕА |
D2. 92
92
12⟌ ECE.46
EA
2E
24
A4
A2
26
0007
24
2
Ответ: D2.92) 16
Пример № 03: 257.8a) 16 ÷ 5,1) 16
Сдвигая шестнадцатеричная точка облегчает проблему. Согласно математическому правилу, если вы сдвинете шестнадцатеричную точку делимого на одно место, то вы должны сдвинуть шестнадцатеричную точку делителя.
После переключения
2578.A÷51
51*1 | 51 |
51*2 | А2 |
51*3 | F3 |
51*4 | 144 |
51*5 | 195 |
51*6 | 1Е6 |
51*7 | 237 |
51*8 | 288 |
51*9 | 2D9 |
51*А | 32А |
51*В | 37Б |
51*С | 3CC |
51*Д | 41Д |
76. 6D
6D
51⟌2578.A
237
208
1E6
22A
1E6
440
41D
33
Answer: 76.6D)16
Newer Post Старый пост Главная
Подписаться на: Комментарии к сообщениям (Atom)
Популярные сообщения
Примеры сложения восьмеричных чисел
Примеры сложения восьмеричных чисел Это моя первая статья о восьмеричной арифметике. В этом посте я объясню два…
Двойственность в электрических цепях
Принцип двойственности в электрических цепях Интересно знать, как системы связаны друг с другом. Как механическая система…
Решенные примеры восьмеричного вычитания
Примеры восьмеричного вычитания Это моя вторая статья о восьмеричной арифметике.
 В этом посте я объясню восьмеричное число…
В этом посте я объясню восьмеричное число…Примеры шестнадцатеричных делений
Примеры шестнадцатеричных делений Это моя четвертая и последняя статья о шестнадцатеричной арифметике. В этом посте я решу некоторые упр…
Примеры шестнадцатеричных умножений
Шестнадцатеричное умножение Это моя третья статья о шестнадцатеричной арифметике. В этом посте я объясню, как умножить два…
Примеры решения восьмеричного деления
Примеры решения восьмеричного деления Это моя четвертая статья о восьмеричной арифметике. В этой статье я собираюсь решить некоторые э…
Анализ линии нагрузки (диоды)
В этом руководстве рассматриваются следующие концепции. Описание: Что такое грузовая линия? Как нарисовать линию нагрузки? Какой характеристический ток…
Матрица набора галстуков | Фундаментальная матрица циклов — граф электрических сетей
Это моя третья статья о графах электрических сетей.
 В этой статье я собираюсь объяснить матрицу набора галстуков. Матрица набора галстуков также…
В этой статье я собираюсь объяснить матрицу набора галстуков. Матрица набора галстуков также…Примеры решения восьмеричного умножения
Примеры решения восьмеричного умножения Это моя третья статья о восьмеричной арифметике. В этой статье я собираюсь объяснить восьмеричное…
Шестнадцатеричное вычитание 16 с дополнением
Шестнадцатеричное вычитание Это моя вторая статья о шестнадцатеричной арифметике. В этой статье я объясню вычитание ч…
Шестнадцатеричный калькулятор
Шестнадцатеричный калькулятор выполняет алгебраические операции над шестнадцатеричными числами. Он может выполнять основные 4 операции, включая сложение, вычитание, умножение и деление.
Выдаст ответ в шестнадцатеричной системе счисления. Вы найдете все математические операции, выполняемые над десятичной формой введенных шестнадцатеричных чисел.
Что такое шестнадцатеричные числа?
Шестнадцатеричная система счисления аналогична десятичной, двоичной и восьмеричной системам счисления. Он использует основание шестнадцать (16). Шестнадцать шестнадцатеричных цифр включают цифры от 0 до 9 и алфавиты от A до F.
Он использует основание шестнадцать (16). Шестнадцать шестнадцатеричных цифр включают цифры от 0 до 9 и алфавиты от A до F.
Буква A означает 10, B — 11, C — 12 и т. д. Эта система счисления используется в различных областях компьютера. Основная цель этой системы заключается в том, что она сжимает двоичные числа, чтобы сэкономить место для лучшей работы.
Алгебраические операции над шестнадцатеричными числами
Операции выполняются как в десятичной системе счисления. Разница возникает там, где задействованы преобразования.
В статье ниже мы последовательно рассмотрим каждую операцию. Но прежде чем перейти к операциям, давайте кратко рассмотрим преобразование десятичного числа в шестнадцатеричное и шестнадцатеричного в десятичное.
Преобразование десятичных дробей в шестнадцатеричные: Разделите число на 16 и запишите частное и остаток. Отметьте этот остаток как единицу и найдите его шестнадцатеричный эквивалент. Теперь возьмите предыдущее частное и повторите.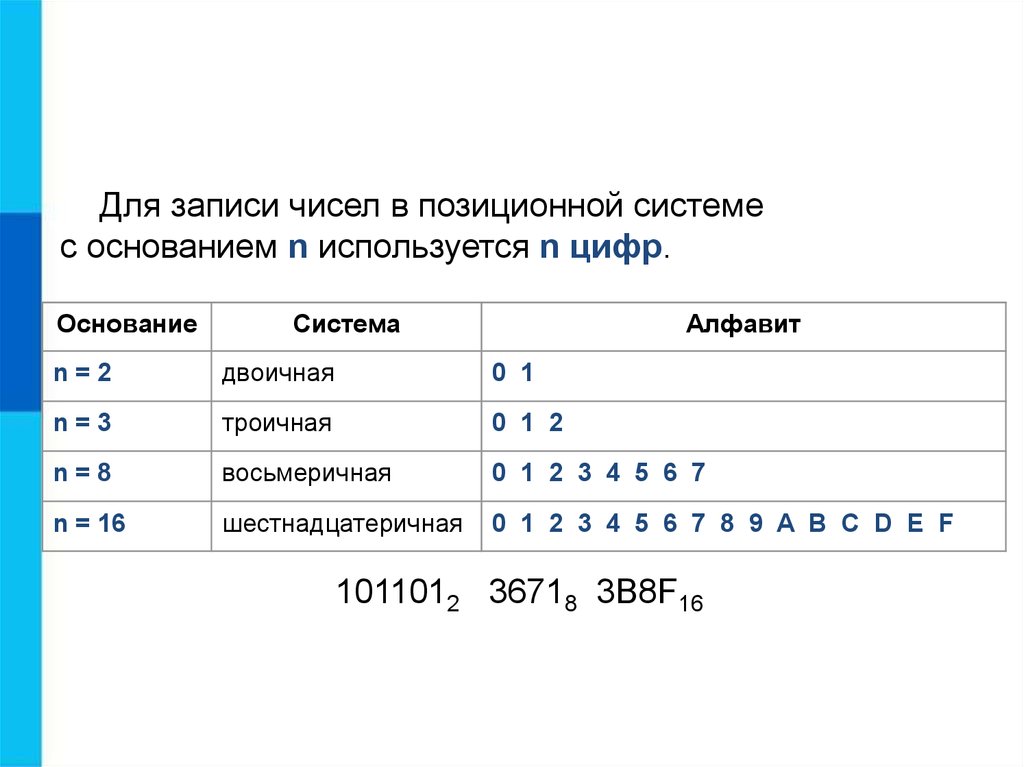 Отметьте этот остаток как два.
Отметьте этот остаток как два.
Продолжайте этот процесс, пока само частное не станет меньше 16. Давайте посмотрим на пример.
Пример:
Преобразование 1256 10 в шестнадцатеричную систему.
Решение:
Дивизион | Коэффициент | .0007 | |||
1256/16 | 78 | 8 | 8 | 0 | |
78/16 | 4 | 14 | E | 1 | |
4/16 | Нет | 4 | 4 | 0007 | 2 |
Запишите цифры снизу вверх как 4E8 16 . Вместо этого используйте десятичный преобразователь в шестнадцатеричный.
Примечание: Цифры начинаются с 0, потому что для обратного преобразования эти числа нужно возводить в степень. Степени в таких преобразованиях начинаются с 0. См. следующий заголовок.
Преобразование шестнадцатеричных чисел в десятичныеШестнадцатеричные числа преобразуются в десятичные таким же образом, как двоичные преобразуются в десятичные. Найдите разрядное значение каждого шестнадцатеричного числа. Возведите 16 в эту степень (разрядное значение) и умножьте на цифру. Добавьте все числа.
Пример:
Найдите десятичное значение DEF .
Решение:
Шаг 1: Найдите разрядные значения.
- F на месте 0
- E на месте 1
- D на месте 2
Шаг 2: Возведите эти значения в степени и умножьте на цифры.
- Как F = 15 10 , 15 10 x 16 0 = 15 10
- E = 14 10 , 14 10 x 16 1 = 224 10
- D = 13 10 , 13 10 x 160777 2 , 13 10 1 2 , 13 10
111 2 2 , 13 10
11 2 2 .
 Шаг 3: Добавьте эти числа.
Шаг 3: Добавьте эти числа.= 3328 10 + 224 10 + 15 10
= 3567 10
Теперь это время. Попробуйте преобразовать шестнадцатеричное число в десятичное.
Как добавить шестнадцатеричные числа?Измените алфавиты на их десятичные эквиваленты и добавьте шестнадцатеричные числа. Но прежде чем их писать, вы должны изменить их на шестнадцатеричные, так как сложение было в десятичных числах.
Пример шестнадцатеричного добавления:
Добавить 1E4 и 33D .
Решение:
В этом вычислении мы сначала добавили 4 и D. Так как D = 13, то 4+13 = 17 10 это 11 16 . Возьмем 1 как перенос в E. Тогда E = 14, поэтому 14+1+3 = 18 10 = 12 16 . Наконец, 1+1+3 = 5 10 , что то же самое в шестнадцатеричной системе.
Как вычитать шестнадцатеричные числа?
Также похоже на шестнадцатеричное сложение. Но вы должны быть осторожны в заимствовании чисел. При шестнадцатеричном вычитании, когда вы заимствуете 1 из предыдущего числа, вы добавляете 16 к текущему числу. Потому что 16 шестнадцатеричных равно 10 десятичных.
Пример шестнадцатеричного вычитания:Вычтите
5AF из F89.Решение:
В первом столбце 9 меньше, чем F, которое на самом деле равно 15. При заимствовании 1 из предыдущей цифры 8 вы получаете следующие вычисления: 9 + 16 — 15 = 10 10 = А 16 . Во втором ряду снова требуется заимствование. 8 стало 7. Таким образом, при заимствовании 16 + 7 — A = 16 + 7 — 10 = 14 10 = D 16 . В последней строке есть E в первой строке, потому что она была уменьшена во время предыдущего заимствования.
Как умножать шестнадцатеричные числа? Итак, Е — 5 = 14 — 5 = 9 10 . То же самое и в шестнадцатеричном формате.
Итак, Е — 5 = 14 — 5 = 9 10 . То же самое и в шестнадцатеричном формате.Умножать шестнадцатеричные числа довольно сложно. Каждый раз, когда строка умножается на цифру, преобразования будут выполняться так же, как и в последний раз при сложении.
Пример шестнадцатеричного умножения:Умножить
44A по FA .Решение:
для первого ряда (44a x a):
A, умноженное на A, на самом деле 10 умножен на 10. Ответ 100 10 преобразуется в HEX 64 16 . 4 остается внизу, а 6 идет в качестве переноса. Далее A x 4 = 40 10 . Теперь добавьте 6 переносов к этому 40 10 , ответ будет 46 10 = 2E 16 . E находится внизу, а 2 снова идет как перенос. Так как А х 4 = 40 10 + 2 10 = 42 10 = 2А 16 .
 Ответ 2AE4.
Ответ 2AE4.Для второго ряда (44A x F):
A x F = 10 10 x 15 10 = 150 10 = 96 16 . Оставьте 6 внизу и поставьте 9 в качестве переноски. F x 4 = 15 10 x 4 10 = 60 10 . Добавьте 9 10 , получится 69 10 , что равно 45 16 . Наконец, используйте те же знания, чтобы снова умножить 4 x F и добавить перенос. Окончательный ответ в этой строке — 4456.
Добавьте 2AD4 и 4456 , используя метод сложения.
Как разделить шестнадцатеричные числа?Лучший способ деления шестнадцатеричных чисел — преобразовать шестнадцатеричные числа в десятичные, выполнить деление в длинное число и затем преобразовать обратно. Или другой способ — разделить, используя сами шестнадцатеричные числа.
Для шестнадцатеричных чисел лучше составить таблицу умножения делителей и затем использовать эти значения для выполнения длинного деления.

В приведенном ниже примере представлены шестнадцатеричные числа.
Пример шестнадцатеричного деления:Разделить
DACE на E .Решение:
Шаг 1: Составьте таблицу умножения.
Multiple
Hex multiple
Decimal value
E x 1
E
14
E x 2
1C
28
E x 3
28
42
E x 4
38
56
E X 5
46
9 9 041 E x 6
54
84
E x 7
62
98
E x 8
70
112
E X
7E
126
E X 10 / E x A
E X 10 / E x A
8C
140
Шаг 2: Выполнить деление в большую сторону.



 Из этого можно сформулировать правило:
Из этого можно сформулировать правило: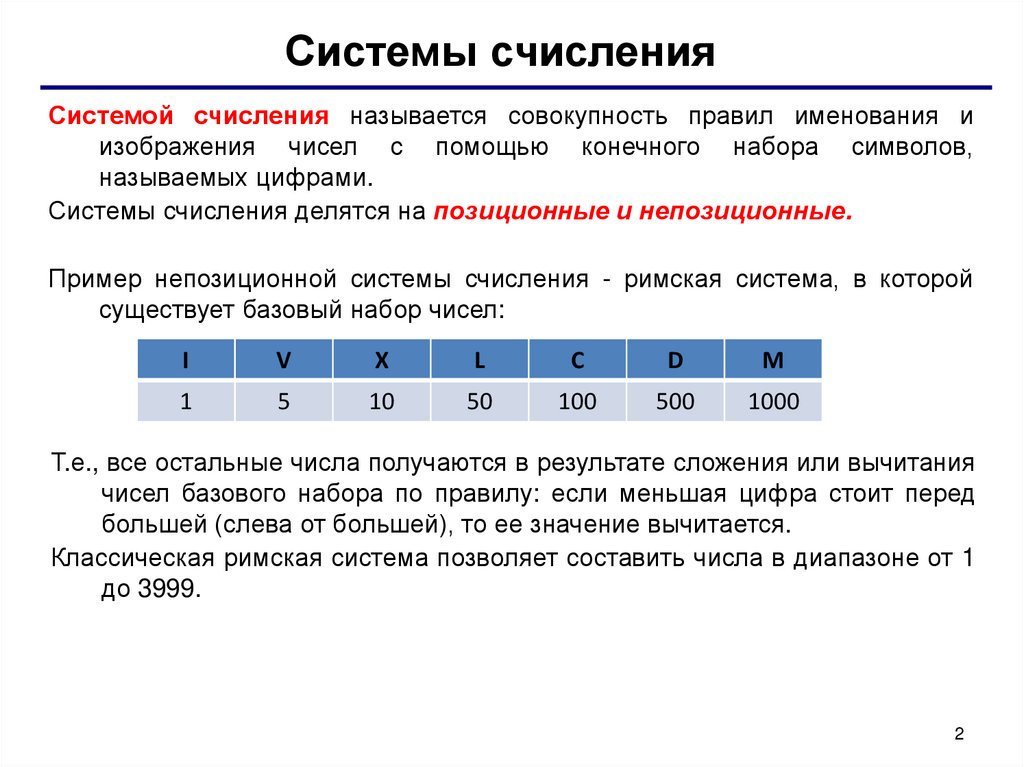


 д.
д.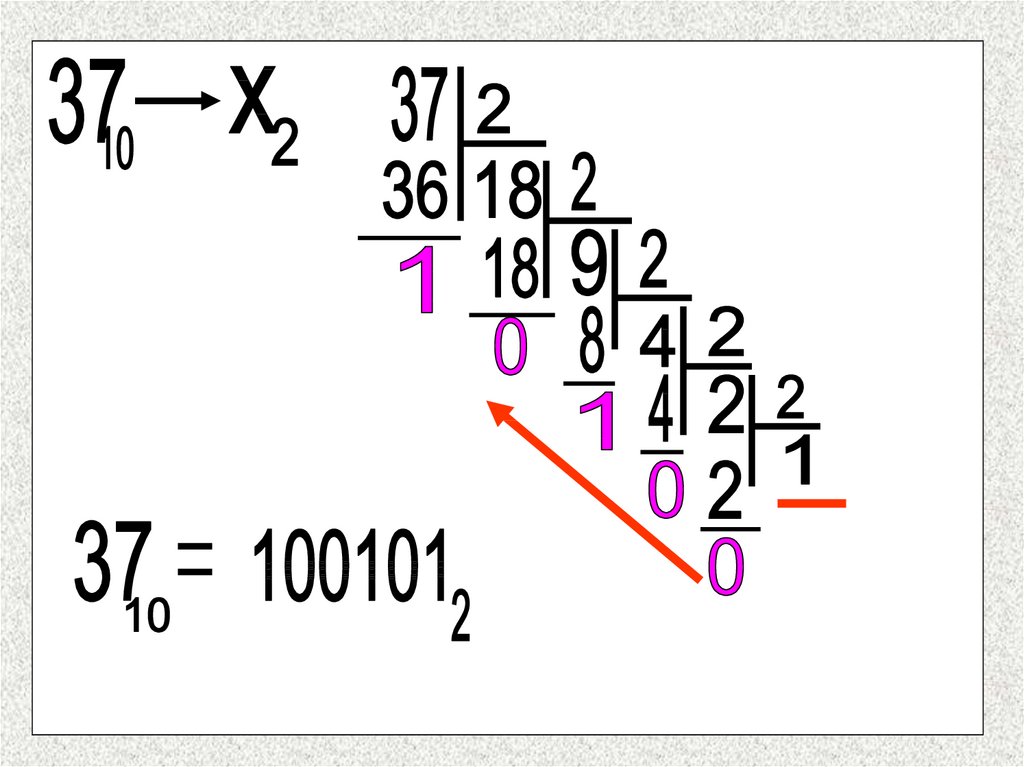 Римская
также использует элемент позиционной системы — большая цифра, стоящая
перед меньшей, прибавляется, меньшая перед большей — вычитается: IV = 4,
но VI = 6, этот метод, правда, применяется исключительно для
обозначения чисел 4, 9, 40, 90, 400, 900, 4000, и производных их
сложением.
Римская
также использует элемент позиционной системы — большая цифра, стоящая
перед меньшей, прибавляется, меньшая перед большей — вычитается: IV = 4,
но VI = 6, этот метод, правда, применяется исключительно для
обозначения чисел 4, 9, 40, 90, 400, 900, 4000, и производных их
сложением.
 д.
д. В этом посте я объясню восьмеричное число…
В этом посте я объясню восьмеричное число…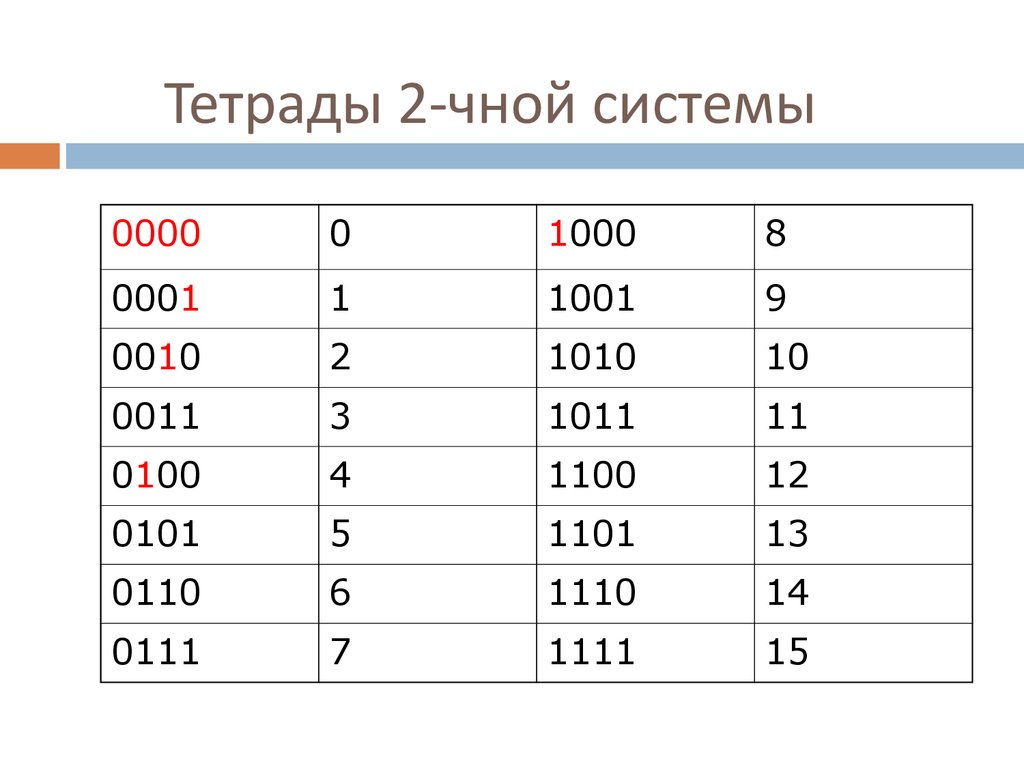 В этой статье я собираюсь объяснить матрицу набора галстуков. Матрица набора галстуков также…
В этой статье я собираюсь объяснить матрицу набора галстуков. Матрица набора галстуков также… Шаг 3: Добавьте эти числа.
Шаг 3: Добавьте эти числа.
 Итак, Е — 5 = 14 — 5 = 9 10 . То же самое и в шестнадцатеричном формате.
Итак, Е — 5 = 14 — 5 = 9 10 . То же самое и в шестнадцатеричном формате. Ответ 2AE4.
Ответ 2AE4.
