Сложение и вычитание векторов, умножение вектора на число

Используй поиск, чтобы найти научные материалы и собрать список литературы

База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны

Содержание статьи

1. Откладывание вектора от данной точки

2. Сложение векторов. Правило треугольника

3. Вычитание векторов

4. Построение разности двух векторов рассмотрим с помощью задачи

5. Умножение вектора на число

6. Пример задачи

Откладывание вектора от данной точки

Перед тем как ввести понятие суммы, разности векторов и умножения вектора на число, вначале разберем такое понятие, как откладывание вектора от точки.

Определение 1

Если точка $A$ начала какого-либо вектора $\overrightarrow{a}$, то говорят, что вектор $\overrightarrow{a}$ отложен от точки $A$ (рис. 1).

Рисунок 1.

Теорема 1

От любой точки $K$ можно отложить вектор единственный $\overrightarrow{a}$.

Доказательство.

Существование: Имеем два следующих случая:

1. Вектор $\overrightarrow{a}$ — нулевой.

   Здесь получаем, что искомый нами вектор совпадает с вектором $\overrightarrow{KK}$.

2. Вектор $\overrightarrow{a}$ не является нулевым.

   Пусть точка $A$ является началом вектора $\overrightarrow{a}$, а точкой $B$ — конец вектора $\overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $\overrightarrow{a}$. Будем откладывать на прямой отрезки $\left|KL\right|=|AB|$ и $\left|KM\right|=|AB|$. Рассмотрим векторы $\overrightarrow{KL}$ и $\overrightarrow{KM}$. Из этих двух векторов нужный нам вектор — вектор, сонаправленный с вектором $\overrightarrow{a}$ (рис.2)

   Рисунок 2.

Из данного выше построения сразу же будет следовать единственность данного вектора.

Сложение векторов. Правило треугольника

Рассмотрим векторы $\overrightarrow{a}$ и $\overrightarrow{b}$.

Определение 2

Вектор $\overrightarrow{c}=\overrightarrow{AC}$ называется суммой векторов $\overrightarrow{a}+\overrightarrow{b}$ который получается из векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ следующим образом: От точки $A$ отложим $\overrightarrow{AB}=\overrightarrow{a}$, от точки $B$ отложим $\overrightarrow{BC}=\overrightarrow{b}$ и соединим точку $A$ c точкой $C$ (рис. 3).

Рисунок 3.

Замечание 1

Также это определение называется правилом треугольника для сложения двух векторов.

Отметим несколько свойств сложения двух векторов:

1. Для произвольного вектора $\overrightarrow{a}$ выполняется равенство

   \[\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{a}\]

2. Для произвольных точек $A,\ B\ и\ C$ справедливо следующее равенство

   \[\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\]

Замечание 2

Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Вычитание векторов

Рассмотрим векторы $\overrightarrow{a}$ и $\overrightarrow{b}$.

Определение 3

Разностью двух векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ называется такой вектор $\overrightarrow{c}$, который при сложении с вектором $\overrightarrow{b}$ дает вектор $\overrightarrow{a}$, то есть

\[\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{a}\]

Обозначение: $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{c}$.

Построение разности двух векторов рассмотрим с помощью задачи

Пример 1

Пусть даны векторы $\overrightarrow{a}$ и $\overrightarrow{b}$. Построить вектор $\overrightarrow{a}-\overrightarrow{b}$.

Решение.

Построим произвольную точку $O$ и отложим от нее векторы $\overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OB}=\overrightarrow{b}$. Соединив точку $B$ с точкой $A$, получим вектор $\overrightarrow{BA}$ (рис. 4).

Рисунок 4.

По правилу треугольника для построения суммы двух векторов видим, что

\[\overrightarrow{OB}+\overrightarrow{BA}=\overrightarrow{OA}\]

То есть

\[\overrightarrow{b}+\overrightarrow{BA}=\overrightarrow{a}\]

Из определения 2, получаем, что

\[\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{BA}\]

Ответ: $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{BA}$.

Из этой задачи получаем следующее правило для нахождения разности двух векторов. Чтобы найти разность $\overrightarrow{a}-\overrightarrow{b}$ нужно от произвольной точки $O$ отложить векторы $\overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OB}=\overrightarrow{b}$ и соединить конец второго вектор с концом первого вектора.

Умножение вектора на число

Пусть нам дан вектор $\overrightarrow{a\ }$ и действительное число $k$.

Определение 4

Произведением вектора $\overrightarrow{a\ }$ на действительное число $k$ называется вектор $\overrightarrow{b\ }$ удовлетворяющий следующим условиям:

1. Длина вектора $\overrightarrow{b\ }$ равна $\left|\overrightarrow{b\ }\right|=\left|k\right||\overrightarrow{a\ }|$;

2. Векторы $\overrightarrow{a\ }$ и $\overrightarrow{b\ }$ сонаправлены, при $k\ge 0$ и противоположно направлены, если $k

Обозначение: $\ \overrightarrow{b\ }=k\overrightarrow{a\ }$.

Пример задачи

Пример 2

Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_1}=\overrightarrow{AC_1}$

Рисунок 5.

Доказательство.

Воспользуемся свойством правила треугольника $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, получим:

\[\overrightarrow{AC_1}=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{CC_1}\]

Так как $\overrightarrow{DC}=\overrightarrow{AB},\ \ \overrightarrow{CC_1}=\overrightarrow{AA_1}$

То есть

\[\overrightarrow{AC_1}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_1}\]

ч.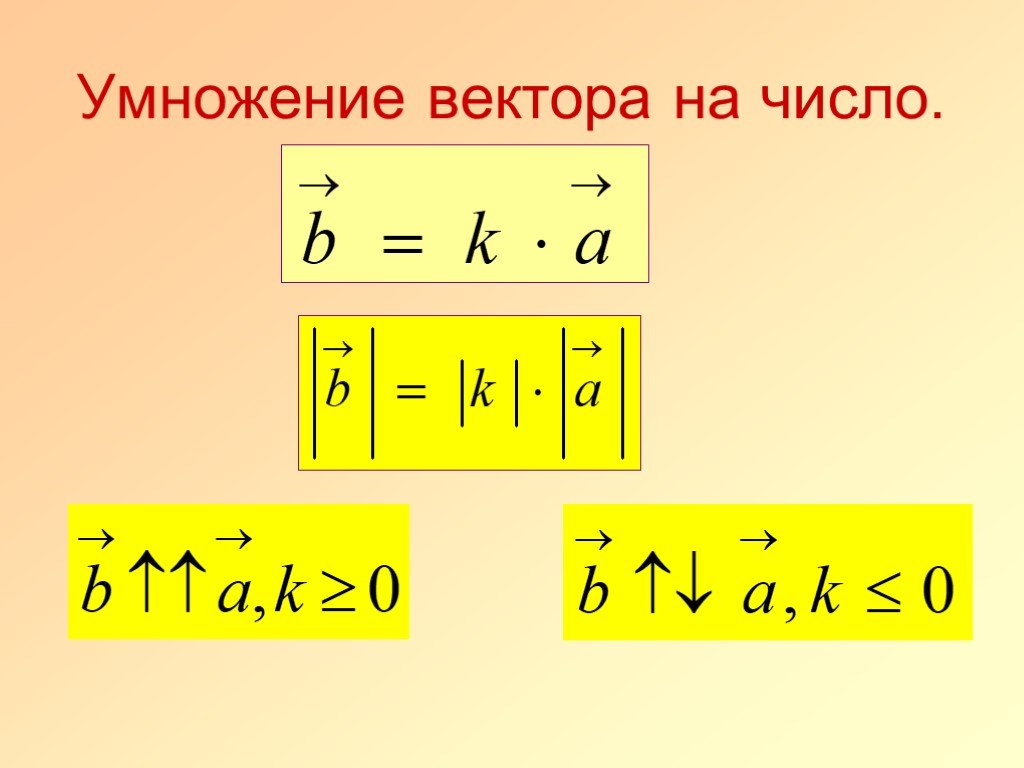 т. д.

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 27.04.2022

Выполнение любых типов работ по математике

Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами

Подбор готовых материалов по теме

Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы

Сложение и вычитание векторов.

Умножение вектора на число в координатах 9 класс онлайн-подготовка на Ростелеком Лицей |

Напоминание предыдущего материала

 

Ранее для выполнения действий с векторами мы применяли правило треугольника, правило параллелограмма, сжимали или растягивали вектор. Теперь мы научимся выполнять действия над векторами в координатах.

 

Пример

Даны векторы , ,  (см. рис. 1).

Рис. 1. Задача о сложении векторов

Найти:

Решение

Из произвольной точки  строим вектор . Далее из конца вектора  строим вектор , он сонаправлен вектору , а длина в два раза больше. Теперь из конца вектора  строим вектор , он противоположно направлен вектору , а длина в 4 раза больше. Теперь соединяем точку  и конец вектора  – получен ответ, вектор  (см. рис. 2).

Рис. 2. Решение задачи

Пусть заданы два неколлинеарных вектора. Будучи отложены из одной точки, они задают косоугольную систему координат (см. рис. 3).

Рис. 3. Косоугольная система координат

Любой третий вектор однозначно выражается через векторы , :

Пара чисел  однозначно задает вектор – это и есть его координаты: .

 

Сложение векторов в координатах

 

 

Теорема

 

Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

Дано:; .

Доказать:.

Доказательство

В системе координат относительно векторов ,  имеем:

;

Тогда сумма:

Что и требовалось доказать: .

 

Умножение вектора на число в координатах

 

 

Теорема

 

Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число.

Дано:.

Доказать:.

Доказательство

В системе координат относительно векторов ,  имеем:

Умножим обе части равенства на число :

Что и требовалось доказать: .

 

Вычитание векторов в координатах

 

 

Рассмотрим разность векторов.

 

Дано: ; .

Координаты вектора  определяем как координаты вектора, умноженного на число:

Тогда разность векторов:

 

Решение примеров

 

 

Пример

 

Доказать, что если два вектора коллинеарны, то их координаты пропорциональны.

Решение

Дано: ; , .

Доказать: ; .

По определению коллинеарных векторов векторы  и  лежат на одной прямой или на параллельных прямых. В таком случае вектор  можно получить из вектора  умножением на некоторое число:

 по условию;  по правилу умножения вектора на число.

Равные векторы имеют равные координаты, отсюда:

;

Что и требовалось доказать.

Пример

; ; ;

Найти попарно коллинеарные векторы.

Решение

Очевидно, что нужно искать пропорциональные координаты. Рассмотрим первый и третий векторы:

Получено верное равенство, следовательно, векторы коллинеарны: .

Рассмотрим второй и четвертый векторы:

Также получено истинное выражение, а значит, векторы коллинеарны: .

Ответ:; .

 

Вывод

 

 

Итак, мы научились складывать и вычитать векторы, умножать вектор на число в координатах.

 

 

Список литературы

1. Атанасян Л.С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.

2. Фарков А.В. Тесты по геометрии: 9 класс. К учебнику Л.С. Атанасяна и др. – М.: Экзамен, 2010.

3. Погорелов А.В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт mathprofi.ru (Источник)

2. Интернет-сайт cleverstudents.ru (Источник)

3. Интернет-сайт edu.dvgups.ru (Источник)

 

Домашнее задание

1. Вектор  с началом в точке  имеет координаты .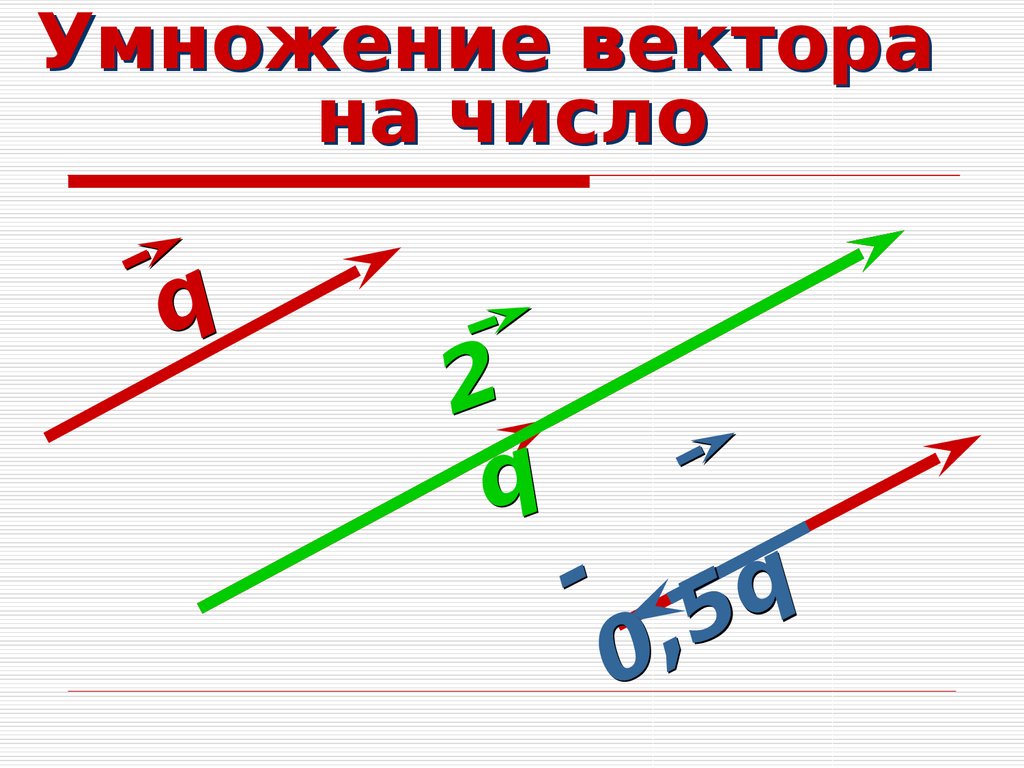 Найдите сумму координат точки .

2. Заданы векторы  и . Найти координаты вектора .

3. Даны векторы  и . Найти векторы ; .

4.Даны векторы ,  и . Найти   и  

 

Деление и умножение на векторы. Какое направление?

Задавать вопрос

спросил 6 лет, 2 месяца назад

Изменено 6 лет, 2 месяца назад

Просмотрено 893 раза

$\begingroup$ 9{-1} \, \hat i$, в каком направлении находится $\vec v$? Точно так же, если бы у вас была величина, разделенная на вектор, $\frac{13 \, \text{kg}}{1,6 \, \text{m}, \, \hat i}$, каково направление?

Я столкнулся с этим в физике и рассматривал единичные векторы почти как единицы, потому что для меня это работает математически (кроме случаев, когда есть два направления). Я знаю, что это неправильно, что и послужило причиной этого вопроса.

Кроме того, правильно ли я записываю векторы?

• векторов

$\endgroup$

6

$\begingroup$

Ваша нотация для векторов подойдет большинству. Однако вы не можете умножать или делить на векторы; вы можете только умножать или делить вектор на скаляр. В вашем случае нет смысла в «квадрате 12,5 метра в секунду на восток» или «13 килограммов, разделенных на 1,6 метра на восток», но «дважды 12,5 метра в секунду на восток» имеет значение: 25 метров в секунду на восток. Поскольку операции, которые вы хотите выполнить, не определены, нет связанного направления.

Интуитивно один из способов увидеть, что системы умножения и деления на векторы для получения векторов не существует, состоит в том, что существует бесконечно много единичных векторов. В этом посте есть больше информации о том, почему деление по векторам не определено.

Есть одно исключение из этого запретного принципа: комплексные числа иногда представляются в виде векторов, и они допускают умножение и деление. Но так как вы добавляете единицы в свои количества, они не являются комплексными числами…

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

комплексных чисел. Почему мы не определяем векторное умножение и деление?

спросил 1 год, 9 месяцев назад

Изменено 1 год, 9 месяцев назад

Просмотрено 104 раза

$\begingroup$

Рассмотрим два плоских вектора:

$$V= a \hat{x} + b \hat{y}$$

И $$ U = a’ \hat{x} + b’ \hat{y}$$

Они аналогичны комплексным числам:

$$ v = a + bi$$

и,

$$u= a’ + b’ i$$

Теперь существуют четкие правила умножения $ v \cdot u$ а также выражение: $ \frac{v}{u}$ , также существует геометрическая интерпретация (если смотреть в полярной форме). Тогда почему мы не упоминаем эти произведения, когда говорим о векторах, а обсуждаем только скалярное и векторное произведение?

• комплексные числа
• векторы

$\endgroup$

2

$\begingroup$

Предложенный вами продукт в некотором смысле является геометрическим, но между ним и точечным и перекрестным произведениями есть принципиальное отличие. Представьте, что у вас есть стол или другая плоская горизонтальная поверхность, и на ней нарисованы две стрелки, обозначающие векторы. Вот вопрос: каково «комплексное число» произведения этих двух векторов?

Ответить на этот вопрос невозможно. Возможно, это легче всего увидеть, заметив, что вы не можете найти полярную форму векторов, потому что угол зависит от системы координат («базис»), а мы ее не указали. Другими словами, произведение «комплексных чисел» зависит не только от векторов, но и от (совершенно произвольного) выбора координат.

Напротив, скалярное произведение и векторное произведение можно понимать без ссылки на какую-либо конкретную систему координат. Скалярное произведение одинаково в любом ортонормированном базисе (то есть в системе координат, состоящей из векторов единичной длины, которые все перпендикулярны друг другу). Это также верно и для перекрестного произведения, при условии, что два основания имеют одинаковую хиральность (то есть вы можете превратить одно основание в другое).