ТОЭ Лекции — №13 Действующее значение переменного тока
Понятие действующего значения тока вводится в связи с необходимостью производства измерений. Что измерять у переменного тока? Если бы мы имели дело только с синусоидами – кривыми одной формы, то можно было бы измерять амплитуды. Но на практике встречаются самые разные кривые, и может оказаться так, что два различных по форме тока имеют одинаковые амплитуды, хотя очевидно, что на электрическую цепь они будут оказывать разное воздействие.
Поэтому наиболее целесообразно оценивать величину тока по той работе, которую он
совершает. При такой оценке действие переменного тока сравнивается с аналогичным действием постоянного
тока. Например, если некоторый переменный ток выделяет на участке цепи такое же количество тепла, что и
постоянный ток силой 10 ампер, то говорят, что величина этого переменного тока составляет 10 ампер.
Итак, действующим значением переменного тока называется численное значение такого постоянного тока, который за время, равное одному периоду, выделяет в сопротивлении такое же количество тепла, что и ток переменный..
Таким образом, для оценки величины переменного тока мы должны сделать следующее.
1.Определить количество теплоты, выделяющейся в сопротивлении R за время Т при протекании переменного тока i. Это количество теплоты равно:
2.Подобрать такой постоянный ток I, который за то же время Т в том же сопротивлении R выделяет такое же количество тепла. При постоянном токе оно равно: W=I2RT.
3. Приравнять W=W:
откуда
Последняя формула и определяет действующее значение переменного тока.
Пример 2.1. На вход некоторой цепи
подается импульсное напряжение треугольной формы (рис.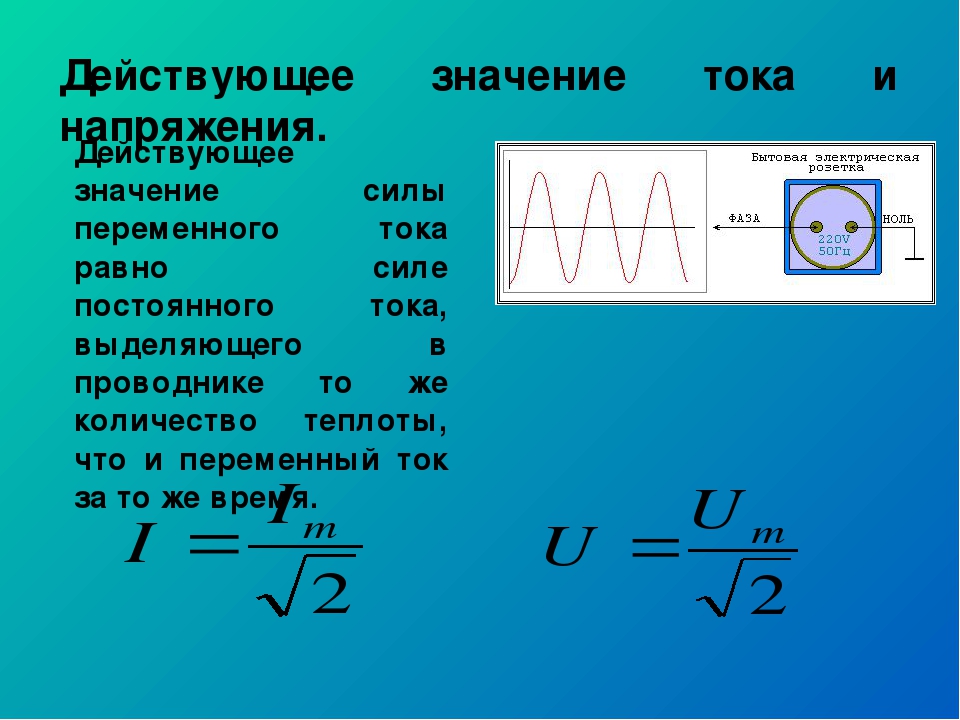 13.1, а). Чему равно его действующее значение?
13.1, а). Чему равно его действующее значение?
Решение
Пример 2.2. На рис. 13.1, б показана кривая напряжения на выходе схемы однофазного однополупериодного выпрямления. Чему равно действующее значение напряжения, если его амплитудное значение Um составляет 311 В?
Решение
Пример 2.3. Определить действующее значение синусоидального тока i=Imsin(ωt):
Решение
Рассмотренные примеры показывают, что действующее значение переменного тока зависит от его формы.
Действующие значения тока и напряжения формулы. Эффективное, действующее напряжение, сила тока
Как известно, переменная э.д.с. индукции вызывает в цепи переменный ток. При наибольшем значении э.д.с. сила тока будет иметь максимальное значение и наоборот. Это явление называется совпадением по фазе. Несмотря на то что значения силы тока могут колебаться от нуля и до определенного максимального значения, имеются приборы, с помощью которых можно замерить силу переменного тока.
Характеристикой переменного тока могут быть действия, которые не зависят от направления тока и могут быть такими же, как и при постоянном токе. К таким действиям можно отнести тепловое. К примеру, переменный ток протекает через проводник с заданным сопротивлением. Через определенный промежуток времени в этом проводнике выделится какое-то количество тепла. Можно подобрать такое значение силы постоянного тока, чтобы на этом же проводнике за то же время выделялось этим током такое же количество тепла, что и при переменном токе. Такое значение постоянного тока называется действующим значением силы переменного тока.
В данное время в мировой промышленной практике широко распространен трехфазный переменный ток , который имеет множество преимуществ перед однофазным током. Трехфазной называют такую систему, которая имеет три электрические цепи со своими переменными э.д.с. с одинаковыми амплитудами и частотой, но сдвинутые по фазе относительно друг друга на 120° или на 1/3 периода. Каждая такая цепь называется фазой.
Каждая такая цепь называется фазой.
Для получения трехфазной системы нужно взять три одинаковых генератора переменного однофазного тока, соединить их роторы между собой, чтобы они не меняли свое положение при вращении. Статорные обмотки этих генераторов должны быть повернуты относительно друг друга на 120° в сторону вращения ротора. Пример такой системы показан на рис. 3.4.б.
Согласно вышеперечисленным условиям, выясняется, что э.д.с., возникающая во втором генераторе, не будет успевать измениться, по сравнению с э.д.с. первого генератора, т. е. она будет опаздывать на 120°. Э.д.с. третьего генератора также будет опаздывать по отношению ко второму на 120°.
Однако такой способ получения переменного трехфазного тока весьма громоздкий и экономически невыгодный. Чтобы упростить задачу, нужно все статорные обмотки генераторов совместить в одном корпусе. Такой генератор получил название генератор трехфазного тока (рис. 3.4.а). Когда ротор начинает вращаться, в каждой обмотке возникает
а) б)
Рис. 3.4. Пример трехфазной системы переменного тока
3.4. Пример трехфазной системы переменного тока
а) генератор трёхфазного тока; б) с тремя генераторами;
изменяющаяся э.д.с. индукции. Из-за того что происходит сдвиг обмоток в пространстве, фазы колебаний в них также сдвигаются относительно друг друга на 120°.
Для того чтобы подсоединить трехфазный генератор переменного тока к цепи, нужно иметь 6 проводов. Для уменьшения количества проводов обмотки генератора и приемников нужно соединить между собой, образовав трехфазную систему. Данных соединений два: звезда и треугольник. При использовании и того и другого способа можно сэкономить электропроводку.
Соединение звездой
Обычно генератор трехфазного тока изображают в виде 3 статорных обмоток, которые располагаются друг к другу под углом 120°. Начала обмоток принято обозначать буквами А, В, С , а концы — X, Y, Z . В случае, когда концы статорных обмоток соединены в одну общую точку (нулевая точка генератора), способ соединения называется «звезда».
Точно так же можно соединять и приемники (рис. 3.5., справа). В этом случае провод, который соединяет нулевую точку генератора и приемников, называется нулевой. Данная система трехфазного тока имеет два разных напряжения: между линейным и нулевым проводами или, что то же самое, между началом и концом любой обмотки статора. Такая величина называется фазным напряжением (Uл ). Поскольку цепь трехфазная, то линейное напряжение будет в v3 раз больше фазного, т. е.: Uл = v3Uф.
Рассмотрим следующую цепь.
Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.
Активное сопротивление
Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. 2) = Um/√2.
2) = Um/√2.
Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R. Получим:
Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний — такие, как амплитуда, частота, период, действующие значения силы тока и напряжения.
Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.
Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.
,
После подстановки значения тока i и последующих преобразований получим, что действующее значение переменного тока равно:
Аналогичные соотношения могут быть получены также для напряжения и ЭДС:
Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.
Учитывая, например, что действующее значение напряжения в нашей сети составляет 220В, можно определить амплитудное значение напряжения в сети: U m =U Ö2=311В. Соотношение между действующим и амплитудным значениями напряжений и токов важно учитывать, например, при проектировании устройств с применением полупроводниковых элементов.
Действующее значение переменного тока
Теория
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т. Для периодического тока имеем
Для периодического тока имеем
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i — мгновенное значение тока ;
u – мгновенное значение напряжения ;
е — мгновенное значение ЭДС ;
р — мгновенное значение мощности .
Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ).
Амплитуда тока;
Амплитуда напряжения;
Амплитуда ЭДС.
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
, |
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:
Значения аргументов синусоидальных функций и называются фазами синусоид, а значение фазы в начальный момент времени (t =0): и — начальной фазой ( ).
Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть , где f– частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .
Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:
Векторное изображение синусоидально изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное ) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:
Каждый из этих токов синусоидален и может быть представлен уравнением
Результирующий ток также будет синусоидален:
Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .
Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
.
Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .
Действующее и среднее значения переменного тока и напряжения.
Среднее или среднеарифметическое значение Fcp произвольной функции времени f (t )за интервал времени Т определяется по формуле:
Численно среднее значение Fср равно высоте прямоугольника, равновеликого по площади фигуре, ограниченной кривой f (t ), осью t и пределами интегрирования 0 – Т (рис. 35).
35).
Для синусоидальной функции среднее значение за полный период Т (или за целое число полных периодов) равно нулю, так как площади положительной и отрицательной полуволн этой функции равны. Для переменного синусоидального напряжения определяют среднее по модулю значение за полный период Т или среднее значение за половину периода (Т /2) между двумя нулевыми значениями (рис. 36) :
Ucp = Um∙ sinwt dt = 2R . Таким образом, количественные параметры электрической энергии на переменном токе (количество энергии, мощность) определяются действующими значениями напряжения U и тока I . По этой причине в электроэнергетике все теоретические расчеты и экспериментальные измерения принято выполнять для действующих значений токов и напряжений. В радиотехнике и в технике связи, наоборот, оперируют максимальными значениями этих функций.
Приведенные выше формулы для энергии и мощности переменного тока полностью совпадают с аналогичными формулами для постоянного тока. На этом основании можно утверждать, что энергетически постоянному току эквивалентно действующее значение переменного тока.
На этом основании можно утверждать, что энергетически постоянному току эквивалентно действующее значение переменного тока.
Что берется за действующее значение силы переменного тока и переменного напряжения
что берется за действующее значение силы переменного тока и переменного напряжения?
Боевое яйцо
Переменный ток, в широком смысле электрический ток, изменяющийся во времени. Обычно в технике под П. т. понимают периодический ток, в котором среднее значение за период силы тока и напряжения равно нулю.
Переменные токи и переменные напряжения постоянно изменяются по величине. В каждое другое мгновение у них другая величина. Возникает вопрос, как же их измерять? Для их измерения введено понятие действующее значение.
Действующим или эффективным значением переменного тока называют величину такого постоянного тока, который по своему тепловому действию равноценен данному переменному току.
Действующим или эффективным значением переменного напряжения называют величину такого постоянного напряжения, которое по своему тепловому действию равноценно данному переменному напряжению.
Все переменные токи и напряжения в технике измеряются в действующих значениях. Приборы измеряющие переменные величины показывают их действующее значение.
Вопрос: напряжение в электросети 220 В, что это значит?
Это значит, что источник постоянного напряжения с напряжением 220 В оказывает такое же тепловое действие как и электросеть.
Действующее значение тока или напряжения синусоидальной формы в 1,41 раз меньше амплитуды этого тока или напряжения.
Пример: Определить амплитуду напряжения электросети с напряжением 220 В.
Амплитуда равна 220 * 1,41=310,2 В.
Значения действующего напряжения и силы тока. Определение. Соотношение с амплитудой для разной формы. (10+)
Понятие эффективных (действующих) значений напряжения и силы тока
Когда мы говорим о переменных напряжении или силе тока, особенно сложной формы, то встает вопрос о том, как их измерять. Ведь напряжение постоянно меняется. Можно измерять амплитуду сигнала, то есть максимум модуля значения напряжения. Такой метод измерения нормально подходит для сигналов относительно гладкой формы, но наличие коротких всплесков портит картину. Еще одним критерием выбора способа измерения является то, для каких целей делается измерение. Так как в большинстве случаев интерес представляет мощность, которую может отдать тот или иной сигнал, то применяется действующее (эффективное) значение.
Такой метод измерения нормально подходит для сигналов относительно гладкой формы, но наличие коротких всплесков портит картину. Еще одним критерием выбора способа измерения является то, для каких целей делается измерение. Так как в большинстве случаев интерес представляет мощность, которую может отдать тот или иной сигнал, то применяется действующее (эффективное) значение.
Вашему вниманию подборка материалов: Действующее (эффективное) значение для сигналов стандартной формыСинусоидальный сигнал (синус, синусоида) [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 2 ] Прямоугольный сигнал (меандр) [Действующее значение ] = [Амплитудное значение ] Треугольный сигнал [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 3 ] Закон Ома и мощность для действующих значений напряжения и силы токаЭффективное значение напряжения измеряется в Вольтах, а силы тока в Амперах. Для эффективных значений верен закон Ома: = / [Сопротивление нагрузки, Ом ] [Рассеиваемая на омической нагрузке мощность, Вт ] = [Действующее значение силы тока, А ] * [Действующее значение напряжения, В ] К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости , чтобы быть в курсе. Если что-то непонятно, обязательно спросите! Еще статьи Микроконтроллеры — пример простейшей схемы, образец применения. Фузы (… Практика проектирования электронных схем. Самоучитель электроники…. Силовой мощный импульсный трансформатор, дроссель. Намотка. Изготовить… Силовой резонансный фильтр для получения синусоиды от инвертора… Бесперебойник своими руками. ИБП, UPS сделать самому. Синус, синусоида… Преобразователь однофазного напряжения в трехфазное. Принцип действия,… Электрическое напряжение. Амплитуда сигнала. Амплитудное. Вольт. Volt…. |
>> Активное сопротивление. Действующие значения силы тока и напряжения
§ 32 АКТИВНОЕ СОПРОТИВЛЕНИЕ. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ
Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.
Сила тока в цени с резистором. Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.
В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряже ния (рис. 4.11), а амплитуда силы тока определяется равенством
Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.
Как правило, нам нужно бывает знать среднюю мощ ностъ тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найчи среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.
Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.
Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой
P = I 2 R. (4.18)
На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.
Поэтому мгновенная моoность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой
P = i 2 R. (4.19)
Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение
График зависимости мгновенной мощности от времени изображен на рисунке 4.12, а. Согласно графику (рис. 4.12, б.), на протяжении одной восьмой периода, когда , мощность в любой момент времени больше, чем . Зато на протяжении следующей восьмой части периода, когда cos 2t
Средняя мощность равна, таким образом, первому члену в формуле (4. 20):
20):
Действующие значения силы тока и напряжения . Из формулы (4.21) видно, что величина есть среднее за период значение квадрата силы тока:
Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы неременного тока. Действующее зртачепие силы неременного тока обозначается через I:
Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты , что и при переменном токе за то же время.
Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:
Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем
Это закон Ома для участка цепи переменного тока с резистором.
Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.
Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.
Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока:
P = I 2 R = UI.
Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.
1. Чему равна амплитуда напряжения в осветительных сетях переменного тока, рассчитанных на напряжение 220 В!
2. Что называют действующими значениями силы тока и напряжения!
Мякишев Г. Я., Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд. , перераб. и доп. — М. : Просвещение, 2008. — 399 с: ил.
, перераб. и доп. — М. : Просвещение, 2008. — 399 с: ил.
Библиотека с учебниками и книгами на скачку бесплатно онлайн , Физика и астрономия для 11 класса скачать , школьная программа по физике, планы конспектов уроков
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиВконтакте
Одноклассники
Google+
Переменное напряжение и его параметры
Всем доброго времени суток! В прошлой статье я рассказал, как рассчитать индуктивность катушки выполненной на разомкнутом сердечнике (например, ферритовой антенны, контурных катушек радиоприёмников, катушек с построечными сердечниками и т. д.). Сегодняшняя статья посвящена переменному напряжению и параметрам, которые его характеризуют.
д.). Сегодняшняя статья посвящена переменному напряжению и параметрам, которые его характеризуют.
Что такое переменное напряжение?
Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.
Постоянное (слева), периодическое (в центре) и непериодическое (справа) переменное напряжение.
Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид
где Т – период.
Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда
Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже
Синусоидальное переменное напряжение.
Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.
Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.
Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла),
φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.
Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.
Таким образом, амплитуда Um, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.
Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда
В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.
Что такое действующее напряжение переменного тока?
Как я писал выше, одним из основных параметров переменного напряжения является амплитуда Um, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному Um ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?
Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения
Для переменного напряжения мгновенное значение выделяемой энергии составит
где u – мгновенное значение напряжения
Тогда количество энергии за полный период от t0 = 0 до t1 = T составит
Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения
Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.
Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.
Действующее значение синусоидального напряжения.
Вычислим действующее значение синусоидального напряжения
Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.
Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение
Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения
Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.
С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.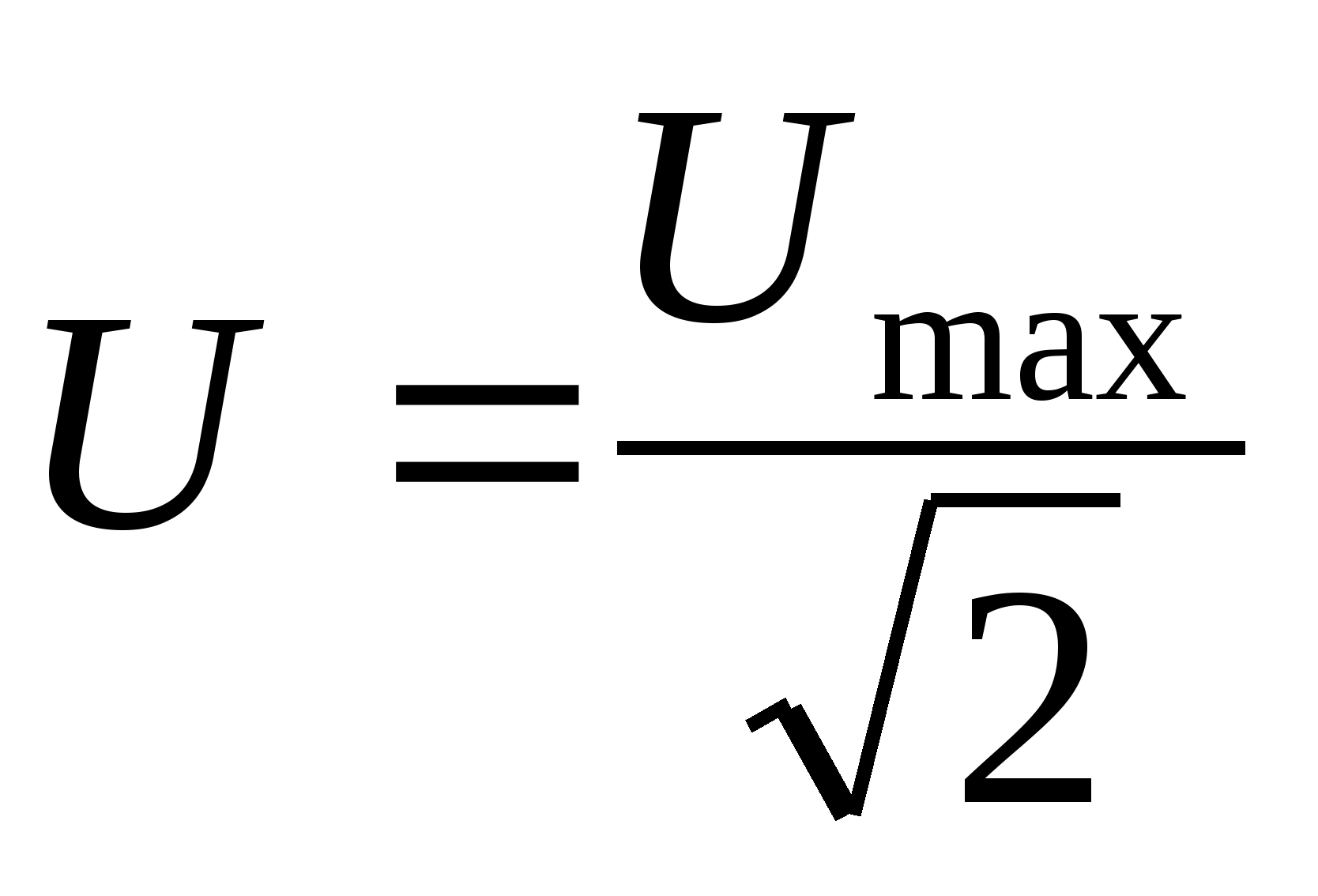
Что такое среднее значение переменного напряжения?
Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением
где Т – период переменного напряжения,
fu(t) – функциональная зависимость напряжения от времени.
Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией fu(t) и осью Ox за период Т.
Среднее значение переменного напряжения.
В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.
Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла).
Какие коэффициенты, характеризуют переменное напряжение?
Иногда возникает необходимость охарактеризовать форму переменного напряжения. Для этой цели существует ряд параметров данного переменного напряжения:
1. Коэффициент формы переменного напряжения kф – показывает как относится действующее значение переменного напряжения U к его среднему значению Ucp.
Так для синусоидального напряжения коэффициент формы составит
2. Коэффициент амплитуды переменного напряжения kа – показывает как относится амплитудное значение переменного напряжения Um к его действующему значению U
Так для синусоидального напряжения коэффициент амплитуды составит
На сегодня всё, в следующей статье я рассмотрю прохождение переменного напряжения через сопротивление, индуктивность и емкость.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Действительное значение тока. Эффективное, действующее напряжение, сила тока. Значение
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В
настоящее время центральное производство
и распределение электрической энергии
осуществляется в основном на переменном
токе. Цепи с изменяющимися – переменными
– токами по сравнению с цепями постоянного
тока имеют ряд особенностей. Переменные
токи и напряжения вызывают переменные
электрические и магнитные поля. В
результате изменения этих полей в цепях
возникают явления самоиндукции и
взаимной индукции, которые оказывают
самое существенное влияние на процессы,
протекающие в цепях, усложняя их анализ.
Цепи с изменяющимися – переменными
– токами по сравнению с цепями постоянного
тока имеют ряд особенностей. Переменные
токи и напряжения вызывают переменные
электрические и магнитные поля. В
результате изменения этих полей в цепях
возникают явления самоиндукции и
взаимной индукции, которые оказывают
самое существенное влияние на процессы,
протекающие в цепях, усложняя их анализ.
Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т. Для периодического тока имеем
Диапазон
частот, применяемых в технике: от
сверхнизких частот (0.01¸10 Гц – в системах
автоматического регулирования, в
аналоговой вычислительной технике) –
до сверхвысоких (3000 ¸ 300000 МГц –
миллиметровые волны: радиолокация,
радиоастрономия).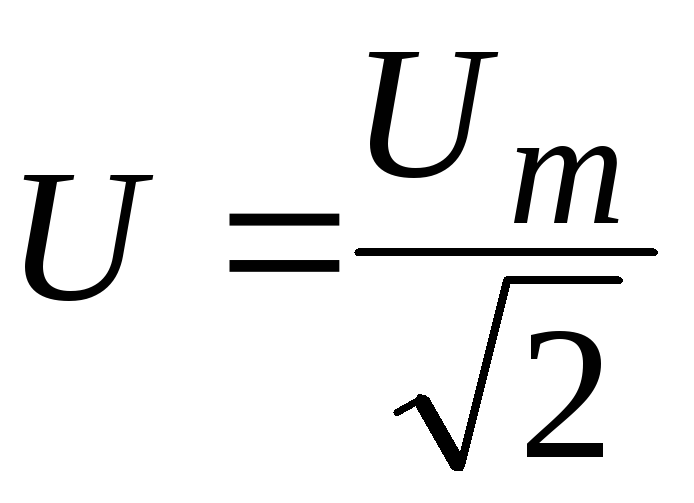 В РФ промышленная
частота f = 50Гц .
В РФ промышленная
частота f = 50Гц .
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i — мгновенное значение тока ;
u – мгновенное значение напряжения ;
е — мгновенное значение ЭДС ;
р — мгновенное значение мощности .
Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ).
Амплитуда тока;
Амплитуда напряжения;
Амплитуда ЭДС.
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из
всех возможных форм периодических токов
наибольшее распространение получил
синусоидальный ток.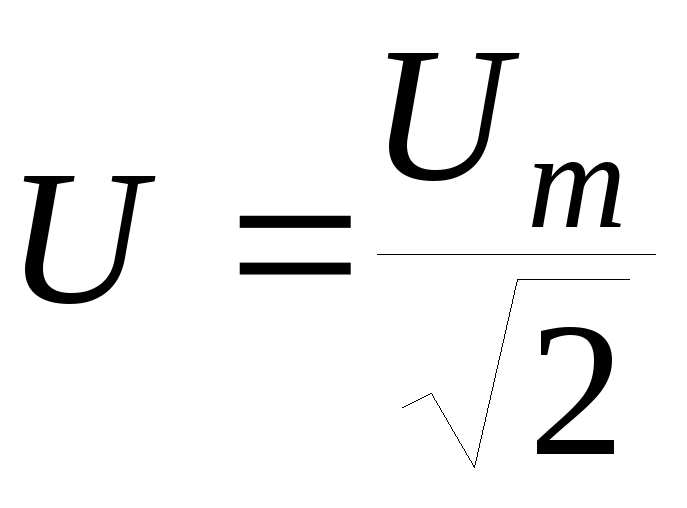 По сравнению с
другими видами тока синусоидальный ток
имеет то преимущество, что позволяет в
общем случае наиболее экономично
осуществлять производство, передачу,
распределение и использование
электрической энергии. Только при
использовании синусоидального тока
удается сохранить неизменными формы
кривых напряжений и токов на всех
участках сложной линейной цепи. Теория
синусоидального тока является ключом
к пониманию теории других цепей.
По сравнению с
другими видами тока синусоидальный ток
имеет то преимущество, что позволяет в
общем случае наиболее экономично
осуществлять производство, передачу,
распределение и использование
электрической энергии. Только при
использовании синусоидального тока
удается сохранить неизменными формы
кривых напряжений и токов на всех
участках сложной линейной цепи. Теория
синусоидального тока является ключом
к пониманию теории других цепей.
Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:
Значения
аргументов синусоидальных функций
иназываютсяфазами синусоид,
а значение фазы в начальный момент
времени (t =0): и
—начальной
фазой ( ).
Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .
Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:
Векторное изображение синусоидально изменяющихся величин
На
декартовой плоскости из начала координат
проводят векторы, равные по модулю
амплитудным значениям синусоидальных
величин, и вращают эти векторы против
часовой стрелки (в
ТОЭ данное направление принято за
положительное )
с угловой частотой, равной w .
Фазовый угол при вращении отсчитывается
от положительной полуоси абсцисс.
Проекции вращающихся векторов на ось
ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих
синусоидально изменяющиеся ЭДС,
напряжения и токи, называют векторными
диаграммами. При
построении векторных диаграмм векторы
удобно располагать для начального
момента времени (t =0), что
вытекает из равенства угловых частот
синусоидальных величин и эквивалентно
тому, что система декартовых координат
сама вращается против часовой стрелки
со скоростью w .
Таким образом, в этой системе координат
векторы неподвижны (рис. 4). Векторные
диаграммы нашли широкое применение при
анализе цепей синусоидального тока. Их
применение делает расчет цепи более
наглядным и простым. Это упрощение
заключается в том, что сложение и
вычитание мгновенных значений величин
можно заменить сложением и вычитанием
соответствующих векторов.
3). Совокупность векторов, изображающих
синусоидально изменяющиеся ЭДС,
напряжения и токи, называют векторными
диаграммами. При
построении векторных диаграмм векторы
удобно располагать для начального
момента времени (t =0), что
вытекает из равенства угловых частот
синусоидальных величин и эквивалентно
тому, что система декартовых координат
сама вращается против часовой стрелки
со скоростью w .
Таким образом, в этой системе координат
векторы неподвижны (рис. 4). Векторные
диаграммы нашли широкое применение при
анализе цепей синусоидального тока. Их
применение делает расчет цепи более
наглядным и простым. Это упрощение
заключается в том, что сложение и
вычитание мгновенных значений величин
можно заменить сложением и вычитанием
соответствующих векторов.
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:
При расчете цепей переменного тока обычно пользуются понятием действующих (эффективных) значений переменного тока, напряжения и э. д. с.
д. с.
Действующие значения тока, напряжения и э. д. с. обозначаются прописными буквами .
На шкалах измерительных приборов и технической документации также указываются действующие значения величин.
Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.
Количество тепла, выделенное переменным током в со противлении за бесконечно малый промежуток времени
а за период переменного тока Т
Приравняв Полученное выражение количеству тепла выделенному в том же сопротивлении постоянным током за то же время Т, получим:
Сократив общий множитель , получим действующее значение тока
Рис. 5-8. График переменного тока и квадрата тока.
На рис. 5-8 построена кривая мгновенных значений тока i и кривая квадратов мгновенных значений Площадь, ограниченная последней кривой и осью абсцисс, представляет собой в некотором масштабе величину, определяемую выражением Высота прямоугольника равновеликого площади, ограниченной кривой и осью абсцисс, равная среднему значению ординат кривой представляет собой квадрат действующего значения тока
Если ток изменяется по закону синуса, т. е.
е.
Аналогично для действующих значений синусоидальных напряжений и э. д. с. можно написать:
Кроме действующего значения тока и напряжения, иногда пользуются еще понятием среднего значения тбка и напряжения.
Среднее значение синусоидального тока за период равно нулю, так как в течение первой половины периода определенное количество электричества Q проходит через поперечное сечение проводника в прямом направлении. В течение второй половины периода то же количество электричества проходит через сечение проводника в обратном направлении. Следовательно, количество электричества, прошедшее через сечение проводника за период, равно нулю, равно нулю и среднее за период значение синусоидального тока.
Поэтому среднее значение синусоидального тока вычисляют за полупериод, в течение которого ток остается положительным. Среднее значение тока равно отношению количества электричества, прошедшего через сечение проводника за половину периода, к продолжительности этого полупериода.
Лекции по ТОЭ/ №13 Действующее значение переменного тока.
Понятие действующего значения тока вводится в связи с необходимостью производства измерений. Что измерять у переменного тока? Если бы мы имели дело только с синусоидами – кривыми одной формы, то можно было бы измерять амплитуды. Но на практике встречаются самые разные кривые, и может оказаться так, что два различных по форме тока имеют одинаковые амплитуды, хотя очевидно, что на электрическую цепь они будут оказывать разное воздействие.
Поэтому наиболее целесообразно оценивать величину тока по той работе, которую он совершает. При такой оценке действие переменного тока сравнивается с аналогичным действием постоянного тока. Например, если некоторый переменный ток выделяет на участке цепи такое же количество тепла, что и постоянный ток силой 10 ампер, то говорят, что величина этого переменного тока составляет 10 ампер. Это значение тока и называют действующим.
Итак, действующим значением переменного тока называется численное значение такого постоянного тока, который за время, равное одному периоду, выделяет в сопротивлении такое же количество тепла, что и ток переменный. .
.
Таким образом, для оценки величины переменного тока мы должны сделать следующее.
1.Определить количество теплоты, выделяющейся в сопротивлении R за время Т при протекании переменного тока i. Это количество теплоты равно:
2.Подобрать такой постоянный ток I, который за то же время Т в том же сопротивлении R выделяет такое же количество тепла. При постоянном токе оно равно: W=I 2 RT.
3. Приравнять W=W:
Последняя формула и определяет действующее значение переменного тока.
Пример 2.1. На вход некоторой цепи подается импульсное напряжение треугольной формы (рис. 2.4, а). Чему равно его действующее значение?
Пример 2.2. На рис. 2.4, б показана кривая напряжения на выходе схемы однофазного однополупериодного выпрямления. Чему равно действующее значение напряжения, если его амплитудное значение Um составляет 311 В?
Пример 2.3. Определить действующее значение синусоидального тока i=I m sin(ωt):
Рассмотренные примеры показывают, что действующее значение переменного тока зависит от его формы.
Желаем удачного изучения материала и успешной сдачи!
Значения действующего напряжения и силы тока. Определение. Соотношение с амплитудой для разной формы. (10+)
Понятие эффективных (действующих) значений напряжения и силы тока
Когда мы говорим о переменных напряжении или силе тока, особенно сложной формы, то встает вопрос о том, как их измерять. Ведь напряжение постоянно меняется. Можно измерять амплитуду сигнала, то есть максимум модуля значения напряжения. Такой метод измерения нормально подходит для сигналов относительно гладкой формы, но наличие коротких всплесков портит картину. Еще одним критерием выбора способа измерения является то, для каких целей делается измерение. Так как в большинстве случаев интерес представляет мощность, которую может отдать тот или иной сигнал, то применяется действующее (эффективное) значение.
Вашему вниманию подборка материалов: Действующее (эффективное) значение для сигналов стандартной формыСинусоидальный сигнал (синус, синусоида) [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 2 ] Прямоугольный сигнал (меандр) [Действующее значение ] = [Амплитудное значение ] Треугольный сигнал [Действующее значение ] = [Амплитудное значение ] / [Квадратный корень из 3 ] Закон Ома и мощность для действующих значений напряжения и силы токаЭффективное значение напряжения измеряется в Вольтах, а силы тока в Амперах. Для эффективных значений верен закон Ома: = / [Сопротивление нагрузки, Ом ] [Рассеиваемая на омической нагрузке мощность, Вт ] = [Действующее значение силы тока, А ] * [Действующее значение напряжения, В ] К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости , чтобы быть в курсе. Если что-то непонятно, обязательно спросите! Еще статьи Микроконтроллеры — пример простейшей схемы, образец применения. Фузы (… Время переключения полевого транзистора. Емкость затвор — сток, исток…. Повышающий импульсный преобразователь напряжения. Силовой ключ — бипол… Удлинитель пульта дистанционного управления, ду, инфракрасного, ик… Цветомузыка, цветомузыкальное оборудование своими руками. Схема ЦМУ, к… Магнитный усилитель — проектирование, формулы, расчет онлайн (online)…. Пушпульный импульсный преобразователь напряжения. Выбор ключа — биполя… |
Значения действующего напряжения и силы тока. Понятие эффективных (действующих) значений напряжения и силы тока Когда мы говорим о переменных напряжении или силе тока, особенно сложной формы, то встает вопрос о том, как их измерять. Ведь напряжение постоянно меняется. Можно измерять амплитуду сигнала, то есть максимум модуля значения напряжения. Такой метод измерения нормально подходит для сигналов относительно гладкой формы, но наличие коротких всплесков портит картину. Еще одним критерием выбора способа измерения является то, для каких целей делается измерение. Так как в большинстве случаев интерес представляет мощность, которую может отдать тот или иной сигнал, то применяется действующее (эффективное) значение.
|
, |
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:
Значения аргументов синусоидальных функций и называются фазами синусоид, а значение фазы в начальный момент времени (t =0): и — начальной фазой ( ).
Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть , где f– частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .
Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:
Векторное изображение синусоидально изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное ) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:
Каждый из этих токов синусоидален и может быть представлен уравнением
Результирующий ток также будет синусоидален:
Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
.
Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .
Действующее и среднее значения переменного тока и напряжения.
Среднее или среднеарифметическое значение Fcp произвольной функции времени f (t )за интервал времени Т определяется по формуле:
Численно среднее значение Fср равно высоте прямоугольника, равновеликого по площади фигуре, ограниченной кривой f (t ), осью t и пределами интегрирования 0 – Т (рис. 35).
Для синусоидальной функции среднее значение за полный период Т (или за целое число полных периодов) равно нулю, так как площади положительной и отрицательной полуволн этой функции равны. Для переменного синусоидального напряжения определяют среднее по модулю значение за полный период Т или среднее значение за половину периода (Т /2) между двумя нулевыми значениями (рис. 36) :
Ucp = Um∙ sinwt dt = 2R . Таким образом, количественные параметры электрической энергии на переменном токе (количество энергии, мощность) определяются действующими значениями напряжения U и тока I . По этой причине в электроэнергетике все теоретические расчеты и экспериментальные измерения принято выполнять для действующих значений токов и напряжений. В радиотехнике и в технике связи, наоборот, оперируют максимальными значениями этих функций.
Приведенные выше формулы для энергии и мощности переменного тока полностью совпадают с аналогичными формулами для постоянного тока. На этом основании можно утверждать, что энергетически постоянному току эквивалентно действующее значение переменного тока.
Что берется за действующее значение силы переменного тока и переменного напряжения
что берется за действующее значение силы переменного тока и переменного напряжения?
Боевое яйцо
Переменный ток, в широком смысле электрический ток, изменяющийся во времени. Обычно в технике под П. т. понимают периодический ток, в котором среднее значение за период силы тока и напряжения равно нулю.
Переменные токи и переменные напряжения постоянно изменяются по величине. В каждое другое мгновение у них другая величина. Возникает вопрос, как же их измерять? Для их измерения введено понятие действующее значение.
Действующим или эффективным значением переменного тока называют величину такого постоянного тока, который по своему тепловому действию равноценен данному переменному току.
Действующим или эффективным значением переменного напряжения называют величину такого постоянного напряжения, которое по своему тепловому действию равноценно данному переменному напряжению.
Все переменные токи и напряжения в технике измеряются в действующих значениях. Приборы измеряющие переменные величины показывают их действующее значение.
Вопрос: напряжение в электросети 220 В, что это значит?
Это значит, что источник постоянного напряжения с напряжением 220 В оказывает такое же тепловое действие как и электросеть.
Действующее значение тока или напряжения синусоидальной формы в 1,41 раз меньше амплитуды этого тока или напряжения.
Пример: Определить амплитуду напряжения электросети с напряжением 220 В.
Амплитуда равна 220 * 1,41=310,2 В.
Переменный синусоидальный ток в течение периода имеет разные секундные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь?
При расчетах цепей переменного тока, также при электронных измерениях неловко воспользоваться моментальными либо амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Не считая того, об электронном эффекте временами изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.
Более комфортным оказалось введение понятий так именуемых действующих значений тока и напряжения . В базу этих понятий положено термическое (либо механическое) действие тока, не зависящее от его направления.
— это значение неизменного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.
Для оценки деяния, производимого переменным током, мы сравним его деяния с термическим эффектом неизменного тока.
Мощность Р неизменного тока I , проходящего через сопротивление r , будет Р = Р 2 r .
Мощность переменного тока выразится как средний эффект моментальной мощности I 2 r за целый период либо среднее значение от (Im х sinωt ) 2 х r за то же время.
Пусть среднее значение t2 за период будет М. Приравнивая мощность неизменного тока и мощность при переменном токе, имеем: I 2 r = Mr, откуда I = √ M ,
Величина I именуется действующим значением переменного тока.
Среднее значение i2 при переменном токе определим последующим образом.
Построим синусоидальную кривую конфигурации тока. Возведя в квадрат каждое секундное значение тока, получим кривую зависимости Р от времени.
Обе половины этой кривой лежат выше горизонтальной оси, потому что отрицательные значения тока (-i ) во 2-ой половине периода, будучи построены в квадрат, дают положительные величины.
Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное с помощью высшей арифметики, будет равно 1/2I 2 m . Как следует, М = 1/2I 2 m
Потому что действующее значение I переменного тока равно I = √ M , то совсем I = Im / √ 2
Аналогично зависимость меж действующим и амплитудным значениями для напряжения U и Е имеет вид:
U = Um / √ 2 , E= Em / √ 2
Действующие значения переменных величин обозначаются строчными знаками без индексов (I , U, Е).
На основании произнесенного выше можно сказать, что действующее значение переменного тока равно такому неизменному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.
Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, демонстрируют действующие значения тока либо напряжения.
При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √ 2 раз. От этого размещение векторов на диаграмме не меняется.
Школа для электрика
Действующее напряжение — что ж ты за зверь-то такой??? | Добрый Аудиофил
фото отсюда https://ru.depositphotos.com/100841854/stock-photo-inventor-with-soldering-iron.html
Всем Доброго Аудиофильского!!!
Идеей данной статьи явился спор с участниками у меня в комметариях. Я со своим циклом статей про Аудиофильскую Инженерию говорил, что Показатель Действующего Напряжения зависит от частоты. А комментаторы целой гурьбой доказывали, что ничего подобного. В формуле частота не указана.
Я же говорил, что данная особенность формулы, есть тест на думающего ученика. Зубрильщик ее вызубрит, а думающий будет неприличные вопросы задавать, из серии паззл не сходится!
Закончилось это все тогда тем, что мне дизлайков понаставили. Что в свою очередь, значительно снизило количество показов материалов данного канала. Что повлекло к падению и других важных показателй. Таких как Аудитория канала например.
В итоге я теперь пребываю в размышлениях на счет идеи отключения комментариев.
Тем более, что текущая статья разложит все по полочкам. В ней будут приведены доказательства зависимости Действующего Напряжения от частоты, как теоретические, так и практические на экране осциллографа. Ну вернее эмулятора.
Готовы? Тогда погнали!!!
********************************************************************
Есть в этом мире такое наблюдение, что формулы движения в механике, электронике, и акустике выглядят весьма похоже. Разница только в том, что в Электронике коэффициентами выступают Емкость и Индуктивность. В механике — сила трения и упругость. А в акустике — плотность да гибкость.
На этом деле основан например процессор Physics от Nvidia. Стоит во многих видеокартах в компах. Суть его — эмулировать в играх поведение, например подвески автомобиля.
Но делает он это не математическими вычисленями. А как в аналоговом эквалайзере с цифровым управлением. Перестраивая настрйоки Аналогового колебательного контура. Одновременно подавая на него с ЦАПа сигнал, например, наезда на кочку. И далее просто оцифровывая через АЦП возникающие колебания в контуре, сообщет программе их знчения.
Такой метод значительно ускоряет расчеты, в которых высокая точность не требуется. Да и себестоимость снижает до приятных показателей.
При этом заметьте. Колебания происходящие в подвеске имитируются колебаниями в электронике. Они в ней значительно компактнее! И даже бесшумнее. Особенно при критических значениях.
А для сегодняшней нашей темы нам понадобится наблюдение за акустикой. И его мы будем проецировать на электричество.
Давайте посмотрим на колонки.
фото отсюда http://yahoo.aleado.ru/lot?auctionID=q300215043
В колонках стоят мощные басовики, раза в 3 меньшей мощности СЧ динамики, и раз в 5-10, относительно басовиков, меньшей мощности пищалки.
Но ведь они воспроизводят умеренно ровную АЧХ.
Т.е. получается, что для получения равной отдачи, нам нужно подводить разный уровень мощности для разных частот.
А это ведь тоже эквивалент действующего напряжения. Если мыслить в обратную сторону, то получим, что при подведении одинаковой мощности, действующее значение громкости звука снижается пропорционально частоте. Т.е. частота ниже и отдача ниже.
И нужно подводить увеличенную мощность, чтобы получить равную отдачу.
Т.е. это Акустчиеский экивалент Действующего Напряжения в Электронике.
********************************************************************
Понятное дело, что такого анализа мало. Я уже опытный. Я знаю, что на такой пример набежит куча комметаторов, которые скажут, что АФФТАР ИДИОТ, и все сосвсем не так и, что вот ни разу не убедил.
Поэтому продолжим.
А продолжим мы с теорией. Причем с двух позиций.
1. Следствие из теории гласит, что Действующее напряжение есть такое напряжение при котором Лампа или Кипятильник будучи подключенными к источнику постоянного тока, с таким же значением напряжения, будут светить и греть точно так же.
Т.е. что действующее, что постоянное напряжения — они оба должны давать одинаковый результат при нагреве.
А давайте мы нагрев представим как накопление Джоулей. А теперь данную механическую среду перенесем на электрическую, и представим это, как накопление электронов в конденсаторе большой емкости.
Ведь там тоже формулы равны, только с разными коэффициентами, зависящими от своих сред.
Тогда давайте проведем такой эксперимент. Подключим конденсатор, включим систему скажем на 1 секунду. И посмотрим до какого напряжения на разных частотах переменного напряжения он зарядится.
Согласно формуле, что не содержит зависимости от частоты, он должен заряжаться с одинаковой скоростью при любой частоте.
фото отсюда Почему современный усилитель выдает больше чем потребляет? И так ли это?
Ссылка как раз на статью, с которой весь спор и разгорелся.
И вот вам скриншот из эмулятора LTspice.
скриншот мойскриншот мой
И да простит меня читатель за столь корявое начертание схем. Я мог их перерисовать, но тут они хранят процесс поиска организации нужного исследовательского процесса.
Дело в том, что спор был про показания стрелочного вольтметра.
И вот здесь я собрал схему его имитирующую.
Разбрем ее слева-направо.
Сначала идет источник напряжения. 20 вольт и как раз его частоту мы и меняем. На первой схеме он с частотой 500 Гц. На второй 5 Гц. А на третьей оно постоянное.
Далее следует диодный мостик. Я забыл как в нем правильно диоды должны быть расположены, а потому пришлось заново синтезировать процесс. Вот и получились они корявенько. Главное ведь помнить, ровно столько, чтобы в любой момент вывести нужный результат.
Хотя конечно это не верно. Знания лишними не бывают! Особенно при создании новых схем и решений. Человек во время креативных процессов, мыслит только тем, что он знает в своей голове.
Дальше резистор. Он использовался в одной из промежуточных схем, а в данный момент просто артефакт с минимальным значением, которым можно пренебречь. Хотя этот эмулятор на него такое слегка реагирует и позволяет посмотреть какой через него течет ток. Я периодически ставлю их в качестве точек Амперметра.
Далее стоит сглаживающий пульсации конденсатор. Им я имитирую инерцию стрелки вольтметра. Ну и далее резистор с номиналом близким к значению вольтметров начального уровня.
Дальше следует цепь развязки заряжаемого конденсатора. Т.е. отдельный источник постоянного напряжения и транзистор. После этого замедляющий процесс заряда конденсатора резистор, ну и собственно сама «банка» в которую мы будем «заливать» действующее напряжение.
Эмулятор у меня хитрый, по умолчанию при включении схемы он ее эмулирует с заряженными конденсаторами. А потому понадобились директивы, что задают начальное его состояние.
Это вот те тексты.
Ну и далее значения. Синяя линия — это заряд конденсатора за 1 сек, от постоянного напряжения. Фиолетовая — заряд от 500 Гц. А зеленая — заряд от 5 Гц. Процесс явно медленнее. Разница в напряжениях заряда через 1 сек в 2 вольта. При том, что на 500 Гц он чуть чуть ниже, чем от постоянного.
Но это не все. Это я продемонстрировал только эксперимент. А сейчас второй теоретический момент.
2. Официальная теория гласит. «Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.» — цитата из: Википедия Действующее значение переменного тока
Ну во первых логично, что включать кипятильник на один период 50 Герцового напряжения никто не будет, для проведения данного замера.
Но давайте вдумаемся. Если период меняется. Т.е. на более высокой частоте он становится короче. То выходит, что у постоянного тока время включения тоже меньше. А значит и времени на работу у него будет меньше.
А значит и нагрев будет меньше. А значит, чтобы получить названное равенство, придется повышать значение постоянного напряжения.
А значит… что это значит??? Что мы имеем зависимость от частоты. Ведь так?
Чем выше частота, тем выше нам нужно напряжение постоянного тока, для обеспечения одинакового нагрева за меньший промежуток времени.
Ведь если формула гласит, что зависимости от частоты нет, то период на частоте в 10 Гц будет дольше, чем период на частоте в 100 Гц. При этом в обоих случаях нам нужно включить постоянный ток который согласно ей на 0.7х ниже, чем амплитудное значение.
Но ведь очевидно же, что кипятильник в первом случае будет работать дольше, а значит и нагреется сильнее?!!!
А значит вопрос «Куда делась привязка к частоте в формуле?» остается актуальным!
В данный момент мы в 3х ключевых средах, доказали зависимость Действующего Напряжения от частоты переменного тока.
И вполне можем сделать вывод, что с общеизвестной формулой что-то не так.
Спасибо, что дочитали!
Всё о напряжении — Мастер 380 вольт
Напряжение — разность потенциалов между двумя точками пространства. Измеряется в вольтах. Так напряжение между плюсовым и минусовым контактом батарейки составляет 1,5 вольта, а между поверхностью земли и грозовым облаком — миллионы вольт!
Всем известно, что в нашей розетке напряжение переменного тока составляет 220 — 230 вольт. А вот, в трёхфазной розетке — 380 вольт. Разница заключается в том, что в первом случае мы получаем фазное, а во втором — линейное напряжение. Так что же такое линейное напряжение и что такое фазное напряжение , и каково соотношение между ними? И по какой причине соотношения именно таковы.
Как в квартиру, так и на предприятие электроэнергия передаётся от генерирующих электростанций по высоковольтным линиям электропередач (в нашей стране — частотой 50 Гц). На трансформаторных подстанциях высокое напряжение понижается, и распределяется по потребителям . Но если у вас в квартире сеть однофазная (надо заметить, что в последнее время у бытовых потребителей имеется возможность подключения к трёхфазной сети), то на производстве — трехфазная, давайте разберёмся, в чём же разница.
Действующее значение и амплитудное значение напряжения
Говоря — 220 или 380 вольт, мы имеем ввиду действующие значения напряжений, другими словами — среднеквадратичные значения напряжений. Фактически амплитудное значение переменного напряжения всегда выше фазного Umф или линейного Umл. Для синусоидального напряжения его амплитуда больше действующего значения в квадратный корень из 2 раз,(1,414 раза).
Отсюда выходит, что фазное напряжение в 220 соответствует амплитудному — 310 вольт, а для линейного напряжения в 380 вольт амплитуда окажется равной 537 вольт. Разумеется, на практике напряжение в розетке часто не соответствует именно 220 вольтам, оно может быть больше или меньше этой величины, но должно укладываться в допустимые параметры.
Что такое фазное напряжение в сети переменного тока?
На электростанции обмотки генератора соединены по схеме «звезда», то есть объединены концами X, Y и Z в одной точке, которая называется нейтралью или нулевой точкой генератора. Такая схема называется четырехпроводной трехфазной схемой. К выводам обмоток A, B и C присоединяются линейные провода, а к нулевой точке — нейтральный или нулевой провод.
Напряжения между выводом A и нулевой точкой, B и нулевой точкой, С и нулевой точкой, — называются фазными напряжениями, их обозначают Ua, Ub и Uc, ну а поскольку сеть симметрична, то можно просто написать Uф — фазное напряжение.
Линейное напряжение трехфазной сети
Действующее напряжение между выводом A и B, между выводом B и C, между выводом C и A, — называются линейными напряжениями, то есть это напряжения между линейными проводами трехфазной сети. Их обозначают Uab, Ubc, Uca, или можно просто написать Uл.
Линейное напряжение в наших электросетях составляет приблизительно 380 вольт. Соотношение фазного и линейного напряжения в любой трёхфазной сети с заземлённой нейтралью составляет 1,732, или квадратный корень из 3. Не смотря на то что фактическое напряжение в сети может изменяться в определённых пределах, в зависимости от загруженности, соотношение между фазным и линейным напряжением остаётся неизменным.
Эффективное напряжение — обзор
В упомянутых ранее методах ШИМ трехфазные опорные напряжения модулируются индивидуально. В отличие от них, существует метод ШИМ, в котором используется другой подход, основанный на концепции пространственного вектора, который называется SVPWM. В методе SVPWM опорные трехфазные напряжения представлены как пространственный вектор vabc в комплексной плоскости, и этот вектор опорного напряжения модулируется векторами выходного напряжения, доступными от инвертора.Технология SVPWM в настоящее время широко используется во многих приложениях с трехфазными инверторами, поскольку она дает выходное напряжение основной гармоники на 15,5% больше, чем напряжение, создаваемое методом SPWM, и дает меньше гармонических искажений тока нагрузки, меньшую пульсацию крутящего момента в двигателях переменного тока и коммутационные потери.
Концепция пространственного вектора, необходимая для этого метода ШИМ, обсуждалась в разделе 4.3. Для этого метода ШИМ, поскольку опорные трехфазные напряжения задаются как пространственный вектор напряжения, возможные выходные напряжения инвертора также должны быть выражены как пространственный вектор.В разделе 7.1.4 мы увидели, что в трехфазном инверторе существует восемь возможных состояний переключения. Векторы выходного напряжения Vo-V7, соответствующие восьми возможным состояниям переключения, показаны в таблице 7.3. Обратитесь к примеру 3, в котором показано, как получить эти векторы. На рис. 7.38 эти векторы выходного напряжения трехфазного инвертора изображены в комплексной плоскости.
Таблица 7.3. Векторы выходного напряжения, соответствующие состояниям переключения
| Состояния переключения | Фазные напряжения | Вектор пространственного напряжения | ||||
|---|---|---|---|---|---|---|
| Sa | Sb | Sc | vas | vbs | vcs | Vn (n = 1 −7) |
| 0 | 0 | 0 | 0 | 0 | 0 | V0 = 0∠0 ° |
| 1 | 0 | 0 | 23Vdc | — 13Vdc | −13Vdc | V1 = 23Vdc∠0 ° |
| 1 | 1 | 0 | 13Vdc | 13Vdc | −23Vdc | V2 = 23Vdc∠60 ° |
| 0 | 0 | −13Vdc | 23Vdc | −13Vdc | V3 = 23Vdc∠120 ° | |
| 0 | 1 | 1 | −23Vdc | 13Vdc | 13Vdc | 900 37 V4 = 23Vdc∠180 °|
| 0 | 0 | 1 | −13Vdc | −13Vdc | 23Vdc | V5 = 23Vdc∠240 ° |
| 1 | 0 | 1 | 13Vdc | −23Vdc | 13Vdc | V6 = 23Vdc∠300 ° |
| 1 | 1 | 1 | 0 | 0 | 0 | V7 = 0∠0 ° |
Рис. 7.38. Векторы выходного напряжения в комплексной плоскости (или d – q осей неподвижной рамы).
Шесть из этих векторов, V1-V6, которые называются вектором активного напряжения или предлагают эффективное напряжение на нагрузку. Амплитуда всех активных векторов равна 2Vdc / 3. Однако они не совпадают по фазе друг с другом на 60 °. Напротив, два вектора, V0 и V7, называются вектором нулевого напряжения , что не может обеспечить эффективное напряжение для нагрузки.
Пример 3
Выразите выходное фазное напряжение трехфазного инвертора как пространственный вектор.
Решение
В качестве примера найдем вектор напряжения V2 для состояния переключения Sa = 1, Sb = 1, Sc = 0.
- •
Определение вектора пространства напряжения:
V = 23 (vas + avbs + a2vcs) = vas + j13 (vbs − vcs)
(Здесь a = ej2π / 3 = −12 + j32, a2 = ej4π / 3 = −12 − j32)
- •
Фазные напряжения: vas = 13Vdc, vbs = 13Vdc, vcs = −23Vdc
- •
Вектор напряжения V2 = (13 + j13) Vdc = 23Vdc∠60 °
Мы можем получить векторы напряжения для остальных состояний переключения аналогично тому, как показано в таблице 7.3.
7.2.4.1 Принцип метода широтно-импульсной модуляции пространственного вектора
Поскольку опорные трехфазные напряжения меняются со временем, опорный вектор напряжения V * вращается против часовой стрелки в комплексной плоскости, как показано на рис. 7.39. Этот вектор совершает один оборот за электрический период опорного напряжения.
Рисунок 7.39. Вращение вектора напряжения.
В методе SVPWM опорное напряжение задается как пространственный вектор V *, и этот опорный вектор напряжения V * генерируется с использованием векторов выходного напряжения трехфазного инвертора.Используя два активных вектора напряжения, смежных с V *, и нулевые векторы среди доступных восьми векторов напряжения, метод SVPWM создает напряжение, которое имеет такое же основное среднее значение в вольт-секундах, что и данный опорный вектор напряжения V * за период модуляции Ts. .
Теперь мы опишем, как сгенерировать опорный вектор напряжения. Предполагается, что опорный вектор напряжения V * находится внутри шестиугольника, который образован шестью векторами выходного напряжения трехфазного инвертора. Только когда это условие выполнено, вектор опорного напряжения может быть правильно модулирован.
Например, рассмотрим опорный вектор напряжения V *, заданный в секторе ① шести сегментов шестиугольника, показанного на рис. 7.39. В этом случае инвертор не может напрямую сгенерировать требуемый опорный вектор напряжения, потому что нет выходного вектора инвертора, который имел бы амплитуду и фазу, равные таковым из опорного вектора напряжения. Таким образом, в качестве альтернативы из шести активных векторов два вектора напряжения, смежные с опорным вектором напряжения, и нулевые векторы используются для генерации напряжения, которое имеет такое же основное среднее значение в вольт-секундах, что и данный опорный вектор напряжения V *.Эта модуляция повторяет каждый период модуляции Ts в зависимости от частоты переключения.
Давайте теперь рассмотрим этот процесс модуляции более подробно. Предполагается, что опорный вектор напряжения V * остается постоянным в течение периода модуляции Ts. Процесс синтеза векторов напряжения для генерации опорного вектора V * состоит из трех этапов, как показано на рис. 7.40.
Рисунок 7.40. Процесс модуляции для генерации напряжения.
На первом этапе один из двух соседних векторов активного напряжения, V1, применяется первым в течение времени T1.В результате создается выходное напряжение с величиной V1⋅ (T1 / Ts) в направлении вектора V1. Затем другой вектор V2 применяется в течение времени T2, чтобы соответствовать величине и фазе вектора V * опорного напряжения. Посредством этих двух шагов можно сгенерировать то же выходное напряжение, что и опорный вектор напряжения в течение периода модуляции Ts. Наконец, если T1 + T2 Продолжительность (T1, T2 и T0) каждого вектора напряжения для генерации заданного опорного вектора V * может быть вычислена следующим образом.Вышеупомянутый процесс модуляции может быть выражен математически как (7,45) ∫0TsV * dt = ∫0TsVndt + ∫T1T1 + T2Vn + 1dt + ∫T1 + T2TsV0,7dt Предполагая постоянное напряжение звена постоянного тока во время Ts, уравнение. (7.45) можно переписать как (7.46) V * ⋅Ts = Vn⋅T1 + Vn + 1⋅T2 В качестве примера, если вектор задания напряжения V * задан в первом секторе ① (0≤θ ≤60 °), уравнение. (7.46) можно разложить на две составляющие: (7.47) {Ts⋅ | V * | cosθ = T1⋅ (23Vdc) + T2⋅ (23Vdc) cos60 ° Ts⋅ | V * | sinθ = T2⋅ (23Vdc) sin60 ° Решение уравнения.(7.47) дает время продолжительности как (7,48) T1 = Ts⋅a⋅sin (60 ° −θ) sin60 ° (7,49) T2 = Ts⋅a⋅sinθsin60 ° (7,50) T0 = Ts− (T1 + T2) Здесь a = | V * | / 23Vdc. Время длительности для вектора опорного напряжения в других секторах ② – можно рассчитать аналогичным образом. Давайте исследуем достижимый диапазон выходного напряжения с помощью метода SVPWM. В методе SVPWM сумма времен длительности для двух активных векторов напряжения не должна превышать периода модуляции, т.е.е., T1 + T2≤Ts. Используя уравнения. (7.48) и (7.49), величина опорного напряжения для удовлетворения этого требования может быть получена как (7,51) T1 + T2≤Ts → V * ≤Vdc31sin (60 ° + θ) Это уравнение показывает, что Возможный диапазон опорного вектора напряжения V * находится внутри шестиугольника, образованного соединением концов шести активных векторов, как показано на рис. 7.41. Однако для вектора опорного напряжения в течение одного электрического периода диапазон вектора опорного напряжения должен находиться внутри вписанной окружности шестиугольника, чтобы получить одинаковую величину.Следовательно, радиус вписанной окружности Vdc / 3 является максимальным фазовым напряжением основной гармоники в методе SVPWM. Это значение примерно на 15,5% больше, чем для метода SPWM, и равно значению для метода THIPWM. Значение соответствует 90,7% выходного напряжения при шестиступенчатом режиме работы. Рисунок 7.41. Возможный диапазон вектора опорного напряжения в SVPWM. В разделе 7.В разделе 2.4.1 мы описали, как получить время продолжительности активного и нулевого векторов напряжения для создания заданного вектора опорного напряжения. Для заданных выбранных векторов и их длительностей существует множество способов поместить их в интервал модуляции Ts. Размещение этих векторов не влияет на среднее значение выходного напряжения в интервале Ts, но существенно влияет на диапазон линейной модуляции и гармонические характеристики выходного напряжения. В частности, важно размещение эффективных векторов напряжения.На рис. 7.42 сравнивается, как величина и частота пульсаций тока нагрузки могут изменяться в зависимости от расположения эффективных векторов напряжения. На рис. 7.42A показан случай, когда вектор эффективного напряжения помещен в середину интервала модуляции. По сравнению с рис. 7.42B, такое размещение приводит к меньшей пульсации тока и более высокой частоте пульсации. Таким образом, размещение рис. 7.42A может дать лучшие гармонические характеристики, чем расположение на рис. 7.42B. Рисунок 7.42. Токовые характеристики по размещению активных импульсов напряжения.(A) в лучшем случае и (B) в худшем случае. Было известно, что размещение эффективных векторов напряжения в центре интервала модуляции показывает превосходные гармонические характеристики, как показано на рис. 7.42A [8,9]. Техника SVPWM этой схемы размещения называется симметричной техникой SVPWM . Более того, это центрирование может дополнительно увеличить ширину импульса для модуляции эффективного напряжения, что приводит к улучшенному диапазону модуляции напряжения.Размещение векторов нулевого напряжения определяет положение эффективных векторов напряжения в пределах интервала модуляции Ts. Таким образом, в методе симметричного SVPWM два нулевых вектора, V0 и V7, в течение равного времени T0 / 2 распределяются в начале и конце интервала модуляции Ts, как показано на рис. 7.43. Кроме того, в этом случае, чтобы получить минимальную частоту переключения, необходимо расположить последовательность переключения в следующем порядке: В 0 (000) → В 1 (100) → В 2 (110) → V 7 (111). Рисунок 7.43. Последовательность переключения. Для этого два нулевых вектора V0 и V7 используются поочередно в интервале Ts. В такой последовательности переключения переход от одного вектора к другому вектору может быть выполнен переключением только одного переключателя. В следующем интервале последовательность переключения меняется на обратную, т.е. V 7 → V 2 → V 1 → V 0 , как показано на рис. 7.44 [9]. Этот интервал также требует только одного переключения для перехода.Такие чередующиеся последовательности переключения на каждом интервале модуляции позволяют снизить частоту переключения. Рисунок 7.44. Альтернативная последовательность переключения. На рис. 7.45 показаны последовательности переключения во всех шести секторах для симметричного метода SVPWM . Рисунок 7.45. Переключение последовательностей в шести секторах. Для этой альтернативной последовательности переключения два интервала 2Ts модуляции становятся одним периодом переключения. Например, интервал модуляции Ts, равный 100 мкс, указывает частоту переключения 5 кГц.Обычно интервал модуляции Ts относится к текущему периоду управления. Это связано с тем, что новое задание напряжения выдается в каждый текущий период регулирования. Пример 4 Опишите полюсное напряжение для метода симметричного SVPWM. Из значений длительности вектора, рассчитанных для каждого сектора, как показано на рис. 7.45, мы можем получить на полюсе напряжение для метода SVPWM. Полюс имеет напряжение для заданного вектора команд V * в первом секторе ① (0 ° ≤θ≤60 °) из формул.(7.48) и (7.49) равны van1 = T1 + T2Ts⋅Vdc2 = 32 | V * | cos (π6 − θ) Аналогичным образом полюсные напряжения для остальных секторов могут быть получены как: Сектор ② (60 ° ≤ θ ≤120 °): van2 = T1 − T2Ts⋅Vdc2 = 32 | V * | cos (π6 − θ) Сектор ③ (120 ° ≤ θ ≤180 °): van3 = −T1 − T2Ts⋅Vdc2 = −32 | V * | cos (π6 − θ) Сектор ④ (180 ° ≤ θ ≤240 °): van4 = −T1 − T2Ts⋅Vdc2 = −32 | V * | cos (π6 − θ) Сектор ⑤ (240 ° ≤ θ ≤300 °): van5 = −T1 + T2Ts⋅Vdc2 = 32 | V * | cos (π6 − θ) Сектор ⑥ (300 ° ≤ θ ≤360 °): van6 = T1 + T2Ts⋅Vdc2 = 32 | V * | cos (π6 − θ) На следующем рисунке показан полюс и напряжение , полученное во всех секторах для MI = 1 (т.е.е., | V * | = Vdc / 3). Как можно увидеть в Примере 4, интересно отметить, что напряжение на полюсе — это не чисто синусоидальная волна, а форма волны, которая содержит третью гармоническую составляющую, аналогичную форме волны модуляции метода THIPWM. В методе THIPWM мы видим, что добавление третьей гармоники к опорному напряжению может увеличить основную частоту фазного напряжения. Поскольку метод SVPWM также использует третью гармоническую составляющую, можно также рассмотреть возможность расширения диапазона линейной модуляции в большей степени, чем метод SPWM. На рис. 7.46 сравниваются выходной крутящий момент и гармонические искажения тока нагрузки для методов SPWM и SVPWM [7]. Легко видеть, что метод SVPWM допускает значение от MI до 1,15 и может создавать более низкие гармонические искажения, чем метод SPWM в высоком диапазоне модуляции. Рисунок 7.46. Сравнение методов SPWM и SVPWM. (A) квадрат среднеквадратичного гармонического тока и (B) гармоники крутящего момента. В отличие от метода симметричного SVPWM, эффективные напряжения в методе SPWM не помещаются в центр, в результате чего гармонические характеристики хуже, чем у метода симметричного SVPWM. Гармонические порядки, содержащиеся в методе SVPWM, аналогичны порядкам в методе SPWM, выраженным в формуле. (7.42). Однако из рис.7.47, можно видеть, что относительная величина гармоник частоты переключения для метода SVPWM меньше, чем у метода SPWM, а метод SVPWM эффективно распределяет энергию гармоник переключения на боковые полосы. Следовательно, THD метода SVPWM меньше, чем THD метода SPWM, даже несмотря на то, что гармоника удвоенных частот переключения для метода SVPWM увеличивается. Рисунок 7.47. Частотный спектр фазных напряжений для ШИМ и ШИМ. Недостатком метода SVPWM является то, что он требует тригонометрических вычислений и больших вычислительных затрат для вычисления времени переключения векторов активного напряжения. Однако в настоящее время этот метод может быть просто реализован методом ШИМ на основе несущей с использованием напряжения смещения. Более подробно этот метод будет рассмотрен в Разделе 7.4. В методе SVPWM, описанном выше, используется метод симметричной модуляции, в котором два нулевых вектора распределяются в течение равного времени.В этом случае все переключатели в трех полюсах работают в каждый период модуляции. Таким образом, это называется трехфазной модуляцией или непрерывной модуляцией . Напротив, мы можем выбрать разное время для двух нулевых векторов. В зависимости от выбора мы можем получить различные методы модуляции, которые различаются характеристиками модуляции, такими как гармонические характеристики, линейность напряжения и коммутационные потери. Таким образом, размещение нулевых векторов является степенью свободы для модуляции в методе SVPWM.Типичным примером неравномерно распределенных нулевых векторов является метод модуляции, при котором переключения только двух из трех полюсов работают для уменьшения частоты переключения. Это называется двухфазной модуляцией или прерывистой модуляцией , при которой переключатели одной ветви остаются неактивными в интервале модуляции, как показано на рис. 7.48. В этом методе прерывистой модуляции используется только один нулевой вектор, либо T0, либо T7. Соответственно, это вызывает потерю симметрии в размещении эффективных векторов напряжения.Однако из-за переключения только двух полюсов из трех общая частота переключения может быть снижена на 1/3 по сравнению с трехфазной модуляцией. В более высоком диапазоне модуляции прерывистая модуляция дает более низкие гармонические искажения из-за более высокой чистой частоты переключения. Однако в низком диапазоне модуляции из-за потери симметрии прерывная модуляция имеет более высокие гармонические искажения, чем непрерывная модуляция. Рисунок 7.48. Последовательность переключения при двухфазной модуляции. Этот калькулятор среднеквадратичного напряжения помогает найти значение среднеквадратичного напряжения из известных значений пикового напряжения, размаха напряжения или среднего напряжения. Он рассчитывает среднеквадратичное значение напряжения на основе заданных уравнений. Среднеквадратичное значение каждого сигнала является эквивалентным напряжением постоянного тока.Давайте возьмем пример, если среднеквадратичное значение синусоидального сигнала составляет 10 вольт, это означает, что вы можете подавать такое же количество энергии через источник постоянного тока на 10 вольт. Не путайте между средним напряжением и среднеквадратичным напряжением, поскольку они не равны. A Пиковое напряжение синусоидальной волны измеряется от горизонтальной оси (которая берется из контрольной точки 0) до пика (который является верхним или максимальным уровнем напряжения) формы волны. Пиковое напряжение показывает амплитуду сигнала . По этой формуле мы можем получить значение V rms относительно пикового напряжения. Разница между максимальным пиковым напряжением и минимальным пиковым напряжением, или сумма положительной и отрицательной амплитуды пиков, известна как межпиковое напряжение . По этой формуле мы можем получить значение V rms по отношению к размаху напряжения. Среднее значение синусоидальной волны равно нулю, потому что область, покрытая положительным полупериодом, аналогична области отрицательного полупериода, поэтому эти значения компенсируют друг друга, когда берется среднее значение.Тогда среднее значение измеряется только за полупериод, обычно мы берем для измерения положительную часть полупериода. Среднее напряжение, определяемое как «отношение площади под формой сигнала к времени». По этой формуле мы можем получить значение V rms по отношению к размаху напряжения. (DC) — постоянный ток Элементы и батареи обеспечивают электрический ток, который всегда течет по цепи одинаково, это называется постоянным током (DC). (AC) — переменный ток В Великобритании электросеть подается примерно при 230 вольт и подается как (переменный) или переменный ток. Это означает, что ток течет в одном направлении, а затем в другом по цепи. Ток постоянно меняет направление (чередуется), поэтому его называют (переменным) переменным током. В Великобритании частота электросети составляет 50 Гц , то есть 50 циклов в секунду. Сигналы переменного тока Мы можем использовать осциллограф для представления сигнала переменного тока. Мы можем использовать осциллограмму осциллографа в качестве вольтметра, если мы знаем, какое усиление по оси Y установлено на осциллографе. Используя диаграмму выше и зная, что усиление по оси Y было установлено на 10 В / дел, мы можем это решить; Когда мы знаем пиковое напряжение (V o ) и сопротивление (R) в цепи, мы можем вычислить пиковый ток (I o ) , используя уравнение V = IR. Среднеквадратичные значения Как п.о. и ток непрерывно изменяются в сигнале переменного тока, нам нужно представить среднее значение для p.d. и ток. Среднеквадратичные значения p.d. (V rms ) и ток (I rms ) представляют собой действующее значение p.d. и ток в цепи переменного тока. Принадлежности
Расширять Элемент в буфере обмена Абдель-Фаттах Аттиа и др.
ISA Trans. . Показать варианты Формат
АннотацияPubMedPMID Элемент в буфере обмена Показать варианты Формат
АннотацияPubMedPMID Ключевые слова: Эффективное использование энергии; ФАКТЫ; Генетически оптимизированный контроллер; Многоступенчатый контроллер нечеткой логики; Коммутируемый модулированный фильтр компенсации-SMFC; Стабилизация напряжения. Заявление о конкурирующих интересах Авторы заявляют, что у них нет известных конкурирующих финансовых интересов или личных отношений, которые могли бы повлиять на работу, описанную в этой статье. Афгул Х., Крим Ф., Чикуш Д., Беддар А.
Afghoul H, et al.
ISA Trans. 2015 сентябрь; 58: 614-21. DOI: 10.1016 / j.isatra.2015.07.008. Epub 2015 30 июля.
ISA Trans. 2015 г.
PMID: 26233491 Гомаа Харун AH, Ли YY.Gomaa Haroun AH, et al.
ISA Trans. 2017 ноябрь; 71 (Pt 2): 364-379. DOI: 10.1016 / j.isatra.2017.09.003. Epub 2017 14 сентября.
ISA Trans. 2017 г.
PMID: 28919286 П. К., Махапатра К. К..
П. К. и др.
ISA Trans. 2012 Янв; 51 (1): 163-9. DOI: 10.1016 / j.isatra.2011.09.004. Epub 2011 5 октября.ISA Trans. 2012 г.
PMID: 21982358 Кумарасабапати Н, Манохаран ПС.
Kumarasabapathy N, et al.
ScientificWorldJournal. 2015; 2015: 304165. DOI: 10,1155 / 2015/304165. Epub 2015 1 октября.
ScientificWorldJournal. 2015 г.
PMID: 26504895
Бесплатная статья PMC. Sathiyanarayanan JS, Kumar AS.
Sathiyanarayanan JS, et al.
ScientificWorldJournal. 2014; 2014: 252645. DOI: 10.1155 / 2014/252645. Epub 2014 15 июня.
ScientificWorldJournal. 2014 г.
PMID: 25028677
Бесплатная статья PMC.
Рассмотрение. Все усилители имеют три основных свойства: усиление , входное сопротивление и выходное сопротивление .Эти свойства могут быть представлены с помощью усилителя общей модели , подобного изображенному на рис. 8-1. Рисунок 8-1. Общая модель усилителя. Ромбовидная форма в модели усилителя представляет коэффициент усиления схемы. Коэффициент усиления — это множитель, который существует между входом и выходом схемы. Например, коэффициент усиления 50 означает, что выходной сигнал в пятьдесят раз больше входного. Существует три типа усиления: усиление по напряжению (), усиление по току () и усиление по мощности (). Технически усиление — это отношение выходного значения к соответствующему входному значению. Это определение иллюстрируется следующими отношениями: Поскольку усиление представляет собой отношение одинаковых значений, у него нет единицы измерения. Этот момент демонстрируется в Примере 8.1 текста. Приведенные выше уравнения вводят в заблуждение, поскольку они подразумевают, что коэффициент усиления схемы определяется ее входными и выходными значениями. Коэффициент усиления схемы фактически определяется значениями ее компонентов.Когда коэффициент усиления схемы вычислен, его можно использовать для определения выхода схемы для указанного входа. Этот момент продемонстрирован в Примере 8.2. Усилитель напряжения — это схема, разработанная для обеспечения определенного значения усиления по напряжению. Общая модель усилителя напряжения показана на рисунке 8-2. Обратите внимание, что ромб был изменен, чтобы представлять произведение коэффициента усиления напряжения схемы и напряжения входного сигнала (). Когда источник сигнала и нагрузка подключены к модели усилителя напряжения, мы получаем схему, показанную на рисунке 8-3. Обратите внимание, что: Также обратите внимание, что и обычно являются резистивными в природе, поэтому их значения можно алгебраически комбинировать с и. Делители входного и выходного напряжения влияют на значения напряжения источника и нагрузки следующим образом: Уравнения делителя напряжения показывают, что и. Эти отношения далее демонстрируются в примерах 8.3 и 8.4 текста. Эффективное усиление по напряжению схемы — это отношение напряжения нагрузки к напряжению источника. Так как и, эффективное усиление напряжения усилителя напряжения ниже, чем рассчитанное усиление напряжения самого усилителя. Идеальный усилитель напряжения , если бы его можно было сконструировать, имел бы следующие характеристики (среди прочего): При значениях и делители входного и выходного напряжения будут эффективно исключены, оставив и. В результате расчетный и эффективный выигрыши по напряжению схемы будут равны. Конфигурации усилителя BJT Существует трех конфигураций усилителя BJT, каждая со своими уникальными входными / выходными характеристиками. Эти конфигурации усилителя показаны на рисунке 8.12 текста. Характеристики трех конфигураций можно обобщить, как показано в Таблице 8-1. ТАБЛИЦА 8-1 Конфигурация Входная клемма Выходная клемма 900 База Коллектор * Общий коллектор (CC) База Излучатель Общая база (CB) Излучатель Коллектор Чтобы определить конфигурацию любого усилителя BJT, вы просто идентифицируете клеммы входа и выхода сигнала. Третий вывод — это общий вывод. В этом можно убедиться, сравнив усилители, перечисленные в таблице, с их входными и выходными клеммами. Классификация усилителей Усилители классифицируются в зависимости от их способности передавать мощность на нагрузку. Четыре основных классификации усилителей BJT перечислены (вместе с их характеристиками) в Таблице 8-2. Усиление достигается путем передачи мощности от источника постоянного тока усилителя на входной сигнал. Идеальный усилитель будет передавать 100% мощности, потребляемой от источника питания постоянного тока, на входной сигнал. На практике это не может произойти (на данном этапе), потому что каждый из компонентов усилителя рассеивает некоторое измеримое количество мощности. (См. Рис. 8.18 текста.) КПД усилителя — это процент мощности, потребляемой от источника постоянного тока, которая фактически передается нагрузке.Как показано в Таблице 8-2, каждая классификация усилителей имеет максимальный теоретический КПД. ТАБЛИЦА 8-2 Классификация * Эффективность Прочие характеристики Класс A Класс B 78,5% Класс AB Немного меньше класса B Класс C 99,9% Децибел Спецификации компонентов и системы часто указывают значения усиления в форме децибел . децибел (дБ) — это отношение выходной мощности к входной мощности, равное десятикратному десятичному логарифму этого отношения. Коэффициент усиления усилителя в дБ находится с использованием где. Пример 8.7 текста демонстрирует расчет усиления мощности в дБ. Одним из преимуществ представления усиления в форме дБ является то, что очень большие (и маленькие) значения могут быть представлены с использованием нескольких цифр. (Например, усиление мощности в 1 000 000 равно 60 дБ.) Однако недостатком использования значений в дБ является то, что они не могут использоваться в стандартных расчетах схемы без предварительного преобразования в стандартную числовую форму. Коэффициент усиления мощности в дБ преобразуется в стандартную числовую форму с использованием После преобразования в стандартную числовую форму его можно использовать (вместе с) для расчета выходной мощности схемы, как показано в Примере 8.9 текста. Еще одним преимуществом выражения усиления в форме дБ является тот факт, что положительные и отрицательные значения в дБ представляют собой взаимные усиления и потери . Например, 3 дБ означает усиление мощности примерно в 2 раза, а — 3 дБ представляют потерю мощности в. Это соотношение может быть выражено математически следующим образом: Последним преимуществом выражения усиления в форме дБ является тот факт, что множественные коэффициенты усиления (и потери) находятся путем простого сложения отдельных значений в дБ.Например, на рисунке 8-4 показана блок-схема двухкаскадного усилителя. Обратите внимание, что общий коэффициент усиления мощности схемы в дБ равен сумме отдельных коэффициентов усиления мощности в дБ. В некоторых спецификациях значения мощности указаны в форме дБм . Значение дБм — это значение мощности, относящееся к 1 мВт. Мощность в дБм определяется с использованием В отличие от стандартных значений в дБ (которые представляют собой отношения мощности ), значение в дБм представляет собой фактический уровень мощности.Эта концепция продемонстрирована в примерах 8.11 и 8.12 текста. Как и коэффициент усиления по мощности, коэффициент усиления по напряжению часто выражается в дБ. Коэффициент усиления усилителя по напряжению в дБ находится с использованием где. Коэффициент усиления усилителя по напряжению в дБ рассчитывается, как показано в Примере 8.13 текста. При изменении усиления схемы по напряжению в дБ усиление по мощности в дБ изменяется с тем же коэффициентом (при условии, что все другие значения остаются постоянными). Эта связь выражается как Оригинальная версия Правило 23.2 23.2 Напряжение (или вольт) означает наивысшее эффективное напряжение между
любые два проводника рассматриваемой цепи, за исключением тех случаев, когда, согласно определенным правилам,
термин напряжение (или вольт) относительно земли используется. Когда одна цепь напрямую
подключен к другой цепи с более высоким напряжением (как в случае
автотрансформатор) оба считаются имеющими более высокое напряжение, если только цепь
низкого напряжения эффективно заземлен.Прямое подключение подразумевает
электрическое соединение в отличие от соединения просто через
электромагнитная или электростатическая индукция. Вычеркнутый
и версия подчеркивания Правило 23.2 23.2 Напряжение (или вольт) означает наивысшее эффективное напряжение между
любые два проводника рассматриваемой цепи, за исключением тех случаев, когда, согласно определенным правилам,
термин напряжение (или вольт) относительно земли используется. Прекращение означает конец
что-то или точка, где это заканчивается, например, где проводник или подполье
кабель стояка заканчивается на оконечном устройстве. Когда одна цепь напрямую
подключен к другой цепи с более высоким напряжением (как в случае
автотрансформатор) оба считаются имеющими более высокое напряжение, если только цепь
низкого напряжения эффективно заземлен. Прямое подключение подразумевает
электрическое соединение в отличие от соединения просто через
электромагнитная или электростатическая индукция. A. Оконечное устройство (обычно
используется вместе с невинцовыми стояками) — это оборудование или части
оборудование, которое используется для заделки переходных кабелей. Это оборудование может быть
заземленный, незаземленный, под напряжением или обесточенный. Это оборудование и его
связанные части включают, помимо прочего, конусы напряжения (термоусадки,
холодная термоусадка, скотч и т. д.), насадки, различные типы клемм и клемм
фитинги и различные типы втулок. Окончательная версия 23,2
Прекращение действия означает конец
что-то или точка, где это заканчивается, например, где проводник или подполье
кабель стояка заканчивается на оконечном устройстве. A. Устройство прерывания (обычно
используется вместе с невинцовыми стояками) — это оборудование или части
оборудование, которое используется для заделки переходных кабелей.Это оборудование может быть
заземленный, незаземленный, под напряжением или обесточенный. Это оборудование и его
связанные части включают, помимо прочего, конусы напряжения (термоусадки,
холодная термоусадка, скотч и т. д.), насадки, различные типы клемм и клемм
фитинги и различные типы втулок. Note Оригинальная версия 23.2
перенесено на 23,4 7.2.4.2 Метод широтно-импульсной модуляции с симметричным пространственным вектором
Решение
Калькулятор среднеквадратичного напряжения
Как рассчитать действующее значение напряжения? RMS (среднеквадратичное значение) Напряжение (В rms )
Vp = √2 * Vrms
V rms = 0,7071 * V p
Пиковое напряжение (В pp )
V pp = 2√2 * V rms
V rms = 0,35355 * V pp
Среднее напряжение (В ср. )
V средн. = 2√2 / π * V rms
V rms = 1.1107 * V средн.
бесплатных карточек по теории переменного тока
Вопрос Ответ В цепи постоянного тока (DC) ток течет в ______ направлении (ах), но в цепи переменного тока (AC) ток течет в _____ направлении (ах). один
два Сигнал переменного тока _____ (не пересекает / не пересекает нулевую ось), а форма сигнала постоянного тока _____ (пересекает / не пересекает). будет
не будет Наиболее распространенная частота в США — _____ Гц, что означает, что форма волны напряжения завершает 60 циклов за _____ секунд (с). 60
1 Легче преобразовать напряжение _____ (AC / DC). AC Почему переменный ток используется в системах распределения электроэнергии чаще, чем постоянный ток? переменного тока можно преобразовывать с одного напряжения на другое. Возможность преобразования мощности переменного тока делает ее менее дорогой и более универсальной, чем мощность постоянного тока. Чтобы снизить потери мощности за счет уменьшения тока, вы должны увеличить _____ на ту же пропорцию, чтобы доставить такое же количество энергии пользователю.Математически это выражается как P = _____. напряжение
P = E x I Когда мощность распределяется по линиям передачи, возникают потери мощности из-за _____ провода, который выделяет тепло в проводнике. Тепло генерируется в результате протекания _____ через проводник. Математическое выражение этой потери? сопротивление
Текущий
P = I²R Потери мощности в линии передачи могут быть уменьшены путем уменьшения _____ провода или количества _____. сопротивление
ток Уменьшение сопротивления провода наполовину уменьшит потери мощности на _____ процентов, но уменьшение тока наполовину уменьшит потери мощности на ____ процентов. 50%
25% Переменный ток преобразуется с одного уровня напряжения для передачи, а затем снижается до другого уровня напряжения для использования конечным пользователем с использованием _____. Трансформаторы Какая будет разница в потерях мощности в линии передачи 1000 ампер при 1000 вольт по сравнению с 10 ампер при 100 киловольт? P = 1000 ампер x 1000 вольт = 1000000 ватт
P = 10 ампер x 100000 вольт = 1000000 ватт
Соотношение 10: 1 Когда синусоидальные волны тока и напряжения равны ____, они имеют одинаковую частоту, одновременно пересекая опорную линию и идя в одном направлении. В фазе Переменный ток используется для обеспечения более ____ процентов мировой потребности в электроэнергии. 90% Переменная ____ при производстве электрического тока имеет большое влияние на эффекты ____ (переменного / постоянного) тока. время
AC Применяются ли правила закона Ома, полученные в теории постоянного тока, к цепям переменного тока? Да. К цепям переменного тока можно применить несколько вариаций закона при различных обстоятельствах.Напряжение, падающее на катушке с проводом при протекании переменного тока, рассчитывается лишь частично с использованием строгой интерпретации закона Ома. Что такое скин-эффект? Создает такие же последствия, как уменьшение площади поперечного сечения проводника, потому что электроны вынуждены течь в меньшей площади, сосредоточенной около поверхности проводника. Что вызывает скин-эффект? Напряжение заставляет ток, протекающий в проводнике, отталкиваться от центра проводника к внешней стороне проводника.Ток вынужден проходить около поверхности проводника. Скин-эффект ____ (увеличивает / уменьшает) эффективное сопротивление проводника. Увеличивает Скин-эффект ____ (меньше / больше) на высоких частотах. больше Каждый раз, когда генерируемое в генераторе переменного тока напряжение меняет полярность, ток во внешней цепи подключается через контактные кольца к генератору переменного тока в ____ направлении. реверсирует Какие изменения в генераторе переменного тока вызывают изменения полярности? Катушка (якорь) проходит под одним полюсом, имеет одну электрическую полярность. Он создает противоположную полярность, когда пересекает противоположный магнитный полюс. Когда якорь генератора делает один полный оборот, он проходит ____ градусов механического вращения. 360 ° Форма волны переменного напряжения имеет положительное направление в течение некоторого периода времени и отрицательное направление в течение некоторого периода времени.Как называется форма волны? синусоида При каких градусах синусоиды напряжение равно нулю? 0 °, 180 °, 360 ° Когда напряжение на синусоиде является максимальным положительным? Максимум отрицательного? 90 °
270 ° Когда проводник перерезает линии магнитного потока на ____ градусов, максимальное напряжение будет индуцировано в проводнике. 90 ° Синусоидальные волны названы так потому, что напряжение в любой точке формы волны равно максимальному или пиковому значению, умноженному на ____ угла поворота. синус Каждый раз, когда генератор переменного тока выполняет один полный оборот (перемещение на 360 °), это называется a (n) _____. цикл Мера количества циклов в секунду напряжения, производимого генератором переменного тока, называется _____ этого напряжения и измеряется в _____. частота
герц Если сигнал прошел 60 положительных и отрицательных циклов за одну секунду, какова частота этого сигнала? 60 Гц Время, необходимое для одного цикла, называется ____. период Какой период для следующих частот?
60 Гц_____
1 МГц____
100 Гц ____ t = 1/60 Гц = 0,0167 секунды
t = 1/1000000 Гц = 0,000001 секунда
t = 1/100 Гц = 0,01 секунды Максимальное (пиковое) напряжение синусоидальной волны составляет 144 В. Каково напряжение после поворота на 45 °? E inst = 144 x sin (45 °)
144 x 0,707 = 101,8 В Какие четыре формы измерения напряжения и тока связаны с синусоидальными волнами? пик
от пика до пика
среднеквадратичное значение (RMS)
среднее значение Как измеряется пиковое значение напряжения? от нуля до наивысшего значения, полученного в положительном или отрицательном направлении. Пиковое значение равно ____ раз (с) пикового значения. 2 Другое название действующего значения — значение ____. RMS Объясните RMS или эффективное значение. Почему это используется? Среднеквадратичное значение сигнала переменного тока — это квадратный корень из среднего квадрата всех мгновенных значений. Это дает эффективное значение переменного тока. Это среднеквадратичное значение имеет тот же эффект нагрева, что и постоянный ток того же значения. Пиковое напряжение было измерено и составило 170 вольт. Какое эффективное напряжение? E rms = 170/1.414 = 120 В Действующее напряжение 480 вольт. Какое пиковое напряжение? Пик E = 480 x 1,414 = 679 В Каково среднее напряжение переменного тока для полного цикла идеальной синусоидальной волны? ноль Напряжение переменного тока, которое будет производить такое же количество энергии, что и аналогичное значение напряжения постоянного тока, называется значением ____. RMS Чистая синусоида переменного тока имеет _____ значение постоянного тока, потому что это ______ нулевая ось точно так же, как _____ нулевой оси. нет
выше
ниже Что обозначают буквы RMS, когда речь идет о значениях напряжения или тока переменного тока? Среднеквадратичное значение — для напряжения или тока среднеквадратичное значение s, вычисленное с использованием пика формы сигнала, деленного на 1,414 (квадратный корень из 2). Приведите следующие значения для эффективного 120 В переменного тока.
Эффективное, Среднее, Пиковое, Размах Эффективное = 120
E ср = 2 x 120 x 1,414 / 3,1416 = 108
Пик E = 120 x 1.414 = 170
E размах = 170 x 2 = 340 Среднее значение напряжения одного чередования можно найти по формуле ____ или умножив пиковое значение на ____. E ср = 2 x E пик / π,
.637 Мощность в цепи — это количество ____, выполненных за единицу времени. работа Пиковое напряжение переменного тока (АС), напряжение от пика до пика, среднеквадратичное (среднеквадратичное) напряжение
Многоступенчатый нечеткий гибкий контроллер для эффективной стабилизации напряжения в энергосистемах
.2021 6 марта; S0019-0578 (21) 00133-6.
DOI: 10.1016 / j.isatra.2021.03.004.
Интернет впереди печати. Принадлежности
Принадлежности
Заявление о конфликте интересов
Похожие статьи
chet_paynter_introduct_6 | Введение в усилители | Краткое содержание главы
Рисунок 8-2.Модель усилителя напряжения.
CE101017 Характеристики 2 91
* эмиттер-повторитель . 7 Нормально содержит один транзистор, проводящий на 360 ° цикла входного сигнала
* Максимальное теоретическое значение. На самом деле значения КПД значительно ниже. SU25 GO95 правило 23.2
SU25 GO95 правило 23.2
Правило 23.2



 …
…
 Как выбрать мощный т…
Как выбрать мощный т… ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ
ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ 
 4.12, б.), на протяжении одной восьмой периода, когда , мощность в любой момент времени больше, чем . Зато на протяжении следующей восьмой части периода, когда cos 2t
4.12, б.), на протяжении одной восьмой периода, когда , мощность в любой момент времени больше, чем . Зато на протяжении следующей восьмой части периода, когда cos 2t
 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М. : Просвещение, 2008. — 399 с: ил.
11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М. : Просвещение, 2008. — 399 с: ил.  Определение. Соотношение с амплитудой для разной формы. (10+)
Определение. Соотношение с амплитудой для разной формы. (10+) 
 …
… Таковым является, например, тепловое
действие тока. Поворот стрелки амперметра,
измеряющего переменный ток, вызывается
удлинением нити, которая нагревается
при прохождении по ней тока.
Таковым является, например, тепловое
действие тока. Поворот стрелки амперметра,
измеряющего переменный ток, вызывается
удлинением нити, которая нагревается
при прохождении по ней тока. Общее количество теплоты, выделяемое
за период, найдется суммированием
теплот, выделяемых за отдельные малые
промежутки времени, или, другими словами,
интегрированием:
Общее количество теплоты, выделяемое
за период, найдется суммированием
теплот, выделяемых за отдельные малые
промежутки времени, или, другими словами,
интегрированием: