Векторы. Действия над векторами. Проекция вектора
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Элементы комбинаторики ( 9-11 классы)
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
ВЕКТОРЫ. ДЕЙСТВИЯ НАД
ВЕКТОРАМИ. ПРОЕКЦИЯ
ВЕКТОРА
ФИЗИКА , 10 КЛАСС
04.09.2013
Плуталов С.Н. МОУ Мальчевская СОШ
1
СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ВЕЛИЧИНЫ
• Величины, характеризующиеся только численным значением, называются
скалярными.
масса
m
время
t
объём
V
температура T и др.
• Величины, характеризующиеся численным значением и направлением,
называются векторными.
сила
F
скорость V
радиус-вектор r и др.
04.09.2013
Плуталов С.Н. МОУ Мальчевская СОШ
2
ВЕКТОР
• На чертежах любой вектор изображается направленным
отрезком(стрелкой). Направление стрелки задает
направление вектора
b
04.09.2013
Плуталов С.Н. МОУ Мальчевская СОШ
3
ПРАВИЛА СЛОЖЕНИЯ ВЕКТОРОВ
• Параллелограмма
• Треугольника
Для двух векторов
04.09.2013
Плуталов С.Н. МОУ Мальчевская СОШ
4
ПРАВИЛА СЛОЖЕНИЯ ВЕКТОРОВ
Многоугольника
Если число векторов больше двух
04.09.2013
R
= F1 +МОУFМальчевская
…. + Fn
2 + F3 +СОШ
Плуталов С.Н.
5
ВЫЧИТАНИЕ ВЕКТОРОВ
04.09.2013
6
ПРОЕКЦИЯ ВЕКТОРА
Проекцией вектора
называется
скалярная величина,
равная длине
отрезка,
заключенного между
основаниями
перпендикуляров,
опущенных из
начала и конца
вектора на ось.
ay
a
ax
04.09.2013
Плуталов С.
 Н. МОУ Мальчевская СОШ
Н. МОУ Мальчевская СОШ7
ПРОЕКЦИЯ
ВЕКТОРА
04.09.2013
Если направление вектора совпадает
с направлением оси координат, то
проекция этого вектора
положительная.
Если направление вектора не
совпадает с направлением оси
координат, то проекция этого вектора
Если вектор перпендикулярен к оси
координат, его проекция равна 0
Если вектор параллелен оси
координат, его проекция равна длине
самого вектора.
Плуталов С.Н. МОУ Мальчевская СОШ
8
Изобразите произвольный вектор, чтобы
:
1.Чтобы его проекция на ось Ох была
положительной, а на ось Оу – отрицательной;
2.Чтобы его проекция на ось Ох была равна нулю , а
на ось Оу положительной;
3.Чтобы проекции данного вектора на обе оси были
отрицательными;
4.Чтобы проекция вектора на ось Оу была равна
длине самого вектора;
5.Чтобы проекция на ось Ох была отрицательной, а
на ось Оу – положительной.
Плуталов С.
 Н. МОУ Мальчевская СОШ
Н. МОУ Мальчевская СОШ9
English Русский Правила
Операции над векторами, формулы и онлайн калькуляторы
Содержание:
- Сложение и вычитание векторов
- Умножение вектора на число
Определение
Линейными операциями над векторами называются операции сложения векторов и умножения вектора на число.
Сложение и вычитание векторов
Определение
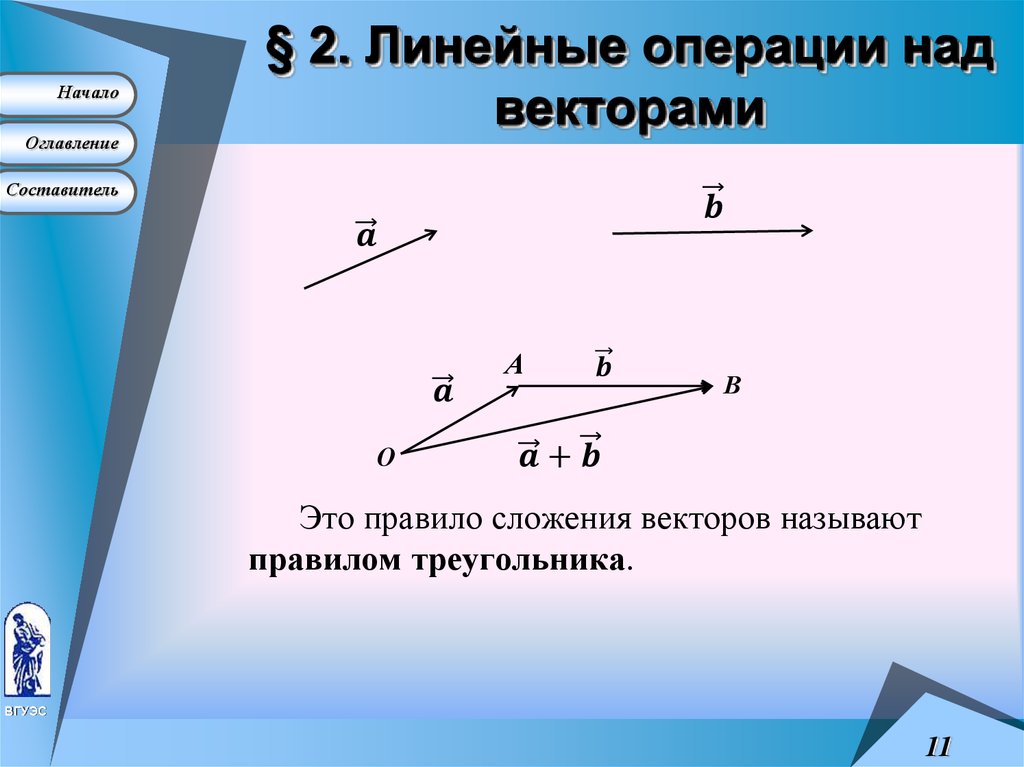
Сложение векторов $\overline{a}$ и $\overline{b}$ осуществляется по правилу треугольника.
Суммой $\overline{a}+\overline{b}$
Для сложения векторов применяется также правило параллелограмма.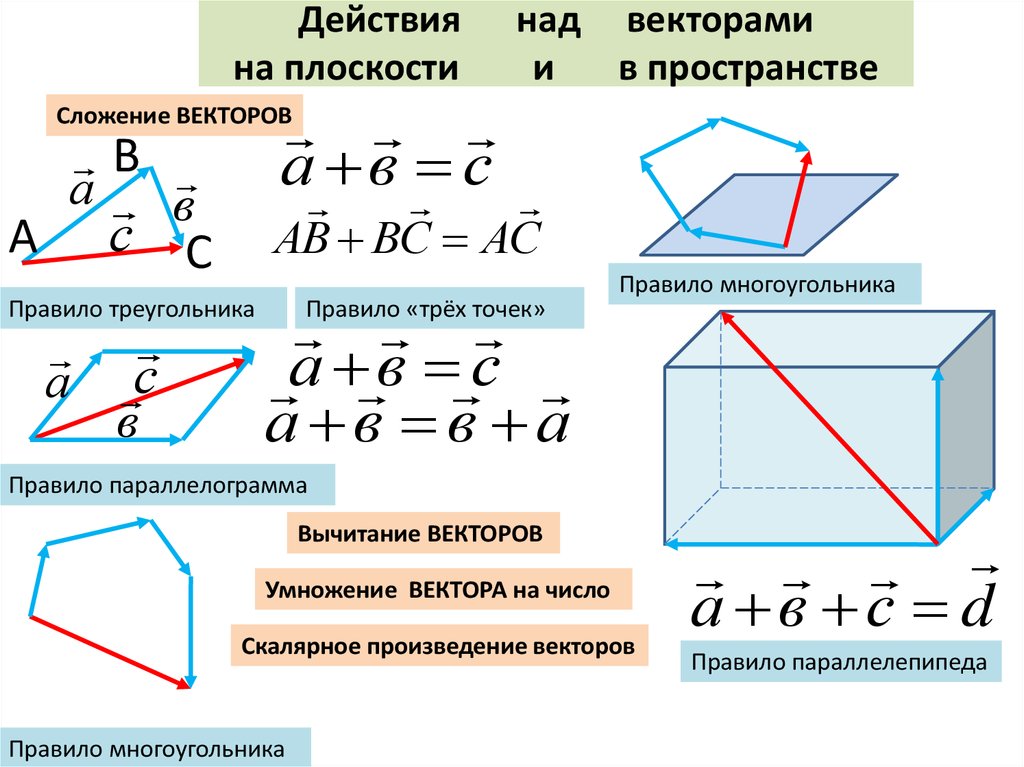
Определение
Правило параллелограмма — если два неколлинеарных вектора $\overline{a}$ и $\overline{b}$ привести к общему началу, то вектор $\overline{c}=\overline{a}+\overline{b}$ совпадает с диагональю параллелограмма, построенного на векторах $\overline{a}$ и $\overline{b}$ (рис. 2). Причем начало вектора $\overline{c}$ совпадает с началом заданных векторов.
Определение
Вектор $-\overline{a}$ называется противоположным вектором к вектору $\overline{a}$, если он коллинеарен вектору $\overline{a}$, равен ему по длине, но направлен в противоположную сторону вектору $\overline{a}$.
Операция сложения векторов обладает следующими свойствами:
- $\overline{a}+\overline{b}=\overline{b}+\overline{a}$ — коммутативность
- $(\overline{a}+\overline{b})+\overline{c}=\overline{a}+(\overline{b}+\overline{c})$ — ассоциативность
- $\overline{a}+(-\overline{a})=\overline{0}$
Определение
Разностью $\overline{a}-\overline{b}$ векторов $\overline{a}$ и $\overline{b}$ называется вектор $\overline{c}$
такой, что выполняется условие: $\overline{b}+\overline{c}=\overline{a}$ (рис.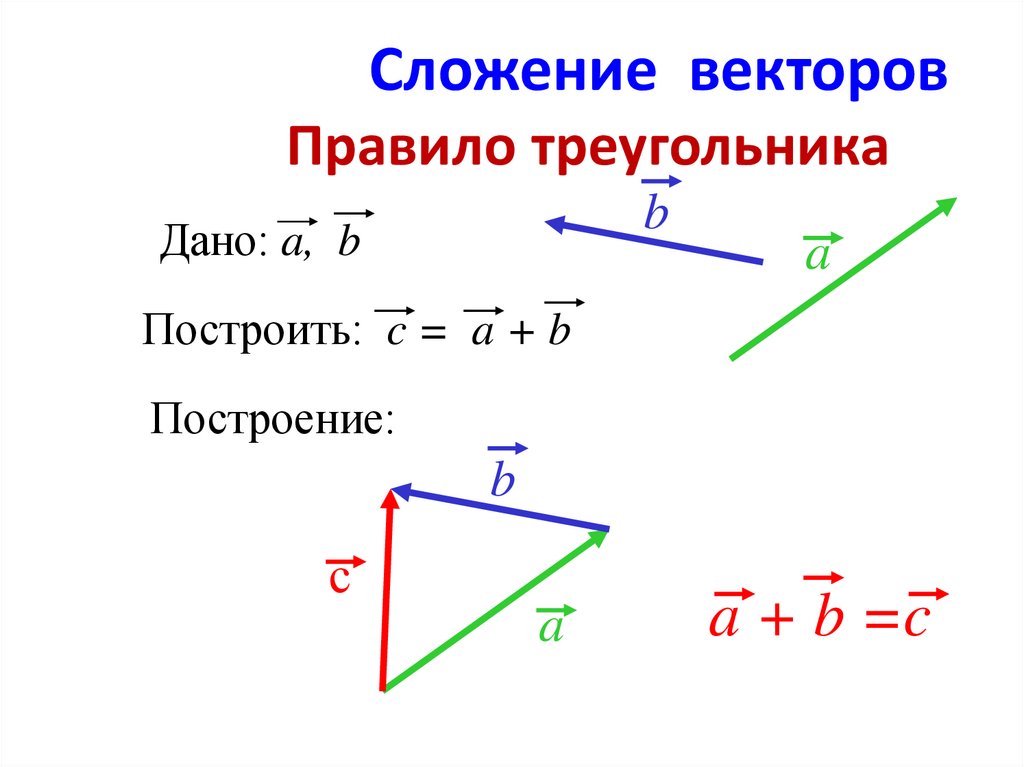 3).
3).
Умножение вектора на число
Определение
Произведением $\alpha \overline{a}$ вектора $\overline{a}$ на число $\alpha$ называется вектор $\overline{b}$, удовлетворяющий условиям:
- $\overline{b}\|\overline{a}$
- $|\overline{b}|=|\alpha||\vec{a}|$
- $\overline{a} \uparrow \uparrow \overline{b}$, если $\alpha>0$, $\overline{a} \uparrow \downarrow \overline{b}$, если $\alpha \lt 0$.
Свойства умножения вектора на число:
- $(\alpha \pm \beta) \overline{a}=\alpha \overline{a} \pm \beta \overline{a}$
- $\alpha(\overline{a} \pm \overline{b})=\alpha \overline{a} \pm \alpha \overline{b}$
- $\alpha(\beta \overline{a})=(\alpha \beta) \overline{a}=\beta(\alpha \overline{a})$
- $1 \cdot \overline{a}=\overline{a}$
- $-1 \cdot \overline{a}=-\overline{a}$
- $0 \cdot \overline{a}=\overline{0}$
Здесь $\overline{a}$ и
$\overline{b}$ — произвольные векторы,
$\alpha$,
$\beta$ — произвольные числа.
Читать дальше: разложение вектора на составляющие.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
векторных путешествий! — Деятельность — TeachEngineering
(2 оценки)Quick Look
Уровень: 9 (8-10)
Необходимое время: 30 минут
Расходные материалы Стоимость/группа: 0,00 долл. США
Размер группы: 1
Activity Depend08: 900
предметных областей: Земля и Космос, Геометрия, Измерение
Поделиться:
TE Информационный бюллетень
Резюме
 Они используют векторы для построения курса на основе времени и скорости. Затем они корректируют положения с помощью векторов, представляющих ветры и течения.
Они используют векторы для построения курса на основе времени и скорости. Затем они корректируют положения с помощью векторов, представляющих ветры и течения.Инженерное подключение
Несмотря на то, что впервые они были описаны математиками, сегодня почти каждая отрасль техники использует векторы в качестве инструмента, особенно для расчета силы и напряжения. Инженеры-механики, аэрокосмические, гражданские и химические инженеры, которые проектируют с использованием концепций гидродинамики, используют векторы в своих расчетах для описания реальных сил, таких как ветер и движение воды. Инженеры-электрики также используют их для описания сил магнитных и электрических полей.
Цели обучения
После этого задания учащиеся должны уметь:
- Объясните , что векторы могут отображать расстояния и направления и являются хорошим способом отслеживания перемещений на картах.

- Используйте векторы, чтобы понимать направления, расстояния и время, связанные с движением и скоростью.
Образовательные стандарты
Каждый урок или занятие TeachEngineering соотносится с одной или несколькими науками K-12, технологические, инженерные или математические (STEM) образовательные стандарты.
Все более 100 000 стандартов K-12 STEM, включенных в TeachEngineering , собираются, поддерживаются и упаковываются сетью стандартов достижений (ASN) , проект D2L (www.achievementstandards.org).
В ASN стандарты структурированы иерархически: сначала по источнику; напр. по штатам; внутри источника по типу; напр. , естественные науки или математика; внутри типа по подтипу, затем по классам, и т.д. .
Общие базовые государственные стандарты — математика
- (+) Признать, что векторные величины имеют как величину, так и направление.
 Представляйте векторные величины в виде направленных отрезков и используйте соответствующие символы для векторов и их величин (например, v, |v|, ||v||, v).
(Оценки
9-
12) Подробнее
Представляйте векторные величины в виде направленных отрезков и используйте соответствующие символы для векторов и их величин (например, v, |v|, ||v||, v).
(Оценки
9-
12) ПодробнееПосмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
- (+) Решайте задачи, связанные со скоростью и другими величинами, которые могут быть представлены векторами.
 (Оценки
9 —
12) Подробнее
(Оценки
9 —
12) ПодробнееПосмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
- (+) Сложение и вычитание векторов.
(Оценки
9 —
12) Подробнее
Посмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
- Сложите векторы встык, по компонентам и по правилу параллелограмма.
 Поймите, что величина суммы двух векторов обычно не является суммой величин.
(Оценки
9 —
12) Подробнее
Поймите, что величина суммы двух векторов обычно не является суммой величин.
(Оценки
9 —
12) ПодробнееПосмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
Международная ассоциация преподавателей технологий и инженерии — Технология
ГОСТ
Предложите выравнивание, не указанное вышеКакое альтернативное выравнивание вы предлагаете для этого контента?
Подписывайся
Подпишитесь на нашу рассылку новостей, чтобы получать внутреннюю информацию обо всем, что связано с TeachEngineering, например, о новых функциях сайта, обновлениях учебных программ, выпусках видео и многом другом!
PS: Мы никому не передаем личную информацию и электронные письма.
Список материалов
Каждому ученику нужно:
- Рабочий лист «Векторное путешествие» 1
- Рабочий лист векторного путешествия 2
- 3 карандаша разного цвета (синий, зеленый и красный соответствуют инструкциям на рабочем листе)
Рабочие листы и вложения
Vector Voyage Worksheet 1 (pdf)
Vector Voyage Worksheet 2 (pdf)
Пустой рабочий лист векторного путешествия (pdf)
Vector Voyage Worksheet 1 Ключ к ответу (pdf)
Vector Voyage Worksheet 2 Ключ ответа (pdf)
Vector Voyage Worksheet 3 Ключ ответа (pdf)
Посетите [www.teachengineering.org/activities/view/cub_navigation_lesson02_activity1], чтобы распечатать или загрузить.Больше учебных программ, подобных этому
Урок средней школы
Навигация на суше, на море, в воздухе и в космосе
Студенты узнают, что методы навигации меняются, когда люди путешествуют по разным местам — по суше, морю, воздуху и космосу. Например, путешественник, путешествующий по суше, использует другие методы и средства навигации, чем моряк или космонавт.
Например, путешественник, путешествующий по суше, использует другие методы и средства навигации, чем моряк или космонавт.
Методы навигации по суше, морю, воздуху и космосу
Урок средней школы
Как стать великим навигатором!
На этом уроке студенты узнают, как великие мореплаватели прошлого не сбивались с курса, то есть исторические методы навигации. Обсуждаются концепции счисления пути и астронавигации.
Как стать Великим Навигатором!
Урок средней школы
Навигация со скоростью спутников
На этом уроке учащиеся изучают фундаментальные концепции технологии GPS — трилатерацию и использование скорости света для расчета расстояний.
Навигация со скоростью спутников
Введение/Мотивация
Можете ли вы описать скорость и расстояние? (Ответ: расстояние = скорость x время; запишите это на доске.) Помните, что для того, чтобы это соотношение работало, единицы измерения должны совпадать. Например, если скорость измеряется в милях в час, то время необходимо преобразовать в часы, чтобы ответ был правильным.
Как древние морские капитаны сохраняли курс своих кораблей во время своих путешествий? (Посмотрите, есть ли у студентов какие-либо идеи.) Они использовали счисления , чтобы выяснить, куда они направляются. Как вы думаете, они следовали за солнцем, береговой линией или даже за звездами? (Подождите, что ответят некоторые ученики.) Да, так и было. Однако, зная скорость, время и курс своего путешествия, они могли определить, где и примерно когда они прибудут, что было большим преимуществом!
Колумб — и большинство других моряков его эпохи — использовали для навигации счисление пути.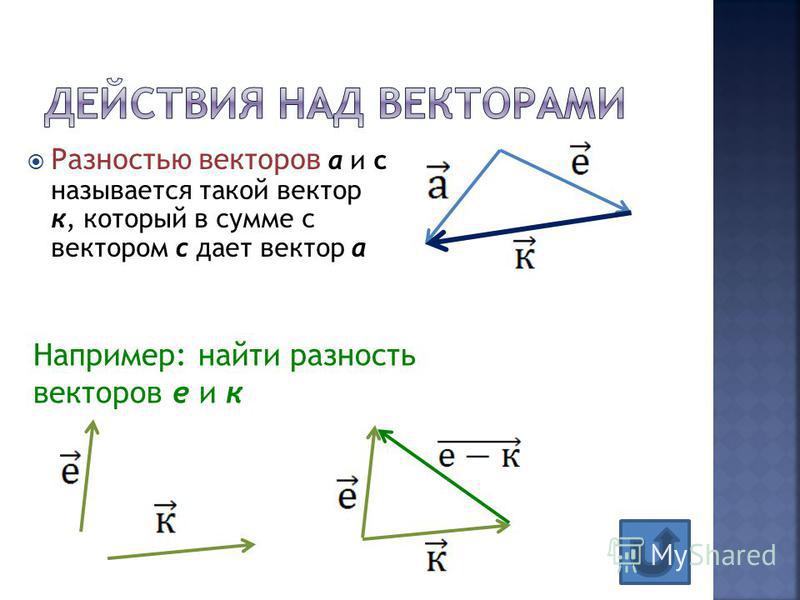 С точным счислением навигаторы определяют свои позиции, оценивая курс и расстояние, которое они прошли от известных точек. Начиная с известной точки, например порта, навигатор измеряет курс и расстояние от этой точки на карте, прокалывая карту булавкой, чтобы отметить новое положение. Эти ранние мореплаватели использовали математику, чтобы помочь им найти свой путь и не сбиться с курса, когда на их путешествия влияли ветер, течение и другие факторы. К сожалению, Колумб так и не достиг места назначения, где, как он думал, он окажется. Как вы думаете, почему это произошло? Насколько точен счисление?
С точным счислением навигаторы определяют свои позиции, оценивая курс и расстояние, которое они прошли от известных точек. Начиная с известной точки, например порта, навигатор измеряет курс и расстояние от этой точки на карте, прокалывая карту булавкой, чтобы отметить новое положение. Эти ранние мореплаватели использовали математику, чтобы помочь им найти свой путь и не сбиться с курса, когда на их путешествия влияли ветер, течение и другие факторы. К сожалению, Колумб так и не достиг места назначения, где, как он думал, он окажется. Как вы думаете, почему это произошло? Насколько точен счисление?
Процедура
Счисление пути — это процесс навигации путем продвижения на известное положение с использованием курса, скорости, времени и пройденного расстояния. Другими словами, выяснение, где вы будете в определенное время, если вы держите скорость , время и курс , по которому вы планируете путешествовать.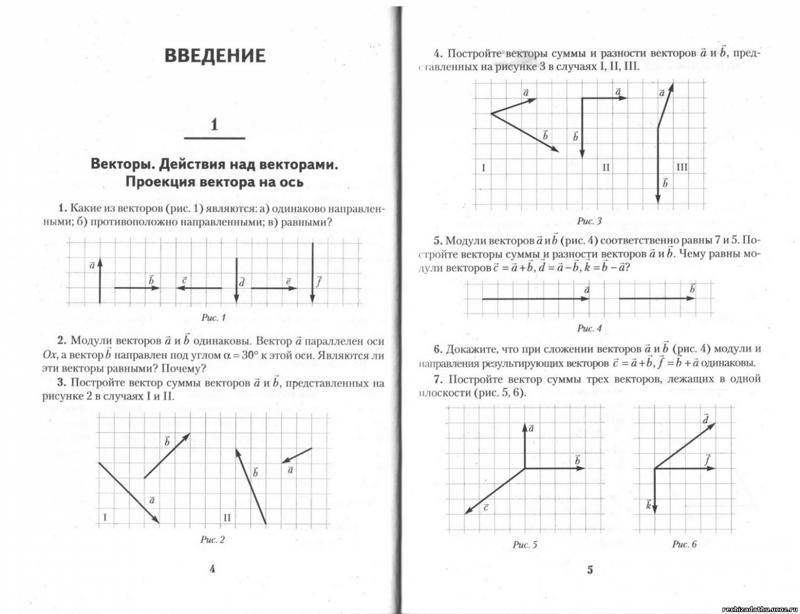
Рис. 1. Графическое изображение рейса судна с использованием векторов.
авторское право
Copyright © 2003 Matt Lippis, Программа ITL, Инженерный колледж, Колорадский университет в Боулдере
Курс — это направление, в котором вы собираетесь вести судно. В этом упражнении «курс» или курс всегда строго на запад (270 градусов по часовой стрелке от 0 градусов северной широты). Направление — это направление, в котором судно движется в данной точке. Путь, по которому фактически следовали, может быть очень кривым из-за действия волн, течения, ветра и рулевого (лица, ответственного за управление судном). «Прекрасный курс» — это фактически пройденный курс.
Векторы — это стрелки, представляющие две части информации: значение величины (длина стрелки) и значение направления (направление стрелки). С точки зрения движения информация, содержащаяся в векторе, представляет собой пройденное расстояние и пройденное направление. Векторы дают нам графический метод для расчета суммы нескольких одновременных движений.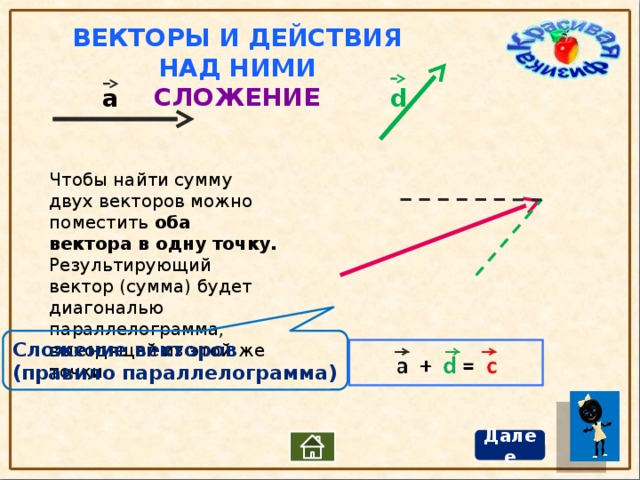 Если на движение влияет только одна переменная (представленная вектором A или B), то судно прибывает в конец этого вектора. Если на движение влияют две переменные (представленные суммой A и B), то конечное положение судна можно найти, соединив два вектора вместе.
Если на движение влияет только одна переменная (представленная вектором A или B), то судно прибывает в конец этого вектора. Если на движение влияют две переменные (представленные суммой A и B), то конечное положение судна можно найти, соединив два вектора вместе.
Рис. 2. Векторы показывают конечное положение рейса судна.
авторское право
авторское право © 2003 Matt Lippis, программа ITL, инженерный колледж, Университет Колорадо в Боулдере
Перед занятием
- Сделайте копии рабочего листа «Векторное путешествие 1» и рабочего листа «Векторное путешествие 2», по одной на каждого учащегося.
- Распечатайте для себя лист ответов 1, 2 и 3 «Векторное путешествие».
- Познакомьте учащихся с векторами.
Со студентами
Спросите учащихся: Должны ли моряки беспокоиться о ветре и течении при путешествии на большие расстояния? (Ответ: Да. Ветер и течения могут увести корабль далеко от курса, которым он следовал бы в противном случае. Если навигатор не уследит за влиянием ветра и течения, корабль может безнадежно заблудиться.)
Если навигатор не уследит за влиянием ветра и течения, корабль может безнадежно заблудиться.)
Спросите учащихся: как векторы связаны со скоростью? (Ответ: вектор [скорости] сообщает как скорость, так и направление [N, S, E, W], в то время как скорость сама по себе не указывает вам направление.)
- Раздайте каждому учащемуся рабочий лист Vector Voyage 1.
- С помощью карандаша указанного цвета попросите учащихся нарисовать 10 квадратных векторов движения прямо по карте и ответить на вопросы рабочего листа.
- Предложите учащимся перерисовать 10 квадратных векторов движения на карте, добавляя поправки на вектор ветра для каждого месяца. Вектор движения каждого месяца должен начинаться с конца вектора ветра предыдущего месяца (см. Рабочий лист 1 «Векторное путешествие»). Предложите учащимся ответить на вопросы рабочего листа.
- Предложите учащимся перерисовать 10 квадратных векторов движения и векторов поправок на ветер на карте, добавляя текущие векторные поправки для каждого месяца.
 Текущий вектор каждого месяца теперь начинается с конца вектора ветра предыдущего месяца. Вектор движения каждого месяца теперь должен начинаться с конца текущего вектора предыдущего месяца (см. Рабочий лист 2 «Векторное путешествие», ключ к ответам). Попросите учащихся ответить на вопросы из рабочего листа Vector Voyage 2.
Текущий вектор каждого месяца теперь начинается с конца вектора ветра предыдущего месяца. Вектор движения каждого месяца теперь должен начинаться с конца текущего вектора предыдущего месяца (см. Рабочий лист 2 «Векторное путешествие», ключ к ответам). Попросите учащихся ответить на вопросы из рабочего листа Vector Voyage 2. - Когда они закончат, укажите, как бы они приземлились в США без воздействия ветра или океанских течений. Однако из-за ветра и океанских течений они оказались на Кубе.
- Сообщите учащимся, что каждый квадрат имеет длину 100 миль. Затем попросите их рассчитать расстояние для Части 1. (Ответ: 3500 миль.)
Словарь/Определения
счисление пути : процесс навигации путем расчета текущего положения с использованием ранее определенного положения и продвижения этого положения на основе известных или расчетных скоростей за истекшее время и курс.
Оценка
Предварительная оценка
Вопрос для обсуждения: Запрашивайте, объединяйте и обобщайте ответы учащихся.
- Должны ли моряки беспокоиться о ветре и течении при путешествии на большие расстояния? (Ответ: Да. Ветер и течения могут увести корабль далеко от курса, которым он следовал бы в противном случае.
- Должен ли штурман обращать внимание на ветер? К текущему? (Ответ: Да. Если штурман не уследит за влиянием ветра и течения, корабль может безнадежно заблудиться.)
Встроенная оценка активности
Рабочие листы: Как указано в разделе «Процедура > Со учащимися», попросите учащихся заполнить рабочие листы и ответить на вопросы из них. Просмотрите их ответы, чтобы оценить их мастерство в предмете.
Оценка после активности
Вопросы, созданные учащимися: Попросите каждого учащегося выбрать место на африканском побережье, а затем определить векторы поправки на ветер и течение, которые приведут туда корабль после 1 месяца плавания на восток на 10 квадратов. Предложите им обменяться этими исправлениями с партнером (не позволяя партнерам видеть свои листы) и рассчитать, куда они прибудут в Африку, используя исправления своего партнера на своих листах.
Советы по устранению неполадок
Приступая к рисованию векторов, учащиеся могут запутаться. При необходимости помогите им, нарисовав первые два вектора на доске так, чтобы их мог видеть весь класс или небольшие группы.
Вектор поправки на ветер добавляется к концу первой стрелки вектора для месяца 1. Векторы для Части 3 рабочих листов должны основываться на добавленных векторах в Части 2. И ветер, и океан влияют на выход на сушу; это точно представлено только путем построения векторов поправок на ветер.
Vector Voyage Worksheet 3 Ключ к ответу предлагает краткое изложение этой деятельности и четко иллюстрирует непосредственное движение вектора. Этот ключ к ответам – отличный справочник для учителей, у которого возникли трудности с этим упражнением.
Расширения деятельности
Предложите учащимся, использующим пустой рабочий лист векторного путешествия, построить свои собственные курсы, записывая движения, направления и исправления по пути. Попросите их дать инструкции по новому курсу партнеру, чтобы определить, могут ли они плыть к новому месту.
Попросите их дать инструкции по новому курсу партнеру, чтобы определить, могут ли они плыть к новому месту.
Масштабирование активности
- Для младших классов выполните часть задания по поправке на ветер всем классом. Затем предложите учащимся попробовать текущее исправление самостоятельно.
- Для старшеклассников попросите учащихся подсчитать фактическое общее расстояние, пройденное кораблем по пути на Кубу. Фактическое расстояние, пройденное кораблем, является результирующим вектором суммы трех векторов движения за каждый месяц. Учащиеся могут нарисовать эти векторы на своих картах, начав с начала сплошного вектора из 10 квадратов для каждого месяца и нарисовав стрелку прямо до конечного положения корабля в этом месяце. Используйте теорему Пифагора (a 2 +b 2 =c 2 ), чтобы найти длины этих векторов. (Ответ: расстояние от Испании до Кубы составляет 3683 мили.) Ожидайте, что учащиеся также смогут рассчитать расстояние от Испании до Флориды таким же образом.
 (Ответ: 3940 миль.)
(Ответ: 3940 миль.) - Для учащихся старших классов попросите учеников рассчитать скорость корабля в милях в месяц и милях в час. (скорость = расстояние/время) (Ответ: Флорида — 1,37 мили в час или 985 миль в месяц, Куба — 1,7 мили в час или 1228 миль в месяц, а Нью-Йорк — 1,39.миль в час или 1000 миль в месяц.) Эти скорости высокие или низкие? Как насчет корабля без двигателей? Что случилось бы с запасами продовольствия, если бы корабль всегда сталкивался с ветром на 6 квадратов на восток?
Авторские права
© 2004 Регенты Университета КолорадоАвторы
Джефф Уайт; Мэтт Липпис; Пенни Аксельрад; Джанет Йоуэлл; Малинда Шефер ЗарскеПрограмма поддержки
Комплексная программа преподавания и обучения, Инженерный колледж Колорадского университета в БоулдереБлагодарности
Содержание этой учебной программы цифровой библиотеки было разработано в рамках грантов Фонда улучшения высшего образования (FIPSE), Министерства образования США и Национального научного фонда (грант GK-12 № 0338326).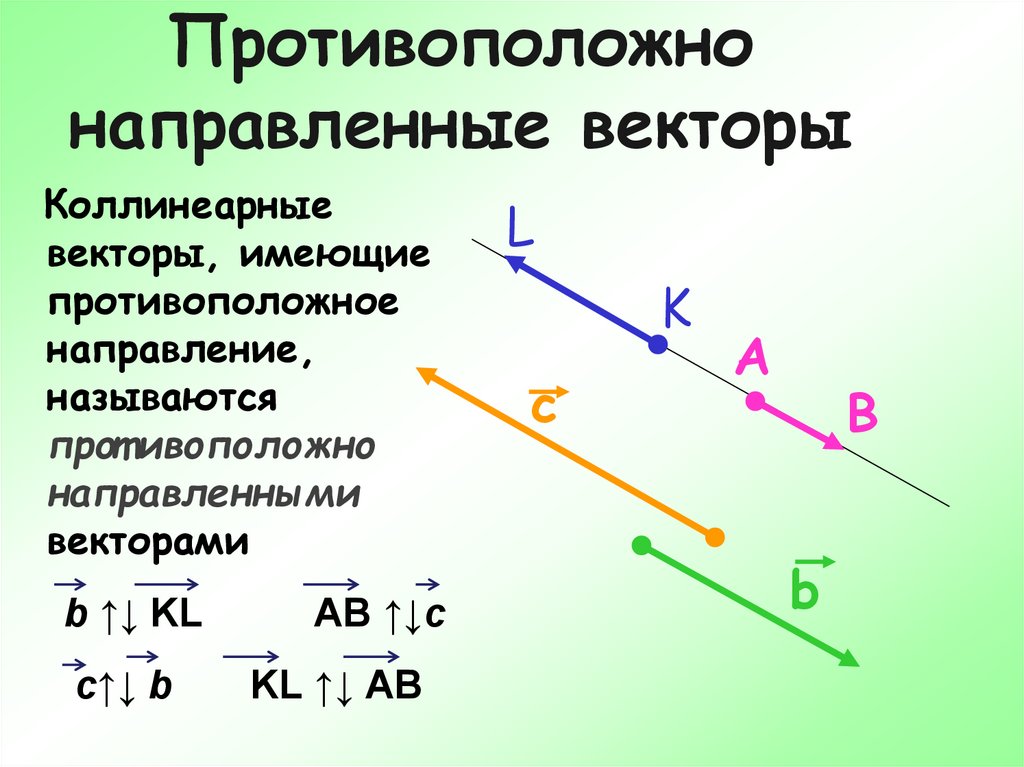 Однако это содержание не обязательно отражает политику Министерства образования или Национального научного фонда, и вы не должны исходить из того, что оно одобрено федеральным правительством.
Однако это содержание не обязательно отражает политику Министерства образования или Национального научного фонда, и вы не должны исходить из того, что оно одобрено федеральным правительством.
Последнее изменение: 21 октября 2020 г.
терминология — Представление групп в виде векторов и изоморфизм между весами и генераторами матриц
Нет, это , а не проблема неоднозначной терминологии.
Я подозреваю, что поиск «изоморфизма» может быть слишком ограниченным … вы могли бы также искать «функтор»! Основной ответ состоит в том, что да, обладание порождающими матрицами T размерности dxd в основном эквивалентен характеристике весов состояний v в d -мерном векторном пространстве, на котором действуют такие матрицы, за исключением того, что последний обычно более непосредственно подводит вас к тому, что вы хотите знать в QM в последнем случай, благодаря соответствующим меткам/корням/весам.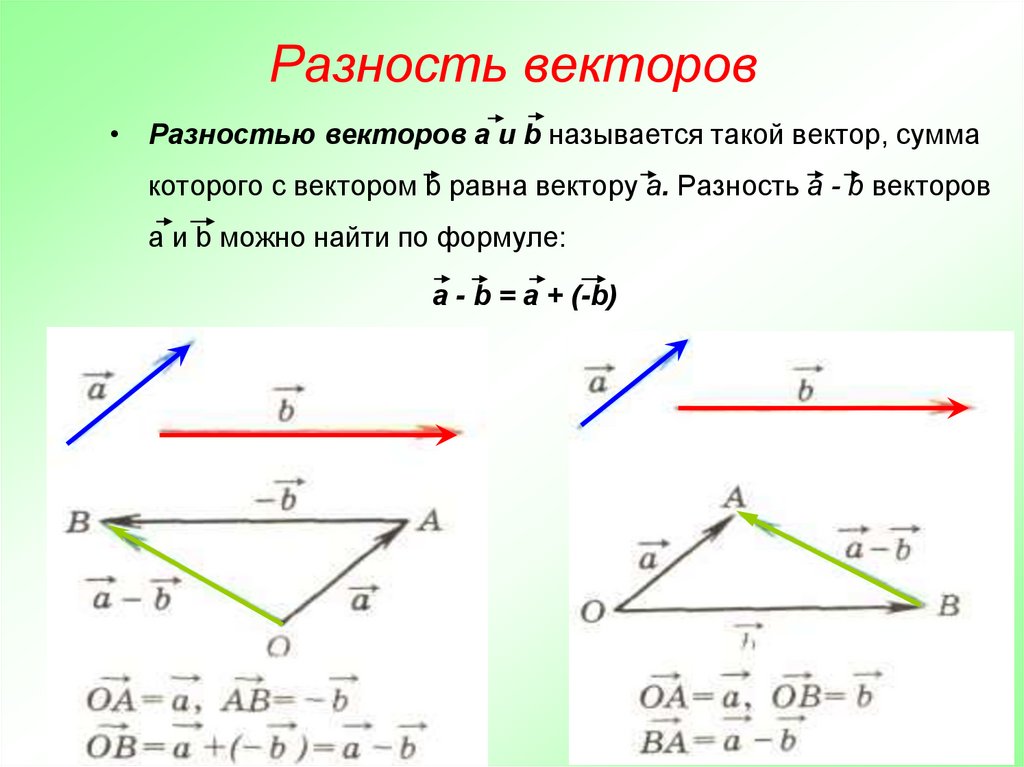
Думайте о SU(2) для простоты, но вы можете обобщить до SU(3) , как только игра станет очевидной. Для поворота произвольного d -dim v на угол θ , вы действуете на него как v → exp( iθJ ) v в классической физике. Заменив основу 3 генераторов J на их версии с подъемной и опускающейся лестницей $J_+, J_-$ и $J_0$, а также замечательные уравнения на собственные значения, которым удовлетворяют их коммутаторы алгебры Ли, вы можете гораздо полезнее организовать эти повороты в КМ, а также в вычислительном отношении — именно так, конечно, эти матрицы более высокой размерности в SU(2) WP-статьи были найдены, во-первых!
То есть, если у вас есть собственные векторы J.J с собственными значениями j(j+1) , с точностью до нормализации вы охарактеризовали размерность собственного вектора v на 2j+1 и его компонент по собственному значению m из J0 на нем, при этом вы знаете, как поднимающие и опускающие J s будут отправлять записи в соседний слот. Таким образом, запись состояний в соответствии с соглашением |j,m> равносильна тому, чтобы подготовить их к вращению простым сдвигом их 92 |j,m\rangle = j(j + 1) |j,m\rangle$, $ J_0 |j,m\rangle = m |j,m\rangle $ и $J_\pm |j,m\rangle = \sqrt{j(j+1)-m(m\pm 1)} |j,m\pm 1 \rangle$: если мы подействуем на них произвольным лифчиком слева, $\langle j\,m’ |$ они дают матричные элементы рассматриваемых матриц, гарантированно удовлетворяющие алгебре SU(2) .
Таким образом, запись состояний в соответствии с соглашением |j,m> равносильна тому, чтобы подготовить их к вращению простым сдвигом их 92 |j,m\rangle = j(j + 1) |j,m\rangle$, $ J_0 |j,m\rangle = m |j,m\rangle $ и $J_\pm |j,m\rangle = \sqrt{j(j+1)-m(m\pm 1)} |j,m\pm 1 \rangle$: если мы подействуем на них произвольным лифчиком слева, $\langle j\,m’ |$ они дают матричные элементы рассматриваемых матриц, гарантированно удовлетворяющие алгебре SU(2) .
Но этот язык проще глупого умножения матриц с целью перехода между состояниями с помощью КМ-операторов, теоремы Вигнера-Экарта и т. д. Переход — это просто линейно-алгебраическое изменение языка.
Для SU(3) таких собственных значений больше: не только аналог j (изоспин), но и гиперзаряд, собственное значение Y=B+S , связанное с квантовым числом странности . И действительно, большее количество лестничных операторов, V+ или U+ (например, U — обмены спинами d и s кварков) перемещают вас между компонентами векторов подходящими способами — они помечены в плоскости узоры с треугольной симметрией, а не линии для простых вращений.



 Представляйте векторные величины в виде направленных отрезков и используйте соответствующие символы для векторов и их величин (например, v, |v|, ||v||, v).
(Оценки
9-
12) Подробнее
Представляйте векторные величины в виде направленных отрезков и используйте соответствующие символы для векторов и их величин (например, v, |v|, ||v||, v).
(Оценки
9-
12) Подробнее (Оценки
9 —
12) Подробнее
(Оценки
9 —
12) Подробнее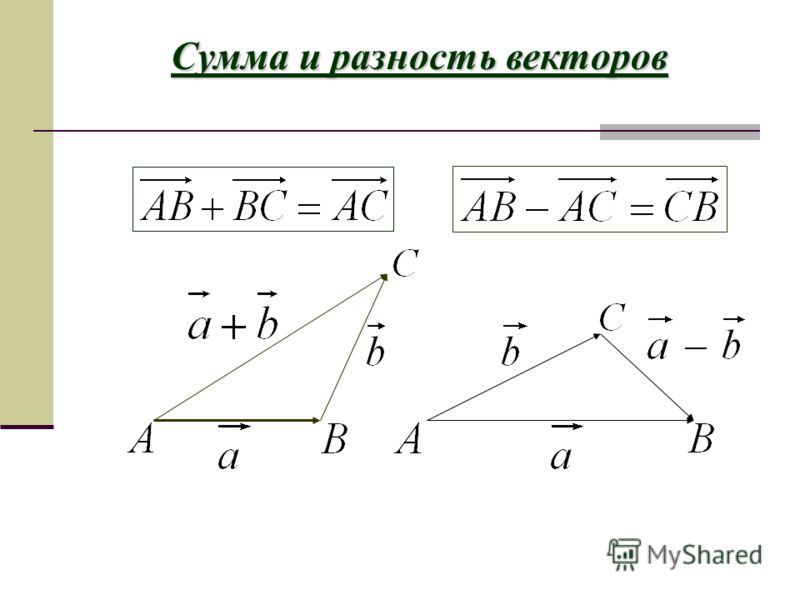 Поймите, что величина суммы двух векторов обычно не является суммой величин.
(Оценки
9 —
12) Подробнее
Поймите, что величина суммы двух векторов обычно не является суммой величин.
(Оценки
9 —
12) Подробнее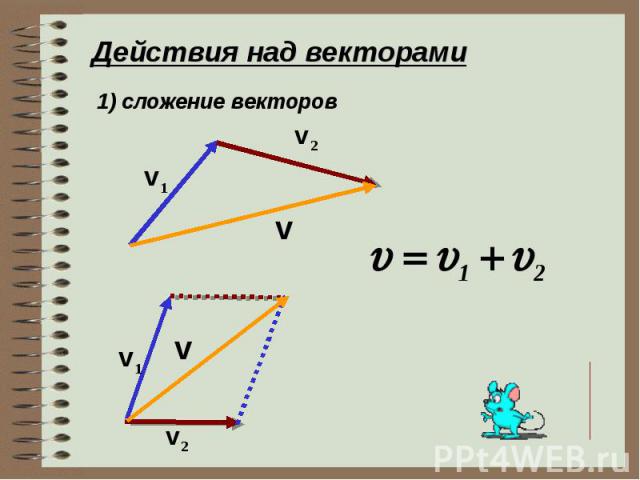 Текущий вектор каждого месяца теперь начинается с конца вектора ветра предыдущего месяца. Вектор движения каждого месяца теперь должен начинаться с конца текущего вектора предыдущего месяца (см. Рабочий лист 2 «Векторное путешествие», ключ к ответам). Попросите учащихся ответить на вопросы из рабочего листа Vector Voyage 2.
Текущий вектор каждого месяца теперь начинается с конца вектора ветра предыдущего месяца. Вектор движения каждого месяца теперь должен начинаться с конца текущего вектора предыдущего месяца (см. Рабочий лист 2 «Векторное путешествие», ключ к ответам). Попросите учащихся ответить на вопросы из рабочего листа Vector Voyage 2. (Ответ: 3940 миль.)
(Ответ: 3940 миль.)