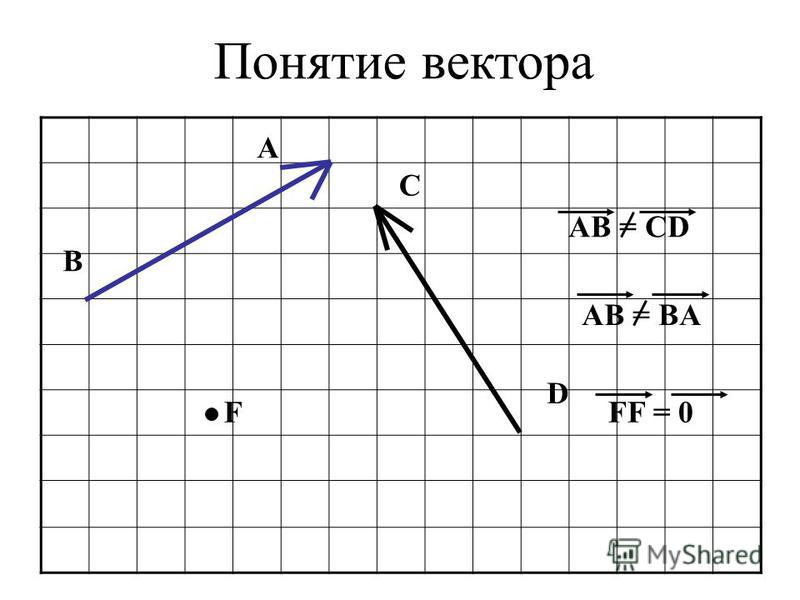
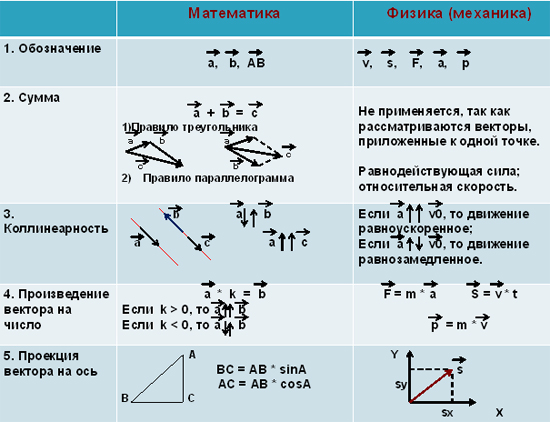
2.2. Действия над векторами

В предыдущем параграфе мы определили вектор как направленный отрезок. Однако вектор можно определять еще и с помощью координат. Это позволяет использовать в векторной алгебре законы алгебры и анализа. Координатами вектора называют проекции вектора на координатные оси [2, гл. II, п. 5.3, 5.4]. Вектор, имеющий координаты а_x, а_y, а_z, можно записывать в двух равнозначных формах:

или

(9)

Выражение (9) называют разложением вектора по базисным векторам ( — единичные взаимно перпендикулярные векторы — базис в пространстве; — базис на плоскости).

Замечание. Если начало вектора находится в точке М₁ (x₁; y₁; z₁), а конец в точке М₂ (x₂; y₂;

z₂), то вектор будет иметь координаты

. (10)

Пример 7 [1, к задачам № 21-30, п. 1]. Даны точки А(1; 6; 5) и В(3; 4; 5). Найти координаты вектора .

Решение

Принимая за начало вектора точку А, а за конец — точку В, по формуле (10) получим

Замечание. В координатной форме векторы считаются равными, если равны их соответствующие координаты, т.е.

Рассмотрим теперь, какие действия производятся над векторами и как они осуществляются. Следует только помнить, что эти действия можно выполнять как в векторной, так и в координатной формах. Все действия над векторами приведены в таблице 2.

Таблица 2

Действия над векторами

Название	Определение в векторной форме	Выражение в координатной форме
1. Сложение векторов	1) по правилу параллелограмма
	2) по правилу треугольника
2. Вычитание векторов	Как действие, обратное сложению:
3. Умножение вектора на число λ
4. Скалярное произведение векторов
5. Векторное произведение векторов
6. Смешанное произведение векторов

Пример 8 [1, к задачам № 21-30]. Даны векторы:

Найти:

Решение

Векторы заданы в виде разложений по базисным векторам. Найдем их координаты:

Выполним вышеуказанные действия над векторами, учитывая, что векторы заданы координатами. Используя таблицу 2, получим:

Рассмотренные операции над векторами, а также получающиеся из них следствия широко используют в практике (табл.

3).

Таблица 3

Основные применения векторов

Словесное название	Выражение в
1	2
1. Длина вектора — длина отрезка
2. Единичный вектор — орт вектора
3. Угол между векторами
4. Условие
5. Условие
6. Условие компланарности векторов

Продолжение таблицы 3

1	2
7. Площадь параллелограмма S, построенного на векторах (SΔ = S)
8. Объем параллелепипеда Vпаралл, построенного на векторах

Пример 9 [1, к задачам № 21-30]. Даны координаты вершин пирамиды ДАВС: А (1; 2; –1), В (0; 1; 5), С (–1; 2; 1), Д (0; 1; 6). Средствами векторной алгебры найти:

1) координаты векторов

2) длину вектора

3) площадь грани АВС;

4) объем пирамиды ДАВС.

Решение

1. Сначала найдем координаты векторов . Как и в примере 7, по формуле (10) получим:

2. Найдем теперь координаты вектора Для этого воспользуемся 1, 2, 3 пунктами таблицы 2. Тогда получим:

Для определения длины вектора можно воспользоваться результатом пункта 1 из таблицы 3:

3. Угол между векторами найдем, используя п. 3 табл. 3:

4. Площадь грани АВС (см. п. 7, табл. 3,) равна:

Так как

то с учетом п. 1 табл. 3 получим

А площадь грани (ед.²).

5. Объем пирамиды ДАВС (см. п. 8 табл. 3) равен

Найдем смешанное произведение (см.

п. 8 табл. 2):

Объем пирамиды .

Контрольные вопросы

1. Дайте понятие базиса на плоскости и в пространстве.

2. Дайте понятие координат вектора на плоскости и в пространстве.

3. Что такое скалярное произведение векторов? Где оно применяется?

4. Дайте определение векторного произведения векторов и укажите, где его применяют.

5. Дайте определение смешанного произведения векторов и укажите, где его применяют.

Аналитическая геометрия

Аналитическая геометрия

Привалов И.И. Аналитическая геометрия. М.: Наука, 1966. — 272 с. Учебник для студентов высших технических заведений. Содержит разделы: Аналитическая геометрия на плоскости, Аналитическая геометрия в пространстве. Много решенных примеров и задач. Оглавление ВВЕДЕНИЕ ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ ГЛАВА I. МЕТОД КООРДИНАТ § 2. Координаты на прямой линии. § 3. Расстояние между двумя точками на прямой линии. § 4. Прямоугольные координаты на плоскости. § 5. Расстояние между двумя точками на плоскости. § 6. Деление отрезка в данном отношении. § 7. Угол между двумя осями. § 8. Основные положения теории проекций. § 9. Проекции направленного отрезка на оси координат. § 10. Площадь треугольника. § 11. Полярные координаты. Упражнения ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ § 1. Составление уравнений заданных линий. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Пересечение двух линий. § 5. Параметрические уравнения линий. § 6. Уравнения линий в полярных координатах. ГЛАВА III. ПРЯМАЯ ЛИНИЯ § 1. Угловой коэффициент прямой. § 2. Уравнение прямой линии с угловым коэффициентом. § 3. Геометрический смысл уравнения первой степени между двумя переменными. § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0. § 5. Уравнение прямой линии в отрезках. § 6. Построение прямой линии по ее уравнению. § 7. Угол между двумя прямыми. § 8. Условия параллельности и перпендикулярности двух прямых. § 9. Уравнение прямой, проходящей через данную точку в данном направлении. § 10. Взаимное расположение двух прямых на плоскости. § 11. Уравнение пучка прямых. § 12. Уравнение прямой, проходящей через две данные точки. § 13. Условие, при котором три данные точки лежат на одной прямой. § 14. Нормальное уравнение прямой линии. § 15. Приведение общего уравнения первой степени к нормальному виду. § 16. Расстояние от дайной точки до данной прямой. § 17. Уравнение прямой в полярной системе координат. Упражнения ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ § 2. Окружность. § 3. Эллипс. § 4. Гипербола и ее асимптоты. § 5. Парабола. § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки. § 7. Эллипс, гипербола и парабола как конические сечения. § 8. Эксцентриситет и директрисы эллипса. § 9. Эксцентриситет и директрисы гиперболы. § 10. Эксцентриситет и директриса параболы. § 11. Уравнение конического сечения в полярных координатах. § 12. Диаметры зллипса. Сопряженные диаметры. § 13. Диаметры гиперболы. Сопряженные диаметры. § 14. Диаметры параболы. § 15. Касательная. § 16. Эллипс как проекция окружности. § 17. Параметрические уравнения эллипса. Упражнения ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ § 2. Перенос начала координат. § 3. Поворот осей координат. § 4. Общий случай. § 5. Некоторые приложения формул преобразования координат. § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных. § 7. Преобразование общего уравнения второй степени. § 8. Классификация линий. Упражнения ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА § 2. Однородная система двух уравнений с тремя неизвестными. § 3. Определители 3-го порядка. § 4. Основные свойства определителей 3-го порядка. § 5. Система трех уравнений первой степени с тремя неизвестными. § 6. Однородная система. § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными. § 8. Некоторые приложения определителей к аналитической геометрии. Упражнения ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ § 2. Основные задачи. § 3. Основные положения теории проекций в пространстве. § 4. Вычисление угла между двумя осями в пространстве. Упражнения ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ § 2. Сложение векторов. § 3. Вычитание векторов. § 4. Умножение вектора на число. § 5. Проекции вектора. § 6. Действия над векторами, заданными своими проекциями. § 7. Скалярное произведение векторов. § 8. Основные свойства скалярного произведения. § 9. Скалярное произведение векторов, заданных проекциями. § 10. Направление вектора. § 11. Векторное произведение. § 12. Основные свойства векторного произведения. § 13. Векторное произведение векторов, заданных проекциями. § 14. Векторно-скалярное произведение. § 15. Векторно-скалярное произведение в проекциях. § 16. Двойное векторное произведение. Упражнения ГЛАВА III. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ § 1. Уравнение поверхности. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Сфера. § 5. Цилиндрические поверхности. § 6. Уравнения линии в пространстве. § 7. Пересечение трех поверхностей. Упражнения ГЛАВА IV. ПЛОСКОСТЬ § 1. Нормальное уравнение плоскости. § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду. § 3. Исследование общего уравнения плоскости. § 4. Уравнение плоскости в отрезках. § 5. Уравнение плоскости, проходящей через данную точку. § 6. Уравнение плоскости, проходящей через три данные точки. § 7. Угол между двумя плоскостями. § 8. Условия параллельности и перпендикулярности двух плоскостей. § 9. Точка пересечения трех плоскостей. § 10. Расстояние от точки до плоскости. Упражнения ГЛАВА V. ПРЯМАЯ ЛИНИЯ § 1. Уравнения прямой линии. § 2. Прямая как линия пересечения двух плоскостей. Общие уравнения прямой. § 3. Угол между двумя прямыми линиями. § 4. Условия параллельности и перпендикулярности двух прямых. § 5. Уравнения прямой, проходящей через две данные точки. § 6. Угол между прямой и плоскостью. § 7. Условия параллельности и перпендикулярности прямой и плоскости. § 8. Уравнение пучка плоскостей. § 9. Пересечение прямой с плоскостью. § 10. Условие, при котором две прямые лежат в одной плоскости. Упражнения ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА § 1. Классификация поверхностей. § 2. Цилиндрические поверхности (общий случай). § 3. Конические поверхности. § 4. Поверхности вращения. § 5. Эллипсоид. § 6. Однополостный гиперболоид. § 7. Двуполостный гиперболоид. § 8. Эллиптический параболоид. § 9. Гиперболический параболоид. § 10. Конус 2-го порядка. § 11. Цилиндры 2-го порядка. § 12. Прямолинейные образующие поверхностей 2-го порядка. Конструкции В. Г. Шухова. Упражнения Ответы

2. Векторы: определения, алгебра

2. Векторы: определения, алгебра

принтер Дружественный Копия

Частица – это тело, размеры которого пренебрежимо малы или чьи размеры приближаются к нулю в математическом смысле, в том смысле, что можно рассматривать как точечную массу. Кроме того, когда размеры тела не имеют отношения к описанию его положения или последствий действие приложенных к нему сил, тело можно рассматривать как частицу.
    Статика частиц имеет дело с эффектами концентрированных силы на частицы, сложение таких сил, их разложение на компонентов, определение равнодействующей системы сил, действующих на частицу, а также связь между силами, действующими на частица в состоянии равновесия. Для их выполнения мы будем необходимо применить правила векторной алгебры.

Силы, действующие на частицу

Сила – это действие/следствие, стремящееся изменить состояние покоя или равномерное движение тела. Сила полностью характеризуется своим величину и направление. Направление силы задается ее точкой приложения и линии действия, которая представляет собой прямую линию, лежащую на одной прямой с вектором силы.

Обратите внимание, что, поскольку частицы идеализируются как точечные массы, система все силы, действующие на частицу, проходят через точку, занимаемую частица. Система сил, проходящая через общую точку, говорят, что они одновременны.

Скаляры и векторы

    Механика имеет дело с двумя видами величин — скаляры и векторы.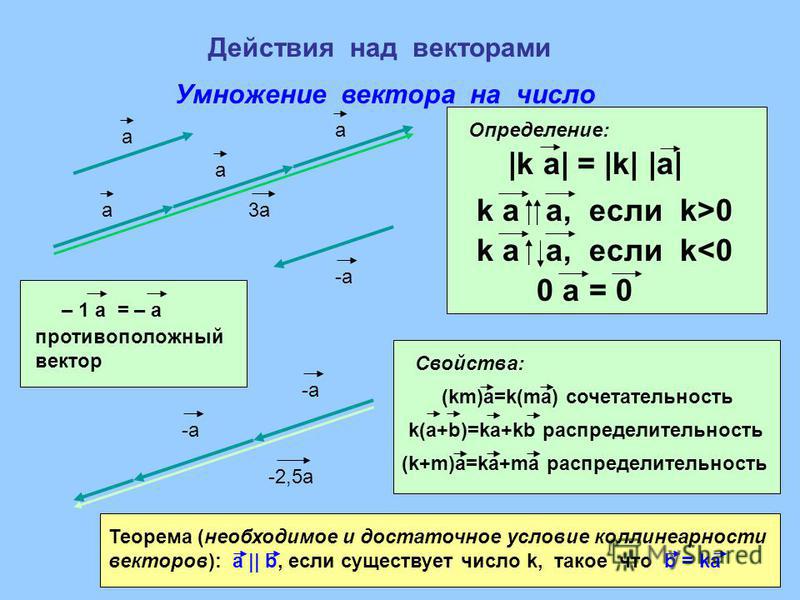 Скалярные величины — это те, величина которых только напр. расстояние, время, объем, плотность, скорость, энергия, масса, длина, температура и т. д. С другой стороны, векторные величины имеют как величина и направление (линия действия и смысл) и должны подчиняться параллелограмму закон сложения. Примеры векторов включают скорость, смещение, ускорение, сила, момент и количество движения.
    Вектор представлен графически стрелкой который определяет величину и направление вектора. Величина вектора обозначается длиной стрелки, направление определяется углом между базовой осью и линией действия стрелки а смысл указан стрелкой. В учебниках векторы представлены полужирными буквами , но в классе мы будем использовать подчеркивание для представления векторов, например. вектор A будет записан как А .

Классификация векторов

    Векторы можно сгруппировать в три класса — бесплатно векторы, скользящие векторы и фиксированные векторы. Физические величины, которые векторы попадают в одну из этих трех категорий. Бесплатные векторы являются векторы, которые могут свободно перемещаться в пространстве, т. е. их линии действия не ограничен или не связан с уникальной линией в пространстве, например. пары, смещение вектор тела, движущегося в пространстве без вращения. Наоборот, скользящий вектор — это тот, для которого единственная линия в пространстве, вдоль которой векторные действия должны поддерживаться, например. внешнее действие силы на твердое тело (сила может быть приложена в любой точке вдоль его линии действия без изменения его действия на организм в целом — принцип трансмиссивности). Фиксированный вектор — это вектор, для которого определена уникальная точка приложения. указан, и поэтому вектор занимает определенную позицию в пространстве например действие силы на деформируемое или нежесткое тело или силы действует на данную частицу. Фиксированный вектор полностью характеризуется по его точке приложения, его величине и направлению (где направление определяется линией действия и смыслом).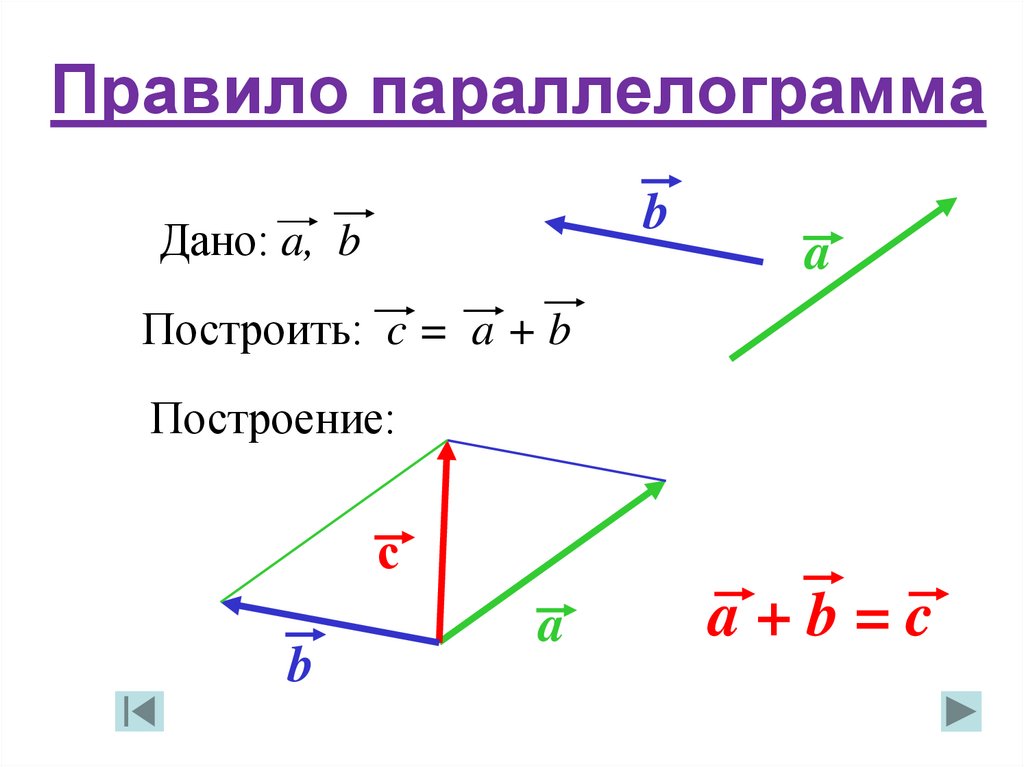 Потому что частица бесконечно мала, силы, действующие на него, имеют одну и ту же точку приложения, следовательно, силы, действующие на частицу, полностью характеризуются своей величиной и направление.
    Два вектора называются равными, если они имеют той же величины, направления и точки приложения. Если векторы являются свободными векторами, они могут не иметь одинаковой точки приложения или одна и та же линия действия, но их величина и направление должны быть одинаковыми, например рассмотрим векторы A , B и C , которые имеют одинаковая величина, но разные точки приложения.

A = B = C тогда и только тогда, когда A , B , C являются бесплатные векторы
А нет = Б нет = С если А , Б , С являются фиксированными векторами
А не = Б а А = С если А , Б , С скользящие векторы

    Два вектора равны и противоположны , если они имеют одинаковую величину, но имеют противоположные направления. (т.е. их линии действия коллинеарны или параллельны, но их смысл противоположен). Нулевой вектор — это вектор с нулевой величиной в любом произвольном направлении.

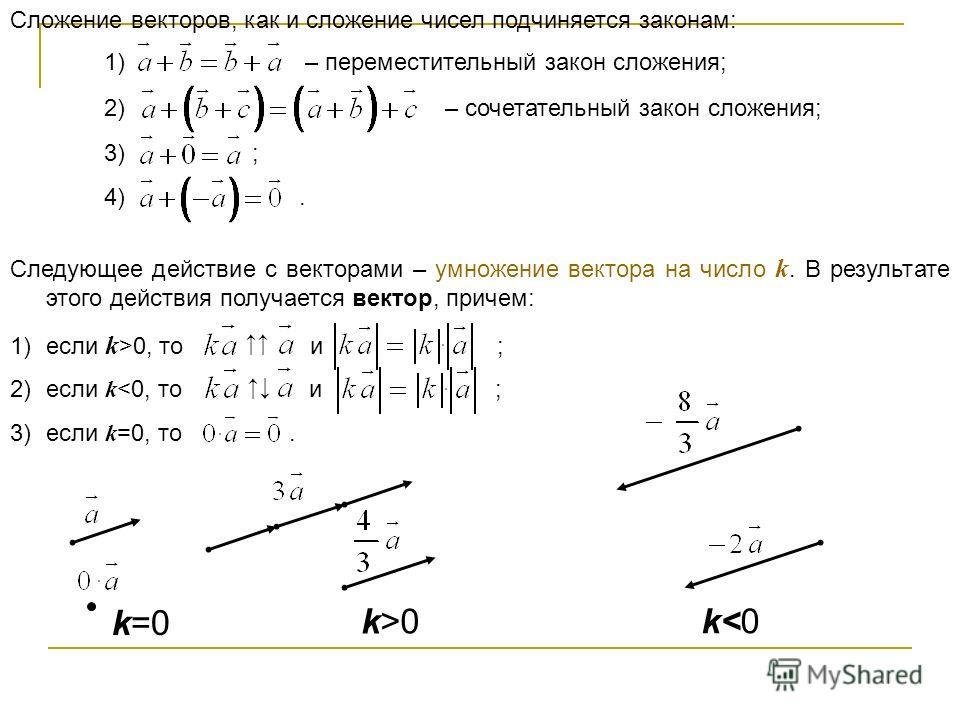
Сложение двух векторов : Закон параллелограмма

    Напомним из определения векторов, которые они добавляют по закону параллелограмма. Сумма двух векторов получается построив параллелограмм с векторами по обеим сторонам параллелограмм. Диагональ параллелограмма представляет собой сумму векторного сложения двух векторов. например

Обратите внимание, что сложение векторов является коммутативным , т.е.
           P + О = О + Р

Свойство коммутативности становится очевидным, если использовать треугольник . Правило сложения векторов.

Вычитание вектора следует рассматривать как сложение соответствующих отрицательный вектор. Следовательно,
           P — Q = P + (- Q )
    Чтобы получить сумму трех или более векторов, примените закон параллелограмма многократно к последовательным парам векторов, пока все векторы заменяются одним вектором, результатом является .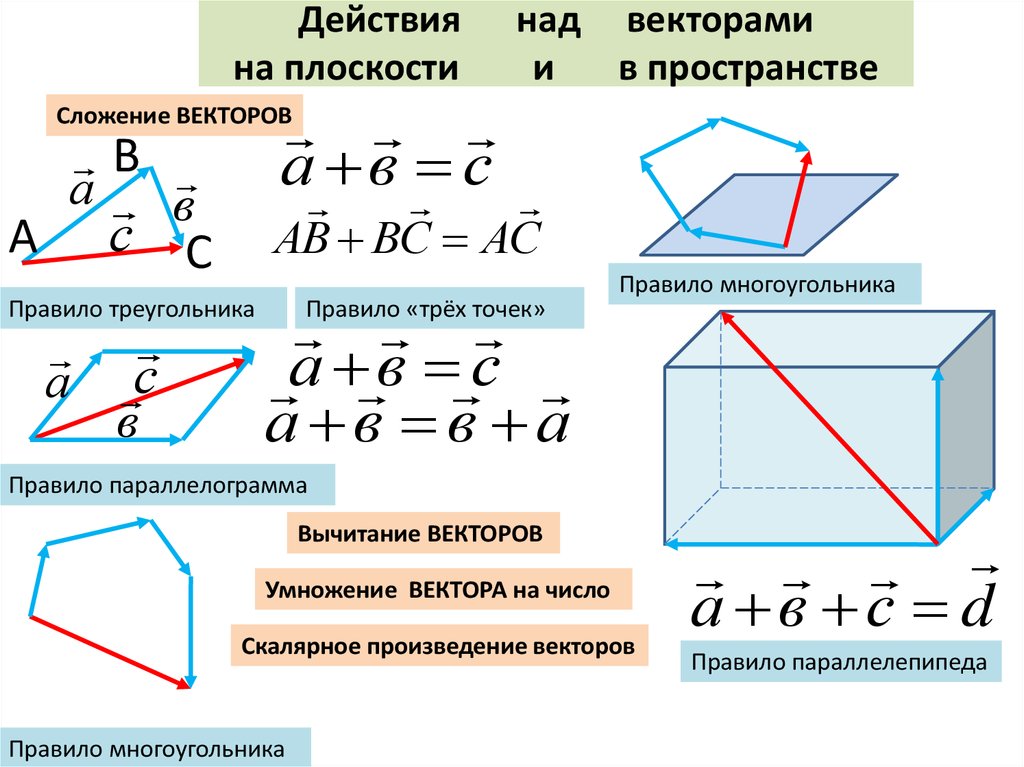

Правило треугольника/многоугольника для сложения двух и более Векторы

    Это означает, что сумма (то есть результирующая) два или более векторов, действующих на тело, можно получить графически, расположив заданные векторы в форме кончик-к-хвосту и соединяющие хвост первый вектор с вершиной последнего при условии, что все векторы компланарны (т.е. все они лежат в одной плоскости). Результирующий из нескольких одновременных компланарных сил также могут быть получены в этом способ. Система сил называется совпадающей, если все силы действовать через одну точку. Обратите внимание, что система сил должна быть компланарной. тоже потому, что рисунок должен быть на плоскости.
    Используя правило многоугольника, легко увидеть, что вектор сложение является одновременно коммутативным и ассоциативным ; то есть
           P + Q = Q + P   (коммутативный закон)
           P + Q + R = ( P + Q ) + R = P + ( Q + Р ) (ассоциативный закон)

Произведение скаляра на вектор

    Произведение скаляра k на вектор P это вектор k P , имеющий то же направление, что и P (если k положительное) или направление, противоположное направлению P (если k отрицательное), и величина которого равна произведению | Р | (и абсолютное значение k, где | Р | величина вектора P

Результат двух сил

    Равнодействующая двух сил, действующих на частицу единая сила, которая действует на частицу так же, как две силы объединились. Такой результат можно получить из Закон параллелограмма сложения двух сил. Обратите внимание, что параллелограмм Закон основан на экспериментальных данных и не может быть доказан или выведен математически.

Разложение вектора на компоненты

    Так же, как две или более сил, действующих на частицу, могут заменить одной силой (равнодействующей), которая имеет тот же эффект на частицу можно также заменить одну силу двумя или больше сил (называемых составляющими одной силы). процесс называется разложением единой силы на составные части .
Обратите внимание, что существует бесконечное количество компонентов для любого отдельного сила F . Однако практическое значение имеет определение двух составляющих силы, когда (1) известна одна из двух составляющих и (2) известна линия действия каждого компонента. В этих и В других случаях необходимые компоненты могут быть получены с помощью треугольника правило или закон параллелограмма.

Рассмотрим силу F , компоненты которой P и Q

(a) F – заданная сила. P известен и только линия действия Q известна; Получите величину Q

• Нарисуйте линию от кончика P к наконечнику F
• Перенести Q в место применения P и Ф
• Получите величину Q либо графически, либо с помощью тригонометрии

 

(b)  Учитывая F и направления действий оба компонента P и Q известны. Получить величины Р и Q

— Построить параллелограмм с F как диагональ и известные линии действий в качестве сторон Тригонометрические решения

Использует правила синуса и косинуса

	a / sin A = b / sin B = c / sin C   (правило синусов)
	а 2 = б 2 + c 2 — 2bc Cos A \ b 2 = a 2 + c 2 — 2ac Cos B (Правило косинуса) c 2 = a 2 + b 2 — 2ab Cos C /

В общем,

    — Когда проблема затрагивает только три силы , используйте силовой треугольник и правила синуса и / или косинуса, чтобы решить его.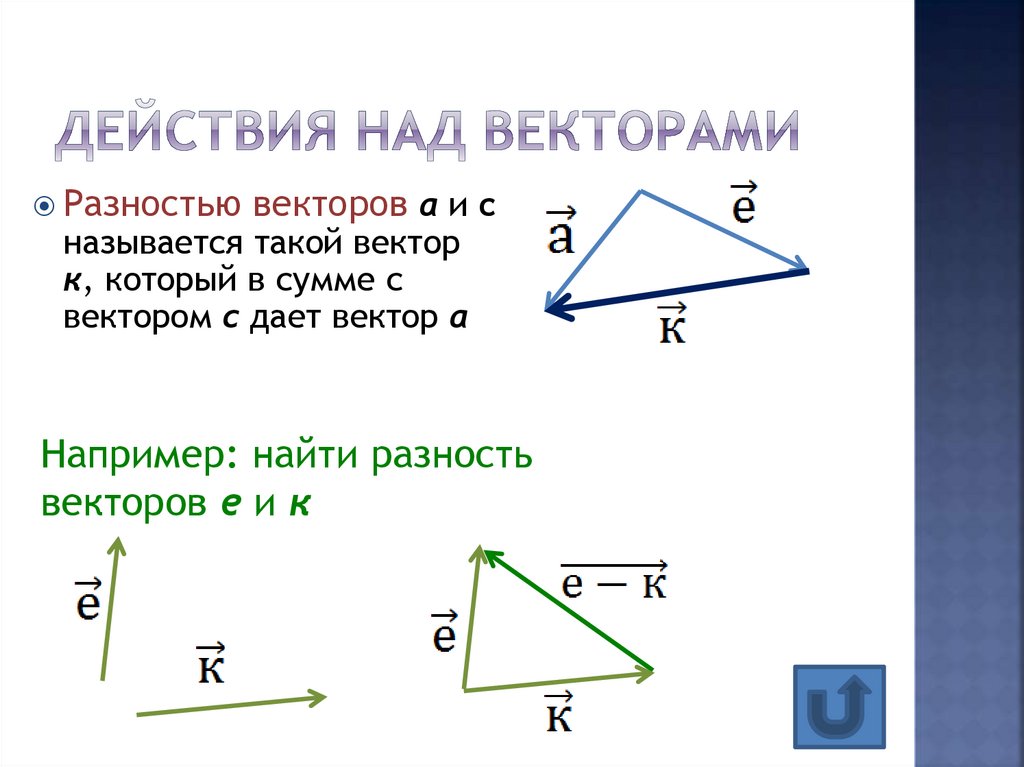
    — Когда проблема включает в себя более трех сил , разложите силы на их прямоугольные компоненты и решите с помощью вектора алгебра.

Пример 2-1

Кабели AB и AC на рис. ниже помогают поддерживать консольный крыша спортивного стадиона. Силы, с которыми тросы действуют на опору, к которой они прикреплены представлены векторами F _AB и F _AC , которые имеют величины 100 кН и 60 кН соответственно. Определить величину и направление суммы приложенных сил. (1) на пилоне за тросы (2) на стадионе за тросы. Получать ваше решение (а) графически и (б) с помощью тригонометрии.

Учитывая : | F _аб | = 100 кН
| F _ак | = 60 кН

Требуется :    Величина и направление сумма сил, действующих на трос
а) на пилоне Используйте     (1) графическое решение
б) на стадионе (2) Тригонометрическое решение

Пример задачи 2.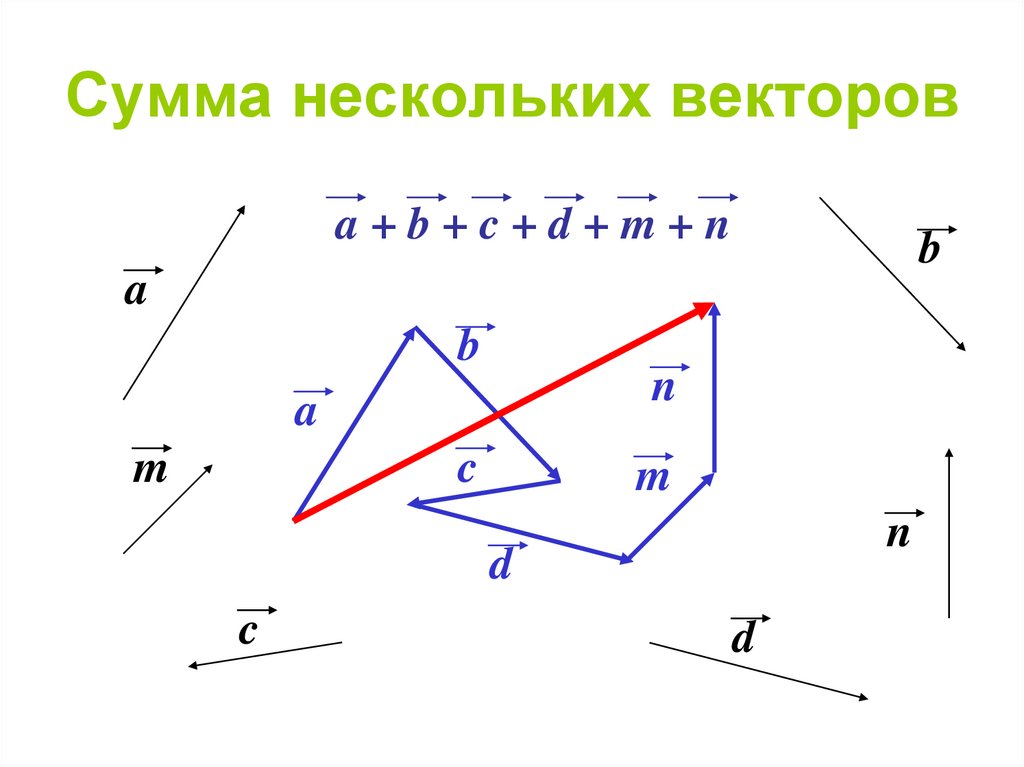 1

Учитывая : Две силы с величиной и направлением, как показано на диаграмме

Требуется :    Величина и направление результирующая сила

Пример задачи 2.2

Дано : Две силы с величиной и направлением как показано на схеме

Требуется :    Величина и направление результирующая сила

Пример задачи 2.10

Дано :    Автомобиль-инвалид, протянутый мимо две веревки АВ и АС. Напряжение в АВ = 4000 Н·а = 20 градусов Результирующая сила действует вдоль оси автомобиля.

Требуется :
     а) Натяжение каната переменного тока
     b) Величина равнодействующей силы приложены две силы
     c) Стоимость такого что напряжение в переменном токе минимально, а R все еще действует вдоль оси автомобиля. Какова величина Т _ак а также результирующая сила, которая все еще действует вдоль оси автомобиля.

Прямоугольные компоненты силы в плоскости и в космосе

—    Компоненты силы, параллельные к прямоугольным/декартовым координатным осям. Такие компоненты перпендикулярны друг другу.

    Любая сила F в трехмерном пространстве может разложить на прямоугольные компоненты F _x , F _y и F _z , которые параллельны осям x и z соответственно. Следовательно, F является суммой или равнодействующей прямоугольных составляющих F _x , Ф _у и F _z , т.е.

Ф = F _x + F _y + Ф _з . . . (1) Концепция единичного вектора
    Единичный вектор — это вектор который имеет величину один (1). Этот вектор очень важен, потому что он устанавливает направление любого заданного вектора. Чтобы получить направление вектора, вычислить единичный вектор, который действует в том же направлении, что и вектор. Это делается путем деления заданного вектора на его величину. направление единичного вектора обычно задается указанием направления углы, которые представляют собой углы, которые вектор образует с положительным x-, оси координат y и z.

    Если  i, j и k являются единичными векторами в x, y, направления и z и F _x , F _y и F _z ортогональных скалярных компонента F , где F _x , Ф _у и F _z являются ортогональными компонентами вектора F и F _x = | F _x | ; Ф _и =| F _у | и F _г = | Ф _з | ,
F _x = F _x i    F _y = F _y j F _z = F _z k
Тогда уравнение 1 может быть выражено как

F = F _x i + F _y j + F _z k . . . (2) и величина F = | Ф | дан кем-то

  Сложение сил (вычисление равнодействующей)
Использование прямоугольных компонентов

    Обратите внимание, что и закон параллелограмма, и треугольник правило позволяет добавить две силы с использованием графического подхода, в то время как Правило многоугольника позволяет добавить три или более сил.
    Силовой треугольник и тригонометрическое решение могут использоваться, когда участвуют только три силы . Когда более задействованы три силы, подход все еще может быть использован последовательным одновременно рассматривая тео сил и находя их равнодействующую. Однако, такой подход обычно утомителен. Когда сложение векторов включает более трех векторов, сложение лучше всего выполнять путем разрешения каждый вектор на его прямоугольные компоненты и сложение этих компонентов для получения прямоугольных составляющих результирующей силы, например.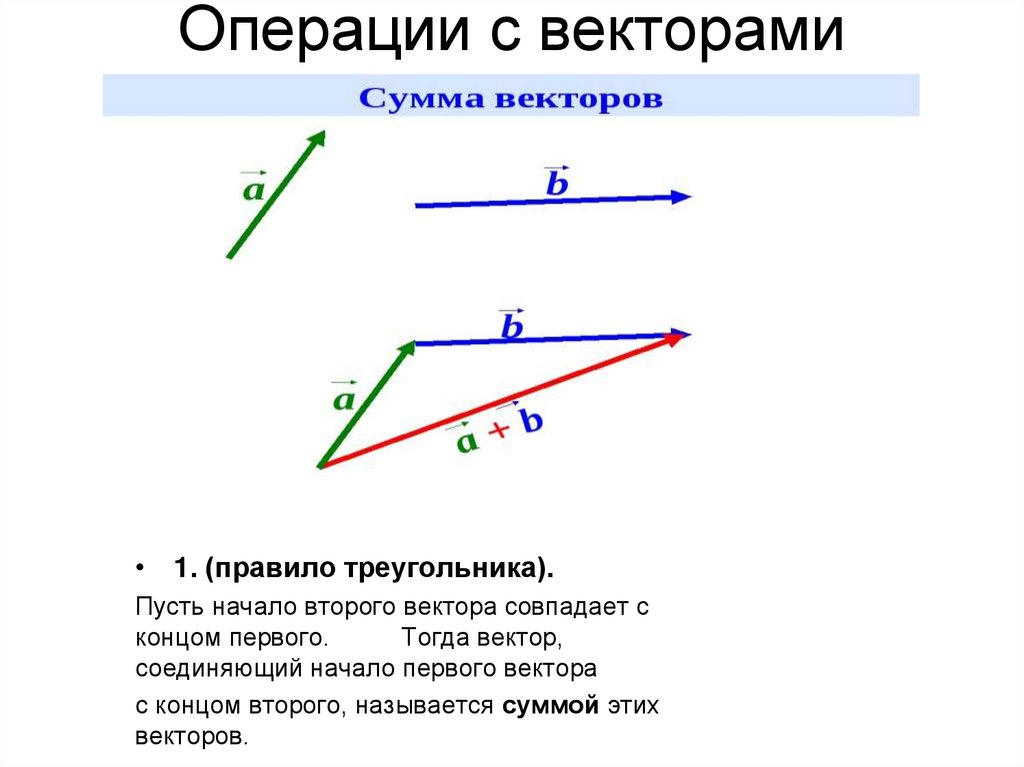 если Р есть равнодействующая сил А , В , С и D , т.е.

           Р = А + В + С + D
Где A = 
           B = 
           C = 
           D = 
           R =

Тогда    R = где

Обратите внимание, что скалярная составляющая R _x , R _y и R _z результирующего R определяется алгебраической суммой соответствующие скалярные компоненты заданных векторов. Величина равнодействующей силы находится из выражения:

Углы направления и косинусы направления

Углы q _x , q _y и q _z , которые вектор составляет с положительные концы осей x, y и z соответственно называются углы направления. Эти углы важны, потому что их косинусы — прямоугольные скалярные компоненты единичного вектора, действующие в одном и том же направление. Для любого вектора R = , направляющие косинусы связаны с его прямоугольными скалярными компонентами и величина следующим образом:

Обратите внимание на соотношение выше, что
, , 

но  R =

и

, где должна быть единица вектор, поскольку величина вектора равно 1. Используя отношение
R =

У нас есть

Следовательно,

    Заметим, что направляющие косинусы вектора равны прямоугольные скалярные компоненты (по трем координатным осям) единичный вектор, действующий в том же направлении, что и вектор.

Обратите внимание, что скалярные компоненты единичного вектора вдоль трех декартовых системы координат равны направляющим косинусам вектора с отношение к осям. Также три угла направления q _x , д _д и q _z не все независимы. Если известны два дирекционных угла, то третий можно определить из уравнение выш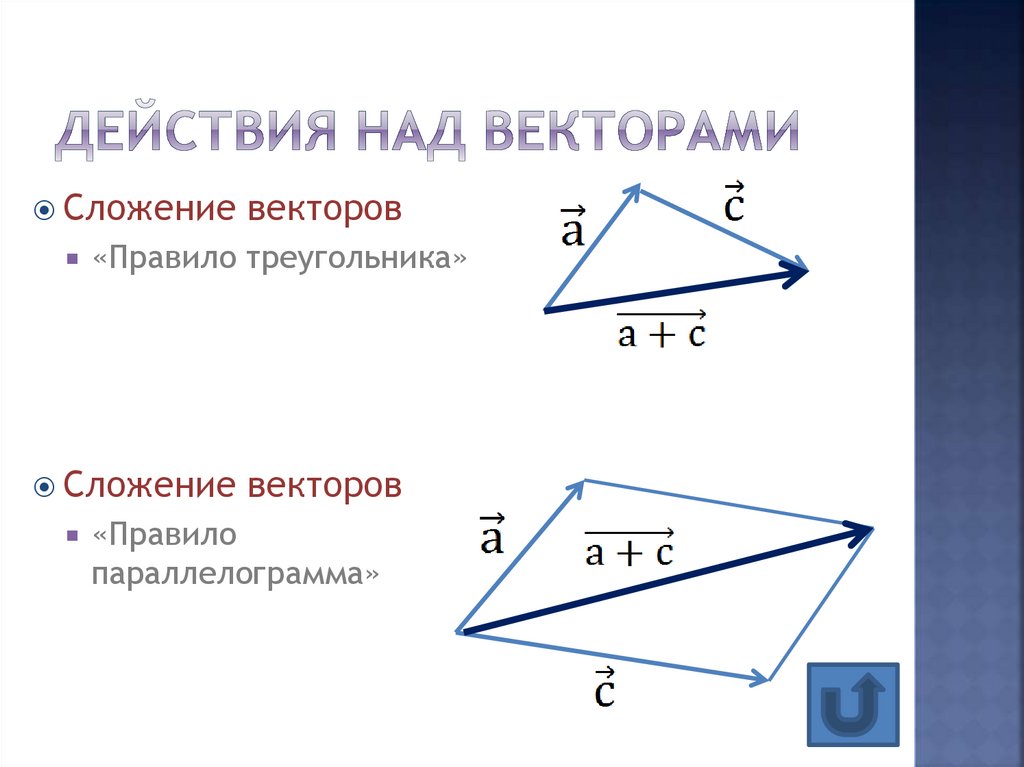е. Также

Пример (см. пример задачи 2.7 на стр. 44)

Дано : Вектор известной величины | В | но линия действия которого определяется двумя точками (x ₁ , y ₁ , z ₁ ) и (x ₂ , y ₂ , z ₂ ).
Требуется : для определения компонентов вектора В в трех ортогональных направлениях. Что такое направляющие косинусы?

Пример задачи 2.59

Дано : Пружина AB и стойка DA, с углом 30 градусов между стойкой и пружиной. Напряжение | Т | = 250 Н

Требуется :   (a) компоненты x, y, z сила, действующая на пластину в точке B
(б) q _x , q _y и q _z , определяющие направление сила в точке В

Пример задачи 2. 61

Дано : F = (240Н)i — (270Н)j + (680Н)k

Требуется : Величина и направление F

Равновесие частиц

Говорят, что частица находится в равновесии, если равнодействующая всех силы, действующие на него, равны нулю. Это означает, что если силовой многоугольник для всех сил, действующих на частицу, находящуюся в равновесии, силовой многоугольник замкнется, как показано ниже (см. учебник стр. 32, рис. 2.27 и 2.28). Алгебраически условие равновесия представляется как

Ч = å Ф = 0
==> 
==>

Задачи на равновесие лучше всего решать с помощью бесплатных схемы тела. Вы должны нарисовать свободные диаграммы тела для своих решений.

Бесплатные диаграммы тела

Диаграмма свободного тела — это диаграмма, на которой показано тело (или частица) и все силы, как известные, так и неизвестные, действующие на него.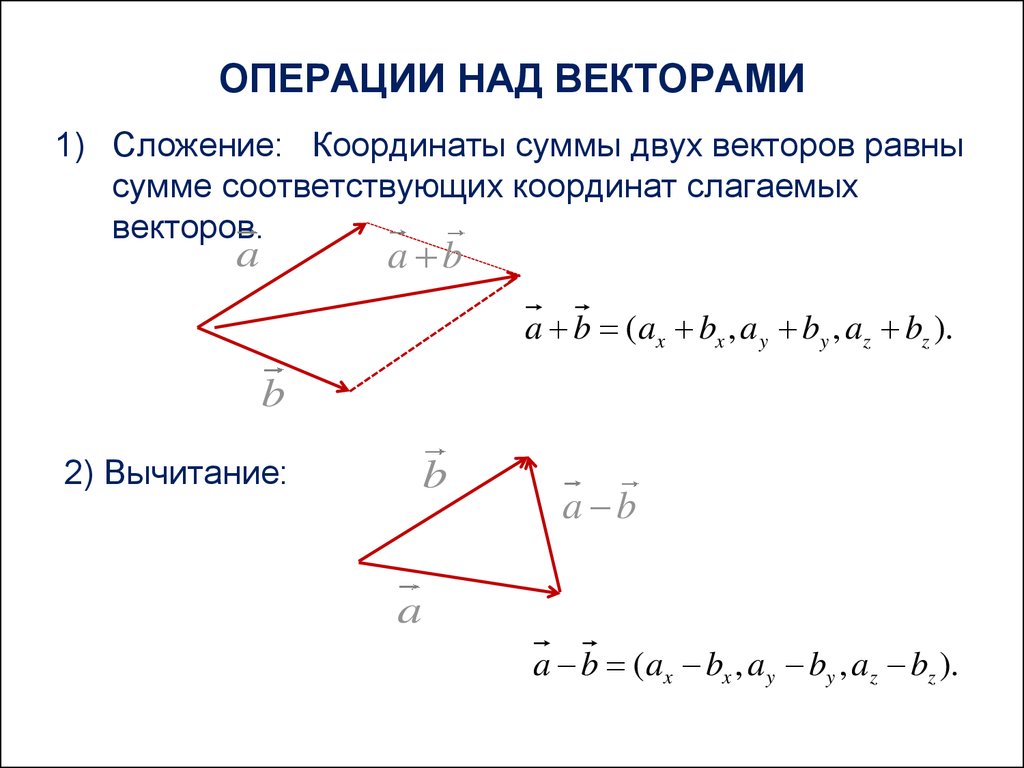

Обратите внимание, что все соответствующие размеры, величины и направления должны показать на диаграмме свободного тела. Все уравнения должны быть написаны на основе на применимых диаграммах свободного тела

Примеры

Для каждой задачи ниже нарисуйте диаграмму свободного тела, которая может быть используется для решения проблемы.

Вопрос 1

Определить силы натяжения канатов AB и AC.

Вопрос 2

Определите горизонтальную силу «P», которую рабочий должен приложить к канат для размещения 50-килограммового ящика непосредственно над транспортным средством?

Вопрос 3

Определить натяжение тросов AC и BC.

Вопрос 4

Две веревки связаны вместе в точке С. Если максимально допустимое натяжение в каждая веревка 2,5 кН, что такое Fmax и соответствующий ей угол наклона, альфа?

Вопрос 5

Определите натяжение тросов AB, AC и AD, необходимое для

удерживайте 60-фунтовый ящик в равновесии.

Вопрос 6

Вышка со срезными опорами используется для буксировки 200-килограммовой сети.

рыбы на причал. Определить сжатие

усилие в каждой из опор AB и CB и напряжение в

кабель БД. Предположим, что сила каждой ноги действует вдоль ее

ось.

Вопрос 7

Хомут А может свободно скользить по горизонтальному гладкому стержню. Весна прикреплен к Кольцо

имеет константу 10 фунтов/дюйм и не деформируется, когда кольцо находится прямо под

опора Б. Определить величину силы Р, необходимой для поддержания равновесие, когда (а) c = 9 дюймов; (б) с = 16 дюймов.

ОБЗОР

Учитывая систему сил в пространстве, действующих на частицу, определить величину и направление равнодействующей силы.

• Получить прямоугольные компоненты каждой силы
• Отдельно добавьте все компоненты x, y и z, чтобы получить компоненты равнодействующей силы вдоль координатных направлений
• Получите величину равнодействующей силы, используя ее прямоугольные компоненты
• Вычислите направляющие косинусы и, следовательно, получите направляющие углы

Дана величина силы и две точки вдоль его линии действия, выразите силу через ее прямоугольные компоненты.

• Используя данные две точки вдоль линии действия, получите единичный вектор по линии действия —
• получить вектор смещения из одной точки в другую;
• получить величину вектора смещения;
• разделите вектор смещения на его величину, чтобы получить единичный вектор
• Умножьте единичный вектор на величину силы, чтобы получить силу вектор

 

---

Вернуться на страницу курса Статика принтер Дружественная копия

---

Пример группового действия G в векторном пространстве V, которое не может быть линейным (т. е. не может быть линейным представлением).

спросил 7 лет, 4 месяца назад

Изменено 2 года, 9несколько месяцев назад

Просмотрено 2к раз

$\begingroup$

Я видел следующее определение представления линейной группы из заметок К. Лента по теории представлений:

линейное представление $ρ$ группы $G$ на комплексном векторном пространстве $V$ является теоретико-множественным действие на $V$, сохраняющее линейную структуру, то есть:

1. $ρ(g)(v_1 + v_2) = ρ(g)v_1 + ρ(g)v_2, ∀v_1,v_2 ∈ V$
2. $ρ(g)(kv) = k · ρ(g)v, ∀k ∈ C, v ∈ V$

Из этого определения следует, что существуют действия $G$ на векторном пространстве $V$, которые не могут сохранить линейную структуру $V$ в этом смысле. Может ли кто-нибудь привести хороший пример?

• теория представлений
• примеры-контрпримеры
• групповые действия

$\endgroup$

1

$\begingroup$ 92}$ определяется как: $n * (x,y) = (x+n, y)$.

Мы можем убедиться, что это действительно формирует групповое действие:

1. $m * (n * (x,y)) = m * (x + n, y) = (x + n + m, y) = (m+n) * (x,y)$
2. $0 * (x,y) = (x + 0, y) = (x,y)$

Однако это действие не учитывает скалярное умножение для $k \neq 0$ и $n \neq 0$, поскольку это дает $n * (k(x,y)) = n * (kx, ky) = (kx + n, ky) \neq (kx + kn, ky) = k(x+n, y) = k (n * (x,y))$.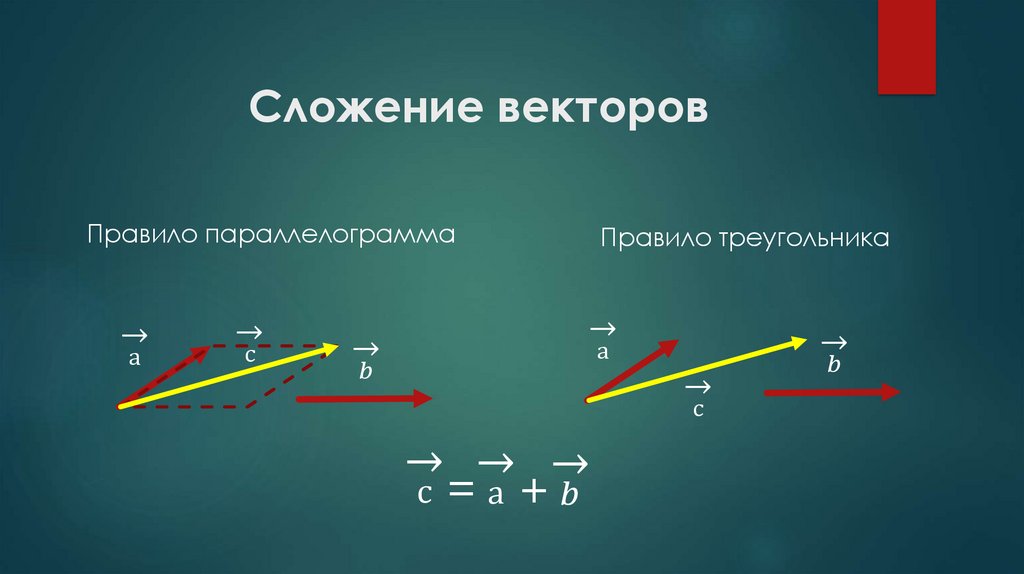

$\endgroup$

$\begingroup$

Если я правильно помню, стандартный пример: возьмем пространство матриц $$ A(k)=\begin{pmatrix} 1 & k \\ 0 & 1 \end{pmatrix}, $$ для реальных $k$. Это группа по умножению с $A(k)A(-m) = A(k-m)$. Определим действие $\rho$ на $\mathbb{R}$ следующим образом: $$ \rho(A(k))(v) = v+k $$ для любого $v \in \mathbb{R}$. Теперь это действие, так как $$\rho(A(k))(\rho(A(m))(v)) = (v+m)+k = v+(k+m) = \rho(A(k)A(m) )(v) \quad \text{and} \quad \rho(A(0))(v)=v,$$ но $$ \rho(A(k))(u+v) = u+v+k \neq u+k+v+k = \rho(A(k))(u)+\rho(A(k) )(v), $$ и $$ \rho(A(k))(\lambda v) = \lambda v+k \neq \lambda(v+k) = \lambda \rho(A(k))(v), $$ поэтому никакой линейной структуры не остается.

$\endgroup$

2

$\begingroup$

Важным примером из теории представлений является так называемое «точечное» действие группы Вейля для полупростой алгебры Ли, действующей на двойственном Картане. Оно задается формулой $w \cdot \lambda = w(\lambda+\rho)-\rho$, где неточечное действие является линейным, поэтому его можно рассматривать как сдвинутое линейное действие, где мы переместили начало координат $-\rho$.

$\endgroup$

$\begingroup$

Вот несколько примеров:

• Самый крайний пример — симметричная группа на базовом множестве $V$.
• Аффинная группа группы $V$, порожденная обратимыми линейными отображениями и сдвигами. Это можно обобщить, заменив ${\rm GL}(V)$ любой матричной подгруппой $G$, чтобы получить $V\rtimes G$. В частности, $G=1$ дает нам группу $V$, действующую на себя сдвигами. 9n$ как вещественное $n$-мерное риманово многообразие, рассмотрим
  • Группа изометрий обратимых карт, сохраняющих расстояние.
  • Группа конформных автоморфизмов обратимых отображений, сохраняющих угол.