Действия над векторами /qualihelpy

Линейные действия над векторами

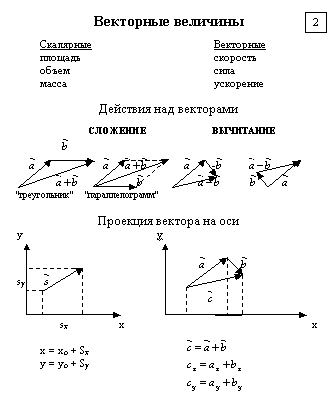
К линейным действиям с векторами относят сложение векторов, вычитание векторов и умножение вектора на число.

Сложение векторов с заданными координатами

Чтобы сложить (вычесть) векторы   и  необходимо сложить (вычесть) их соответствующие координаты: (3.8)

Умножение вектора на число

Чтобы умножить вектор   на число , необходимо каждую координату вектора   умножить на это число: (3.9)

Сочетая действия сложения и вычитания векторов, а также умножение вектора на число, получим линейную комбинацию векторов. 

Аналогично выполняются линейные действия над -мерными векторами. 

Скалярное произведение векторов

Скалярным произведением векторов   и   называется число, равное произведению длин этих векторов на косинус угла между ними:  (3.10)Угол между векторами    и     находят по формуле:. (3.11)Векторы    и     перпендикулярны, если угол между ними равен  . Поскольку   то скалярное произведение перпендикулярных векторов равно нулю.  

Проекцией вектора  на вектор    называют длину отрезка, концами которого являются основания перпендикуляров, опущенных из начала и конца вектора   на вектор   . 

Записывают: пр.  На рисунке 3.7  пр 

Проекцию вектора  на вектор  находят по формуле:  

пр (3.12) 

где  – угол между векторами  и .

Свойства скалярного произведения:

1) 2)  где 3) 4) Скалярное произведение векторов   и   можно найти и по формуле: (3.13)Аналогично в -мерном пространстве: (3.13.1)

Векторное произведение векторов

Векторное произведение векторов   и   находят по формуле: , (3.14)где векторы    и  – орты.Площадь параллелограмма, построенного на векторах  и , находят по формуле:  (3.15)

Площадь треугольника, построенного на этих же векторах, находят по формуле: 

 (3.16)

Смешанное произведение векторов

Рассмотрим векторы  ,  и  Смешанным произведением этих векторов называют число, которое получено в результате скалярного умножения вектора   на векторное произведение векторов   и  Смешанное произведение векторов  и   и   находят по формуле: . (3.17)Объем параллелепипеда, построенного на векторах  ,    и  , находят по формуле:  (3.18)Объем пирамиды, построенной на векторах  ,    и  , находят по формуле:  (3.19)

Конспект на тему » Векторы и действия над ними»

Казахско-Американский Университет Школа при КАУ Класс 9B Семестр осенний 2017-2018 учебный год Урок 1. Векторы и действия над ними. Проекция вектора на координатную ось Преподаватель: Шокпарбаева Э.Е

Понятие вектора

Векторы занимают особое место среди объектов, рассматриваемых в высшей математике, поскольку каждый вектор имеет не только числовое значение — длину, но и физическое и геометрическое — направленность. Вектор, представленный направленным отрезком, идущим от точки A к точке B, обозначается так: .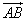

Физическими примерами

 векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на неё сила.

Векторы занимают особое место среди объектов, рассматриваемых в высшей математике, поскольку каждый вектор имеет не только числовое значение — длину, но и физическое и геометрическое — направленность. Вектор, представленный направленным отрезком, идущим от точки A к точке B, обозначается так: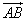

.

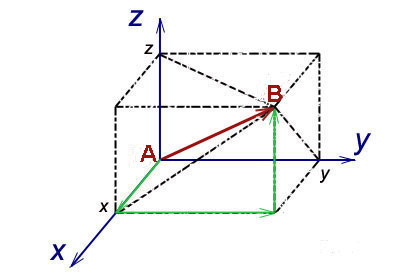
Вектор — это вид представления точки, до которой требуется добраться из некоторой начальной точки. Например, трёхмерный вектор, как правило, записывается в виде (х, y, z). Говоря совсем просто, эти числа означают, как далеко требуется пройти в трёх различных направлениях, чтобы добраться до точки.

Пусть дан вектор. При этом x = 3 (правая рука указывает направо), y = 1 (левая рука указывает вперёд), z = 5 (под точкой стоит лестница, ведущая вверх). По этим данным вы найдёте точку, проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении, указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец, окажетесь в искомой точке.

Все остальные термины — это уточнения представленного выше объяснения, необходимые для различных операций над векторами, то есть, решения практических задач. Пройдёмся по этим более строгим определениям, останавливаясь на типичных задачах на векторы.

Физическими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на неё сила.

Геометрический вектор представлен в двумерном и трёхмерном пространстве в виде направленного отрезка, т.е. отрезка, у которого различают начало и конец.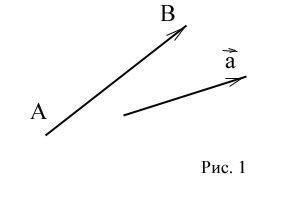

Если A — начало вектора, а B — его конец, то вектор обозначается символом 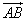или одной строчной буквой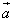

. На рисунке конец вектора указывается стрелкой (рис. 1)

Длиной (или модулем) геометрического вектора 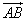называется длина порождающего его отрезка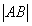

Два вектора называются равными, если они могут быть совмещены (при совпадении направлений) путём параллельного переноса, т.е. если они параллельны, направлены в одну и ту же сторону и имеют равные длины.

В физике часто рассматриваются закреплённые векторы, заданные точкой приложения, длиной и направлением. Если точка приложения вектора не имеет значения, то его можно переносить, сохраняя длину и направление в любую точку пространства. В этом случае вектор называется свободным. Мы договоримся рассматривать только свободные векторы.

Линейные операции над геометрическими векторами

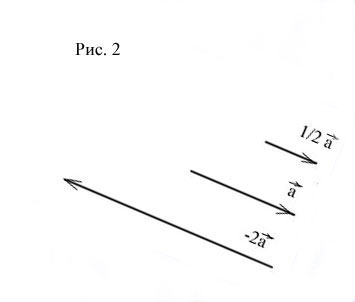
Умножение вектора на число

Произведением вектора 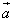на число 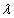называется вектор, получающийся из вектора 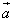растяжением (при 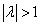) или сжатием (при 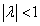) в 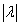раз, причём направление вектора 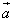сохраняется, если 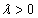, и меняется на противоположное, если 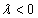. (Рис. 2)

Из определения следует, что векторы 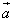и 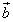= 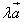всегда расположены на одной или на параллельных прямых. Такие векторы называются коллинеарными. (Можно говорить также, что эти векторы параллельны, однако в векторной алгебре принято говорить «коллинеарны».) Справедливо и обратное утверждение: если векторы 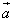и 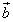коллинеарны, то они связаны отношением

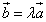.   (1)

Следовательно, равенство (1) выражает условие коллинеарности двух векторов.

Глоссарий

осьі

направленность

orientation

Бағытталған

пространство

space

кеңістік

скорость

speed

жылдамдық

Вопросы:

1. Что называется вектором? Изображение вектора. Примеры.

2. Что называется скаляром? Примеры.

3. Чем отличаются векторные величины от скалярных?

4. Как производится сложение векторов?

5. Как производится вычитание векторов?

6. Что называют проекцией вектора?

СРС: Даны длины векторов 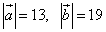 и длина суммы этих векторов 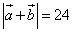. Найти длину разности этих векторов .

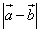Литература: Физика 9 класс

Урок-презентация «Вектор. Действия над векторами»

Этап урока	Время	Учитель	Ученики
Организационный момент	1 мин.	Приветствие друг друга.	Готовятся к уроку.
Актуализация знаний	5 мин.	Из курса физики вам известно, что все физические величины имеют численное значение, но есть физические величины, например, такие как скорость и силы (слайд 1), которые имеют не только численные значения, но и направление. То есть все физические величины можно разделить на те, которые имеют только численное значение. Их называют скалярными. И физические величины, которые характеризуются численным значение и направлением. Такие физические величины называют векторными (слайд 2).	Слушают учителя и делают записи в тетрадях. Отвечают на вопросы
		Сейчас перед вами будут появляться физические величины. Ваша задача распределить их на группы (слайд 3). Давай проверим правильность вашего ответа. Бывает так, что на тело действует несколько сил и необходимо знать куда будет двигаться тело, а для этого надо знать, как можно обращаться с векторными величинами. Сегодня мы с вами и будем говорить о векторах и действиях над ними.	Учащиеся делают свои предположения
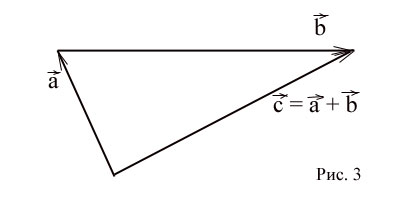
Изучение нового материала	38 мин.	Тема  урока “Векторные величины. Действия над векторами”. (слайд 4). Учитель дает определение вектора (слайд 5). Рассмотрим правила действия над векторами. Вектора можно складывать. Сложение векторов возможно по правилу параллелограмма и треугольника. Рассмотрим их последовательно. Учитель объясняет правила сложения векторов (слайд 6). Правило треугольника позволяет нам складывать несколько векторов. Учитель объясняет, как складывать несколько векторов (слайд 7). Вектора не только можно складывать их так же можно и вычитать. Учитель объясняет правила вычитания векторов (слайд 8).	Слушают учителя и делают записи и чертежи в тетрадях
		Рассмотрим пример физической задачи на сложение векторов (слайд  9). “Крокодил переплывает реку перпендикулярно берегу. Скорость, с которой он гребет равна v1. Скорость течения реки равна v2. Чему будет равна скорость крокодила относительно берега реки?” В курсе физики 7 класса вы находили равнодействующую сил, действующих на тело. Давайте вспомним как складывать и вычитать вектора, направленные вдоль одной прямой (слайд 10). Приведу пример из сказки про репку. (слайд 11)	учащиеся решают задачу
		Теперь перейдем к нахождению проекций вектора на оси координат. Учитель дает определение проекции и объясняет, как найти проекцию вектора на оси координат и модуль вектора (слайд 12, 13).	Учащиеся смотрят на экран. Учащиеся слушают и делают записи в тетрадь
		Решим задачу (слайд 14). “Найдем проекции силы тяжести, которая действует на тело массой 1 кг, на оси координат.” После того как учащиеся получили ответ, учитель показывает правильное решение данной задачи.	Учащиеся решают задачу
Домашнее задание	1 мин.	Учащимся задается домашнее задание.	Записывают д.з.

Действия над векторами

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Понятие вектора является одним из основных в математике, объединяющим такие ее разделы, как геометрия, алгебре, математический анализ. Оно имеет большое прикладное значение, так как многие физические величины (сила, скорость и другие) характеризуются не только величиной, но и направлением, то есть являются векторными величинами.

В стереометрии изучаются векторы в пространстве. Их определение и свойства аналогичны определению и свойствам векторов на плоскости.

Цели урока:

• Образовательные: повторение теоретических сведений по теме; рассмотрение правил треугольника и параллелограмма сложения векторов в пространстве, законы сложения векторов; изучение правил сложения нескольких векторов в пространстве и его применение при нахождении векторных сумм, не прибегая к рисункам; рассмотрение правил умножения вектора на число и основные свойства этого действия, а так же их применение при решении задач.
• Развивающие: развитие памяти, математической речи, наблюдательности, развитие графических навыков у учащихся.
• Воспитательные: формирование культуры ученического труда.

Тип урока: урок изучения нового материала

Оборудование:

1) Учебник: Геометрия, 10-11: Учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 11-е изд. – М. : Просвещение, 2002. – 206 с. : ил.
2) раздаточный материал (Приложение 1)
3) мультимедийный проектор, Презентация «Действия над векторами».

ХОД УРОКА

1. Организационный момент

Сообщение темы и цели урока

Учитель: Ребята, тема нашего урока «Действия над векторами» (Слайд 1). Сегодня мы рассмотрим правила треугольника и параллелограмма сложения векторов в пространстве; изучим правило сложения нескольких векторов в пространстве и его применение при нахождении векторных сумм, не прибегая к рисункам; рассмотрим правила умножения вектора на число и основные свойства этого действия, а так же их применение при решении задач. (Слайд 2).

2. Актуализация знаний (Устная работа)

Учащиеся отвечают на вопросы учителя. Если учащиеся затрудняются ответить, учитель помогает.

Учитель: 1вопрос. Что называется вектором в пространстве? Его обозначения.

Ученик: Отрезок, для которого указано, какой из его концов считается началом, а какой концом, называется вектором.

Учитель: 2 вопрос. Что называется длиной вектора? Ее обозначение.

Ученик: Длиной ненулевого вектора  называется длина отрезка АВ.

Учитель: 3 вопрос. Какой вектор называется нулевым?

Ученик: Любая точка пространства может рассматриваться как вектор. Такой вектор называется нулевым.

Учитель: 4 вопрос. Какие векторы называются коллинеарными?

Ученик: Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Учитель: 5 вопрос. Какие векторы называются сонаправленными? Обозначение.

Ученик: Если два ненулевых вектора и  коллинеарны и если при этом лучи АВ и СД сонаправленны, то векторы и  называются сонаправленными. .

Учитель: 6 вопрос. Какие векторы называются противоположно направленными? Обозначение.

Ученик: Если два ненулевых вектора и  коллинеарны и если при этом лучи АВ и СД противоположно направленны, то векторы и  называются противоположно направленными. .

Учитель: 7 вопрос. Каким (сонаправленным или противоположно направленным) принять нулевой вектор?

Ученик: Нулевой вектор принято считать сонаправленным с любым вектором.

3. Изучение нового материала

Задача учителя подчеркнуть, что сложение и вычитание векторов в пространстве вводится так же, как и на плоскости, и подчиняется тем же законам. Раздать опорную схему по теме и дать время для работы над конспектом в тетради.

Учитель: Введем правило сложения двух произволь­ных векторов и .Отложим от какой-нибудь точки А вектор , равный . Затем от точки В отложим вектор , равный . Вектор называется суммой векторов и : =+ .
Это правило сложения векторов называется правилом треугольника (Слайд 3, 4, 5).

Для любых трех точек А, В и С имеет место равенство  + = .

Учащиеся делают записи  в тетрадях (Слайд 6).

 Учитель: Для сложения двух неколлинеарных векто­ров можно пользоваться также правилом параллело­грамма, известным из курса планиметрии. Это правило пояснено на рисунке (Слайд 7).

Учитель: Два ненулевых вектора называются проти­воположными, если их длины равны и они противоположно направлены. Вектором, противоположным нулевому вектору, считается нулевой вектор. Очевидно, вектор   является противоположным вектору  .

Учитель: Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору  (Слайд 6).
Разность – векторов и можно найти по формуле  – = + (– ), где (– ) – вектор, противоположный вектору

Учитель: Для любых трех векторов справедливы переместительный и сочетательный законы (Слайд 6).

Учитель просит учащихся записать законы в тетрадь.

Учитель: Сформулируем правило многоугольника. Сложение нескольких векторов в простран­стве выполняется так же, как и на плоскости: первый вектор складывается со вторым, затем их сумма — с третьим вектором и т. д. Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются (Слайд 8).

4. Закрепление изученного материала (выполнение задач)

а) Применение знаний в стандартной ситуации

Учащиеся выполняют № 327: один учащийся у доски, учитель комментирует (Слайд 9)

№ 327. На рисунке 97 изображен параллелепипед АВСДА1В1С1Д1. Назовите вектор, начало и конец которого является вершинами параллелепипед, равный сумме векторов:

а)
б)
в)
г)
д)

Учащиеся выполняют № 328: один учащийся у доски, учитель комментирует (Слайд 10)

№ 328 (а).  Тетраэдр АВСД. Докажите, что .

Дано: АВСД – тетраэдр
Докажите, что .
Решение: ,   .
Следовательно, .

б) Самостоятельная работа обучающего характера с последующей самопроверкой (решение на обратной стороне доски) (Слайд 11)

Задача. Дан тетраэдр АВСД. Найдите сумму:

а)  
б)
в)

5. Изучение нового материала

Учитель: Сформулируем правило умножения вектора на число: ; (Слайд 12)

Если , то,  при ;
 при .
Если , то .

Рассмотреть законы умножения вектора на число и попросить ребят изобразить схему в тетрадях. (Слайд 12)

6. Закрепление изученного материала (выполнение задач)

Учащиеся выполняют № 345: один учащийся у доски, учитель комментирует (Слайд 14)

№ 345. Точки E и F – середины сторон АВ и ВС параллелограмма АВСД, а О – точка произвольная точка пространства. Выразите вектор  через вектор .

Решение:  

Так как EF – средняя линия треугольника АВС, EF|| АС и EF = 1/2  АС.
Поэтому ,     ,  

№ 347. Упростить выражение:

а)

7. Домашнее задание (с комментарием учителя)

§ 2 (п. 36, 37, 38), № 335, № 337 (а, б), № 347 (б). (Слайд 15)

8. Подведение итогов урока

В конце урока желательно с помощью ребят перечислить понятия, правила, свойства, которые были рассмотрены на уроке и которые необходимо запомнить. Выставление оценок.

Учитель: Давайте подведем итоги урока.

Блиц-опрос по вопросам:

– Что называется произведением ненулевого вектора на число?
– Что называется произведением нулевого вектора на число?
– Свойства умножения вектора на число.
– Справедливо ли утверждение:

а) любые два противоположно направленных вектора коллинеарны;
б) любые два вектора коллинеарных противоположно направленны;
в) любые два равных вектора коллинеарны;
г) любые два сонаправленных вектора равны?

(Слайд 16)

Презентация к уроку по физике (10 класс) на тему: презентация «Векторы.Действия над векторами.Проекция вектора»

Слайд 1

Физика, 10 класс Векторы. Действия над векторами. Проекция вектора 04.09.2013 1 Плуталов С.Н. МОУ Мальчевская СОШ

Слайд 2

Скалярные и векторные величины Величины, характеризующиеся только численным значением, называются скалярными. масса m время t объём V температура T и др. Величины, характеризующиеся численным значением и направлением , называются векторными. сила F скорость V радиус-вектор r и др. 04.09.2013 2 Плуталов С.Н. МОУ Мальчевская СОШ

Слайд 3

Вектор На чертежах любой вектор изображается направленным отрезком(стрелкой). Направление стрелки задает направление вектора а b 04.09.2013 3 Плуталов С.Н. МОУ Мальчевская СОШ

Слайд 4

Правила сложения векторов Параллелограмма Треугольника Для двух векторов 04.09.2013 4 Плуталов С.Н. МОУ Мальчевская СОШ

Слайд 5

Правила сложения векторов Многоугольника Если число векторов больше двух R = F 1 + F 2 + F 3 + …. + F n 04.09.2013 5 Плуталов С.Н. МОУ Мальчевская СОШ

Слайд 6

Вычитание векторов 04.09.2013 6 Плуталов С.Н. МОУ Мальчевская СОШ

Слайд 7

Проекция вектора a a x a y Проекцией вектора называется скалярная величина, равная длине отрезка, заключенного между основаниями перпендикуляров, опущенных из начала и конца вектора на ось . 04.09.2013 7 Плуталов С.Н. МОУ Мальчевская СОШ

Слайд 8

Проекция вектора Если направление вектора совпадает с направлением оси координат, то проекция этого вектора положительная. Если направление вектора не совпадает с направлением оси координат, то проекция этого вектора отрицательная Если вектор перпендикулярен к оси координат, его проекция равна 0 Если вектор параллелен оси координат, его проекция равна длине самого вектора. 04.09.2013 8 Плуталов С.Н. МОУ Мальчевская СОШ

Слайд 9

04.09.2013 Плуталов С.Н. МОУ Мальчевская СОШ 9 Изобразите произвольный вектор, чтобы : 1.Чтобы его проекция на ось Ох была положительной, а на ось Оу – отрицательной; 2.Чтобы его проекция на ось Ох была равна нулю , а на ось Оу положительной; 3.Чтобы проекции данного вектора на обе оси были отрицательными; 4.Чтобы проекция вектора на ось Оу была равна длине самого вектора; 5.Чтобы проекция на ось Ох была отрицательной, а на ось Оу – положительной.